Journal of Modern Physics
Vol. 2 No. 8 (2011) , Article ID: 6760 , 8 pages DOI:10.4236/jmp.2011.28097
Light-Front Hamiltonian and Path Integral Formulations of the Conformally Gauge-Fixed Polyakov D1 Brane Action with a Scalar Dilation Field
1Department of Physics, Kirori Mal College, University of Delhi, Delhi, India
2Department of Physics and Astrophysics, University of Delhi, Delhi, India
E-mail: {ushakulsh, dskulsh}@gmail.com
Received March 31, 2011; revised May 1, 2011; accepted May 22, 2011
Keywords: Light-Front Quantization, Hamiltonian Quantization, Path Integral Quantization, Constrained Dynamics, Constraint Quantization, Gauge Symmetry, String Gauge Symmetry, String Theory, D-brane Actions, Polyakov Action, Light-Cone Quantization
ABSTRACT
Recently we have studied the instant-form quantization (IFQ) of the conformally gauge-fixed Polyakov D1 brane action with and without a scalar dilaton field using the Hamiltonian and path integral formulations in the equal world-sheet time framework on the hyperplanes defined by the world-sheet time . The light-front quantization (LFQ) of this theory without a scalar dilaton field has also been studied by us recently. In the present work we study the LFQ of this theory in the equal light-cone world-sheet time framework, on the hyperplanes of the light-front defined by the light-cone world-sheet time
. The light-front quantization (LFQ) of this theory without a scalar dilaton field has also been studied by us recently. In the present work we study the LFQ of this theory in the equal light-cone world-sheet time framework, on the hyperplanes of the light-front defined by the light-cone world-sheet time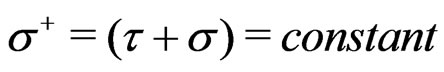 , using the Hamiltonian and path integral formulations. The light-front theory is seen to be a constrained system in the sense of Dirac. The light-front theory is seen to possess a set of twenty seven primary second-class contraints. In the present work Hamiltonian and path integral quantizations of this theory are studied on the light-front.
, using the Hamiltonian and path integral formulations. The light-front theory is seen to be a constrained system in the sense of Dirac. The light-front theory is seen to possess a set of twenty seven primary second-class contraints. In the present work Hamiltonian and path integral quantizations of this theory are studied on the light-front.
1. Introduction
The Polyakov action is almost the starting point in any studies on string theories and it is therefore also one of the most widely studied and discussed topics in this field in the recent times [1-13]. The action possesses three well-known local gauge symmetries [14] given by the two-dimensional world-sheet (WS) reparametrization invariance (WSRI) and the Weyl invariance (WI) [1-14]. When the action is considered under the conformal gaugefixing it looses the above said string gauge symmetries [9-14] as expected (owing to the conformal gauge-fixing). Recently we have studied instant-form (IF) quantization (IFQ) [12] of the conformally gauge-fixed Polyakov D1 brane action (CGFPD1BA) with and without a scalar dilaton field, using the equal world-sheet (WS)-time (EWST) framework, on the hyperplanes defined by the WS-time 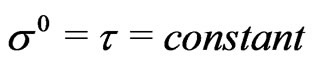 [9,12,15-17]. The theory without a scalar dilaton field is seen to be an unconstrained system in the sense of Dirac [18], whereas in the presence of a scalar dilaton field it is seen to be a constrained system, possessing one primary and one secondary Gauss law constraint [18]. In a recent paper [11] we have studied the Hamiltonian and path integral formulations [18-22] of this theory without the scalar dilaton field [11] using the equal light-cone (LC) worldsheet time (ELCWST) framework on the hyperplanes of the light-front (LF) defined by the LC world-sheet time
[9,12,15-17]. The theory without a scalar dilaton field is seen to be an unconstrained system in the sense of Dirac [18], whereas in the presence of a scalar dilaton field it is seen to be a constrained system, possessing one primary and one secondary Gauss law constraint [18]. In a recent paper [11] we have studied the Hamiltonian and path integral formulations [18-22] of this theory without the scalar dilaton field [11] using the equal light-cone (LC) worldsheet time (ELCWST) framework on the hyperplanes of the light-front (LF) defined by the LC world-sheet time 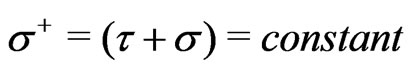 [23-28]. The LF theory becomes a constrained system in the sense of Dirac [11,13, 18-22] (in contrast to the corresponding case of the IF theory, and it is seen to possess a set of 26 primary second-class constraints [10]. In Reference [11], we have quantized this LF theory using the standard constraint quantization techniques in the Hamiltonian and path integral formulations [9-17,20-22], It is needless to say that the LF quantization (LFQ) has several distinct advantages over the usual IFQ [23-28]. For a recent review on LFQ of field theories we refer to the work of Brodsky, Pauli and Pinsky [24].
[23-28]. The LF theory becomes a constrained system in the sense of Dirac [11,13, 18-22] (in contrast to the corresponding case of the IF theory, and it is seen to possess a set of 26 primary second-class constraints [10]. In Reference [11], we have quantized this LF theory using the standard constraint quantization techniques in the Hamiltonian and path integral formulations [9-17,20-22], It is needless to say that the LF quantization (LFQ) has several distinct advantages over the usual IFQ [23-28]. For a recent review on LFQ of field theories we refer to the work of Brodsky, Pauli and Pinsky [24].
In the present work, we study the LF Hamiltonian and path integral formulations of this action for the D1 brane in the conformal gauge (CG), in the presence of a scalar dilation field using the Dirac’s front-form (FF) of dynamics. In the next section we briefly recapitulate some basics of this theory and then in Section 3, we study the LFQ of this theory in the presence of the scalar dilation field. The summary and discussion is finally given in Section 4.
2. Recapitulation of Instant-Form Theory
We first recapitulate very briefly the IF theory. The Polyakov D1 brane action in a d-dimensional curved background  (with d = 10 for the fermionic and d = 26 for bosonic D1 brane) is defined by [1-14]:
(with d = 10 for the fermionic and d = 26 for bosonic D1 brane) is defined by [1-14]:
 (1a)
(1a)
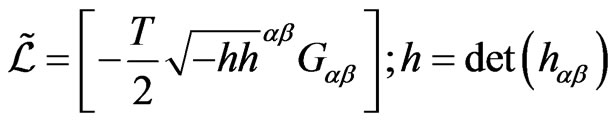 (1b)
(1b)
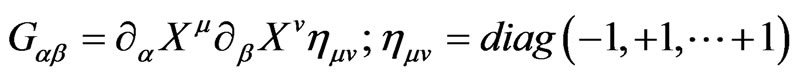 (1c)
(1c)
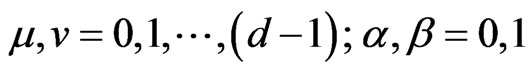 (1d)
(1d)
Here 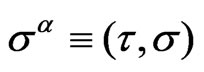 are the two parameters describing the worldsheet (WS). The overdots and primes would denote the derivatives with respect to
are the two parameters describing the worldsheet (WS). The overdots and primes would denote the derivatives with respect to  and
and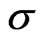 .
. 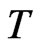 is the string tension.
is the string tension.  is the induced metric on the WS and
is the induced metric on the WS and 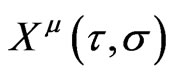 are the maps of the WS into the
are the maps of the WS into the 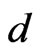 -dimensional Minkowski space and describe the strings evolution in space-time [1-14].
-dimensional Minkowski space and describe the strings evolution in space-time [1-14]. 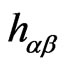 are the auxiliary fields (which turn out to be proportional to the metric tensor
are the auxiliary fields (which turn out to be proportional to the metric tensor 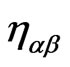 of the two-dimensional surface swept out by the string). One can think of
of the two-dimensional surface swept out by the string). One can think of  as the action describing
as the action describing 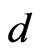 massless scalar fields
massless scalar fields  in two dimensions moving on a background
in two dimensions moving on a background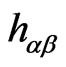 . Also because the metric components
. Also because the metric components 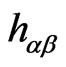 are varied in the above equation, the 2- dimensional gravitational field
are varied in the above equation, the 2- dimensional gravitational field  is treated not as a given background field, but rather as an adjustable quantity coupled to the scalar fields [1-14]. The action
is treated not as a given background field, but rather as an adjustable quantity coupled to the scalar fields [1-14]. The action 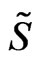 possesses the well-known three local gauge symmetries given by the two-dimensional WS reparametrization invariance (WSRI) and the Weyl invariance (WI) [1-14]:
possesses the well-known three local gauge symmetries given by the two-dimensional WS reparametrization invariance (WSRI) and the Weyl invariance (WI) [1-14]:
 (2a)
(2a)
 (2b)
(2b)
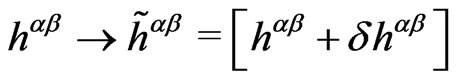 (2c)
(2c)
 (2d)
(2d)
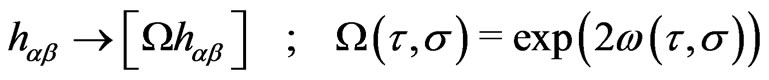 (2e)
(2e)
Here 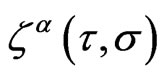 is a gauge parameter corresponding to the WSRI and
is a gauge parameter corresponding to the WSRI and  is a gauge parameter corresponding to the Weyl symmetry. The WSRI is defined by the first four equations involving the two gauge parameters
is a gauge parameter corresponding to the Weyl symmetry. The WSRI is defined by the first four equations involving the two gauge parameters 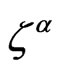 and the WI is defined by the last equation and is specified by the gauge parameter
and the WI is defined by the last equation and is specified by the gauge parameter  (or equivalently by
(or equivalently by ). Also the above theory being a gauge-invariant theory (possessing the local gauge symmetries including two WSRI and one WI symmetries), could be studied under approriate gauge-fixing the way one likes. However, one could also use the above three local gauge symmeties of the theory to choose
). Also the above theory being a gauge-invariant theory (possessing the local gauge symmetries including two WSRI and one WI symmetries), could be studied under approriate gauge-fixing the way one likes. However, one could also use the above three local gauge symmeties of the theory to choose  to be of a particular form [1-14] e.g., as follows:
to be of a particular form [1-14] e.g., as follows:
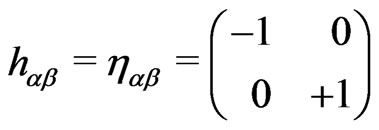 (3)
(3)
This is the so-called conformal gauge (CG). In this CG we have
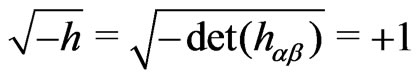 (4)
(4)
and the action 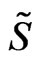 in this CG now becomes:
in this CG now becomes:
 (5a)
(5a)
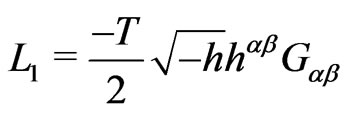 (5b)
(5b)
 (5c)
(5c)
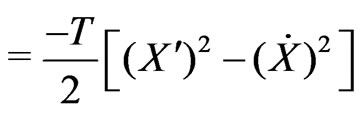 (5d)
(5d)
 (5e)
(5e)
This is the CGFPD1BA. The IFQ of this action has been studied by us recently in Reference. This theory is easily seen to be an unconstrained system in the sense of Dirac [18]. It may be important to remark here that an unconstrained system like this represents a gaugenoninvariant theory and is some what akin to a gaugefixed gauge-invariant theory which makes it a gaugenoninvariant system. In the presence of a scalar dilaton field the theory of course, becomes a constrained system in the sense of Dirac as shown in our earlier work [12]. The above theory in the presence of a scalar dilation field  in a
in a 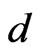 -dimensional flat background
-dimensional flat background 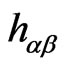 reads as [13]:
reads as [13]:
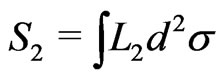 (6a)
(6a)
 (6b)
(6b)
 (6c)
(6c)
 (6d)
(6d)
This theory is easily seen to possess two constraints [1]:
 (7a)
(7a)
 (7b)
(7b)
where  is a primary constraint and
is a primary constraint and  is a secondary Gauss law constraint and
is a secondary Gauss law constraint and 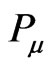 and
and  here are the momenta conjugate canonically respectively to
here are the momenta conjugate canonically respectively to  and
and . The matrix of the Poisson brackets of the constraints
. The matrix of the Poisson brackets of the constraints  and
and  is seen to be nonsingular implying that the set of these constraints is second-class and that the theory is gauge-noninvariant (which does not respect the usual string gauge symmetries WSRI and WI). The Hamiltonian and path integral formulations of this theory have been studied by us earlier [12]. It may be worth mentioning here that the IF theory in the absence of a scalar dilaton field [12], is not a constrained system in the sence of Dirac (implying that theory is equivalent to a gauge-fixed gauge-invariant theory) whereas the theory in the presence of a scalar dilaton field represents a constrained system in the sence of Dirac possessing a set of two second-class constraints where one constraint is primary and the other one is the secondary Gauss law constraint [12]. A comparasion of the IFQ results of the theory with those of the present LFQ results is given in the last section.
is seen to be nonsingular implying that the set of these constraints is second-class and that the theory is gauge-noninvariant (which does not respect the usual string gauge symmetries WSRI and WI). The Hamiltonian and path integral formulations of this theory have been studied by us earlier [12]. It may be worth mentioning here that the IF theory in the absence of a scalar dilaton field [12], is not a constrained system in the sence of Dirac (implying that theory is equivalent to a gauge-fixed gauge-invariant theory) whereas the theory in the presence of a scalar dilaton field represents a constrained system in the sence of Dirac possessing a set of two second-class constraints where one constraint is primary and the other one is the secondary Gauss law constraint [12]. A comparasion of the IFQ results of the theory with those of the present LFQ results is given in the last section.
3. Light-Front Quantization
In LFQ of the theory we use the three local gauge symmetries of the theory for choosing 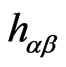 to be of a particular form as follows:
to be of a particular form as follows:
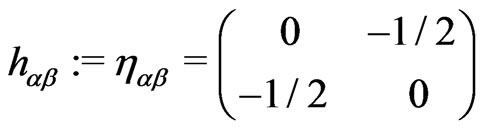 (8a)
(8a)
and
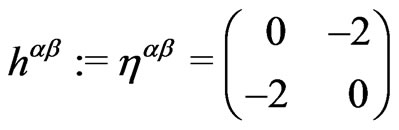 (8b)
(8b)
with
 (8c)
(8c)
This is the so-called conformal gauge (CG) in the LFQ of the theory. Also, in the LFQ we use the LC variables defined by [23,24]:
 (9)
(9)
The action  in the above CG in the LFQ reads:
in the above CG in the LFQ reads:
 (10a)
(10a)
 (10b)
(10b)
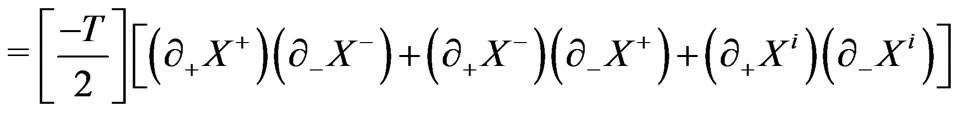
(10c)
 (10d)
(10d)
This theory is easily seen to possess twenty six primary constraints [11]:
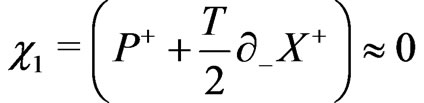 (11a)
(11a)
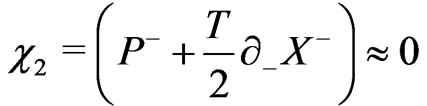 (11b)
(11b)
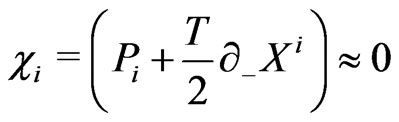 (11c)
(11c)
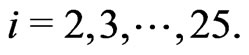 (11d)
(11d)
where  and
and  denote the canonical momenta conjugate respectively to
denote the canonical momenta conjugate respectively to 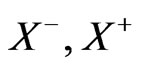 and
and . Demanding that the primary constraints
. Demanding that the primary constraints  and
and  be preserved in the course of time one does not get any secondary constraints. The theory is thus seen to possess only twenty six constraints
be preserved in the course of time one does not get any secondary constraints. The theory is thus seen to possess only twenty six constraints 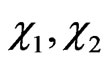 and
and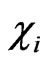 . Matrix of the Poisson brackets of the constrains
. Matrix of the Poisson brackets of the constrains 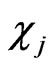 namely,
namely,

 is seen to be nonsingular implying that the theory is GNI and it does not respect the standard string gauge symmetries defined by the WSRI and the WI. The LF Hamiltonian and path integral formulations of the theory have been studied by us in our recent work [10,11] and the details could be found in Ref. [10,11]. In the present work we study this theory in the presence of a scalar dilaton field
is seen to be nonsingular implying that the theory is GNI and it does not respect the standard string gauge symmetries defined by the WSRI and the WI. The LF Hamiltonian and path integral formulations of the theory have been studied by us in our recent work [10,11] and the details could be found in Ref. [10,11]. In the present work we study this theory in the presence of a scalar dilaton field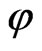 .
.
In the following we now proceed to study the LFQ of this theory in the presence of a scalar dilation field  defined in the LF coordinates by the action [13]:
defined in the LF coordinates by the action [13]:
 (12a)
(12a)
 (12b)
(12b)
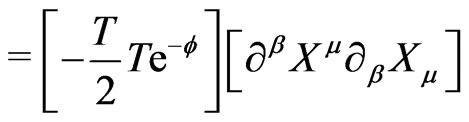 (12c)
(12c)
 (12d)
(12d)
 (12e)
(12e)
where (as before) 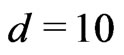 for the fermionic string and 26 for the bosonic string. In the present work we consider only the bosonic string. In the following we would study the LFQ of the above action
for the fermionic string and 26 for the bosonic string. In the present work we consider only the bosonic string. In the following we would study the LFQ of the above action  (which describes the Polyakov
(which describes the Polyakov  -brane action in the LF coordinates). The canonical momenta
-brane action in the LF coordinates). The canonical momenta  and
and 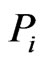 conjugate respectively to
conjugate respectively to  and
and 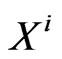 obtained from (12) are [13]:
obtained from (12) are [13]:
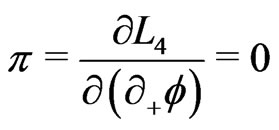 (13a)
(13a)
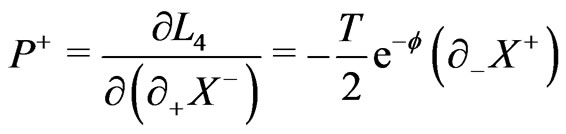 (13b)
(13b)
 (13c)
(13c)
 (13d)
(13d)
The above equations imply that the theory possesses four primary constraints:
 (14a)
(14a)
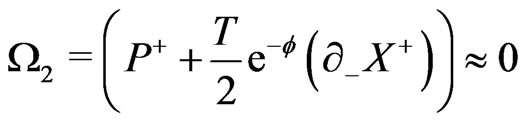 (14b)
(14b)
 (14c)
(14c)
 (14d)
(14d)
The canonical Hamiltonian density corresponding to 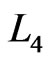 is
is
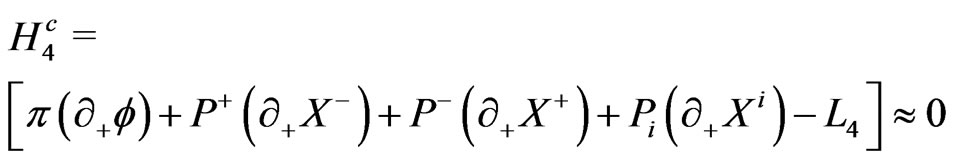 (15)
(15)
After including the primary constraints 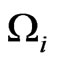 in the canonical Hamiltonian density
in the canonical Hamiltonian density  with the help of Lagrange multiplier fields
with the help of Lagrange multiplier fields  and
and , the total Hamiltonian density
, the total Hamiltonian density 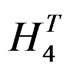 could be written as
could be written as
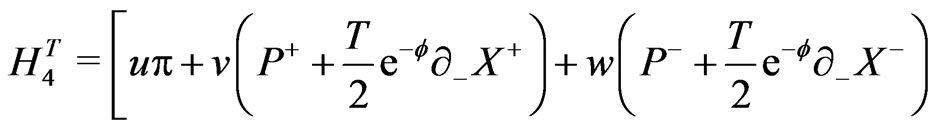
 (16)
(16)
We now treat the Lagrange multiplier fields  and
and 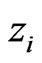 as dynamical. The Hamiltons equations obtained from the total Hamiltonian:
as dynamical. The Hamiltons equations obtained from the total Hamiltonian:
 (17)
(17)
e.g., for the closed bosonic strings with periodic boundary conditions are now defined as:
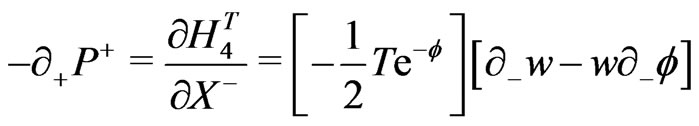
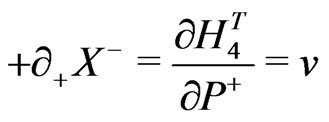
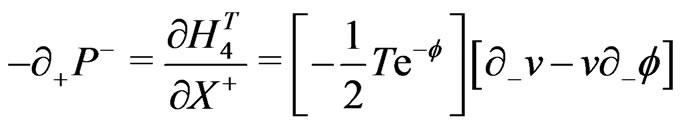


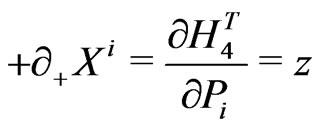
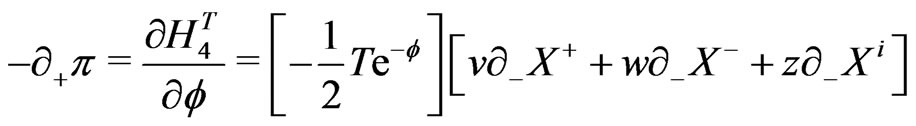
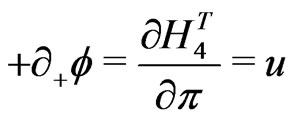
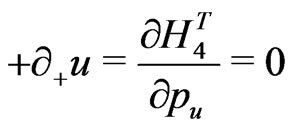


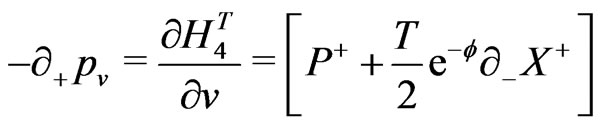
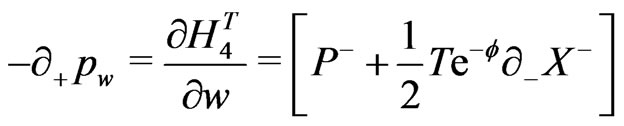


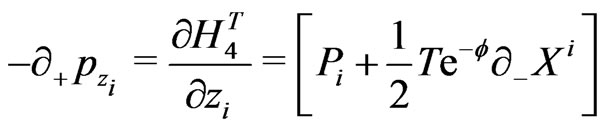 (18)
(18)
Demanding that the primary constraints 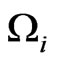 be preserved in the course of time one does not get any secondary constraints. The theory is thus seen to possess only four constraints
be preserved in the course of time one does not get any secondary constraints. The theory is thus seen to possess only four constraints 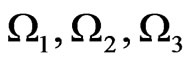 and
and . The first-order Lagrangian density of the theory is
. The first-order Lagrangian density of the theory is


 (19)
(19)
The matrix of the Poisson brackets of the constraints 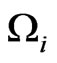 namely,
namely, 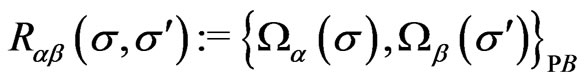 is then conculated. The nonvanishing elements of the matrix
is then conculated. The nonvanishing elements of the matrix  are now obtained as
are now obtained as
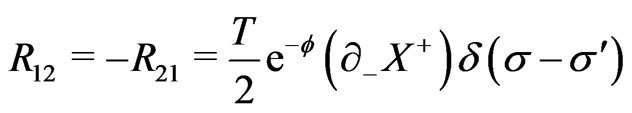 (20a)
(20a)
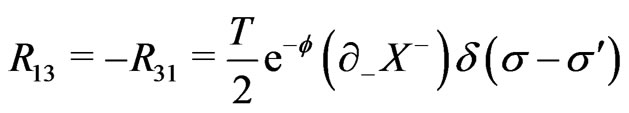 (20b)
(20b)
 (20c)
(20c)
 (20d)
(20d)
Here 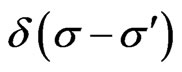 is the Dirac distribution function. The matrix
is the Dirac distribution function. The matrix  is seen to be nonsingular with the determinant given by
is seen to be nonsingular with the determinant given by
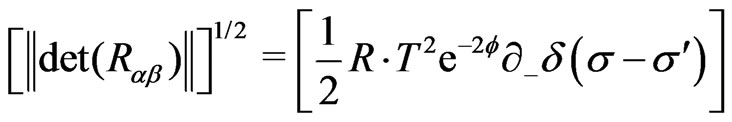 (21a)
(21a)
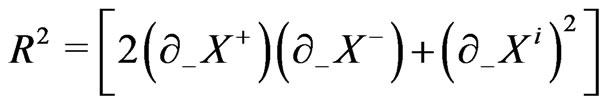 (21b)
(21b)
and the nonvanishing elements of the inverse of the matrix  (i.e., the elements of the matrix
(i.e., the elements of the matrix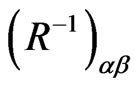 ) are obtained as:
) are obtained as:
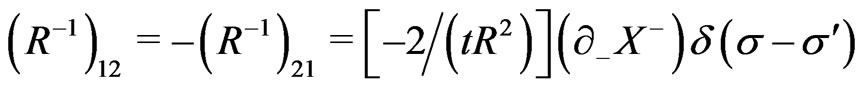
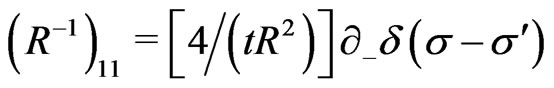
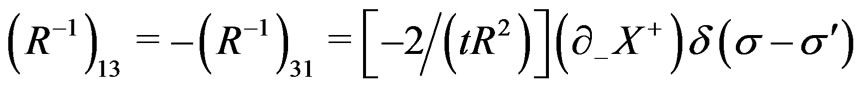
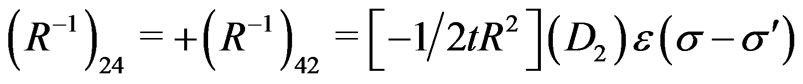
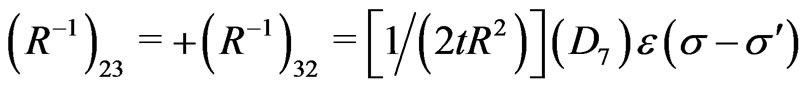
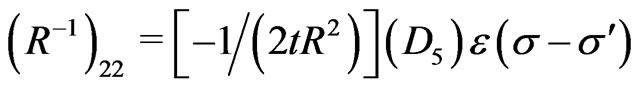


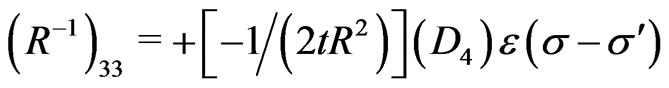
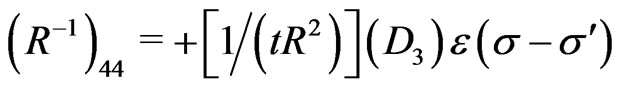 (22)
(22)
where
 (23a)
(23a)
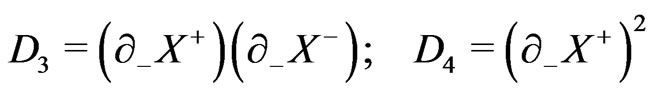 (23b)
(23b)
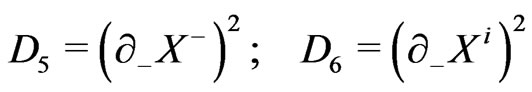 (23c)
(23c)
 (23d)
(23d)
and
 (24)
(24)
Now following the Dirac qunatization procedure in the Hamiltonian formulation [18], the nonvanishing ELCWST Dirac brackets of the theory described by the Polyakov 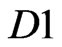 brane action
brane action 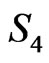 in the presence of scalar dilation field
in the presence of scalar dilation field  are formally obtained as [18]:
are formally obtained as [18]:
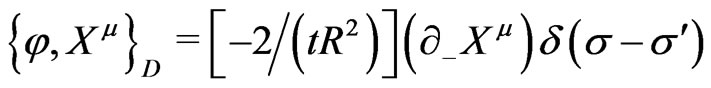 (25a)
(25a) 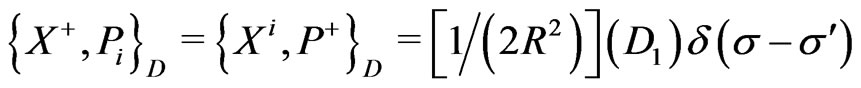 (25b)
(25b)
 (25c)
(25c)
 (25d)
(25d)
 (25e)
(25e)
 (25f)
(25f)
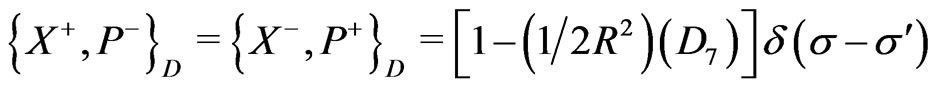 (25g)
(25g)
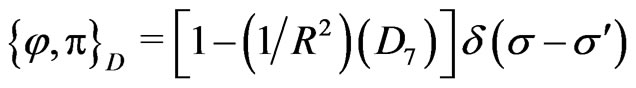 (25h)
(25h)
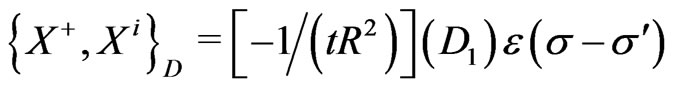 (25i)
(25i)
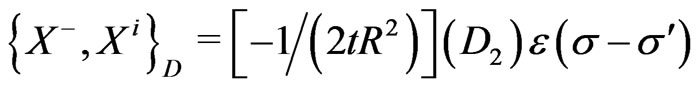 (25j)
(25j)
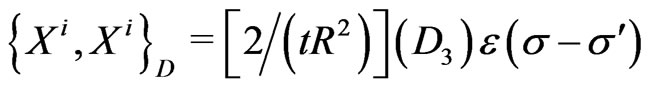 (25k)
(25k)
 (25l)
(25l)
 (25m)
(25m)
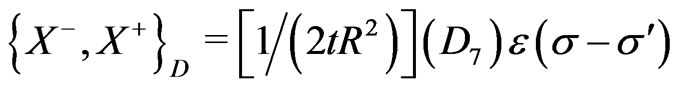 (25n)
(25n)
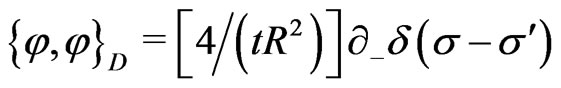 (25o)
(25o)
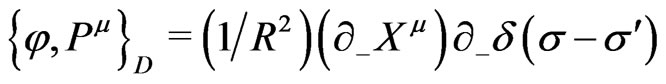 (25p)
(25p)
 (25q)
(25q)
 (25r)
(25r)
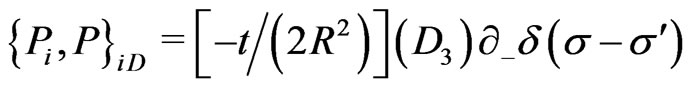 (25s)
(25s)
 (25t)
(25t)
 (25u)
(25u)
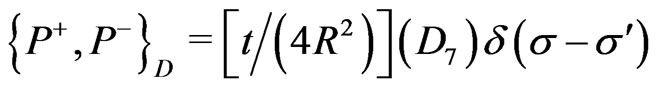 (25v)
(25v)
where the step function 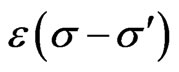 is defined as
is defined as
 (26)
(26)
In the path integral formulation, the transition to quantum theory is now made by writing the generating fucntional  for the theory in the presence of the external sources
for the theory in the presence of the external sources  as [20-22]:
as [20-22]:
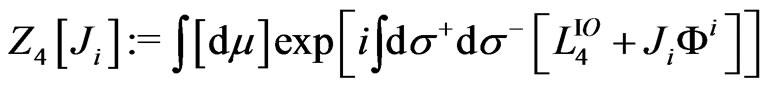 (27)
(27)
where the phase space variables of the theory defined by the action 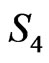 are
are 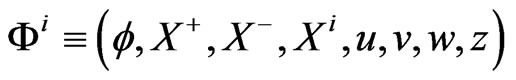 with the corresponding respectively canonical conjugate momenta:
with the corresponding respectively canonical conjugate momenta: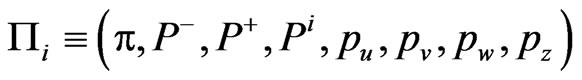 . The functional measure
. The functional measure  of the generating functional
of the generating functional  is obtained as [20-22]:
is obtained as [20-22]:
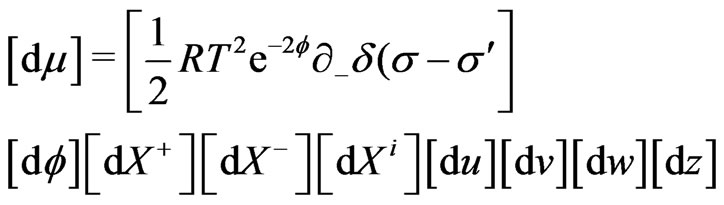


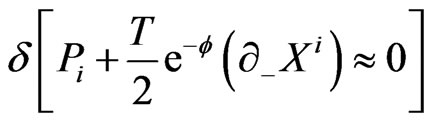 (28)
(28)
The LF Hamiltonian and path integral quantization of the Polyakov D1 brane action  in the presence of the scalar dilaton field
in the presence of the scalar dilaton field 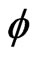 is now complete.
is now complete.
Now in the canonical quantization of the theory while going from equal WS-LC time (ELCWST) Dirac brackets of the theory to the corresponding ELCWST commutation relations one would encounter here the problem of operator ordering [29] because the product of canonical variables of the theory are involved in the classical description of the theory (like in the expressions for the constraints of the theory) as well as in the calculation of the Dirac brackets. These variables are envisaged as noncommuting operators in the quantized theory leading to the problem of so-called operator ordering [29]. This problem could, however, be resolved [29] by demanding that all the string fields and momenta of the theory are Hermitian operators and that all the canonical commutation relations be consistent with the hermiticity of these operators [29].
It is important to mention here in our work we have not imposed any boundary conditions (BC’s) for the open and closed strings separately. There are two ways to take these BC's into account: a) one way is to impose them directly in the usual way for the open and closed strings separately in an appropriate manner [1,2], b) an alternative second way is to treat these BC's as the Dirac primary constraints [30] and study the theory accordingly [30].
4. Summary and Discussion
In this work we have studied the LF Hamiltonian and path integral quantization of the CGFPD1BA in the presence of the scalar dilation field under the conformal gauge in the absence of boundary conditions (BC’s). The action under this gauge-fixing becomes GNI as expected. Also because this is a (conformally) gauge-fixed action, the theory is therefore gauge noninvariant as expected and the associated constraints of the theory form a set of second-class constraints. It is important to recap here that the original Polyakov D1 brane is defined by the action  in a curved background and it is gauge-invaraint possessing the three well known local gauge symmetries defined by the 2-dimensional WSRI and the WI. On the other hand, the theory under our present investigation defined by the action
in a curved background and it is gauge-invaraint possessing the three well known local gauge symmetries defined by the 2-dimensional WSRI and the WI. On the other hand, the theory under our present investigation defined by the action 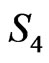 is a conformally gauge-fixed theory and consequently gauge-anomalous and gaugenoninvariant as it should be. We have studied this conformally gauge-fixed gauge anomalous (and GNI) theory in the presence of a scalar dilation field in the LF formulation using the ELCWST framework on the hyperplanes of the world-sheet defined by: LC world-sheet time
is a conformally gauge-fixed theory and consequently gauge-anomalous and gaugenoninvariant as it should be. We have studied this conformally gauge-fixed gauge anomalous (and GNI) theory in the presence of a scalar dilation field in the LF formulation using the ELCWST framework on the hyperplanes of the world-sheet defined by: LC world-sheet time 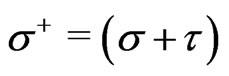 = const.
= const.
The problem of operator ordering occurring here while making a transition from the Dirac brackets to the corresponding commutation relations can be resolved as explained in the foregoing by demanding that all the string fields and momenta of the theory are Hermitian operators and that all the canonical commutation relations be consistent with the hermiticity of these operators [29].
Polyakov D1 brane action action possesses three wellknown local gauge symmetries given by the two-dimensional world-sheet reparametrization invariance and the Weyl invariance. When the action is considered under the conformal gauge-fixing it looses the above said string gauge symmetries as expected. In a very recent paper [12], we have studied the CGFPD1BA with and without a scalar dilaton field in the usual instant-form (IF) of dynamics, using the equal world-sheet-time framework, on the hyperplanes defined by the WS-time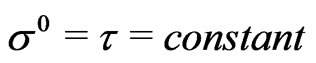 . The LFQ of the theory without the scalar dilaton field has also been studied by us recently [10,11]. In the present work, the CGFPD1BA in the presence of scalar dilaton field is studied on the LF (using the front-form of dynamics) in the equal light-cone worldsheet time (ELCWST) framework on the hyperplanes of the LF defined by the light-cone world-sheet time
. The LFQ of the theory without the scalar dilaton field has also been studied by us recently [10,11]. In the present work, the CGFPD1BA in the presence of scalar dilaton field is studied on the LF (using the front-form of dynamics) in the equal light-cone worldsheet time (ELCWST) framework on the hyperplanes of the LF defined by the light-cone world-sheet time  [13,23,24]. The LF theory is seen to become a constrained system in the sense of Dirac [9-21], and it is seen to possess a set of 26 primary second-class constraints when considered without the scalar dilaton field [11], and possessing a set of 27 primary second-class constraints when it is considered in the presence of the scalar dilaton field as is seen in the present work. For a comparative study, it may be important to mention here that the present theory when considered in the IFQ without the scalar dilaton field is seen [12] to be an unconstrained system in the sence of Dirac (implying that it is equivalent to a gauge-fixed gauge-invariant theory) and the same theory when considered in the presence of the scalar dilaton field in IFQ implies that the theory becomes a constrained system in the sence of Dirac possessing a set of two second-class constraints [12] where one constraint is primary and the other one is a secondary Gauss law constraint [12]. The LF theory with or without the scalar dilaton field could now in principle, also be used to construct the corresponding equivalent gauge-invariant theory using the techniques of constrained dynamics (albeit constraint quantization) which is however, outside the scope of the present work.
[13,23,24]. The LF theory is seen to become a constrained system in the sense of Dirac [9-21], and it is seen to possess a set of 26 primary second-class constraints when considered without the scalar dilaton field [11], and possessing a set of 27 primary second-class constraints when it is considered in the presence of the scalar dilaton field as is seen in the present work. For a comparative study, it may be important to mention here that the present theory when considered in the IFQ without the scalar dilaton field is seen [12] to be an unconstrained system in the sence of Dirac (implying that it is equivalent to a gauge-fixed gauge-invariant theory) and the same theory when considered in the presence of the scalar dilaton field in IFQ implies that the theory becomes a constrained system in the sence of Dirac possessing a set of two second-class constraints [12] where one constraint is primary and the other one is a secondary Gauss law constraint [12]. The LF theory with or without the scalar dilaton field could now in principle, also be used to construct the corresponding equivalent gauge-invariant theory using the techniques of constrained dynamics (albeit constraint quantization) which is however, outside the scope of the present work.
The LF theory is quantized using the standard constraint quantization techniques in the Hamiltonian and path integral formulations. It is needless to say that the LF quantization (LFQ) has undisputedly several distinct advantages [23,24] over the usual IF quantization (IFQ). One of the most important advantages of the LF framework e.g., is that the LF theory provides the largest number of kinematical generators of the Poincare transformations in Hamiltonian dynamics. For a recent review on LFQ of field theories we refer to the work of Brodsky, Pauli and Pinsky [24].
Also, we like to make a few comments about further solving the LF theory. It is possible to write down the solutions of the LF theory on the reduced hypersurface of the constraints of the theory where one implements the constraints of the theory strongly and this could be achieved in the Hamiltonian as well as in the path integral formulation of the theory. This is however, outside the scope of the present work. One well known example of this concerns the Batalin-Fradkin-Vilkovisky quanization of a gauge-noninvariant theory where one enlarges the phase space of a classical theory or the Hilbert space of the corresponding quantum theory by introducing some additional fields in to the theory by modifying the second-class constraints of the theory in such a manner that each of the second-class constraint of the theory becomes a first-class constraint. This in principle, could be done with the present LF theory because its constraint structure is known.
REFERENCES
- D. Luest and S. Theisen, “Lectures in String Theory,” Lecture Notes in Physics, Springer Verlag, Berlin, Vol. 346, 1989.
- L. Brink and M. Henneaux, “Principles of String Theory,” Plenum Press, New York, 1988.
- C. V. Johnson, “D-Brane Primer,” hep-th/0007170.
- M. Aganagic, J. Park, C. Popescu and J. Schwarz, “Dual D-Brane Actions,” Nuclear Physics B, Vol. 496, No. 1-2, 1997, pp. 215-230. doi:10.1016/S0550-3213(97)00257-5
- M. Abou Zeid and C. M. Hull, “Intrinsic Geometry of D-Branes,” Physics Letters B, Vol. 404, No. 3-4, 199, pp. 7264-270.
- C. Schmidhuber, “D-Brane Actions,” Nuclear Physics B, Vol. 467, No. 1-2, 1996, pp. 146-158. doi:10.1016/0550-3213(96)00092-2
- S. P. de Alwis, K. Sato, “D-Strings and F-Strings from String Loops,” Physical Review D, Vol. 53, No. 12, 1996, pp. 7187-7196. doi:10.1103/PhysRevD.53.7187
- A. A. Tseytlin, “Self Duality of Born-Infeld Action and Dirichlet Three-Brane of Type IIB Super String Theory,” Nuclear Physics B, Vol. 469, No. 1-2, 1996, pp. 51-67. doi:10.1016/0550-3213(96)00173-3
- Usha kulshreshtha and D. S. Kulshreshtha, “Conformally Gauge-Fixed Polyakov D1 Brane Action in the Presence of a 2-Form Gauge Field: The Instant-Form and FrontForm Hamiltonian and Path Integral Formulations,” Physics Letters B, Vol. 555, No. 3-4, 2003, pp. 255-263.
- D.S. Kulshreshtha, “Polyakov D1 Brane Action on the Light-Front,” Invited Talk at the Light-Cone 2008: Relativistic Nuclear and Particle Physics (2008), Mulhouse, 7-11 July, 2008, Published in PoS LC2008: 007, 2008, hep-th/0809.1038.
- Usha Kulshreshtha and D. S. Kulshreshtha, “Light-Front Hamiltonian and Path Integral Formulations of the Conformally Gauge-Fixed Polyakov D1 Brane Action,” Journal of Modern Physics, Vol. 2, No. 5, 2011, pp. 335-340 (in Press).
- Usha Kulshreshtha and D. S. Kulshreshtha, “Hamiltonian and Path Integral Quantization of the Conformally GaugeFixed Polyakov D1 Brane Action in the Presence of a Scalar Dilation Field,” International Journal of Theoretical Physics, Vol. 48, No. 4, 2009, pp. 937-944. doi:10.1007/s10773-008-9866-z
- D. S. Kulshreshtha, “Light-Front Quantization of the Polyakov D1 Brane Action with a Scalar Dilaton Field,” Invited Talk at the Light-Cone 2007: Relativistic Hadronic and Nuclear Physics (LC2007), Columbus, 14-18 May 2007, hep-th/0711.1342.
- D. S. Kulshreshtha, “String gauge Symmetries in the LightFront Polyakov D1 Brane Action,” Invited Talk at the International Conference Light-Cone 2010: Relativistic Hadronic and Particle Physics (LC2010), Valencia, 14-18 June 2010, Published in PoS LC2010: 006, 2010, SISSA, Trieste, Italy.
- Usha kulshreshtha and D. S. Kulshreshtha, “Hamiltonian and Path Integral Formulations of the Dirac-Born-InfeldNambu-Goto D1 Brane Action with and without a Dilaton Field under Gauge-Fixing,” European Physical Journal, Vol. C29, No. 3, 2003, pp. 453-461.
- Usha kulshreshtha and D. S. Kulshreshtha, “Hamiltonian and Path Integral Formulations of the Nambu-Goto D1 Brane Action With and Without a Dilaton Field under Gauge-Fixing,” International Journal of Theoretical Physics, Vol. 43, No. 12, 2004, pp. 2355-2369. doi:10.1007/s10773-004-7704-5
- U. kulshreshtha and D. S. Kulshreshtha, “Hamiltonian and Path Integral Formulations of the Born-Infeld-NambuGoto D1 Brane Action with and without a Dilaton Field under Gauge-Fixing,” International Journal of Theoretical Physics, Vol. 44, No. 5, 2005, pp. 587-603. doi:10.1007/s10773-005-3985-6
- P. A. M. Dirac, “Generalized Hamiltonian Dynamics,” Canadian Journal of Mathematics, Vol. 2, 1950, pp. 129- 148. doi:10.4153/CJM-1950-012-1
- M. Henneaux and C. Teitleboim, “Quantization of Gauge Systems,” Princeton University Press, New Jersey, 1992.
- P. Senjanovic, “Path Integral Quantization of Field Theories with Second-Class Constraints,” Annals Physics, Vol 100, No. 1-2, 1976, pp. 227-261.
- Usha Kulshreshtha, “Hamiltonian, Path Integral and BRST Formulations of the Chern-Simons-Higgs Theory in the Broken Symmetry Phase,” Physica Scripta, Vol. 75, No. 6, 2007, pp. 795-802. doi:10.1088/0031-8949/75/6/009
- Usha Kulshreshtha and D. S. Kulshreshtha, “Gauge-Invariant Reformulation of the Vector Schwinger Model with a Photon Mass Term and Its Hamiltonian, Path Integral and BRST Formulations,” International Journal of Modern Physics, Vol. A22, No. 32, 2007, pp. 6183-6201.
- P. A. M. Dirac, “Forms of Relativistic Dynamics,” Reviews of Modern Physics, Vol. 21, No. 3, 1949, pp. 392- 399. doi:10.1103/RevModPhys.21.392
- S. J. Brodsky, H. C. Pauli and S. S. Pinsky, “Quantum Chromodynamics and Other Field Theories on the LightCone,” Vol. 301, No. 4-6, 1998, pp. 299-486.
- Usha Kulshreshtha, “Hamiltonian and BRST Formulations of the Nelsen-Olesen Model,” International Journal of Theoretical Physics, Vol. 41, No. 2, 2002, pp. 273-291. doi:10.1023/A:1014058806710
- Usha Kulshreshtha, “Light-Front Hamiltonian, Path Integral and BRST Formulations of the Nelsen-Olsen (Bogomol’nyi) Model in the Light-Cone Gauges,” International Journal of Theoretical Physics, Vol. 46, No. 10, 2007, pp. 2516-2530. doi:10.1007/s10773-007-9367-5
- Usha Kulshreshtha, D. S. Kulshreshtha and J. P. Vary, “Light-Front Hamiltonian, Path Integral and BRST Formulations of the Chern-Simons-Higgs Theory under Appropriate Gauge-Fixing,” Physics Scripta, Vol. 82, No. 5, 2010, 055101.
- Usha Kulshreshtha, D. S. Kulshreshtha and J. P. Vary, “Light-Front Hamiltonian, Path Integral and BRST Formulations of the Chern-Simons Theory Under Appropriate Gauge-Fixing,” Journal of Modern Physics, Vol. 1, No. 6, 2010, pp. 385-392.
- J. Maharana, “Quantization of Nonlinear Sigma Model in Constrained Hamiltonian Formalism,” Physics Letters B, Vol. 128, No. 6, 1983, pp. 411-414. doi:10.1016/0370-2693(83)90928-0
- M. M. Sheikh-Jabbari and A. Shirzad; “Boundary Conditions as Dirac Constraints,” European Physical Journal C, Vol. 19, No. 2, 2001, pp. 383-390. doi:10.1007/s100520100590

