Journal of Modern Physics
Vol.2 No.9(2011), Article ID:7138,7 pages DOI:10.4236/jmp.2011.29117
Spin-Flip Scattering at Quantum Hall Transition
1Shamoon College of Engineering, Bialik/Basel St., Israel
2I. Institut für Theoretische Physik, Universität Hamburg, Hamburg, Germany
3Max-Planck-Institut für Physik Komplexer Systeme, Nöthnitzer Str., Dresden, Germany
E-mail: achudnov@physik.uni-hamburg.de
Received February 2, 2011; revised April 15, 2011; accepted April 29, 2011
Keywords: 73.43.Nq, 72.25.Rb, 73.20Jc
ABSTRACT
We formulate a generalized Chalker-Coddington network model that describes the effect of nuclear spins on the two-dimensional electron gas in the quantum Hall regime. We find exact analytical expression for spin-dependent transmission coefficients of a charged particle through a saddle point potential in a perpendicular magnetic field. Spin-flip scattering creates a metallic state in a finite range around the critical energy of quantum Hall transition. As a result we find that the usual insulating phases with Hall conductance 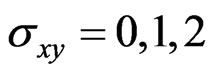 are separated by novel metallic phases.
are separated by novel metallic phases.
1. Introduction
Transition between the quantized values of Hall conductance in integer quantum Hall effect represents a profound example of electronic delocalization. Properties of this transition remain a subject of intensive theoretical and experimental investigations since the discovery of the integer quantum Hall effect (QHE) [1]. Theory of the delocalization transition in the QHE predicts the existence of a single delocalized critical electronic state at the center of Landau level (LL) [2-5]. Other states of a given LL are localized by disorder due to the Anderson localization phenomenon. Effective theoretical treatment of QHE delocalization transition is provided in frame of the Chalker-Coddington (CC) network model [6]. In this model electrons move along unidirectional links that form closed loops in analogy with semiclassical motion on contours of constant potential. Scattering between links is allowed at nodes, in analogy with tunneling through saddle-point potentials in the semiclassical model. Subsequent generalizations of CC model allowed to include spin degree of freedom [7] and to describe systems belonging to various symmetry classes [8,9].
In this paper we study the effect of spin-flip scattering by magnetic nuclei on the QHE transition. The spin-flip scattering by nuclei mixes two components of electron spin, and results in the mutual influence of electron and nuclear spins. The interplay of electron and nuclear spin degrees of freedom has been investigated earlier, focusing on measurement of nuclear-spin-lattice relaxation mediated by hyperfine interaction with two-dimensional electron system in QH regime [10,11]. In contradistinction, we concentrate on the effect of nuclear spins on the electron motion and resulting changes in the QH phase diagram.
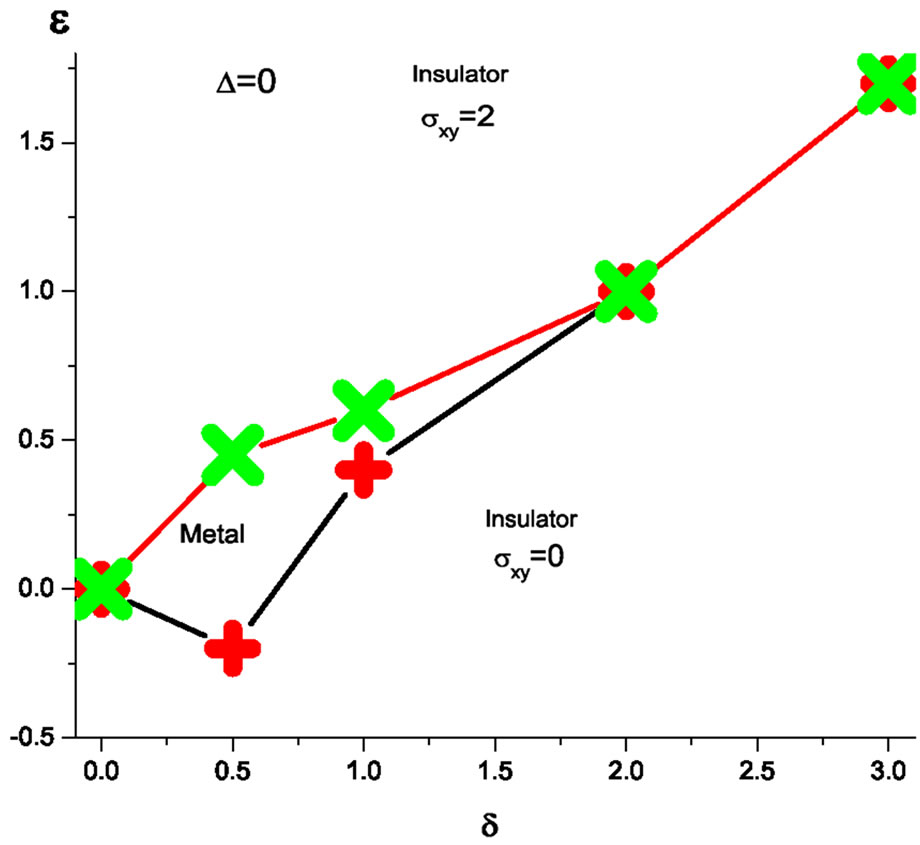
We adopt the model of point-like exchange interaction between nuclear and electron spins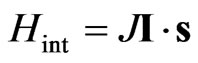 , where I and s denote the spins of the nucleus and of the electron respectively. Throughout the paper we assume spin-1/2 nuclei. In the absence of spin-flip scattering there are two Zeeman-split critical energies for each Landau level, where the QH delocalization transition takes place. We find that the spin-flip scattering results in the appearance of a finite region of delocalized states around the critical QHE states. The energetical width of the delocalized region depends on the strength of the exchange interaction relative to the Zeeman splitting in a nonmonotonous way. It increases with the exchange strength for weak exchange, reaches its maximum, and then shrinks back to two critical states at very large exchange interaction. Our results are summarized in phase diagram shown in Figure 1. To obtain this phase diagram, we constructed an effective network model based on the original CC model for the QH transition.
, where I and s denote the spins of the nucleus and of the electron respectively. Throughout the paper we assume spin-1/2 nuclei. In the absence of spin-flip scattering there are two Zeeman-split critical energies for each Landau level, where the QH delocalization transition takes place. We find that the spin-flip scattering results in the appearance of a finite region of delocalized states around the critical QHE states. The energetical width of the delocalized region depends on the strength of the exchange interaction relative to the Zeeman splitting in a nonmonotonous way. It increases with the exchange strength for weak exchange, reaches its maximum, and then shrinks back to two critical states at very large exchange interaction. Our results are summarized in phase diagram shown in Figure 1. To obtain this phase diagram, we constructed an effective network model based on the original CC model for the QH transition.
In general, scattering of electrons by nuclear spins induces many-electron Kondo correlations. In this paper
 (a)
(a)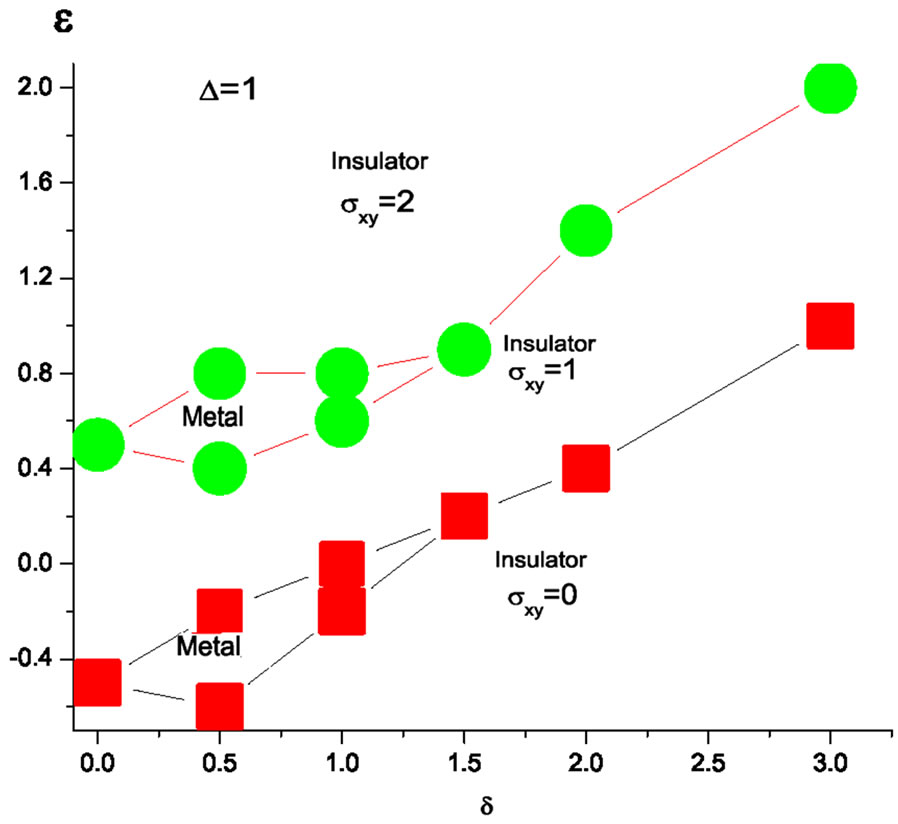 (b)
(b)
Figure 1. (a) Phase diagram at zero Zeeman splitting. (b) Phase diagram with finite Zeeman splitting.
however we consider regime, when Kondo correlations are suppressed by large Zeeman splitting and/or temperature larger than the Kondo temperature. In that case, collisions of different electrons with a nucleus lead to a loss of coherence of the nuclear wave function. In what follows we find a way to incorporate phenomenologically the loss of coherence of nuclear spins into modified CC network model. As a starting point, we consider a many particle wave function 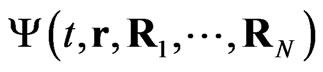 that describes a single electron and N nuclear spins. Here r denotes the coordinate of the mobile electron and Ri, (I = 1, ..., N) are the coordinates of nuclear spins. Furthermore, the short range of interaction between the electron and a nuclear spin allows for a series of simplifications that lead to an effective description in frame of CC model formulated for the reduced two-particle wave function. This wave function is a bi-spinor that describes propagation of an electron and an effective nuclear spin through the network.
that describes a single electron and N nuclear spins. Here r denotes the coordinate of the mobile electron and Ri, (I = 1, ..., N) are the coordinates of nuclear spins. Furthermore, the short range of interaction between the electron and a nuclear spin allows for a series of simplifications that lead to an effective description in frame of CC model formulated for the reduced two-particle wave function. This wave function is a bi-spinor that describes propagation of an electron and an effective nuclear spin through the network.
2. Spin-Dependent Scattering: Exact Solution
The spin-flip process requires conservation of energy between the initial and final states. However, because of the small nuclear magnetic moment, the change of its Zeeman energy cannot compensate the change in the Zeeman energy of the electron after the spin-flip. The energy conservation can still be fulfilled, if the center of mass of the electron wave function shifts in space in the act of spin scattering to the position with different potential energy. This difference has to compensate for the Zeeman energy. The favorable conditions for such process occur close to the saddle points of the disorder potential [12], which correspond to the nodes in the network model. Therefore, in terms of CC model, the spin-flip scattering is effective only at the nodes of the network.
Second, the act of scattering in each node involves only the coordinates of the electron and a single nucleus that is located at the node. Considered alone, this scattering event can be described in terms of the scattering matrix for the two-particle wave function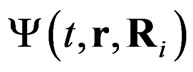 , where r is the coordinate of the electron and Ri is the coordinate of the nucleus in the node i.
, where r is the coordinate of the electron and Ri is the coordinate of the nucleus in the node i.
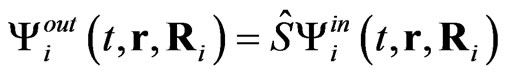 (1)
(1)
The explicit expression for the scattering matrix elements is obtained along the lines of [13] generalized on the problem with spin-flip scattering. We assume that the scattering at saddle points of the potential is accompanied by the interaction with nuclear spin, and hence allows for spin flips. Thereby, the states 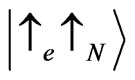 and
and 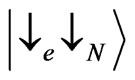 (where indices e, N) correspond to the spin state of electron and nucleus respectively) cannot flip the spin because of conservation of the total angular momentum by scattering. The scattering matrix for these two states can be obtained directly from the expression of [13] by shifting the height of the saddle point by Zeeman energy of the electron. In what follows we neglect Zeeman energy of a nucleus, which does not change the results of this paper qualitatively. We note, that the model that takes into account the Zeeman energy of the localized spin scatterers can also be applied to the scattering by localized magnetic impurities as it takes place, for example, in semimagnetic semiconductors [14]. The states
(where indices e, N) correspond to the spin state of electron and nucleus respectively) cannot flip the spin because of conservation of the total angular momentum by scattering. The scattering matrix for these two states can be obtained directly from the expression of [13] by shifting the height of the saddle point by Zeeman energy of the electron. In what follows we neglect Zeeman energy of a nucleus, which does not change the results of this paper qualitatively. We note, that the model that takes into account the Zeeman energy of the localized spin scatterers can also be applied to the scattering by localized magnetic impurities as it takes place, for example, in semimagnetic semiconductors [14]. The states 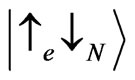 and
and 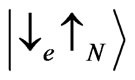 can be mixed in the spinflip process. To obtain the transmission coefficients for those states, we find the eigenstates and eigenenergies of the Hamiltonian
can be mixed in the spinflip process. To obtain the transmission coefficients for those states, we find the eigenstates and eigenenergies of the Hamiltonian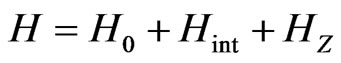 , where H0 is the Hamiltonian describing the motion of the electron in the scalar saddle point potential [13], and HZ describes the Zeeman energy. We choose the basis of singlet and triplet states that are the eigenstates of the interaction part of the Hamiltonian. The two-dimensional Hilbert space for the spin-flip scattering problem is then formed by the states
, where H0 is the Hamiltonian describing the motion of the electron in the scalar saddle point potential [13], and HZ describes the Zeeman energy. We choose the basis of singlet and triplet states that are the eigenstates of the interaction part of the Hamiltonian. The two-dimensional Hilbert space for the spin-flip scattering problem is then formed by the states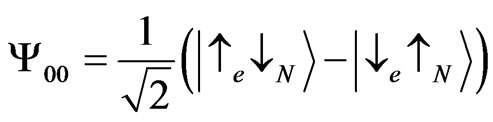 ,
, 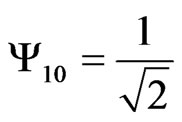
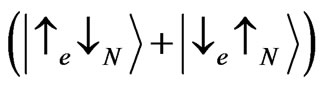 . Similarly to [10] we seek the solution of the Schrödinger equation in the form
. Similarly to [10] we seek the solution of the Schrödinger equation in the form 
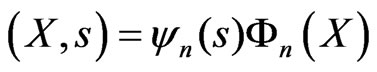 , where
, where 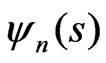 and
and 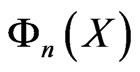 describe the cyclotron motion and the motion of the guiding center respectively, and n denotes the number of Landau level (LL). Explicit expression for
describe the cyclotron motion and the motion of the guiding center respectively, and n denotes the number of Landau level (LL). Explicit expression for 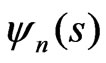 is provided in [13]. Without the loss of generality we restrict the further consideration to the lowest Landau level and suppress the Landau level index. The equation for the guiding center wave function in the basis
is provided in [13]. Without the loss of generality we restrict the further consideration to the lowest Landau level and suppress the Landau level index. The equation for the guiding center wave function in the basis 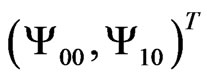 is given by
is given by
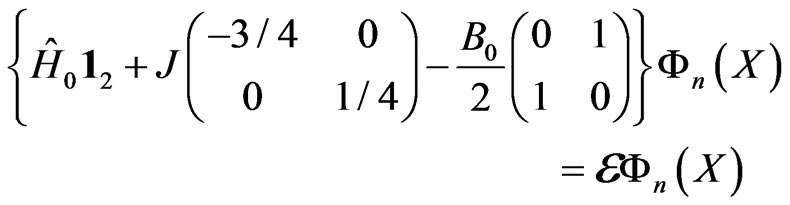 (2)
(2)
In writing Equation (2) we omitted the spatial dependence of the exchange interaction. The transitions between different Landau levels caused by such dependence can be neglected in high magnetic fields, while the transitions within a given Landau level can be taken into account by the random potential scattering term in the scalar part . We seek for the solution of Equation (2) in the form
. We seek for the solution of Equation (2) in the form
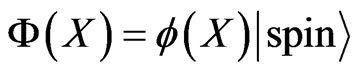 , (3)
, (3)
where 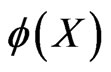 describes the spatial dependence of the wave function, and
describes the spatial dependence of the wave function, and 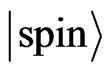 is its spinor part. Let
is its spinor part. Let 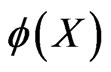 be the solution of the Schrödinger equation
be the solution of the Schrödinger equation
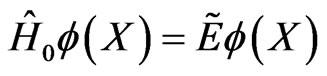 (4)
(4)
Diagonalization of the spinor part of Equation (2) for a fixed 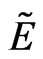 leads to the two eigenvectors and corresponding eigenergies
leads to the two eigenvectors and corresponding eigenergies
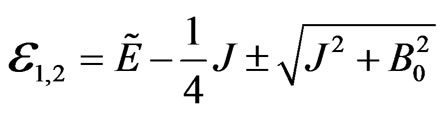 (5)
(5)
The energies 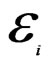 correspond to the total energies of the two-particle states. By the energy conservation, both energies are to be equal to the energy of the incoming electron,
correspond to the total energies of the two-particle states. By the energy conservation, both energies are to be equal to the energy of the incoming electron,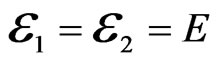 . This leads to the two different values for the energy
. This leads to the two different values for the energy 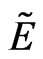 that determines the effective height of the potential barrier
that determines the effective height of the potential barrier
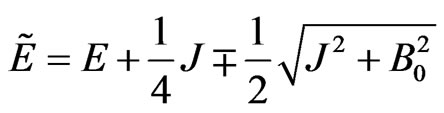 (6)
(6)
Following [13], we introduce the dimensionless measure of energy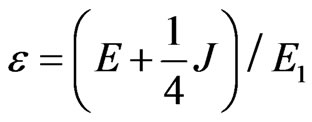 , where E1 is the energetic parameter characterizing the form of the saddle point potential. Furthermore, we denote the dimensionless strength of the Zeeman coupling as
, where E1 is the energetic parameter characterizing the form of the saddle point potential. Furthermore, we denote the dimensionless strength of the Zeeman coupling as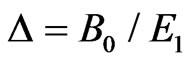 , and the relative exchange strength as
, and the relative exchange strength as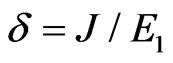 .
.
Therefore, there are two solutions of Equation (2) corresponding to the energy E of the incoming electron, 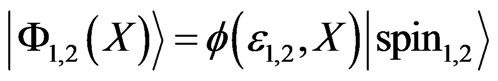 , where
, where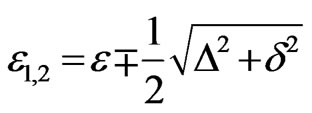 , and
, and 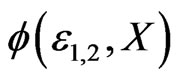 is the solution of Equation (4) for the energy
is the solution of Equation (4) for the energy 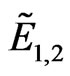 respectively. The explicit form of
respectively. The explicit form of 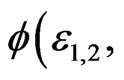
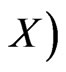 is given in [13]. The relations between the functions
is given in [13]. The relations between the functions 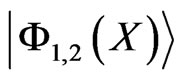 and
and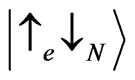 ,
, 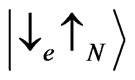 are given by
are given by
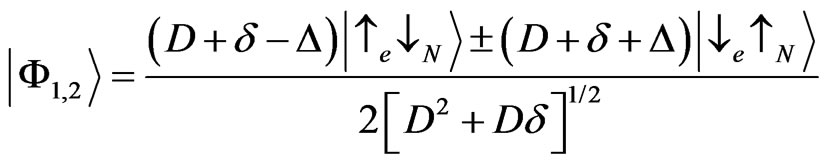 , (7)
, (7)
where .
.
The energies 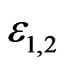 together with the energies
together with the energies 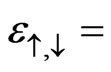
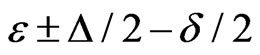 of the states
of the states 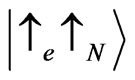 and
and 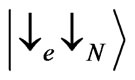 determine the transmission coefficients [13]
determine the transmission coefficients [13]
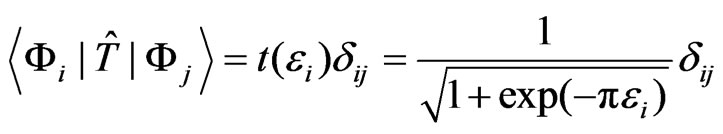 . (8)
. (8)
Using Equations (7) and (8) we obtain the transmission coefficients for the scattering with spin flip:
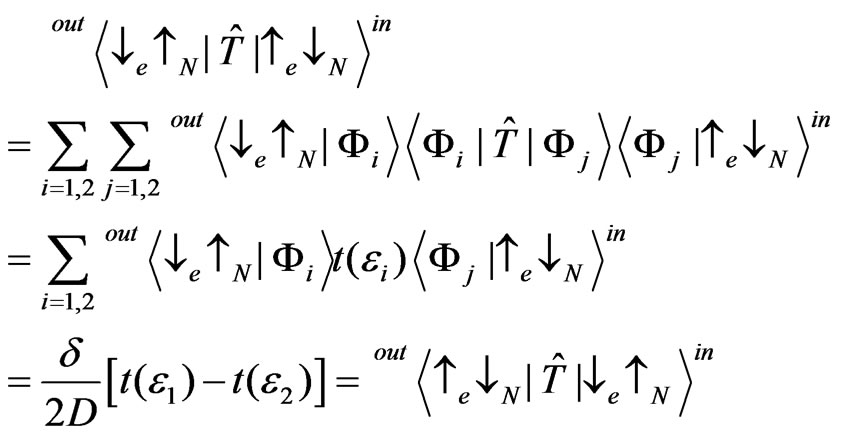 (9)
(9)
The transmission coefficients without spin flip are obtained in the similar way
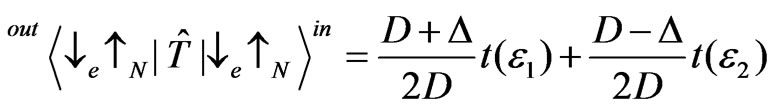 , (10)
, (10)
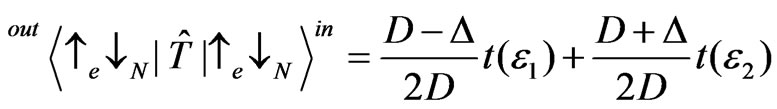 , (11)
, (11)
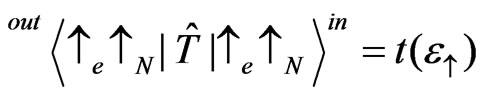 , (12)
, (12)
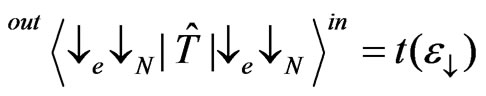 , (13)
, (13)
The reflection coefficients are given by the exchange 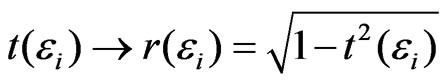 everywhere.
everywhere.
Furthermore, using the expressions for transmission and reflection coefficients, we construct the scattering matrix in the node relating the incoming and outgoing waves (see Figure 2). From that we derive the transfer matrix relating the waves on the left and on the right sides of the node. The system is, on average, invariant under  rotation if the transmission and reflection (of each channel) are interchanged at the next neighbor node, i.e.
rotation if the transmission and reflection (of each channel) are interchanged at the next neighbor node, i.e.  [6].
[6].
3. Bi-Spinor Network Model
In the standard formulation of the CC network model, the outgoing wave after the scattering at the node i and acquiring a random phase on the link plays the role of the incoming wave for the scattering by the next node (let’s number it with i + 1). The latter allows to get the information about the propagation through the network by dividing the network into slices and multiplying the transfer matrices slice by slice. Such a direct approach is inapplicable if one replaces the exact many-particle scattering matrix by the two-particle scattering matrix though. Namely, the outgoing two-particle wave function from the node i contains no information about the phase and the spin direction of the nucleus in the node i + 1. However, both being the spin-1/2 state, the outgoing state of the nucleus i and the state of the nucleus i + 1 can always be transformed to each other by a unitary rotation
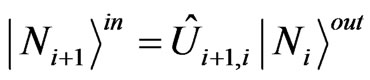 , (14)
, (14)
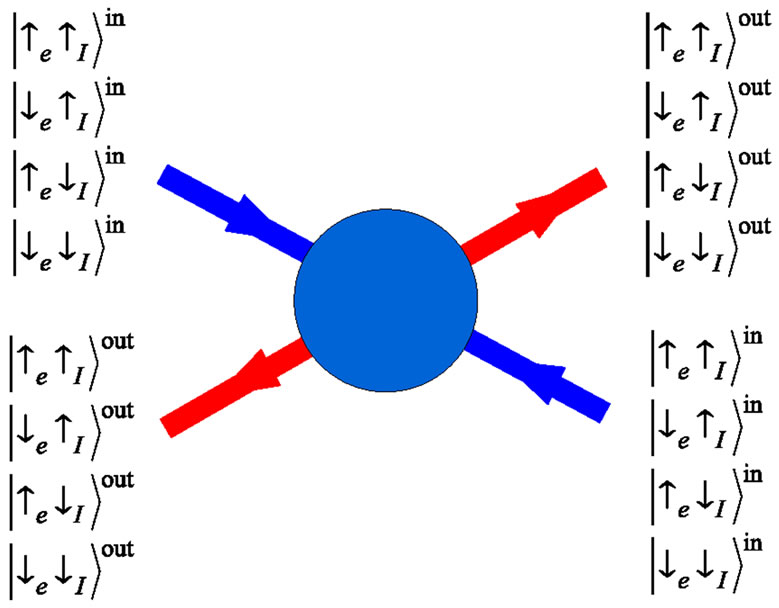
Figure 2. Incoming and outgoing states at a single node.
where 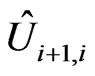 is a matrix of SU(2) group. One can imagine the matrix
is a matrix of SU(2) group. One can imagine the matrix  as residing on the link connecting the nodes i and i + 1. Therefore, if one had a knowledge of matrices
as residing on the link connecting the nodes i and i + 1. Therefore, if one had a knowledge of matrices 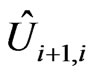 on all links connecting the neighbor nuclei, one could replace the many-particle wave function of all nuclei by a single spin-1/2 spinor that changes its state by propagation through each link according to the states of real nuclei. Taking into account the electron part of the wave function, the propagation of an electron though the network with scattering by nuclear spins can be described as a propagation of a bi-spinor that consists of the electron and nuclear parts. The scattering of the bispinor at each node is described by Equations (9)-(13). To illustrate this procedure, let us consider propagation of an electron through a single path in the network, and number the nodes on that path consequently from 1 to n. The many-particle wave function can be expanded in the basis of states
on all links connecting the neighbor nuclei, one could replace the many-particle wave function of all nuclei by a single spin-1/2 spinor that changes its state by propagation through each link according to the states of real nuclei. Taking into account the electron part of the wave function, the propagation of an electron though the network with scattering by nuclear spins can be described as a propagation of a bi-spinor that consists of the electron and nuclear parts. The scattering of the bispinor at each node is described by Equations (9)-(13). To illustrate this procedure, let us consider propagation of an electron through a single path in the network, and number the nodes on that path consequently from 1 to n. The many-particle wave function can be expanded in the basis of states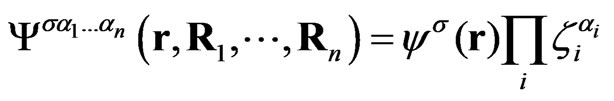 , where
, where 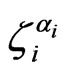 denotes the wave function of the nucleus at node i,
denotes the wave function of the nucleus at node i, 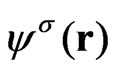 denotes the electron wave function,
denotes the electron wave function, 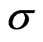 is the spin-index of the electron, and
is the spin-index of the electron, and 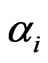 is the spin index of the nucleus at site i (both
is the spin index of the nucleus at site i (both 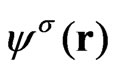 and
and 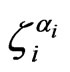 have a structure of spin-1/2 spinors). The incoming and outgoing amplitudes at a given node i are related through the scattering matrix
have a structure of spin-1/2 spinors). The incoming and outgoing amplitudes at a given node i are related through the scattering matrix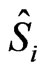 ,
,
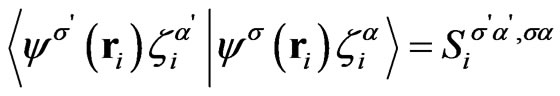 , the states of nuclei on other nodes being unchanged. According to the construction of CC network, the electron amplitude acquires a spin dependent random phase
, the states of nuclei on other nodes being unchanged. According to the construction of CC network, the electron amplitude acquires a spin dependent random phase 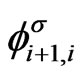 at each link. The spin projection of the electron propagating on the link remains conserved. Therefore, we obtain the relation between the electron amplitude outgoing from the node i, and the one incoming to the node i + 1,
at each link. The spin projection of the electron propagating on the link remains conserved. Therefore, we obtain the relation between the electron amplitude outgoing from the node i, and the one incoming to the node i + 1, 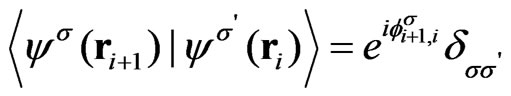 Then the discussed amplitude P can be written as a chain of scattering events by subsequent nodes and propagations on the links
Then the discussed amplitude P can be written as a chain of scattering events by subsequent nodes and propagations on the links
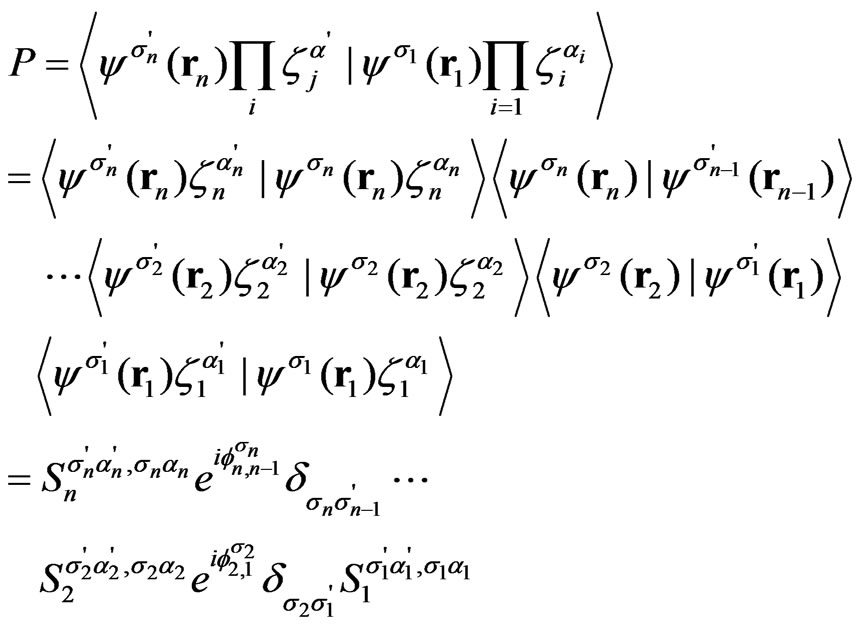 (15)
(15)
Note that in Equation (15) the spin states of the nuclei before (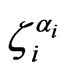 ) and after (
) and after (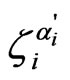 ) the scattering are fixed by initial and final many-particle states, while summation over the repeating indices of intermediate states of electrons is implied (the indices
) the scattering are fixed by initial and final many-particle states, while summation over the repeating indices of intermediate states of electrons is implied (the indices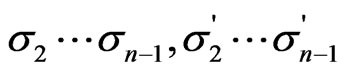 ).
).
To rewrite Equation (15) in bi-spinor notations, we introduce an SU(2) matrix 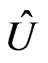 on each link according to Equation (14),
on each link according to Equation (14), 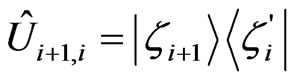 , where
, where 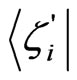 is the outgoing state of the nucleus i and
is the outgoing state of the nucleus i and 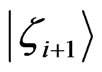 is the incoming state of the nucleus i + 1 as chosen by the many-particle amplitude in Equation (15). Now we can describe the evolution of the states of the nuclei by a single spacedepentend spinor
is the incoming state of the nucleus i + 1 as chosen by the many-particle amplitude in Equation (15). Now we can describe the evolution of the states of the nuclei by a single spacedepentend spinor . The propagation of this spinor on the link between the nodes i and i + 1 is governed by the matrix
. The propagation of this spinor on the link between the nodes i and i + 1 is governed by the matrix . So, if the state of the spinor after the scattering by the node i equals the final state of the nucleus i in the many particle formulation,
. So, if the state of the spinor after the scattering by the node i equals the final state of the nucleus i in the many particle formulation, 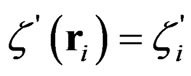 , then the matrix
, then the matrix 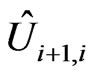 transforms this state into initial state of the nucleus at the node i + 1,
transforms this state into initial state of the nucleus at the node i + 1,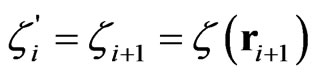
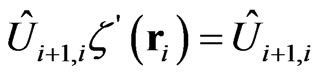 . Introducing now a bi-spinor
. Introducing now a bi-spinor 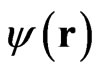
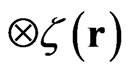 , we obtain the for the propagation on the link (i + 1, i)
, we obtain the for the propagation on the link (i + 1, i)
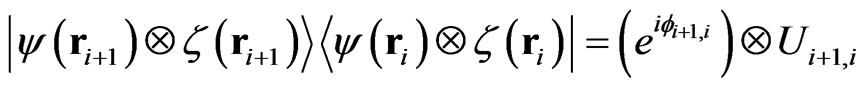 (16)
(16)
where 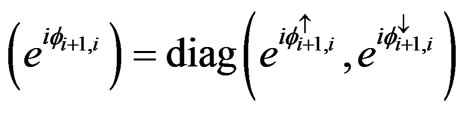 is the diagonal matrix of phases acquired by the electron wave function.
is the diagonal matrix of phases acquired by the electron wave function.
Using Equation (16) we can represent the amplitude in Equation (15) in the equivalent form
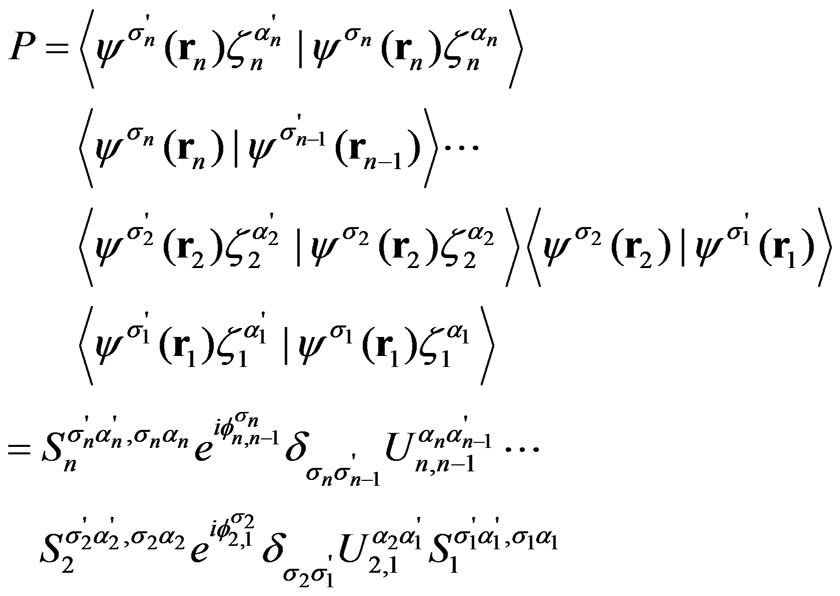 (17)
(17)
Let us stress that in contrast to Equation (15), summation over repeating indices in Equation (17) extends on the intermediate states of the nucleus 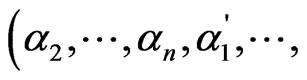
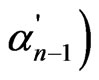 as well. However, due to the special form of matrices
as well. However, due to the special form of matrices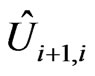 , the only nonzero contributions to the sum over nuclear indices are provided when the indices
, the only nonzero contributions to the sum over nuclear indices are provided when the indices 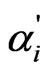 and
and  correspond to the states of nuclei i and i + 1 chosen in the many particle amplitude Equation (15). Therefore, in the bi-spinor formulation, the information about the many-particle state is contained in the special choice of SU(2) matrices on links.
correspond to the states of nuclei i and i + 1 chosen in the many particle amplitude Equation (15). Therefore, in the bi-spinor formulation, the information about the many-particle state is contained in the special choice of SU(2) matrices on links.
The explicit form of matrices 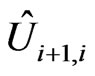 is determined by the states of the two nuclei connected by the link in a given partial trajectory, and is unknown. In general, the matrices
is determined by the states of the two nuclei connected by the link in a given partial trajectory, and is unknown. In general, the matrices 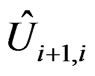 depend not only on the position of the link but also on the form of the whole trajectory. Moreover, as it was mentioned above, due to collisions of nuclear spins with different electrons, matrices
depend not only on the position of the link but also on the form of the whole trajectory. Moreover, as it was mentioned above, due to collisions of nuclear spins with different electrons, matrices 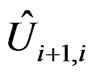 acquire stochastic time-dependence that eventually leads to decoherence of the bi-spinor wave function, and hence to the appearance of delocalized states. We incorporate this effect phenomenologically, replacing the SU(2) matrices
acquire stochastic time-dependence that eventually leads to decoherence of the bi-spinor wave function, and hence to the appearance of delocalized states. We incorporate this effect phenomenologically, replacing the SU(2) matrices 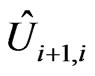 by a random ensemble of
by a random ensemble of 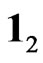 and
and 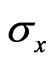 matrices, appearing with probability 1/2 on each link and acting on the state of the nucleus. As it is shown below by numerical simulations, finite regions of delocalized states appear in frame of this model.
matrices, appearing with probability 1/2 on each link and acting on the state of the nucleus. As it is shown below by numerical simulations, finite regions of delocalized states appear in frame of this model.
4. Results and Discussion
Our numerical calculations proceed as follows. We study a system of size 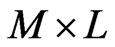 where M is the width of the system and L is its length. For a given M, the eigenvalues of
where M is the width of the system and L is its length. For a given M, the eigenvalues of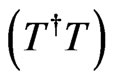 , where T is the full transfer matrix, behave as
, where T is the full transfer matrix, behave as 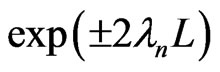 defining the Lyapunov exponents
defining the Lyapunov exponents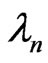 ; the smallest positive one,
; the smallest positive one, 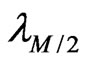 , defines the localization length
, defines the localization length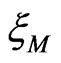 . The M dependence of renormalized localization length
. The M dependence of renormalized localization length 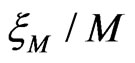 identifies the phases: 1) a decreasing ratio corresponds to localized state, i.e., an insulator, 2) a constant ratio corresponds to a critical state, and 3) an increasing ratio corresponds to a metallic phase.
identifies the phases: 1) a decreasing ratio corresponds to localized state, i.e., an insulator, 2) a constant ratio corresponds to a critical state, and 3) an increasing ratio corresponds to a metallic phase.
The results of our numerical calculations lead to phase diagrams presented in Figure 1. The phase diagram in Figure 1(a) corresponds to the spin-degenerate case with zero Zeeman splitting. In the absence of spin-flip scattering 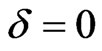 there is a transition between the two insulating phases with Hall conductances
there is a transition between the two insulating phases with Hall conductances 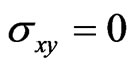 and
and 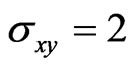 at energy
at energy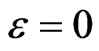 . At nonzero
. At nonzero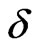 , a metallic phase appears in the finite range of energies, as described above.
, a metallic phase appears in the finite range of energies, as described above.
As a typical example of numerical results we show renormalized localization length 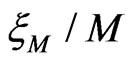 as a function of energy
as a function of energy 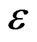 for zero Zeeman splitting
for zero Zeeman splitting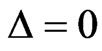 , and fixed exchange interaction
, and fixed exchange interaction 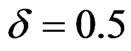 in Figure 3. Different point-sets correspond to different widths M of the system. The data imply that the region within approximate boundaries
in Figure 3. Different point-sets correspond to different widths M of the system. The data imply that the region within approximate boundaries 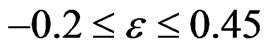 demonstrates a typical metallic behavior with
demonstrates a typical metallic behavior with 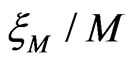 increasing with M. We cannot completely rule out that this increase is still an artifact of finite-size errors. But even if the latter is true, the data still provide a strong indication of a drastic increase in the localization length caused by spin-flip processes.
increasing with M. We cannot completely rule out that this increase is still an artifact of finite-size errors. But even if the latter is true, the data still provide a strong indication of a drastic increase in the localization length caused by spin-flip processes.
The phase diagram for finite Zeeman splitting 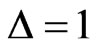 is shown in Figure 1(b). Without the spin-flip scattering there are two critical energies
is shown in Figure 1(b). Without the spin-flip scattering there are two critical energies 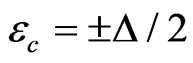 separating the insulating phases with
separating the insulating phases with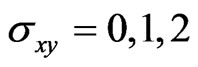 . A finite spin-flip scattering induces the appearance of two metallic regions around each critical energy, in analogy with Figure 1(a).
. A finite spin-flip scattering induces the appearance of two metallic regions around each critical energy, in analogy with Figure 1(a).
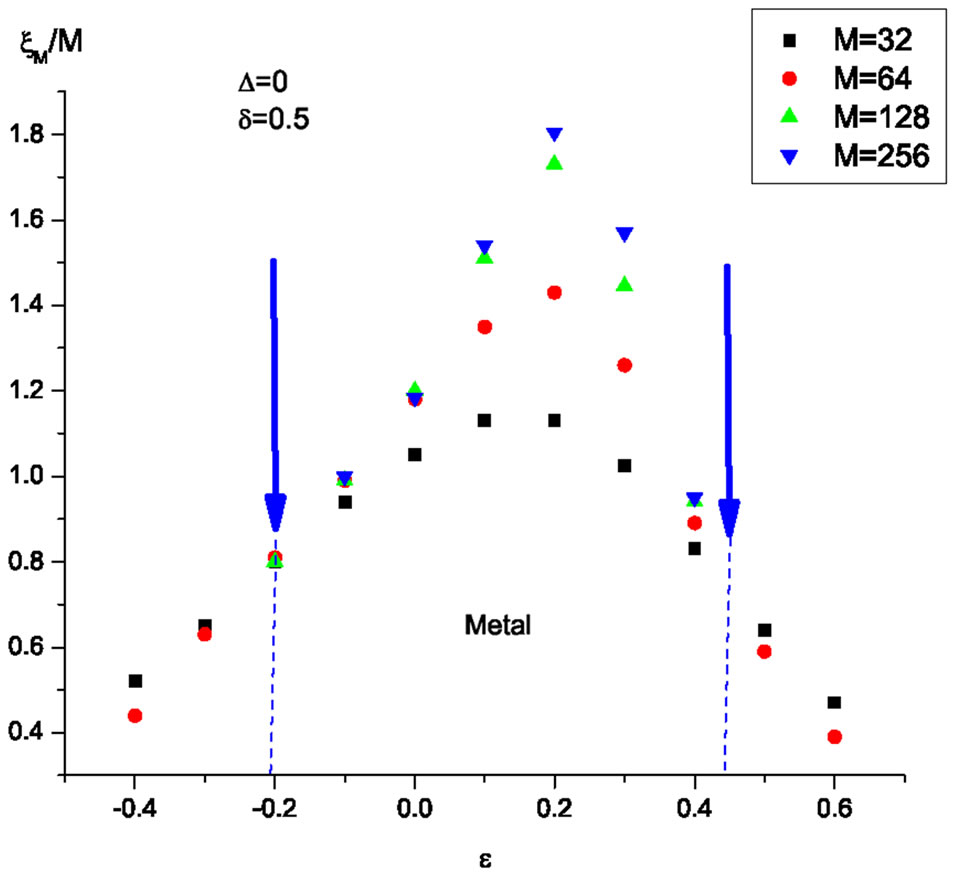
Figure 3. Renormalized localization lengths 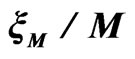 as functions of energy
as functions of energy 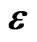 for zero Zeeman splitting
for zero Zeeman splitting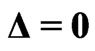 , and fixed exchange interaction
, and fixed exchange interaction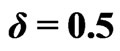 . Different point-sets correspond to different widths M of the system.
. Different point-sets correspond to different widths M of the system.
As the spin-flip scattering rate grows further, the size of each metallic region diminishes and finally collapses to single critical states at energies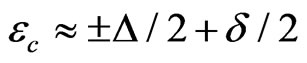 .
.
The appearance and the subsequent collapse of delocalized phase with the increase of the spin-flip scattering 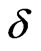 can be qualitatively explained by the mutual influence of the spin-flip scattering at nodes and mixing of the states on links. To simplify the consideration, let us use the eigenfunctions of the Hamiltonian in Equation (2) as basis states.
can be qualitatively explained by the mutual influence of the spin-flip scattering at nodes and mixing of the states on links. To simplify the consideration, let us use the eigenfunctions of the Hamiltonian in Equation (2) as basis states.
The basis states can be united into the vector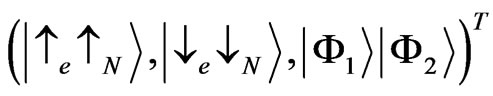 . In this basis, the scattering matrix on the nodes becomes block-diagonal, consisting of four blocks corresponding to the four basis states. The states are mixed however on the links. By transformation to the new basis, the mixing matrix
. In this basis, the scattering matrix on the nodes becomes block-diagonal, consisting of four blocks corresponding to the four basis states. The states are mixed however on the links. By transformation to the new basis, the mixing matrix 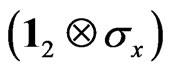 goes over into the matrix
goes over into the matrix
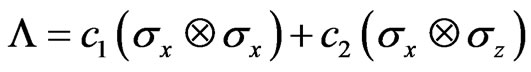 (18)
(18)
The coefficients 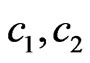 are given by the transformation matrix between the vectors
are given by the transformation matrix between the vectors 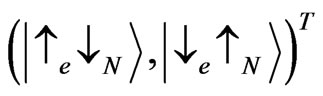 and
and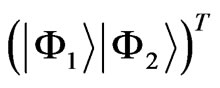 , they can be read off from Equation (7)
, they can be read off from Equation (7)
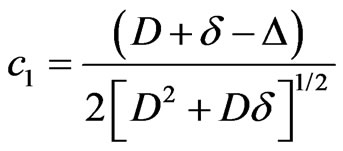 ,
,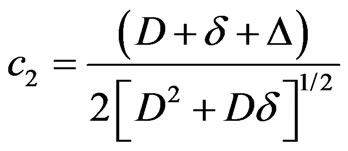 (19)
(19)
The matrix elements 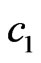 provide the mixing of the states
provide the mixing of the states 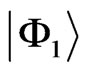 with
with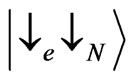 , and
, and 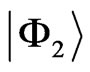 with
with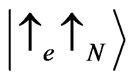 . At finite Zeeman splitting and exchange coupling, the critical energies of those states lie close to each other (see Figure 4). The matrix elements
. At finite Zeeman splitting and exchange coupling, the critical energies of those states lie close to each other (see Figure 4). The matrix elements 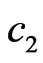 mix the other
mix the other
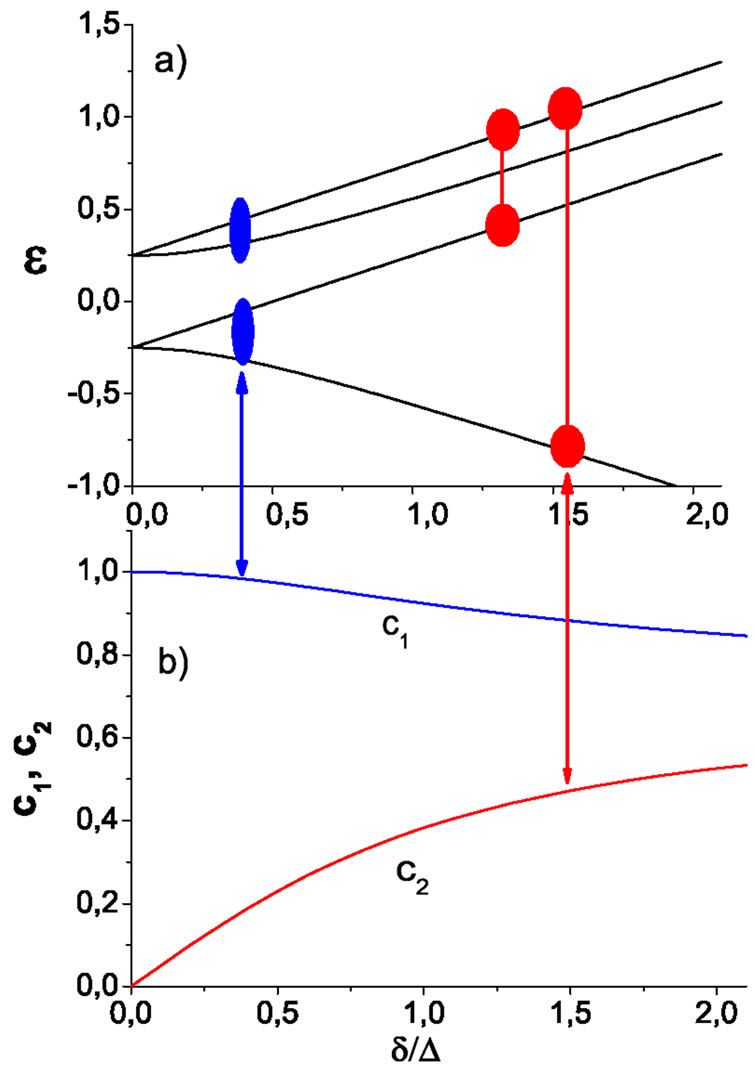
Figure 4. (a) Eigenenergies of Hamiltonian in Equation (2). Blue ovals and connected red circles show the states mixed on the links by the matrix elements 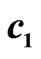 (blue) and
(blue) and 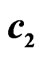 (red). (b) Matrix elements
(red). (b) Matrix elements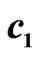 ,
, 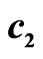 of the mixing matrix
of the mixing matrix 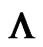 (Equation (18)) as functions of exchange coupling
(Equation (18)) as functions of exchange coupling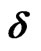 .
.
pairs of states, 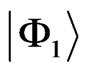 with
with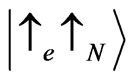 , and
, and 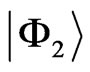 with
with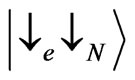 . If the energy is equal to the critical energy of one of the states, for instance the state
. If the energy is equal to the critical energy of one of the states, for instance the state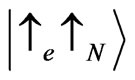 , this state is extended but the mixing on the links couples it to other states that are localized at the given energy. As long as the critical energies of the mixed states are close, the localization length of the admixed state is large, and the overall effect of the mixing results in the appearance of a finite energy region of delocalized states. This is the case for relatively small exchange couplings
, this state is extended but the mixing on the links couples it to other states that are localized at the given energy. As long as the critical energies of the mixed states are close, the localization length of the admixed state is large, and the overall effect of the mixing results in the appearance of a finite energy region of delocalized states. This is the case for relatively small exchange couplings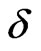 . In the regime of small
. In the regime of small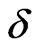 , the coefficients
, the coefficients 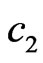 of the mixing matrix
of the mixing matrix 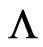 are small, and the mixing occurs only between the states with close critical energies due to the matrix element
are small, and the mixing occurs only between the states with close critical energies due to the matrix element 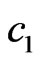 (see Figure 4(b)).
(see Figure 4(b)).
For large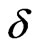 , the coefficients
, the coefficients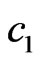 ,
, 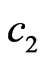 become approximately equal to
become approximately equal to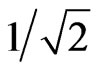 . At the same time, the critical energy of the state
. At the same time, the critical energy of the state 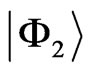 moves far away from the critical energies of other states (the lowest line in Figure 4(a)). As a result, at the critical energy
moves far away from the critical energies of other states (the lowest line in Figure 4(a)). As a result, at the critical energy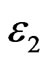 , the extended state
, the extended state 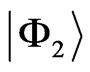 is coupled to strongly localized states, and becomes localized itself. The upper three lines in Figure 4(a) show the critical energies for the states (from top to bottom)
is coupled to strongly localized states, and becomes localized itself. The upper three lines in Figure 4(a) show the critical energies for the states (from top to bottom)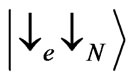 ,
, 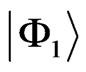 ,
,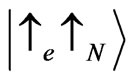 . The distance between the critical energies of those states saturates at large
. The distance between the critical energies of those states saturates at large 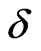 to the value of half of the Zeeman splitting
to the value of half of the Zeeman splitting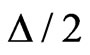 . Due to the relatively small energy distance between the critical energies, two delocalized states at the energies close to
. Due to the relatively small energy distance between the critical energies, two delocalized states at the energies close to 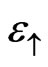 and
and 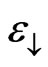 remain preserved. Note that the collapse of the delocalized regions to just two critical states at large exchange coupling
remain preserved. Note that the collapse of the delocalized regions to just two critical states at large exchange coupling 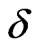 provides a strong evidence that our numerical results are not an artifact of the finite size of the system but rather a nontrivial effect due to the mixing of localized and extended states. Indeed, four critical states exist without the mixing on the links, and all four states should have reappeared at large
provides a strong evidence that our numerical results are not an artifact of the finite size of the system but rather a nontrivial effect due to the mixing of localized and extended states. Indeed, four critical states exist without the mixing on the links, and all four states should have reappeared at large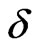 , if our results had been due to the finite system size.
, if our results had been due to the finite system size.
In conclusion, we derived the exact solution of spinflip scattering problem in quantum Hall regime, and used it to construct the network model that describes integer QH transition in presence of scattering by nuclear spins. With increase of the exchange coupling between electron and nuclear spins, we predict the appearance of metallic regions in the QH phase diagram that subsequently collapse to the critical lines. Those critical lines correspond to a standard QH transition. Our investigation can also shed light on the QH transition in presence of scattering by magnetic impurities.
5. Acknowledgements
We are grateful to I. Burmistrov, J. Chalker, I. Gornyi, and A. Mirlin for fruitful discussions. Authors acknowledge financial support from DFG through Sonderforschungsbereich 668 and of the SCE internal research grant.
REFERENCES
- K. V. Klitzing, G. Dorda and M. Pepper, “New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance,” Physical Review Letters, Vol. 45, No. 6, 1980, pp. 494-497. doi:10.1103/PhysRevLett.45.494
- R. B. Laughlin, “The Quantized Hall Conductivity in Two Dimensions,” Physical Review B, Vol. 23, No. 10, 1981, pp. 5632-5633. doi:10.1103/PhysRevB.23.5632
- B. I. Halperin, “Quantized Hall Conductance, Current-Carrying Edge States, and the Existence of Extended States in a Two-Dimensional Disordered Potential,” Physical Review B, Vol. 25, No. 4, 1982, pp. 2185-2190. doi:10.1103/PhysRevB.25.2185
- H. Levine, S. B. Libby and A. M. M. Pruisken, “Electron Delocalization by a Magnetic Field in Two Dimensions,” Physical Review Letters, Vol. 51, No. 20, 1983, pp. 1915-1918. doi:10.1103/PhysRevLett.51.1915
- D. E. Khmel’nitskii, “Quantization of Hall Conductivity,” Journal of Experimental and Theoretical Physics Letters, Vol. 38, No. 9, 1983, pp. 552-556.
- J. T. Chalker and P. D. Coddington, “Percolation, Quantum Tunnelling and the Integer Quantum Hall Effect,” Journal of Physics C, Vol. 21, No. 14, 1988, pp. 2665- 2679.
- D. K. K. Lee and J. T. Chalker, “A Unified Model for Two Localisation Problems: Electron States in Spin-Degenerate Landau Levels, and in a Random Magnetic Field,” Physical Review Letters, Vo. 72, No. 10, 1994, pp. 1510-1513.
- V. Kagalovsky, B. Horovitz, Y. Avishai and J. T. Chalker, “Quantum Hall Plateau Transitions in Disordered Superconductors,” Physical Review Letters, Vol. 82, No. 17, 1999, pp. 3516-3519. doi:10.1103/PhysRevLett.82.3516
- J. T. Chalker, N. Read, V. Kagalovsky, B. Horovitz, Y. Avishai and A. W. W. Ludwig, “Thermal Metal in Network Models of a Disordered Two-Dimensional Superconductor,” Physical Review B, Vol. 65, No.1 , 2001, Article ID: 012506.
- A. Berg, M. Dobers, R. R. Gerhardts and K. V. Klitzing, “Magnetoquantum Oscillations of the Nuclear-Spin-Lattice Relaxation near a Two-Dimensional Electron Gas,” Physical Review Letters, Vol. 64, No. 21. 1990. pp. 2563-2566. doi:10.1103/PhysRevLett.64.2563
- I. D. Vagner and T. Maniv, “Nuclear Spin-Lattice Relaxation: A Microscopic Local Probe for Systems Exhibiting the Quantum Hall Effect,” Physical Review Letters, Vol. 61, No. 12, 1988, pp. 1400-1403. doi:10.1103/PhysRevLett.61.1400
- V. Kagalovsky and I. Vagner, “Hyperfine Interaction Induced Critical Exponents in the Quantum Hall Effect,” Physical Review B, Vol. 75, No. 11, 2007, Article ID: 113304. doi:10.1103/PhysRevB.75.113304
- H. A. Fertig and B. I. Halperin, “Transmission Coefficient of an Electron through a Saddle-Point Potential in a Magnetic Field,” Physical Review B, Vol. 36, No. 15, 1987, pp. 7969-7976. doi:10.1103/PhysRevB.36.7969
- T. Jungwirth, J. Sinova, J. Masek, J. Kucera and A. H. MacDonald, “Theory of Ferromagnetic (III,Mn)V Semiconductors,” Reviews of Modern Physics, Vol. 78, No. 3, 2006, pp. 809-864. doi:10.1103/RevModPhys.78.809

