ABSTRACT

In this paper, we construct two sets of vertex operators $S_{+}$ and $S_{-}$ from a direct sum of two sets of Heisenberg algebras. Then by calculating the vacuum expectation value of some products of vertex operators, we get Macdonald function in special variables $x_i=t^{i-1}$ ( $i=0,1,2,\cdots$ ). Hence we obtain the operator product formula for a special Macdonald function $P_{\lambda }\left(\mathrm{1,}t\mathrm{,}\cdots \mathrm{,}{t}^{n-1}\mathrm{<mo>\; ;\; </mo>}q\mathrm{,}t\right)$ when n is finite as well as when n goes to infinity.

Keywords:

Macdonald Function, Vertex Operator, Heisenberg Algebra

1. Introduction

The study of topological string on Calabi-Yau manifolds is interested in mathematical physics for many years. It was found that gauge theories with certain gauge groups can be geometrically engineered from some Calabi-Yau threefolds, and the topological string partition functions on such spaces are related to instanton sums in gauge theories [1] .

The topological vertex formalism provides a powerful method to calculate the topological string partition function for non-compact toric Calabi-Yau 3-fold. By transfer matrix approach, A. Okounkov, N. Reshetikhin and C. Vafa proposed the topological vertex $C_{\lambda \mu \nu }$ using Schur and skew Schur functions [2] :

$C_{\lambda \mu \nu }\left(q\right)=q^{\frac{\kappa \left(\mu \right)}{2}}{s}_{{\nu }^t}\left(q^{-\rho }\right){\displaystyle \sum _{\eta }}{s}_{{\lambda }^t/\eta }\left(q^{-\nu -\rho }\right)s_{\mu /\eta }\left(q^{-{\nu }^t-\rho }\right)$

where $\lambda \mathrm{,}\mu \mathrm{,}\nu$ are Young diagrams, ${\lambda }^t$ denotes the transpose of λ, and $\rho =\left(-1/2,-3/2,-5/2,\cdots \right)$ . The topological vertex $C_{\lambda \mu \nu }$ has a nice interpretation by statistical mechanics of the melting crystal model [2] [3] . In this paper two sets of vertex operators constructed specifically by the annihilation and creation generators of Heisenberg algebra play important roles in realizing Schur and skew Schur functions.

On the other hand, gauge theory partition function is a function with two equivariant parameters. In 2007, based on the arguments of geometric engineering, concerning the K-theoretic lift of the Nekrasov partition functions, A. Iqbal, C. Kozçaz and C. Vafa introduced a refined version of topological vertex [4] . In this refinement, one more parameter t comes in and the theory seems to be deeply related to a Macdonald function with special variables, or what we call a special Macdonald function, $P_{\lambda }\left(t^{-\rho }\mathrm{<mo>\; ;\; </mo>}q\mathrm{,}t\right)$ :

$\begin{array}{c}{C}_{\lambda \mu \nu }\left(t,q\right)={\left(\frac{q}{t}\right)}^{\frac{{\Vert \mu \Vert }^2+{\Vert \nu \Vert }^2}{2}}{t}^{\frac{\kappa \left(\mu \right)}{2}}{P}_{{\nu }^t}\left(t^{-\rho };q,t\right)\\ \times {\displaystyle \sum _{\eta }}{\left(\frac{q}{t}\right)}^{\frac{\left|\eta \right|+\left|\lambda \right|-\left|\mu \right|}{2}}{s}_{{\lambda }^t/\eta }\left(t^{-\rho }{q}^{-\nu }\right)s_{\mu /\eta }\left(t^{-{\nu }^t}{q}^{-\rho }\right)\end{array}$

where ${\Vert \lambda \Vert }^2={\displaystyle {\sum }_i}{\lambda }_i^2$ . Moreover H. Awata and H. Kanno proposed another formula [5] which is expressed entirely in terms of the special (skew) Macdonald functions:

$\begin{array}{c}{C}_{\mu \lambda }^{\nu }\left(q,t\right)=P_{\lambda }\left(t^{\rho };q,t\right)f_{\nu }{\left(q,t\right)}^{-1}\\ \times {\displaystyle \sum _{\sigma }}\iota P_{{\mu }^t/{\sigma }^t}\left(-t^{{\lambda }^t}{q}^{\rho };t,q\right)P_{\nu /\sigma }\left(q^{\lambda }{t}^{\rho };q,t\right){\left(q^{1/2}/t^{1/2}\right)}^{\left|\sigma \right|-\left|\nu \right|},\end{array}$

where $f_{\lambda }\left(q\mathrm{,}t\right)={\left(-1\right)}^{\left|\lambda \right|}{q}^{n\left({\lambda }^t\right)+\left|\lambda \right|/2}{t}^{-n\left(\lambda \right)-\left|\lambda \right|/2}$ and $\iota$ is the involution on the algebra of symmetric functions defined by $\iota \left(p_n\right)=-p_n$ , here $p_n\left(x\right)={\displaystyle {\sum }_{i=1}^{\infty }}{x}_i^n$ . Although $C_{\lambda \mu \nu }\left(t\mathrm{,}q\right)$ and $C_{\mu \lambda }^{\nu }\left(q\mathrm{,}t\right)$ have different expressions, they are supposed to give the same result.

Therefore it seems that the key problem is to change Schur function for the unrefined case to Macdonald function for the refined one. Hence to find a vertex operator formalism for the refined topological vertex will be interesting. The essential step is to realize the special Macdonald function $P_{\lambda }\left(t^{-\rho }\mathrm{<mo>\; ;\; </mo>}q\mathrm{,}t\right)$ . However a vertex operator formalism for $P_{\lambda }\left(t^{-\rho }\mathrm{<mo>\; ;\; </mo>}q\mathrm{,}t\right)$ does not exist so far.

In this paper, we get the operator product formula for the special Macdonald function $P_{\lambda }\left(\mathrm{1,}t\mathrm{,}\cdots \mathrm{,}{t}^{n-1}\mathrm{<mo>\; ;\; </mo>}q\mathrm{,}t\right)$ . We also extend this formula to the case when n goes to infinity.

2. Preliminaries

2.1. Notations

• $\mathbb{Q}$ : the set of rational numbers;

• $\mathbb{Q}\left(q\mathrm{,}t\right)$ : the field of rational functions of q, t over $\mathbb{Q}$ ;

• The q infinite product: ${\left(x;q\right)}_{\infty }:={\displaystyle \prod _{n\ge 0}}\left(1-x{q}^n\right)$ .

2.2. Partitions

A partition is any (finite or infinite) sequence $\lambda =\left({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_r,\cdots \right)$ of non-negative in decreasing order: ${\lambda }_1\ge {\lambda }_2\ge \cdots \ge {\lambda }_r\ge \cdots$ and containing only finitely many non-zero terms. We denote by $\left|\lambda \right|$ the size of the partition, i.e. $\left|\lambda \right|={\displaystyle {\sum }_i}{\lambda }_i$ and by $l\left(\lambda \right)$ the number of non-zero ${\lambda }_i$ . The set of all partitions is denoted by $\mathcal{P}$ .

A pictorial representation of a partition λ is called 2D Young diagram , it can be obtained by placing ${\lambda }_i$ boxes at the i-th row. For example, Figure 1 represents a partition $\lambda =\left(5,4,4,1\right)$ .

The transpose of λ is denoted by ${\lambda }^t$ , ${\lambda }^t=\left({\lambda }_1^t,{\lambda }_2^t,\cdots \right)$ , here ${\lambda }_j^t=\text{Card}\left\{i\mathrm{<mo>\; |\; </mo>}{\lambda }_i\ge j\right\}$ . For example, the transpose of $\lambda =\left(5,4,4,1\right)$ is ${\lambda }^t=\left(4,3,3,3,1\right)$ .

We denote by $s=\left(i\mathrm{,}j\right)\in {\mathbb{Z}}^2$ for each square of a partitionλ, here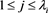. For each square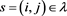, let

The numbers 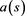and 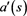may be called respectively the arm-length and the arm-colength of s, and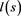, 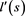the leg-length and the leg-colength.

2.3. Macdonald FunctionWe

define a scalar product

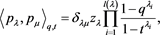(1)

here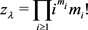, where 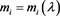is the number of parts of λ equal to i; 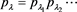for each partition 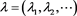and.

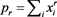Macdonald function 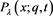depends rationally on two parameters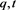, i.e.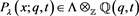, here 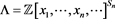and means tensor product over. They are characterized by the following two properties [6]:

1) is of the form:, where;

2), if.

When, reduce to the schur function.

In particular,

(2)

here and.

Let,

(3)

3. Operator Product Formula for.

3.1. Algebra

We introduce an algebra generated by bosons and, they satisfy the following relations:

Let be the vacuum state which satisfies the conditions and. For a partition, we use a short notation.

The bosonic Fock space is generated from the vacuum state:

The dual vacuum state is defined by the conditions and. The dual boson Fock space is generated by the dual vacuum state:

There is a paring denoted by between two spaces, defined by the following properties:

3.2. The Vertex Operators

To construct the vertex realization for, we propose two sets of vertex operators depending on q and t.

We define

(4)

(5)

Since

we can obtain

(6)

We define another set of vertex operators

(7)

(8)

Since

likewise we obtain

(9)

3.3. Operator Product Formula for

With the help of the vertex operator, we define vertex operators and as follows:

(10)

and

(11)

We propose operator product formula

(12)

After some careful computation via the commutative relation (6) and (9), the Formula (12) is equal to

Using the identity (we will prove it in the appendix)

(13)

we get the vacuum expectation value of this operator product formula

(14)

In other words,

(15)

Therefore we get the operator product formula for.

Similarly, by using the identity

(16)

we get

(17)

Hence we get the operator product formula for.

4. Conclusion

The operator product formula for a special Macdonald function when n is finite as well as when n goes to infinity are given in this paper. A further investigation is to find a possible relation with the refined topological vertex.

The Proof of Identity (13) and (16)

Firstly, we will proof the identity (13).

Suppose, the infinite product of the left side (13) can be separated into three parts, and.

For the first part

(18)

(19)

For the second part

(20)

(21)

For the third part, the numerator and denominator cancel out each other.

Next, we will simplify the left hand side of the (13).

Since, we can get

Before combing them all, we can check

(22)

(23)

In conclusion,

(24)

To show the identity (13), we need to use some properties of Young diagram λ, namely we need to interpret those powers of q in terms of arm lengths, leg lengths, arm co-lengths and leg co-lengths of those squares of Young diagram λ.

Now let us take i-th row as an example. We can classify all the arm lengths denoted as (where s means a specific square) of all squares of this row according to their leg lengths (denoted as). For example, for all squares s whose leg length, there must be squares counting from the end of row i. Likewise for leg length, there must be squares (See Figure 2). For, there must be squares etc. The leg length for i-th row must satisfy where r is the number of rows of λ. For there must be squares. For there must be squares.

For those squares which have leg length, their arm lengths are ranged from 0 to. For, those squares have arm lengths ranged from to. Similarly for, those squares have arm lengths ranged from to. Therefore the set on the i-th row with leg length becomes (where).

Similarly for leg co-length, these squares have arm co-lengths ranged from 0 to. For, these squares have arm co-lengths ranged from 0 to. At most.

Now from previous computation of and the analysis about the properties of Young diagram, we can deduce the identity (13).

Next we will prove the identity (16).

we notice that if n goes to infinity

So when n goes to infinity,

From previous analysis about the properties of Young diagram, we can deduce the identity (16).

Acknowledgements

This work is partially supported by National Natural Science Foundation of China (No. 11475116, 11401400, 11626084, 11647123).

Cite this paper

Wang, L.F., Wu, K. and Yang, J. (2018) Operator Product Formula for a Special Macdonald Function. Applied Mathematics, 9, 459-471. https://doi.org/10.4236/am.2018.94033

References