Applied Mathematics
Vol.07 No.16(2016), Article ID:71597,16 pages
10.4236/am.2016.716163

Vibrational Stabilization by Reshaping Arnold Tongues: A Numerical Approach

Joaquin Collado1, Hildeberto Jardón-Kojakhmetov2

1Automatic Control Department, CINVESTAV-IPN, Mexico City, Mexico

2Engineering and Technology Institute, University of Groningen, Groningen, The Netherlands

Copyright © 2016 by authors and Scientific Research Publishing Inc.

This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).

http://creativecommons.org/licenses/by/4.0/

Received: July 28, 2016; Accepted: October 25, 2016; Published: October 28, 2016

ABSTRACT

This paper presents two contributions to the stability analysis of periodic systems modeled by a Hill equation: The first is a new method for the computation of the Arnold Tongues associated to a given Hill equation which is based on the discretization of the latter. Using the proposed method, a vibrational stabilization is performed by a change in the periodic function which guarantees stability, given that the original equation has unbounded solutions. The results are illustrated by some examples.

Keywords:

Vibrational Stabilization, Hill Equation, Periodic Systems, Arnold Tongues

1. Introduction

The Hill equation is a second order differential equation of the form

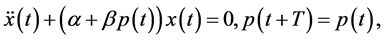(1)

where 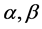are real numbers and T is the minimal period of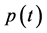. Without loss of generality, it is assumed through this document that the periodic function 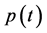is of zero average, i.e.

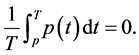(2)

Equation (1) can always be rewritten as a two dimensional first order Linear Periodic (LP) system

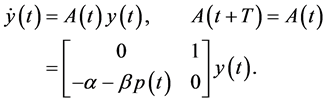(3)

As Lyapunov proved in [1] , the asymptotic stability of an LP system is equivalent to the asymptotic stability of a Linear Time Invariant (LTI) system under a periodic change of coordinates. Unfortunately, in order to obtain the LTI system, it is required to explicitly have the solution of the original LP system, and with some few exceptions, this is in general impossible.

1.1. Background

There exist plenty of references regarding the stability analysis of Hill equations (or more generally of periodic systems) as well as for the study of Arnold Tongues [2] - [6] . Some classical references are: [1] [7] - [9] , while more recently there are [10] - [13] , and some others. Less attention has been dedicated to the Arnold Tongues computation [10] , maybe because the most common method of study would be numerical integ- ration. There exist some other ways to obtain the stability/instability diagrams based on: infinite Hill determinants [14] , the computation of the discriminant [15] [16] , or per- turbation methods. In the method of infinite determinants, an infinite dimensional matrix has to be truncated at some dimension, and the number of Tongues to be computed is proportional to the dimension of such truncated matrix [16] . On the other hand, perturbation method, which expresses the solution and some parameters as (truncated) power series of, necessarily requires to be small; so the applicability of that method is limited. Then, it seems that there is a necessity of new and efficient techniques to compute Arnold Tongues. That is one of the motivations of this document.

1.2. Motivation

Stability analysis of periodic systems is a topic of high interest in e.g. engineering. In particular, due to the existence of parametric resonance [3] [11] [17] , it becomes crucial to be able to design controllers that can overcome such effects. Some examples of physical systems modeled by a Hill equation and the effects of parametric resonance can be found in [17] - [20] . Moreover, the understanding and control of parametric resonance for electric applications is currently receiving much attention [21] - [23] . Then, techniques to eliminate (or promote) parametric resonance have immediate impact in such applications. As shown below, Arnold Tongues are a graphical way to visualize the parameter set of a Hill equation prone to such effect. Thus, developing new and fast techniques to obtain Arnold Tongues and to modify them is very relevant for the above context, and in fact those are the contributions of this paper.

1.3. Contribution

In this paper, the first result shows a new method for computing Arnold Tongues which is valid for a wide range of values of parameters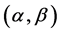. It also offers infor- mation on whether the given parameters correspond to a stable or unstable solution of (1). One advantage of the presented numerical method is that it is faster compared to numerical integration. Our second contribution is the design of a vibrational controller that stabilizes an operating point of a Hill equation. The basic idea of our second contribution is presented on “On Vibrational Control and Vibrational Stabilization” [24] . The main difference with [24] is that Meerkov considers LTI systems with negative trace and introduces a periodic variation of some parameters. In this paper, in contrast, we consider an unstable linear periodic systems with no restriction on the trace of the system matrix. So, in a way, we extend the results of [24] .

The organization of the paper is as follows. In section 2, some preliminaries as Floquet theory, the stability of linear periodic systems and some results of linear algebra are reviewed. Next, in section 3, (1) is transformed to a Linear Shift Invariant approxi- mation of it; then, the proposed numerical method to compute the Arnold Tongues is presented and a computational time comparison is provided. In section 4, the main result of this document is presented, namely, a novel scheme to stabilize a linear periodic system is provided and afterwards, the result is illustrated with an example. Finally, in section 5 some concluding remarks as well as some discussion are provided.

The following notation is used through the paper: represents the natural numbers, given a square matrix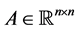, its determinant is denoted as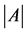, the set of its eigenvalues counting multiplicities is denoted as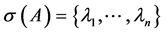. The polyno- mials 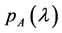and 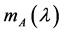represent the characteristic and minimal polynomial of 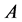respectively.

2. Preliminaries

This section reviews the Floquet Theorem, which provides a factorization of the state transition matrix of a Linear Periodic System, this factorization allows to determine the stability of the LP system (3) from the algebraic localization of the eigenvalues of the Monodromy Matrix. Also, a result concerning the determinant of some special sum of matrices is given.

Consider (3), its solution is given by

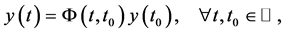(4)

where 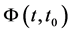is the state transition matrix and is given by the solution of [7] [14] [25]

(5)

The periodicity of the system leads to the periodicity of the state transition matrix

(6)

The transition matrix over one period is defined as the Monodromy matrix M

(7)

Remark 2.1. is independent on [26] [27] .

One of the basic tools used for the stability analysis of periodic systems is based on Floquet theory.

Theorem 2.1 (Floquet [27] ). Consider the homogeneous system given by (3), then there exists a periodic invertible matrix and a constant matrix such that the state transition matrix of the system can be written as

(8)

where.

Evaluating (8) over one period T leads to

(9)

That is, the Monodromy matrix M is similar to. Assume, then, where and, then

(10)

In (10), the factor and are bounded, therefore will be bounded if and only if is bounded; i.e., boundedness of the solution of (3) depends only on the eigenvalues of the Monodromy Matrix which from (9) are the same as the eigenvalues of, there the importance of the calculation of M.

Theorem 2.2 (Lyapunov [17] ). The periodic system (3) is:

1) Exponentially stable if.

2) Stable if and if such that then is a simple root of.

3) Unstable if such that, or if and such that and it is a multiple root of

The following results are useful in the analysis of the rest of the paper. Let represent the identity matrix of dimension.

1In (*) we have used the fact:, and in (**) we have used: if, then.

Theorem 2.3. Let R denote an matrix, S an matrix, T an matrix, and U an matrix. If R and T are non singular then

(11)

Proof.1

(12)

Lemma 2.1 ( [28] ) For all, and for all:

(13)

The previous Lemma states that, and therefore,.

Corollary 2.1. Consider a set of matrices:, where, all matrices of dimensions, then

(14)

The same conclusion of Lemma 2.1 applies, i.e.

(15)

3. From a Linear Periodic System to a Discrete Shift Invariant System

Consider a system given by (1). There are, in principle, two ways to determine its stability. One using numerical integration of the solution and the other is to approximate (1) by a discrete time system and solve it. Then, the solution of the latter is an approximation of. In this paper the last method is used. The advantage of such approach is that it is always possible to find an analytical solution of the approximated discrete problem.

Lemma 3.1 ( [29] ). Any p-norm of the approximation error, under finite difference methods, of functions defined on a finite interval is bounded.

Remark 3.1. Observe that knowing the solution of (3) in the interval allows to know the solution everywhere.

Performing a discretization based on the centered finite-difference method [30] to (1), the following approximation is obtained

(16)

where, and with, is the sampling period.

Remark 3.2.

・ Centered finite-difference has an error of approximation of of order.

・ In the sampling process, the continuous-time period T has to be divided in an integer number of samples per period, K; i.e., , with K a positive integer. This restriction guarantees that the obtained discrete-time system is K-periodic. If this constrain is not satisfied, the resulting discrete-time system is quasi-periodic and the Floquet Theory is not longer valid [31] .

As decreases, (16) approximates better to the behavior of the original Equation (1). In state space (16) is rewritten as

(17)

In (17) is K-periodic. During one period K, the index k takes the values, so it follows that

(18)

but in the next period

(19)

and so on. Then, using the Lifting Technique [26] the next Shift Invariant system is obtained.

(20)

where

(21)

Remark 3.3. Roughly speaking, the Lifting Technique augments the dimension of the state K times. Then the augmented system evaluated every K samples turns to be shift-invariant.

In (20), so the dimension of the Shift Invariant System increases as the sampling period decreases. Equation (20) is equivalent to (17), so as decreases, the solution of (20) gives a better approximation of the solution of (1), but it is important to notice that the stability problem of (20) can be solved analytically. The stability analysis of (17) is now simpler: is a block diagonal Matrix and because of Corollary 2.1 each block of has the same eigenvalues. Moreover, the last block of results to be the Discrete Monodromy Matrix associated to (17), then the stability of the Shift Invariant System (20) is reduced to the analysis of any of the diagonal blocks of. The first contribution of this paper is then stated as follows.

Theorem 3.1. Consider an homogeneous periodic differential equation

(22)

where and T is the minimum period, and its sampled approximation

(23)

where with K an integer. Then

1) (23) can always be solved analytically via Lifting Technique, which leads to a Shift Invariant System

(24)

2) The stability of (23)2 is given by the eigenvalues of any of the blocks of the constant matrix .

2Recall that the shift invariant system is

(a) Exponentially stable if.

(b) Stable if and if such that then is a simple root of.

(c) Unstable if such that, or if and it is a multiple root of.

Remark 3.4. The solution of the Shift Invariant System (23) and its stability analysis under small sampling periods, are approximately equivalent to their counterparts in the continuous time system (22).

Example 3.1. As an example let the periodic function in (22) by given by. In Figure 1 the Arnold Tongues computed with the method proposed in this document are shown. The gray zones represent unstable solutions of (22) while white zones represent stable solutions. Only this graph is presented since its difference to the one obtained via numerical integration is indistinguishable.

Notation: The first instability region is labeled as 0, and the following accordingly

with natural numbers, the Arnold Tongues starts at and we refer to the k-th

Arnold Tongue [7] .

The same stability diagrams were also computed using numerical integration, both algorithms on a computer with a Intel Core 2 Duo processor at 2.6 GHz and 1 Gb of RAM, having in both cases 360 samples per period, and the same increment for the parameters and, the computational time comparison is shown in Table 1.

Table 1 shows that the computational time of the proposed method is much lower (approximately 20 times faster) than the time needed for computing the same chart using numerical integration.

Figure 1. Arnold Tongues computed using the method proposed in this document. Observe in Table 1 that the computation based on the lifting technique is considerably faster than the classical numerical integration method.

Table 1. Time comparison of computation methods of the stability diagram of Figure 1. The parameters are and.

4. Vibrational Stabilization

3, where we denote by n the number of the Arnold Tongue to which the pair belongs.

In this section the second contribution of this paper is presented. Suppose that the pair is fixed, where, such that

(25)

has unbounded solutions. Let us introduce a vibrational control scheme which consists on modifying by, where is -periodic3, i.e.,

. This results in the forced system

(26)

The goal is to design a controller such that the system

(27)

is stable for. The following result shows how to design and.

Theorem 4.1. Consider two linear periodic systems, of the same dimensions, and of the same structure

(28)

where

(29)

and

(30)

where

(31)

Denote by and the corresponding monodromy matrices and suppose that both systems are unstable, i.e., and, under the ad- ditional condition that. Then there exists a constant such that for the system:

(32)

where

(33)

Note that, and therefore (32) it is stable.

Remark 4.1. If belongs to the n-th Arnold Tongue for (28) and belongs to the Arnold Tongue for (30), then the condition holds.

Proof. The proof is performed in discrete time. The Monodromy Matrix associated to (32) is:

Then, define

which is a polynomial and therefore a continuous function of. It follows that

(34)

Therefore, from the hypothesis and from the con- tinuity of, we have that there exists a constant for which.

Remark 4.2.

・ Theorem 4.1 does not only guarantees the existence of a stabilizing constant, but provided with Theorem 3.1, it is possible to explicitly compute such constant.

・ In the proof it is possible to choose and the same stability result holds. By choosing a stable point more or less at the middle of the corresponding stable interval is obtained.

Figure 2 shows schematically how the vibrational stabilization method performs.

Theorem 4.1 might be also written for Hill systems as follows.

Corollary 4.1. Assume that the pair, where, is given such that the solution of the system

(35)

is unstable. Then there exists a constant and a -periodic function

such that for the same pair, the system

4. (36)

has a stable solution.

Proof. Recall that denotes the number of the Arnold Tongue to which the pair belongs for the stability chart of (35). From what has been mentioned in this paper, if for it happens that, the effect is that the right contiguous Tongue is going to be modified [5] .

Remark 4.3. Let the Fourier series of be written as. Then the boundaries of the k-th Arnold Tongue are tangent at and if and

only if, and are transversal if and only if [5] . Such results means that we can design a controller that modifies a specific Tongue.

It only rests to find. Let

(37)

Figure 2. A 3 dimensional view of the vibrational stabilization method. The control scheme introduced changes the shape of the stability chart in such a way that for some, the pair belongs to a stable zone.

therefore (36) is rewritten as

(38)

It is clear that (38) is in the same format given in Theorem 4.1. Then, it is guaranteed the existence of such that the solution of (36) is stable.

Example

Consider the system (Kapitza Pendulum [32] [33] ) shown in Figure 3 (this is the prototype example used to witness the effects of parametric resonance, see e.g. [13] or

[34] ), where: and, then, the Hill equation

which models the system is

(39)

Or after linearization around the lower equilibrium point

(40)

Note: Even though this paper developed the stabilization method for linear systems, we will show that it also works for the nonlinear system.

The operation point, i.e., the point produces an unstable response as can be seen in Figure 4.

The solution of (39) is shown in Figure 5 and the solution of its linearisation, given by (40), is shown in Figure 6. Note the beating phenomenon on the non-linear solution.

The results of this paper show the existence of a constant gain and a periodic function such that the new system given by

Figure 3. Kapitza pendulum.

Figure 4. Arnold Tongues for the example. The operating point is located at .

Figure 5. Solution of the non-linear model.

(41)

has a stable solution. In this example, the resulting equation turns to be

(42)

The corresponding stability diagram of (42) is shown in Figure 7.

The response of (42) is depicted in Figure 8. The same stabilization scheme might be applied to the non-linear equation, this means

The corresponding response is shown in the Figure 9. Note that for small am-

Figure 6. Solution of the linear model.

Figure 7. Modified Arnold Tongues by the vibrational controller.

Figure 8. Stable solution of the linear model under the action of the vibrational control.

plitudes, the linear model resembles very good to the non-linear one. Also, note that in general, the stable solutions of a Linear Periodic System are not periodic, but almost- periodic [31] .

Figure 9. Stable solution of the non-linear model under the action of the vibrational control.

5. Conclusions

This paper presents an alternate and new method to compute the Arnold Tongues of a Hill equation, which is much faster than the traditional numerical integration method. Since the proposed algorithm calculates an approximation of the Monodromy matrix, it is possible to know, with some small errors due to the approximation, whether a given pair is a stable or an unstable operation point.

Moreover, a vibrational stabilization scheme for a given (unstable) Linear Periodic System is given. The approach presented is based on the capability of modifying the shape of the Arnold Tongues. Although the method proposed here was based on re- shaping the contiguous Tongue from which the pair belongs to, com- putationally speaking we may modify any Tongue as long as it is different from the Tongue to which the pair belongs originally. The proof follows the same lines developed in this paper.

Acknowledgements

H.J.K. thanks CONACyT and CINVESTAV-IPN for their support during his M.Sc. studies, while this document was written.

Cite this paper

Collado, J. and Jardón-Kojakhmetov, H. (2016) Vibrational Stabilization by Reshaping Arnold Tongues: A Numerical Approach. Applied Mathematics, 7, 2005-2020. http://dx.doi.org/10.4236/am.2016.716163

References

  1. 1. Lyapunov, A. (1992) General Problem of the Stability of Motion (Original in Russian (1892)). English Translation, Taylor and Francis, London.

  2. 2. Grigo’ev, A.I. and Golovanov, A. (1999) Deformations and Overlap of Instability Zones in the Mathieu-Hill Equation. Technical Physics Letters, 25, 806-808.
    http://dx.doi.org/10.1134/1.1262642

  3. 3. Broer, H. and Simó, C. (2000) Resonance Tongues in Hill’s Equations: A Geometric Approach. Journal of Differential Equations, 166, 290-327.
    http://dx.doi.org/10.1006/jdeq.2000.3804

  4. 4. Gel’fand, I.M. and Lidskii, V.B. (1958) On the Structure of the Regions of Stability of Linear Canonical Systems of Differential Equations with Periodic Coefficients. Uspekhi Matematicheskikh Nauk, 10, 3-40 (English Translation: AMS Translations, Series 2, 2, 143-181).

  5. 5. Arnold, V.I. (1983) Remarks on the Perturbation Theory for Problems of Mathieu Type. Russian Mathematical Surveys, 38, 215-233.
    http://dx.doi.org/10.1070/RM1983v038n04ABEH004210

  6. 6. Broer, H. and Levi, M. (1995) Geometrical Aspects of Stability Theory of Hill’s Equations. Archive for Rational Mechanics and Analysis, 131, 225-240.
    http://dx.doi.org/10.1007/BF00382887

  7. 7. Yakubovich, V. and Starzhinskii, V.M. (1975) On Linear Differential Equations with Periodic Coefficients. Vol. 17. 2 Vols., Wiley, London.

  8. 8. Starzhinskii, V.M. (1955) A Survey of Works on the Conditions of Stability of the Trivial Solution of a System of Linear Differential Equations with Periodic Coefficients. American Mathematical Society Translations, 1, 189-237.

  9. 9. Starzhinskii, V.M. (1963) On the Stability of Periodic Motions I and II. Buletinul Institutului Politehnic din Iasi, Serie Noua, 5, 51-100 (Buletinul Institutului Politehnic din Iasi, Serie Noua, 4, 9-68, 1958).

  10. 10. Schilder, F. and Peckham, B.B. (2007) Computing Arnold Tongue Scenarios. Journal of Computational Physics, 220, 932-951.
    http://dx.doi.org/10.1016/j.jcp.2006.05.041

  11. 11. Broer, H. (2008) Tongues in Parametric Resonance. ENOC, Saint Petersburg.

  12. 12. Mailybaev, A.A. and Seyranian, A.P. (2009) Stabilization of Statically Unstable Systems by Parametric Excitation. Journal of Sound and Vibration, 323, 1016-1031.
    http://dx.doi.org/10.1016/j.jsv.2009.01.042

  13. 13. Seyranian, A.P. (2008) Parametric Resonance in Mechanics: Classical Problems and New Results. Journal of Sound and Vibration, 2, 664-683.

  14. 14. Jordan, D. and Smith, P. (2004) Nonlinear Ordinary Differential Equations: An Introduction for Scientists and Engineers. 4th Edition, Oxford University Press, USA.

  15. 15. Magnus, W. and Winkler, S. (1966) Hill’s Equation. Interscience Publishers, New York.

  16. 16. Magnus, W. (1959) The Discriminant of Hill’s Equation. Research Report No.BR-28, New York University, New York.

  17. 17. Seyranian, A.P. and Mailybaev, A.A. (2004) Multiparameter Stability Theory with Mechanical Applications. World Scientific Publishing, Singapore.

  18. 18. Seyranian, A. (2004) The Swing: Parametric Resonance. Journal of Applied Mathematics and Mechanics, 68, 757-764.
    http://dx.doi.org/10.1016/j.jappmathmech.2004.09.011

  19. 19. Vázquez, C., Collado, J. and Fridman, L. (2013) Control of a Parametrically Excited Crane: A Vector Lyapunov Approach. IEEE Transactions on Control Systems Technology, 21, 2332-2340.

  20. 20. Vázquez, C., Collado, J. and Fridman, L. (2014) Super Twisting Control of a Parametrically Excited Overhead Crane. Journal of the Franklin Institute, 351, 2283-2298.

  21. 21. Jia, Y. and Seshia, A.A. (2014) An Auto-Parametrically Excited Vibration Energy Harvester. Sensors and Actuators A: Physical, 220, 69-75.
    http://dx.doi.org/10.1016/j.sna.2014.09.012

  22. 22. Jia, Y., Yan, J., Soga, K. and Seshia, A.A. (2014) Parametric Resonance for Vibration Energy Harvesting with Design Techniques to Passively Reduce the Initiation Threshold Amplitude. Smart Materials and Structures, 23, Article ID: 065011.
    http://dx.doi.org/10.1088/0964-1726/23/6/065011

  23. 23. Scapolan, M., Tehrani, M.G. and Bonisoli, E. (2016) Energy Harvesting Using Parametric Resonant System Due to Time-Varying Damping. Mechanical Systems and Signal Processing, 79, 149-165.
    http://dx.doi.org/10.1016/j.ymssp.2016.02.037

  24. 24. Meerkov, S.M. (1980) Principle of Vibrational Control: Theory and Applications. IEEE Transactions on Automatic Control, 25, 755-762.
    http://dx.doi.org/10.1109/TAC.1980.1102426

  25. 25. Nayfeh, A. and Mook, D. (1995) Nonlinear Oscillations. John Wiley and Sons, Hoboken.
    http://dx.doi.org/10.1002/9783527617586

  26. 26. Bittanti, S. and Colaneri, P. (2009) Periodic Systems, Filtering and Control. John Wiley and Sons, Hoboken.

  27. 27. Brockett, R. (1970) Finite Dimensional Linear Systems. John Wiley and Sons, Hoboken.

  28. 28. Chen, T. (1998) Linear System Theory and Design. 3rd Edition, Oxford University Press, Oxford.

  29. 29. LeVeque, R.J. (2007) Finite Difference Methods for Ordinary and Partial Differential Equations. SIAM.
    http://dx.doi.org/10.1137/1.9780898717839

  30. 30. Golub, G. and Ortega, J. (1992) Scientic Computing and Differential Equations, an Introduction to Numerical Methods. Academic Press, Pittsburgh.

  31. 31. Corduneanu, C. (2009) Almost Periodic Oscillations and Waves. Springer, Berlin.
    http://dx.doi.org/10.1007/978-0-387-09819-7

  32. 32. Kapitza, P.L. (1965) Dynamical stability of a Pendulum When Its Point of Suspension Vibrates. Pergamon Press, Oxford, Vol. 2, 714-725.

  33. 33. Kapitza, P.L. (1965) Pendulum with a Vibrating Suspension. Pergamon Press, Oxford, Vol. 2, 726-737.

  34. 34. Seyranian, A.P., Yabuno, H. and Tsumoto, K. (2005) Instability and Periodic Motion of a Physical Pendulum with Vibrating Suspension Point (Theoretical and Experimental Approach). Doklady Physics, 50, 467-472.
    http://dx.doi.org/10.1134/1.2074117

NOTES

4Here, although the function q(mt) is not of period T (since m Î N) p(t) + q(mt) is of period T.

Journal Menu>>