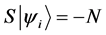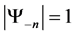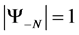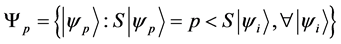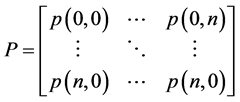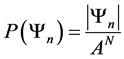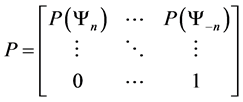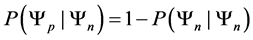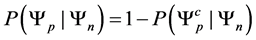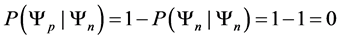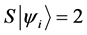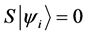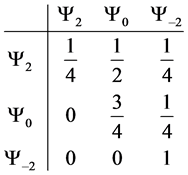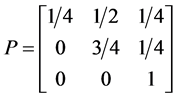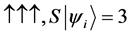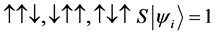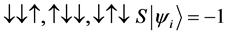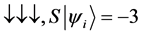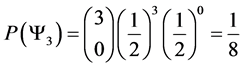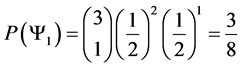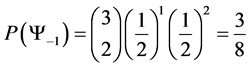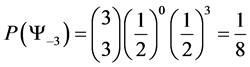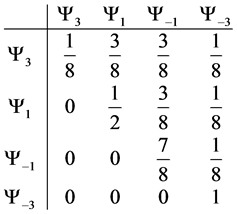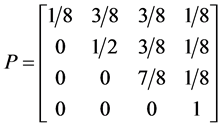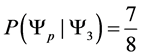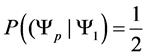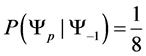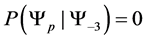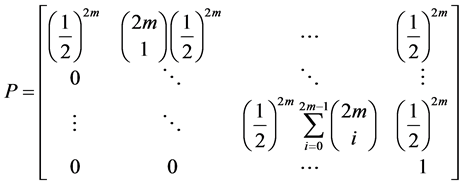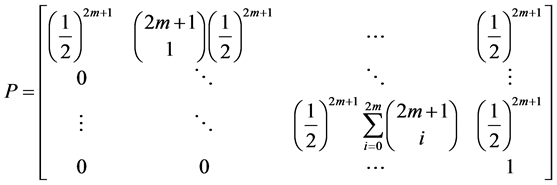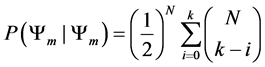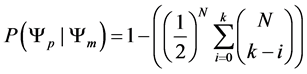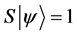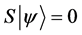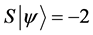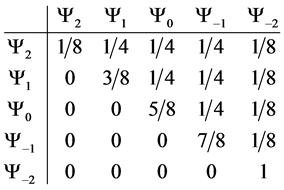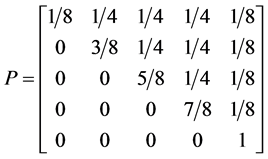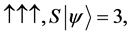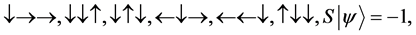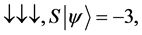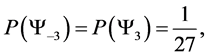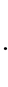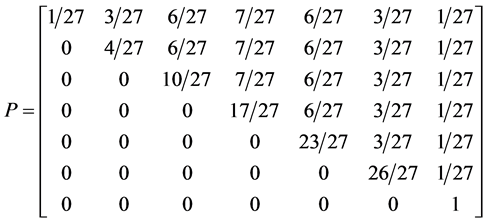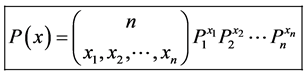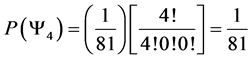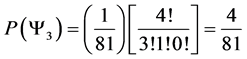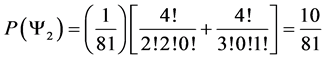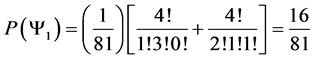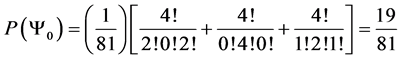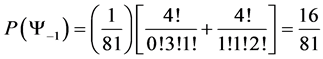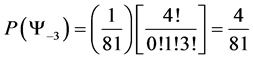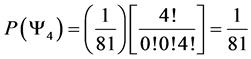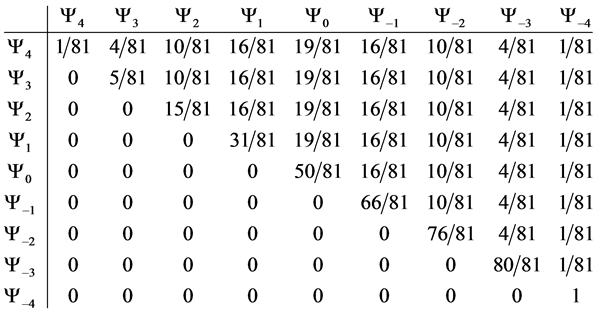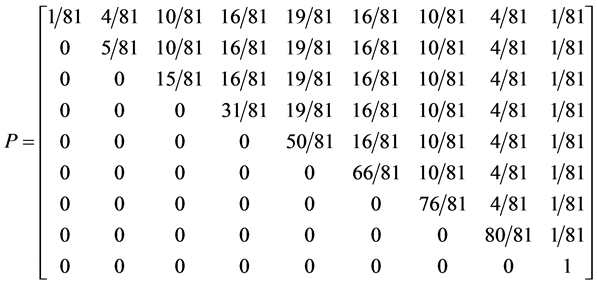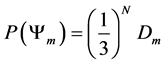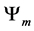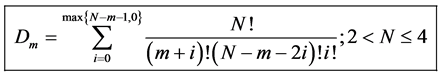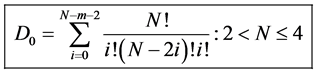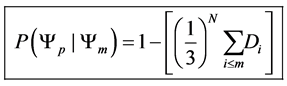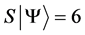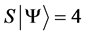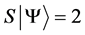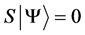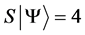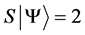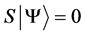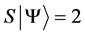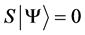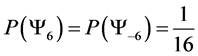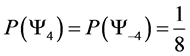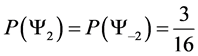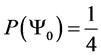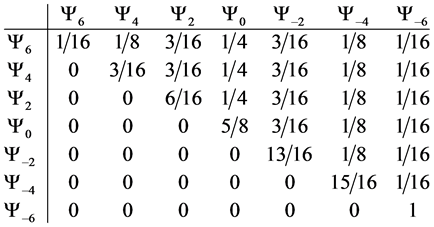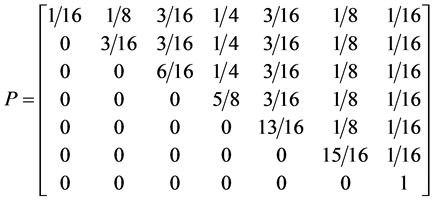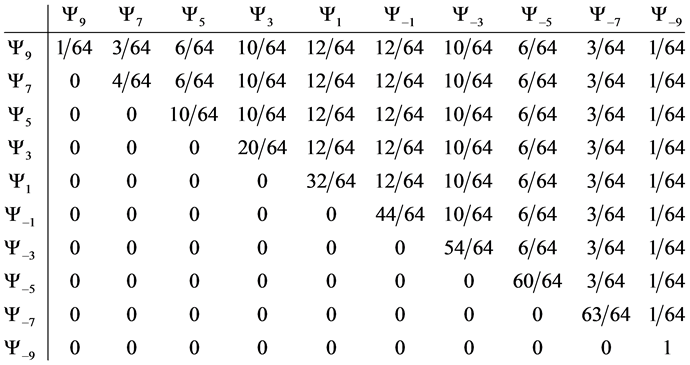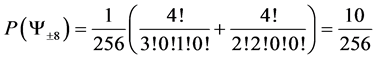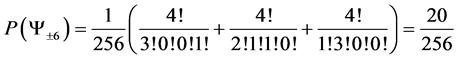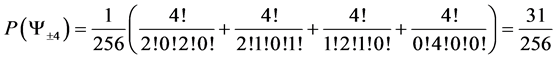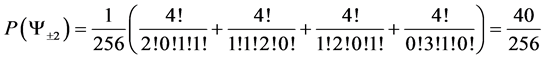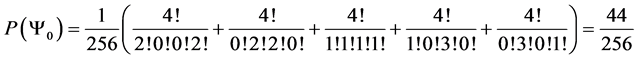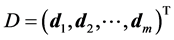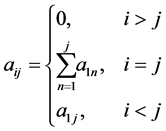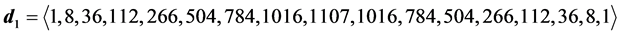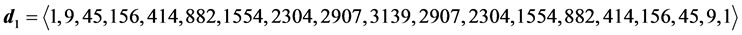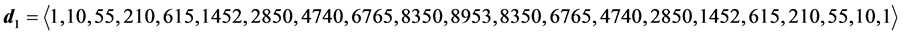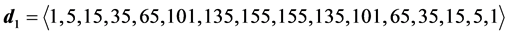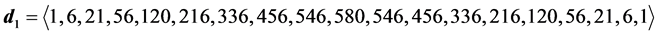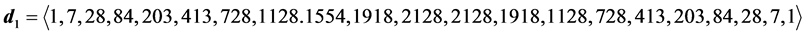Received 7 March 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

In this paper, an algorithm to produce a transition matrix between all states in ideal anti-para- magetic system under the simulated annealing condition that only moves to lower energy states are accepted. The check the accuracy of the transition matrix is confirmed by computer simulation, showing close agreement between model and simulation results.

Keywords:

Markov Chain Monte Carlo, Simulated Annealing, Spin 1/2 Particles

1. Introduction

In this paper we compute all transition probabilities of a system of N isolated particles of spin M to move to any lower energy state. In each move, the current state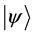, is compared with a random trial state,. The move is accepted if it the trial state has a lower energy, and rejected if the energy is equal, or higher. No restrictions are placed upon the trial state: it is totally random, thus the states form a Markov chain [1] which the next state chosen at random, via the Monte Carlo method [2] . This is a kind of simulated annealing [3] , but with a simulation temperature of zero [4] , which continues to be relevant within the context of recent work [5] . The system will approach its idealized energy state, with net magnetic moment , where is the magnetic moment of one particle, with energy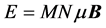, with entropy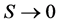. For the context of this paper, we will consider the system to be an diamagnet, with the external magnetic field pointing up, the ground state (lowest energy) for the system will be when all spins point down.The least preferred state will be the state that has all spins up. Results are essentially the same for paramagnetic systems, but with the transition matrix is the flipped.

This is an unusual use of simulated annealing. Normally, simulated annealing is used to find a solution to a complex problem, such as the optimal path in the traveling salesman problem. In complex magnetic systems, such as spin glasses, simulated annealing is used to find the optimal ground state [6] . By contrast, in this paper, the system is rather simple and the optimal state is known. Thus we can compute the probability to move from any state to any other state which should lend insight into how this very powerful tool (simulated annealing) operates. We can pause the simulation at any point, and since we know the optimal state, measure how far the system is from optimal, The number of moves to find the best state increases rapidly with the complexity of the system. In the magnetic systems we study in this paper, this complexity can be increased by increasing the number of spins in the system, or by increasing the spin of each particle. Either way greatly increases the number of states for the system to explore.

1.1. Plan of the Paper

Beginning with two, three and four spin one half particle states, the transition probabilities between all states are enumerated. These lists of probabilities are formed into matrices. This is repeated for spin one particles in section 2 where the transition probabilities are derived from the degeneracy of the states. These degeneracies employ the generalized binomial coefficients, called the multinomials. In Section 3, the spin 3/2 particles are considered. Then, in Section 4, the entries in the transition matrices are derived from the degeneracy of the states, using a simple summation rule. In Section 5, degeneracy vectors are given for various systems. In Section 6, the results of numerical simulations are provided which confirm the results of the matrix calculations.

1.2. Assumptions of Model

Our underlying assumptions are:

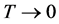・ , thus eliminating the effects of entropy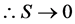

・ states gravitate towards more preferred states of lower magnetism number due to our model being an anti-paramagnet

・ Particles in are indistinguishable.

In any system N-particles with spin we will assign values. Those values will be relative to the system we are working with. We will assign +1 for spin up, and values −1 for spin down in a spin one half system. +1, 0, −1 for a spin one system, and, for a spin 3/2 system. The magnetism number will be achieved by virtue of the magnetism operator S.

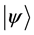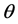Definition 1.1. For any state in a N-particle system we define S to be the operator such that where is the total spin up, Total spin down.

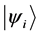
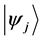
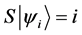
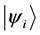
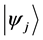
Definition 1.2. For any two states, with, we say is preferred to iff.

Definition 1.3. For any N-particle system. 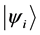will be the idealized ground state iff

Definition 1.4. let 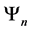be defined as the set

Definition 1.5. The cardinality of the set, denoted is the total number of states with magnetism number n.

This leads us to the following proposition.

Proposition 1.6. There can only be one idealized Ground state;

that is

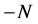
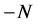
Poof. The only way to get magnetism number for an N-particle system, is to have all the particles in that system be spin down. Since particles are indistinguishable by assumption 3, there is only one state that gives magnetism number, thus

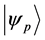
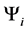
Definition 1.7. let denote a preferred state to then

is the set of all states that are preferred to a state with magnetism number

1.3. Markov Chains

Definition 1.8. A system with a finite or countably infinite number of states with the property that given a present state, past states have no influence on the future is known as a Markov chain

Definition 1.9. Markov chains have the property that for a random variable,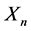

where 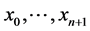are in the state space .This property is known as the Markov property.

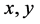
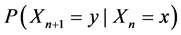
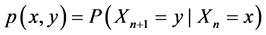
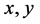
Definition 1.10. Let be in the state space. The conditional probabilities are known as transition probabilities of the the Markov chain. The function for any in the sample space is known as the transition function.

From the transition function 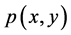we construct a square matrix of the form

P is known as the transition matrix for the Markov chain. We will now apply the concepts of a Markov chain directly to our model.

2. Markov Chains and Our Model

We will use Markov chains to model the transition states for spin 1/2, spin 1, or spin 3/2 particles. For our model of N-spin particles the state space will be composed of all with different magnetism numbers.

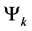
We begin by defining the probability function for our model.

Definition 2.1. Let be the probability of being on a state such that. This probability function is defined as

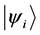
where N is total number of particles in the system,

and 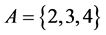for spin 1/2, spin 1, spin 3/2 particles respectively.

Since our Markov chain has the property of only transferring to preferred states, our transition probabilities are defined by the following transition function.

This transition function shows how transition probabilities are absorbed when we move to a preferred state from a less desired state. This probability absorption allows us to construct upper triangular square transition matrices of the following form.

Our understanding of the transition function and the transition matrix of our model leads to the following 2 propositions .

Proposition 2.2.

Poof. Staring with, we can quickly see that

Now will be the probability of all of the states that are not preferred to. Thus

Giving us the desired result.

Proposition 2.3. For the idealized ground state

Poof. By proposition 4.2

We will now look at Markov chains and the spin 1/2 particle.

3. Spin 1/2 Particles

3.1. Two Spin One Half Particles

For a two spin one half particles, the only possibilities of spin configuration of the fermions look like this

・ ,

・ ,;

・ ,

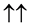
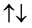
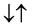
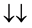
Thus make up the state space of the two fermion system with our underlying 3 assumptions.

Giving us the following probability transition table

With transition matrix

For example we would read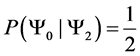, and; it is our assumption 2 that makes all of

our probability matrices upper triangular. Which for our model denotes that system is probabilistically approaching the idealized ground state. Since read then is an absorbing state, physically it shows that it is the idealized ground state.

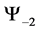
3.2. Three Spin One Half Particles

For a system of three spin one half particles, the only possibilities of spin configuration of the fermions look like this

・

・

・

・

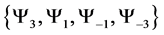
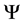
Thus make up the state space of the three fermion system with our underlying 3 assumptions.

Although we can clearly see what the probability of landing in each state is, we can use basic counting arguments to show our results mathematically. Thus

・

・

・

・

Giving us the following probability transition table

With transition marix

Example 3.1. Given the transition matrix for the three spin one half particle system, above, we can calculate the probablity of moving to a preferred state.

・

・

・

・

With our understanding of the three spin one half particle case and counting arguments, we can develop a generalization for any N spin one half particle system.

3.3. N-Spin One Half Particle System

Now given our understanding of the probabilities we can build the probability transition matrix for any N-fer- mion system. If with our transition matrix looks like this

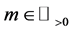
And with s.t we get the probability transition matrix

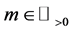
Leading us to the following definition.

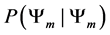
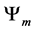
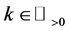
Definition 3.2. For any N-fermion system we can calculate where is not the idealized ground state. Let be the number of spin up or spin down particles for magnetism number m. Then

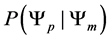
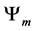
Definition 3.3. For any N-fermion system we can calculate where is not the idealized ground state.

With these result we can calculate the probability of our system moving to a better state, given any N-fer- mions and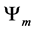. We now turn our attention to systems of spin one particles.

4. Spin One Particles

For the spin one particles we will assign for respectively. The assumptions to the model will not change. The goal is examine N-spin one systems, and to see how their transition matrices look.

4.1. System of Two Spin One Particles

A system with two spin one particles has the following states:

・ , ,

・ ,

・ , ,

・ ,

・ , ,

・ ,

・ , ,

・ ,

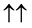
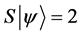
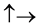
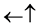
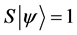
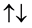
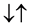
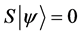
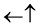
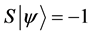
Thus for a system of two spin one particles, the state space has possible states.,., , which give us the following transition table

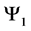
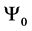
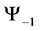
With the following transition matrix

4.2. System of Three Spin One Particles

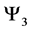
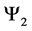
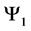
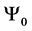
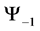
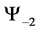
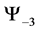
For a system of three spin one particles the possible states are given by the macro-states,.,., ,. Whose micro-state configuration looks like this.

・

・

・

・

・

・

・

Thus in terms of probabilities:

These probabilities give us the following transition table.

With the following transition matrix.

Notice that listing out all appropriate micro states gets a bit cumbersome, but unlike the spin 1/2 particles, the spin one particles have 3 possible spins. So to calculate their probabilities with the aid multinomial probability formula.

Now with this formula we are able to calculate the probability of the macro states for a 4 spin one particle system.

4.3. 4 Spin One Particle System

For a spin one system with 4 particles we find macro states such that. We do this by calculating their degenerate states via the multinomial formula. Giving us the following results:

・

・

・

・

・

・

・

・

・

Giving us the following Transition table

Along with the following transition matrix

We now generalize our results with the following formulas

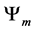
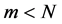
Definition 4.1. For any N-spin one particle system and a given macro state s.t. the following hold.

where 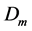is the degeneracies for

If n-even m-even, or n-odd m-odd

If N-even m-odd, or N-odd m-even

And for the zero case we get the following.

Definition 4.2. Let 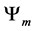be a macro state, for any N spin one particle system, then the probability of moving to a preferred state is

Now with this result we can calculate the probability of our system moving to a preferred state, given N-spin one particles and.

We now turn our attention to a system of spin 3/2 particles.

5. Spin 3/2 Particles

Now we turn our attention to spin 3/2 particles. We will de-note all the possible states a particle can take with

the set.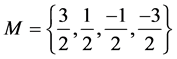

To give the spin 3/2 particles integer coefficients we simply represent them in the set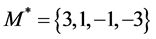. Once again we will hold the assumptions as the spin 1/2, and spin 1 cases to find the Probability transition matrix between macro states.

5.1. Two Spin 3/2 Particle System

A two spin 3/2 particle system has the following states

・ +3, +3

・ +3, +1

・ +3, −1

・ +3, −3

・ +1, +3

・ +1, +1

・ +1, −1

・ +1, −3

・ −1, +3

・ −1, +1

・ −1, −1

・ −1, −3

・ −3, +3

・ −3, +1

・ −3, −1

・ −3, −3

The two particle system gives us the following states with the pro- babilities ;

・

・

・

・

Giving us the following probability transition table

With the following transition matrix

5.2. Three Spin 3/2 Particle System

For a system of three spin 3/2 particles we calculate the state space in the same manner as we did in the two spin 3/2 particle system. Giving us the following state space

With the following probabilities:

This results in the following transition table

With the following transition matrix

5.3. Four Spin 3/2 Particle System

With the aid of the multinomial formula we are able to calculate the probabilities of the state space

・

・

・

・

・

・

・

Which gives us the following degeneracy transition table, with 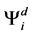being the degeneracies for state

And the transition matrix

With D being the following matrix

With D being the degeneracy matrix. Notice that we can construct any transition probability matrix from just understanding degeneracy matrix D. Thus given our systems it suffices to understand degeneracies in order to construct their transition probabilities.

6. Degeneracy Matrix Algorithm

As we saw in the previous section we can find all the transition probabilities from any j spin-N particle system under assumptions:

・ , thus eliminating the effects of entropy

・ states gravitate towards more preferred states of lower magnetism number due to our model being an anti-paramagnet

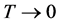
・ Particles in 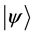are indistinguishable.

With Probability transition matrix P

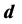
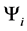
To construct D let be the degeneracy vector, composed from all the degeneracies form all the states

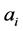
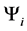
With = number of degeneracies from state and

We will now use the degeneracy vector to construct the degeneracy matrix.

6.1. Algorithm for Constructing D

For simplicity we will construct D from our degeneracy vector which we will denote 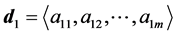s.t

Thus it follows that

thus we can rewrite with

Using as the base for constructing D. We can construct the entire degeneracy matrix D from our degeneracy vector Now with this generalized algorithm we can construct any degeneracy matrix D, which allows us to construct any probability transition matrix P.

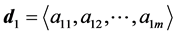
6.2. Degeneracy Vector (d₁) for Spin One Particles for n = 5, 6, 7, 8, 9, 10

From the preceding section, we see that we can construct the probability transition matrix of a system solely by means of the degeneracy vector. Now here are the degeneracy vectors for n = 5, 6, 7, 8, 9, 10.

・ for n = 5

・ for n = 6

・ for n = 7

・ for n = 8

・ for n = 9

・ for n = 10

6.3. Degeneracy Vector (d₁) for Spin 3/2 Particles for n = 5, 6, 7, 8

・ for n = 5

・ for n = 6

・ for n = 7

・ for n = 8

7. Results from Numerical Simulations

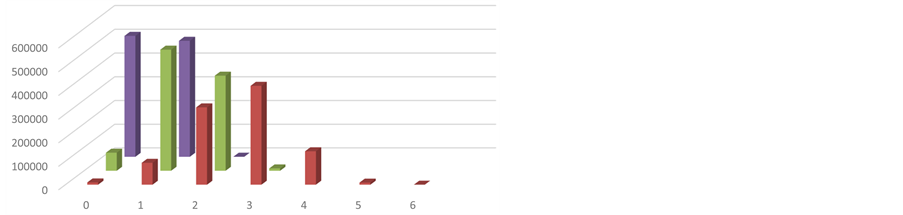
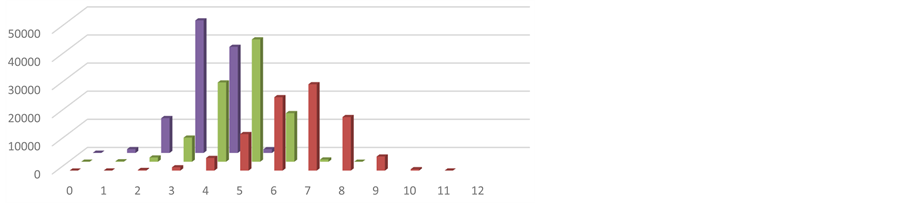
Two systems are studied: a small system with 10 spin 1/2 particles giving 1024 possible states, and a larger system with 20 spin 1/2 particles, with about a million possible states. The system begins in the least optimal state, all spins pointing up, and at each move, a random trial state is generated. If the trial state is more optimal, meaning it has fewer spins pointing up, it is accepted. It is highly probable the first move will be accepted. After many moves, the likelihood of improvement diminishes. We consider three “times” to illustrate the relative movement slowing at large time: after 9, 81 and 729 moves, so the moves are evenly spaced in log time. The simulation is run one million times for the small system, and one hundred thousand times for the large system. The results are displayed in Figure 1 and Figure 2, and are consistent with the calculation of predicted number at each, as shown in Table 1 and Table 2, below.

8. Conclusion

For ideal anti-paramagnetic systems, an algorithm for generating a transition matrix is given, with the constraint that the simulated annealing rule is followed; that only transitions to lower energy are allowed. This matrix is confirmed by direct simulated annealing simulations.

Acknowledgements

We thank the Editor and the referee for their comments.

Cite this paper

Ricardo Suarez,Gregory G. Wood, (2016) Energy-States of Particles with Representational Spin. Applied Mathematics,07,650-664. doi: 10.4236/am.2016.77060

References