Received 30 December 2015; accepted 26 February 2016; published 29 February 2016

ABSTRACT

We revisit one of the classical search problems in which a diffusing target encounters a stationary searcher. Under the condition that the searcher’s detection region is much smaller than the search region in which the target roams diffusively, we carry out an asymptotic analysis to derive the decay rate of the non-detection probability. We consider two different geometries of the search region: a disk and a square, respectively. We construct a unified asymptotic expression valid for both of these two cases. The unified asymptotic expression shows that the decay rate of the non- detection probability, to the leading order, is proportional to the diffusion constant, is inversely proportional to the search region, and is inversely proportional to the logarithm of the ratio of the search region to the searcher’s detection region. Furthermore, the second term in the unified asymptotic expansion indicates that the decay rate of the non-detection probability for a square region is slightly smaller than that for a disk region of the same area. We also demonstrate that the asymptotic results are in good agreement with numerical solutions.

Keywords:

Detection of a Random Target, Asymptotic Solutions, Decay of the Non-Detection Probability

1. Introduction

Searching is a common activity in our everyday life. For example, we look for lost car keys in a big parking lot, search for hidden natural resources such as oil and metals in a vast field, and search for missing people in a national park; the U.S. Coast Guards conduct thousands of open ocean search and rescue missions every year; the police hunts for drug smugglers; the military searches for Improvised Explosive Devices (IEDs) and insur- gents in Iraq and Afghanistan. More examples can be found in Koopman’s classical book [1] and in a recent article by Beckhusen [2] .

Historically, the search for enemy submarines during World War II stimulated intensive scientific studies, giving rise to a branch of operations research now known as search theory [3] - [9] . The continued importance of finding maritime targets as well as other hidden objects keeps providing new research challenges in the field.

In search theory, we call the object being sought the target. The search region is the region that both the target and the searcher are confined to. Generally speaking, search problems can be loosely divided into two cate- gories: one-sided search and two-sided search. In one-sided search, the searcher tries to detect the target while the target does not know the presence of the searcher, i.e., the target does not try to avoid the searcher in any active way. In two-sided search, the target has some capability of sensing the presence or the approaching of the searcher and may design a way to avoid being detected by the searcher. In one-sided search, the main objective is to maximize the probability of detection in a given time period and/or to minimize the cost or time of the search for a given tolerance of the non-detection probability. One-sided search can be further characterized by the constraints placed on the searcher’s actions and the target motion. This includes stationary target problems and moving target problems. Different approaches have been taken to address these problems. For example, Stone [8] derived necessary and sufficient conditions for optimal detection problems. Mangel [10] calculated joint probability density for target location and unsuccessful search by the ray method. Mangel also formulated the search and mining problems as constrained optimization problems and then solved the problems by vari- ational techniques [11] . Washburn [12] found the searcher path that minimized the mean time to locate a random stationary target where the starting point could be chosen by the searcher. Eagle and his co-workers found a searcher path that maximized the probability of detecting a moving target in a fixed time duration [13] - [15] . Washburn [16] compared several branch-and-bound methods for solving a moving-target search problem. Dell and collaborators applied an optimal branch-and-bound procedure to find a feasible path that maximized the probability of detecting a moving target using multiple searchers with constrained path [17] . MacPhee and Jordan considered the optimal search problem for a leprechaun that moves randomly between two sites and the movement was modeled with a two-state Markov chain [18] . Majumdar and Bray calculated the survival pro- bability of a tracer particle moving along a deterministic trajectory in the presence of diffusing traps [19] . Fernando and Sritharan computed the non-detection probability of infinitely many diffusing Brownian targets by a moving searcher which traveled along a deterministic path with constant speed in the two-dimensional plane [20] . Wang and Zhou conducted numerical studies to calculate the non-detection probability of a randomly moving target by a stationary or moving searcher in a square search region [21] . They also considered the search problem where a target moves between a hiding area and an operating area via multiple pathways where the searchers are equipped with either cookie-cutter sensors [22] or stochastically intermittent sensors [23] . In con- trast, the two-sided search problem is traditionally addressed by formulating the problem as a game-theory problem [24] [25] . It involves a searcher and a target who knows that it is being chased and attempts to avoid detection or capture. Early work on search games was presented in the classic book of Shmuel Gal [26] . This monograph mainly addresses the problem of finding optimal search trajectories in order to locate a target. Recent developments on the theory of search games and rendezvous are discussed in the books [27] [28] . More references on the two-sided search problem can be found in the review paper by Chung, Hollinger and Isler [5] .

One of the classical one-sided search problems involves a lone searcher looking for a single moving target. A classical mathematical problem is to examine the non-detection probability of a diffusing target by a stationary sensor such as fixed acoustic sensors, sonobuoys, or possibly mines. This problem has been investigated by Eagle [29] . A diffusion equation is used to describe the probability density of a diffusing target (modeled as a Brownian particle). When the search region is a disk and the cookie cutter detector (a detector whose detection region is a circle of a given radius) is fixed at the center of the search region, analytical solution to the boundary value problem can be formulated using separation of variables. The solution by separation of variables contains an infinite sum of Bessel functions. For large time, the solution is well approximated by the slowest decaying mode. For a rectangular search region, analytical solutions are still unknown. Instead Eagle carried out Monte Carlo simulations and numerically estimated the probability of non-detection.

In this paper we revisit this classical problem of detecting a moving target by a stationary sensor or searcher. We first nondimensionalize the problem, then we derive asymptotic approximations to the decay rate of the non-detection probability of a diffusing target by a fixed searcher in a large detection region for two different geometries of the search region: a disk and a square, respectively. For the disk-shaped search region, we show that the asymptotic solution agrees very well with an accurate numerical solution obtained by solving an algebraic equation involving Bessel functions. For a square search region, asymptotic solutions show that the decay rate of the non-detection probability is slightly smaller than that for a disk search region of the same area. Finally, we combine the two cases into a unified form by expressing the decay rate of non-detection probability in terms of a large parameter: the ratio of the search region to the searcher’s detection region. The significance of our results lies in the simple and explicit asymptotic expressions of the decay rate of the non-detection pro- bability. It shows that the decay rate of the non-detection probability, to the leading order, is inversely propor- tional to the logarithm of the ratio of the search region to the searcher’s detection region.

2. Mathematical Formulations

Consider a search region A of “characteristic” radius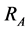. For a disk, the characteristic radius 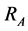is the true radius; for a square, the characteristic radius 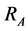could be half the width, for example. Suppose the searcher is capable of detecting target within distance R. That is, the searcher covers a disk of radius R centered at the location of the searcher, which is called the detection region of the searcher. Once the target gets inside the detection region, it is detected instantaneously. This is the so-called cookie-cutter sensor/searcher in search theory. In this paper we study two cases: a disk search region and a square search region.

We consider the situation where the searcher is fixed at 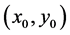and the target moves randomly with a diffusion coefficient D, confined in region A (the search region). Let 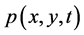be the probability of the target being at position 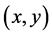at time t. 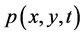is governed by the diffusion equation with boundary and initial conditions:

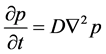(1)

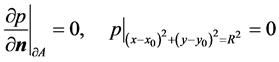
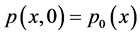
where 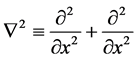denotes the Laplace operator and 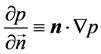represents the directional derivative of

p along the normal vector 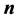of 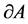(the boundary of search region A). Of the two boundary conditions, the first one corresponds to the reflecting condition at the boundary of the search region A, and the second one refers to the absorbing condition at the boundary of the searcher’s detection region.

The objective of this paper is to seek asymptotic solutions when the detection radius R of the searcher is much smaller than the characteristic radius 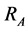of the search region A. Mathematically, that is. We first perform non-dimensionalization to make the problem dimensionless. Let

The function has the meaning of probability density with respect to new variables. It satisfies the initial boundary value problem below (we drop the subscript “” for simplicity):

(2)

.

After non-dimensionalization, the characteristic radius of the search region is 1 and the detection radius of the searcher is.

3. Asymptotic Solutions

The initial boundary value problem (2), in principle, can be solved using the method of separation of variables. More specifically, the solution can be expressed as

(3)

where are the eigenvalues and the associated eigenfunctions of the Sturm-Liouville problem described by

(4)

In the expression of given in (3), is the slowest decaying term. Over long time, the slowest decaying term dominates and consequently has the approximate expression

. (5)

Let, which is the survival probability. Note that is also called the probability of non-detection by time t in search theory. Here we use these two terms interchangeably. Over long time, has the approximate expression

(6)

That is, over long time, the decay rate of the survival or non-detection probability is given by the smallest eigenvalue. The quantity corresponds to the time scale of being detected (absorbed) by the searcher. When is small, time scale is large. In contrast, corresponds to the time scale of re- laxation of probability within the region and is not very much affected by small. As a result, , independent of. This separation of time scales makes it possible to derive asymptotic expressions for the smallest eigenvalue. In the following we study two different geometries of the search region: a disk and a square, respectively, and we derive the corresponding asymptotic expressions.

3.1. Search in a Disk Region

We consider a disk-shaped search region as illustrated in Figure 1. After non-dimensionalization the search region A is a unit disk. The searcher is fixed at the center of the disk, and the detection radius of the searcher is. In this case it is more convenient to use polar coordinates. Since the whole problem is axisymmetric, u is simplified to be a function of r only:. Consequently, the Sturm-Liouville problem (4) becomes

(7)

In (Muskat, 1934), it is shown that is the nth positive root of the equation

(8)

where and are the zero-th order Bessel functions of the first and the second kind, respectively; and are the first order Bessel functions of the first and the second kind, respectively. Thus, an accurate numerical solution for can be obtained by solving algebraic Equation (8). We will use this accurate numerical solution to validate our asymptotic solutions.

To derive an asymptotic solution, we view the right-hand side of (7) as a source term and recast the equation for in the form of conservation of probability.

(9)

where.

When is small, we can make a few comments about Equation (9):

・ probability flows out at the absorbing boundary and gets added back in as the source term; the total probability is conserved and does not change with time;

・ the source term is small because is small;

・ the probability outflow (detection by the searcher) is slow;

・ the relaxation within the region is relatively fast.

From these observations, it follows that as long as the total amount of the source term is correctly counted, the distribution of the source term should not significantly affect the solution. The relaxation within the region is relatively fast and is capable of spreading the source within the region in a time scale much shorter than the time scale of detection by the searcher (the separation of time scales discussed above).

We use a delta function at to replace in Equation (9), which means the probability flowing out at is added back in at. The boundary condition is no longer valid due to the delta function source term at. Since both and are unknown, the boundary condition at becomes unknown after we approximate the source term as a delta function at. However, notice that eigenfunction is determined only up to a constant multiple. We proceed by solving for with only the absorbing condition at. Eigenfunction satisfies approximately

(10)

A general solution of Equation (10) is. Enforcing the absorbing condition, we get:

. (11)

The probability out-flow at the absorbing boundary is. The total amount of the source term in Equation (9) is. Equating these two quantities, we express in terms of (it is more convenient to work with than working with). We use this method to calculate based on the approximate given in (11).

(12)

In the calculations above, we have ignored terms smaller than. It is important to point out that the expression for given above is not accurate up to or not even accurate up to because the error in is not included in the calculation of (12).

Note that given in (11) is a first approximation of the true, obtained by setting to a delta function in Equation (9). We can improve the approximation iteratively. Once we have the approximate given in (11), we use it to replace in Equation (9) and derive a more accurate differential equation.

Specifically, in Equation (9), we set. For convenience, we pick since a non-zero

multiple of an eigenfunction is still an eigenfunction. Equation (9) with boundary conditions becomes

(13)

A particular solution of Equation (13) is. A general solution of the inhomogeneous Equation (13) without boundary condition is

Enforcing the boundary conditions and, we get an improved approximation for:

(14)

where is defined in (12). This is a more accurate approximation of than the one given in (11). A new approximation for can be calculated by equating the probability out-flow at the absorbing boundary

and the total amount of the source term. Using the updated approximation of

given in (14), we obtain

. (15)

In the calculations above, we have neglected terms smaller than. Again, that does not imply that the expression for given above is accurate up to because the error in the approximate is not included in the calculation. We do, however, expect that in the iterative approach, each iteration yields one more term in the asymptotic expansion. Thus, the expansion in (15) is accurate up to term. That is, the first two coefficients in (15) are correct.

With the new approximation of given in (14), we can repeat the iterative improvement on and. We go back to Equation (9) and replace by the most recent approximation of. Note that a

constant multiple of an eigenfunction is still an eigenfunction. We set

and we pick. Now Equation (9) with boundary conditions takes the form

(16)

For each term on the right-hand side of (16), we find a corresponding particular solution. A particular solution of is; a particular solution of is. Using these results, we write out a general solution of (16) without boundary condition:

. (17)

Determining coefficients and from the boundary conditions and, we arrive at

. (18)

We now have 3 approximations for eigenfunction obtained in 3 iterations. The approximation given in (11) is the leading term approximation; the one in (14) is the 2-term expansion, and the one in (18) is accurate for the first 3 terms. Figure 2 shows these 3 asymptotic solutions for along with the accurate numerical solution when. Note that eigenfunction is only determined up to a constant multiple. To compare these approximations of eigenfunction, we normalized each function by its value at. So, after normalization, we have for every function. In Figure 2, it is clear that even for this moderate, as we carry out the iterative improvements and include more terms in the asymptotic expansion, the approximation converges to the true solution.

Based on the most recently updated, a more accurate expansion of is calculated by equating the

probability out-flow at the absorbing boundary and the total amount of the source term. In this new round of improvement iteration, we expect to get the coefficient of. So, in the calculation, we ignore terms smaller than.

(19)

where as defined in in (12). In Figure 3 we compare our one-term, two-term and three-term

asymptotic results for the normalized decay rate of non-detection probability, , given in (12), (15), and (19). For comparison, an accurate numerical solution from (8) is also plotted in Figure 3. When is small, all of the three asymptotic results match the accurate numerical solution quite well. As increases, one-term and two-term asymptotic results start to deviate from the accurate numerical solution whereas the three-term asymptotic expression remains very accurate even for.

Going back to the physical quantities before non-dimensionalization, we conclude that, over long time, the decay rate of non-detection probability for a disk search region has the asymptotic expression:

(20)

where.

3.2. Search in a Square Region

Next we study the case of a square search region as shown in Figure 4. The search region A after non-dimen- sionalization is a square of width 2. The searcher is at the center of the square, , and the detection radius of the searcher is.

Even though the search region is not axisymmetric, we will not completely abandon the polar coordinates. The motivation for using the polar coordinates is follows. When is small, the local effect of the absorbing boundary is becoming singular. Fortunately, this singular local effect is nearly axisymmetric, and is best captured using the polar coordinates. The non-axisymmetry of the region does affect the solution of the eigenvalue problem. The effect of the square boundary is not axisymmetric. Fortunately, this non-axisymmetric effect is not singular and it can be conveniently described in Cartesian coordinates, independent of the small parameter. So, in the case of a square search region, we use both the polar coordinates and the Cartesian co- ordinates. Some coefficients in the asymptotic expansion have to be calculated using accurate numerical solutions.

For a square of size 2 centered at, the Sturm-Liouville problem (4) becomes

(21)

We use a similar approach as we did in the case of a disk region. We treat the right-hand side as a source term and view, the eigenfunction corresponding to the smallest eigenvalue (), as the steady state solution of the diffusion equation with a source term. In other words, we rewrite the differential equation above as

(22)

where. Similar to the case of a disk region, when is small, system (22) has several properties:

・ probability flows out at the absorbing boundary and gets added back in as the source term; at the steady state, the out-flow is balanced by the source term, and does not vary with time;

・ the input of probability from the source term is relatively slow (slow time scale);

・ in contrast, the relaxation of probability distribution within the region is relatively fast (fast time scale).

Due to the separation of slow and fast time scales, the exact distribution of the source term, to the leading order, will not affect solution. The relaxation of probability distribution within the region driven by diffusion is relatively fast and is capable of spreading out the distribution of the source term. In the leading order expansion, we put the source term along the boundary of the square. For simplicity, we distribute the source term along the boundary of the square in a way such that the solution is axisymmetric. It follows that the approximate satisfies

(23)

.

The exact solution of (23) is given by

. (24)

The probability out-flow at the absorbing boundary is. The total amount of the source term in Equation (22) is

where function is defined as

. (25)

Geometrically, when we look at the intersection of the circle of radius r and the square, is the fraction of the circle inside the square. For,; for,. This geometric meaning of function is illustrated in Figure 5.

Equating the out-flow and the source term, we have an expression of in terms of. Using the approximate given in (24), we obtain

(26)

where

(27)

. (28)

Note that given in (24) is a first approximation of the true. We improve the approximation iteratively. We use the approximate given in (24) to replace in Equation (22) and derive a new

approximate differential equation for. Specifically, in Equation (22), we set and

we choose. After this updating, Equation (22) along with the absorbing boundary condition has the form

(29)

Both the differential equation and the absorbing boundary are still axisymmetric. When the reflecting condition at the square boundary is put away, the system allows axisymmetric solutions. We first solve for an axisymmetric solution of this system and then we use superposition to take care of the reflecting condition at the

boundary of the square. A particular axisymmetric solution of (29) is. The

general axisymmetric solution of (29) with the absorbing boundary condition can be written as

(30)

where

(31)

. (32)

Note that in the general solution, both coefficients and are associated with, a solution of the homogeneous equation. But in the asymptotic analysis, is the coefficient of term while

is the coefficient of term. So, in the asymptotic analysis, we treat and separately by enforcing the reflecting boundary condition separately for and for.

For each of and, the reflecting boundary condition is taken care of in two steps. In step 1, we adjust coefficient in solution such that the probability out-flow integrated over the boundary of the square is zero. In step 2, we solve numerically a non-singular Neumann boundary value problem in the Cartesian coordinates, and then we add the solution to to make the probability out-flow zero everywhere on the boundary of the square. We notice that the problem is still invariant with respect to a rotation

of an integer multiple of. As a result, the integral of probability out-flow over the entire square boundary

is zero if and only if the integral over one side of the square is zero. Specifically, in step 1 for, we require that

. (33)

Substituting (31) into (33), we obtain

(34)

In step 2 for, to make the probability out-flow zero everywhere on the square boundary, we add to counter the probability out-flow of. Function satisfies

(35)

.

The last condition is an approximation of the absorbing boundary condition. This appro- ximation is valid since has no singularity. Without the condition, solution exists and is determined up to an additive constant. Solution is then uniquely determined by the condition. This well-posedness of the Neumann boundary value problem for follows directly from the fact that the integral of the prescribed probability out-flow over the outer boundary is zero. The zero total probability out-flow at the outer boundary also implies that the total probability out-flow at the absorbing boundary for is zero. That is,

. (36)

This property plays an important role in the calculation of below. can be calculated accurately using a numerical discretization in Cartesian coordinates. The accurate numerical solution of is made possible by the fact that is independent of and has no singularity. Based on the numerical solution, the integral of over the square region A has the value

. (37)

This quantity is also important in the calculation of below.

Next, we enforce the reflecting boundary condition for solution. In step 1 for, we require that

. (38)

Using Equation (38) to determine coefficient in (32) leads to

. (39)

In step 2 for, to make the probability out-flow zero everywhere on the square boundary, we add to counter the probability out-flow of. Function satisfies

(40)

.

Similar to the situation for, the zero total probability out-flow for at the outer square boundary implies that the total out-flow at the inner absorbing boundary for is zero:

. (41)

The exact expression of is not needed in the 2-term expansion below.

Putting all components together, the solution of (29) with both the absorbing boundary condition and the reflecting boundary condition is approximately

(42)

where functions and are given in (31) and (32) with coefficients and given in (34) and (39). Using the improved approximation of given in (42), we derive a 2-term expansion of. In the calculation, we will use properties (36) and (41). In addition, we will use the short notation and the constant defined as

(43)

. (44)

As before, is calculated by matching the out-flow at the absorbing boundary and the

source term. Thus, we find that

(45)

where the coefficients, , , and are given in (27), (28), (34), (37) and (44), respectively. For reader’s convenience, these coefficients are summarized below:

The 2-term asymptotic expansion of (for a square region) has the expression

(46)

where.

We like to find the accuracy of the asymptotic solutions we derived above for a square search region. Unfortunately, for a square search region, no analytical or semi-analytical solution is known yet. A very accurate numerical solution is also difficult to compute. The circular cookie-cutter detector is incompatible with the square search region in a numerical discretization. It is difficult to design a numerical grid to accommodate both the square outer boundary and the circular inner boundary. Instead, we use Monte Carlo simulations to compute the decay rate of non-detection probability density.

To gauge the accuracy of Monte Carlo simulations, we first carry out Monte Carlo simulations in the case of a disk search region for which a very accurate numerical solution is known. Figure 6 compares the Monte Carlo solution for a disk search region and the very accurate numerical solution obtained by solving an algebraic equation involving Bessel functions. In Figure 6, each point is based on a Monte Carlo simulation of 100,000 particles integrated over more than 40 million time steps. Each time step () typically moves a particle less than (as a scale reference, the search region has radius 1 after non-dimensionalization). The large number of particles and the tiny numerical time step work together to keep the errors low in Monte Carlo simulations. As shown in Figure 6, the Monte Carlo solution agrees very well with the accurate numerical solution in the case of a disk search region. The goal of this comparison in the case of a disk search region is to identify the number of particles, the time step size, and the number of time steps needed for a reasonably high accuracy in Monte Carlo simulations. In Monte Carlo simulations of a square search region, we use the same numerical parameters (100,000 particles integrated over more than 40 million time steps with).

In the case of a square search region, we use the Monte Carlo solution as the accurate solution and we compare it with the two asymptotic expansions. Figure 7 shows that the asymptotic solutions have good agreement with the accurate Monte Carlo solution when is small.

In terms of the physical quantities before non-dimensionalization, we conclude that over long time, the decay rate of non-detection probability for a square search region has the asymptotic expression:

(47)

where, R is the the detection radius of the searcher and is the half width of the square search region.

3.3. A unified Form

Finally, we compare the results of the two cases that we have analyzed so far. We define the large parameter as the ratio of the area of search region A (disk or square) to the searcher’s detection area:

.

. (48)

Since we only have a two-term expansion for a square search region, in the comparison we will use only two terms from the asymptotic expansion for a disk search region. We write the results of these two cases in a unified form:

(49)

(50)

where the shape factor contains the effect of the search region shape while the area of the search region is fixed. The values of for a disk and a square are respectively

Note that in the unified form (50), the normalized decay rate is defined slightly differently from the one used in the discussion of a disk or a square search region. In the discussion of case 1 and case 2, we used, a “characteristic” radius of the search region, to define the normalized decay rate. To avoid the ambiguity associated with a “characteristic” radius, we use the area of the search region to define the normalized decay rate in the unified form.

In summary, for both a disk search region and a square search region, the decay rate of the survival probability, to the leading order, is proportional to the diffusion constant, is inversely proportional to the search area, and is inversely proportional to the logarithm of the ratio of the search area to the searcher’s detection area. Furthermore, the second term in the asymptotic expansion implies that the decay rate of the non-detection probability for a square region is slightly smaller than that for a disk region of the same area.

4. Concluding Remarks

We have derived asymptotic expressions for the decay rate of non-detection probability of a diffusing target in the presence of a stationary searcher in a large disk or square search region. The asymptotic expansions agree well with a very accurate numerical result obtained by solving an algebraic equation involving Bessel functions in the case of a disk search region. In the case of a square search region, the asymptotic expansions are validated by comparing them with an accurate result computed in large scale Monte Carlo simulations. Based on the asymptotic expansions obtained, respectively, for a disk and for a square, we write out a unified asymptotic expression valid for both of these two cases, in which the effect of the area of the search region is separated from the effect of the shape of the search region. The unified asymptotic expression shows that the decay rate of non-detection probability, to the leading order, is proportional to the diffusion constant, is inversely proportional to the search area, and is inversely proportional to the logarithm of the ratio of the search area to the searcher’s detection area. The leading term is not affected by the shape of the search region provided that the area of the search region is kept unchanged. The second term in the unified asymptotic expansion is affected by the shape of the search region. It indicates that the decay rate of non-detection probability for a square region is slightly smaller than that for a disk region of the same area.

Acknowledgements

Hong Zhou would like to thank Professor James Eagle, Professor Jim Scrofani and Professor Sivaguru Sritharan for helpful discussions.

Cite this paper

HongyunWang,HongZhou, (2016) Non-Detection Probability of a Diffusing Target by a Stationary Searcher in a Large Region. Applied Mathematics,07,250-266. doi: 10.4236/am.2016.73023

References

NOTES

^*The views expressed in this document are those of the authors and do not reflect the official policy or position of the Department of Defense or the U.S. Government.