Applied Mathematics
Vol.06 No.12(2015), Article ID:61465,12 pages
10.4236/am.2015.612180
Numerical Study for Simulation the MHD Flow and Heat-Transfer Due to a Stretching Sheet on Variable Thickness and Thermal Conductivity with Thermal Radiation
Mohamed M. Khader1,2, Mohammed M. Babatin1, Ali Eid3, Ahmed M. Megahed2
1Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia
2Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt
3Department of Physics, College of Science, Al-Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 6 October 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT
The main aim of this article is to introduce the approximate solution for MHD flow of an electrically conducting Newtonian fluid over an impermeable stretching sheet with a power law surface velocity and variable thickness in the presence of thermal-radiation and internal heat generation/absorp- tion. The flow is caused by the non-linear stretching of a sheet. Thermal conductivity of the fluid is assumed to vary linearly with temperature. The obtaining PDEs are transformed into non-linear system of ODEs using suitable boundary conditions for various physical parameters. We use the Chebyshev spectral method to solve numerically the resulting system of ODEs. We present the effects of more parameters in the proposed model, such as the magnetic parameter, the wall thickness parameter, the radiation parameter, the thermal conductivity parameter and the Prandtl number on the flow and temperature profiles are presented, moreover, the local skin-friction and Nusselt numbers. A comparison of obtained numerical results is made with previously published results in some special cases, and excellent agreement is noted. The obtained numerical results confirm that the introduced technique is powerful mathematical tool and it can be implemented to a wide class of non-linear systems appearing in more branches in science and engineering.
Keywords:
Newtonian Fluid, Stretching Sheet, Variable Thermal Conductivity, Thermal Radiation, Chebyshev Spectral Method

1. Introduction
The previous investigations ([1] -[6] ) did not study the effects of radiation on the flow and heat transfer. In manufacturing industries, the radiative heat transfer flow is very important for the design of reliable equipments, nuclear plants, gas turbines and various propulsion devices for aircraft, missiles, satellites and space vehicles. Also, the effect of thermal radiation on the forced and free convection flows is important in the context of space technology and processes involving high temperature. Historically in ([7] - [10] ), the study on boundary layer flows over a stretching sheet with variable thickness is presented. From these considerations, we can see that the effects of the non-flatness on the stretching sheet problems considering a variable sheet thickness have not presented. So, the main goal of this paper is to introduce the numerical simulation using Chebyshev spectral method ([11] -[16] ) for the proposed model.
2. Formulation of the Model
In this section, we will consider a steady, 2Dim boundary layer flow of an incompressible Newtonian fluid over a continuously impermeable stretching sheet. The origin is located at a slit, through which the sheet is drawn through the fluid medium (see Figure 1). The velocity of the stretching surface is given by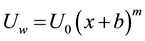 ,
,
where 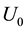 is the reference velocity. We suppose that the sheet is not flat and defined as
is the reference velocity. We suppose that the sheet is not flat and defined as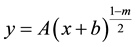 ,
,
where A is a very small constant so that the sheet is sufficiently thin and m is the velocity power index. We must note that the proposed model is satisfied only for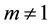 , because for
, because for , the model changes to a flat sheet. Likewise, the fluid properties are assumed to be constant except for thermal conductivity variations in the temperature. In this work, we will suppose that the variable magnetic field
, the model changes to a flat sheet. Likewise, the fluid properties are assumed to be constant except for thermal conductivity variations in the temperature. In this work, we will suppose that the variable magnetic field 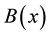 is applied normal to the sheet and that the induced magnetic field is neglected, which is justified for MHD flow at small magnetic Reynolds number.
is applied normal to the sheet and that the induced magnetic field is neglected, which is justified for MHD flow at small magnetic Reynolds number.
In case of approximations for the usual boundary layer of the Newtonian fluid, we can write, the steady 2D im boundary-layer equations taking into account the thermal radiation effect in the energy equation in the following form:
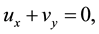 (1)
(1)
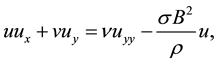 (2)
(2)
 (3)
(3)
Figure 1. Illustration of a stretching sheet with variable sheet thickness.
where u and v are the velocity components in the x and y directions, respectively.  and
and 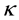 are the fluid density and the thermal conductivity, respectively. T is the temperature of the fluid,
are the fluid density and the thermal conductivity, respectively. T is the temperature of the fluid,  is the fluid kinematic viscosity, B is the strength of the applied magnetic field,
is the fluid kinematic viscosity, B is the strength of the applied magnetic field, 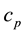 is the specific heat at constant pressure,
is the specific heat at constant pressure, 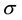 is the electrical conductivity of the fluid,
is the electrical conductivity of the fluid, 

The radiative heat flux 

where 





The physical and mathematical advantage of the Rosseland formula (4) consists of the fact that it can be combined with Fourier’s second law of conduction to an effective conduction-radiation flux 

where 
ing the net contribution of the radiation emitted from the hot wall and absorbed in the colder fluid, takes the form

To obtain similarity solutions, it is assumed that the magnetic field 

where 


The mathematical analysis of the problem is simplified by introducing the following dimensionless coor- dinates

where 




In this study, the equation for the dimensionless thermal conductivity 

where 

Upon using these variables, the boundary layer governing Equations (1)-(3) can be written in a non-dimensional as follows


where 



Also, the boundary conditions transformed to the following form


where 

cates the plate surface. We can write the Equations (13)-(14) in a simple form and to facilitate the computation, if we take into the account the transformation 





The physical quantities of primary interest are the local skin-friction coefficient 


where 

3. Application of Chebyshev Spectral Method
In this section, we implement Chebyshev spectral method to solve the resulting system of non-linear ODEs of the form (17)-(18) with boundary conditions (19)-(20). To achieve this aim, and since the Gauss-Lobatto nodes
inside

form


also the boundary conditions will transform to the following form

where 















Also using the boundary conditions (24), the constants of integration
Now, the approximations to the Equations (25) and (26) will take the following forms

where 

And with implementation the transformation (27), we can write the system (22)-(23) to a form of system of non- linear equations in the highest derivative as follows:


These equations are non-linear system of 2n + 2 algebraic equations in 2n + 2 unknowns 



4. Results and Discussion
In Table 1 and Table 2, we presented the numerical solution using the Chebyshev spectral method with
In Figure 4, Figure 5, we presented the obtained numerical results to show the effects of wall thickness parameter on the fluid flow and the temperature distribution. From Figure 4, we can see that the velocity at any point near to the plate decreases as the wall thickness parameter increases. Also from these figures, we can note that the thickness of the boundary layer becomes thinner for a higher value of 

Figure 5 displays that the wall thickness parameter decreased the thickness of the thermal boundary layer and enhanced the rate of heat transfer. Physically, increasing the value of 

Table 1. The approximate values of



Table 2. The approximate values of



Figure 2. The velocity distribution for different values of M.
Figure 3. The temperature distribution for different values of M.
Figure 4. The velocity distribution for different values of
From Figure 6, we can ensure that the velocity increases with a decrease in the values of the velocity power index m along the sheet and the reverse is true away from it. This implies that the momentum boundary thickness becomes thicker as m increases.
The influence of the velocity power index parameter m on the temperature profiles is displayed in Figure 7. From this figure, we can see that increasing the value of m produces an increase in the temperature profiles. It further shows that the larger the value of m, the higher the magnitude of the thermal boundary thickness will be.
From Figure 8, we can reveal that the temperature profile as well as the thickness of the thermal boundary layer increase when 

In Figure 9, we presented the effects of R on the temperature profiles with fixed the values of all other parameters. From this figure, we noted that the temperature field and the thermal boundary layer thickness increase with the increase in R. Also, from Figure 10, we can observe that an increase in the Prandtl number results in decreases the heat transfer profiles. The reason is that increasing values of Prandtl number equivalent for decreasing the thermal conductivities and therefore heat is able to diffuse away from the heated sheet more rapidly. Hence in the case of increasing Prandtl number, the boundary layer is thinner and the heat transfer is reduced.
Figure 11 illustrates the affect on the profiles of temperature distribution with different values of the parameter 
Figure 5. The temperature distribution for different values of
Figure 6. The velocity distribution for different values of m.
Figure 7. The temperature distribution for different values of m.
Figure 8. The temperature distribution for different values of
Figure 9. The temperature distribution for different values of R.
Figure 10. The temperature distribution for different values of Pr.
Figure 11. The temperature distribution for different values of
increase when the internal heat generation parameter 



Table 3 shows the influence of the magnetic parameter M, wall thickness parameter




Table 3. Comparison between 


5. Conclusion
In this work, we implemented the Chebyshev spectral method to solve the non-linear system of ODEs of the proposed model. The fluid thermal conductivity is assumed to vary as a linear function of temperature. Asystematic study on the effects of the various parameters on flow and heat transfer characteristics is carried out. It has found that the effect of increasing values of the magnetic parameter, the velocity power index parameter, thermal conductivity parameter and the radiation parameter reduce the local Nusselt number. On the other hand, it is observed that the local Nusselt number increases as the Prandtl number and wall thickness parameter increases. Moreover, it is interesting to find that as the magnetic parameter, wall thickness parameter and the velocity power index parameter increases in magnitude, causes the fluid to slow down past the stretching sheet, the skin-friction coefficient increases in magnitude. A comparison with previously published work is given to ensure that the obtained numerical results are in excellent agreement, and this confirms that the validity of the proposed method to solve the presented model. Finally, we can make the error is smaller by increasing the terms in the series (27). All computations in this paper are done using Mathematica 8.
Acknowledgements
The first three authors thank Deanship of Academic Research, Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, KSA, for the financial support of the project number (351227).
Cite this paper
Mohamed M.Khader,Mohammed M.Babatin,AliEid,Ahmed M.Megahed, (2015) Numerical Study for Simulation the MHD Flow and Heat-Transfer Due to a Stretching Sheet on Variable Thickness and Thermal Conductivity with Thermal Radiation. Applied Mathematics,06,2045-2056. doi: 10.4236/am.2015.612180
References
- 1. Crane, L.J. (1970) Flow past a Stretching Plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 645-647.
http://dx.doi.org/10.1007/BF01587695 - 2. Gupta, P.S. and Gupta, A.S. (1979) Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing. Canadian Journal of Chemical Engineering, 55, 744-746.
http://dx.doi.org/10.1002/cjce.5450550619 - 3. Soundalgekar, V.M. and Ramana, T.V. (1980) Heat Transfer past a Continuous Moving Plate with Variable Temperature. Warme-Und Stoffuber Tragung, 14, 91-93.
http://dx.doi.org/10.1007/BF01806474 - 4. Grubka, L.J. and Bobba, K.M. (1985) Heat Transfer Characteristics of a Continuous Stretching Surface with Variable Temperature. Journal of Heat Transfer, 107, 248-250.
http://dx.doi.org/10.1115/1.3247387 - 5. Chen, C.K. and Char, M. (1988) Heat Transfer on a Continuous Stretching Surface with Suction or Blowing. Journal of Mathematical Analysis and Applications, 35, 568-580.
http://dx.doi.org/10.1016/0022-247X(88)90172-2 - 6. Hayat, T., Abbas, Z. and Javed, T. (2008) Mixed Convection Flow of a Micropolar Fluid over a Non-Linearly Stretching Sheet. Physics Letters A, 372, 637-647.
http://dx.doi.org/10.1016/j.physleta.2007.08.006 - 7. Hossain, M.A., Alim, M.A. and Rees, D. (1999) The Effect of Radiation on Free Convection from a Porous Vertical Plate. International Journal of Heat and Mass Transfer, 42, 181-191.
http://dx.doi.org/10.1016/S0017-9310(98)00097-0 - 8. Hossain, M.A., Khanfer, K. and Vafai, K. (2001) The Effect of Radiation on Free Convection Flow of Fluid with Variable Viscosity from a Porous Vertical Plate. International Journal of Thermal Sciences, 40, 115-124.
http://dx.doi.org/10.1016/S1290-0729(00)01200-X - 9. Bataller, R.C. (2008) Radiation Effects in the Blasius Flow. Applied Mathematics and Computation, 198, 333-338.
http://dx.doi.org/10.1016/j.amc.2007.08.037 - 10. Fang, T., Zhang, J. and Zhong, Y. (2012) Boundary Layer Flow over a Stretching Sheet with Variable Thickness. Applied Mathematics and Computation, 218, 7241-7252.
http://dx.doi.org/10.1016/j.amc.2011.12.094 - 11. Khader, M.M. (2015) Shifted Legendre Collocation Method for the Flow and Heat Transfer Due to a Stretching Sheet Embedded in a Porous Medium with Variable Thickness, Variable Thermal Conductivity and Thermal Radiation. Mediterranean Journal of Mathematics, 1-18.
http://dx.doi.org/10.1007/s00009-015-0594-3 - 12. Khader, M.M. (2011) On the Numerical Solutions for the Fractional Diffusion Equation. Communications in Nonlinear Science and Numerical Simulation, 16, 2535-2542.
http://dx.doi.org/10.1016/j.cnsns.2010.09.007 - 13. Sweilam, N.H. and Khader, M.M. (2010) A Chebyshev Pseudo-Spectral Method for Solving Fractional Order Integro-Differential Equations. ANZIAM Journal, 51, 464-475.
http://dx.doi.org/10.1017/S1446181110000830 - 14. Khader, M.M. and Megahed, A.M. (2013) Numerical Solution for the Effect of Fluid Properties Effect on the Flow and Heat Transfer in a Non-Newtonian Maxwell Fluid over an Unsteady Stretching Sheet with Internal Heat Generation. Ukrainian Journal of Physics, 58, 353-361.
- 15. Khader, M.M. and Megahed, A.M. (2014) Differential Transformation Method for Studying Flow and Heat Transfer Due to a Stretching Sheet Embedded in a Porous Medium with Variable Thickness, Variable Thermal Conductivity and Thermal Radiation. Applied Mathematics and Mechanics, 35, 1387-1400.
http://dx.doi.org/10.1007/s10483-014-1870-7 - 16. Khader, M.M. and Megahed, A.M. (2014) Differential Transformation Method for the Flow and Heat Transfer Due to a Permeable Stretching Surface Embedded in a Porous Medium with a Second Order Slip and Viscous Dissipation. Journal of Heat Transfer, 136, Article ID: 072602.
http://dx.doi.org/10.1115/1.4027146 - 17. Raptis, A. (1998) Flow of a Micropolar Fluid past a Continuously Moving Plate by the Presence of Radiation. International Journal of Heat and Mass Transfer, 41, 2865-2866.
http://dx.doi.org/10.1016/S0017-9310(98)00006-4 - 18. Raptis, A. (1999) Radiation and Viscoelastic Flow. International Communications in Heat and Mass Transfer, 26, 889-895.
http://dx.doi.org/10.1016/S0735-1933(99)00077-9 - 19. Chiam, T.C. (1997) Magnetohydrodynamic Heat Transfer over a Non-Isothermal Stretching Sheet. Acta Mechanica, 122, 169-179.
http://dx.doi.org/10.1007/BF01181997 - 20. Mahmoud, M.A.A. and Megahed, A.M. (2009) MHD Flow and Heat Transfer in a Non-Newtonian Liquid Film over an Unsteady Stretching Sheet with Variable Fluid Properties. Canadian Journal of Physics, 87, 1065-1071.
http://dx.doi.org/10.1007/BF01181997 - 21. El-Gendi, S.E. (1969) Chebyshev Solution of Differential, Integral and Integro-Differential Equations. Computer Journal, 12, 282-287.
http://dx.doi.org/10.1093/comjnl/12.3.282















