Applied Mathematics
Vol.06 No.11(2015), Article ID:60603,11 pages
10.4236/am.2015.611167
Assessments of Some Simultaneous Equation Estimation Techniques with Normally and Uniformly Distributed Exogenous Variables
O. O. Alabi1, B. A. Oyejola2
1Department of Statistics, Federal University of Technology, Akure, Nigeria
2Department of Statistics, University of Ilorin, Ilorin, Nigeria
Email: a.olatayoolusegunvictor@gmail.com, alabioo@futa.edu.ng, boyejola@unilorin.edu.ng
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 September 2015; accepted 24 October 2015; published 27 October 2015
ABSTRACT
In each equation of simultaneous Equation model, the exogenous variables need to satisfy all the basic assumptions of linear regression model and be non-negative especially in econometric studies. This study examines the performances of the Ordinary Least Square (OLS), Two Stage Least Square (2SLS), Three Stage Least Square (3SLS) and Full Information Maximum Likelihood (FIML) Estimators of simultaneous equation model with both normally and uniformly distributed exogenous variables under different identification status of simultaneous equation model when there is no correlation of any form in the model. Four structural equation models were formed such that the first and third are exact identified while the second and fourth are over identified equations. Monte Carlo experiments conducted 5000 times at different levels of sample size (n = 10, 20, 30, 50, 100, 250 and 500) were used as criteria to compare the estimators. Result shows that OLS estimator is best in the exact identified equation except with normally distributed exogenous variables when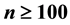 . At these instances, 2SLS estimator is best. In over identified equations, the 2SLS estimator is best except with normally distributed exogenous variables when the sample size is small and large,
. At these instances, 2SLS estimator is best. In over identified equations, the 2SLS estimator is best except with normally distributed exogenous variables when the sample size is small and large,
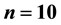 and
and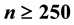 ; and with uniformly distributed exogenous variables when n is very large,
; and with uniformly distributed exogenous variables when n is very large,
 , the best estimator is either OLS or FIML or 3SLS.
, the best estimator is either OLS or FIML or 3SLS.
Keywords:
Normally Distributed Exogenous Variables, Uniformly Distributed Exogenous Variables, Identification Status, Estimators, Exact Identified Equation, Over Identified Equation

1. Introduction
A simultaneous equation system is a regression equation system where two types of variables (the endogenous, the predetermined or exogenous variable) appear with disturbance terms. [1] defined simultaneous equation as the process of modeling more than one equation at a time; a multi-equation modeling. It is proposed to solve the problem of correlation.
In a multi-equation model, the dependent variable Y appears as endogenous variable in one equation and as explanatory variable in another equation of the model. The X variable appears as the explanatory variable in the equations. This creates problems of equation identification, multicollinearity and choice of estimation techniques among others.
Identification problem which creates estimation problems has the same features with multicollinearity [2] . Correlation between the pairs of exogenous or independent variables is an important problem in econometrics especially in single equation estimation. The impact of multicollinearity is less serious when attention is focused on predicting or forecasting values of the endogenous variables than when the analyst is interested in estimating the parameters [3] .
Econometric variables are often non-negative and can exhibit violation against the normality assumption of classical models which inevitably influences the performances of the estimation techniques. This study therefore examines the performances of four (4) common estimation techniques namely; Ordinary Least squares (OLS), Two-stage Least squares (2SLS), Three-stage Least squares (3SLS) and Full Information Maximum Likelihood Estimators under both normally and uniformly distributed exogenous variables for different equation identification status. Here it is assumed that there is no form of correlation in the simultaneous equation model.
Most economic data are often positive [4] and correlated [5] . However, various works done in the recent time especially on correlation studies on simultaneous equation model have being with normally distributed exogenous variables, exhibiting both positive and negative values [6] [7] .
2. Methodology
The methodology followed in this research work is as follows:
The Model and Its Description
Consider the simultaneous Equation model of the for
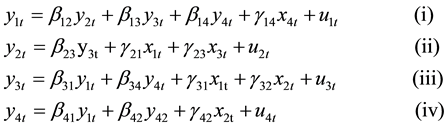 (1)
(1)
where
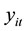 is an endogenous variable,
is an endogenous variable, ;
;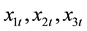 and
and
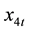 are the exogenous variables
are the exogenous variables

where
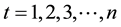 and
and
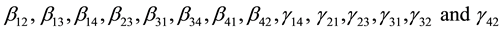 are the structural parameters of the model. Equations (i) and (iii) are exactly identified while Equations (ii) and (iv) were over identified by both order and rank condition.
are the structural parameters of the model. Equations (i) and (iii) are exactly identified while Equations (ii) and (iv) were over identified by both order and rank condition.
For the simulation study, Equation (1) was expressed as follows:
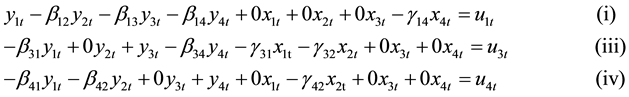 (4)
(4)
This can be written in matrix form as:
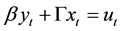 (5)
(5)
where
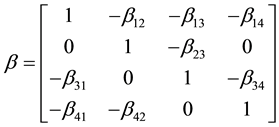 ,
,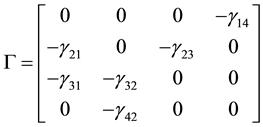 ,
,
 ,
,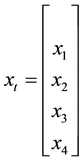 and
and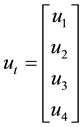
Now, from (5),

Equation (6) was used to generate the endogenous variables by taking the true value of the parameters as:
Monte Carlo experiments were performed 5000 times for seven sample sizes (n = 10, 20, 30, 50, 100, 250 and 500) when there is no correlation of any form among exogenous variables and the error terms. The two forms of exogenous variables are generated to follow normal and uniform distribution.
3. Data Generation of Exogenous Variables
The generation was done as follows:
1) Normally Distributed Exogenous Variables
The exogenous were generated to be normal with mean zero and variance unity i.e.



2) Correlated Uniformly Distributed Variables
Using the generated normally distributed exogenous variables above,


3) Generation of Correlated Error Terms
Equation provided by [8] was modified when the mean of the error terms are zero and variance is unit (1). Also,


4) Method of Generating the Data of Endogenous Variables
Equation (6) was used to generate the endogenous variables by taking the true value of the parameters as:
5) Criteria Used for Assessment of the Estimators
To assess the performance of the estimators, the finite properties were used (Bias, Absolute bias, Variance and Mean Square Error):
Mathematically, MSE is the addition of the Bias squared to the variance. For any estimator



where R = 5000
as a measure of dispersion.
In this paper,

4. Results and Discussion
4.1. Performance of the Estimator Based on the Bias Criterion
The performances of the estimators was examined, ranked and summed over all the parameters in each equation, having examined and summed the rank of the bias of each parameter over all the parameters in each equation the outcome is given in Table 1.
The preferred estimators for different identification status differ. The preferred estimators are also slightly affected by the two exogenous variables.
In the exact identified equation with normally distributed exogenous variables, OLS or 2SLS or both are generally preferred except for very large samples sizes
In the over identified equation with normally distributed exogenous variable, 2SLS estimator is generally preferred except when


Also, with uniformly distributed exogenous variable 2SLS estimator is generally preferred except at very large sample sizes when


4.2. Performances of the Estimators Based on Absolute Bias Criterion
The performances of the estimators was examined, ranked and summed over all the parameters in each equation, having examined and summed the rank of absolute bias of each parameter over all the parameters in each equation the outcome is given in Table 3.
From Table 3, at each level of sample size the sum rank were further added over the equations and preferred estimator under both exact and over identification model with the two exogenous variables were bolded. Table 4 gives the summary of the findings as follows:
The preferred estimators differ in term of identification status. The preferred estimators are slightly affected
Table 1. Summary of the total ranks of the parameter based on bias criterion when there is no correlation.
Source: Computed from simulated results of bias criterion.
by the two exogenous variables. In the exact identified equation with normally distributed exogenous variables under the absolute bias criterion the OLS estimators is preferred when


With uniformly distributed exogenous variables the OLS estimator is generally preferred.
In the over identified equation with normally distributed exogenous variables under the absolute bias criterion, the OLS estimator is preferred when the sample size is small


With uniformly distributed exogenous variables the 2 SLS estimator is preferred over all the sample sizes. Thus, the preferred estimators are more stable in performance with uniformly distributed exogenous variables than the normally distributed exogenous variables.
4.3. Performances of the Estimators Based on Variance Criterion
The performances of the estimators was examined, ranked and summed over all the parameters in each equation, having examined and summed the rank of the variance of each parameter over all the parameters in each equation the outcome is given in Table 5.
From Table 5, at each level of sample size the sum rank were further added over the equations, and preferred estimator under both exact and over identification model with the two exogenous variables were bolded. Table 6 gives the summary of the findings as follows:
From Table 6, the following are observed about the preferred estimators under the variance criterion.
The preferred estimators differ in term of identification status. The preferred estimators are slightly affected by the two exogenous variables.
In the exact identified equation, the OLS estimator is generally preferred in all the sample sizes for both exogenous variables. In the over identified equation with normally distributed exogenous variables, OLS or 2SLS estimator are preferred when


4.4. Performances of the Estimators Based on Mean Squared Error Criterion
The performances of the estimators was examined, ranked and summed over all the parameters in each equation, having examined and summed the rank of the mean squared error of each parameter over all the parameters in each equation the outcome is given in Table 8.
From Table 8 the following are observed about the preferred estimators under the mean squared error criterion.
The preferred estimators differ in term of identification status. The preferred estimators are slightly affected by the two exogenous variables. In the exact identified equation with normally distributed exogenous variables, the OLS estimator is generally preferred except when the sample size is large




4.5. Performances of the Estimators Based on All the Criteria
From Table 10, the following are observed about the preferred estimators under the overall criteria.
The preferred estimators differ in term of identification status. The preferred estimators are slightly affected by the two exogenous variables.
In the exact identified equation with normally distributed exogenous variables the OLS estimator is generally preferred except when the sample size is large when
In the over identified equation with normally exogenous variables the OLS estimators is preferred when the samples sizes is small




With uniformly distributed exogenous variable, the 2SLS estimator is preferred except when the sample sizes is large
From Table 1, at each level of sample size the sum rank were further added over the equations, and preferred estimator under both exact and over identification model with the two exogenous variables were bolded. Table 2 gives the summary of the preferred estimators.
From Table 3, at each level of sample size, the sum rank were further added over the equations, and preferred estimator under both exact and over identification model with the two exogenous variables were bolded. Table 4 gives the summary of the preferred estimators.
From Table 5, at each level of sample size the sum rank were further added over the equations. The preferred
Table 2. Summary of the preferred estimators based on bias criterion.
Source: Table 1.
Table 3. Performances of the estimator based on absolute bias criterion.
Source: Computed from simulated results of Absolute bias criterion.
Table 4. Summary of the preferred estimators based on absolute bias criterion.
Source: Table 3.
Table 5. Performances of the estimators based on variance criterion.
Source: Computed from simulated results of variance criterion.
estimators under both exact and over identification model with the two exogenous variables were made bold. Table 6 gives the summary of the preferred estimators.
From Table 7, at each level of sample size the sum rank were further added over the equations and preferred
Table 6. Summary of the preferred estimators under variance criterion.
Source: Table 5.
Table 7. Performances of the estimators based on mean squared error criterion.
Source: Computed from simulated results of Mean squared error criterion.
estimator under both exact and over identification model with the two exogenous variables were bolded. Table 8 gives the summary of the preferred estimators.
4.6. Overall Examination of the Model Parameters
The overall summary of the performances of the estimators having examined and obtained by adding the total ranks over all the criteria is given in Table 9.
From Table 9, at each level of sample size the sum of the rank were further added over all the criteria and preferred estimator under both exact and over identification model with the two exogenous variables were bolded. Table 10 gives the summary of the preferred estimators.
Table 8. Summary of the preferred estimators when there is no correlation under mean squared error criterion.
Source: Table 7.
Table 9. Overall performances of the estimators based on all criteria.
Source: Computed from Table 1, Table 3, Table 5 and Table 7.
Table 10. Overall summary of the best estimators on the basis of all criteria.
5. Conclusions
The performances of the estimators are affected by the distribution of the exogenous variables. The best estimators are more stable over the levels of sample size with uniformly distributed exogenous variables than the normally distributed exogenous variables.
In exact identified equation with normally distributed exogenous variables the following were observed.
For low sample sizes, OLS is the best performed estimator. In medium sample sizes, OLS or 2SLS is the best performed estimator and 2SLS estimator is the best performed in the large sample sizes. Whereas with uniformly distributed exogenous variables, OLS is the best performed estimator in the entire sample sizes category.
In over identified equation with normally distributed exogenous variables, the following are observed.
For low sample sizes, OLS or 2SLS is the best performed estimator, in medium sample sizes 2SLS\3SLS is the best performed estimator and FIML estimator performed best in the large sample sizes. Whereas with uniformly distributed exogenous variables, 2SLS is the best in low and medium sample sizes category, but 2SLS/ 3SLS estimator is the best in large sample sizes category.
Hence, when there is no correlation of any form in the model the performances of the estimators are affected by the distribution of the exogenous variables in simultaneous equation models.
Cite this paper
O. O.Alabi,B. A.Oyejola, (2015) Assessments of Some Simultaneous Equation Estimation Techniques with Normally and Uniformly Distributed Exogenous Variables. Applied Mathematics,06,1902-1912. doi: 10.4236/am.2015.611167
References
- 1. Schmidt, J.S. (2005) Econometrics. McGraw-Hill International Edition.
- 2. Koutsoyainnis, A. (1977) Theory of Econometrics. 2nd Edition, Palgrave Publishers Ltd., New York.
- 3. Odunta, E.A. (2004) A Monte Carlo Study of the Problem of Multicollinearity in a Simultaneous Equation Model. Unpulished Ph.D. Thesis, Department of Statistics University of Ibadan, Ibadan.
- 4. Kmenta, J. and Gilberet, R.F. (1967) Small Sample Properties of Alternative Estimators of Seemingly Unrelated Regression. Journal of the American Statistical Association, 63, 1180-1200.
http://dx.doi.org/10.1080/01621459.1968.10480919 - 5. Chatterjee, S. and Ali, S.H. (2012) Regression Analysis by Example. 5th Edition, John Wiley and Sons, Hoboken.
- 6. Johnson, T.L., Ayinde, K. and Oyejola, B.A. (2010) Effect of Correlations and Equation Identification Status on Estimators of a System of Simultaneous Equation Model. Electronic Journal of Applied Statistical Analysis EJASA, 3, 115-125.
http://siba-ese.unile.it/index.php/ejasa/index - 7. Ayinde, K., Johnson, T.L. and Oyejola, B.A. (2011) Effect of Equation Identification Status and Correlation between Error Terms on Estimators of System of a Simultaneous Equation Model. American Journal of Scientific and Industrial Research, 2, 184-190.
http://dx.doi.org/10.5251/ajsir.2011.2.2.184.190 - 8. Ayinde, K. (2007) Equation to Generate Normal Variates with Desired Intercorrelations Matrix. International Journal of Statistics and System, 2, 99-111.
- 9. Schumann, E. (2009) Generating Correlated Uniform Variates.
http://comisef.wikidot.com/tutorial:correlated











