Received 29 July 2015; accepted 18 August 2015; published 21 August 2015

ABSTRACT

This paper presents discontinuous Legendre wavelet Galerkin (DLWG) approach for solving one- dimensional advection-diffusion equation (ADE). Variational formulation of this type equation and corresponding numerical fluxes are devised by utilizing the advantages of both the Legendre wavelet bases and discontinuous Galerkin (DG) method. The distinctive features of the proposed method are its simple applicability for a variety of boundary conditions and able to effectively approximate the solution of PDEs with less storage space and execution. The results of a numerical experiment are provided to verify the efficiency of the designed new technique.

Keywords:

Advection-Diffusion Equation, Legendre Wavelet, Discontinuous Galerkin Method, Discontinuous Legendre Wavelet Galerkin Method

1. Introduction

The advection-diffusion equation arises in many important applications, such as fluid dynamics, heat transfer and mass transfer etc. [1] -[9] . In this paper, we shall consider the one-dimensional convection-diffusion equation, which takes the form

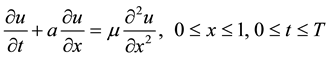, (1.1)

where 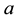and are the speed of advection and diffusion coefficients respectively, and the function 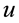is unknown. The initial and boundary conditions are

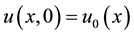, (1.2)

and the boundary conditions satisfy

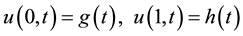, (1.3)

where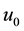, g and h are known functions.

There has been little progress in obtaining analytical solution to the advection-diffusion equation when initial and boundary conditions are complicated, even with constant coefficients a and ν [7] . This is the reason why numerical solution of Equation (1.1) is very important. It is pointed out that a lot of numerical techniques for Equation (1.1) are by now well developed such as finite differences, finite elements, spectral procedures, Wavelet-Galerkin (WG) methods, DG methods and Graphical methods etc. [9] - [25] . Among these approaches, we need to emphasize on Wavelet Galerkin method, especially, Legendre Wavelet Galerkin technique and DG approach for solving partial differential equations (PDEs) because these methods are applied to constructing the DLWG approach proposed in this article.

Firstly, the DG method has emerged as an attractive tool for simulating the convection-diffusion problem [9] -[14] . The main advantage of the DG method lies in its accuracy and flexibility thanks to its high degree of locality. Secondly, the reason for such fast development of the WG approach may be the fact that many nonlinear PDEs have solutions containing local phenomena and interactions among several scales, which can be well-represented in wavelet bases owing to their nice properties, such as compact support and vanishing moment [15] -[22] . However, their main limitations are the difficulties to adapt them to non-periodic geometries and to append specific boundary conditions. Thirdly, what most interests us is that the Legendre wavelet approach is widely implemented to solve PDEs because of its rich properties, for example, expressions in closed form, orthogonality, compact support and vanishing moments [14] -[25] .

In this paper, the DLWG technique is constructed by borrowing the idea of the DG method. The DLWG approach is based on the variational formulation for the solution of Equation (1.1) and takes advantage of an elementwise discontinuous Legendre wavelet approximation, where numerical information only communicates locally via numerical fluxes, to cope with complicated geometries and to represent the dynamics and structure of highly complex solutions. Especially, compared with the LWG method, the discontinuity of Legendre wavelet functions at interfaces of element to element and the boundary conditions are easy to be solved by using the numerical fluxes. Furthermore, the rich properties of Legendre wavelet bases and the use of the discontinuous elements can produce block-diagonal, sparse and lower dimensional mass matrices, which can be easily inverted by hand and stored efficiently in computer-memory compared with the WG method. Of course, the stability and approximate error of the DLWG approach are also addressed in this article. Finally, the DLWG approach utilizes the discontinuous feature at nodes of the Legendre wavelet bases combined with discontinuous finite elements to discretize the space variable and the spacial derivatives to produce a system of first-order ODEs in time for Equation (1.1). We solve this system by using the TVD Runge-Kutta method [11] , and obtain good numerical results, illustrating that this scheme is very simple and computationally efficient.

This paper is organized as follows: in Section 2, descriptions of the Legendre wavelet and its rich properties are given. Section 3 obtains the variational form of Equation (1.1) by the DLWG method. Section 4 derives the computations of the derivative operator and the numerical fluxes. Through these calculations, Equation (1.1) is transformed into an ODE system with time. Section 5 addresses the stability analysis of the DLWG approach. In Section 6, the results of a numerical experiment are presented to demonstrate the efficiency of the DLWG method. Conclusions of the proposed method and some suggestions for future research are given at the end of Section 7.

2. Legendre Wavelet

In this section, we briefly review the Legendre wavelet bases, and introduce our notations and some auxiliary results that will be used later [22] -[24] . Let 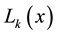denote the Legendre polynomial of degree k, which is inductively defined as follows:

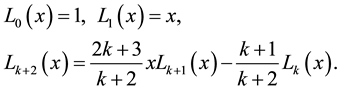(2.1)

Let denote the Legendre scale function defined as

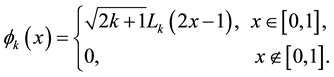(2.2)

For, and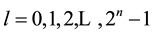, define the interval. For, define 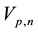as a subspace of piecewise polynomial functions, { is a polynomial of degree strictly less than p; and f vanishes elsewhere}.

The whole set forms an orthonormal basis for. Generally, the subspace is spanned by functions which are obtained from by dilations and translations, i.e.,

spa

which forms an orthonormal basis and

. (2.3)

In order to intuitively understand the Legendre scale functions, we let the scale level and, respectively. Figure 1 plots the scale functions.

The approximation of a function in is represented by only scale functions as follows

, (2.4)

where is the finest scale projection and are scale coefficients. Furthermore, the approximate estimation satisfies

, (2.5)

which demonstrates the approximation error exponentially convergences with the level n of resolution and the order p of the Legendre wavelet bases [22] . The above nice properties demonstrate that the Legendre wavelet bases can be very efficiently applied to the numerical solution of Equation (1).

3. Discontinuous Legendre Wavelet Galerkin Variational Form

In this section, we derive the weak formulation of Equation (1.1) by the DLWG technique in detail. The computational domain is firstly divided into elements, i.e., subintervals as described in Section 2,

so the size of each element is. Secondly, the spaces of the approximation solutions and the test functions are defined as the Legendre wavelet functions spaces introduced in Section 2. Thirdly, for a specific, the numerical solution for in space can be approximated by

, (3.1)

where is unknown time-dependent quantity to be determined from the initial conditions and the weak solution form of Equation (1.1), and

is the vector of the Legendre wavelet bases at the finest decomposition level n.

Now we utilize and to denote the values of u at, from right and left, respectively,

.

We also let the usual notations and represent the mean and the jump of function u at each element boundary point, respectively. Then the semi-discrete i.e., space discretization, the DLWG approach is applied to Equation (1.1) and the corresponding initial and the boundary conditions,

(3.2)

In order to determine the approximate solution, we implement a weak formulation to multiply Equation (1.1) and (3.2) by all test functions, that is to say, Legendre wavelet functions for any and integrate over each element, and then obtain the following

, (3.3a)

, (3.3b)

where. After a simple formal integration by parts over Equation (3.3), we have

(3.4)

for each element. The functions and in Equation (3.4) are convection and diffusion numerical fluxes, respectively, which are single-valued functions defined at the element interfaces and in general depend on the values of numerical solution or its derivatives from both sides of the interfaces. Since the function is discontinuous at the points, we must also replace the nonlinear convection and diffusion fluxes by the numerical fluxes and, which appear from integration by parts. A suitable choice for these numerical fluxes is the key ingredient for the stability of the DLWG scheme.

There are two types of numerical fluxes: one is the convection numerical flux; the other is the diffusion numerical flux. In this work, the convection flux is chosen to be the local Lax-Friedrichs flux [11]

. (3.5)

In addition, the diffusion flux is chosen as [11]

. (3.6)

We note that the choice of numerical fluxes follows the same principle as those for the LDG method. However, numerical experience suggests that as the degree k of the approximate solution increases, the choice of the numerical fluxes does not have significant impact on the quality of the approximations [11] .

4. Computation of the Variational Form

In this section, we concretely evaluate each term of Equation (3.4) obtained in Section 3 by taking advantage of the characteristics of the Legendre wavelet bases.

4.1. Calculating the Matrix of Derivatives

Since the Legendre basis functions are discontinuous at nodes when the order of the bases is odd, representations of derivative operators do not exist in the usual sense. The proposed approach by Beylkin et al. [22] is based on defining weak representations of the derivative operator. The transition matrices have large dimensions, although they have block diagonal structures. In this subsection, we can adopt another calculation technique of the differential operator, i.e., computing on each element other than whole interval. This approach consists of the DG method for solving the PDEs and avoids the discontinuity of the Legendre wavelet bases at interfaces. Furthermore, the interactions of the adjacent elements are jointed by using the convection and diffusion fluxes. As we shall show below, this representation of the derivative on each element is an important advantage of the lower dimension transition matrices.

We now let D denote the derivative operator and consider (the projection of D on) for some fixed resolution level n. Then let us consider solution u and with expansions by the Legendre scale functions,

, (4.1)

. (4.2)

Our goal is to find the transition matrices for, which satisfy

. (4.3)

Then the coefficient would necessarily be given by

, (4.4)

where

is the representation of D on the coarsest scale. Also, because we compute the transition matrices on each element, only the same element is involved, that is. Consequently, the matrix in (4.4) is replaced by

, (4.5)

which again is a formal expression at this point, where and is a matrix. Additionally, the representation of transition matrix on the decomposition level n can be found on each element by rescaling

. (4.6)

We now return to how to provide explicit calculation for each element of the matrix in (4.4) for the Legendre scale bases. Using a relation for the Legendre polynomials

, (4.7)

we obtain for the first derivative

(4.8)

Substituting (4.8) into (4.4), we find that the (i + 1, j + 1)-th element of the matrix satisfies

, (4.9)

where and

(4.10)

For example, let p = 3, we can obtain

. (4.11)

The transition matrix derived above is applied to numerical solution of Equation (1.1). They can also be used to solve problems such as calculus of variations, differential equations, optimal control and integral equations.

4.2. Transformation PDE into ODE and Time Discretization

In this subsection, we use the matrix of differential operator and the fluxes proposed in above subsections to transform Equation (1.1) into a system of ODEs in time.

For any test function, , we firstly substitute (3.1) into the first term in (3.4) and then have

. (4.12)

Secondly, taking advantage of the result of (4.6), we obtain the concrete calculation of the second term in (3.4) satisfying

(4.13)

where are the presentation coefficients of the numerical solution on a certain subinterval, and denotes the (k + 1)-th column of the derivative transition matrix.

Up to present, we need to compute the convection and diffusion fluxes, i.e., the third and fourth terms in (3.4). According to the definitions of the fluxes (3.5) and (3.6), we must first evaluate the approximate values of and with needed accuracy at notes. We use the following properties of the Legendre polynomials

(4.14)

and obtain the corresponding results of the Legendre basis functions such that

. (4.15)

Thus, for, we have

(4.16)

where we let. Similarly, we obtain

. (4.17)

Additionally, for and, the boundary conditions (1.3) are subsituted into these computations.

Using (4.16) and (4.17), we have

(4.18)

(4.19)

Now, using (3.5) and (3.6), we can obtain the computations of the fluxes satisfying

(4.20)

(4.21)

With (4.20) and (4.21), we obtain

. (4.22)

Finally, we use (4.12), (4.13) and (4.22) to obtain the ODE systems from the DLWG space discretization. For each k and l, , we have

. (4.23)

In addition, the initial condition (1.2) is represented as

, (4.24)

where are the coefficients of the initial numerical solution. When l = 0 and, each term in (4.23) can be computed by using the boundary conditions (1.3). We now rewrite the p ODE systems (4.23) to a short-handed ODE system of the form

. (4.25)

where is the vector of the coefficients of the numerical solution on the subinterval of Equation (1.1) by using the DLWG method proposed in this paper.

In the current work, the ODE system (4.25) is discretized over time by using the total variation diminishing (TVD) high-order Runge-Kutta method as follows [11]

,

,

, (4.26)

where denotes the time discretization step, and is the time step.

Solving (4.25) by the above time discretization approach, we can obtain the finest resolution scale coefficients on each subinterval in space. Consequently, for all l, the numerical approximate solution to Equation (1.1) is obtained on the n resolution. In comparison with the WG method, we do have more equations to solve. However, the reason why our technique is valid is that we do not try to solve a large system but solve effectively small p systems. This results in a dimensional reduction, which is quite appealing for h-p adaptivity. If the resolution level n is large enough, the lower dimensional matrices would remarkably reduce the storage and time cost complexity needed to solve the full system.

5. Stability Analysis

In this section, we shall address the stability property of the DLWG scheme we just proposed. For simplicity of discussion, we shall only consider the case of being positive from now on, and only consider periodic boundary conditions, which is the type of boundary conditions analyzed in this article. For general boundary conditions, the choice of the numerical fluxes should be adjusted at the boundary. See [11] for details.

Theorem 1. The numerical scheme (3.4) with the fluxes choices (3.5) and (3.6), respectively, is stable, i.e.

.

Proof. According to the Equation (1.1), we let and. In (3.4), we let and sum over l to obtain

, (5.1)

where, is the numerical flux for the function. It is now

easy to show that following the proof of the cell entropy inequality in [11] , using the

fact that is a monotone flux. Consequently,

(5.2)

Choosing suitable parameters, of the flux in (3.6), following the same argument as the literature [11] , we have

. (5.3)

Thus, we can obtain in (5.2)

, (5.4)

which finishes the proof.

6. Numerical Experiment

In this section, we provide numerical experiment for numerically solving Equation (1.1) to illustrate the performance of the DLWG approach.

The values of various used parameters are, , respectively. This means that we consider the equation

(6.1)

defined on,. The exact solution is taken by [7] and given as

. (6.2)

The corresponding initial and boundary conditions are decided by (6.1). Because the exact solution of the Equation (6.2) is known, we can compute the error between numerical solution and exact solution.

We calculate the solution up to. The parameters of the numerical flux in (3.6) are chosen as,. We list the computational results in Table 1 and Table 2 at time and, respectively.

In the tables, Column 1 indicates the spatial order k, Column 2 shows the finest scale n used, and Column 3 contains the size of time steps. In Column 4, we evaluate the error of the solution on 100 × 100 points and comparing it with the exact solution in (6.2). Additionally, in order to describe the evolution at desired accuracy, Figure 2 describes the numerical solution of Equation (6.1) at different time and on the decomposition level and, respectively.

As shown in the numerical experiment, the numerical solution from the DLWG method is in good agreement with the exact one and illustrates the accuracy and capacity of the DLWG approach proposed in this article.

7. Conclusion

In this paper, the numerical method has been used to solve the advection-diffusion equation with specified initial and boundary conditions. The numerical experiment is presented to demonstrate the high order accuracy and validity of this technique. In particular, this method can be generalized to multi-dimensional cases and be applied to other kinds of PDEs and integro-differential equations.

Acknowledgements

This work is supported by Technological Research Program of Chongqing Municipal Education Commission (Grant No. KJ130818 and KJ130810) and is funded by Fundamental and Advanced Research Project of Chongqing CSTC of China, the project No. are CSTC2013JCYJA00022 and cstc2012jjA00018.

Cite this paper

XiaoyangZheng,ZhengyuanWei, (2015) Discontinuous Legendre Wavelet Galerkin Method for One-Dimensional Advection-Diffusion Equation. Applied Mathematics,06,1581-1591. doi: 10.4236/am.2015.69141

References