Received 3 June 2015; accepted 10 July 2015; published 14 July 2015

ABSTRACT

We study the asymptotic behavior of the solutions of a Hybrid System wrapping an elliptic operator.

Keywords:

Hybrid System, Compressible, Stabilization, Asymptotic Behavior, Decay Rate, Generator Infinitesimal, Polynomial Decay

1. Introduction

In this paper, we address some issues related to the asymptotic behavior a hybrid system with two types of vibrations of different nature. The model under consideration is inspired in and introduced in [1] . However, there are some important differences between these two models. In [1] the flexible part of the boundary 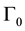is occu- pied by a flexible damped beam instead of a flexible. Most of the relevant properties see [2] . In [3] the authors are interested on the existence of periodic solutions of this system. Due to the localization of the damping term in a relatively small part of the boundary and to the effect of the hybrid structure of the system, the existence of periodic solutions holds for a restricted class of non homogeneous terms. Some resonance-type phenomena are also exhibited. Cindea, Sorin and Pazoto [4] consider the motion of a stretched string coupled with a rigid body at one end and we study the existence of periodic solution when a periodic force facts on the body. The main difficulty of the study is related to the weak dissipation that characterizes this hybrid system, which does not ensure a uniform decay rate of the energy. For more examples of hybrid systems see [5] [6] . We refer to [7] for a discussion on the model and references therein. In [8] the authors to discern exact controllability properties of two coupled wave equations, one of which holds on the interior of a bounded open domain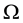, and the other on a segment 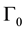of the boundary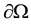. Moreover, the coupling is accomplished through terms on the boundary. Because of the particular physical application involved the attenuation of acoustic waves within a chamber by means of active controllers on the chamber walls control is to be implemented on the boundary only.

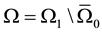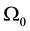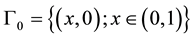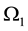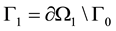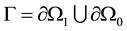We consider the bi-dimensional cavity and that an open class C² with limited boundary contained in Ω₁, filled with an elastic, in viscid, compressible fluid, in which the acoustic vibrations are coupled with the mechanical vibration of a string located in the subset a part of the boundary of omega of, and with 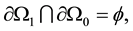is boundary of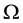. The subset 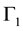is assumed to be rigid and we impose zero normal velocity of the fluids on it. The subset 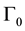is supposed to be flexible and occupied by a flexible string that vibrates under the pressure of the fluid on the plane where 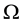lies. The displacement of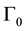, described by the scalar function, obeys the one-dimensional dissipa- tive wave equation. As is compressible fluid where the velocity field is given by the potential All deformations are supposed to be small enough so that linear theory applies.

The linear motion of this system is described by means of the coupled wave equations

(1)

where denote the unit outward normal to.

We define the energy associated with this system. Proceeding formally, multiply the first equation by and then integrate over.

(2)

However, the integral

which leads us

(3)

Replacing (3) into (2) we obtain

(4)

Multiplying by w in the second equation of the system (1) and then integrate over

(5)

Integrating by parts

Replacing the above equation over (5) we obtain

(6)

which leads us to assert that, the energy of the system is given by

(7)

for each.

Remark 1 The first two terms represents the energy of acoustic wave and the other terms is the energy of bungee wave.

The system has a natural dissipation. Indeed, to observe this fact multiply the first equation of (1) by and then the second equation of (1) by, as was done in previous calculations

(8)

if Micu, S. in his doctoral thesis [7] shows non-exponential decay of the energy of the hybrid system (1).

2. Mathematical Formulation

Define the face space endowed with the Hilbertian scalar product given by

(9)

for all We can show that the pair is a Hilbert space.

Since the first and second equation of the system (1), we obtain

These equations lead us to define the operator by

in this sense for all

(10)

Note that if and only if

Now, we consider the problem with Neumann boundary conditions

(11)

where we can say that see [9] . Similarly, consider the problem

(12)

We can say that In this sense we can define the domain of the operator which we denote, as the set of such that satisfying

Remark 2 By previous observations we can say that the hybrid system (1) is equivalent to the Cauchy problem

(13)

where and

3. Solution Existence

We want to show that is a dissipative operator and (The resolvent set of).

Remark 3 The operator is dissipative, ie for all

Applying (9), we get

Resolvent Equation:

Given, we find

(14)

In particular, if and only if, there is

that is,

where By previous observations that there have Using the application of Lummer Phillips Theorem [10] [11] , we have the following result.

Theorem 1 The operator set to (10) is the infinitesimal generator of a contraction semigroup

Theorem 2 The is the infinitesimal generator of a semigroup and verifies then the solution of (13) satisfies

(15)

4. Asymptotic Behavior

We now show that the energy associated with the system decays exponentially. Multiplying by the first equation in (1) and integrating over yields

equivalently

(16)

Observe that

(17)

From the second equation in (1), we obtain

(18)

On the other hand,

(19)

From (17)-(19), we obtain

(20)

Replacing (20) into (16)

(21)

or equivalently

(22)

Now, since Poincaré inequality we have

(23)

where is the Poincaré constant. In a similar way,

(24)

From (22), (23) and (24) we have

(25)

We define the operator

(26)

Differentiating (26) and using (8) we obtain

(27)

Considering n large enough, we can obtain a constant C such that

(28)

On the other hand, using Poincaré, we can obtain

(29)

In a similar way

(30)

Moreover, from trace

(31)

Replacing (31) into (30) we have

(32)

From (23), (29), (32) and (26) we can to claim that there is a constant and such that

(33)

leading to decay exponentially energy

(34)

where. The result follows.

Remark 4 In the case of can be also said that a power decays exponentially.

The above results support the conclusion.

Theorem 3 If and then the solution of the hybrid system (1) decays exponentially over time.

Acknowledgements

Octavio Vera thanks the support of the Fondecyt project 1121120.

Cite this paper

PedroGamboa,Jaime E.Muñoz,OctavioVera,MargarethAlves, (2015) Asymptotic Behavior of a Bi-Dimensional Hybrid System. Applied Mathematics,06,1228-1234. doi: 10.4236/am.2015.68115

References