Received 30 March 2015; accepted 12 May 2015; published 14 May 2015

ABSTRACT

In this paper, we consider an initial-boundary value problem for a nonlinear viscoelastic wave equation with strong damping, nonlinear damping and source terms. We proved a blow up result for the solution with negative initial energy if p > m, and a global result for p ≤ m.

Keywords:

Viscoelastic Equation, Blow Up, Global Existence

1. Introduction

A purely elastic material has a capacity to store mechanical energy with no dissipation (of the energy). A complete opposite to an elastic material is a purely viscous material. The important thing about viscous materials is that when the force is removed it does not return to its original shape. Materials which are outside the scope of these two theories will be those for which some, but not all, of the work done to deform them can be recovered. Such materials possess a capacity of storage and dissipation of mechanical energy. This is the case for viscoelastic material. The dynamic properties of viscoelastic materials are of great importance and interest as they appear in many applications to natural sciences. Many authors have given attention to this problem for quite a long time, especially in the last two decades, and have made a lot of progress.

In [1] , Messaoudi considered the following initial-boundary value problem:

(1.1)

where 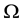was a bounded domain of 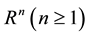with a smooth boundary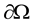, , 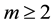p > 2, and 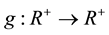was a positive nonincreasing function. He proved a blow up result for the solution with negative initial energy if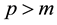, and a global result for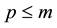. This result was later improved by Messaoudi [2] , to certain solutions with positive initial energy. A similar result was also obtained by Wu [3] using a different method.

For the problem (1.1) in 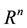and with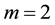, concerning Cauchy problems, Kafini and Messaoudi [4] established a blow up result for the problem

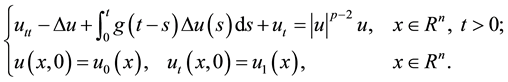(1.2)

where 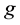satisfied 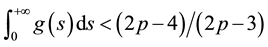and the initial data were compactly supported with negative

energy such that.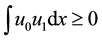

In the absence of the viscoelastic term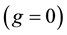, the problem has been extensively studied and results concerning existence and nonexistence have been established. In bounded domains, for the equation

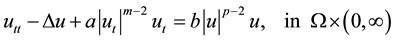(1.3)

, , , it is well known that, for, the source term causes finite time blow up of solutions with negative initial energy (see [5] ). In contrast, for, the damping term assures global existence for arbitrary initial data (see [6] ). The case of linear damping and nonlinear source has been first considered by Levine [7] [8] . He showed that solutions with negative initial energy blew up in finite time. Furthermore, the interaction between the nonlinear damping and the source terms was studied by Georgiev and Todorova [9] , for a bounded domain with Dirichlet boundary conditions. For the same problem, Messaoudi [10] extended the blow up result to solutions with negative initial energy.

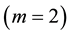
In [11] , Berrimi and Messaoudi considered

(1.4)

in a bounded domain and. They established a local existence result and showed that the local solution was global and decays uniformly if the initial data were small enough.

In [12] , Song and Xue considered with the following viscoelastic equation with strong damping:

(1.5)

where was a bounded domain of with a smooth boundary, , , and was a positive nonincreasing function. They showed, under suitable conditions on, that there were solutions of (1.5) with arbitrarily high initial energy that blow up in a finite time. For the same problem (1.5), in [13] , Song and Zhong showed that there were solutions of (1.5) with positive initial energy that blew up in finite time. For more related works, we refer the reader to [14] - [18] .

In this work, we intend to study the following initial-boundary value problem:

(1.6)

where is a bounded domain with a smooth boundary, , p > 2, , ,

for the problem (1.6), the memory term (see [19] [20] ) replaces,

and we consider the strong damping term and the nonlinear damping term.

Now, we shall add a new variable to the system which corresponds to the relative displacement history. Let us define

(1.7)

A direct computation yields

(1.8)

Thus, the original memory term can be written as

(1.9)

and we get a new system

(1.10)

(1.11)

with the initial conditions

(1.12)

and boundary conditions

(1.13)

The paper is organized as follows. In Section 2, we first prove the blow up result, and then in Section 3, we prove the global existence result.

For convenience, we denote the norm and scalar product in by and, and let. denotes a general positive constant, which may be different in different estimates.

2. Blow Up

In this section, we present some materials needed in the proof of our results, state a local existence result, which can be established, combining the argument of [21] , and prove our main result. For this reason, we assume that

(G1) is a differentiable function satisfying;

(G2);

(G3) There exists a constant such that,;

We start with a local existence theorem which can be established by the Faedo-Galerkin methods. The interested readers are referred to Cavalcanti, Domingos Cavalcanti and Soriano [22] for details:

Theorem 2.1. Assume (G1) holds. Let and

(2.1)

Then for any initial data

,

with compact support, problem (1.10) has a unique solution

for some.

Lemma 2.2. Assume (G1), (G2), (G3) and (2.1) hold. Let be a solution of (1.10), then is nonincreasing, that is

. (2.2)

where

. (2.3)

Proof. By multiplying the Equation in (1.10) by and intergrating over, we get

(2.4)

For the fourth term on the left side (2.4), by using (1.11), (G2) and (G3), we have

(2.5)

where

(2.6)

Then, we obtain

(2.7)

So, we have

(2.8)

where

Our main result reads as follows.

Lemma 2.3. Suppose that (2.1) holds. Then there exists a positive constant such that

(2.9)

for any and.

Proof. If, by Sobolev embedding theorem Young’s inequality, then we have

So, we obtain

If, then

Therefore (2.9) follows.

We get

(2.10)

and use, throughout this paper, C to denote a generic positive constant.

As a result of (2.3) and (2.5), we have

Corollary 2.4. Suppose that (2.1) holds. Then, we have

(2.11)

for any and.

Lemma 2.5. (inequality) Let a, b is arbitrary real, then we have

(2.12)

where

(2.13)

Proof. We set, that is to proof

By taking a derivative of, we obtain

If, then we know is monotone decreasing on and monotone increasing on, and

Then, we have

If, then we know is monotone increasing on and monotone decreasing on. So, we have

The proof is completed.

Next, we have the following theorem concerning blow up.

Theorem 2.6. Assume (G1), (G2), (G3) and (2.1) hold. Let, satisfy (2.1). Assume further that

(2.14)

if and satisfy, then the solution of problem(1.10)blow up in finite time.

Proof. From (2.2), we have

(2.15)

consequently, we have

(2.16)

Similar to [18] , then we define the weighed functional

(2.17)

where shall be chosen in what follows. Let

(2.18)

By multiplying (1.10) by and taking a derivative of (2.17), we obtain

(2.19)

By using Holder inequality and Young’s inequality to estimate the fourth term on the right hand side of (2.19)

(2.20)

for some number with. From (2.3) we have

(2.21)

Then, we have

(2.22)

that is

(2.23)

By using Holder inequality and Young’s inequality to estimate the last two terms on right hand side of (2.24), we obtain

(2.24)

and

(2.25)

and

(2.26)

Substituting (2.24), (2.25) and (2.26) and to (2.23), we have

(2.27)

by taking so that, so, for large K to be specified later, and substituting in (2.28) we obtain

(2.28)

by taking proper, , such that

(2.29)

so, we have

(2.30)

From (2.16), we have

(2.31)

Then, hence (2.31) yields

(2.32)

where, , and taking proper, , such that

,.

Writing, for, we know. By using Corollary2.4 we have

(2.33)

where.

From (2.3) and (G1) we have

(2.34)

writing, where, estimate (2.34) yields

(2.35)

at this point, we choose large enough, so is small enough. Then there exists such that

. (2.36)

By using Holder inequality and Young’s inequality, we next estimate

(2.37)

and

(2.38)

which implies

(2.39)

where, we take, to get by (2.18). We then use Corollary 2.4

(2.40)

By using inequality we have

(2.41)

According to (2.36) and (2.41), we get

(2.42)

where. According to the theorem of Ordinary Differential Equation, we have

(2.43)

So, we know blow up in finite time. The proof is completed.

3. Global Existence

In this section, we show that solution of (1.10) is global if.

Lemma 3.1. For, , is the convexity of the function.

Proof.

,

so, is convex.

Theorem 3.2. Assume (G1), (G2) and (G3) hold. Let satisfy (2.1). If for any initial data with compact support, so problem (1.7) has a unique global solution, such that

for any.

Proof. Similar to [23] , we set

(3.1)

from (2.3), we have

(3.2)

By differentiating and using (2.2), we get

(3.3)

By using Holder inequality and Young’s inequality, we next estimate

(3.4)

Setting, we know is the convexity of function by Corollary 3.1. Since 2 < p ≤ m, we obtain

(3.5)

Substituting (3.5) to (3.3), we have

(3.6)

so, there exist a small enough constant such that

(3.7)

Then, by using Gronwall inequality and continuation principle, we complete the proof of the global existence result.

Acknowledgements

The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.

This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057

References