Received 24 March 2015; accepted 22 April 2015; published 27 April 2015

ABSTRACT

We consider the nonlinear boundary value problems for elliptic partial differential equations and using a maximum principle for this problem we show uniqueness and continuous dependence on data. We use the strong version of the maximum principle to prove that all solutions of two-point BVP are positives and we also show a numerical example by applying finite difference method for a two-point BVP in one dimension based on discrete version of the maximum principle.

Keywords:

Two-Point Boundary, Variational Problem, Stability Restriction

1. Introduction

In this paper, we have considered a simple two-point boundary value problem (BVP) for a second order linear ordinary differential equation. Using a maximum principle for this problem, we show uniqueness and continuous dependence on data.

We write the BVP in variational form and use this together (with elements from functional analysis) we prove existence, uniqueness and continuous dependence on data. The finite difference method is a method for early development of numerical analysis to differential equations. In such a method, an approximate solution is sought at the points of a finite grid of points reducing the problem to a finite linear system of algebraic equations [1] .

In this paper, we illustrate this for a two-point BVP in one dimension in which the analysis is based on discrete versions of maximum principle. Much attention has been paid to the development, analysis and implementation of accurate methods for the numerical solution of this problem in the literature. Many problems are modeled by smooth initial conditions and Dirichlet boundary conditions, see [2] and [3] . We can say that three classes of solution techniques have emerged for solution of BVP for differential equations: the finite difference techniques, the finite element methods and the spectral techniques (see [4] and [5] ). The last one has the advantage of high accuracy attained by the resulting discretization for a given number of nodes [6] [7] and [8] .

2. Variational Formulation

We treat the two-point boundary value problem in Hilbert space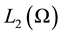. We consider the problem

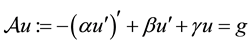
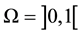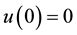in with and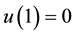. Here the coefficients 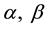and are smooth and

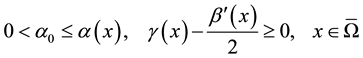
Let 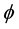an auxiliary function on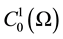, so multiplying Equation (1) by and integrating over 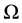we have

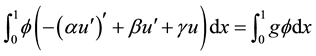
By using integration by parts with 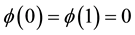we obtain

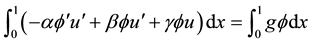
Here (4) is the variational formulation of the problem (1). If we introduce the bilinear form

with the functional, we can write (3) as

for all. We can say that function is a weak solution of the problem (1) provided that and (6) holds.

Next we show two theorems that demonstrate the existence of a solution of the variational equation (6).

Theorem 1. Let and we assume that (2) holds. Then there exists a unique solution of the problem (6) satisfying the condition.

Theorem 2. Let and we assume that (2) holds. Furthermore let and be the solution of the problem (6), then for all where

In theorem 1, we obtain the weak solution u of (6) and this solution is more regular than stated there, therefore exists as a weak function (derivative) and. Hence, it follows that and also

This expression together with where implies the regularity estimates.

We can see that the weak solution of (1) is a strong solution, but we can also see that with less smooth we still obtain a weak solution in.

The next nonlinear boundary problem shows that all solutions are positive by using the strong version of maximum principle.

2.1. Numerical Examples

We consider the nonlinear boundary value problem

in. In the maximum principle, we need to consider a differential operator, i.e. in this case we have

for all. We can see that usually takes the general form

Therefore, we have and. Now, the maximum principle states that for a differential operator and a function with the property that in, if in, then

u and respect the conditions of the principle, the boundary conditions of the problem are. Thus, all solutions of u are

The strong version of the principle refers to the case when there is a minimum interior point inside, which results in a constant value of the function u inside the domain. We know already that, and if we assume that u has a minimum point inside say x₀ then

After this assumption, the expression, but by the initial hypothesis. Here, we have a contradiction, because the assumption that there is a minimum interior point is false. In the other words, the minimum 0 is attained only at the boundaries and all solutions inside the interval are positive, i.e.

2.2. Variation Formulation and Existence of

In this case, we are going to solve

with the following boundary conditions:

2.2.1. Solution with BCs:

Let an auxiliary function with the homogeneous boundary conditions as u,. Multiplying the initial differential operator and the function f by, then expression (7) becomes

Next, integrate over we have

By using integration by parts, we can write the left hand side as

The last term comes down to 0,

therefore, the Equation (8) becomes

which is the variational form of the (7).

Lax-Milgram lemma may allow us to prove existence of a solution. First we consider the LHS and the RHS as a bilinear form and a linear functional respectively, in fact

* (LHS) is a bilinear form because on is a function. Now it is linear in each argument separately,

then is symmetric. To show coercivity of, we can apply Cauchy-Schwarz inequality

Coercivity of in follows

* (RHS). We can see that is a function and L is linear, in fact

The Equation (9) can be written as

since is a bounded bilinear form, coercive in the Hilbert space and is a bounded linear form in the same space, so the Lax-Milgram theorem states that there exists a unique vector i.e. a solution of u exists.

2.2.2. Solution with BCs:

Similar to (7), this equation can be written using the auxiliary function and integration over the domain and in this case.

Therefore, we can see that this function has the same variational formulation, i.e.

Then, we can use the bilinear form and linear functional. Lax-Milgram lemma shows can be subsequently applied to prove the existence of solution in a similar way as before.

2.2.3. Solution with BCs:

Let the auxiliary function with the same boundary conditions,. In this case, the LHS of (7) can be written as

We can see that this quantity represents still a bilinear form

therefore, on is a function and it is linear each argument separately, i.e.

then, is also symmetric. In this case the coercivity on the Hilbert space also applies, in fact

hence Lax-Milgram lemma can be applied to

where is a bilinear, symmetric coercive form and L a linear functional. A solution of u needs to exist in the domain.

3. Case of the Beam Equation

In this section, we give the variational formulation for the beam equation and we prove the existence and uniqueness of solution. We consider the beam equation

with the boundary conditions.

Now, using an auxiliary function with the same BCs as u, and integrating on we get

therefore

Thus, the variational form of the beam equation is

Again, let the bilinear form and linear functional and to be equal to

We can see that is a function and it is linear in each argument separately (as shown previously). Finally is also symmetric, i.e.

Here, the Lax-Milgram theorem can be applied to this system and show existence of a solution for u.

Note: In mechanical representations, the boundary conditions represent the

deflection and the slope of the deflection at the boundaries is 0 which means that the ends of the beam are fixed.

4. Maximum of the Error at the Mesh-Points for 2-Point BVP

In this example, we consider the two-point boundary value problem [9]

with. Applying the finite difference method

with we show in Figure 1 the exact solution and the maximum of the error at the mesh-points.

Figure 1(a) and Figure 1(b) present similar plots. However, a h twice as small decreases the maximal error a 4 fold, shown in Figure 1(c). At the same point x = 0.6, the error is 2.209 × 10⁻⁵ vs. 8.829 × 10⁻⁵. The Logarithmic plot in Figure 1(d) shows a linear relationship between the error and h with slope 8 units.

Acknowledgements

We would like to thank the referee for his valuable suggestions that improved the presentation of this paper and group GEDNOL of the Universidad Tecnológica de Pereira-Colombia.

References