Applied Mathematics
Vol.06 No.03(2015), Article ID:54598,26 pages
10.4236/am.2015.63049
The Weighted Mean Standard Deviation Distribution: A Geometrical Framework
R. Caimmi
Physics and Astronomy Department, Padua University, Padova, Italy
Email: roberto.caimmi@unipd.it
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 February 2015; accepted 11 March 2015; published 12 March 2015
ABSTRACT
The current attempt is aimed to extend previous results, concerning the explicit expression of the arithmetic mean standard deviation distribution, to the general case of the weighted mean standard deviation distribution. To this respect, the integration domain is expressed in canonical form after a change of reference frame in the 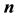 -space, which is recognized as an infinitely thin
-space, which is recognized as an infinitely thin 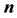 -cy- lindrical corona where the axis coincides with a coordinate axis and the orthogonal section is an infinitely thin, homotetic
-cy- lindrical corona where the axis coincides with a coordinate axis and the orthogonal section is an infinitely thin, homotetic 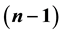 -elliptical corona. The semiaxes are formulated in two different ways, namely in terms of (1) eigenvalues, via the eigenvalue equation, and (2) leading principal minors of the matrix of a quadratic form, via the Jacobi formulae. The distribution and related parameters have the same formal expression with respect to their counterparts in the special case where the weighted mean coincides with the arithmetic mean. The reduction of some results to ordinary geometry is also considered.
-elliptical corona. The semiaxes are formulated in two different ways, namely in terms of (1) eigenvalues, via the eigenvalue equation, and (2) leading principal minors of the matrix of a quadratic form, via the Jacobi formulae. The distribution and related parameters have the same formal expression with respect to their counterparts in the special case where the weighted mean coincides with the arithmetic mean. The reduction of some results to ordinary geometry is also considered.
Keywords:
Standard Deviation, 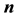 -Spaces, Direction Cosines, Quadratic Forms, Matrix Theory
-Spaces, Direction Cosines, Quadratic Forms, Matrix Theory

1. Introduction
Hyperspace geometry is useful, if not essential, for the interpretation of theories involving many branches of knowledge and, in particular, general relativity (e.g., [1] ) and superstring theory (e.g., [2] ). Though further insight could be gained exploiting a geometrical framework, still pure mathematical analysis is preferred owing to a much greater difficulty in handling with hyperspace geometry.
The geometrical framework of a well known statistical problem, concerning the explicit expression of the arithmetic mean standard deviation distribution, has been considered in an earlier investigation [3] .
The current attempt is aimed at extenting the above mentioned results to the general case of the weighted mean, or in other words searching the explicit expression of the weighted mean standard deviation distribution, under the safely motivated restriction of independent measures obeying Gaussian distributions. Accordingly, the weighted mean standard deviation depends only on the uncertainties on the input data, which is not in con- tradiction with its counterpart inferred from a different approach based on the least-squares method [4] .
The extension of the procedure followed in the parent paper [3] yields results which reduce to their counter- parts therein, in the special case where the weighted mean reduces to the arithmetic mean.
The paper is organized as follows. The problem is outlined in Section 2 together with three steps towards the solution. The first, second, third step are exploited in Sections 3, 4, 5, respectively. In addition, three different attempts are exploited in Section 4. The solution of the problem is shown in Section 6, where a number of (well known) related parameters are also inferred for sake of completeness. The conclusion is drawn in Section 7. Further details are shown in the Appendix, including extension of analytic geometry formulation to 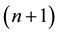 - spaces, Jacobi formulae, reduction of the results to ordinary geometry, and a corrigendum to the parent paper [3] .
- spaces, Jacobi formulae, reduction of the results to ordinary geometry, and a corrigendum to the parent paper [3] .
2. The Problem
Let 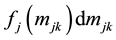 be distributions related to assigned measure methods,
be distributions related to assigned measure methods, 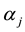 ,
, 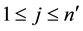 , and a specified
, and a specified
statistical system, where the occurrence of the events, 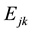 , has been designed by the value of the random var- iables,
, has been designed by the value of the random var- iables, 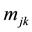 ,
,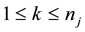 . The special case of Gaussian distributions, which well holds for independent measures, reads:
. The special case of Gaussian distributions, which well holds for independent measures, reads:
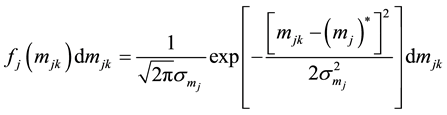 (1)
(1)
where 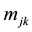 is a generic measure related to the method,
is a generic measure related to the method,  , and
, and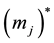 ,
, 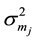 ,
, 

Let 









where 




The additional condition on the coefficients:

ensures that in the special case of distributions with equal expected values, which is the one under consideration,


The further condition that the variance, defined by Equation (4), has to be minimum for fixed data, implies for the coefficients, 

and Equations (2), (3), (4), (6), reduce to:




where 



Expected value and rms error estimators are known to be the weighted mean, 




where 

means the rms error and the deviation relate to the weighted mean: neither 


where 





The substitution of Equation (8) into (12) yields the explicit expression of the deviation in terms of the measures, 

where 
Using a theorem of statistics (e.g., [5] , Chapter 8; [6] , Chapter 2), the deviation distribution reads:


by use of Equation (10).
With regard to Equation (11), the weighted mean standard deviation distribution reads:

where the random variables, 







The deviations, 


Aiming to calculate the multiple integral on the right-hand side of Equation (17), three steps shall be per- formed as in the parent paper [3] , where the weighted mean, 

ed mean standard deviation, 

In dealing with the geometrical framework, for sake of simplicity, the formalism has to be specified as in the parent paper [3] , to which an interested reader is addressed. The extension of useful formulation of analytic geometry to 
3. Expression of 

The generic deviation, 




according to the general definition of error. It is apparent the error of the weighted mean equals the weighted mean of the errors. The substitution of Equation (20) into (18) yields:

which shows the deviation of a measure from the weighted mean of the measures equals the deviation of the related error from the weighted mean of the errors. The right-hand side relation appearing in Equation (21)
represents a 


The substitution of Equation (21) into (11) after some algebra yields:

which represents a one-sheet 


respectively1, and the equator is the intersection between the 


The asymptotes of the 





which may be considered as the equation of the 
The generatrixes lying on the principal plane, 

which can be extended to a generic direction, 


Using general formulation of analytic geometry extended to 












Keeping in mind the 


which implies

that is equivalent to:

where, in the case under discussion of generatrixes, the square coefficient, 


1In the special case of the arithmetic mean, 




and the condition of parallelism between 




Owing to Equation (113), the result is:

where, in the case under discussion of the generatrix, 





Accordingly, the generatrix of the 


which is the 



Let 






which is the 



Let 








where 
Let






which implies 



In summary, the weighted mean standard deviation, 



where the polar axis coincides with the coordinate axis, 


tion that the weighted mean of deviations is null, Equation (21), defines a 


















4. Expression of 

According to the above results, (i) the points, 





where the polar semiaxis of the 

In terms of the errors, 




where, with regard to the middle side, the single sum is made of 






After performing some algebra, Equation (36) may be cast under the equivalent form [6] , Chapter 4:

which is a 


The canonical form of the above mentioned 















Following the procedure outlined in the parent paper [3] , the direction cosines, 


conformly to Equation (32). The remaining coordinate axes, 



gruent provided the Jacobian determinant is orthogonal,
The term, 

which is independent of the coordinate, 




where its counterpart related to 






The 

where the contribution related to the coordinate axis, 



where the coefficients, 







The coordinate, 










4.1. First Attempt
The explicit expression of the coefficients, 



Particularize Equations (39) and (40) to the special case, 






Express the square differences, 

Substitute the above expressions into the second term on the right-hand side of Equation (41) particularized to the case under discussion,
Substitute the result into the right-hand side of Equation (42) particularized to the case under discussion, 


The result is [6] , Chapter 4:




and the recursive application of Equations (43a) and (43c), with due account taken of (43b) and (43d), after some algebra yields:


with regard to 


with regard to 
Finally, the symmetry relations:

are due to the appearence of related coefficients in the expression of a quadratic form on the middle side of Equation (42).
With regard to the 



4.2. Second Attempt
With regard to the 

where the determinant, 
the case under consideration. Due to the symmetry of the elements of quadratic forms, 

Let 




where the coordinates define the same vector in the appropriate reference frame.
The linear transformation reduces to an orthogonal transformation if and only if the elements of the matrix, 

concerning lines and columns, respectively.
According to the theory of linear transformations, the expression of the quadratic form on the left-hand side of Equation (36), in canonical form, takes place via the determination of an orthogonal matrix, 




With regard to the 

where the matrix, 







which is an algebraic equation of degree, 

where the coefficients, regardless of an inessential multiplicative constant, may be expressed as [6] , Chapter 4:

and, in particular:

where the last relation comes from Equation (47) after summation of all lines or columns on a selected line or column which, via Equation (5), yields a line or column made of null elements implying, in turn, a null deter- minant.
With regard to Equation (51a), the existence of 




According to the general theory (e.g., [8] , Tome III, Part I, Chapter II; [9] , Vol. I, Chapter 10), a generic quadratic form where the coefficients are real, as:

can be reduced to the canonical form:

by use of a convenient linear orthogonal transformation, where
In the case under discussion, with regard to Equations (23), (47), (51a), Equation (56) reduces to:

which defines a 





The semiaxes of the 


accordingly, the features of the 



It is apparent from Equation (51a) that the determination of eigenvalues is not an easy matter in the general case,
4.3. Third Attempt
4For sake of convenience, the polar axis here is denoted as 

With regard to the quadratic form, expressed by Equation (55), let 



where


where, in turn, 

(1) The number of positive, 


(2) With regard to the whole set of linear transformations, defined by Equation (60), the number of negative
coefficients, 


for any element of the set, according to the theorem of inertia of quadratic forms (e.g., [8] , Tome III, Part I, Chapter II; [9] , Vol. I, Chapter 10).
Further considerations shall be restricted to linear transformations defined by Jacobi formulae. For additional details, an interested reader is addressed to Appendix B. Using the Jacobi formulae, Equation (60) reduces to:

which is valid in general.
In the case of interest, 

according to Equation (47), and Equation (115) reduces to (47). Finally, Equation (114) reads:

and Equations (116) take the explicit form [6] , Chapter 4:


in addition, Equation (64a) may be expressed via a recursive formula, as:


where inequalities are due to the constraints, 

Let 


where the rank of the matrix, 




By use of Jacobi formulae, Equations (118), the 

which defines a 





4.4. Explicit Expressions
With regard to the 

where the resulting coordinates, 


which implies a rigid rotation around the origin in a 
Let 





in terms of eigenvalues of the matrix, 
The semiaxes of the 



where the leading principal minors, 
In the special case where the weighted mean reduces to the arithmetic mean, 


and the substitution of Equation (72) into (71a) yields:


which shows the current procedure is conceptually different from its counterpart related to the arithmetic mean, where the orthogonal section of the 

The apparent discrepancy can be explained in the following way. Jacobi formulae are grounded on non orthogonal linear transformations which, in themselves, imply changes in metric relations. On the other hand, eigenvalue equations are grounded on orthogonal linear transformations which, in themselves, imply conserva- tion of metric relations.
According to the general theory of linear transformations and quadratic forms (e.g., [8] , Tome III, Part I, Chapter II; [9] , Vol. I, Chapter 10), the coefficients of the eigenvalue equation, expressed by Equations (51)-(52), regardless of an inessential multiplicative constant, coincide with the invariants of the matrix, 
invariants, 








Let



where



where the elements, 



According to the general theory of linear transformations and quadratic forms (e.g., [8] , Tome III, Part I, Chapter II; [9] , Vol. I, Chapter 10), the above mentioned systems of equations read:

where 





The validity of the eigenvalue equation, expressed by Equation (51), necessarily implies the determinant of the system, defined by Equation (77), is null in the case of interest or, in other words, the existence of infinite solutions. On the other hand, the condition of unit norm:

allows the selection of a special solution (regardless of the sign) among infinite others.
The particularization of the system, defined by Equation (77), to the case of interest, 


which is equivalent to:

accordingly, the following relations hold:

and the substitution of Equation (81) into (78), particularized to

where the positive sign relates to Equation (38).
Using the definition of matrix product, Equation (76) takes the explicit form:


where, in the case under discussion of orthogonal linear transformations, the inverse matrix, 



which is related to the eigenvalue, 


In summary, the weighted mean standard deviation distribution can be expressed as a function of the errors, 

where 




Finally, 


where 


5. Expression of 


The substitution of Equations (10) and (86) into (85), after little algebra yields:

the special case, 
With regard to the resulting reference frame, 

which necessarily implies the following:

conformly to Equation (82).
The weighted mean of the errors, expressed by Equation (20), by use of Equations (83b) and (89), after little algebra may be cast under the equivalent form:

and the substitution of Equations (23) and (90) into (35) yields:

in terms of a single resulting coordinate,
Figure 1. The integration domain, 







The transformation, 

With regard to the resulting reference frame, 



where the integration domain, 



With regard to the principal 







5A negative Jacobian determinant, 


where 

Figure 2. The integration domain, 












and the particularization of Equation (93a) to the simplest cases, 

with regard to points, segments, ellipses, ellipsoids, respectively.
In particular, 


Accordingly, the 0-ellipse coincides with the origin of the reference frame, 


may safely be put equal to 0, hence

The 


which is independent of the reference frame.
In summary, the weighted mean standard deviation distribution, 





where the integration domain of the ordinary and the multiple integral are the axis and the 


6. The Solution
The substitution of Equations (58) and (96) into (97), after long but stimulating algebra yields [6] , Chapter 4:

where due account has been paid to Equations (94a), (94c), together with the normalizing condition:

which, after integration as outlined above via Equation (97), is equivalent to:

according to Equation (98) that, in addition, can be related to a chi square distribution with 
The distribution, 





The expected values, 



and the rms error of the weighted mean standard deviation distribution, 

which, for

where the ratio, 
In summary, the weighted mean standard deviation distribution is explicitly expressed by Equation (98) and related expectation values, 


tively. Finally, an asymptotic formula involving 
7. Conclusions
6In ordinary plane and space, ellipses and triaxial ellipsoids are referred to as having biaxial and triplanar symmetry, respectively. By extension to 





The weighted mean standard deviation distribution and related parameters have been determined following a procedure where the geometrical framework is clearly shown using typical formulation generalized to 


In the special case where the weighted mean reduces to the arithmetic mean, the results of the current paper reduce to their counterparts (where present) in the parent paper [3] . In particular, the integration domain reduces to an infinitely thin 


Acknowledgements
A more extended version of the current attempt appears in a specific textbook [6] by the author.
Cite this paper
R.Caimmi, (2015) The Weighted Mean Standard Deviation Distribution: A Geometrical Framework. Applied Mathematics,06,520-546. doi: 10.4236/am.2015.63049
References
- 1. Misner, C.W., Wheeler, J.A. and Thorne, K.S. (1973) Gravitation. W.H. Freeman & Company.
- 2. Greene, B. (1999) The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory. W.W. Norton, New York.
- 3. Caimmi, R. (2013) The Arithmetic Mean Standard Deviation Distribution: A Geometrical Framework. Applied Mathematics, 4, 1-10.
- 4. Malkin, Z.M. (2013) On the Calculation of Mean-Weighted Value in Astronomy. Astronomy Reports, 57, 882-887.
http://dx.doi.org/10.1134/S1063772913110048 - 5. Gnedenko, B. (1978) The Theory of Probability. Mir, Moscow.
- 6. Caimmi, R. (2014) Il Problema della Misura. Aracne, Roma. (In Italian, In Press)
- 7. Papoulis, A. (1965) Probabilities, Random Variables, and Stochastic Processes. McGraw-Hill, New York.
- 8. Smirnov, V. (1970) Cours de Mathè matiques Supè rieures. Mir, Moscow.
- 9. Gantmacher, F.R. (1966) Théorie des Matrices. Dunod, Paris.
- 10. Spiegel, M.R. (1969) Mathematical Handbook of Formulas and Tables. Schaum’s Outline Series, McGraw-Hill, New York.
Appendix
A. Analytic Geometry Formulation Extended to 
Analytic geometry formulation extended to 

Let 




where 





Let



which, in the case of interest

where 


Let 

where 



Let




which, in the case of interest (







where 




The condition of parallelism between the straight line, 



which, in the case of interest

where 

B. Jacobi Formulae
With regard to the quadratic form, defined by Equation (51), let the following linear forms be defined:

where 

and let the leading principal minors of the discriminant of the quadratic form, 


where 


and let 









which allow an explicit expression of Equation (60).
For further details, an interested reader is addredded to specific textbooks (e.g., [8] , Tome III, Part I, Chapter II; [9] , Vol. I, Chapter 10).
C. Reduction to Ordinary Geometry
Aiming to get further insight on the general results related to 


C.1. Ordinary Planes
In the special case, 

and the related eigenvalue equation, expressed by Equation (51), reduces to:

where eigenvalues can be calculated by equating each factor to zero, using Equation (5). The result is:

The canonical equation of the quadratic form, expressed by Equations (56)-(57), reduces to:

and the related orthogonal transformation, defined by Equation (69), reduces to:

finally, the system of equations, expressed by Equation (77), reduces to:

and the substitution of Equation (121) into (124), using Equation (5), after some algebra yields:

On the other hand, the condition of unit norm, expressed by Equation (78), reduces to:

and the combination of Equations (125) and (126) yields:

finally, the substitution of Equation (127) into (123) produces:

where, in addition, the substitution of Equation (128) into (122) yields Equation (120), as expected.
The coefficients and the linear forms appearing in Jacobi formulae, expressed by Equations (64) and (66), respectively, using Equation (5), reduce to:


and the canonical expression of the quadratic form, appearing on the left-hand side of Equation (67), reduces to:

where, in addition, the substitution of Equation (130) into (131) yields Equation (119), as expected.
The equivalence of alternative canonical formulations, expressed by Equation (68), reduces to:

and the substitution of Equation (121) into (132) yields:

which shows the connection between coordinates, 

The canonical equation of the 



where the substitution of Equation (121) into (134) yields:

with regard to eigenvalue equation and, using Equation (132):

which is equivalent to:

with regard to Jacobi formulae. In any case, the 
C.2. Ordinary Spaces
In the special case, 

and the related eigenvalue equation, expressed by Equation (51), reduces to:

where eigenvalues can be calculated by equating each factor to zero, using Equation (5). The result is:




where the discriminant, 
The canonical equation of the quadratic form, expressed by Equations (56) and (57), reduces to:

and the related orthogonal transformation, defined by Equation (69), reduces to:

finally, the system of equations, expressed by Equation (77), reduces to:

and the substitution of Equations (140) into (143), using Equation (5), after some algebra yields:

On the other hand, the condition of unit norm, expressed by Equation (78), reduces to:

and the combination of Equations (144) and (145) yields:

where 


and the substitution of Equation (147) into (144) after some algebra yields:

according to the condition of unit norm.
The system of equations, expressed by Equation (143), 
Concerning the special case, 

where the condition of unit norm selects the solution:

which completely specifies the orthogonal transformation, defined by Equation (142).
The substitution of Equation (142) into (141), via comparison with Equation (138) term by term, after some algebra yields [6] , Chapter 4:






which have been cheched numerically for assigned choices of the input parameters, 


The coefficients and the linear forms appearing in Jacobi formulae, expressed by Equations (64) and (66), respectively, using Equation (5), reduce to:



and the canonical expression of the quadratic form, appearing on the left-hand side of Equation (67), reduces to:

where, in addition, the substitution of Equations (153)-(154) into (155) yields Equation (138), as expected.
The equivalence of alternative canonical formulations, expressed by Equation (68), reduces to:


and the substitution of Equations (140a), (140b), into (156), (157), respectively, after some algebra yields:


which shows the connection between coordinates, 

The canonical equation of the 



where the substitution of Equations (140a)-(140b), into (160) yields:

with regard to eigenvalue equation and, using Equations (156)-(157):

with regard to Jacobi formulae. In any case, the 


with regard to eigenvalue equation, and:


with regard to Jacobi formulae.
D. Corrigendum [3]
Additional help to an interested reader could arise from the following corrigendum to a quoted earlier attempt devoted to the arithmetic mean [3] .
p. 2, right column: Equations (9) and (10) are inferred via Equation (8) instead of Equation (6).
p. 3, left column: the extension of usual formulation of analytic geometry has to be intended to 

p. 3, right column: Equation (18) relates to the polar intead of equatorial semiaxis.
p. 4, right column: Equation (30) relates to a 




p. 4, right column: Equation (30) relates to the polar intead of equatorial semiaxis.
p. 4, right column: the intersection, 


p. 5, left column:


p. 5, left column: to avoid ambiguity, the direction cosines should be defined as 









p. 6, left column: the integration domain, 


p. 8, left column: 

p. 8, left column: Equation (49) has to be considered instead of (18) for determining Equation (60).
NOTES
2In particular, 2-sector reads bisector, 3-sector reads trisector, 4-sector reads quadrisector, and so on.
3In particular, 2-ant reads versant, 4-ant reads quadrant, 8-ant reads octant, and so on.









