Received 15 August 2014; revised 10 September 2014; accepted 6 October 2014

ABSTRACT

We propose and demonstrate an original geometric argument for the ancient Babylonian square root method, which is analyzed and compared to the Newton-Raphson method. Based on simple geometry and algebraic analysis the former original iterated map is derived and reinterpreted. Time series, fixed points, stability analysis and convergence schemes are studied and compared for both methods, in the approach of discrete dynamical systems.

Keywords:

Babylonian Square Root Method, Newton-Raphson Method, Iterated Map, Dynamical Systems

1. Introduction

The oldest known algorithm for successive numerical approximations to the square root of a real number was created by the Babylonians (1950 BC-648 BC) as reported by the Greek mathematician Heron of Alexandria [1] in the first century of our era, named as the Babylonian Method (BABM) in this work. The equivalent mathematical problem has been addressed in the seventeenth century by a more general method to solve numerically the equation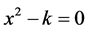, the famous Newton-Raphson method (NRM) [2] . In spite of having been studied and applied for centuries, the lack of a geometric argument to the Babylonian square root method has been a missing link for a better understanding of the ancient Babylonian’s mathematics.

Recent applications of iterated maps in numerical analysis have been found in literature, using and extending the techniques of dynamical systems to the study of numerical algorithms and number theory [3] - [5] . Application in technology and hardware devices are also frequent nowadays [6] - [9] .

In this work, we study and compare two methods that are based on iterated maps, and some common tools from nonlinear dynamics [10] [11] are used to study the orbits, i.e., the numerical time series obtained for each map are investigated. The numerical approximations 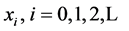to solve the general equation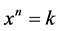, where 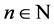and 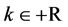are obtained, and the results are valid for positive real values of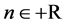. The exact solution is found at the fixed point of each map and its stability is tested. We propose an original geometric argument to construct graphically the BABM basic equation and fill the gap left by this early Babylonian method. We show that both NRM and BABM reduce to a common map for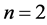, in spite of having different geometric arguments, and also that the BABM cobwebs are simpler than the NRM ones.

2. The Numerical Methods

From the point of view of discrete dynamic systems BABM is a one-dimensional iterated map defined over the set of real numbers 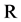and over a one-dimensional parameter space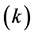. The basic idea implemented in this map is that if 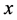is an overestimation for the square root of a real number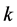, then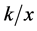, will be underestimated and thus the arithmetic mean of these two numbers can be used as best numerical approximation to the exact root. Repeating this procedure with the new value obtained, the approximation can be refined, and so on. The demonstration that this method usually depends on the inequality between arithmetic and geometric mean shows that this average is always an overestimation of the square root, ensuring convergence to the exact root. This algorithm has a quadratic convergence, which means that the number of digits of the numerical approximations nearly doubles at each iteration [12] .

The Babylonian method (BABM) is based on the iterated map defined by

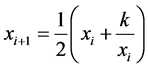(1.1)

where 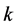is the radicand and 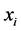are the successive numerical approximations for the square root of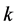. The initial condition is arbitrarily chosen. For example, Table 1 shows the BABM approximations for the square root of 2, i.e., in Equation (1.1) parameter and. In this case, after six iterations the approximation converges to the exact numerical value of within the standard double precision, i.e., to 16 significant digits.

The BABM can be seen as particular case of the more general NRM used to evaluate a zero of the function

(1.2)

The geometric construction used by NRM can be reduced to the following geometric path: 1) take an initial value as an approximation of the root of; 2) find the value of the function; 3) draw a tangent line from the function at that point using its derivative at this point; 4) determines the intersection of the tangent with the -axis, to find the next approximation to the root; 5) increment to and return to step 2). This algorithm is graphically illustrated in Figure 1(a).

The numerical approximations generated by the NRM method are in general represented by the iterated map

(1.3)

where indicates the i-th iteration of the map and is the derivative of the function at. For the case we are studying the function is used (1.2) and the derivative of this function is, assigning these values in Equation (1.3) we obtain

(1.4)

which is exactly the same BABM iterated map function.

3. The Hidden Geometry

There is no historical report showing any geometric argument perhaps used to construct the BABM, but in this section we propose a simple and original one, in the same spirit of that used to construct the NRM. Figure 1(b) shows the schematic geometric path used by the BABM, so that we gain a more intuitive understanding of the convergence schema of this map that permits to demonstrate Equation (1.1).

The root of the function (1.2) is found by approximation, from the initial condition, doing arithmetic mean between two numbers. We assume that the root is between two points, do the arithmetic mean between these two points we are closer and closer to the root. These two points are and and the average between them is the next point in the series, closer to the exact root. So, from the initial condition, the auxiliary point is found, and their average renders the next point of the map series, as shown in Figure 1(b). This point is obtained by knowing the equation of the auxiliary straight line, that intersect the -axis at the auxiliary point. This line contains the auxiliary point, vertex of the parabola.

Given an initial condition we start the geometric path construction. The first step is to find out the equation of the first auxiliary line, whose slope is. According to Figure 1(b), and, and the slope is, and replacing for their function (1.2) we find the slope,

(1.5)

that generates the series recursively.

Drawing the straight line whose linear coefficient is passing through the point, we have, and the auxiliary point can be found when, which is the intersection point of the line with the -axis, and solving we finally find the auxiliary points, for, and the original Equation (1.1) of BABM is exactly recovered. The term corresponds to the auxiliary point, and the BABM basically works by doing the arithmetic mean between these points.

The convergence analysis of time series generated by BABM will be done analytically and graphically by determining the its fixed point and testing its stability. By inspecting Equation (1.1) we see its general form, with the mapping function

(1.6)

where is a fixed parameter, that will be analyzed below.

In general, the first values of the series are irregular, not having a well defined pattern, and this irregular initial behaviour is called the transient. After discarding the transient, the values of can basically: 1) cycle between fixed values, or a period- orbit; 2) assume an aperiodic bounded sequence of values that are never repeated, or a chaotic orbit; 3) an unbound orbit, or divergence.

When a series converges asymptotically to a single fixed value, the fixed point, we have an orbit of period-. An attractive fixed point of a function is a fixed point of such that for any value of in the domain that is close enough to, the iterated function sequence, , , , , converges to. An expression of prerequisites and proof of the existence of such solution is given by Banach’s fixed point theorem [13] . An attractive fixed point is also called a stable fixed point. However, if the map is continuously differentiable in an open neighbourhood of a fixed point, the stability criterion (1.10) is satisfied.

4. Fixed Points and Stability Analysis

For the analytical determination of a fixed point, we have to solve the equation, or

(1.7)

that for BABM is

(1.8)

whose solution for renders

(1.9)

and the existence of this fixed points is the starting point to use the map for square root extraction. For the stability of the fixed point of the map, we have to ensure that

(1.10)

which is the general condition for stability of fixed points of any onedimensional map [14] . Since is the derivative of the function (1.6), we have,

(1.11)

and according to the stability criterion (1.10), that at the point fixed (1.9) is

(1.12)

and its fixed points are both stable, regardless of the value of, so the stability criterion is verified with no dependence on this parameter.

Another important tool to analyze the orbit of a map and its evolution in time is called return diagram or cobweb. A cobweb is built with all the values of obtained in series to construct a graph that has coordinates to the -axis and for the -axis, recursively following the steps: 1) choose an initial condition and iterate the map to obtain the next point; 2) draw the line segment from to; 3) join this point to point on the identity line; 4) use this point to return to -axis, joining it to point; 5) go to to step 2).

Figure 2(a) shows the BABM cobweb for the square root of 2. Plotted on the graph is the equation of BABM, the identity function and the return diagram, for the initial condition. Figure 2(b) plots separately the linear and nonlinear terms of Equation (1.4) indicating that when the linear term has a weight greater than he nonlinear one the map converges to the root, independent of the values of parameters and. For parameter, Figure 2(b) shows in red the linear term in NRM, in green the nonlinear term and in blue the sum of both terms, according Equation (1.4). The identity function is drawn in black and yellow is used for

the tangent line at the fixed point of the map. The linear term has a greater weight ensuring that,

what guarantees that the fixed point is stable. Other important information we can obtain from this figure is the stability of the fixed point, since the map function has a minimum exactly at fixed point, and thus the derivative of the map is zero at this point. According to the stability criterion this is necessary and sufficient condition for the fixed point to be stable.

5. Conclusions

The use of iterated maps to solve the fundamental mathematical problem of square root estimation by numerical approximations was revisited and some tools from nonlinear dynamics were used to predict their stable fixed points and test the behaviour of the corresponding time series over a large region of parameter.

The main result of this paper is fulfilled once we have proposed and demonstrated an original geometric argument to the underlying geometry in the Babylonian square root method, the oldest known and one of the most efficient methods to solve this classical and current problem. The proposed argument is very simple and intuitive, and can be easily extended to other similar maps, and perhaps its basic idea could be useful for constructing new iterated maps, from the geometrical point of view.

Acknowledgements

This work was partially supported by the Brazilian agency Conselho Nacional de Desenvolvimento Cientfico e Tecnológico―CNPq and Universidade do Estado de Santa Catarina―UDESC.

References

NOTES

^*Corresponding author.