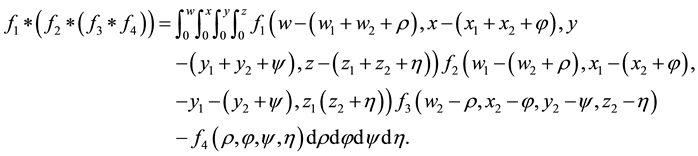Applied Mathematics
Vol.05 No.21(2014), Article ID:52117,10 pages
10.4236/am.2014.521314
A Computational Quadruple Laplace Transform for the Solution of Partial Differential Equations
Hamood Ur Rehman1, Muzammal Iftikhar1, Shoaib Saleem1, Muhammad Younis2, Abdul Mueed3
1Department of Mathematics, University of Education, Okara Campus, Okara, Pakistan
2Center for Undergraduate Studies, University of the Punjab, Lahore, Pakistan
3Air University Multan Campus, Multan, Pakistan
Email: hamood84@gmail.com, muzamil.iftikhar@ue.edu.pk, shaby455@yahoo.com, younis.pu@gmail.com, abdulmueed3@hotmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 11 October 2014; revised 2 November 2014; accepted 16 November 2014
ABSTRACT
In this paper, we proposed new results in quadruple Laplace transform and proved some properties concerned with quadruple Laplace transform. We also developed some applications based on these results and solved homogeneous as well as non-homogeneous partial differential equations involving four variables. The performance of quadruple Laplace transform is shown to be very encouraging by concrete examples. An elementary table of quadruple Laplace transform is also provided.
Keywords:
Quadruple Laplace Transform, Exact Solution, Convolution, Partial Differential Equation, Homogeneous and Non-Homogeneous Problems

1. Introduction
Many engineering and science fields encounter linear or non-linear partial differential equations describing the physical phenomena. A number of methods (for example, approximate and exact methods) can be used to determine the solutions of differential equations. Mostly, it may be complicated to solve these equations analytically. Such equations are commonly solved by integral transforms such as Laplace and Fourier transforms and the worth of Laplace and Fourier transforms lies in their ability to transform differential equations into algebraic equations, which allows a systematic and simple way to find solution. The numerical methods can provide approximate solutions rather than analytic solutions of the problems [1] . A number of aspects of these methods have been studied in [2] [3] .
The Laplace transform has been effectively used to solve linear and non-linear ordinary and partial differential equations and is used extensively in electrical engineering. The Laplace transform reduces a linear differential equation to an algebraic equation, which can be solved by rules of algebra. The original differential equation can then be solved by applying the inverse Laplace transform. The Heaviside first proposed a scheme, without using the Laplace transform (see [4] and references therein).
Eltayeb and Kiliçman [5] applied double Laplace transform to find the solution of general linear telegraph and partial integro-differential equations. Dahiya and Najafai [6] established new theorems for calculating the Laplace transforms of n-dimensions and application of these theorems to a number of commonly used special functions was considered, and in the end, authors solved one-dimensional wave equation involving special functions using two dimensional Laplace transforms. Aghili and Moghaddam [7] presented a new theorem and corollary on multi-dimensional Laplace transformations. Authors further developed some applications based on these results. Kiliçman and Eltayeb [8] discussed the relationship between Sumudu and Laplace transforms and further made some comparison on the solutions. Authors provided some counter examples. Cheniguel and Reghioua [9] investigated the solution of three-dimensional diffusion equation with non-local condition using Adomian decomposition method. Atangana [4] introduced the triple Laplace transform. Author discussed some properties and theorems about the triple Laplace transform. Moreover, author used the operator to solve some kind of third-order differential equation.
The aim of this paper is to discuss some properties and theorems about the quadruple Laplace transform and give a good strategy for solving the fourth order partial differential equations in engineering and physics fields, by quadruple Laplace transform.
First of all, we recall the following definitions.
The double Laplace transform of a continuous function 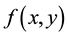 can be defined [5] [10] as
can be defined [5] [10] as
 (1.1)
(1.1)
where x, y > 0 and p, q are Laplace variables.
The inverse double Laplace transform is defined as
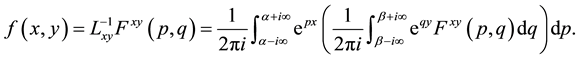 (1.2)
(1.2)
The triple Laplace transform [4] of a continuous function 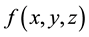 can be defined as
can be defined as
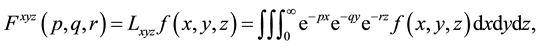 (1.3)
(1.3)
where x, y, z > 0 and p, q, r are Laplace variables.
The inverse triple Laplace transform is defined as
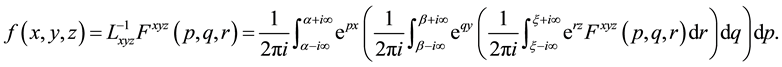 (1.4)
(1.4)
In the following section definitions of quadruple Laplace transform, its inverse and some of its properties are presented.
2. Definitions and Properties
Before launching into the main part of the paper, we define some notations and terminologies which will remain standard.
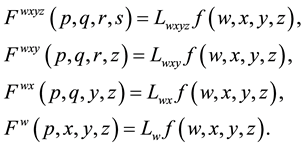
Quadruple Laplace transform: Let f be a continuous function of four variables, then, the quadruple Laplace transform of 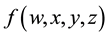 is defined by
is defined by
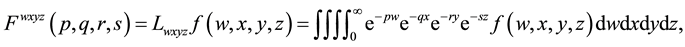 (2.1)
(2.1)
where w, x, y, z > 0 and p, q, r, s are Laplace variables.
It is to be noted that the quadruple Laplace transform operator is linear.
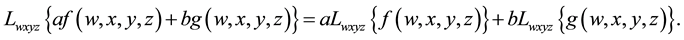 (2.2)
(2.2)
Now, if the quadruple Laplace transform is known, its inverse is given by
 (2.3)
(2.3)
Quadruple Laplace transform for some partial derivatives of function of four variables are given as
1) Quadruple Laplace transform for first order partial derivative of function of four variables
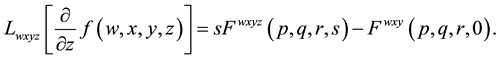 (2.4)
(2.4)
2) Quadruple Laplace transform for second order partial derivative of function of four variables
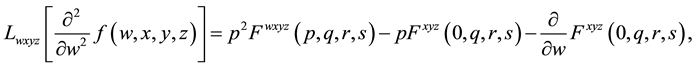 (2.5)
(2.5)
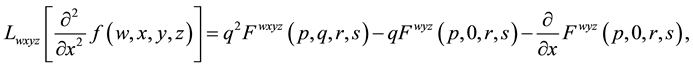 (2.6)
(2.6)
 (2.7)
(2.7)
3) Quadruple Laplace transform for the mixed fourth order partial derivative of function of four variables
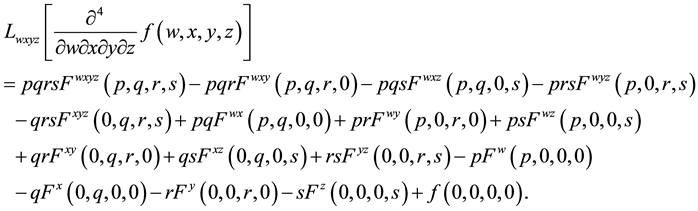 (2.8)
(2.8)

The uniqueness and existence of the quadruple Laplace transform is discussed in the following section.
3. Uniqueness and Existence of the Quadruple Laplace Transform
Consider 





The quadruple Laplace transform

exists for all



Theorem 1. Let 





Proof If 

Using the hypothesis, 

this completes the proof.
4. Convolution Theorem for the Quadruple Laplace Transform
In this section, we will give some definitions of convolution for functions and state the convolution theorem of the quadruple Laplace transform.
Consider the functions



The convolution of functions 


The convolution of functions



Similarly, the convolution of functions



Theorem 2. (Convolution Theorem) If



are convergent at the point 

is absolutely convergent, then, the following expression

is the Laplace transform of the function

and the integral

is convergent at the point
5. Properties of Quadruple Laplace Transform
In this sectioon, some properties of quadruple Laplace transform are presented
Property (1)

Proof: By definition (2.1) of quadruple Laplace transform left hand side of (5.1) can be solved as

The inner integral with respect to z in Equation (5.2) can be solved after proper substitution as

Equation (5.2) becomes

The inner integral with respect to y in Equation (5.4) can be solved after proper substitution as

After substituting the value from Equation (5.5) in Equation (5.4), we can get

On the similar lines, integrating Equation (5.6) twice accordingly, we can obtain required result Equation (5.1).
Property (2)

Proof: By definition (2.1) of quadruple Laplace transform right hand side of (5.7) can be solved as

The inner integral with respect to z can be solved, after proper substitution as

On the similar lines, integrating Equation (5.9) with respect to y, x, w after proper substitution, we can obtain required result Equation (5.7).
Property (3)

Proof: By definition (2.1) of quadruple Laplace transform left hand side of (5.10) can be solved as

The inner integral with respect to z can be solved by parts and gives

Equation (5.11) becomes
On the similar lines, integrating Equation (5.13) accordingly with respect to y, x, w, we can obtain required result Equation (5.10).
Theorem 3. A function 



To check the efficiency of the theorem, we consider the following example.
Let 

Taking higher order mixed derivatives of Equation (5.14), leads
Using (5.14) and theorem 5.1, yields
Using the application of logarithm and the L’Hospital’s rule on the previous expression reveals

6. Numerical Examples
To illustrate the applicability and effectiveness of our method, some examples are constructed in this section.
Example 4.1. Consider the following fourth order partial differential equation
Applying quadruple Laplace transform 

where

After substituting the value, Equation (6.1) becomes

Applying the quadruple inverse Laplace transform on (6.3)

Example 4.2. Consider the following three-dimensional diffusion equations [9]
Applying quadruple Laplace transform 

where

After substituting the value of

Applying the quadruple inverse Laplace transform on (6.7)

Example 4.3. Consider the following non-homogeneous fourth order partial differential equation
Applying quadruple Laplace transform 

where

After substituting the value of

Applying the quadruple inverse transform on (11)

Example 4.4. Consider the following non-homogeneous three-dimensional diffusion equation
Applying quadruple Laplace transform 

where

After substituting the value

Applying the quadruple inverse transform on (6.15)

7. Conclusion
In this paper, we extend the work of [4] [5] to quadruple Laplace transform. Existence and uniqueness of the quadruple transform are also discussed in this work. Some properties, theorems using the new quadruple Laplace transform and a table in which quadruple Laplace transform applied on some functions have also been presented. It is analyzed that our proposed method is well suited for use in partial differential equation involving four variables. Therefore, the present method is an accurate and reliable technique for the partial differential equations.
References
- Kurnaz, A. and Oturanç, G. (2005) N-Dimensional Differential Transformation Method for Solving Partial Differential Equations. International Journal of Computer Mathematics, 167, 369-380. http://dx.doi.org/10.1080/0020716042000301725
- Evans, D.J., Ergu, M. and Bulut, H. (2003) Variational Iteration Method―A Kind of Nonlinear Analytical Technique: Some Examples. International Journal of Computer Mathematics, 80, 1189-1198. http://dx.doi.org/10.1080/00207160310001597161
- Inc, M. and Evans, D.J. (2004) An Efficient Approach to Approximate Solutions of Eighth-Order Boundary-Value Problems. International Journal of Computer Mathematics, 81, 685-692. http://dx.doi.org/10.1080/0020716031000120809
- Atangana, A. (2013) A Note on the Triple Laplace Transform and Its Applications to Some Kind of Third-Order Differential Equation. Abstract and Applied Analysis, 2013, Article ID: 769102. http://dx.doi.org/10.1155/2013/769102
- Eltayeb, H. and Kiliçman, A. (2013) A Note on Double Laplace Transform and Telegraphic Equations. Abstract and Applied Analysis, 2013, Article ID: 932578. http://dx.doi.org/10.1155/2013/932578
- Dahiya, R.S. and Saberi-Nadjaf, J. (1999) Theorems on N-Dimensional Laplace Transforms and Their Applications. 15th annual Conference of Applied Mathematics, Univ. of Central Oklahoma, Electronic Journal of Differential Equations, 02, 61-74.
- Aghili, A. and Moghaddam, B.S. (2008) Laplace Transform Pairs of n-Dimensions and Second Order Linear Partial Differential Equations with Constant Coefficients. Annales Mathematicae et Informaticae, 35, 3-10.
- Kiliçman, A. and Eltayeb, H. (2012) Some Remarks on the Sumudu and Laplace Transforms and Applications to Differential Equations. ISRN Applied Mathematics, 2012, Article ID: 591517. http://dx.doi.org/10.5402/2012/591517
- Cheniguel, A. and Reghioua, M. (2013) Ton the Numerical Solution of Three-Dimensional Diffusion Equation with an Integral Condition. Proceedings of the World Congress on Engineering and Computer Science 2013, II, 23-25.
- Ditkin, V.A. and Prudnikov, A.P. (1962) Operational Calculus in Two Variables and Its Applications. Pergaman Press, New York. (English Translation from Russian)
- Kanwal, R.P. (2013) Generalized Functions Theory and Applications. Proceedings of the World Congress on Engineering and Computer Science 2013, II, 23-25.
Appendix
Table 1. of quadruple Laplace transform Lwxyz for functions of four variables.