Applied Mathematics
Vol.5 No.16(2014), Article
ID:49429,8
pages
DOI:10.4236/am.2014.516240
Entanglement and Quantum Discord of Two Moving Atoms
Nour Zidan
Mathematics Department, Faculty of Science, Sohag University, Sohag, Egypt
Email: nazidan@yahoo.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 June 2014; revised 31 July 2014; accepted 12 August 2014
ABSTRACT
In this paper we discuss two measures for the quantumness of correlations (quantum discord and entanglement) of two isolated moving atoms which are initially in Werner state. We compare and analyze the effect of the atomic motion in quantum discord and entanglement. The results show that the atomic motion related to the field mode structure parameter can make the entanglement and quantum discord evolve periodically. The results also indicate that the entanglement suddenly disappears during the evaluation but quantum discord remains non zero, so quantum discord is considered as indicator of disentanglement.
Keywords:Quantum Discord, Concurrence, Moving Atoms, Werner State

1. Introduction
Entanglement is a kind of quantum correlation that has been regarded as a valuable resource for quantum information processing [1] . However, it is was shown both theoretically [2] and experimentally [3] that some mixed separable states allow one to realize the advantages of quantum algorithms in comparison with their classical analogies and quantum nonlocality has been observed in the systems without entanglement [4] [5] . Such observations suggest us to conclude that the entanglement is not the only type of quantum correlation for quantum technology. A new but promising candidate is quantum discord first introduced by Ollivir and Zurek, which is used to quantify all nonclassical correlation in a system [6] . Quantum discord is built on the fact that two classical equivalent ways of defining the mutual information turn out to be inequivalent in the quantum domain. It is observed that quantum discord is a more general measure of quantum correlation that may include entanglement but is an independent one. Moreover, quantum discord provides a larger region of quantum states with nonclassical correlations, and a nonzero quantum discord but not entanglement may be responsible for the efficiency of a quantum computer [3] -[7] . Therefore, quantum discord could be a new resource for quantum information processing. Recently, numerous works have been devoted to the study of quantum discord [8] -[12] . Usually, quantum discord is somewhat difficult to calculate and we cannot obtain analytical solutions. But in [13] , the authors evaluated the quantum discord for a family of two-qubit states and obtained analytical formulas. For more general quantum states, such as the so-called 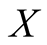 states, the authors [14] -[21] derived explicit expressions for quantum discord and found that the quantum discord, entanglement and classic correlation were independent measures of correlations with no simple relative ordering. An extreme example is realized in the search of maximally discordant mixed states. It has revealed that states maximizing the quantum discord for given value of the classical correlations do not maximize the entanglement and are, in some cases, even separable [22] . Very recently a reliable and effective algorithm for the evaluation of the quantum discord of the general two-qubit states was presented, where the optimization problem for the quantum discord was expressed in a compact form [23] . In this work, we calculate and compare the time evolution of quantum discord and concurrence of two moving isolated atoms. This paper is organized as follows. In Section 2, we give the model and its solution. In Section 3, we give two types of measures including quantum discord and concurrence to analyze quantum correlation. Numerical results and discussion are given in Section 4. Finally we conclude in Section 5.
states, the authors [14] -[21] derived explicit expressions for quantum discord and found that the quantum discord, entanglement and classic correlation were independent measures of correlations with no simple relative ordering. An extreme example is realized in the search of maximally discordant mixed states. It has revealed that states maximizing the quantum discord for given value of the classical correlations do not maximize the entanglement and are, in some cases, even separable [22] . Very recently a reliable and effective algorithm for the evaluation of the quantum discord of the general two-qubit states was presented, where the optimization problem for the quantum discord was expressed in a compact form [23] . In this work, we calculate and compare the time evolution of quantum discord and concurrence of two moving isolated atoms. This paper is organized as follows. In Section 2, we give the model and its solution. In Section 3, we give two types of measures including quantum discord and concurrence to analyze quantum correlation. Numerical results and discussion are given in Section 4. Finally we conclude in Section 5.
2. The Model and Its Solution
We consider two identical moving two-level atoms labeled  and
and 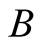 interact with two single-mode thermal cavity fields labeled
interact with two single-mode thermal cavity fields labeled ![]() and
and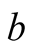 . Each atom-cavity system is isolated (atom
. Each atom-cavity system is isolated (atom 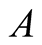 at a constant velocity interacting only with field
at a constant velocity interacting only with field ![]() and similarly for the atom
and similarly for the atom 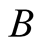 and the field
and the field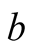 ). For simplicity, we suppose that these two atoms be coupled to the field with the same coupling constant
). For simplicity, we suppose that these two atoms be coupled to the field with the same coupling constant![]() , and the field mode be resonant with the transition frequency of both atoms. The interaction Hamiltonian under the rotating wave approximation
, and the field mode be resonant with the transition frequency of both atoms. The interaction Hamiltonian under the rotating wave approximation 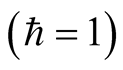 is
is
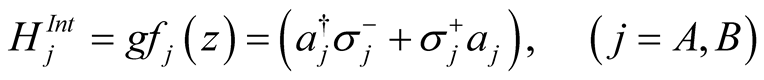 (1)
(1)
where 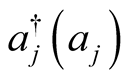 is the creation (annihilation) for
is the creation (annihilation) for 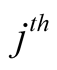 mode of the cavity field and
mode of the cavity field and ,
,  are the raising and lowering operators respectively.
are the raising and lowering operators respectively. 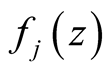 denotes the mode structure of cavity field which can be defined specially as [24]
denotes the mode structure of cavity field which can be defined specially as [24]
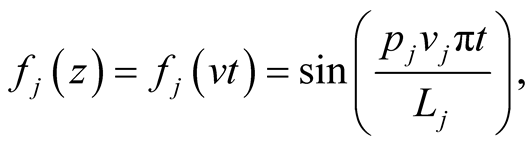 (2)
(2)
where, 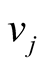 denotes the velocity of the
denotes the velocity of the  atom and
atom and 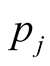 represents the half-wave number of cavity field with length
represents the half-wave number of cavity field with length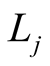 . We restrict our study for atomic in the
. We restrict our study for atomic in the  -axis direction, so that only the
-axis direction, so that only the 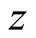 -dependent field mode function needs to be taken into account. For simplicity we assume that
-dependent field mode function needs to be taken into account. For simplicity we assume that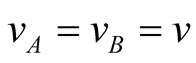 ,
, 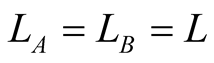 and
and 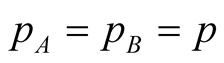 . Using standard technique, it can show that
. Using standard technique, it can show that  in Equation (1) gives rise to the following time evolution operator
in Equation (1) gives rise to the following time evolution operator
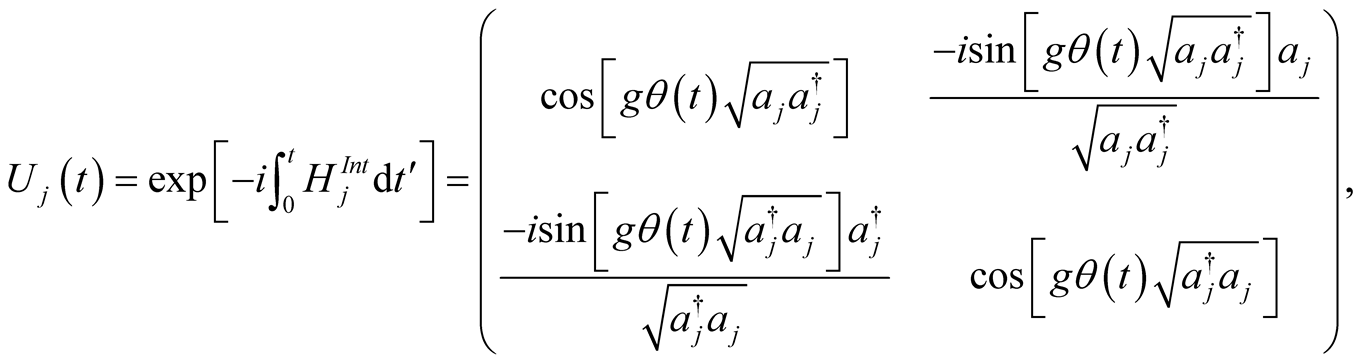 (3)
(3)
where, 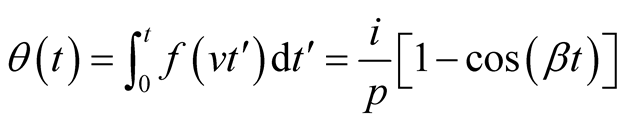 and
and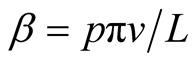 . For a particular choice of the atomic motion velocity
. For a particular choice of the atomic motion velocity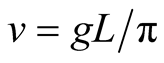 ,
, 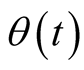 becomes
becomes
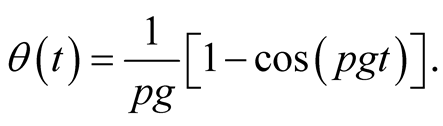 (4)
(4)
We assume that the two atoms are initially in the Werner state
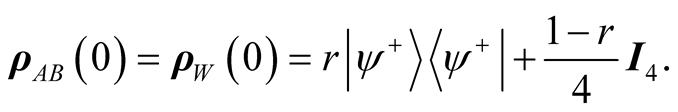 (5)
(5)
Here, 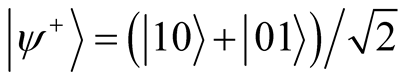 ,
,  is the
is the 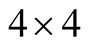 identity matrix and
identity matrix and 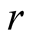 varies from 0 to 1, and for
varies from 0 to 1, and for  the Werner becomes maximally states, while for
the Werner becomes maximally states, while for 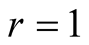 they are the well known Bell states. The two cavity fields
they are the well known Bell states. The two cavity fields ![]() and
and 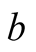 are initially in single-mode thermal field states
are initially in single-mode thermal field states
 (6)
(6)
The weight function 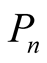 and
and 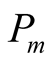 are,
are,
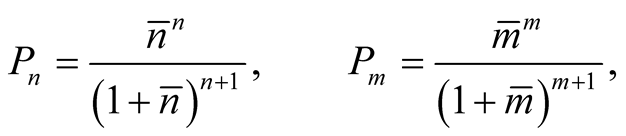 (7)
(7)
where  and
and  are the mean photon numbers of the two thermal cavity fields a and b corresponding to the equilibrium cavity temperatures Ta and Tb respectively,
are the mean photon numbers of the two thermal cavity fields a and b corresponding to the equilibrium cavity temperatures Ta and Tb respectively,  is the Boltzmann constant and
is the Boltzmann constant and 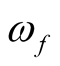 is the frequency of the field.
is the frequency of the field.
Using the evolution operator, we can generate the density operator of the system at time 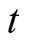 as
as
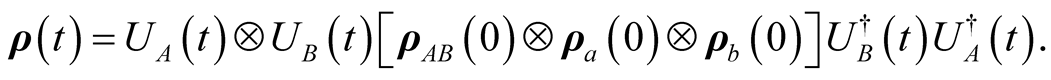 (8)
(8)
We can obtain the reduced density matrix for the two atoms at time t by tracing over the field variables. Under the standard basis 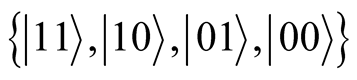 the reduced density matrix
the reduced density matrix 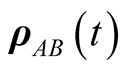 can be obtained in the form
can be obtained in the form
 (9)
(9)
where the matrix elements are expressed as follow



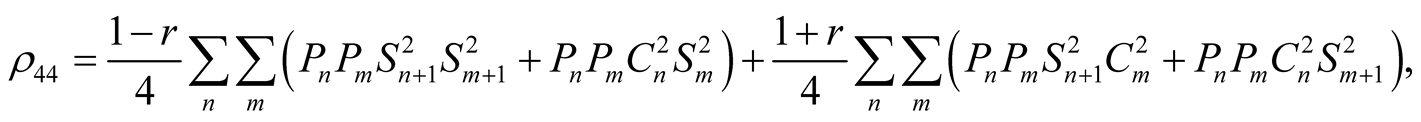
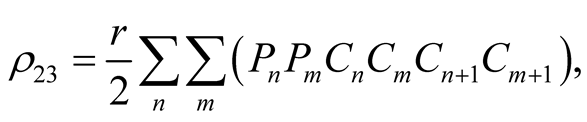 (10)
(10)
with 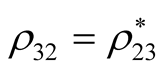 (the asterisk denotes complex conjugation) and all matrix elements are zero,
(the asterisk denotes complex conjugation) and all matrix elements are zero, 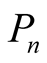 and
and 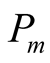 are given in Equation (7), and the time-dependent operations are expressed by
are given in Equation (7), and the time-dependent operations are expressed by
 (11)
(11)
where 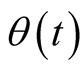 is given in Equation (4).
is given in Equation (4).
3. Quantum Discord and Entanglement
In the following, we will investigate the quantum discord and entanglement between two moving atoms by using above results. In order to follow the entanglement of the two atoms, we choose the Wootters entanglement measure [25] , the concurrence C defined as
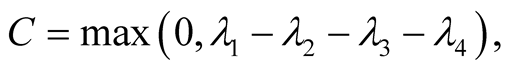 (12)
(12)
where the quantities 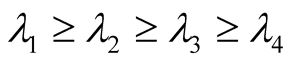 are the square roots of the eigenvalues of the matrix
are the square roots of the eigenvalues of the matrix
 . The concurrence
. The concurrence  corresponds to an unentangled states and
corresponds to an unentangled states and  to a maximally entangled state.
to a maximally entangled state.
On the other hand, quantum discord is based on the difference between the quantum mutual information and the classical correlation [26] . For a two-qubit quantum system, the total correlation is measured by their quantum mutual information
 (13)
(13)
where  and
and  denote the reduced density matrix of
denote the reduced density matrix of  and the density of the bipartite system respectively, and
and the density of the bipartite system respectively, and 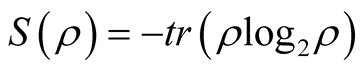 is the von Neumann entropy. Quantum discord, which quantifies the quantumness of correlation between
is the von Neumann entropy. Quantum discord, which quantifies the quantumness of correlation between 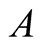 and
and , is then defined as the difference between the total correlation and classical correlation,
, is then defined as the difference between the total correlation and classical correlation,
 (14)
(14)
Here the classical correlation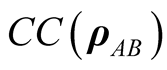 , which quantifies the maximum information that one can obtain from the composite system by measurement on one of the subsystem, can be expressed as
, which quantifies the maximum information that one can obtain from the composite system by measurement on one of the subsystem, can be expressed as
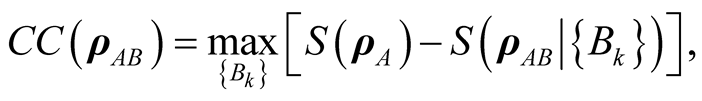 (15)
(15)
where 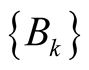 denotes a complete set of projective measurements performed locally on subsystem
denotes a complete set of projective measurements performed locally on subsystem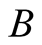 , and
, and
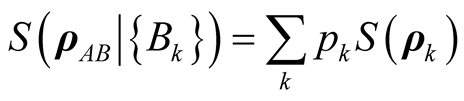 is the quantum conditional entropy with
is the quantum conditional entropy with  and
and
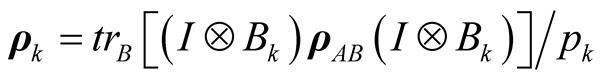 . By substituting from Equations (13) and (15) into Equation (14), one can obtain the quantum discord as
. By substituting from Equations (13) and (15) into Equation (14), one can obtain the quantum discord as
 (16)
(16)
For a class of two-qubit states of qubits 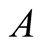 and
and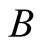 , i.e. the two-qubit
, i.e. the two-qubit 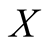 states in standard basis
states in standard basis  ,
,
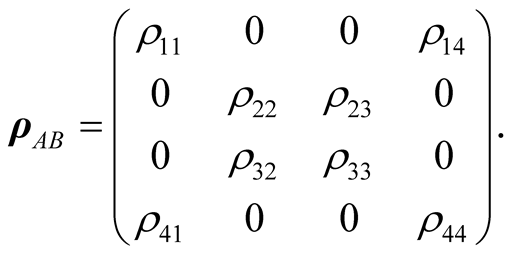 (17)
(17)
It is easy to show that
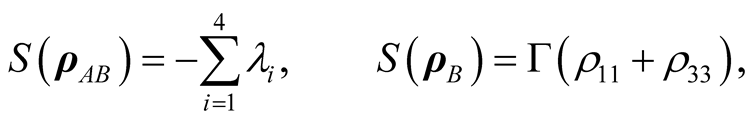 (18)
(18)
where, 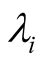 being the four eigenvalues of
being the four eigenvalues of 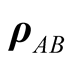 and
and 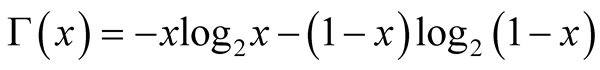 is the Shannon entropy.
is the Shannon entropy.
According to Ref. [14] [27] ,  can be obtained as
can be obtained as
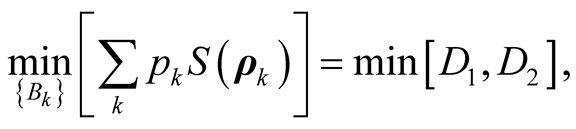 (19)
(19)
where

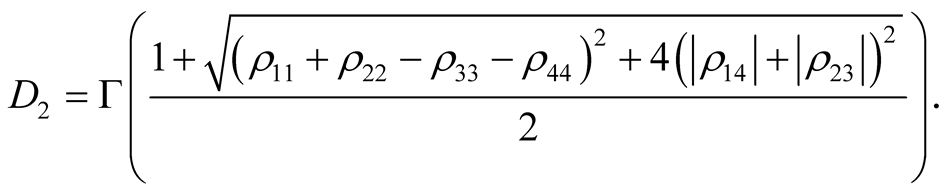
For our system under consideration above, for the density matrix in Equation (9), one can obtain the explicit expressions of the concurrence  and quantum discord
and quantum discord  in the form
in the form
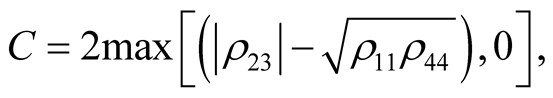 (20)
(20)
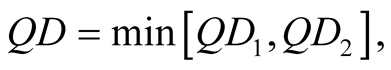 (21)
(21)
where
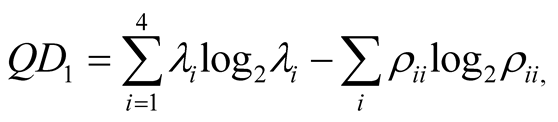 (22)
(22)
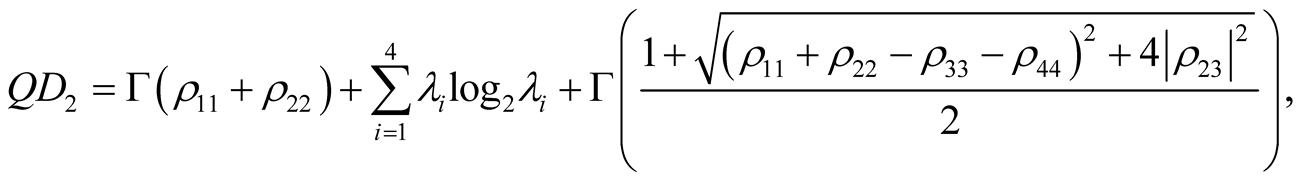 (23)
(23)
with
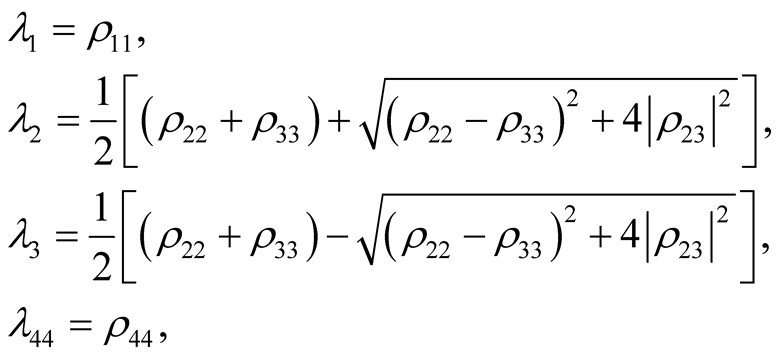 (24)
(24)
where, the non zero elements 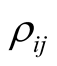 are given in Equation (10).
are given in Equation (10).
Having obtained the results above, we are therefore in a position to discuss the dynamics behavior of the quantum discord and entanglement to the system consider in the following section.
4. Numerical Results and Discussion
Our goal in this article is to clarify what peculiar dynamics happened for quantum discord and entanglement (measured by concurrence) of the system under consideration as follow. In Figure 1, we plotted the concurrence 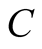 as a function of scaled time
as a function of scaled time 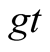 and
and . It is apparent that when
. It is apparent that when 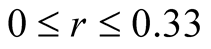 the concurrence is zero,
the concurrence is zero,
 (a) (b)
(a) (b)
Figure 1. Concurrence C plotted as a function of scaled time  and
and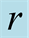 , for (a)
, for (a) 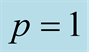 and (b)
and (b)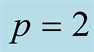 .
.
while , one can see that the concurrence evolves periodically and entanglement sudden death phenomenon occurs, as r increases the local maximum value of the concurrence increases and tends to 1 when r = 1. To study the effect of the atomic motion related to the field-mode structure parameter p in entanglement, we compare between Figure 1(a)
, one can see that the concurrence evolves periodically and entanglement sudden death phenomenon occurs, as r increases the local maximum value of the concurrence increases and tends to 1 when r = 1. To study the effect of the atomic motion related to the field-mode structure parameter p in entanglement, we compare between Figure 1(a)  and Figure 1(b)
and Figure 1(b)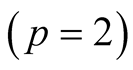 , it is observed that when p increases the evolution period of the concurrence decreases and the time interval for zero entanglement becomes more and its wide becomes shorted. On the other hand, the quantum discord
, it is observed that when p increases the evolution period of the concurrence decreases and the time interval for zero entanglement becomes more and its wide becomes shorted. On the other hand, the quantum discord 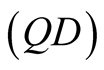 is plotted versus scaled time gt and r in Figure 2. The time behavior of quantum discord is periodical with period
is plotted versus scaled time gt and r in Figure 2. The time behavior of quantum discord is periodical with period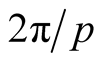 , and its evolution periods are shorten with the increased parameter p. In order to compare between the quantum discord and concurrence, we plotted quantum discord and concurrence as a function of scaled time gt for different values of p and r in Figure 3. We have two main regions responding r: first region 0 ≤ r ≤ 0.33, in this region the concurrence
, and its evolution periods are shorten with the increased parameter p. In order to compare between the quantum discord and concurrence, we plotted quantum discord and concurrence as a function of scaled time gt for different values of p and r in Figure 3. We have two main regions responding r: first region 0 ≤ r ≤ 0.33, in this region the concurrence
 (a) (b)
(a) (b)
Figure 2. Quantum discord QD plotted as a function of scaled time gt and r, for (a) 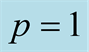 and (b)
and (b)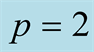 .
.
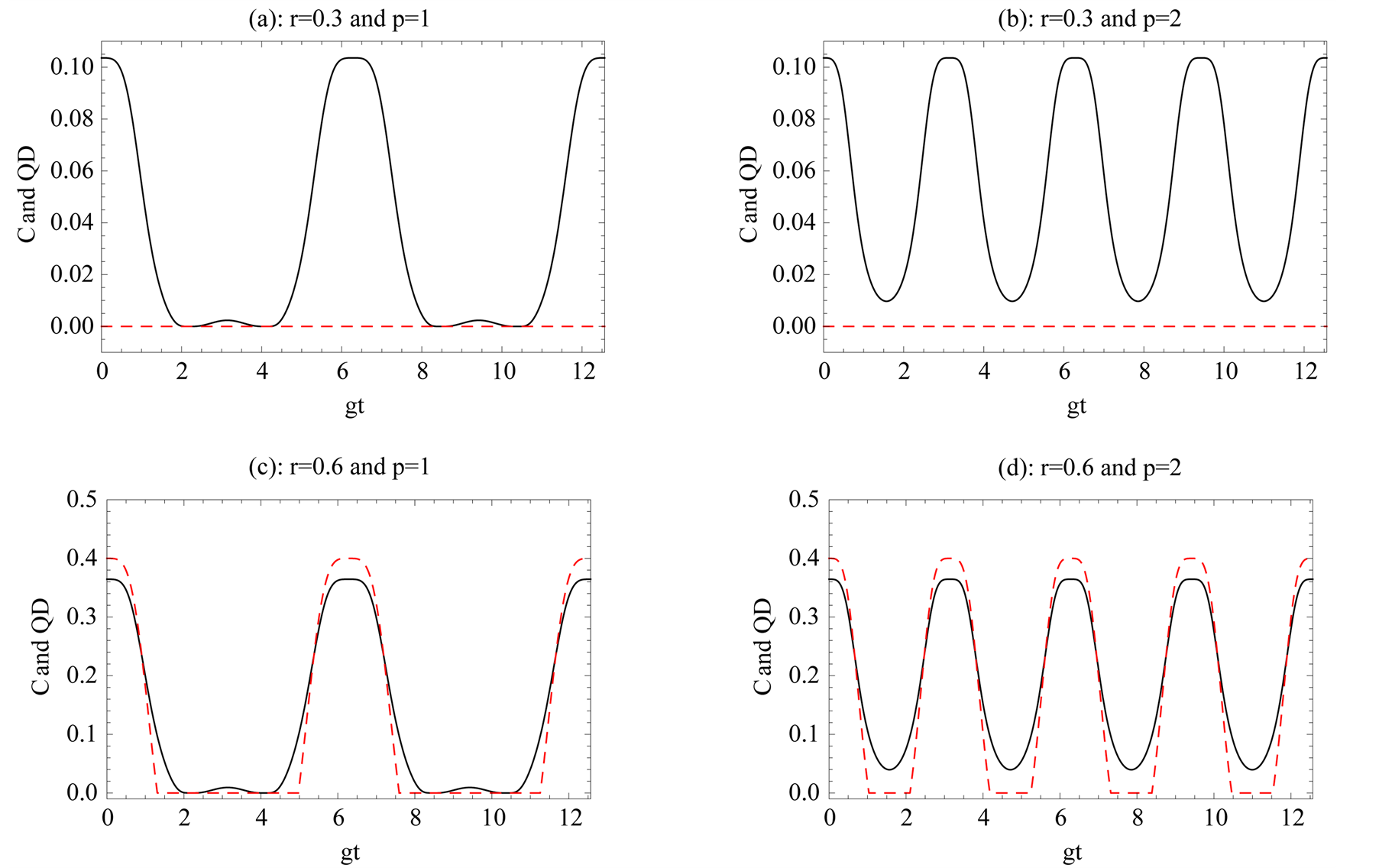
Figure 3. Concurrence C and quantum discord QD versus scaled time gt. The black solid and red dashed lines denote respectively QD and C.
always zero but the quantum discord remains non zero. Second region 0.33 < r ≤ 1, the concurrence vanishes periodically and entanglement sudden death happens, while the quantum discord remains non zero with its corresponding fluctuations. Also the frequencies of quantifiers in unit time are the same for concurrence and quantum discord. Whereas the amplitude of concurrence is greater than the amplitude of quantum discord. However, the dynamic of quantum discord is quite different, although entanglement suddenly disappears during the evaluation, the quantum discord remains non zero. It means that the absence of entanglement does not indicate the absence of quantum discord, so quantum discord still can capture the quantum correlation between the two atoms when the entanglement is zero.
5. Conclusion
We have investigated the quantum discord and entanglement between two isolated two-level atoms which are initially prepared in Werner state and each atom interacts with a thermal cavity field by considering the atomic motion and the field-mode structure. It is shown that the entanglement vanishes periodically and sudden death of entanglement appears, while the quantum discord remains non zero with its corresponding fluctuations. We observe that the atomic motion and the field-mode structure have the same effect on the behavior of quantum discord and entanglement. Although entanglement suddenly disappears during the evaluation, the quantum discord remains non zero. Quantum discord still can capture the quantum correlation between the two atoms when the entanglement is zero.
References
- Bennett, C.H. and Di Vincenzo, D.P. (2000) Quantum Information and Computation. Nature, 404, 247. http://dx.doi.org/10.1038/35005001
- Mayer, D.A. (2000) Sophisticated Quantum Search without Entanglement. Physical Review Letters, 85, 4 p.
- Lanyon, B.P., Barbieri, M., Almeida, M.P. and White, A.G. (2008) Experimental Quantum Computing without Entanglement. Physical Review Letters, 101, Article ID: 200501. http://dx.doi.org/10.1103/PhysRevLett.101.200501
- Vedral, V. (2003) Classical Correlations and Entanglement in Quantum Measurements. Physical Review Letters, 90, Article ID: 050401. http://dx.doi.org/10.1103/PhysRevLett.90.050401
- Datta, A., Flammia, S.T. and Caves, C.M. (2005) Entanglement and the Power of One Qubit. Physical Review A, 72, Article ID: 042316. http://dx.doi.org/10.1103/PhysRevA.72.042316
- Ollivier, H. and Zurek, W.H. (2001) Quantum Discord: A Measure of the Quantumness of Correlations. Physical Review Letters, 88, Article ID: 017901. http://dx.doi.org/10.1103/PhysRevLett.88.017901
- Datta, A., Shaji, A. and Caves, C.M. (2008) Quantum Discord and the Power of One Qubit. Physical Review Letters, 100, Article ID: 050502. http://dx.doi.org/10.1103/PhysRevLett.100.050502
- Zidan, N. (2014) Quantum Discord of a Two-Qubit Anisotropy XXZ Heisenberg Chain with Dzyaloshinskii-Moriya Interaction. Journal of Quantum Information Science, 4, 104. http://dx.doi.org/10.4236/jqis.2014.42011
- Berrada, K., Fanchini, F.F. and Abdel-Khalek, S. (2012) Quantum Correlation between Each Qubit in a Two-Atom System and the Environment in Terms of Interatomic Distance. Physical Review A, 85, Article ID: 052315. http://dx.doi.org/10.1103/PhysRevA.85.052315
- Wang, C.-Z., Li, C.-X., Nie, L.-Y. and Li, J.-F. (2011) Classical Correlation and Quantum Discord Mediated by Cavity in Two Coupled Qubit. Journal of Physics B: Atomic, Molecular and Optical Physics, 44, Article ID: 015503. http://dx.doi.org/10.1088/0953-4075/44/1/015503
- Zhang, J.S. and Chen, A.X. (2012) Review of Quantum Discord in Bipartite and Multipartite Systems. Quantum Physics Letters, 1, 69.
- Mohamed, A.B. (2013) Pairwise Correlations via Quantum Discord and Its Geometric Measure in a Four-Qubit Spin Chain. Journal of the Egyptian Mathematical Society, 21, 68-74. http://dx.doi.org/10.1016/j.joems.2012.10.005
- Luo, S. (2008) Quantum Discord for Two-Qubit Systems. Physical Review A, 77, Article ID: 042303. http://dx.doi.org/10.1103/PhysRevA.77.042303
- Ali, M., Rau, A.R.P. and Alber, G. (2010) Quantum Discord for Two-Qubit X States. Physical Review A, 81, Article ID: 042105. http://dx.doi.org/10.1103/PhysRevA.81.042105
- Chen, Y.X., Li, S.W. and Yin, Z. (2010) Quantum Correlations in a Clusterlike System. Physical Review A, 82, Article ID: 052320. http://dx.doi.org/10.1103/PhysRevA.82.052320
- Hassan, A., Lari, B. and Joag, P. (2010) Thermal Quantum and Classical Correlations in a Two-Qubit XX Model in a Nonuniform External Magnetic Field. Journal of Physics A: Mathe-matical and Theoretical, 43, Article ID: 485302.
- Yuan, J.B., Kuang, L.M. and Liao, J.Q. (2010) Amplification of Quantum Discord between Two Uncoupled Qubits in a Common Environment by Phase Decoherence. Journal of Physics B: Atomic, Molecular and Optical Physics, 43, Article ID: 165503.
- Hao, X., Ma, C.L. and Sha, J. (2010) Decoherence of Quantum Discord in an Asymmetric-Anisotropy Spin System. Journal of Physics A: Mathematical and Theoretical, 43, Article ID: 425302.
- Sun, Z., Lu, X.M. and Song, L. (2010) Quantum Discord Induced by a Spin Chain with Quantum Phase Transition. Journal of Physics B: Atomic, Molecular and Optical Physics, 43, Article ID: 215504.
- Mi, Y.J. (2012) Classical Correlation and Quantum Discord in a Two-Qubit System under Dissipation Environments. International Journal of Theoretical Physics, 51, 544-553. http://dx.doi.org/10.1007/s10773-011-0933-5
- Ji, Y.H. and Liu, Y.M. (2013) Investigations into Quantum Correlation of Coupled Qubits in a Squeezed Vacuum Reservoir. Chinese Physics B, 22, Article ID: 020305.
- Galve, F., Giorgi, G.L. and Zambrini, R. (2011) Maximally Discordant Mixed States of Two-Qubits. Physical Review A, 83, Article ID: 012102. http://dx.doi.org/10.1103/PhysRevA.83.012102
- Girolami, D. and Adesso, G. (2011) Quantum Discord for General Two-Qubit States: Analytical Progress. Physical Review A, 83, Article ID: 052108. http://dx.doi.org/10.1103/PhysRevA.83.052108
- Schlicher, R.R. (1989) Jaynes-Cummings Model with Atomic Motion. Optics Communications, 70, 97-102. http://dx.doi.org/10.1016/0030-4018(89)90276-9
- Wootters, W.K. (1998) Entanglement of Formation of an Arbi-trary State of Two-Qubits. Physical Review Letters, 80, 2245. http://dx.doi.org/10.1103/PhysRevLett.80.2245
- Henderson, L. and Vedral, V. (2001) Classical, Quantum and Total Correlations. Journal of Physics A: Mathematical and General, 34, 6899.
- Sarandy, M.S. (2009) Classical Correlation and Quantum Discord in Critical Systems. Physical Review A, 80, Article ID: 022108. http://dx.doi.org/10.1103/PhysRevA.80.022108

