Applied Mathematics
Vol.5 No.6(2014), Article ID:44587,11 pages DOI:10.4236/am.2014.56087
Some Remarks on the Non-Abelian Fourier Transform in Crossover Designs in Clinical Trials
Peter Zizler
Department of Mathematics/Physics and Engineering, Mount Royal University, Calgary, Canada
Email: pzizler@mtroyal.ca
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 21 November 2013; revised 21 December 2013; accepted 30 December 2013
ABSTRACT
Let G be a non-abelian group and let  be a finite dimensional Hilbert space of all complex valued functions for which the elements of G form the (standard) orthonormal basis. In our paper we prove results concerning G-decorrelated decompositions of functions in
be a finite dimensional Hilbert space of all complex valued functions for which the elements of G form the (standard) orthonormal basis. In our paper we prove results concerning G-decorrelated decompositions of functions in . These Gdecorrelated decompositions are obtained using the G-convolution either by the irreducible characters of the group G or by an orthogonal projection onto the matrix entries of the irreducible representations of the group G. Applications of these G-decorrelated decompositions are given to crossover designs in clinical trials, in particular the William’s
. These Gdecorrelated decompositions are obtained using the G-convolution either by the irreducible characters of the group G or by an orthogonal projection onto the matrix entries of the irreducible representations of the group G. Applications of these G-decorrelated decompositions are given to crossover designs in clinical trials, in particular the William’s  design with 3 treatments. In our example, the underlying group is the symmetric group
design with 3 treatments. In our example, the underlying group is the symmetric group .
.
Keywords:Non-Abelian Fourier Transform, Group Algebra, Irreducible Representation, Irreducible Character, G-Circulant Matrix, G-Decorrelated Decomposition, Crossover Designs in Clinical Trials

1. Preliminaries
Consider a finite group , typically non-abelian, and let
, typically non-abelian, and let 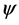 and
and 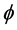 be two functions in
be two functions in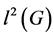 , the finite Hilbert space of all complex valued functions (usual inner product
, the finite Hilbert space of all complex valued functions (usual inner product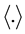 ) for which elements of
) for which elements of  form the (standard) basis. We assume that this basis
form the (standard) basis. We assume that this basis  is ordered and make the natural identification, as vector spaces, with
is ordered and make the natural identification, as vector spaces, with , where
, where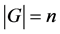 .
.
A  -convolution of
-convolution of  and
and  is defined by the following action,
is defined by the following action, 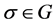
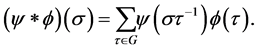
Definition. A function  is called a multiplicative character if
is called a multiplicative character if

In the cyclic case multiplicative characters are eigenfunctions of the convolution operator and we have  multiplicative characters, the Fourier complex exponentials, for example, see [1] for more details. The main problem with the non-abelian group, as opposed to the abelian one, is the lack of multiplicative characters. Multiplicative characters for any group
multiplicative characters, the Fourier complex exponentials, for example, see [1] for more details. The main problem with the non-abelian group, as opposed to the abelian one, is the lack of multiplicative characters. Multiplicative characters for any group  are constant on its conjugacy classes.
are constant on its conjugacy classes.
Definition. A finite dimensional representation of a finite group 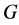 is a group homomorphism
is a group homomorphism
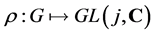
where  denotes the general linear group of degree
denotes the general linear group of degree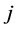 , the set of all
, the set of all 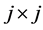 invertible matrices. We refer to
invertible matrices. We refer to  as the degree of the group representation. The field of complex numbers is denoted by
as the degree of the group representation. The field of complex numbers is denoted by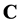 .
.
Definition. Two group representations

are said to be equivalent if there exists an invertible matrix 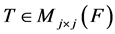 such that
such that
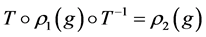
for all .
.
Every finite dimensional group representation is equivalent to a representation by unitary matrices. For more information on group representations see [2] for example.
Definition. Let 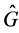 be the set of all (equivalence classes) of irreducible representations of the group
be the set of all (equivalence classes) of irreducible representations of the group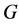 . Let
. Let 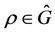 be of degree
be of degree  and let
and let . Then the Fourier transform of
. Then the Fourier transform of  at
at 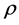 is the
is the  matrix
matrix
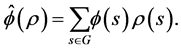
The Fourier inversion formula, 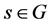 , is given by
, is given by

We alert the reader to an involution switch 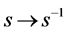 in the summand functions. We refer the reader to [3] for more details. Let
in the summand functions. We refer the reader to [3] for more details. Let  be the algebra of complex valued functions on
be the algebra of complex valued functions on  with respect to
with respect to 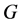 -convolution. Let
-convolution. Let 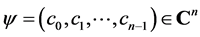 and identify the function
and identify the function  with its symbol
with its symbol
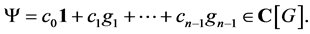
Let 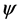 and
and 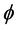 be two elements in
be two elements in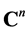 . We have a natural identification
. We have a natural identification
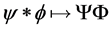
understood with respect to the induced group algebra multiplication. We have a non-abelian version of the classical 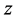 transform. The action of
transform. The action of 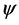 on
on  through
through  -convolution is captured by the matrix multiplication by the
-convolution is captured by the matrix multiplication by the  -circulant matrix
-circulant matrix , in particular
, in particular
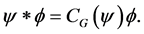
The character of a group representation  is the complex valued function
is the complex valued function

defined by

For all 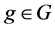 the quantity
the quantity  is a sum of complex roots of unity. Moreover, we have
is a sum of complex roots of unity. Moreover, we have  for all
for all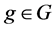 . A character is called irreducible if the underlying group representation is irreducible. We define an inner product on the space of class functions, functions on
. A character is called irreducible if the underlying group representation is irreducible. We define an inner product on the space of class functions, functions on  that are constant its conjugacy classes
that are constant its conjugacy classes

Note that a character is a class function. We have as many irreducible characters as there are conjugacy classes of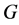 . If
. If  is abelian, then we have
is abelian, then we have 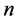 irreducible characters. With respect to the usual inner product we have
irreducible characters. With respect to the usual inner product we have

where  is the Kronecker delta. Irreducible characters form a basis for the space of class functions on
is the Kronecker delta. Irreducible characters form a basis for the space of class functions on .
.
Definition. Let . The adjoint of
. The adjoint of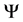 , denoted by
, denoted by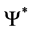 , in the group algebra
, in the group algebra 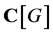 is the element
is the element

Associate  and
and  with the corresponding functions
with the corresponding functions 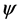 and
and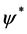 . We collect a few simple facts. Let
. We collect a few simple facts. Let 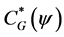 be the adjoint of the
be the adjoint of the 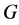 -circulant matrix
-circulant matrix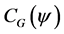 . Then we have
. Then we have . The matrix
. The matrix 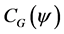 is normal if and only if
is normal if and only if 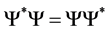 and selfadjoint if and only if
and selfadjoint if and only if .
.
The Fourier transform gives us a natural isomorphism

where

with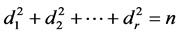 . A typical element of
. A typical element of  is a complex valued function
is a complex valued function
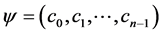
and the typical element of 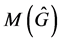 is the direct sum of Fourier transforms
is the direct sum of Fourier transforms
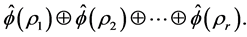
Fourier transform turns convolution into (matrix) multiplication
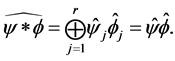
In the abelian setting the Fourier transform is a unitary linear transformation (proper scaling required). In the non-abelian setting we recapture this property if we define the right inner product on the space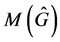 . We will provide more details on this later on. Let
. We will provide more details on this later on. Let 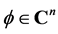 and define for
and define for 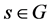
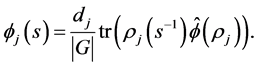
Note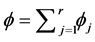 . We are able to decompose a function
. We are able to decompose a function  into a sum of
into a sum of 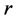 functions which is the number of conjugacy classes of
functions which is the number of conjugacy classes of .
.
Every group  admits a trivial irreducible representation
admits a trivial irreducible representation 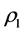 for which
for which  for all
for all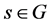 . For
. For 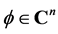 the Fourier transform of
the Fourier transform of 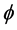 at
at 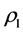 is given by
is given by
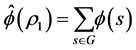
and

Thus the constant mean function is always represented in our decomposition. The decomposition  must be orthogonal. The following can be, for example, found in [4] . The notation
must be orthogonal. The following can be, for example, found in [4] . The notation  refers to the Frobenius norm.
refers to the Frobenius norm.
Proposition 1.1. Let  be given as above. We have
be given as above. We have

Corollary 1.1. Let  then
then
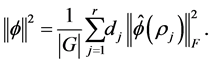
Equip the space 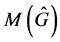 with the following inner product. Let
with the following inner product. Let  and
and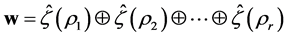 . Then
. Then

whete  denotes the adjoint of
denotes the adjoint of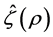 .
.
Corollary 1.2. The Fourier transform is a unitary transformation from 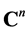 onto
onto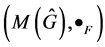 .
.
For more information of non-abelian Fourier transform see the works of [5] -[11] , for example.
2. Main Results
Consider for a moment , where
, where  is a cyclic group of size
is a cyclic group of size . Given a vector
. Given a vector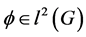 , we can writ
, we can writ

where the Fourier complex exponentials 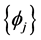 are orthonormal vectors and
are orthonormal vectors and  are the Fourier coefficients. Being multiplicative characters for
are the Fourier coefficients. Being multiplicative characters for , these functions
, these functions  are
are 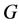 -decorrelated, in particular, for
-decorrelated, in particular, for ,
,

This important property makes the Fourier exponentials vital in signal analysis. The need for time shift de-correlation or spatial shift de-correlation is reflected in the cyclic group structure of .
.
We extend these observations to non-abelian groups , recall that finite abelian groups are direct sums of cyclic groups. We say that two vectors
, recall that finite abelian groups are direct sums of cyclic groups. We say that two vectors ,
,  in
in  are
are 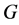 -decorrelated if
-decorrelated if
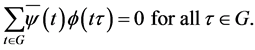
We observe that even in the non-abelian case the linearly independent multiplicative characters are G-decorrelated as the following simple observation reveals

as linearly independent multiplicative characters are orthogonal.
Definition. For given vectors 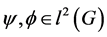 the
the  cross-correlation function is defined by
cross-correlation function is defined by

Note that  and
and  are
are  -decorrelated if and only if
-decorrelated if and only if . Recall we view the following three objects
. Recall we view the following three objects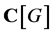 ,
, 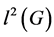 and
and 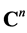 as isomorphic vector spaces.
as isomorphic vector spaces.
Lemma 2.1. Consider  and the corresponding
and the corresponding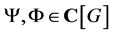 . Then we have
. Then we have
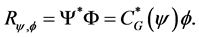
Proof: We have
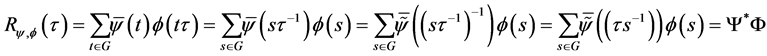
where .
.
Corollary 2.1. Let 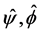 be the Fourier transforms of
be the Fourier transforms of  and
and  respectively. Then we have
respectively. Then we have

Thus functions 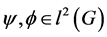 are
are  -decorrelated if and only if
-decorrelated if and only if
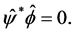
Corollary 2.2. Let . Then
. Then 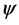 and
and 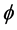 are
are 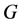 -decorrelated if and only if
-decorrelated if and only if

Observe that if 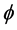 is a multiplicative character then
is a multiplicative character then
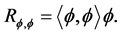
However, these are not the only functions with this property, i.e.  is a multiple of
is a multiple of . In fact, we have the following, note that
. In fact, we have the following, note that  below could be complex.
below could be complex.
Lemma 2.2. Let . Then
. Then

if and only if
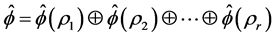
with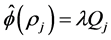 , where
, where 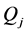 is a projection matrix for all
is a projection matrix for all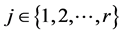 . Note
. Note  in independent of
in independent of , but
, but  can depend on
can depend on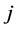 .
.
Proof: Using Corollary 2.1, the function 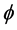 has the property
has the property  if and only if
if and only if
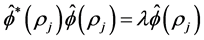
for all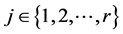 . Observe that, as a result, the matrix
. Observe that, as a result, the matrix 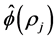 has to be normal. Therefore, we can orthogonally diagonalize
has to be normal. Therefore, we can orthogonally diagonalize  with the diagonal matrix
with the diagonal matrix . Now the above matrix equality translates to the following
. Now the above matrix equality translates to the following

which forces all the non-zero diagonal entries of  to be the same. This is exactly the claim that
to be the same. This is exactly the claim that  is a multiple of some projection matrix
is a multiple of some projection matrix  that could depend of
that could depend of .
.
We say a set of functions 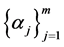 in
in  is
is 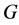 -orthogonal if
-orthogonal if
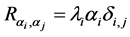
where  is the Kronecker delta and
is the Kronecker delta and .
.
Theorem 2.1. Let 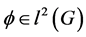 and
and  be the set of all irreducible characters of
be the set of all irreducible characters of . Then we have
. Then we have
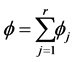
where
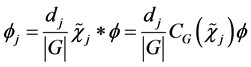
and the set of functions 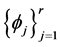 is
is 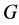 -decorrelated. If
-decorrelated. If 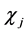 is a multiplicative character,
is a multiplicative character, 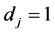 , then
, then

Note that if  and
and 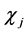 are real valued then so is the corresponding
are real valued then so is the corresponding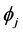 . Moreover, the set
. Moreover, the set 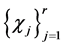 is G-orthogonal.
is G-orthogonal.
Proof: Recall

Now define an (orthogonal) projection  on
on 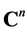 by the following action,
by the following action, 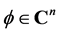

The action of the linear operator  in the Fourier domain is given by the (matrix) multiplication by the vector
in the Fourier domain is given by the (matrix) multiplication by the vector

where the 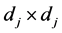 idenity matrix
idenity matrix  is in the jth position. The inverse Fourier transform of this vector is the function (evaluated at
is in the jth position. The inverse Fourier transform of this vector is the function (evaluated at )
)

Therefore for all 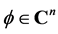 we have
we have

where  is the (inverted) character of the irreducible representation
is the (inverted) character of the irreducible representation . Now Proposition 1.1, Lemma 2.1 and Corollary 2.1 can be used to show that
. Now Proposition 1.1, Lemma 2.1 and Corollary 2.1 can be used to show that 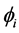 and
and  are
are 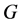 -decorrelated. Using Lemma 2.2 we conclude that the set
-decorrelated. Using Lemma 2.2 we conclude that the set  is
is  -orthogonal.
-orthogonal.
It is important to note that if 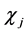 is not a multiplicative character, then
is not a multiplicative character, then

in general.
In order to obtain the above  -decorrelated decomposition one does not need to know explicitly the irreducible group representations, just the irreducible characters for the group
-decorrelated decomposition one does not need to know explicitly the irreducible group representations, just the irreducible characters for the group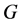 . For any group
. For any group  these (irreducible) characters are much easier to find than the corresponding irreducible group representations. This alone makes the above decomposition amicable for applications. Also note that in a case of multiplicative character
these (irreducible) characters are much easier to find than the corresponding irreducible group representations. This alone makes the above decomposition amicable for applications. Also note that in a case of multiplicative character , the corresponding decomposition function
, the corresponding decomposition function  is a multiple of the (inverted) character
is a multiple of the (inverted) character .
.
However, in the case of (irreducible) character 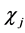 stemming from a higher dimensional irreducible representation, this is no longer the case. The intuitive interpretation of the function
stemming from a higher dimensional irreducible representation, this is no longer the case. The intuitive interpretation of the function  then becomes more difficult.
then becomes more difficult.
Corollary 2.3. Let 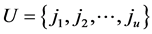 be a subset of
be a subset of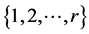 . Then
. Then
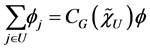
where
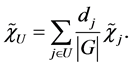
In the cyclic case we can talk about frequencies in the context of the Fourier complex exponentials. As a result, we can design filters, that can isolate specific frequencies and block others. In the non-abelian case this becomes less clear as the concept of frequencies is lost in the irreducible characters.
We can go further and obtain a  -decorrelated decomposition of any function
-decorrelated decomposition of any function 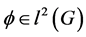 that consists of
that consists of 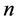 summands. Moreover, this
summands. Moreover, this 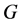 -decorrelated decomposition is obtained by orthogonal projections. However, the drawback is that we have to know the irreducible representations of the group
-decorrelated decomposition is obtained by orthogonal projections. However, the drawback is that we have to know the irreducible representations of the group  and not just the irreducible characters.
and not just the irreducible characters.
Theorem 2.2. Let  and let
and let  be the set of all irreducible representations of
be the set of all irreducible representations of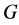 ,
, 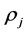 has size
has size . Let
. Let 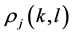 be the
be the  entry in the
entry in the  matrix of
matrix of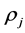 . Consider the (involuted) function
. Consider the (involuted) function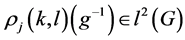 . Then
. Then  can be written as a
can be written as a 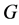 -decorrelated sum of vectors
-decorrelated sum of vectors 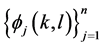 where
where
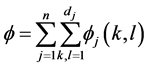
where
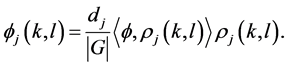
Moreover, the (diagonal) set of functions 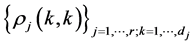 is
is 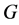 -orthogonal.
-orthogonal.
Proof: We invoke the Schur’s orthogonality relations, see [12] , for example. With notation as in Theorem 2.1, we observe, using the Schur’s orthogonality relations
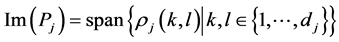
and conclude, using Proposition 1.1, the functions

form an orthonormal basis for . Therefore, we have
. Therefore, we have
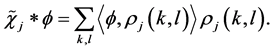
Note that
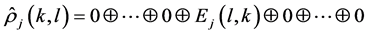
where  is a matrix whose entries are all zero except
is a matrix whose entries are all zero except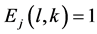 . Therefore
. Therefore

unless  and
and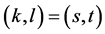 . Now using Lemma 2.2 we conclude that the (diagonal) set of functions
. Now using Lemma 2.2 we conclude that the (diagonal) set of functions 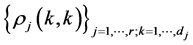 is
is  -orthogonal.
-orthogonal.
Note the (non-diagonal) set of functions.
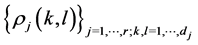 is not necessarily
is not necessarily  -orthogonal. Also, unlike the irreducible characters, we have
-orthogonal. Also, unlike the irreducible characters, we have 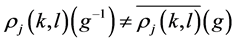 in general.
in general.
3. Example: The Symmetric Group S3
We will consider the symmetric group 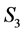 in our example. The group
in our example. The group  consists of elements
consists of elements


The group 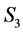 has three conjugacy classes
has three conjugacy classes
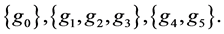
We have three irreducible representations, two of which are one dimensional, 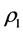 is the identity map,
is the identity map, 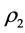 is the map that assigns the value of 1 if the permutation is even and the value of
is the map that assigns the value of 1 if the permutation is even and the value of 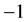 if the permutation is odd. Finally, we have
if the permutation is odd. Finally, we have , the two dimensional irreducible representation of
, the two dimensional irreducible representation of , defined by the following assignment
, defined by the following assignment

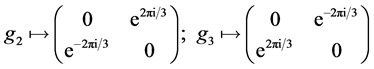

The irreducible characters of  are given by
are given by

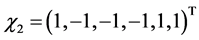
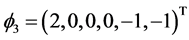
where  and
and 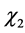 are also multiplicative characters. Moreover, we have
are also multiplicative characters. Moreover, we have


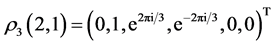
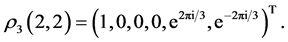
Observe that all three irreducible characters are real valued and hence all the decomposition functions 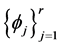 are also real valued if
are also real valued if  is real valued as well. The
is real valued as well. The 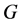 -convolution by a function
-convolution by a function 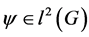 can be induced by a
can be induced by a  -circulant matrix
-circulant matrix  given by
given by

and specifically, note that ,
,
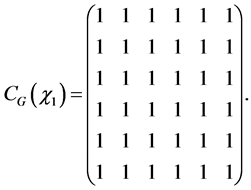


Set  and we obtain
and we obtain
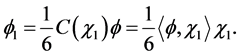
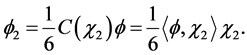
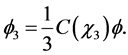
4. Applications to Crossover Designs in Clinical Trials
The application of non-abelian Fourier analysis has been studied extensively; we refer the reader to the works of [13] for example. However, we believe that the property of 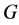 -decorrelation among functions in
-decorrelation among functions in 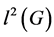 has to be further investigated. We have to capture a natural scenario where the underlying group structure
has to be further investigated. We have to capture a natural scenario where the underlying group structure  is relevant to the corresponding
is relevant to the corresponding 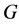 -decorrelation. One of the places this does appears is the crossover designs in clinical trials, in particular the William’s
-decorrelation. One of the places this does appears is the crossover designs in clinical trials, in particular the William’s 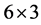 design with 3 treatments.
design with 3 treatments.
During a crossover trial each patient receives more than one treatments in a pre-specified sequence. Therefore, as a result, each subject acts as his or her own control. Each treatment is administered for a pre-selected time period. A so called washout period is established between the last administration of one treatment and the first administration of the next treatment. In this manner the effect of the preceding treatment should wear off, at least in principle. Still there will be some carry-over effects in all the specified treatment sequences, clearly starting with the second treatment. For more information on crossover designs in clinical trials see [14] or [15] for example.
In our example, we record the sum of all carry-over effects of the treatments in any given treatment sequence. We will follow the William’s 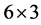 design with 3 treatments
design with 3 treatments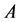 ,
,  and
and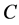 . In particular we have 6 treatment sequences
. In particular we have 6 treatment sequences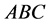 ,
,  ,
,  ,
,  ,
, 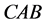 ,
,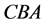 . For example, suppose the order of treatment administration is
. For example, suppose the order of treatment administration is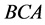 , with
, with  first. We decide to collect the sum of all carry-over effects of the treatments in this sequence (starting with the second one),
first. We decide to collect the sum of all carry-over effects of the treatments in this sequence (starting with the second one),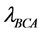 . We observe the sequence
. We observe the sequence  as a permutation of the sequence
as a permutation of the sequence 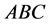 by the permutation
by the permutation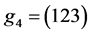 , an element of the group
, an element of the group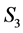 . Thus we can write
. Thus we can write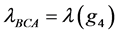 . Similarly, a permutation sequence
. Similarly, a permutation sequence  would result in
would result in .
.
It is here where we can capture the essence of 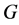 -decorrelation. We can start with some initial treatment order say
-decorrelation. We can start with some initial treatment order say  and then administer crossover designs involving all 6 treatment permutations, denoted by
and then administer crossover designs involving all 6 treatment permutations, denoted by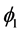 . Similarly, we could have started with a different initial combination of treatments, say
. Similarly, we could have started with a different initial combination of treatments, say  and then administer all 6 treatment permutations, denoted by
and then administer all 6 treatment permutations, denoted by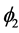 . Now it is natural to request for the data sequences
. Now it is natural to request for the data sequences 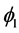 and
and 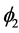 to be
to be 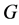 -decorrelated, meaning that our data sequences are decorrelated even when we allow the initial treatment permutation to vary.
-decorrelated, meaning that our data sequences are decorrelated even when we allow the initial treatment permutation to vary.
Let us be specific and give a hypothetical example. Suppose we obtain a carryover sequence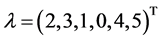 , with the order of the elements respecting the group structure. Assume that the
, with the order of the elements respecting the group structure. Assume that the  values refer to the sums of all carryover effects of the treatments in the given sequence. For example
values refer to the sums of all carryover effects of the treatments in the given sequence. For example 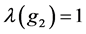 and
and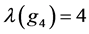 . We now wish
. We now wish 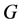 -decorrelate the vector
-decorrelate the vector 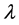 over the group
over the group . We obtain
. We obtain
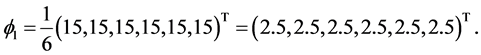

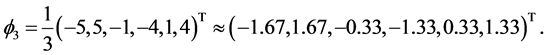
Observe ,
, 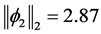 and
and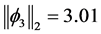 . Observe that the function
. Observe that the function  is a multiple of the multiplicative character
is a multiple of the multiplicative character , and similarly, the function
, and similarly, the function 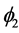 is a multiple of the multiplicative character
is a multiple of the multiplicative character . However, the function
. However, the function  is not a multiple of the (irreducible) character
is not a multiple of the (irreducible) character , recall, the (irreducible) character
, recall, the (irreducible) character  is not a multiplicative character.
is not a multiplicative character.
In the  -decorrelated sum the function
-decorrelated sum the function  represents the carry-over effect from the administration of the three treatments
represents the carry-over effect from the administration of the three treatments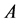 ,
,  and
and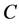 , reflecting the permutation independence in all of the carry-over effects from all 6 permutation options. The function
, reflecting the permutation independence in all of the carry-over effects from all 6 permutation options. The function 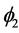 reflects the sign permutation dependence, meaning how sensitive the carry-over effects are to switche from permuting two treatments versus three treatments. The interpretation of the function
reflects the sign permutation dependence, meaning how sensitive the carry-over effects are to switche from permuting two treatments versus three treatments. The interpretation of the function  is more involved, the best is to view
is more involved, the best is to view 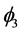 as
as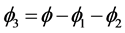 .
.
Let us now decompose the function 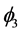 further into a
further into a  -decorrelated sum. Now we have to use the irreducible representations of
-decorrelated sum. Now we have to use the irreducible representations of 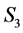 themselves, in particular the two dimensional irreducible representation
themselves, in particular the two dimensional irreducible representation . We obtain the following
. We obtain the following
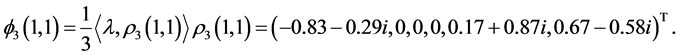
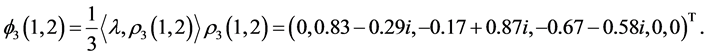


As complex decompositions have little interpretation in our context, we can write a decomposition of 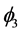 with two vectors,
with two vectors, 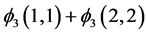 and
and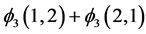 ,
,


References
- Davis, P.J. (1979) Circulant Matrices. John Wiley and Sons.
- Dummit, D.S. and Foote, R.N. (1999) Abstract Algebra. John Wiley and Sons.
- Morrison, K.E. (1998) A Generalization of Circulant Matrices for Non-Abelian Groups. Private Communication. http://www.math.uh.edu/molshan/ftp/pub/proceed_cd.pdf
- Zizler, P. (2013) On Spectral Properties of Group Circulant Matrices. Pan American Mathematical Journal, 23, 1-23.
- Foote, R., Mirchandani, G., Rockmore, D., Healy, D. and Olson, T. (2000) A Wreath Product Group Approach to Signal and Image Processing: Part I—Multiresolution Analysis. IEEE Transaction in Signal Processing, 48, 102-132. http://dx.doi.org/10.1109/78.815483
- Healy, D., Mirchandani, G., Olson, T. and Rockmore, D. (1996) Wreath Products for Image Processing. Proceedings of the ICASSP, 6, 3582-3586.
- Malm, E.J. (2005) Decimation-in-frequency Fast Fourier Transforms for the Symmetric Group. Thesis, Department of Mathematics, Harvey Mudd College.
- Maslen, D. and Rockmore, D. (1997) Generalized FFTs—A Survey of Some Recent Results. In: Finkelstein, L. and Kantor, W., Eds., Proceedings of the DIMACS Workshop on Groups and Computation, 183-237.
- Rockmore, D.N. (2003) Recent Progress and Applications in Group FFTs. NATO Advanced Study Institute on Computational Noncommutative Algebra and Applications.
- Sagan, B.E. (1991) The Symmetric Group: Representations, Combinatorial Algorithms, and Symmetric Functions. Wadsworth & Brooks/Cole, Pacific Grove.
- Terras, A. (1999) Fourier Analysis on Finite Groups and Applications. Cambridge.
- Stankovic, R.S., Moraga, C. and Astola, J.T. (2005) Fourier Analysis on Finite Groups with Applications in Signal Processing and System Design. IEEE Press, John Wiley and Sons.
- Karpovsky, M.G. (1977) Fast Fourier Transforms on finite Non-Abelian Groups. IEEE Transaction on Computers, C-26, 1028-1030. http://dx.doi.org/10.1109/TC.1977.1674739
- Senn, S. (2002) Cross-Over Trials in Clinical Research. 2nd Edition, Wiley. http://dx.doi.org/10.1002/0470854596
- Chow, S.-C. and Liu, J.-P. (2013) Design and Analysis of Clinical Trials: Concepts and Methodologies. Wiley.

