Applied Mathematics
Vol.5 No.4(2014), Article ID:43571,9 pages DOI:10.4236/am.2014.54062
Four Color Theorem and Applied Geophysics
Lev V. Eppelbaum
Department of Geophysical, Atmospheric and Planetary Sciences, Tel Aviv University, Tel Aviv, Israel
Email: levap@post.tau.ac.il
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 2 November 2013; revised 2 December 2013; accepted 9 December 2013
ABSTRACT
A selection of a number of geophysical methods to solve different geological, geodynamical, environmental, archaeological and other problems usually has no theoretical substantiation. The solution to this “four color” mathematical problem is able to assume that two independent geophysical methods are sufficient theoretically to characterize the geological-geophysical peculiarities of the area under study.
Keywords: Logical-Heuristic Model; Geophysical Method Integration; Geophysical Map Coloring

1. Introduction
It is well-known that the majority of the inverse problem solutions in geophysics are ill-posed (e.g., [1] [2] ). It means, according to Hadamard [3] , that the solution does not exist, or is not unique, or is not a continuous function of observed geophysical data (when small perturbation in the observations will cause arbitrary mistake in the solution). This fact, in particular, calls to wide application of informational and probabilistic methodologies in applied geophysics. Main results of geophysical data measurements, processing and interpretation are usually reflected in various maps of different kinds, patterns and scales. Thus, the informational and probabilistic methods application in geophysical maps could have a greatest importance.
2. Formalization of Geological-Geophysical Investigations
Geophysical maps are one of the most important tools for the condensed and effective geophysical-geological (seismological, ecological, atmospheric etc.) data presentation (Figure 1). The compiled maps are employed at different stages (levels) of common and concrete investigations. It is necessary to underline that the same data may be used for different aims; at the same time different data may be applied for solving the same problem.

Figure 1. Simplified scheme of geophysical data processing.
Geophysical observations are notoriously complicated by numerous factors (complex surrounding media, uneven topography, oblique polarization, instrumental errors, etc.) [4] [5] . To eliminate many of these disturbances modern interpretational methodologies have been developed (e.g., [4] [6] [7] ). However, at times the complexity of the geological environment (extreme variability in lateral and vertical physical properties), the presence of several anomalous targets in close proximity and additional disturbances makes it impossible or unfeasible to apply these methodologies. In such cases information-probabilistic methods are effective tools to recognize and classify targets, estimate the potential information value of geophysical methods and decide upon a workable solution. The objective of geophysical surveys application is to obtain qualitative and quantitative information about the geometric and physical characteristics of buried objects; e.g., to develop physical-geological models (PGM) of target objects. PGMs of varying degrees of complexity (the simplest PGMs are simply target identification and complex PGMs can be 3D models of the objects under study) can be used for substantiation of different types of industrial (drilling, excavation, economic minerals exploitation, building, etc.) and scientific (geophysical monitoring, geological-geophysical mapping, construction of new PGMs, etc.) activity, and generation of future strategies for geological-geophysical investigations in the areas under study.
Estimating the information value of geophysical and other means can be formalized on the basis of the following criteria [8] :
(1) Informativeness of the application (informational criterion G);
(2) Cost of implementing the method (cost criterion C);
(3) Time required to carry out the method (time criterion criteria C and T are easy to calculate directly, but criterion G is a non-trivial research problem. A simplified algorithm can be written as:
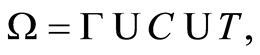 (1)
(1)
where 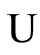 is the symbol of unification.
is the symbol of unification.
All the available geological-geological information can be represented as the classic three-level model (Figure 2): 1) syntactic-quantity of information, 2) semantic-content of information, and 3) pragmatic-value of information. The logical-heuristic model for describing environmental information thus takes the following form:
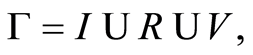 (2)
(2)
where I is the quantitative estimation of information, R is the estimation of informational reliability corresponding to the semantic criterion, and V is the estimation of informational value in terms of feasibility according to the pragmatic criterion.
Algorithm (2) is based on the fundamental terms of information theory and is combined with the structural (hierarchical) approach. This approach defines each indicator as a structure reflecting a set of typical situations and is then used to calculate the value of each estimator using the informational measure. Parameters V and R should be estimated geologically and by informational way, but there are beyond the scope of this paper. Here parameters V and R will be neglected, and it is assumed that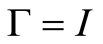 .
.
Thus, the main aim of geophysical prospection is to obtain the maximum effectiveness by minimum expenditures.
3. Evaluating the Efficiency of Geophysical Methods with Informational-Statistical Procedures
Choosing the right method (or number of methods) can be based on a quantitative estimate (Figure 2). For this purpose, reliable informational and statistical criteria are needed. The first issue is the quantity of information that can be obtained by a single method or a set of methods. The second is to define a criterion to express the

Figure 2. A scheme of desired geophysical target recognition and PGM construction with elements of information theory.
decision-making risk as a function of the geophysical data. Nevertheless, informational criteria are preferable, because geophysical prospecting is a permanent process of acquisition and analysis of information [8] .
The classic information theoretic works by Shannon [9] and Brillouin [10] prompted Khalfin [11] to apply these criteria to geophysics. It has been shown [4] [5] that informational and statistical approaches represent two aspects of a shared approach. For instance, the solution to an identification problem using the criterion of minimal average risk or that of maximum information (minimal residual uncertainty) under certain conditions results in the same expressions [12] [13] .
The applied geophysical fields usually have maximal and minimal intensity within studied areas. The difference between the maximal and minimal intensities may be subdivided into some intervals (gradations). Gradations of indicators can be also used to obtain information about the types of the desired objects. Physical fields, geochemical analyses, some geological features, etc. can serve as indicators.
3.1. Some General Considerations
Here are considered some key elements of the theory of information conformably to geophysical studies. Illustrating how these methods can yield valuable results should highlight commonalities in geophysical theory and hence optimize PGM development and successful solving geological-geophysical problems.
As shown in countless publications on geophysical prospecting (e.g., [5] -[7] [14] [15] ), there are typically no more than two or three geophysical methods employed to solve problems of detection, contouring and the development of 3-D models of the objects under study. Let us consider the results of the application of two methods (e.g., gravity and magnetic surveys). They are designated in Table 1 as follows: 1 = negative field, 2 = positive field, 3 = roughly zero field, 4 = alternating field, and 5 = high-gradient field.
Four combinations of two parameters can represent four classes of desired targets, each ranging from 1 to 5. The number of possible combinations of two parameters divided into five categories is 25. The geological features (each class) can be characterized by one of these 25 combinations. It is also necessary to take into account concrete geological situation. For example, in Table 1 value 11 can be obtained for aqueous marl (instead of gabbroid), and this may lead to an erroneous conclusion in the process of geological-geophysical interpretation. Therefore, a certain abundance of the set of geophysical methods sometimes is advisable.
Each class of geological features can be characterized by one of these 25 combinations. The number of combinations can be increased at the expense of secondary parameters arising due to certain transformations of the fields (e.g., downward and upward continuation, various derivatives). Thus, measurements of two geophysical fields can provide sufficient data to resolve mapping problems.
Let’s assume that there is only one anomalous target (AT) in the area. This area is divided into N equal cells. For simplicity each cell is assumed to have the same probability of containing the AT. Thus, the probability of finding the AT is equal to  in each cell. Hence, the entropy of experiment b (discovery of AT) is
in each cell. Hence, the entropy of experiment b (discovery of AT) is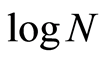 . The entropy is determined using following expression:
. The entropy is determined using following expression:
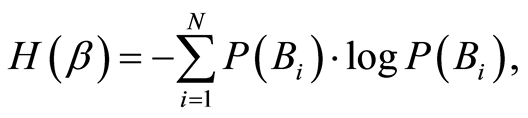 (3)
(3)
where 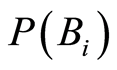 is the probability of a Bi outcome (B is the range of outcomes of experiment b).
is the probability of a Bi outcome (B is the range of outcomes of experiment b).
In this situation  value
value 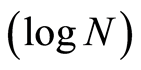 is maximum possible uncertainty. Experiment a (geophysical ob
is maximum possible uncertainty. Experiment a (geophysical ob
Table 1. An example of integrated interpretation.
servation) gives additional information. The A value is a range of outcomes for experiment a.
The difference between uncertainties in the b results before and after experiment a serves to estimate the information in a as related to b:
 (4)
(4)
where  is the conditional entropy for experiment b (provided that experiment a has been conducted).
is the conditional entropy for experiment b (provided that experiment a has been conducted).
The conditional entropy is the average value of a random variable taking a 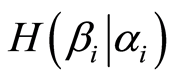 value with a probability of
value with a probability of :
:
 (5)
(5)
3.2. Estimating the Efficiency of Individual Geophysical Methods
When selecting methods for integration, it makes sense to evaluate the amount of information provided by each geophysical method.
Starting from a well-investigated site (with an equal distance between observation points) typical of the area under study, it is assumed that 1/50 of it contains an AT. It is known that in the AT part the magnetic field is always positive, whereas in the empty part of the area it may be either positive or negative with equal probability. In other words, it is known a-priori that 2% and 98% of the area are target-containing and empty, respectively, and in 49% and 51% of this area the magnetic fields, respectively, are negative and positive. The results of experiment b can be designated as follows: B—AT occupying part of the area, —empty part of the area. Thus,
—empty part of the area. Thus, 
 According to expression (3)
According to expression (3) .
.
The result of experiment a is expressed as follows: A is a positive field, 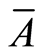 is a negative field. The relative partial entropy (after recording the positive magnetic field at the measurement point) can be calculated in the following way:
is a negative field. The relative partial entropy (after recording the positive magnetic field at the measurement point) can be calculated in the following way: 

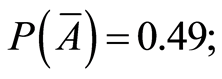
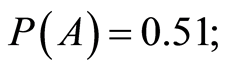 Thus,
Thus,  . According to the recorded negative magnetic field, the area is certainly empty:
. According to the recorded negative magnetic field, the area is certainly empty:  Consequently, the partial entropy for experiment b under the conditions of a, as stated in Equation (5), is
Consequently, the partial entropy for experiment b under the conditions of a, as stated in Equation (5), is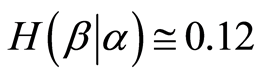 . Thus, the uncertainty of the determination of AT decreases after magnetic field measurement from 0.14 to 0.12.
. Thus, the uncertainty of the determination of AT decreases after magnetic field measurement from 0.14 to 0.12.
3.3. Advantages of Geophysical Method Integration
What information can be obtained from geophysical field measurements? Assume that a magnetic field is observed in a range D, and the measurement precision is given by t. The next step is to fit an integer number of small intervals x into the intervals D and t. It is known after measurement that the value of the field in x units (with a precision up to x) fits into the interval t. Using Equation (4) and considering that the entropy in this expression before and after measurement is expressed by logarithms 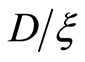 and
and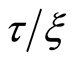 , respectively, one easily obtains (on the basis of [16] ):
, respectively, one easily obtains (on the basis of [16] ):
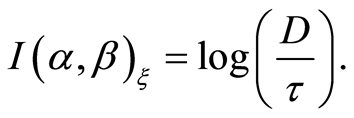 (6)
(6)
With decreasing x, these entropies increase unlimitedly, but the information remains unchanged. With unrestricted increase in measurement accuracy the information also increases unlimitedly, but slowly: an n-fold increase in accuracy leads to only 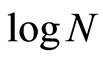 of information units.
of information units.
An essential property of composite experiments is as follows. If certain tests y, j and q are independent, experiments y and q can have zero information about j. However, an integrated experiment y and q can completely determine the outcome of experiment j. Consequently, whereas separate geophysical methods give no information on the presence (or absence) of a target, this can be obtained by integrating these methods. It follows from Equation (6) that the development of integrated investigations is more effective than increasing the accuracy of separate methods.
4. Minimizing the Number of Combined Methods by the “Four Colors Theorem”
How many geophysical methods should be applied for searching economic deposits, localization of archaeological remains or revealing some dangerous geological phenomena (e.g., karst terrane)? Extending a set of methods could be considered to be at variance with its economic efficiency, and complicated from both an organizational and a technical point of view. In addition, there is a basic limitation imposed on the number of methods. As noted Duda and Hart [17] , a growing number of target indicators require larger amounts of standard information. However, sufficient standards are only available in well-explored areas, where quantitative prediction is obviously less urgent. Therefore, a survey set should involve the minimum number of methods.
The intuitive use of a small number of integration elements in practice can be theoretically substantiated applying the well-known mathematical and cartographic “four colors” solution [18] -[21] for integrating geophysical methods by solving different geological, environmental and other problems.
Geophysical investigation is usually a multistage procedure and for simplicity it is assumed that the goal of each prospecting stage is the selection of an area for more detailed operations at the next stage. The result of prospecting is primarily a substantiated evaluation of the areas under investigation and their classification into two groups: those worthy and unworthy of further study. The objective of prospecting is to obtain the maximum information at a given cost.
Let us now examine the “four colors theorem” from this standpoint. Using elementary notions of graph theory the problem can be formulated as follows: prove that all vertices of an arbitrary planar graph can be colored with four colors in such a way that no two vertices joined by a common edge are the same color. It was proved as early as the middle of the 19th century that four colors suffice to color different counties on the map of England. However, a solution to this theorem was only found more than 100 years later [18] [19] . The authors subdivided all possible maps into almost 2000 types and developed a computer program for their investigation. For each type the problem—whether a map which cannot be colored with four colors can be found among the variety of maps—was solved. After lengthy investigations, an answer of “no” was obtained for all types, and this fact confirms the above solution.
A new (general) proof of the theorem was put forward recently [20] . Figure 3 shows seventeen of 633 reducible configurations which are displayed using the indicated convention. The whole set can be found in [20] .
Any area under study can be divided into separate sub-areas according to certain indicators. The following system of prospect classification has been adopted in the USA [22] : high (H), medium (M), low (L) and unknown (U). The objective is to single out promising areas (if any) from the entire set by an integrated geophysical survey. The colors refer to different combinations of geophysical methods. A positive conclusion for a certain prospecting method is labeled (+), and a negative (–).
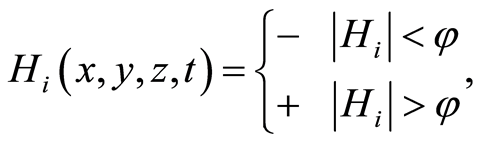 (7)
(7)
where j is some assumed value indicating the split between negative and positive values of geophysical field Hi, 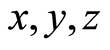 are the space coordinates and t is the time. On the right side of Equation (7) Hi is assigned an absolute value since often anomalous targets may be reflected by negative geophysical anomalies.
are the space coordinates and t is the time. On the right side of Equation (7) Hi is assigned an absolute value since often anomalous targets may be reflected by negative geophysical anomalies.
Clearly a combination of at least two independent geophysical methods is necessary for the first three gradations (H, M and L); gradation U implies no application of the method set (on a scale or not at all) in the area under investigation (Table 2).
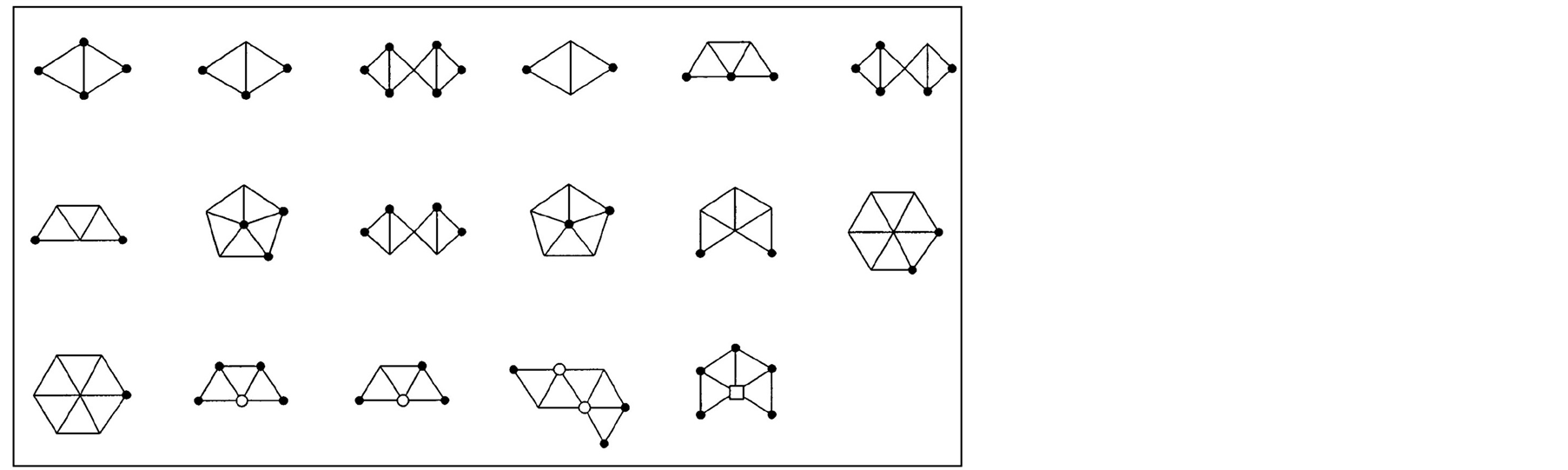
Figure 3. An example of possible configurations (after [18] ).
The geophysical methods employed are a priori assumed to be of equal significance. The threshold field values (the split between plus and minus) and specific types of geophysical investigations are determined according to the prospecting results for similar objects investigated previously and other geological and geophysical considerations. The split refers to the threshold for field values representing specified physical characteristics. These physical characteristics may, for example, include amplitudes of observed fields, field gradients or indicators of field variability. The necessary condition is that we assume the geophysical anomalies are produced by the same targets.
Let us demonstrate an applicability of this approach on a simple example. In an area of porphyry copper deposit in Kazakhstan (Figure 4), marginal values of electrical resistivity of 50 Ohm×m, and magnetic field of 0 nanoTesla have been selected (deposits of this type are characterized by low resistivity (<50 Ohm×m) and negative magnetic field) [23] . Figure 4(a) shows isolines of resistivity, 3b—isolines of magnetic field, and 3c—coloring in four colors according to Table 2. The contour of the deposit is clearly revealed on the basis of the data of two methods.

Figure 4. Electric (a) and magnetic (b) prospecting results at Benkaly porphyry copper deposit and their processing according to four colors problem solution (c) (a), (b) and contour of deposit from [23] .
Table 2. Subdivision of an area according to geophysical survey results.
5. Conclusions
It can be concluded from the foregoing that an optimum geophysical set consists of two independent geophysical methods. A map of geophysical results colored with four colors by the above technique serves as a basis for more detailed investigation. In this connection, a certain redundancy of the set is needed. It should, however, be kept in mind that the employed geophysical set is usually oriented to a particular problem and substantiated by a corresponding physical-geological model of the medium. Any change in the problem (e.g. an increase in the necessary depth of investigation) or in geological and geophysical pattern of the area may bring a change in the set of methods. In this context, this division of the theory of graphs can be attributed to information theory.
At the same time, change of geophysical methods may, in turn, affect the “coloring” of the area under study [24] . Therefore, it is generally a good practice to use three geophysical methods which are effective under given conditions. For instance, a radiometric channel combined with aerial magnetic and electromagnetic surveys will give a negligible increase in cost, but increasing in informativeness may be a significant one.
References
- Tikhonov, A.N. and Arsenin, V.Y. (1977) Solutions of Ill-Posed Problems. Winston, New York.
- Zhdanov, M.S. (2002) Geophysical Inverse Theory and Regularization Problems. In: Ser.: Methods in Geochemistry and Geophysics, 36, Elsevier, Amsterdam.
- Hadamard, J. (1902) Sur les Problèmes aux Dérivées Partielles et Leur Signification Physique. Princeton University Bulletin, 13, 49-52.
- Khesin, B.E., Alexeyev, V.V. and Eppelbaum, L.V. (1996) Interpretation of Geophysical Fields in Complicated Environments. In: Bookseries: Modern Approaches in Geophysics, Kluwer Academic Publishers, Dordrecht.
- Eppelbaum, L.V., Khesin, B.E. and Itkis, S.E. (2001) Prompt Magnetic Investigations of Archaeological Remains in Areas of Infrastructure Development: Israeli Experience. Archaeological Prospection, 8, 163-185. http://dx.doi.org/10.1002/arp.167
- Parasnis, D.S. (1997) Principles of Applied Geophysics. Chapman & Hall, London.
- Telford, W.M., Geldart, L.P. and Sheriff, R.E. (1990) Applied Geophysics. 2nd Edition, Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9781139167932
- Eppelbaum, L.V., Eppelbaum, V.M. and Ben-Avraham, Z. (2003) Formalization and Estimation of Integrated Geological Investigations: Informational Approach. Geoinformatics, 14, 233-240. http://dx.doi.org/10.6010/geoinformatics.14.233
- Shannon, C.E. (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379-432, 623-656. http://dx.doi.org/10.1002/j.1538-7305.1948.tb01338.x
- Brillouin, L.N. (1962) Science and Information Theory. 2nd Edition, Academic Press, New York.
- Khalfin, L.A. (1958) Information Theory of Geophysical Interpretation. Doklady Akademii Nauk SSSR, 122, 1007- 1010.
- Svetov, B.S. (1992) Information Theory Basis of Geophysics. In: Bookseries: Advanced Geophysics. Russian Experience, Issue No. 1, Electromagnetic Research Centre, Moscow.
- Nikitin, A.A. (1993) Statistical Processing of Geophysical Data. In: Bookseries: Advanced Geophysics. Russian Experience, Issue No. 2, Electromagnetic Research Centre, Moscow.
- Gadallah, M.R. and Fisher, R. (2009) Exploration Geophysics. Springer, Berlin.
- Eppelbaum, L.V. and Khesin, B.E. (2012) Geophysical Studies in the Caucasus. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-76619-3
- Ventsel, E.S. (1969) The Probability Theory. 3rd Edition, Nauka, Moscow. (in Russian)
- Duda, R.O. and Hart, P.E. (1973) Pattern Classification and Scene Analysis. John Wiley & Sons, Hoboken.
- Appel, K. and Haken, W. (1977) Every Planar Map Is Four Colorable: Part 1, Discharging. Illinois Journal of Mathematics, 21, 429-490.
- Appel, K., Haken, W. and Koch, S. (1977) Every Planar Mar Is Four Colorable: Part 2, Reducibility. Illinois Journal of Mathematics, 21, 491-567.
- Robertson, N., Sanders, D.P., Seymour, P.D. and Thomas, R. (1997) The Four Color Theorem. Journal of Combinatorial Theory, Series B, 70, 2-44. http://dx.doi.org/10.1006/jctb.1997.1750
- Thomas, R. (1998) An Update on the Four-Color Theorem. Notices of the AMS, 45, 848-859.
- Hansen, W.R. (1978) Suggestions to Authors of the Reports of the United States Geological Survey. 6th Edition, US Government Publishing Office, Washington DC.
- Nikitin, A.A. (1986) Foundation of Integrated Interpretation of Geophysical Data. In: Brodovoi, V.V. and Nikitin, A.A., Eds., Integration of Geophysical Methods, Nedra, Moscow, 42-57. (in Russian)
- Eppelbaum, L.V. (1989) The Development of Methods for Processing and Interpretation of Natural Geophysical Fields in Prospecting for Pyrite Ores in Mountainous Conditions. PhD Thesis, Institute of Geophysics (Georgia Academy of Science), Tbilisi. (in Russian)


