Applied Mathematics
Vol. 4 No. 9 (2013) , Article ID: 36532 , 6 pages DOI:10.4236/am.2013.49174
On (2, 3, t)-Generations for the Rudvalis Group Ru
Department of Mathematics and Statistics, Faculty of Science, Al Imam Mohammad Ibn Saud Islamic University, Riyadh, Saudi Arabia
Email: FaryadA@hotmail.com
Copyright © 2013 Faryad Ali. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 19, 2013; revised July 19, 2013; accepted July 26, 2013
Keywords: Generating Triple; Sporadic Group; Simple Group; Rudvalis Group; 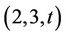 -Generation
-Generation
ABSTRACT
A group G is said to be 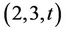 -generated if it can be generated by an involution x and an element y so that
-generated if it can be generated by an involution x and an element y so that 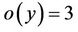 and
and . In the present article, we determine all
. In the present article, we determine all 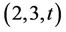 -generations for the Rudvalis sporadic simple group Ru, where t is any divisor of
-generations for the Rudvalis sporadic simple group Ru, where t is any divisor of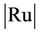 .
.
1. Introduction
A group G is said to be  -generated if it can be generated by two of its elements x and y so that
-generated if it can be generated by two of its elements x and y so that ,
, 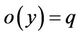 and
and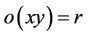 . It is well known that every finite simple group can be generated by just two of its elements. Since the classification of all finite simple groups, more recent work in group theory has involved the study of internal structure of these group and generation type problems have played an important role in these studies. Recently, there has been considerable amount of interest in such type of generations. A
. It is well known that every finite simple group can be generated by just two of its elements. Since the classification of all finite simple groups, more recent work in group theory has involved the study of internal structure of these group and generation type problems have played an important role in these studies. Recently, there has been considerable amount of interest in such type of generations. A  -generated group is a homomorphic image of the projective special linear group
-generated group is a homomorphic image of the projective special linear group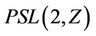 . It has been known since 1901 (see [1]) that the alternating groups An
. It has been known since 1901 (see [1]) that the alternating groups An 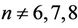 are
are 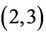 -generated. Macbeath [2] proved that projective special linear groups
-generated. Macbeath [2] proved that projective special linear groups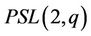 ,
,  are
are 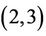 -generated. With the exception of Matheiu groups M11, M22, M23, and Maclarin’s group McL, all sporadic simple groups are
-generated. With the exception of Matheiu groups M11, M22, M23, and Maclarin’s group McL, all sporadic simple groups are 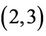 -generated (Woldar [3]). Guralnick showed that any non-abelian finite simple group can be generated by an involution and a Sylow 2-subgroup. In addition, a large number of Lie groups and classical linear groups are
-generated (Woldar [3]). Guralnick showed that any non-abelian finite simple group can be generated by an involution and a Sylow 2-subgroup. In addition, a large number of Lie groups and classical linear groups are 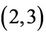 -generated as well. Recently, Liebeck and Shalev proved that all finite classical groups (with some exceptions) are
-generated as well. Recently, Liebeck and Shalev proved that all finite classical groups (with some exceptions) are 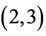 -generated.
-generated.
We say that a group G is 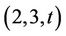 -generated (or
-generated (or 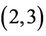 -generated) if it can be generated by just two of its elements x and y such that x is an involution,
-generated) if it can be generated by just two of its elements x and y such that x is an involution, 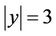 and
and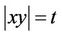 . Moori in [4] computed all
. Moori in [4] computed all 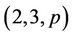 -generations for the smallest Fischer group
-generations for the smallest Fischer group , where p is a prime divisor of
, where p is a prime divisor of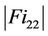 . Further, Ganief and Moori determined the
. Further, Ganief and Moori determined the 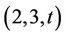 -generations for the Janko’s third sporadic simple group J3 (see [5]). Recently, the author with others computed
-generations for the Janko’s third sporadic simple group J3 (see [5]). Recently, the author with others computed  -generations for the Held’s sporadic simple group He, Tits simple group
-generations for the Held’s sporadic simple group He, Tits simple group 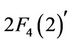 and Conway’s two sporadic simple groups Co3 and Co2 (see [6-8]). Darafsheh and Ashrafi [9] computed generating pairs for the sporadic group Ru. In the present article, we compute all the
and Conway’s two sporadic simple groups Co3 and Co2 (see [6-8]). Darafsheh and Ashrafi [9] computed generating pairs for the sporadic group Ru. In the present article, we compute all the 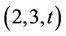 -generations for the Rudvalis simple group Ru, where t is any divisor of
-generations for the Rudvalis simple group Ru, where t is any divisor of .
.
2. Preliminaries
In this article, we use same notation as in [6]. In particular, for C1, C2 and C3 conjugacy classes of elements the group Ru and g3 is a fixed representative of C3, we define 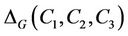 to be the number of distinct pairs
to be the number of distinct pairs 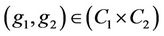 such that
such that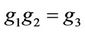 . We can compute the structure of G,
. We can compute the structure of G,  for the conjugacy classes C1, C2 and C3 from the character table of G by the following formula
for the conjugacy classes C1, C2 and C3 from the character table of G by the following formula 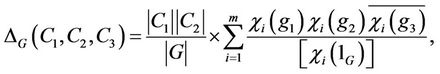 where
where  are the irreducible complex characters of the group G. Further let,
are the irreducible complex characters of the group G. Further let, 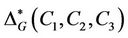 denotes the number of distinct tuples
denotes the number of distinct tuples 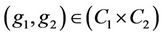 such that
such that  and
and . If
. If 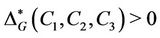 , then clearly G is
, then clearly G is 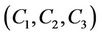 -generated. If H any subgroup of G containing the fixed element
-generated. If H any subgroup of G containing the fixed element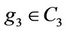 , then
, then 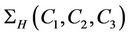 denotes the number of distinct ordered pairs
denotes the number of distinct ordered pairs 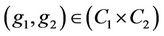 such that
such that  and
and 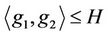 where
where  is obtained by summing the structure constants
is obtained by summing the structure constants 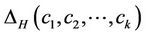 of H over all H-conjugacy classes
of H over all H-conjugacy classes 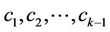 satisfying
satisfying 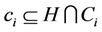 for
for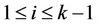 .
.
A general conjugacy class of elements of order n in G is denoted by nX. For examples, 2A represents the first conjugacy class of involutions in a group G. Most of the time, it will clear from the context to which conjugacy classes lX, mY and nZ we are referring. In such case, we suppress the conjugacy classes, using  and
and  as abbreviated notation for
as abbreviated notation for 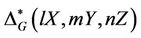 and
and 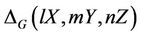 , respectively.
, respectively.
Lemma 2.1 ([10]) Let G be a finite centerless group and suppose lX, mY, nZ are G-conjugacy classes for which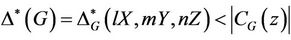 ,
,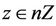 . Then
. Then  and therefore G is not
and therefore G is not 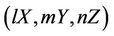 -generated.
-generated.
Theorem 2.2 ([5]) Let G be a finite group and H a subgroup of G containing a fixed element x such that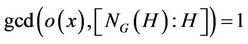 . Then the number h of conjugates of H containing x is
. Then the number h of conjugates of H containing x is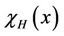 , where
, where 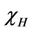 is the permutation character of G with action on the conjugates of H. In particular,
is the permutation character of G with action on the conjugates of H. In particular,
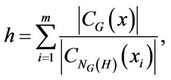
where 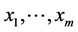 are representatives of the
are representatives of the  - conjugacy classes that fuse to the G-class
- conjugacy classes that fuse to the G-class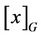 .
.
3. Main Results
The Rudvalis group Ru is a sporadic simple group of order
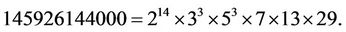
Wilson [11] completely determined the maximal subgroups of the group Ru. It has exactly 15 conjugacy classes of maximal subgroups (see Table 1) as also listed in the  of Finite Group (see [12]). It has precisely two classes of involution, namely 2A and 2B and a unique class 3A of elements of order 3 in Ru.
of Finite Group (see [12]). It has precisely two classes of involution, namely 2A and 2B and a unique class 3A of elements of order 3 in Ru.
It is a well known that if G is 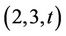 -generated finite simple group, then
-generated finite simple group, then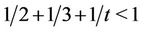 . It follows that we need to consider the cases when
. It follows that we need to consider the cases when
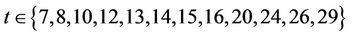 .
.
The cases when t is prime has already been discussed in [9], so we need to investigate the cases when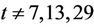 . Next, we investigate each case separately starting with the conjugacy class 15A of Ru.
. Next, we investigate each case separately starting with the conjugacy class 15A of Ru.
Lemma 3.1 The sporadic simple Rudvalis group Ru is 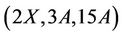 -generated for all
-generated for all .
.
Proof: The maximal subgroups of the group Ru having elements of order 15, up to isomorphism, are H3, H8, H11 and H15.
First we consider the case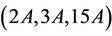 . Using
. Using 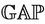 [13], we compute the structure constant
[13], we compute the structure constant 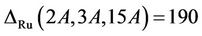 . From the above list of maximal subgroups, Ru class 2A does not meet the maximal subgroup H9. The fusion map of the maximal subgroups H3 into the group Ru yields
. From the above list of maximal subgroups, Ru class 2A does not meet the maximal subgroup H9. The fusion map of the maximal subgroups H3 into the group Ru yields

where 2a, 3a, 3b, 15a, 15b and 2A, 3A, 15A are conjugacy classes of elements in the groups H3 and Ru, respectively. With the help of this fusion map, we calculate the structure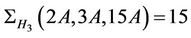 . Further, since a fixed element
. Further, since a fixed element 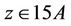 in Ru is contained in a two conjugates of the maximal subgroup H3, the total contribution from the maximal subgroup H3 to the structure constant
in Ru is contained in a two conjugates of the maximal subgroup H3, the total contribution from the maximal subgroup H3 to the structure constant 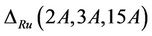 is 2 × 15. Similarly by considering the fusion maps from the maximal subgroups H8, H11 and H15 we compute that
is 2 × 15. Similarly by considering the fusion maps from the maximal subgroups H8, H11 and H15 we compute that ,
,  and
and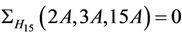 . Since the fixed element z is contained in two conjugates of H8 and in a unique conjugate copy of H11, we obtain
. Since the fixed element z is contained in two conjugates of H8 and in a unique conjugate copy of H11, we obtain
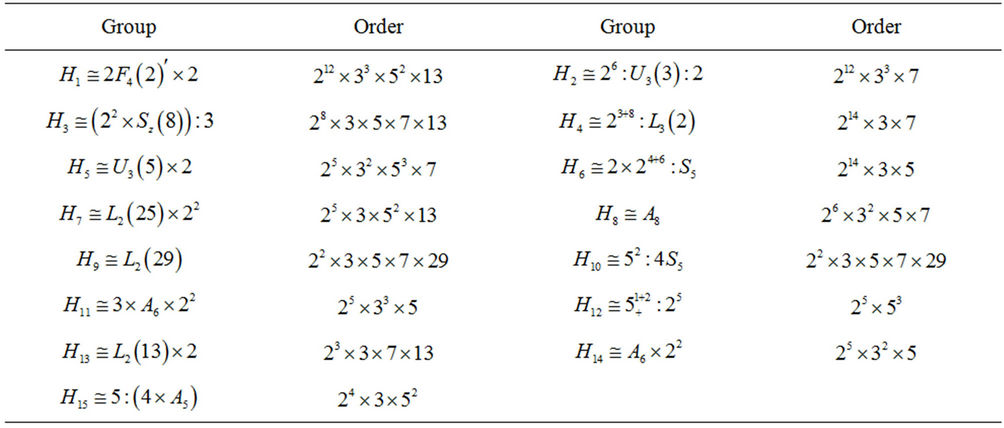
Table 1. Maximal subgroups of rudvalis group Ru.
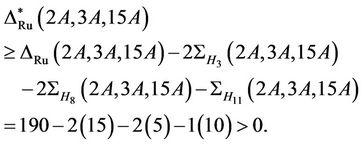
Hence, the group Ru is 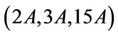 -generated.
-generated.
Next, consider the case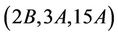 . We compute the algebra structure constant as
. We compute the algebra structure constant as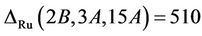 . From the maximal subgroups of Ru, we see that the maximal subgroups that may contain
. From the maximal subgroups of Ru, we see that the maximal subgroups that may contain 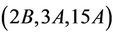 -generated proper subgroups are isomorphic to H3, H9, H11 and H15. By considering the fusion maps from the these maximal subgroups into the group Ru and the values of h which we compute using Theorem 1, we obtain
-generated proper subgroups are isomorphic to H3, H9, H11 and H15. By considering the fusion maps from the these maximal subgroups into the group Ru and the values of h which we compute using Theorem 1, we obtain
 ,
,
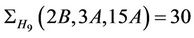 ,
,
 .
.
Hence,
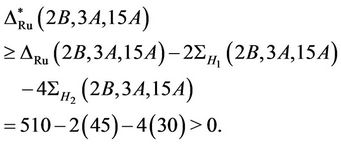
Therefore, 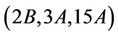 is generating triple of the group Ru and the proof is complete.
is generating triple of the group Ru and the proof is complete.
Lemma 3.2 The Rudavalis group Ru is 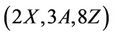 - generated if and and only if
- generated if and and only if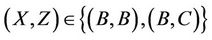 , where
, where  and
and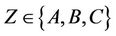 .
.
Proof: Our main proof will consider a number of cases.
Case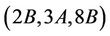 : From the list of maximal subgroups of Ru (Table 1) we observe that, up to isomorphism, H4 and H6 are the only maximal subgroups that admit
: From the list of maximal subgroups of Ru (Table 1) we observe that, up to isomorphism, H4 and H6 are the only maximal subgroups that admit 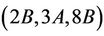 -generated subgroups. From the structure constant we calculate
-generated subgroups. From the structure constant we calculate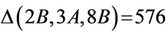 ,
, 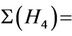 0 and
0 and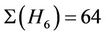 . Since a fixed element
. Since a fixed element 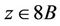 in Ru is contained in three conjugate copies of subgroup H6, we have
in Ru is contained in three conjugate copies of subgroup H6, we have , and therefore Ru is
, and therefore Ru is 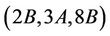 -generated.
-generated.
Case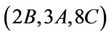 : For this triple we calculate the structure constant
: For this triple we calculate the structure constant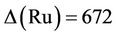 . Up to isomorphism, H4, H6 and H14 are the only maximal subgroups subgroups of Ru that meet the conjugacy classes 2B, 3A and 8C. We compute that
. Up to isomorphism, H4, H6 and H14 are the only maximal subgroups subgroups of Ru that meet the conjugacy classes 2B, 3A and 8C. We compute that 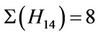 and
and . A fixed element a fixed element of order 8 in Ru-class 8C is contained in eight copies of the subgroup H14. We obtain
. A fixed element a fixed element of order 8 in Ru-class 8C is contained in eight copies of the subgroup H14. We obtain , showing that
, showing that 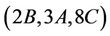 is a generating triple of the group Ru.
is a generating triple of the group Ru.
Cases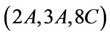 ,
, 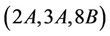 ,
, : In order to investigate these triples, we construct the group Ru explicitly by using its standard generators given by Wilson [14]. The Rudvalis group Ru has a 28 dimensional irreducible representation over
: In order to investigate these triples, we construct the group Ru explicitly by using its standard generators given by Wilson [14]. The Rudvalis group Ru has a 28 dimensional irreducible representation over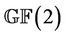 . Using
. Using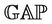 , we generate the group
, we generate the group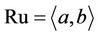 , where a and b are 28 × 28 matrices over
, where a and b are 28 × 28 matrices over 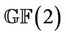 with orders 2 and 4 respectively such that ab has order 13. We see that
with orders 2 and 4 respectively such that ab has order 13. We see that ,
, 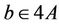 and
and . We produce
. We produce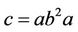 ,
,
 ,
,
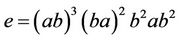 ,
,
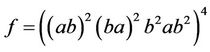 ,
,
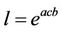 ,
, 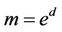 and
and 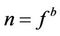 such that
such that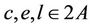 ,
, 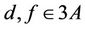 ,
, 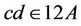 ,
,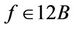 . Let
. Let 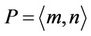 then
then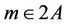 ,
,  and
and 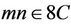 such that
such that 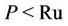 with
with  and
and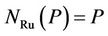 . By investigating maximal subgroups of P and looking at the fusion maps of these maximal subgroups into the groups P and Ru we calculate
. By investigating maximal subgroups of P and looking at the fusion maps of these maximal subgroups into the groups P and Ru we calculate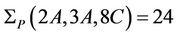 . Consequently we obtain
. Consequently we obtain
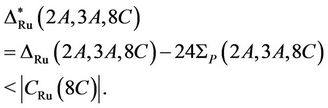
Hence by Lemma 2.1, we obtain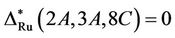 , proving that Ru is not generated by the triple
, proving that Ru is not generated by the triple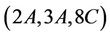 . By using the standard generators a and b of Ru together with above produced elements c, d, e, f, l, m, n in a similar way we explicitly generate
. By using the standard generators a and b of Ru together with above produced elements c, d, e, f, l, m, n in a similar way we explicitly generate 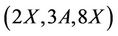 -subgroups and observed that Ru is also not generated by the triple
-subgroups and observed that Ru is also not generated by the triple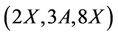 . This completes the lemma.
. This completes the lemma. 
Lemma 3.3 The sporadic group Ru is 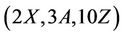 - generated for all
- generated for all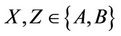 .
.
Proof: We will investigate each triple separately.
Case : We compute the algebra structure constant for this triple as
: We compute the algebra structure constant for this triple as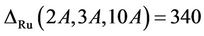 . Amongst the maximal subgroups of Ru having nonempty intersection with the classes 2A, 3A and 10A are isomorphic to H1, H5, H6, H7, H10 and H15. Now, by considering the fusion maps from these maximal subgroups into the group Ru we calculate
. Amongst the maximal subgroups of Ru having nonempty intersection with the classes 2A, 3A and 10A are isomorphic to H1, H5, H6, H7, H10 and H15. Now, by considering the fusion maps from these maximal subgroups into the group Ru we calculate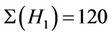 ,
, 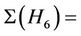 20,
20, 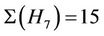 and
and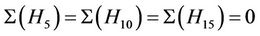 . Since a fixed element of order 10 is contained in two conjugate copies of H1, four conjugate copies of H7 and a unique conjugate copy of H6. Therefore
. Since a fixed element of order 10 is contained in two conjugate copies of H1, four conjugate copies of H7 and a unique conjugate copy of H6. Therefore
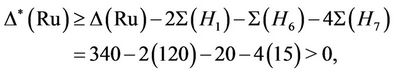
proving the generation of Ru by the triple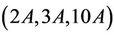 .
.
Case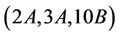 : The only maximal subgroups of Ru that may contain
: The only maximal subgroups of Ru that may contain 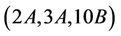 -generated subgroups, up to isomorphisms, are H3, H11, H14 and H15. However, we calculate that
-generated subgroups, up to isomorphisms, are H3, H11, H14 and H15. However, we calculate that . That is, no maximal subgroup of Ru is
. That is, no maximal subgroup of Ru is 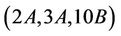 - generated and we obtain
- generated and we obtain , showing that
, showing that  is a generating triple for the group Ru.
is a generating triple for the group Ru.
Case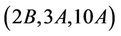 : From the list of maximal subgroup (see Table 1) of Ru, observe that, up to isomorphism, H6, H7 and H15 are only maximal subgroups that may admit
: From the list of maximal subgroup (see Table 1) of Ru, observe that, up to isomorphism, H6, H7 and H15 are only maximal subgroups that may admit 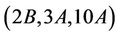 -generated subgroups. We compute in
-generated subgroups. We compute in 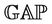 that
that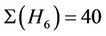 ,
,  and
and . Thus by we have
. Thus by we have
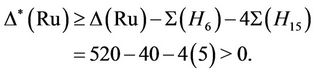
This shows that Ru is 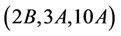 -generated.
-generated.
Case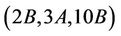 : For this triple we compute
: For this triple we compute  and H3, H11, H14 and H15 are the only maximal subgroups of Ru that meet the classes in this triple. We calculate
and H3, H11, H14 and H15 are the only maximal subgroups of Ru that meet the classes in this triple. We calculate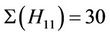 ,
, 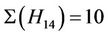 ,
,  and a fixed element
and a fixed element  of order 10 in the group Ru is contained in exactly two copies of each of H11 and H14. Therefore,
of order 10 in the group Ru is contained in exactly two copies of each of H11 and H14. Therefore,
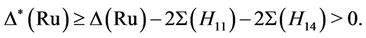
Hence the group Ru is 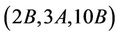 -generated and the lemma is complete.
-generated and the lemma is complete.
Lemma 3.4 Let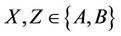 . The group Ru is
. The group Ru is 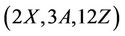 -generated if and only if
-generated if and only if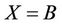 .
.
Proof: We will consider each case separately.
Case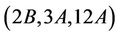 : The maximal subgroups of Ru with order divisible by 12 and non-empty intersection with the classes 2B and 3A are isomorphic to H4, H6, H7 and H11. We calculate that
: The maximal subgroups of Ru with order divisible by 12 and non-empty intersection with the classes 2B and 3A are isomorphic to H4, H6, H7 and H11. We calculate that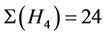 ,
,  while
while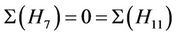 . It follows
. It follows
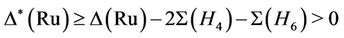 proving the generation by this triple.
proving the generation by this triple.
Case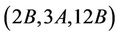 : Up to isomorphism H3, H4, H6, H7, H11, H13 and H15 are maximal subgroups of Ru that may contain
: Up to isomorphism H3, H4, H6, H7, H11, H13 and H15 are maximal subgroups of Ru that may contain 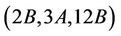 -generated proper subgroups. We compute that
-generated proper subgroups. We compute that ,
, 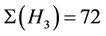 ,
, 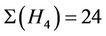 ,
, 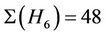 ,
, 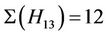 and
and
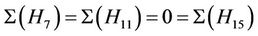 . It follows that
. It follows that

Hence the group Ru is 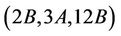 -generated.
-generated.
Case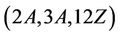 : We show that the group Ru is not
: We show that the group Ru is not 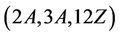 -generated by using the 28-dimensional irreducible representation of Ru over
-generated by using the 28-dimensional irreducible representation of Ru over  as we used in Lemma 3.2 above. We generate
as we used in Lemma 3.2 above. We generate 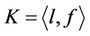 with
with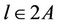 ,
,  such that
such that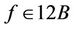 . We have
. We have 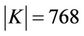 and
and . By investigating the group K, we see that
. By investigating the group K, we see that 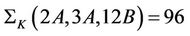 and consequently
and consequently
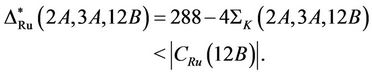
Hence by Lemma 2.1 Ru is not generated by the triple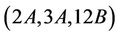 . Similar technique and arguments show that
. Similar technique and arguments show that 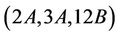 is also not a generating triple for Ru. The lemma is complete.
is also not a generating triple for Ru. The lemma is complete.
Lemma 3.5 The group Ru is 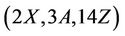 -generated for all
-generated for all 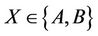 and
and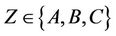 .
.
Proof: We calculate the structure constants 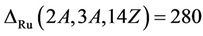 ,
, . From Table 1, the only maximal subgroups of Ru that meet the classes 2A, 3A and 14Z are isomorphic to H3, H4 and H13. Further, H4 is the only maximal subgroup that contribute to the structure constant
. From Table 1, the only maximal subgroups of Ru that meet the classes 2A, 3A and 14Z are isomorphic to H3, H4 and H13. Further, H4 is the only maximal subgroup that contribute to the structure constant  as
as  and
and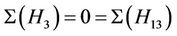 . Thus, we have
. Thus, we have 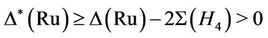 and the generation of Ru by this triple follows.
and the generation of Ru by this triple follows.
Next, we consider the triple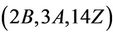 . For this triple, the maximal subgroups that meet the Ru classes 2B, 3A and 14Z, up to isomorphism, are H3, H4, H9 and H13. Our computation shows that
. For this triple, the maximal subgroups that meet the Ru classes 2B, 3A and 14Z, up to isomorphism, are H3, H4, H9 and H13. Our computation shows that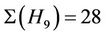 ,
, 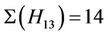 and
and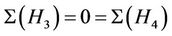 . Thus, for this triple
. Thus, for this triple
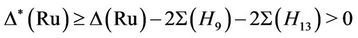 proving that
proving that 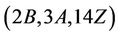 is a generating triple for the group Ru. This completes the proof.
is a generating triple for the group Ru. This completes the proof.
Lemma 3.6 The Rudvalis group Ru is  - generated if and only if
- generated if and only if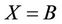 , where
, where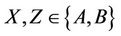 .
.
Proof: We calculate structure constant 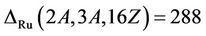 and
and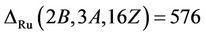 . First we consider the case when
. First we consider the case when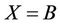 . From the fusion maps of maximal subgroups in Table 1 into the Rudvalis group Ru, we observed that the
. From the fusion maps of maximal subgroups in Table 1 into the Rudvalis group Ru, we observed that the 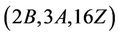 -generated proper subgroups are contained in the maximal subgroups isomorphic to H4 and H6. Further, since
-generated proper subgroups are contained in the maximal subgroups isomorphic to H4 and H6. Further, since 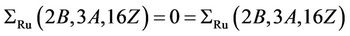 we obtain that H4 and H6 are not
we obtain that H4 and H6 are not 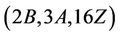 -generated. Hence we have
-generated. Hence we have 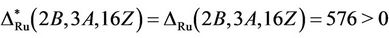 and generation of Ru by the triple
and generation of Ru by the triple  follows.
follows.
For the triple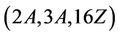 , we use random element generation method as described in Conder [15] to show that Ru is not
, we use random element generation method as described in Conder [15] to show that Ru is not 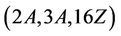 -generated. Since
-generated. Since  . This is, there are 288 pairs
. This is, there are 288 pairs 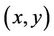 with
with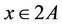 ,
, 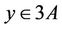 and
and . We apply a procedure (an analogous procedure given in Conder [15] for CAYLEY), in the computer algebra system
. We apply a procedure (an analogous procedure given in Conder [15] for CAYLEY), in the computer algebra system  (see [16]). It turns out that all 288 pairs generate proper subgroup of Ru and so
(see [16]). It turns out that all 288 pairs generate proper subgroup of Ru and so 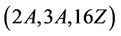 is not a generating triple of Ru.
is not a generating triple of Ru.
Lemma 3.7 The group Ru is 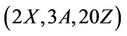 -generated where
-generated where  and
and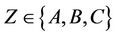 .
.
Proof: The maximal subgroups of the group Ru which contains element of order 20, up to isomorphism, are H1, H5, H10 and H15 (see Table 1). We now consider each case separately.
Case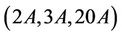 : We observed that 20A class of Ru does not meet the maximal subgroup H15. So, the maximal subgroups of Ru having non-empty intersection with the classes 2A, 3A and 20A are, up to isomorphism, H1, H5, H6 and H10. We compute that
: We observed that 20A class of Ru does not meet the maximal subgroup H15. So, the maximal subgroups of Ru having non-empty intersection with the classes 2A, 3A and 20A are, up to isomorphism, H1, H5, H6 and H10. We compute that 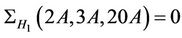 ,
, 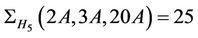 ,
, 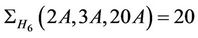 and
and 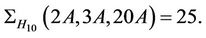 Thus,
Thus,
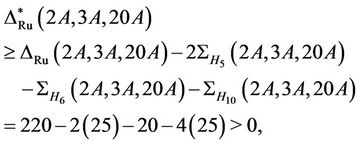
and therefore Ru is  -generated.
-generated.
Case  where
where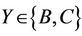 : The only maximal subgroups of Ru that may contain
: The only maximal subgroups of Ru that may contain 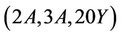 - generated proper subgroups are isomorphic to H6 and H15. Further since
- generated proper subgroups are isomorphic to H6 and H15. Further since 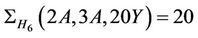 and
and  we have
we have
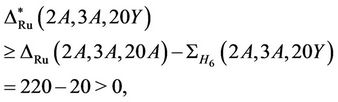
and so Ru is 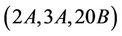 -, and
-, and 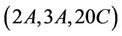 -generated.
-generated.
Case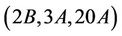 : We compute the algebra structure constant as
: We compute the algebra structure constant as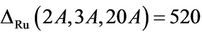 . The only maximal subgroup of Ru having non-empty intersection with the classes 2B, 3A and 20A is isomorphic to H6. Since
. The only maximal subgroup of Ru having non-empty intersection with the classes 2B, 3A and 20A is isomorphic to H6. Since 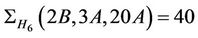 and a fixed element
and a fixed element  is contained in a unique conjugate of M6, we have
is contained in a unique conjugate of M6, we have
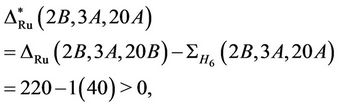
proving that Ru is 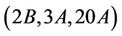 -generated.
-generated.
Case 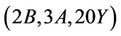 where
where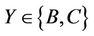 : First we calculate that the values of structure constant
: First we calculate that the values of structure constant 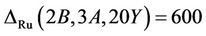 . Again, the only maximal subgroups of Ru which may contain
. Again, the only maximal subgroups of Ru which may contain 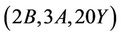 -generated proper subgroups are isomorphic to H6 and H15. We compute
-generated proper subgroups are isomorphic to H6 and H15. We compute 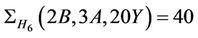 and
and 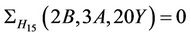 . Hence we obtain
. Hence we obtain
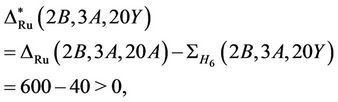
and the generation of Ru with the triples 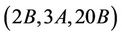 and
and 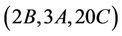 follows. This completes the lemma.
follows. This completes the lemma.
Lemma 3.8 The Rudvalis group Ru is 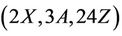 - generated, where
- generated, where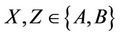 .
.
Proof: The maximal subgroups of Ru having elements of order 24 are isomorphic to H6, H7, H10 and H11 (see Table 1).
First we consider the triple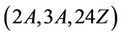 . By looking at the fusion maps from the above maximal subgroups into the group Ru, in each case, we obtain
. By looking at the fusion maps from the above maximal subgroups into the group Ru, in each case, we obtain
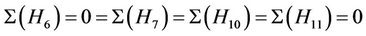 .
.
Now, since  we have
we have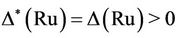 . Thus, Ru is
. Thus, Ru is 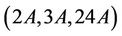 -, and
-, and 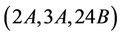 -generated.
-generated.
Next, for the triple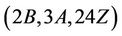 , we compute
, we compute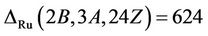 . From the above maximal subgroups H10 does the Ru-class 2B. For the maximal subgroups H6 and H11 we obtain
. From the above maximal subgroups H10 does the Ru-class 2B. For the maximal subgroups H6 and H11 we obtain 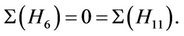 For the maximal subgroup H7 we calculate
For the maximal subgroup H7 we calculate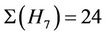 . Hence
. Hence 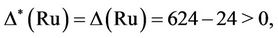 proving the generation of Ru by the triples
proving the generation of Ru by the triples 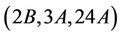 and
and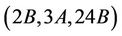 . This completes the proof.
. This completes the proof.
Lemma 3.9 The Rudvalis simple group Ru is 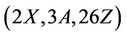 -generated, where
-generated, where 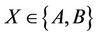 and
and 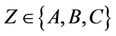 .
.
Proof: Up to isomorphism, H3 and H7 are the only maximal subgroups of Ru which contain an element of order 26 (see Table 1).
Case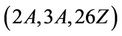 : In this case we compute
: In this case we compute 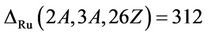 . However, in both cases we obtain
. However, in both cases we obtain 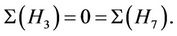 This implies that there is no contribution from these maximal subgroups to the structure constant
This implies that there is no contribution from these maximal subgroups to the structure constant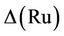 . Hence generation of Ru by the triple follows as we have
. Hence generation of Ru by the triple follows as we have 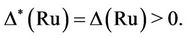
Case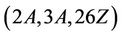 : For this triple we have
: For this triple we have 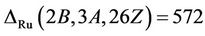 . By considering the fusion maps from the maximal subgroups H3 and H7 into Ru we calculate
. By considering the fusion maps from the maximal subgroups H3 and H7 into Ru we calculate 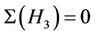 and
and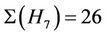 . Thus
. Thus
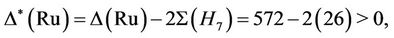
and we conclude that Ru is 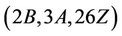 -generated, which completes the proof.
-generated, which completes the proof.
4. Acknowledgements
The author gratefully acknowledges partial financial support from the Deanship of Academic Research (Project No. 301209) at Al Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia.
REFERENCES
- G. A. Miller, “On the Groups Generated by Two Operators,” Bulletin of the AMS—American Mathematical Society, Vol. 7, No. 10, 1901, pp. 424-426. doi:10.1090/S0002-9904-1901-00826-9
- A. M. Macbeath, “Generators of Linear Fractional Groups,” Proceedings of Symposia in Pure Mathematics, Vol. 12, No. 1, 1969, pp. 14-32.
- A. J. Woldar, “On Hurwitz Generation and Genus Actions of Sporadic Groups,” Illinois Journal of Mathematics, Vol. 33, No. 3, 1989, pp. 416-437.
- J. Moori, “(2, 3, p)-Generations for the Fischer Group F22,” Communications in Algebra, Vol. 22, No. 11, 1994, pp. 4597-4610. doi:10.1080/00927879408825089
- S. Ganief and J. Moori, “(2, 3, t)-Generations for the Janko Group J3,” Communications in Algebra, Vol. 23, No. 12, 1995, pp. 4427-4437. doi:10.1080/00927879508825474
- F. Ali and M. A. F. Ibrahim, “On the Simple Sporadic Group He Generated by (2, 3, t) Generators,” Bulletin of the Malaysian Mathematical Sciences Society, Vol. 35, No. 3, 2012, pp. 745-753.
- M. A. Al-Kadhi and F. Ali, “(2, 3, t)-Generations for the Conway Group Co3,” International Journal of Algebra, Vol. 4, No. 25-28, 2010, pp. 1341-1353.
- M. A. Al-Kadhi and F. Ali, “(2, 3, t)-Generations for the Conway Group Co2,” Journal of Mathematics and Statistics, Vol. 8, No. 3, 2012, pp. 339-341. doi:10.3844/jmssp.2012.339.341
- M. R. Darafsheh and A. R. Ashrafi, “Generating Pairs for the Sporadic Group Ru,” Journal of Applied Mathematics and Computing, Vol. 12, No. 1-2, 2003, pp. 143-154. doi:10.1007/BF02936188
- M. D. E. Conder, R. A. Wilson and A. J. Woldar, “The Symmetric Genus of Sporadic Groups,” Proceedings of the American Mathematical Society, Vol. 116, No. 3, 1992, pp. 653-663. doi:10.1090/S0002-9939-1992-1126192-2
- R. A. Wilson, “The Geometry and Maximal Subgroups of the Simple Groups of A. Rudvalis and J. Tits,” Proceedings London Mathematical Society, Vol. 48, No. 3, 1984, pp. 533-563.
- J. H. Conway, R. T. Curtis, S. P. Norton, R. A. Parker and R. A. Wilson, “
 of Finite Groups,” Oxford University Press, Clarendon, Oxford, 1985.
of Finite Groups,” Oxford University Press, Clarendon, Oxford, 1985. - The GAP Group, “
 -Groups, Algorithms and Programming, Version 4.3,” St Andrews, Aachen, 2002. http://www.gap-system.org
-Groups, Algorithms and Programming, Version 4.3,” St Andrews, Aachen, 2002. http://www.gap-system.org - R. A. Wilson, et al., “A World-Wide-Web,” Atlas of Group Representations, 2006. http://brauer.maths.qmul.ac.uk/Atlas/v3
- M. D. E. Conder, “Random Walks in Large Finite Groups,” The Australasian Journal of Combinatorics, 4, No. 1, 1991, pp. 49-57.
- W. Bosma, J. Cannon and C. Playoust, “The Magma Algebra System. I. The User language,” Journal of Symbolic Computation, Vol. 24, No. 3, 1997, pp. 235-265.

