Applied Mathematics
Vol.4 No.6(2013), Article ID:32657,4 pages DOI:10.4236/am.2013.46125
On the Convergence of Monotone Lattice Matrices*
1School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan, China
2The College of Mathematics and Statistics, Chongqing University of Arts and Sciences, Chongqing, China
Email: jiangjingstu@163.com
Copyright © 2013 Jing Jiang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 29, 2013; revised June 3, 2013; accepted June 4, 2013
Keywords: Distributive Lattice; Lattice Matrix; Convergence
ABSTRACT
Since lattice matrices are useful tools in various domains like automata theory, design of switching circuits, logic of binary relations, medical diagnosis, markov chains, computer network, traffic control and so on, the study of the properties of lattice matrices is valuable. A lattice matrix A is called monotone if A is transitive or A is monotone increasing. In this paper, the convergence of monotone matrices is studied. The results obtained here develop the corresponding ones on lattice matrices shown in the references.
1. Introduction
In the field of applications, lattice matrices play major role in various areas such as automata theory, design of switching circuits, logic of binary relations, medical diagnosis, markov chains, computer network, traffic control (see e.g. [1]). Since several classical lattice matrices, for example transitive matrix, monotone increasing matrix, nilpotent matrix, have special applications, many authors have studied these types of matrices. In fact, a transitive matrix can be used in clustering, information retrieval, preference, and so on (see e.g. [2,3]); a nilpotent matrix represents an acyclic graph that is used to represent consistent systems and is important in the representation of precedence relations (see e.g. [4]). Recently, the transitive closure of lattice matrix has been used to analyze the maximum road of network. In this paper, we continue to study transitive lattice matrices and monotone increasing matrices. The main results obtained in this paper develop the previous results on transitive lattice matrices [5] and monotone increasing matrices [6].
2. Definitions and Preliminaries
At this section, we shall give some definitions and lemmas. Let  be a partially ordered set (simply denoted by poset) and
be a partially ordered set (simply denoted by poset) and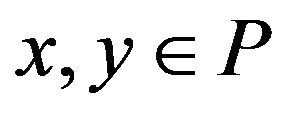 . If
. If 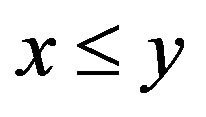 or
or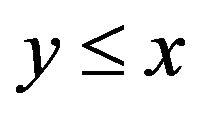 then
then ![]() and
and ![]() are called comparable. Otherwise,
are called comparable. Otherwise, ![]() and
and ![]() are called incomparable, noted by
are called incomparable, noted by . If for any
. If for any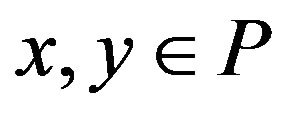 ,
, ![]() and
and ![]() are comparable, then P is called a chain. An unordered poset is a poset in which
are comparable, then P is called a chain. An unordered poset is a poset in which 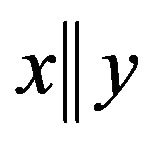 for all
for all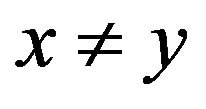 . A chain c in a poset P is a nonempty subset of P, which, as a subposet, is a chain. An antichain C in a poset P is a nonempty subset which, as a subposet, is unordered. A lattice is a poset in which every two elements have a unique least upper bound and a unique greatest lower bound. For any x and y in L, the least upper bound and the greatest lower bound will be denoted by
. A chain c in a poset P is a nonempty subset of P, which, as a subposet, is a chain. An antichain C in a poset P is a nonempty subset which, as a subposet, is unordered. A lattice is a poset in which every two elements have a unique least upper bound and a unique greatest lower bound. For any x and y in L, the least upper bound and the greatest lower bound will be denoted by 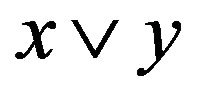 and
and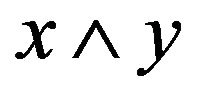 , respectively. It is clear that any chain is a lattice, which is called a linear lattice. It is obvious that if
, respectively. It is clear that any chain is a lattice, which is called a linear lattice. It is obvious that if 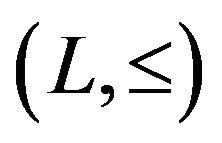 is a linear lattice (especially, the fuzzy algebra [0,1] or the binary Boolean algebra
is a linear lattice (especially, the fuzzy algebra [0,1] or the binary Boolean algebra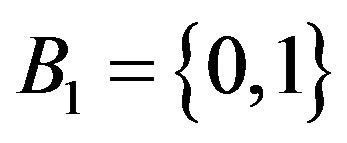 ) then
) then and
and 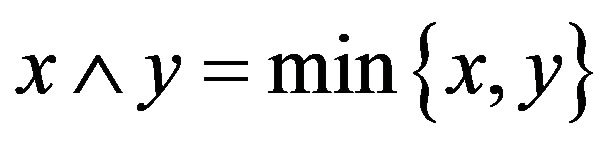 for all x and y in L. Let
for all x and y in L. Let 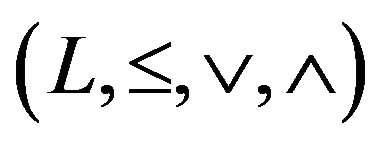 be a lattice and
be a lattice and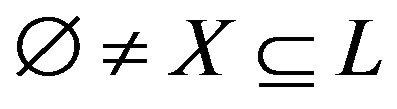 . X is called a sublattice of L if for any
. X is called a sublattice of L if for any 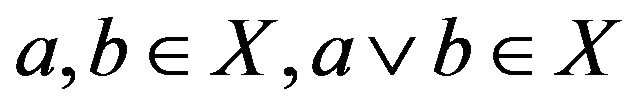 and
and 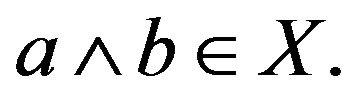 A lattice
A lattice 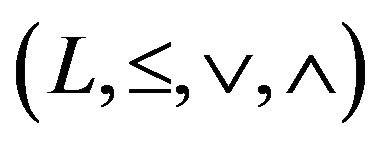 is said to be distributive if the operations
is said to be distributive if the operations  and
and  are distributive with respect to each other. A matrix is called a lattice matrix if its entries belong to a distributive lattice. In this paper, the lattice
are distributive with respect to each other. A matrix is called a lattice matrix if its entries belong to a distributive lattice. In this paper, the lattice 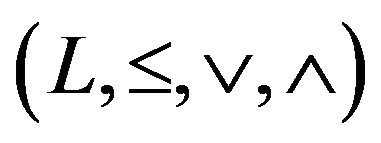 is always supposed to be a distributive lattice with the least and greatest elements 0 and 1, respectively. Let
is always supposed to be a distributive lattice with the least and greatest elements 0 and 1, respectively. Let  be all
be all ![]() matrices over L. For any A in
matrices over L. For any A in , we shall denote by
, we shall denote by 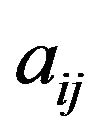 or
or 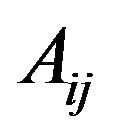 the element of L which stands in the
the element of L which stands in the 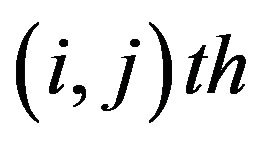 entry of A. For convenience, we shall use the set N to denote the set
entry of A. For convenience, we shall use the set N to denote the set 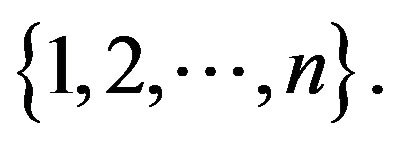
For any A, B, C in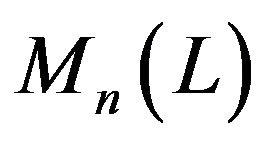 , we define:
, we define:
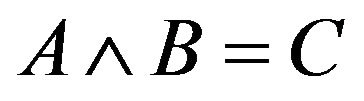 iff
iff 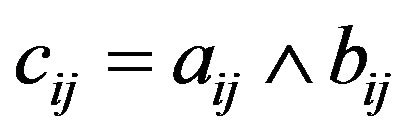 for
for  in N;
in N;
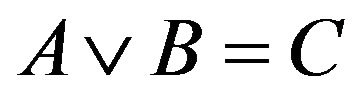 iff
iff 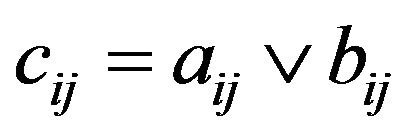 for
for 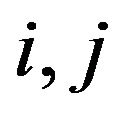 in N;
in N;
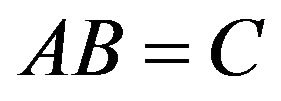 iff
iff 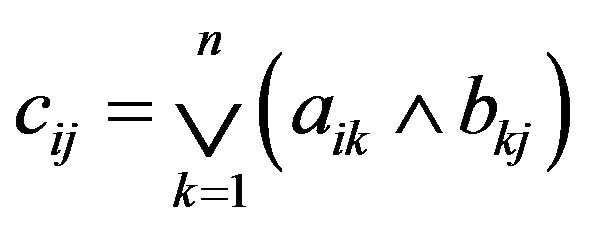 for
for  in N;
in N;
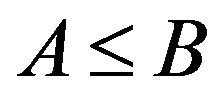 iff
iff 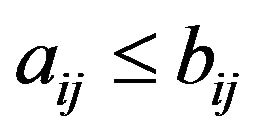 for
for 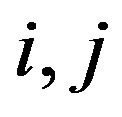 in N and
in N and 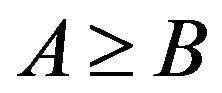 iff
iff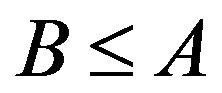 ;
;
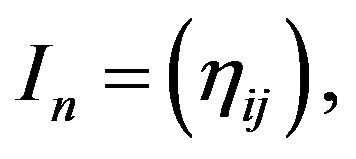 where
where 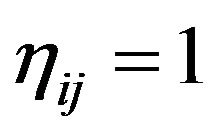 if
if 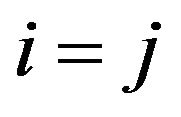 and
and 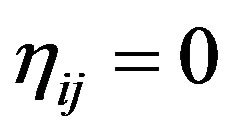 if
if 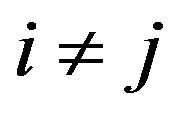 for
for 
For any A in 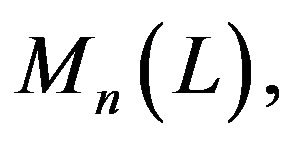 the powers of A are defined as follows:
the powers of A are defined as follows: 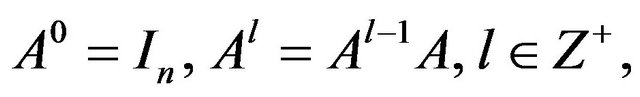 where Z+ denotes the set of all positive integers. The
where Z+ denotes the set of all positive integers. The 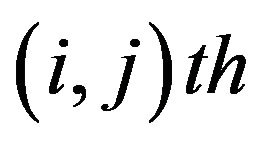 entry of
entry of  is denoted by
is denoted by  and
and
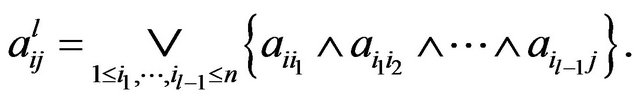
Let 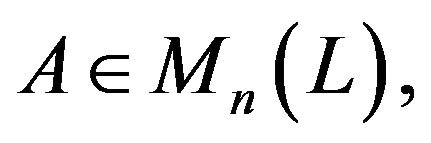 A is called transitive if
A is called transitive if 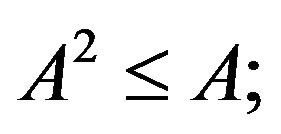
A is called monotone increasing if 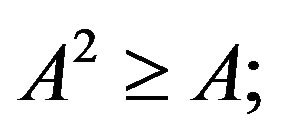 A is called reflexive if
A is called reflexive if 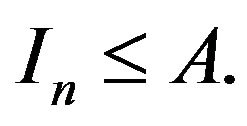 In this paper, A lattice matrix A is called monotone if A is transitive or A is monotone increasing.
In this paper, A lattice matrix A is called monotone if A is transitive or A is monotone increasing.
For any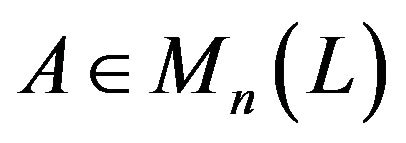 , A is said to be almost periodic if there exist positive integers k and d such that
, A is said to be almost periodic if there exist positive integers k and d such that 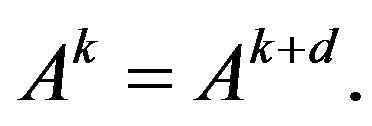 The least positive integers k and d are called the index and the period of A, and denoted by
The least positive integers k and d are called the index and the period of A, and denoted by 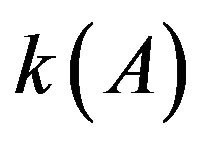 and
and 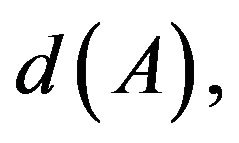 respectively. In particular, if
respectively. In particular, if 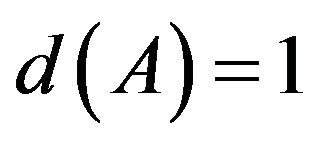 then A is said to converges in a finite number of steps.
then A is said to converges in a finite number of steps.
3. Convergence of Monotone Lattice Matrices
In this section, we shall discuss the convergence of Monotone Lattice Matrices. In [5,6], Tan studied the convergence index of transitive matrices and monotone increasing matrices. In the following, we continue to study the convergence index of these matrices which discussed by Tan [5,6], and the convergence index of these discussed matrices is smaller than previous considered index.
Theorem 3.1. Let 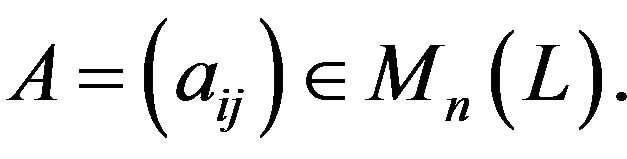 if
if 
holds for all  then 1)
then 1) 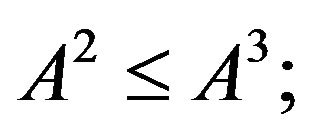
2) 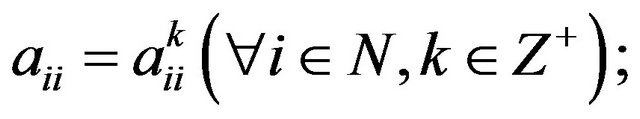
3)  converges to
converges to 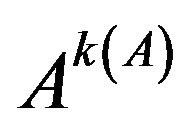 with
with 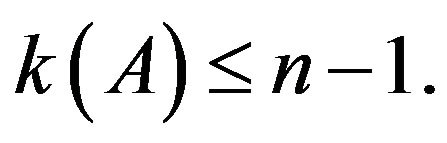
Proof. 1) Let
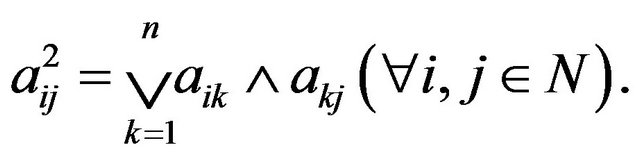
By the hypothesis 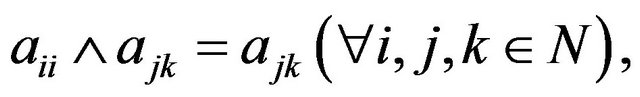 it follows that
it follows that
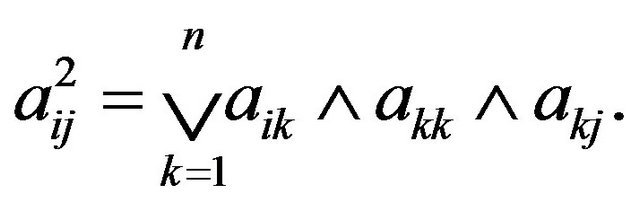
Since 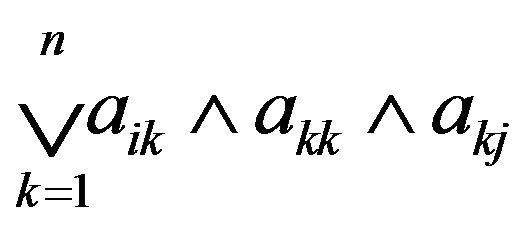 is the sum of some term in
is the sum of some term in 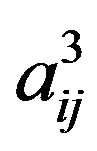 we have
we have

Thus 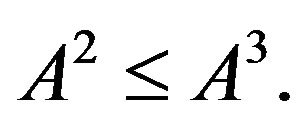
2) By  we have
we have
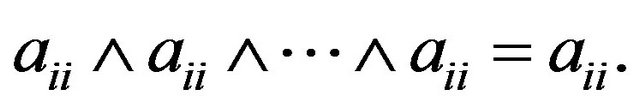
Then
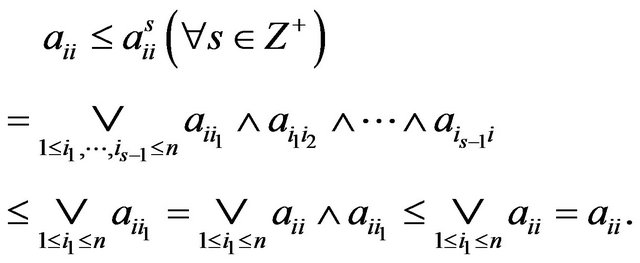
Therefore, 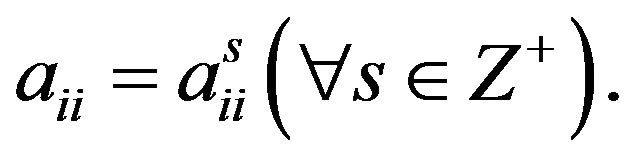
3) By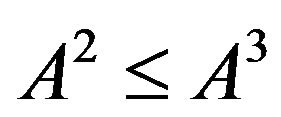 , it follows that
, it follows that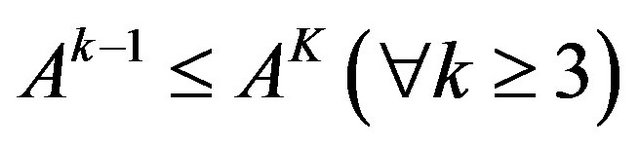 . Hence,
. Hence, 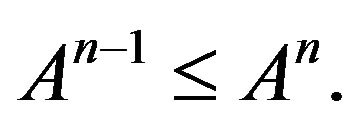 In the following, we shall prove that
In the following, we shall prove that 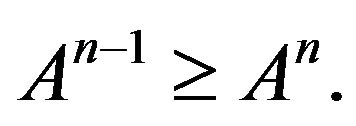
By the result of 2), we only need to show that 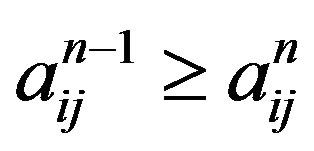 for
for 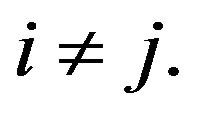 Let
Let
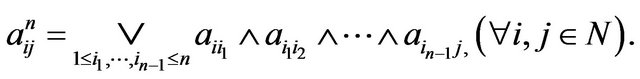
Since the number of indices in 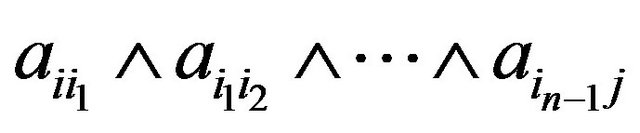 is
is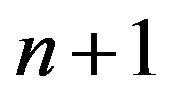 , there must be two indices
, there must be two indices 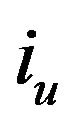 and
and 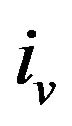 such that
such that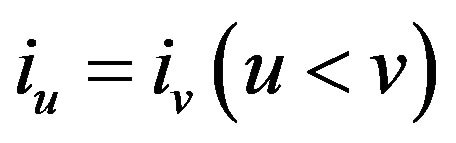 . Then
. Then
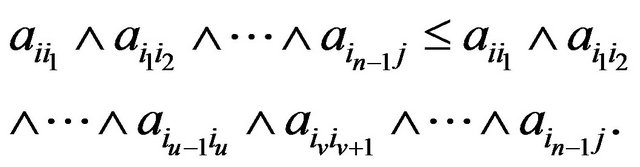
Since  is a term of
is a term of 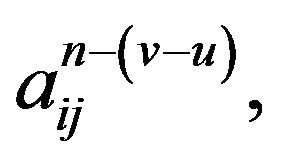 we have
we have

Thus 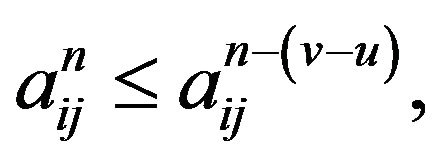 then
then
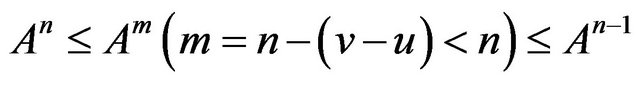 (since
(since 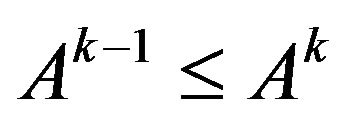 for
for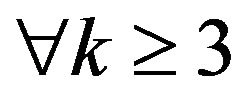 ).
).
From above, we can get 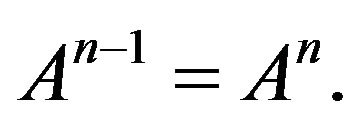 This completes the proof.
This completes the proof.
Corollary 3.1. Let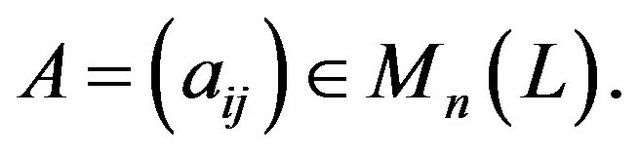 if
if 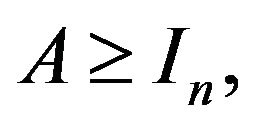 then 1)
then 1) 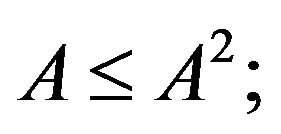
2) 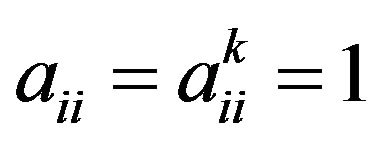 for all
for all 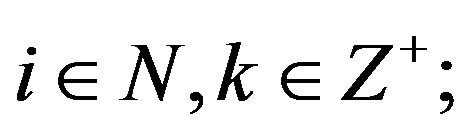
3) A converges to 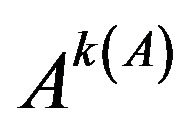 with
with 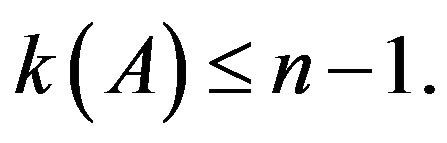
Proof. It follows from Theorem 3.1.
Theorem 3.2. Let  If
If  and
and
 holds for all
holds for all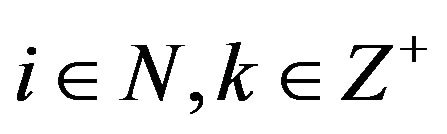 , then A converges to
, then A converges to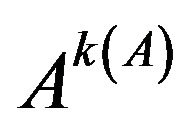 with
with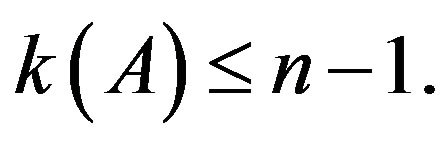
Proof. Since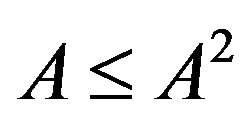 we have
we have 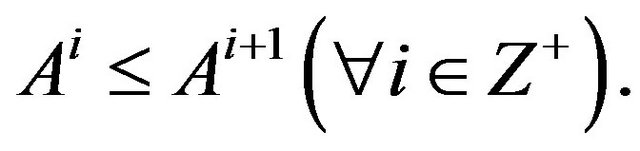
Then

Let 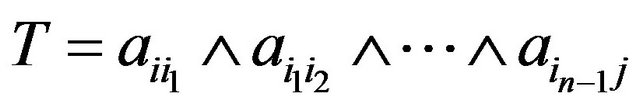 be any term of
be any term of 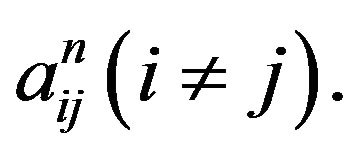
Since the number of indices in T is greater than![]() , there must be two indices
, there must be two indices 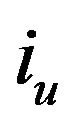 and
and 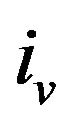 such that
such that 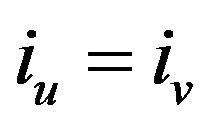
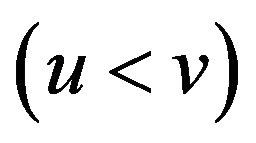 . Then
. Then
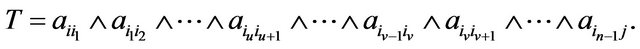 Now delete the term
Now delete the term  in
in![]() , thus we can get a new term
, thus we can get a new term
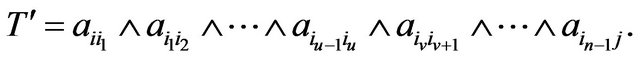
Since 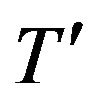 is a term of
is a term of 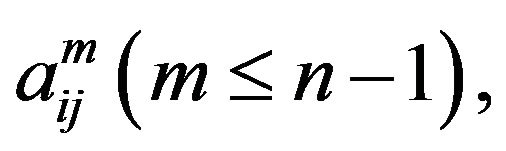 we have
we have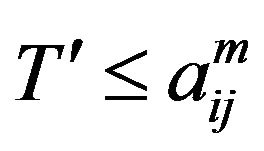 . But by the property of the operation
. But by the property of the operation , we have
, we have
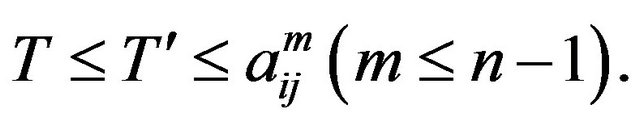
Thus  On the other hand, by the hypothesis
On the other hand, by the hypothesis 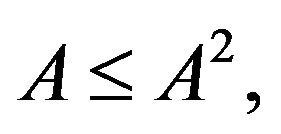 we have
we have
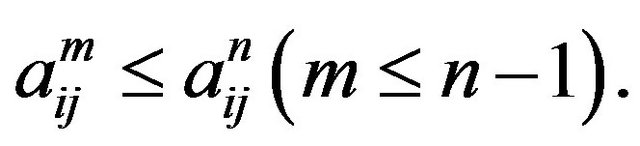
From above, we can get 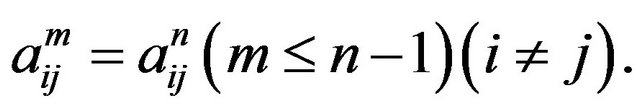
Since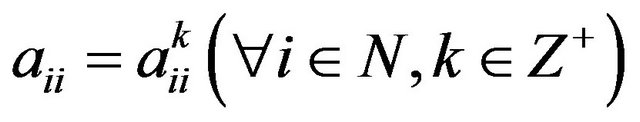 , we have
, we have
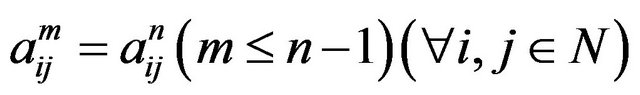 and so
and so
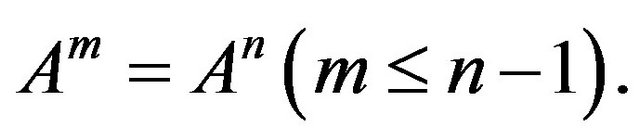
This completes the proof.
Theorem 3.3. Let . If for any
. If for any
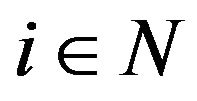 ,
,  or
or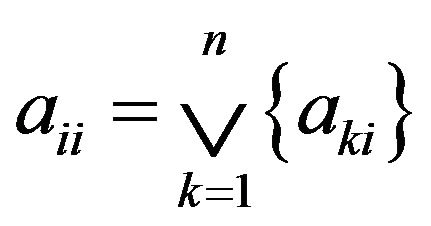 , then 1)
, then 1) ;
;
2)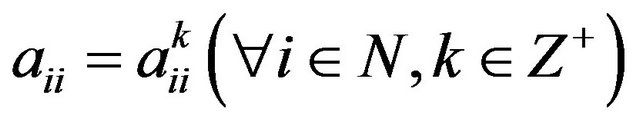 ;
;
3) A converges to 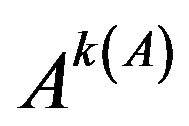 with
with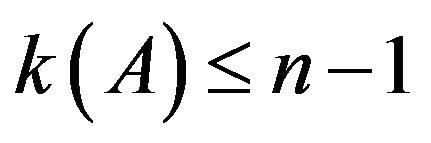 .
.
Proof. 1) Let
 .
.
If , then
, then

If , then
, then
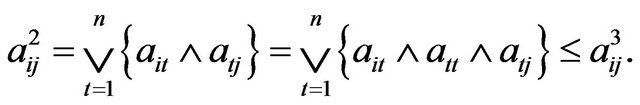
Thus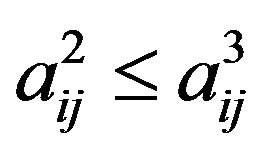 , and so
, and so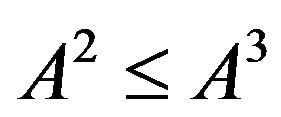 . Therefore
. Therefore
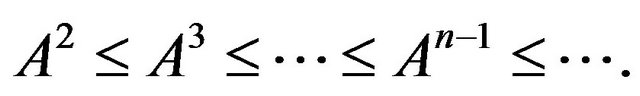
2) for any ,
,  ,
,
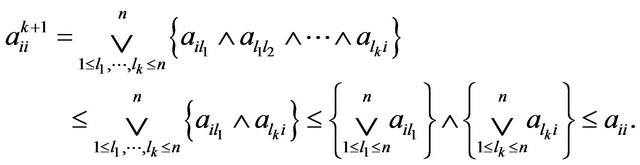
On the other hand, by the result 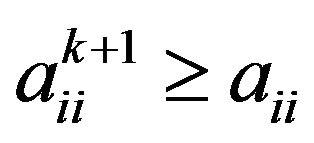 in 1), we have
in 1), we have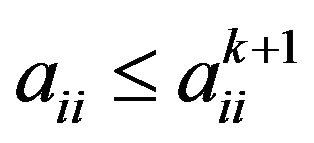 .
.
3) It follows from Theorem 3.2. This completes the proof.
Corollary 3.2. Let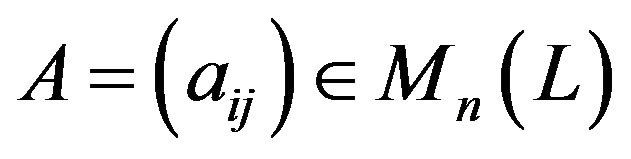 . If for any
. If for any 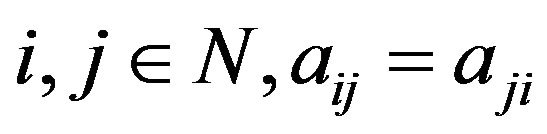 and
and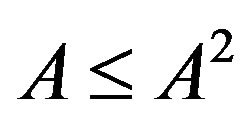 , then 1)
, then 1)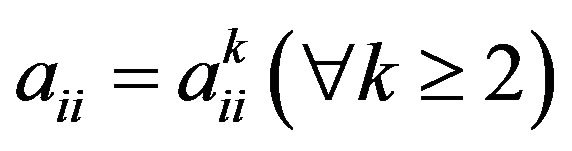 ;
;
2) A converges to 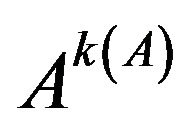 with
with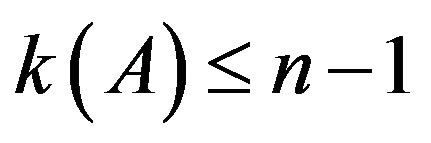 .
.
Proof. 1) By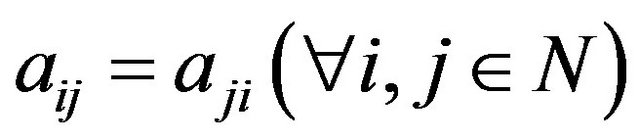 , we can get
, we can get
Since
We have . On the other hand, since
. On the other hand, since , we have
, we have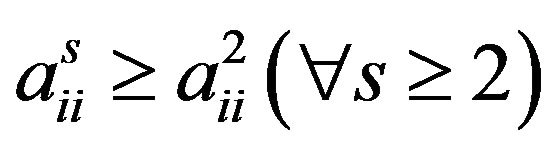 . Therefore
. Therefore
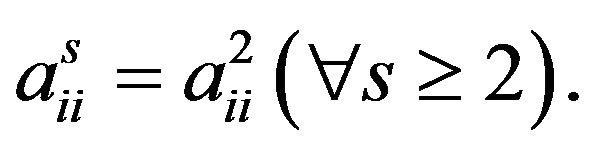
2) It follows from Theorem 3.2. This completes the proof.
Theorem 3.4. If A is transitive and . Where
. Where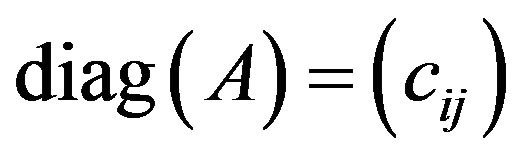 , with
, with 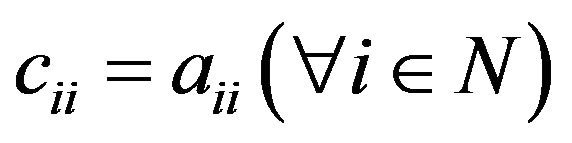 and
and
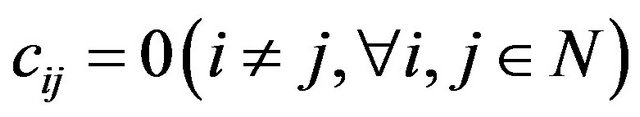 , then 1)
, then 1) 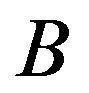 converges to
converges to 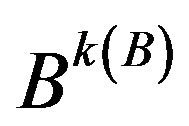 with
with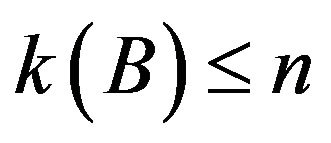 ;
;
2) If A satisfies  (or
(or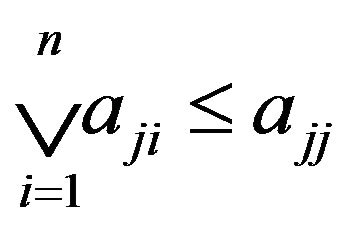 ) for some
) for some
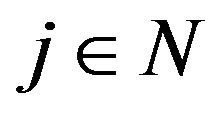 , then B converges to
, then B converges to 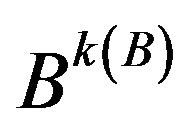 with
with ;
;
3) If B satisfies 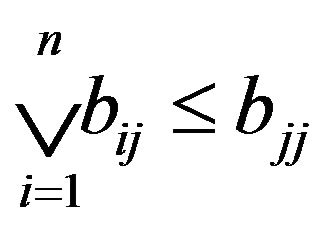 (or
(or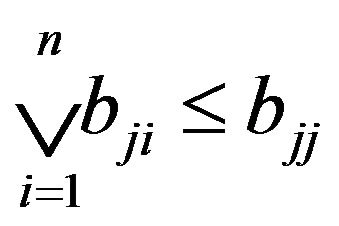 ) for some
) for some
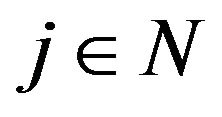 , then B converges to
, then B converges to  with
with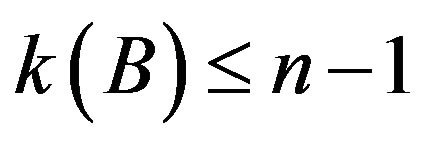 .
.
Proof. First by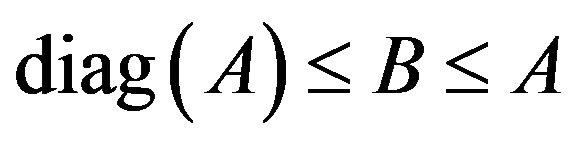 , we have
, we have 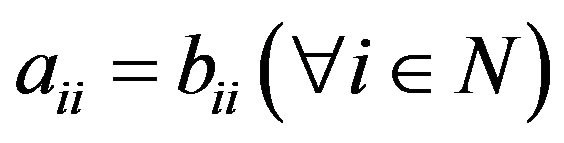 .
.
1) Let
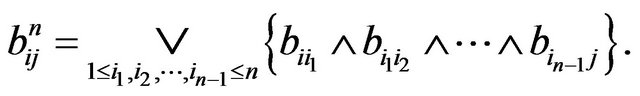
Now, we consider any term T of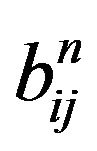 . Since the number of indices in T is greater than n, there must be two indices
. Since the number of indices in T is greater than n, there must be two indices 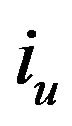 and
and 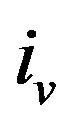 such that
such that . Then
. Then
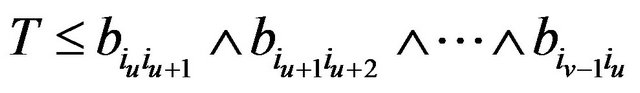
And
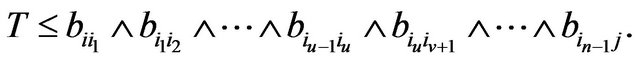
Since  is transitive, we have
is transitive, we have  for all
for all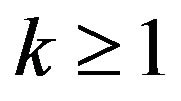 , and so
, and so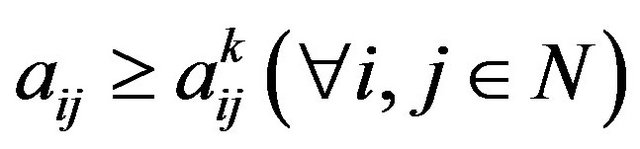 . Thus
. Thus
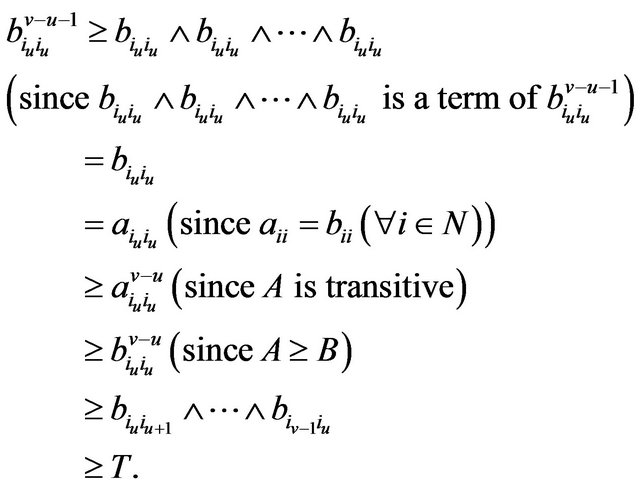
Since 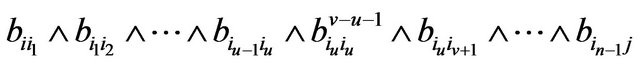 is a term of
is a term of , we have
, we have
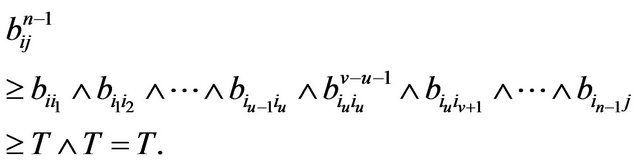
Then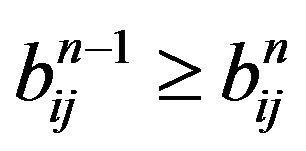 , and so
, and so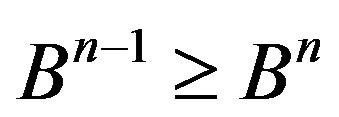 . Therefore
. Therefore 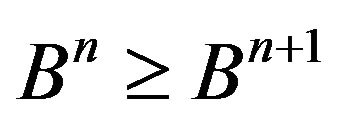 . On the other hand, since
. On the other hand, since

We have , then
, then . From above, we can get
. From above, we can get , and so
, and so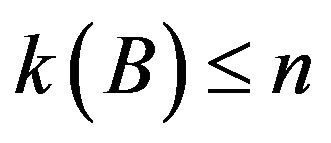 .
.
2) By the proof of 1), we have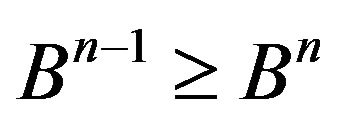 . In the following we shall prove that
. In the following we shall prove that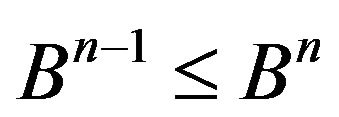 .
.
Let
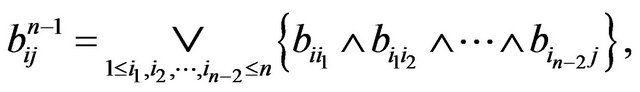
Now consider any term 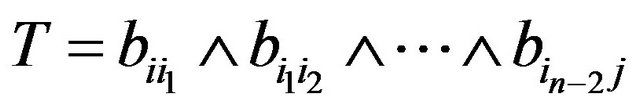 of
of .
.
a) If 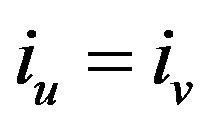 for some
for some ![]() and
and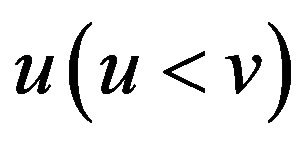 , then
, then
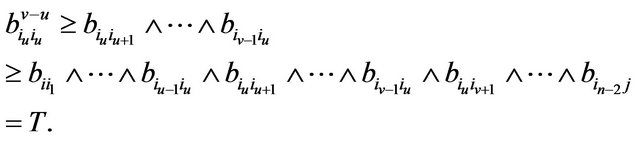
And so
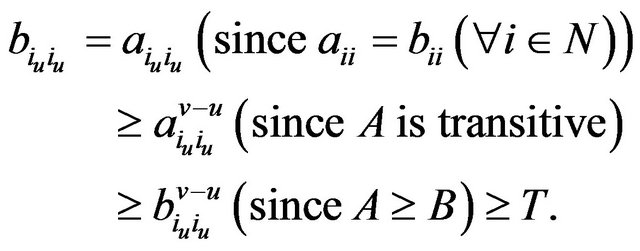
Then
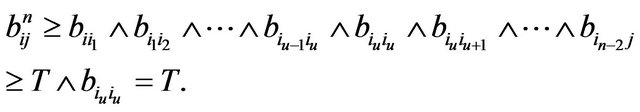
b) Suppose that 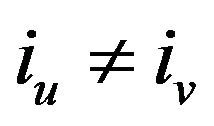 for all
for all . By the hypothesis,
. By the hypothesis, 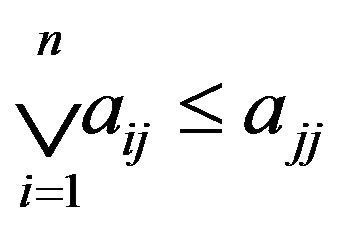 (or
(or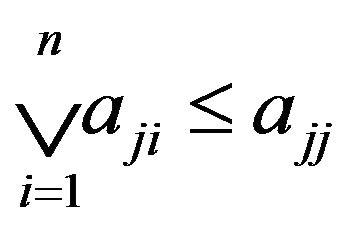 ) for some
) for some 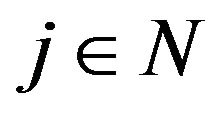 and
and
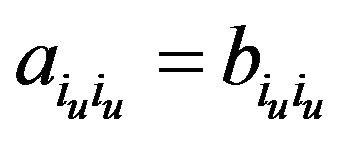 , we can get
, we can get 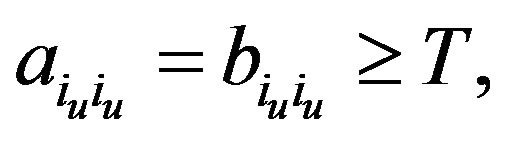 Thus
Thus
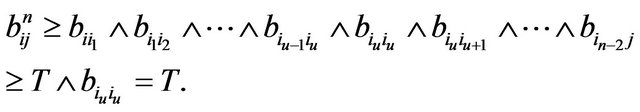
From above, we have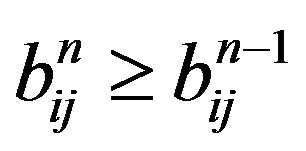 , and so
, and so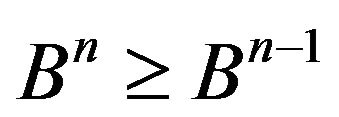 . Therefore
. Therefore .
.
3) The proof of 3) is similar to that of 2). This completes the proof.
Theorem 3.4 is an improvement of Theorem 4.1 [6].
As a special of Theorem 3.4, we obtain the following Corollary.
Corollary 3.3. If  is transitive, then 1)
is transitive, then 1)  converges to
converges to 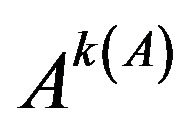 with
with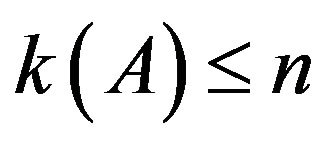 ;
;
2) If A satisfies 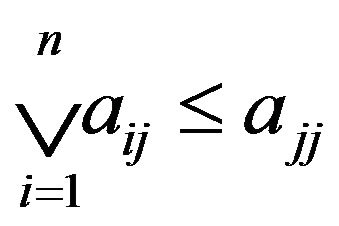 (or
(or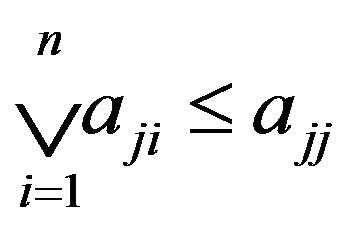 ) for some
) for some
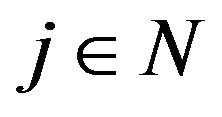 , then A converges to
, then A converges to 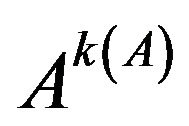 with
with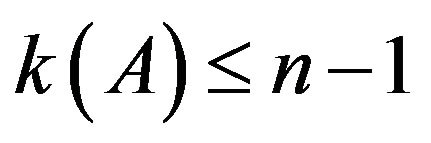 .
.
Corollary 3.3 is an improvement of Corollary 4.1 [6].
REFERENCES
- F. A. Deng and S. Y. Liu, “Application of Fuzzy Concept Networks in Fault Diagnosis,” Control and Decision, Vol. 16, 2001, pp. 834-836.
- S. V. Ovchinnikov, “Structure of Fuzzy Binary Relations,” Fuzzy Sets and Systems, Vol. 6, No. 2, 1981, pp. 169-195. doi:10.1016/0165-0114(81)90023-3
- V. Tahani, “A Fuzzy Model of Document Retrieval Systems,” Information Processing Management, Vol. 12, No. 3, 1976, pp. 177-187. doi:10.1016/0306-4573(76)90004-2
- F. Harary, “On the Consistency of Precedence Matrices,” Journal of the ACM, Vol. 7, No. 3, 1960, pp. 255-259. doi:10.1145/321033.321038
- Y. J. Tan, “On the Power of Matrices over a Distributive Lattice,” Linear Algebra and Its Applications, Vol. 336, 2001, pp. 1-14. doi:10.1016/j.laa.2004.11.016
- Y. J. Tan, “On the Transitive Matrices over Distributive Lattices,” Linear Algebra and Its Applications, Vol. 400, 2005, pp. 169-191.
NOTES
*This work was supported by the Foundation of National Nature Science of China (Grant No.11071178) and the Fundamental Research Funds for the Central Universities.

