Applied Mathematics
Vol.3 No.12A(2012), Article ID:26005,7 pages DOI:10.4236/am.2012.312A284
Strong Law of Large Numbers under an Upper Probability
Graduate Department of Financial Engineering, Ajou University, Suwon, South Korea
Email: cxy_161977@163.com
Received September 3, 2012; revised October 3, 2012; accepted October 10, 2012
Keywords: Strong Law of Large Numbers; Upper Probability; Weakly Compact; Independence; Quasi-Continuous
ABSTRACT
Strong law of large numbers is a fundamental theory in probability and statistics. When the measure tool is nonadditive, this law is very different from additive case. In 2010 Chen investigated the strong law of large numbers under upper probability V by assuming V is continuous. This assumption is very strong. Upper probabilities may not be continuous. In this paper we prove the strong law of large numbers for an upper probability without the continuity assumption whereby random variables are quasi-continuous and the upper probability is generated by a weakly compact family of probabilities on a complete and separable metric sample space.
1. Introduction
Strong law of large numbers under nonadditive probabilities is a much important theory in uncertainty theories and has more applications in statistics, risk measures, asset pricings and many other fields. In 1999 Marinacci [1] first investigated the strong law of large numbers for sequences of independent and identically distributed (IID for short) random variables ![]() relative to a capacity
relative to a capacity ![]() which is continuous and totally monotone and proved that under regularity condition the limit inferior and limit superior of
which is continuous and totally monotone and proved that under regularity condition the limit inferior and limit superior of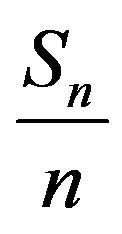 , where
, where , lie between the two Choquet integrals
, lie between the two Choquet integrals 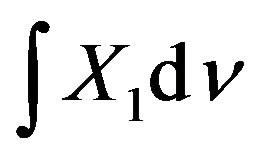 (submean) and
(submean) and 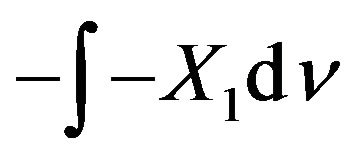 (supermean) induced by this capacity with probability 1 under
(supermean) induced by this capacity with probability 1 under ![]() (that is, quasi surely), and furthermore, if
(that is, quasi surely), and furthermore, if ![]() is null-additive, then that limit inferior attains the submean and the limit superior attains the supermean quasi surely, respectively. This is different from the law under probability measure P whereby under suitable conditions, such as for IID sequences,
is null-additive, then that limit inferior attains the submean and the limit superior attains the supermean quasi surely, respectively. This is different from the law under probability measure P whereby under suitable conditions, such as for IID sequences, 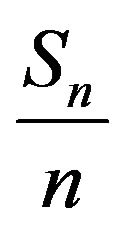 converges to the mathematical expectation of
converges to the mathematical expectation of 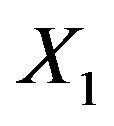 almost surely relative to
almost surely relative to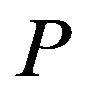 . In 2005 Maccheroni and Marinacci [2] extended the results of Marinacci [1] for a totally monotone capacity on Polish space whereby the bounded variables
. In 2005 Maccheroni and Marinacci [2] extended the results of Marinacci [1] for a totally monotone capacity on Polish space whereby the bounded variables 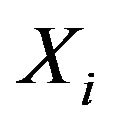 are continuous or simple, or the capacity
are continuous or simple, or the capacity ![]() is continuous. But the conditions of these two articles on capacity are too strong and not easy to test. And generally capacities can not uniquely determine the (nonlinear) expectations relative to the capacities. Motivated by robust statistics and limit theories under sublinear expectations given by Peng in 2007, Chen [3] in 2010 investigated the strong law of large numbers for a pair of lower and upper probabilities
is continuous. But the conditions of these two articles on capacity are too strong and not easy to test. And generally capacities can not uniquely determine the (nonlinear) expectations relative to the capacities. Motivated by robust statistics and limit theories under sublinear expectations given by Peng in 2007, Chen [3] in 2010 investigated the strong law of large numbers for a pair of lower and upper probabilities 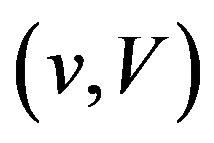 which are induced by a sublinear expectation
which are induced by a sublinear expectation  (see Peng (2012) [4])
(see Peng (2012) [4])
whereby the sequence ![]() is IID under
is IID under  (the independence is different from classical case and the one in Marinacci [1], see Peng (2012) [4]). He proved if
(the independence is different from classical case and the one in Marinacci [1], see Peng (2012) [4]). He proved if
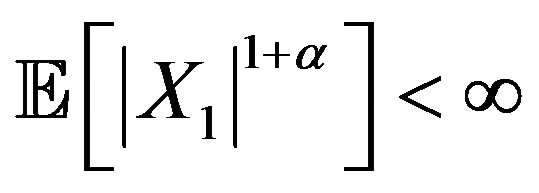 for some
for some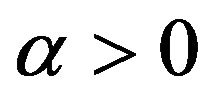 , then those limit inferior and limit superior lie between another submean
, then those limit inferior and limit superior lie between another submean 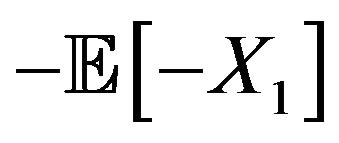 and supermean
and supermean 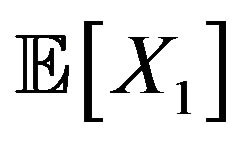 which may not equal the ones given by Choquet integrals (see Chen, Wu and Li (2012) [5] for details). Furthermore, if we futher assume that
which may not equal the ones given by Choquet integrals (see Chen, Wu and Li (2012) [5] for details). Furthermore, if we futher assume that 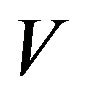 is continuous, then
is continuous, then
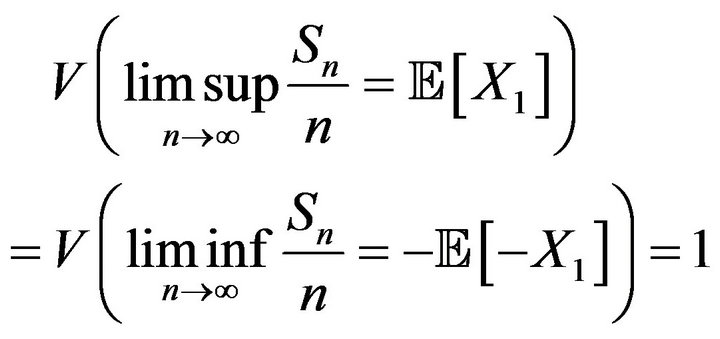 (1)
(1)
Hu (2012) [6] extends the results of Chen [3] to the sequence of non-identically distributed random variables for the same independence and continuity assumptions. Chen and Wu (2011) [7] extends Chen [3] to more weaker independence condition without identical distribution assumption, and proves if we further assume that
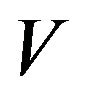 is continuous, for any subsequence
is continuous, for any subsequence ![]() of
of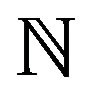 ,
, 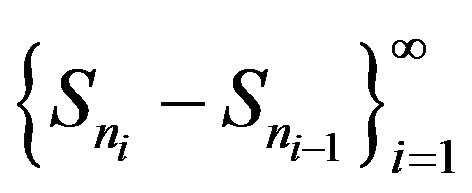 are pairwise weakly independent under
are pairwise weakly independent under
![]() , and there exist some constants
, and there exist some constants 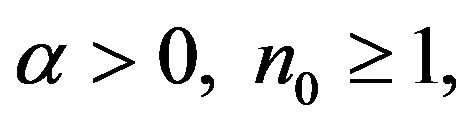 and
and 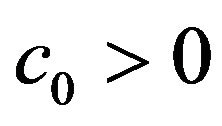 such that
such that

then (1) still holds.
We can see that for the strong law of large numbers (1) under an upper probability, there are two key conditions: well-defined independence and continuity of the upper probability V. The continuity assumption of V is based on the second Borel-Cantelli lemma to get 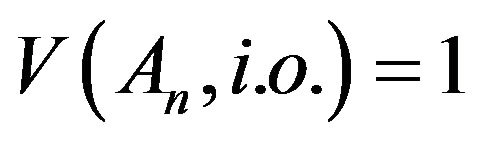 for certain sequence of measurable events
for certain sequence of measurable events 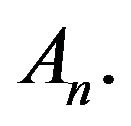 But as we know in general V is not continuous, since for nonclosed nonincreasing sequence of measurable events
But as we know in general V is not continuous, since for nonclosed nonincreasing sequence of measurable events , even if
, even if 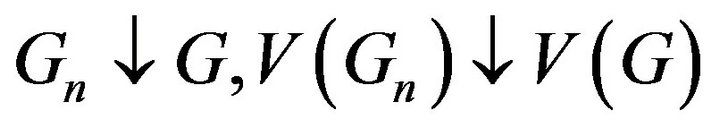 may not hold (see Xu and Zhang (2010) [8] for an example). Hence a natural question is: if
may not hold (see Xu and Zhang (2010) [8] for an example). Hence a natural question is: if 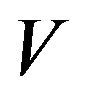 is not continuous, whether does (1) hold? In this paper we will give a confirmative answer. We assume a1)
is not continuous, whether does (1) hold? In this paper we will give a confirmative answer. We assume a1)  is a complete and separable metric space, F is a
is a complete and separable metric space, F is a ![]() -algebra of all Borel subsets of
-algebra of all Borel subsets of , P is a nonempty subset of
, P is a nonempty subset of  which is a family of all probabilities on
which is a family of all probabilities on , and
, and 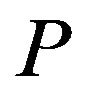 is also weakly compact;
is also weakly compact;
a2) For each 
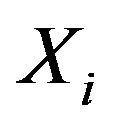 is quasi-continuous, and
is quasi-continuous, and
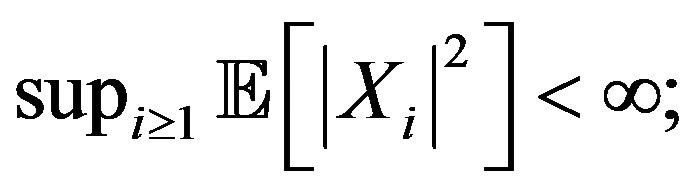
a3) ![]() is independent sequence of random variables under
is independent sequence of random variables under where
where  is a sublinear expectation corresponding to
is a sublinear expectation corresponding to . In this paper we successfully proved the strong law of large numbers under assumptions a1)-a3) without the continuity assumption of V by transforming that an event
. In this paper we successfully proved the strong law of large numbers under assumptions a1)-a3) without the continuity assumption of V by transforming that an event 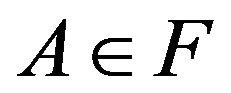 occures with probability 1 under V (that is,
occures with probability 1 under V (that is, ) to the problem of its complementary event
) to the problem of its complementary event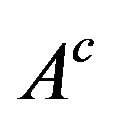 , i.e.,
, i.e.,  where
where ![]() is the conjugate lower probability of V and proving
is the conjugate lower probability of V and proving 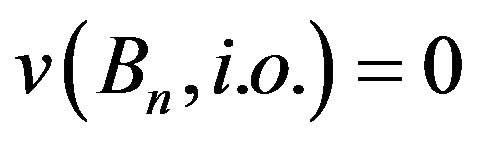
for some appropriate events 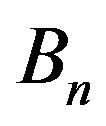 with
with 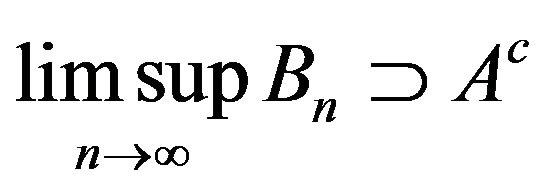
by using properties of V and![]() .
.
This paper is organized as follows. In Section 2 we give some basic concepts and useful lemmas. In Section 3 we mainly prove the strong law of large numbers without continuity assumption of upper probability V for IID and continuous sequences. Section 4 extends results of Section 3 and gets the law for non-identically distributed sequence. Section 5 gives an example.
2. Preliminaries
Let  be a separable and complete metric space.
be a separable and complete metric space.  is a σ-algebra of all Borel subsets of
is a σ-algebra of all Borel subsets of . We introduce an upper probability
. We introduce an upper probability 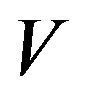 by
by
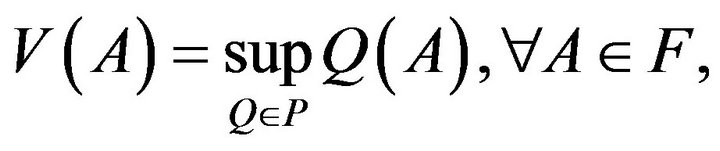
where P is a family of probabilities on 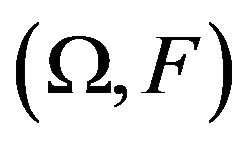 and weakly compact. Thus its conjugate capacity (see Choquet (1954) [9]), i.e., lower probability is
and weakly compact. Thus its conjugate capacity (see Choquet (1954) [9]), i.e., lower probability is
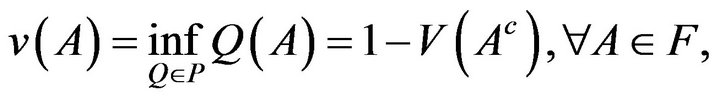
where 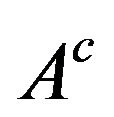 is the complementary set of A. From Huber and Strassen (1973) [10] V and v also satisfy the following properties.
is the complementary set of A. From Huber and Strassen (1973) [10] V and v also satisfy the following properties.
Proposition 1.
1) 
2) 
3) 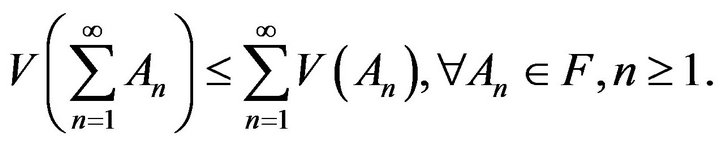
4) 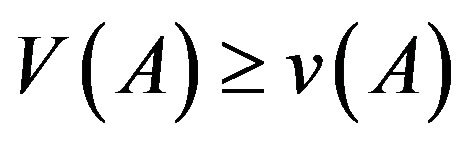 for all
for all 
5) lower-continuity of  for all sets in
for all sets in : if
: if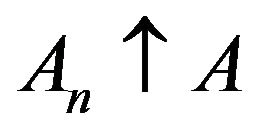 ,
,  then
then 
6) upper-continuity of V for all closed sets: if  closed,
closed, 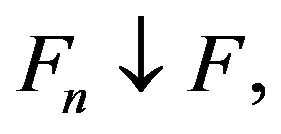 then
then 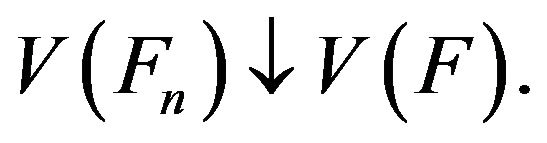
7) lower-continuity of ![]() for all open sets: if
for all open sets: if  open, then
open, then 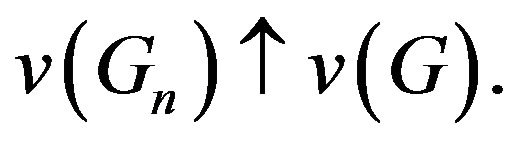
8) upper-continuity of ![]() for all sets: if
for all sets: if 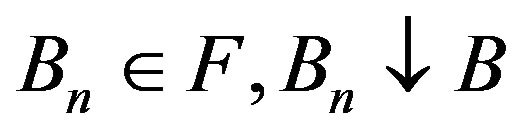 , then
, then 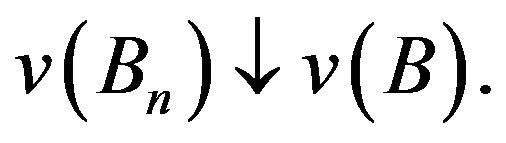
Now we introduce an upper expectation  by
by  in the following
in the following
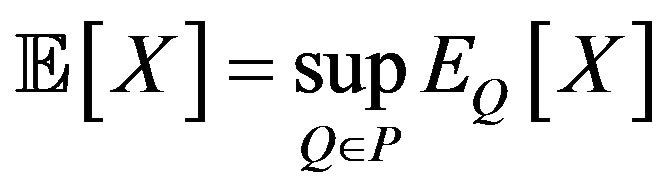
for all  such that
such that 
 is the linear expectation corresponding to
is the linear expectation corresponding to 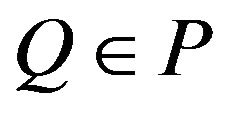 such that
such that 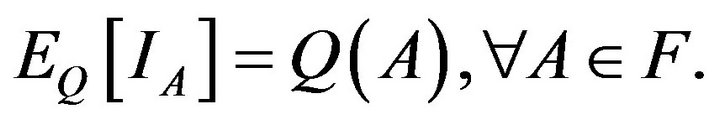
Then  is a sublinear expectation (see Peng [4]) on
is a sublinear expectation (see Peng [4]) on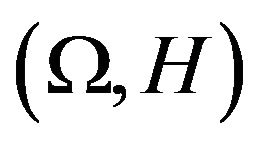 , where
, where  is a set of all real-valued random variables
is a set of all real-valued random variables 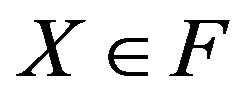 such that
such that 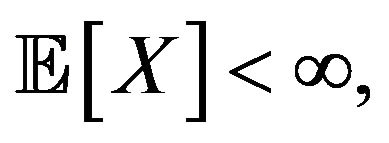 that is,
that is,  satisfies that for all
satisfies that for all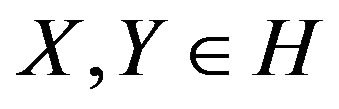 1) Monotonicity:
1) Monotonicity: 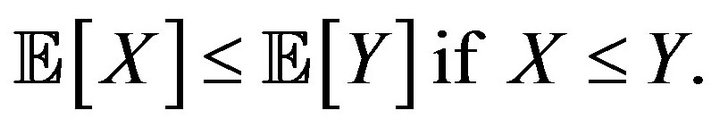
2) Constant preserving: 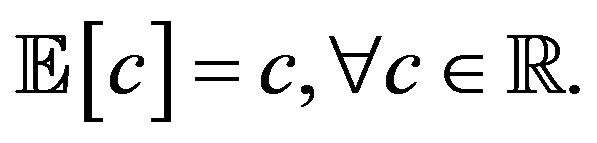
3) Sub-additivity: 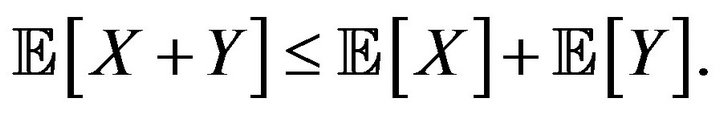
4) Positive homogeneity: 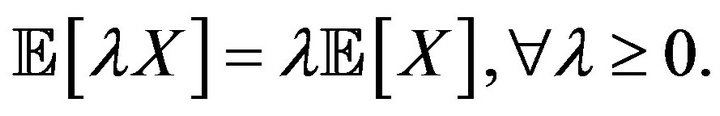
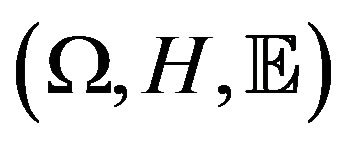 is called a sublinear expectation space in contrast with probability space. Given
is called a sublinear expectation space in contrast with probability space. Given 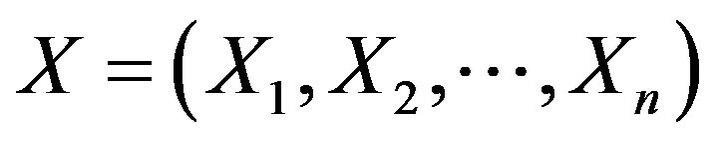 , we say
, we say 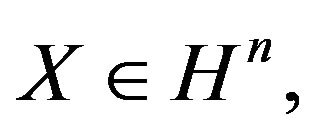 if
if 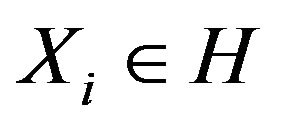 for all
for all 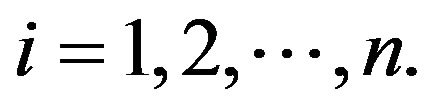 For
For 
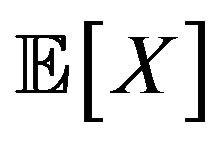 is called its supermean, whereas
is called its supermean, whereas 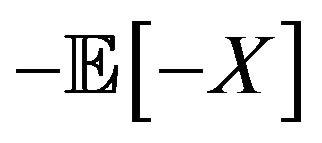 is called its submean. If
is called its submean. If 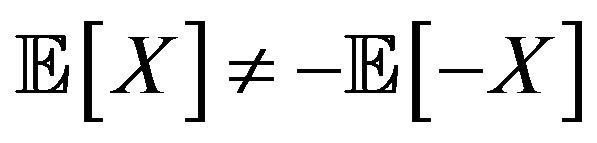 , then
, then  is said to have mean uncertainty.
is said to have mean uncertainty.
In the following we introduce some useful concepts (one can refer to Peng (2010) [4] for details).
Definition 2. An n-dimensional random vector 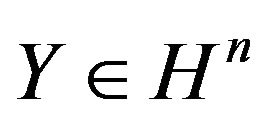 is said to be independent from an m-dimensional random vector
is said to be independent from an m-dimensional random vector 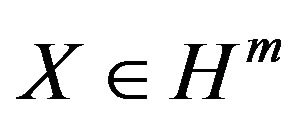 under
under , if for all bounded Lipschitz continuous functions
, if for all bounded Lipschitz continuous functions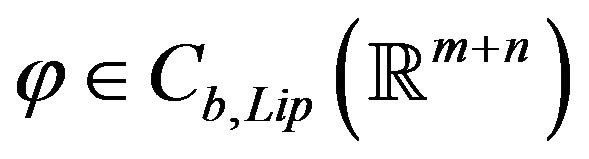 , we have
, we have
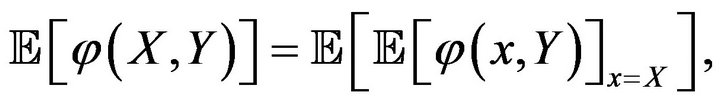
where 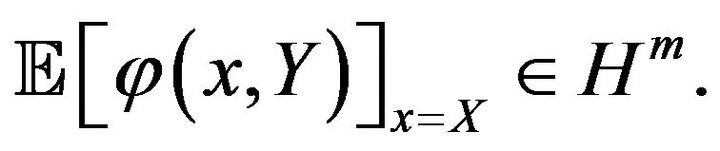
Remark 3. In general Y being independent of X under  does not imply X being independent of Y. See Example 3.13 of Chapter I in Peng (2012) [4] as a counterexample.
does not imply X being independent of Y. See Example 3.13 of Chapter I in Peng (2012) [4] as a counterexample.
Definition 4. A sequence ![]() on
on  is said to be a sequence of independent random variables under
is said to be a sequence of independent random variables under , if for any
, if for any 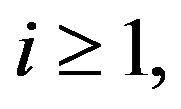
![]() is independent of
is independent of 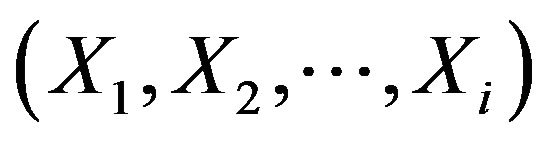 under
under 
Definition 5. A real random variable 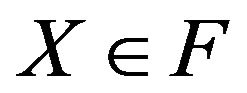 is said to be quasi-continuous (q.c. for short) if for any
is said to be quasi-continuous (q.c. for short) if for any 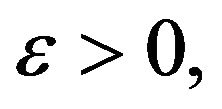 there exists an open set
there exists an open set  with
with 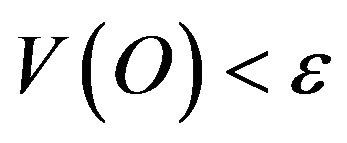 such that
such that  is continuous on
is continuous on 
Lemma 6. (Denis-Hu-Peng (2011) [11] Theorem 2) For any 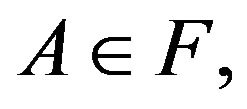
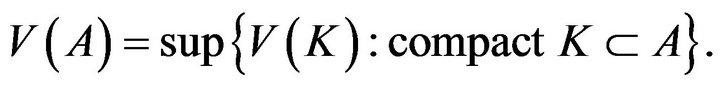
Remark 7. Lemma 6 implies that for any 
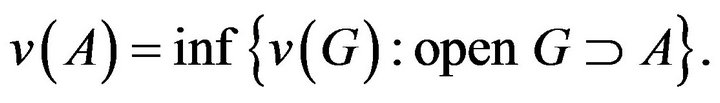
The following Borel-Cantelli lemma is obvious (the readers also can refer to Peng [4] or Chen [3]).
Lemma 8 (Borel-Cantelli Lemma). For any sequence of events ![]() in
in , if
, if 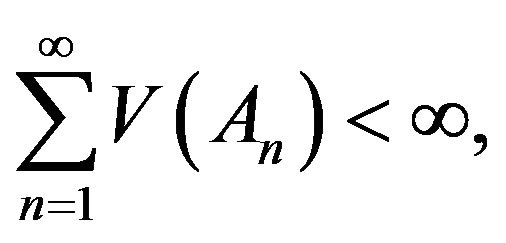 then
then

Lemma 9 (Hu [6] Theorem 3.1). Let ![]() be a sequence of independent random variables on
be a sequence of independent random variables on
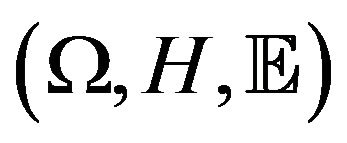 . We assume 1) For any
. We assume 1) For any 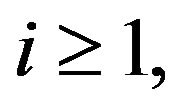 there exist real constants
there exist real constants 
such that 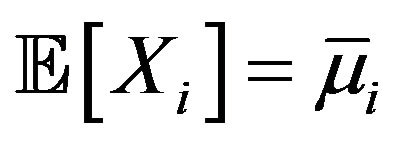 and
and 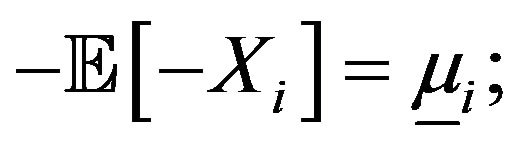
2) There exist two real constants 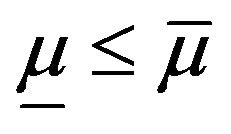 such that
such that
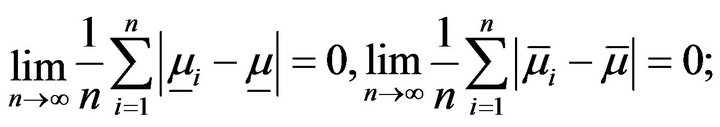
3) 
Set  Then for any continuous function
Then for any continuous function ![]() with linear growth on
with linear growth on , we have
, we have

Lemma 10 (Hu [6] Theorem 3.2 (I)). Let ![]() satisfy all the conditions given in Lemma 9, then
satisfy all the conditions given in Lemma 9, then
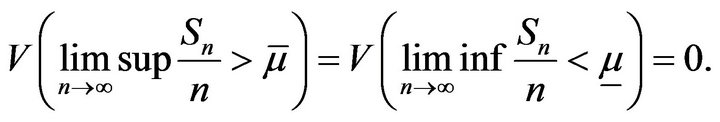
3. Strong Law of Large Numbers
Theorem 11. Let ![]() be an independent and continuous sequence under
be an independent and continuous sequence under . We assume there exist two real constants
. We assume there exist two real constants 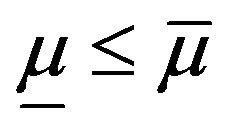 such that
such that 
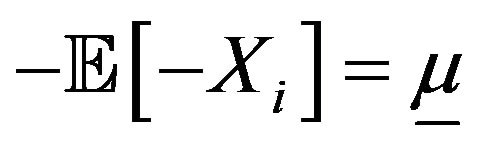 for all
for all 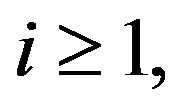 and
and 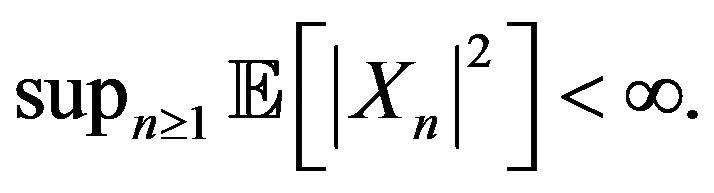
Set  Then
Then
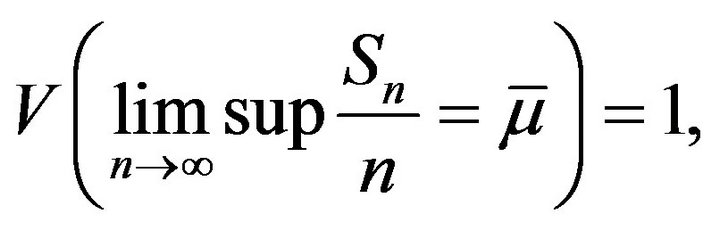 (2)
(2)
 (3)
(3)
Proof. It is obvious that we only need to prove one of the Equations (2) and (3), since on 
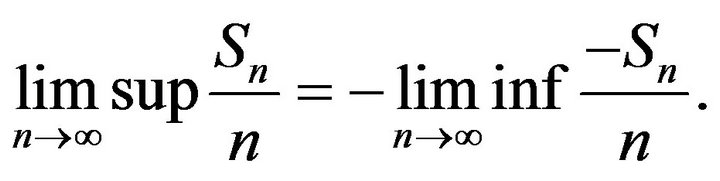
In the following we will prove the Equation (2). It is trivial for 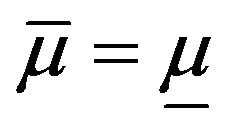 and this theorem obviously holds true in this case from (I) of Theorem 1.1 of Chen and Wu [7] or Lemma 10. Hence we only need to consider
and this theorem obviously holds true in this case from (I) of Theorem 1.1 of Chen and Wu [7] or Lemma 10. Hence we only need to consider  By Lemma 10 or (I) of Theorem 1.1 of Chen and Wu [7], we have
By Lemma 10 or (I) of Theorem 1.1 of Chen and Wu [7], we have
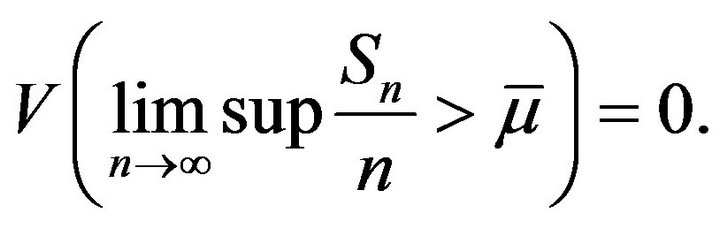
Hence we only need to prove

For any subsequence ![]() of
of , we denote
, we denote
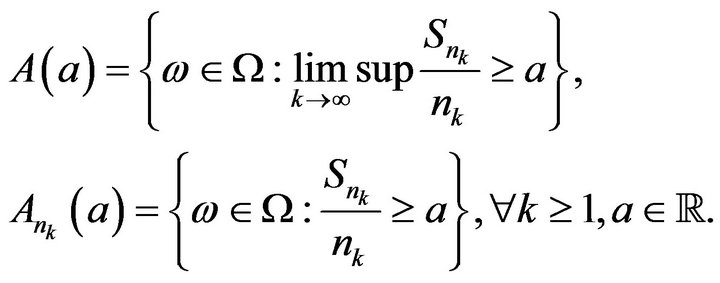
Since ![]() is a sequence of continuous random variables, thus
is a sequence of continuous random variables, thus 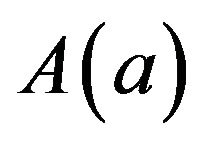 and
and 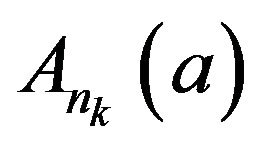 are both closed sets in
are both closed sets in  for all
for all 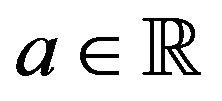 and
and 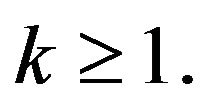 Thus
Thus 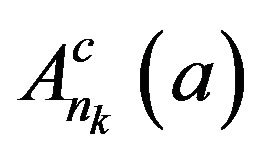 is an open set in
is an open set in  for any
for any 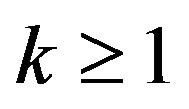 and
and 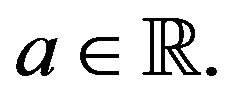 Then by the upper-continuity of
Then by the upper-continuity of 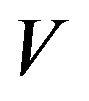 (see Proposition 1 (6)) for closed sets in
(see Proposition 1 (6)) for closed sets in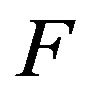 , we only need to prove for any fixed constant
, we only need to prove for any fixed constant 
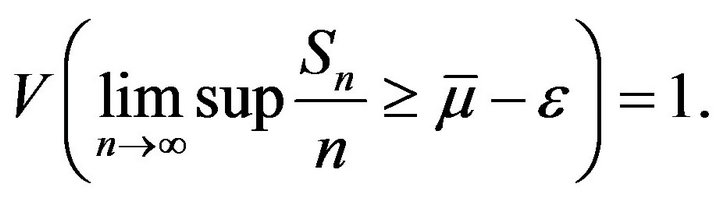
Equivalently, we only need to prove for any fixed
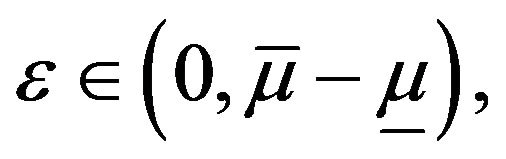
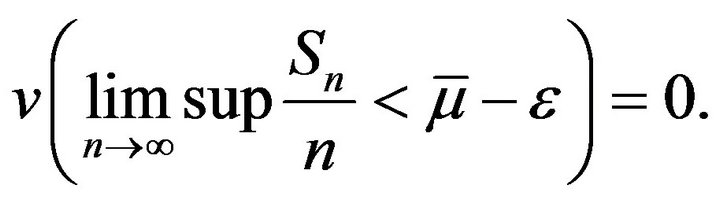
Then it is sufficient to find an increasing subsequence ![]() of
of  such that for any fixed
such that for any fixed 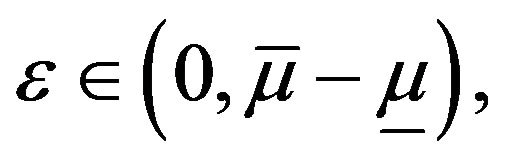
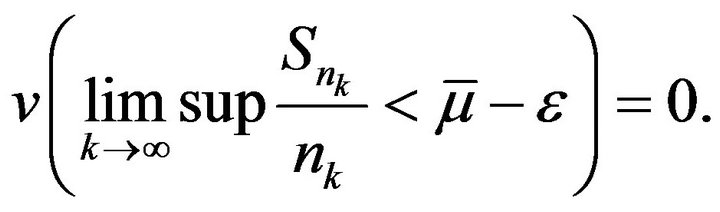 (4)
(4)
Noticing that
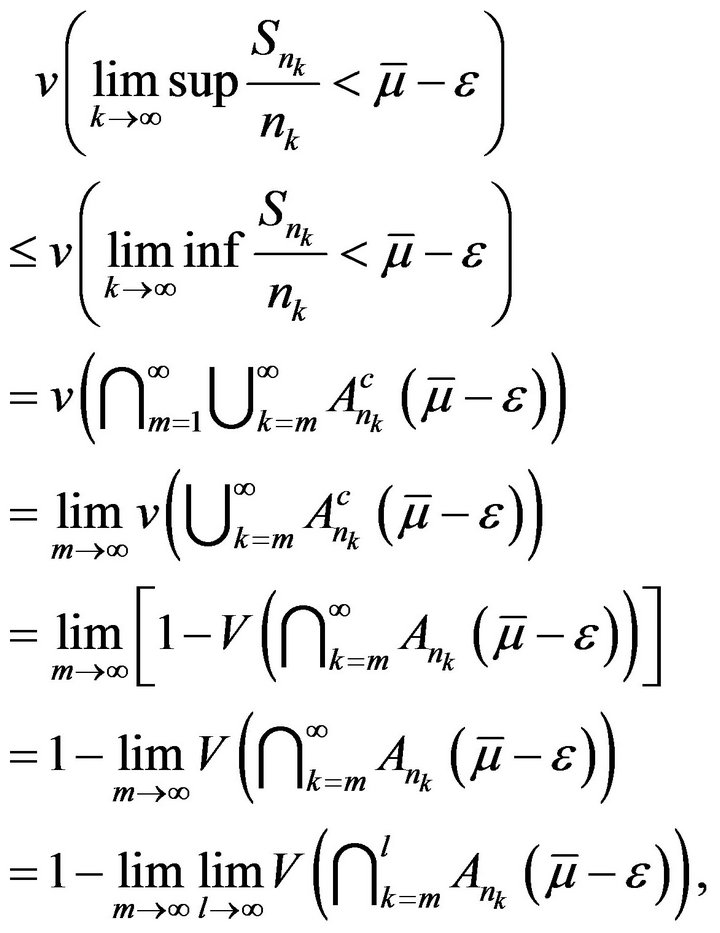 (5)
(5)
since 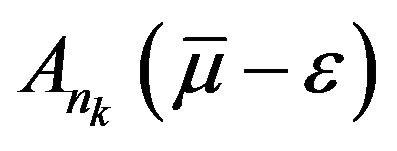 are all closed sets and V is uppercontinuous for closed sets.
are all closed sets and V is uppercontinuous for closed sets.
In addition, for any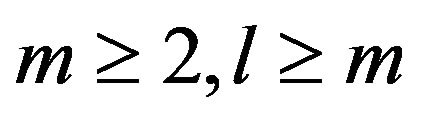 ,
,
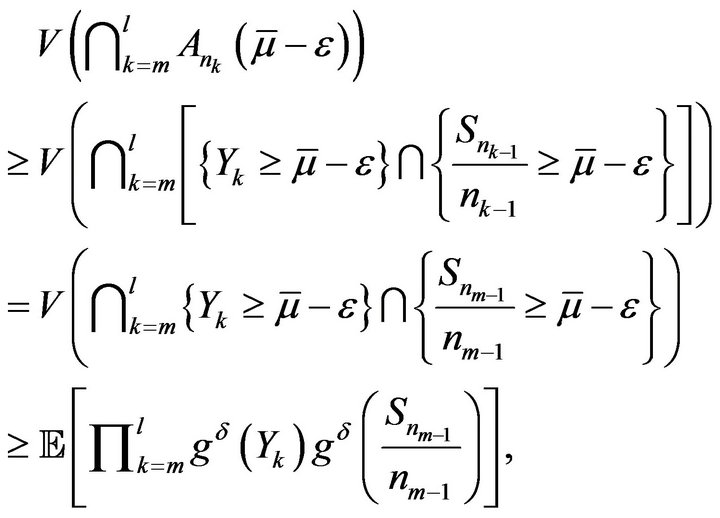
where 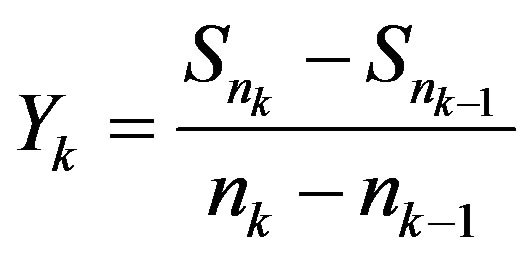 and
and
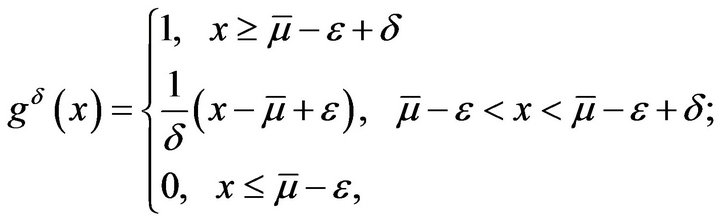
where ![]() is any fixed constant in
is any fixed constant in . It is obvious that for any fixed
. It is obvious that for any fixed 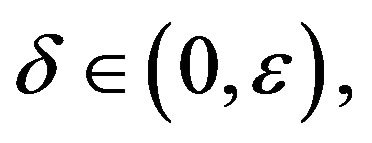
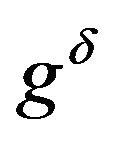 is a bounded and Lipschitz continuous function on
is a bounded and Lipschitz continuous function on . Thus by the independence assumption we know that
. Thus by the independence assumption we know that

And then by Lemma 9 for any fixed 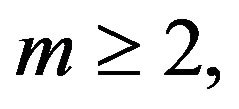 and
and
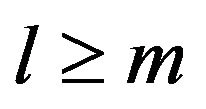 , if we choose a small constant
, if we choose a small constant 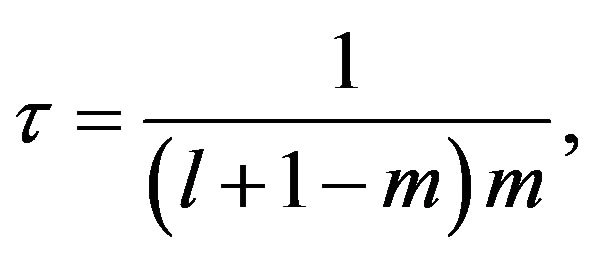
then there exists an integer 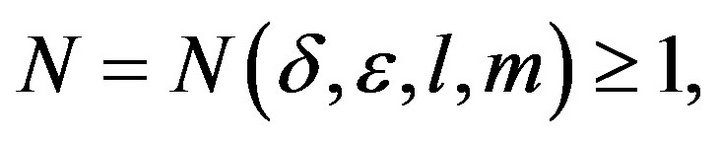 such that for any
such that for any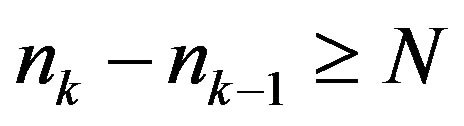 , we have
, we have
 (6)
(6)
where we denote 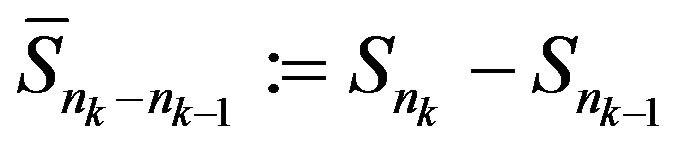 for all fixed
for all fixed 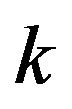 with
with 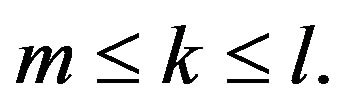
Taking  for any
for any 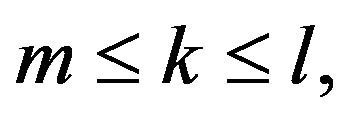 we can obtain
we can obtain
 (7)
(7)
Then letting 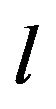 tend to
tend to  and then letting m tend to
and then letting m tend to  on both sides of inequality (7), by Lemma 9 again, we can get
on both sides of inequality (7), by Lemma 9 again, we can get
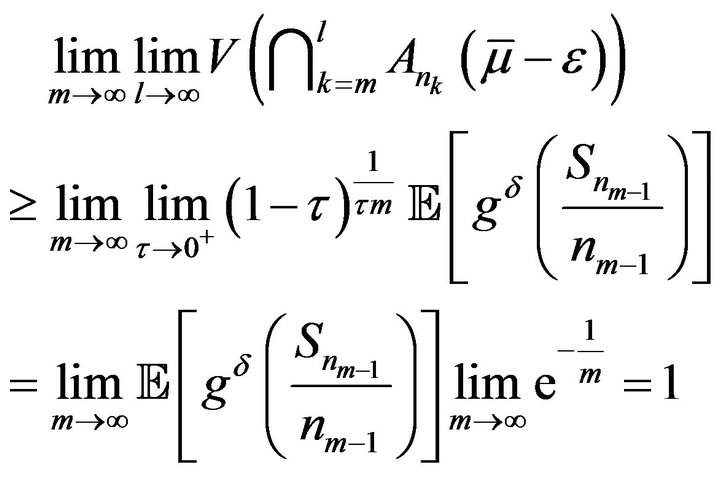 (8)
(8)
Thus from (5) and (8) we can obtain
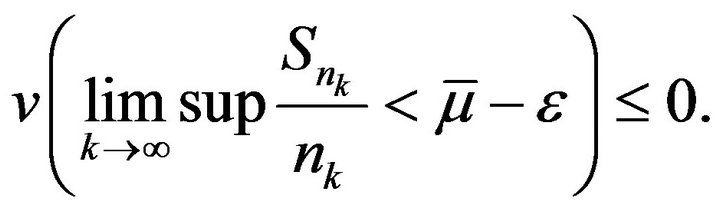
Therefore, (4) holds true. We complete the whole proof. □
Remark 12. If 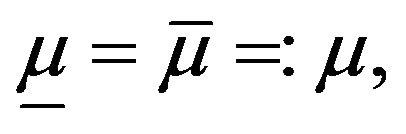 then from the Theorem 11 we can see that
then from the Theorem 11 we can see that 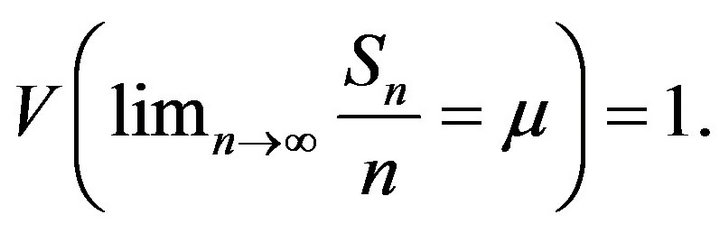 This is just a trivial case for sequences without mean uncertainty.
This is just a trivial case for sequences without mean uncertainty.
Corollary 13. Let ![]() be a sequence of quasicontinuous random variables and satisfy all other conditions except for the continuity given in Theorem 11, then Theorem 11 still holds.
be a sequence of quasicontinuous random variables and satisfy all other conditions except for the continuity given in Theorem 11, then Theorem 11 still holds.
Proof. Similarly as the arguments in the proof of Theorem 11, we only need to prove
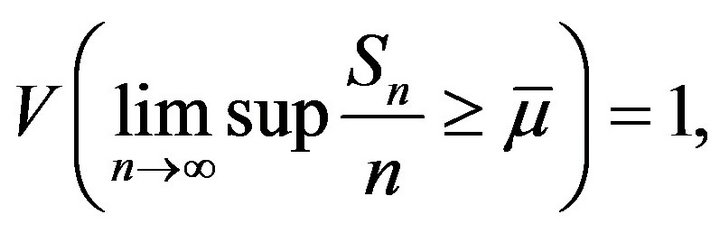 (9)
(9)
when 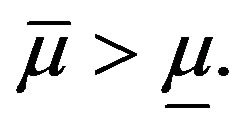
By the assumptions we know that for each 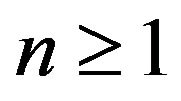 and any constant
and any constant 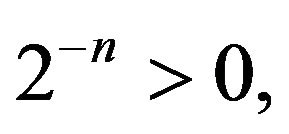 there exists an open subset
there exists an open subset 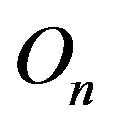 of
of  with
with 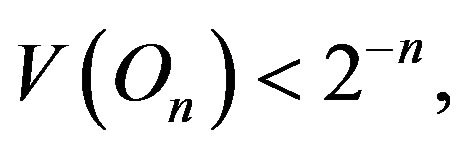 such that
such that 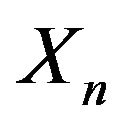 is continuous on
is continuous on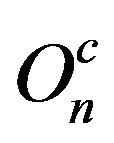 . Denote
. Denote ![]() then by Borel-Cantelli lemma (see Lemma 8) we can obtain
then by Borel-Cantelli lemma (see Lemma 8) we can obtain
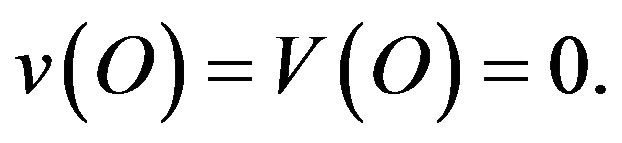
For any  there exist an increasing subsequence
there exist an increasing subsequence ![]() of
of , an integer
, an integer 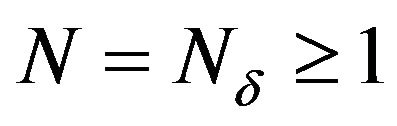 and an open set
and an open set  (by Remark 7) satisfying
(by Remark 7) satisfying
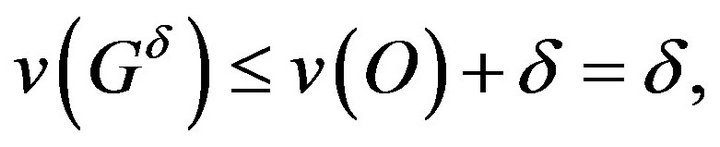
such that when 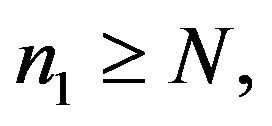 we have
we have
![]()
Then  is continuous on
is continuous on  By Lemma 6, for any
By Lemma 6, for any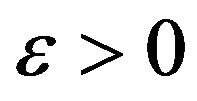 , we can find a compact set
, we can find a compact set 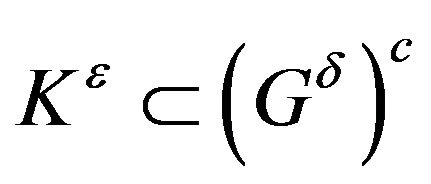
with  such that
such that
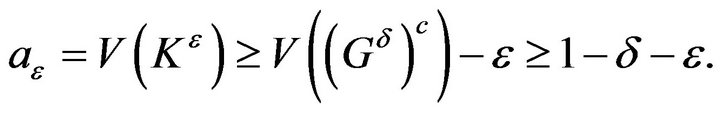
Then we have
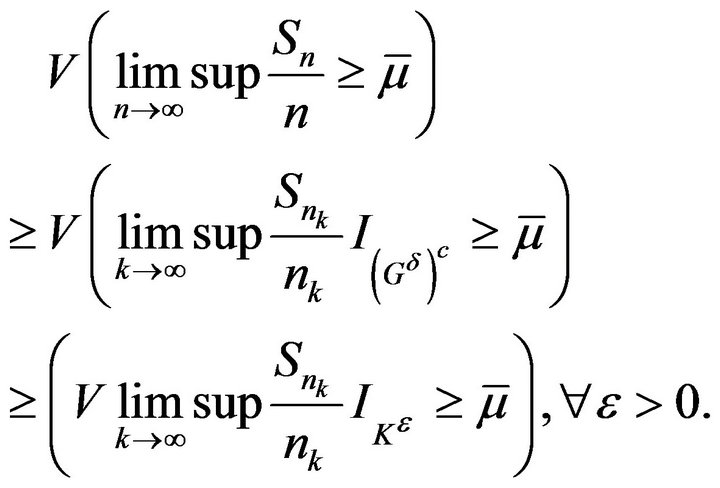 (10)
(10)
For  we define
we define
 (11)
(11)
Then it is obvious that 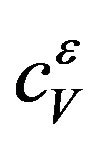 is a capacity on
is a capacity on 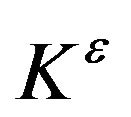 and satisfies all the properties of
and satisfies all the properties of  given in Proposition 1 where
given in Proposition 1 where  is substituted by
is substituted by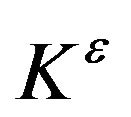 . We also denote by
. We also denote by 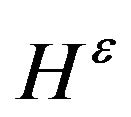 the set of all random variables
the set of all random variables  such that
such that
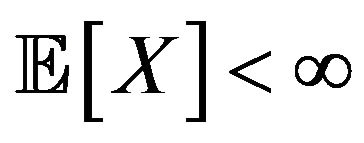 . Thus on
. Thus on ,
, 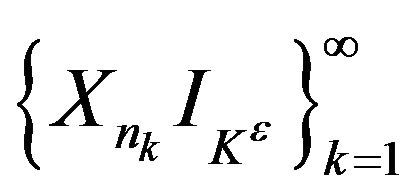 is an independent and continuous sequence. Since
is an independent and continuous sequence. Since  is also a complete and separable metric space, by Theorem 11 we have
is also a complete and separable metric space, by Theorem 11 we have
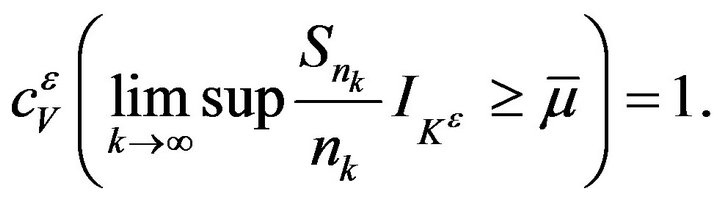 (12)
(12)
Then from (10)-(12) we have
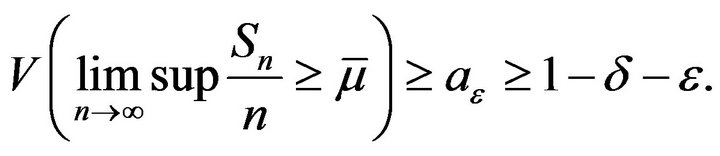 (13)
(13)
Letting ![]() and
and ![]() tend to 0 in inequality (13) we can derive
tend to 0 in inequality (13) we can derive
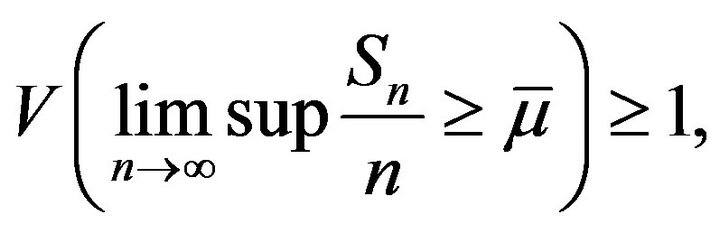
which implies (9). We complete the whole proof of this corollary. □
4. Extensions
In Section 3 we get that the submean 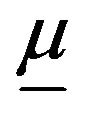 and the supermean
and the supermean 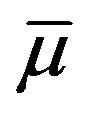 are the inferior and superior limits of the arithmetic average of the first
are the inferior and superior limits of the arithmetic average of the first ![]() random variables
random variables 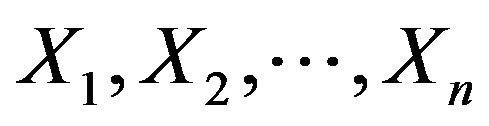 given in Theorem 11, respectively, with probability 1 under the upper probability
given in Theorem 11, respectively, with probability 1 under the upper probability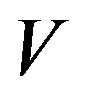 . In fact, except the two values, any other value
. In fact, except the two values, any other value  is still the limit of some subsequence of
is still the limit of some subsequence of![]() , with probability 1 under
, with probability 1 under . We can see it in the following theorem.
. We can see it in the following theorem.
Theorem 14. Under assumptions of Theorem 11, we have for any 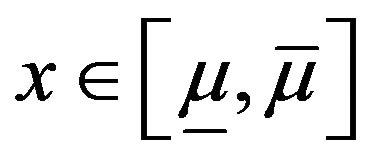

where  is a cluster of limit points of a real sequence
is a cluster of limit points of a real sequence ![]()
Proof. For  and
and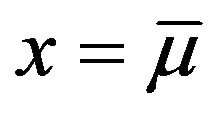 , the result has been obtained in Theorem 11. For the trivial case,
, the result has been obtained in Theorem 11. For the trivial case,  it is obvious. Now we consider
it is obvious. Now we consider 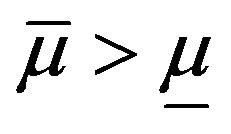 and any
and any 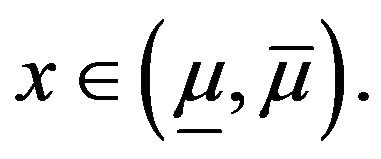 We can notice that
We can notice that
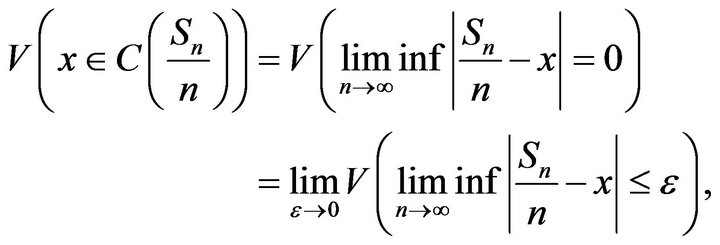
where ![]() is any constant in
is any constant in 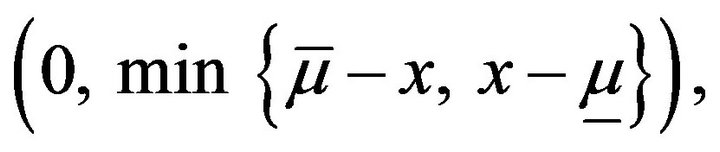
since  is upper-continuous for closed sets. Thus we only need to find an increasing subsequence
is upper-continuous for closed sets. Thus we only need to find an increasing subsequence ![]() of
of  such that for any
such that for any 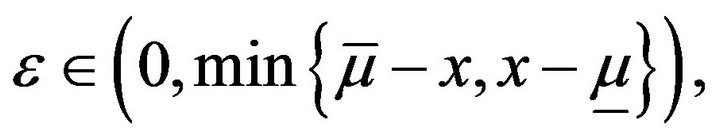 we have
we have
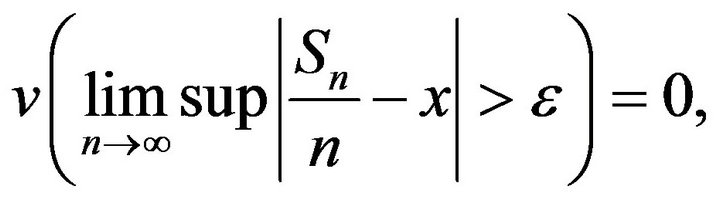 (14)
(14)
Following the arguments in the proof of Theorem 11 we can obtain
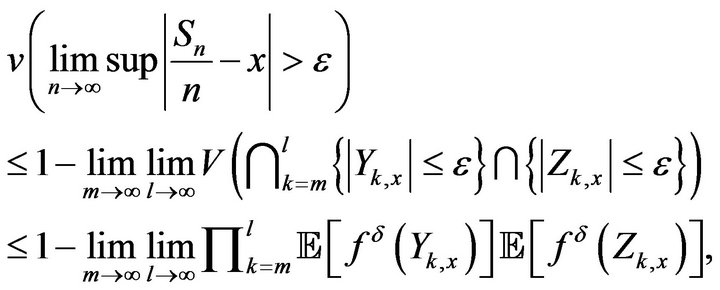
where 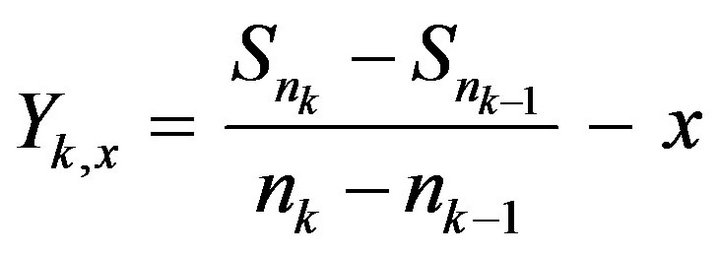 and
and 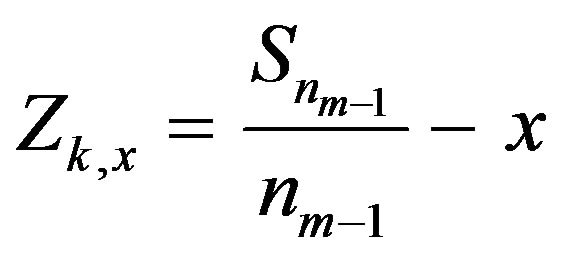 for any
for any 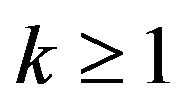 and
and 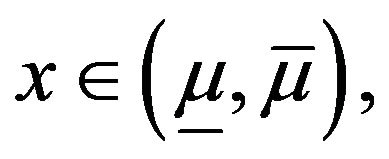
![]() is any given constant in
is any given constant in  and
and
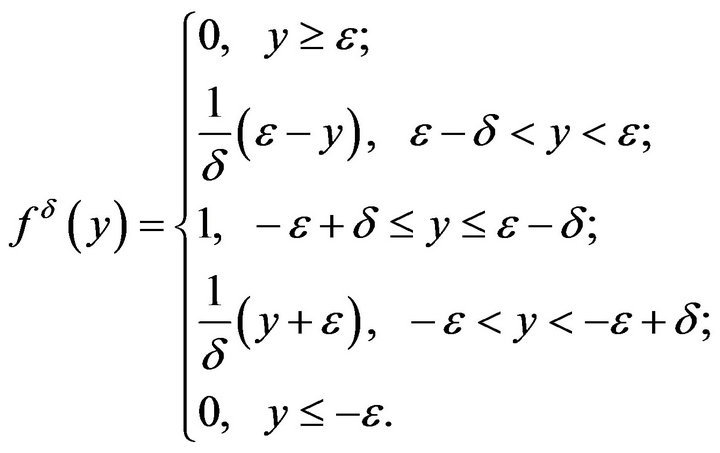
Then by using the same arguments as in the proof of Theorem 11 we also can prove that (14) holds true. The whole proof is complete. □
The following corollary is obvious.
Corollary 15. Under the conditions of Theorem 11, for any continuous real function ![]() on
on , we have for all
, we have for all 
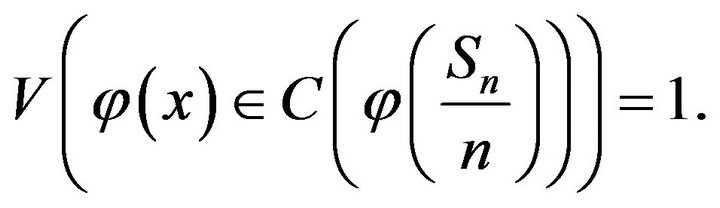
In particular,
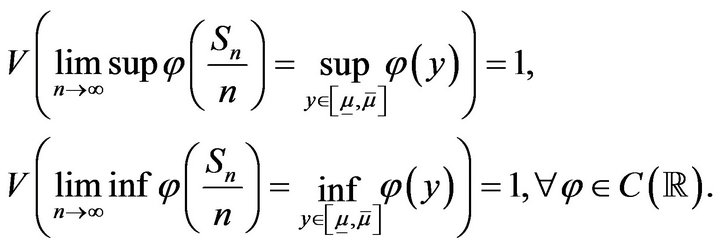
We also can extend Theorem 11, Theorem 14 and Corollary 15 to the sequences with different submeans and supermeans as follows.
Theorem 16. Let ![]() be an independent and continuous sequence under
be an independent and continuous sequence under  and satisfy conditions
and satisfy conditions
(1)-(3) of Lemma 9. Set 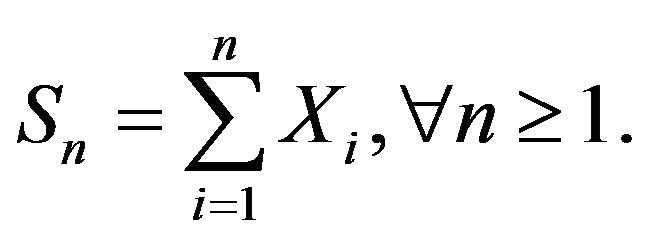 Then for any
Then for any 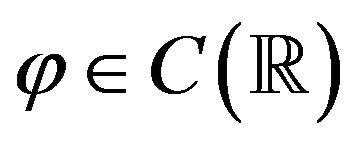 we have
we have
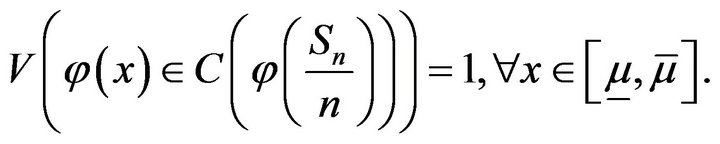
Proof. By Lemma 10 and the proofs of Theorem 11 and Theorem 14 we only need to check whether (6) and (8) hold true under our assumptions of this theorem. In fact, from Lemma 9 they are obviously satisfied. Hence this theorem holds. □
From the proof of Corollary 13 and Theorem 16 we can immediately obtain the following corollary.
Corollary 17. Theorem 16 still holds when continuity assumption is substituted by quasi-continuity condition and condition (2) of Lemma 9 is replaced by the following condition:
(2') there exist real constants 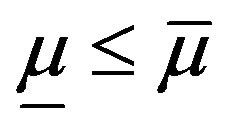 such that
such that
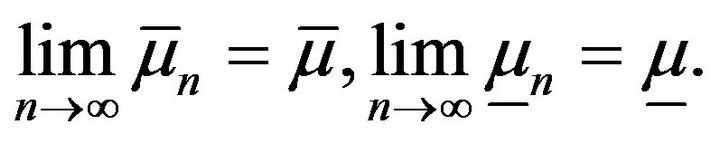
5. An Example
Let 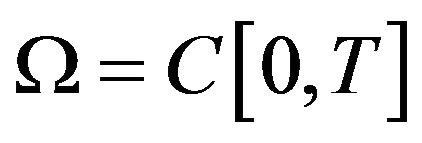 with the supremum norm. Then
with the supremum norm. Then  is a Banach space and compact, thus it is a separable and complete metric space with the distance generated by the norm of the space. Then we can define a G-expectation
is a Banach space and compact, thus it is a separable and complete metric space with the distance generated by the norm of the space. Then we can define a G-expectation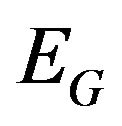 , a special sublinear expectation (see Peng [4] for details), where
, a special sublinear expectation (see Peng [4] for details), where 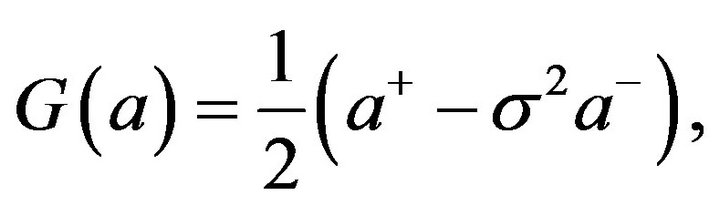
![]() is a nonnegative real number less than 1. Then for any bounded and independent sequence
is a nonnegative real number less than 1. Then for any bounded and independent sequence ![]() with the same submean
with the same submean  and supermean
and supermean  in
in 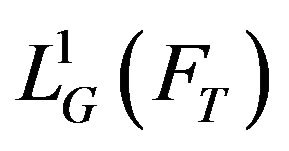 under
under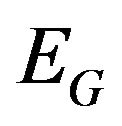 , by Theorem 11 we have
, by Theorem 11 we have

where V is generated by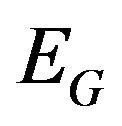 , since this sequence is a sequence of quasi-continuous random variables and from Denis, Hu and Peng [11]
, since this sequence is a sequence of quasi-continuous random variables and from Denis, Hu and Peng [11] 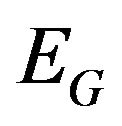 can be represented as supremum of a family of linear expectations corresponding to a family of probabilities which is weakly compact.
can be represented as supremum of a family of linear expectations corresponding to a family of probabilities which is weakly compact.
6. Acknowledgements
This research is supported by WCU (World Class University) program through the National Research Foundation of Korea funded by the Ministry of Education, Science and Technology (R31-20007). The author gratefully thanks the referees for their careful reading.
REFERENCES
- M. Marinacci, “Limit Laws of Non-Additive Probabilities and Their Frequentist Interpretation,” Journal of Economic Theory, Vol. 84, No. 2, 1999, pp. 145-195. doi:10.1006/jeth.1998.2479
- F. Maccheroni and M. Marinacci, “A Strong Law of Large Numbers for Capacities,” Annals of Probability, Vol. 33, No. 3, 2005, pp. 1171-1178. doi:10.1214/009117904000001062
- Z. Chen, “Strong Laws of Large Numbers for Capacities,” Unpublished, 2010. http://arxiv.org/abs/1006.0749
- S. Peng, “Nonlinear Expectations and Stochastic Calculus under Uncertainty-with Robust Central Limit Theorem and G-Brownian Motion,” Unpublished, 2012. http://arxiv.org/abs/1002.4546
- Z. Chen, P. Wu and B. Li, “A Strong Law of Large Numbers for Non-additive Probabilities,” International Journal of Approximate Reasoning, 2012. http://www.sciencedirect.com/science/article/pii/S0888613X12000783
- F. Hu, “General Laws of Large Numbers under Sublinear Expectations,” 2012. http://arxiv.org/abs/1104.5296
- Z. Chen and P. Wu, “Strong Laws of Large Numbers for Bernoulli Experiments under Ambiguity,” Nonlinear Mathematics for Uncertainty and Its Applications, Advances in Intelligent and Soft Computing, Vol. 100, 2011, pp. 19- 30. http://link.springer.com/chapter/10.1007%2F978-3-642-22833-9_2?LI=true
- J. Xu and B. Zhang, “Martingale Property and Capacity under G-Framework,” Electronic Journal of Probability, Vol. 15, No. 67, 2010, pp. 2041-2068.
- G. Choquet, “Theory of Capacities,” Annales de Institute Fourier, Vol. 5, 1954, pp. 131-295.
- P. J. Huber and V. Strassen, “Minimax Tests and the Neyman-Pearson Lemma for Capacities,” The Annals of Statistics, Vol. 1. No. 2, 1973, pp. 251-263. doi:10.1214/aos/1176342363
- L. Denis, M. Hu and S. Peng, “Function Spaces and Capacity Related to a Sublinear Expectation: Application to G-Brownian Motion Paths,” Potential Analysis, Vol. 34, No. 2, 2011, pp. 139-161. doi:10.1007/s11118-010-9185-x

