Applied Mathematics
Vol. 3 No. 6 (2012) , Article ID: 20087 , 5 pages DOI:10.4236/am.2012.36083
Adaptive Lag Synchronization of Lorenz Chaotic System with Uncertain Parameters*
1College of Science, Guilin University of Technology, Guilin, China
2Guangxi Key Laboratory of Spatial Information and Geomatics, Guilin, China
Email: chenyanfei2010@126.com, jjjzzz0@163.com, dgm@glite.edu.cn
Received March 22, 2012; revised April 19, 2012; accepted April 22, 2012
Keywords: Lag Synchronization; Adaptive Technique; Uncertain Parameters; Lorenz Chaotic System
ABSTRACT
The paper discusses lag synchronization of Lorenz chaotic system with three uncertain parameters. Based on adaptive technique, the lag synchronization of Lorenz chaotic system is achieved by designing a novel nonlinear controller. Furthermore, the parameters identification is realized simultaneously. A sufficient condition is given and proved theoreticcally by Lyapunov stability theory and LaSalle’s invariance principle. Finally, the numerical simulations are provided to show the effectiveness and feasibility of the proposed method.
1. Introduction
Since the original work on chaos synchronization by Pecora and Carroll [1] in the drive-response systems, chaos synchronization has attracted much attraction due to its potential applications in many practical engineering fields, such as secure communication [2], information processing [3], image encryption [4], and so on. In the past two decades, many schemes for chaos synchronization have been proposed, including linear and nonlinear feedback approach [5,6], adaptive technique [6], backstepping method [7], impulsive control method [8], etc. At present, the researchers are concentrating on the following types of synchronization phenomena: complete synchronization [9], generalized synchronization [10], phase synchronization [11], lag synchronization [12], dislocated synchronization [13] and so on.
Lag synchronization, where the corresponding state vectors of response system follow the drive system with time delay. Recently, some literatures have been devoted to lag synchronization of chaotic systems. In Reference [14], the lag synchronization of Rössler system and Chua circuit has been investigated via a scalar signal. Li et al. [15] applied a nonlinear observer to lag synchronization of hyperchaotic Rössler system and hyperchaotic Matsumoto-Chua-Kobayashi (MCK) circuit. Zhang et al. [16] studied the same problem for hyperchaotic Lü system. These design of a controller depends on the considered dynamical system, the method can be used in the system with certain parameters. But in some real physical systems and experimental situations, chaotic systems may have some uncertain parameters, so a systematic design process of lag synchronization of chaotic systems with uncertain parameters is important.
In this paper, we investigate the lag synchronization of Lorenz chaotic system with uncertain parameters. Based on the adaptive technique, a novel controller and parameter adaptive laws are designed such that parameters identification is realized, and lag synchronization of Lorenz chaotic system is achieved simultaneously. Theoretically proof and numerical simulations are given to demonstrate the effectiveness and feasibility of the proposed method.
2. Problem Formulation
The Lorenz chaotic system [17] is proposed in 1963, the nonlinear differential equations for describing it are
 (1)
(1)
having a chaotic attractor when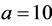 ,
, 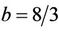 ,
, . The phase portrait is shown in Figure 1.
. The phase portrait is shown in Figure 1.
Considering the drive system (1), the response system is controlled Lorenz chaotic system as following
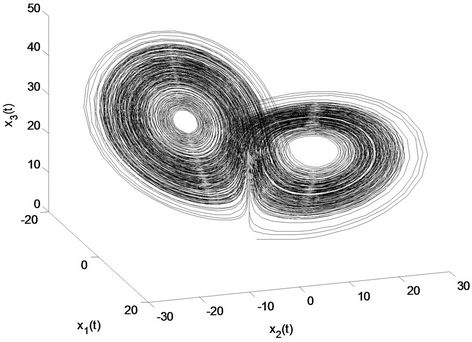
Figure 1. The phase portrait of Lorenz chaotic system (1) with parameter values a = 10, b = 8/3, c = 28.
 (2)
(2)
where as, bs, cs of (2) are unknown parameters which need to be identified in the response system,

is the controller which should be designed such that two systems can be lag synchronized.
Let
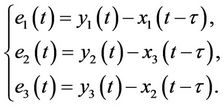 (3)
(3)
where 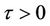 is the time delay for the errors dynamical system.
is the time delay for the errors dynamical system.
Therefore, the goal of parameters identification and lag synchronization is to find an appropriate controller  and parameter adaptive laws of as, bs, cs, such that the synchronization errors
and parameter adaptive laws of as, bs, cs, such that the synchronization errors
 as
as 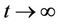 (4)
(4)
and the unknown parameters
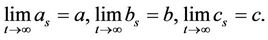 (5)
(5)
Remark 1. When , the lag synchronization will appear. When
, the lag synchronization will appear. When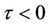 , the anticipated synchronization will appear. More in general, complete synchronization will appear when
, the anticipated synchronization will appear. More in general, complete synchronization will appear when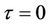 .
.
Remark 2. For the anticipated synchronization and complete synchronization, the discussions are similar to the method given in this paper.
3. Adaptive Lag Synchronization of Lorenz Chaotic System
In this section, based upon the nonlinear adaptive feedback control technique, a systematic design process of parameters identification and lag synchronization of Lorenz chaotic system under the situation of response system with unknown parameters is provided.
According to the systems (1) and (2), we have the errors dynamical system
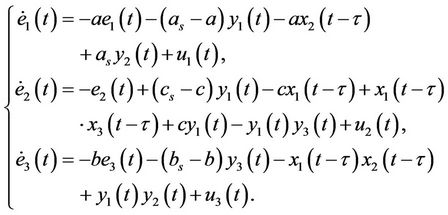 (6)
(6)
Obviously, lag synchronization of systems (1) and (2) appears if the errors dynamical system (6) has an asymptotically stable equilibrium point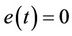 , where
, where
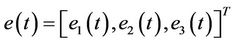 .
.
Then, we get the following theorem.
Theorem Assuming that the Lorenz chaotic system (1) drives the controlled Lorenz chaotic system (2), take
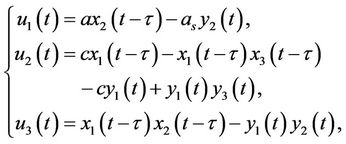 (7)
(7)
and parameter adaptive laws
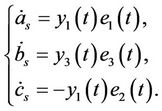 (8)
(8)
Systems (1) and (2) can realize lag synchronization and the unknown parameters will be identified, i.e., Equations (4) and (5) will be achieved.
Proof Equation (6) can be converted to the following form under the controller (7)
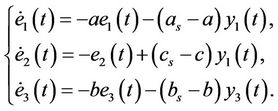 (9)
(9)
Consider a Lyapunov function as
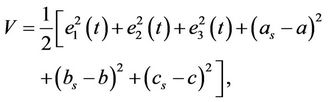
Obviously, V is a positive definite function. Taking its time derivative along with the trajectories of Equations (8) and (9) leads to
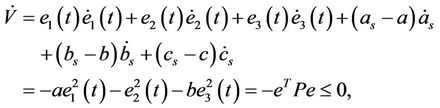
where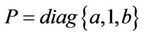 . It is obvious that
. It is obvious that  if and only if
if and only if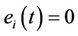 ,
, 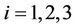 , namely the set
, namely the set
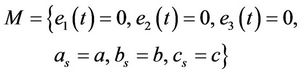
is the largest invariant set contained in  for Equation (9). So according to the LaSalle’s invariance principle [18], starting with arbitrary initial values of Equation (9), the trajectory converges asymptotically to the set M, i.e.,
for Equation (9). So according to the LaSalle’s invariance principle [18], starting with arbitrary initial values of Equation (9), the trajectory converges asymptotically to the set M, i.e., 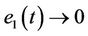 ,
, 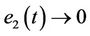 ,
, 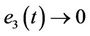 ,
,  ,
,  and
and 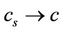 as
as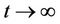 . This indicates that the lag synchronization of Lorenz chaotic system is achieved and the unknown parameters as, bs, cs, can be successfully identified by using controller (7) and parameter adaptive laws (8). Now the proof is completed.
. This indicates that the lag synchronization of Lorenz chaotic system is achieved and the unknown parameters as, bs, cs, can be successfully identified by using controller (7) and parameter adaptive laws (8). Now the proof is completed.
Remark 3. Taking our adaptive synchronization method, we can not only achieve synchronization but also identify the system parameters. The values for parameters a, b, c of drive system (1) should be confined to it has a chaotic attractor.
Remark 4. Although this process is focused on the Lorenz chaotic system, the systematic design process could be used for many other complex dynamical systems with uncertain parameters.
4. Numerical Simulations
In order to verify the effectiveness and feasibility of the proposed method, we give some numerical simulations about the lag synchronization and parameters identification between systems (1) and (2). In the numerical simulations, all the differential equations are solved by using the fourth-order Runge-Kutta method.
For this numerical simulations, we assume that the initial states of drive system and response system are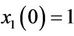 ,
, 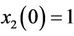 ,
, 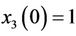 and
and ,
, 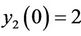 ,
, 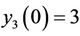 and the unknown parameters have zero initial condition, the time delay is chosen as
and the unknown parameters have zero initial condition, the time delay is chosen as . The drive signals are from the Lorenz chaotic system (1) with system parameters
. The drive signals are from the Lorenz chaotic system (1) with system parameters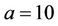 ,
,  ,
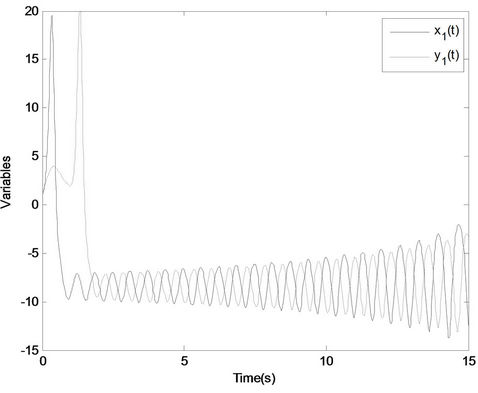
,  so that it exhibits a chaotic attractor. The simulation results are shown in Figures 2-4. Figures 2 and 3 display the lag synchronization state variables and errors response of systems (1) and (2), respectively. Figure 4 shows the identification results of unknown parameters as, bs, cs.
so that it exhibits a chaotic attractor. The simulation results are shown in Figures 2-4. Figures 2 and 3 display the lag synchronization state variables and errors response of systems (1) and (2), respectively. Figure 4 shows the identification results of unknown parameters as, bs, cs.
 (a)
(a)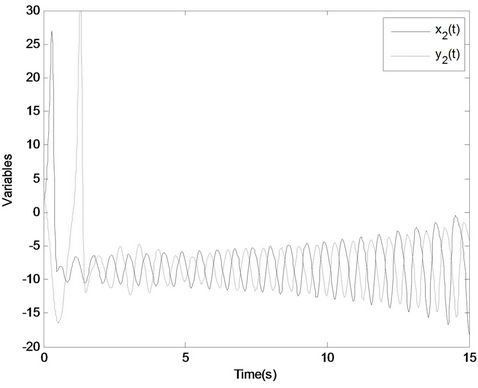 (b)
(b)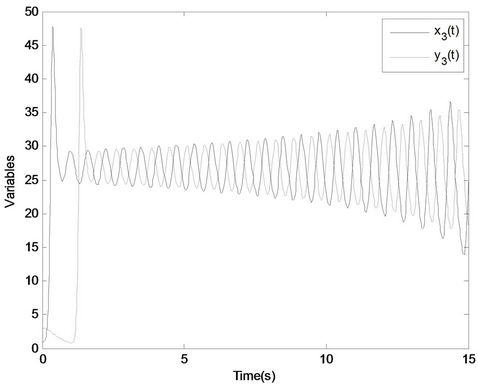 (c)
(c)
Figure 2. The lag synchronization state variables of systems (1) and (2): (a) Variables x1(t), y1(t); (b) Variables x2(t), y2(t); (c) Variables x3(t), y3(t).
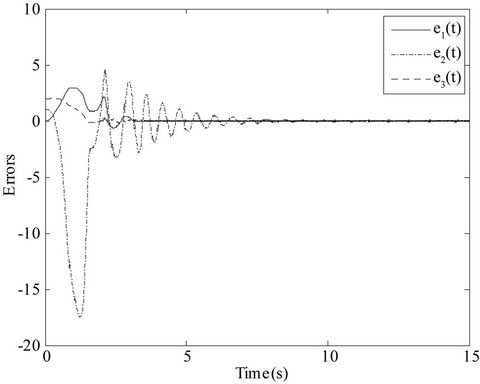
Figure 3. The lag synchronization error evolutions of systems (1) and (2).
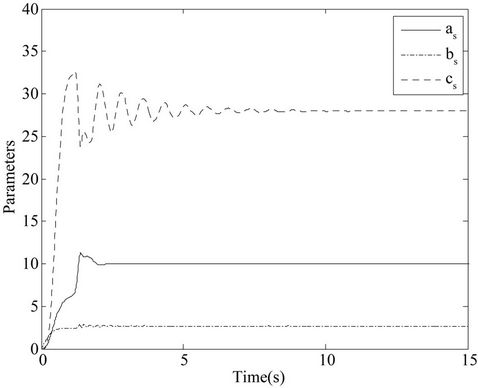
Figure 4. The parameters identification results of response system (2): a = 10, b = 8/3, c = 28.
5. Conclusion
This paper investigates the adaptive lag synchronization for the classical Lorenz chaotic system with the response system parameters unknown. Based on Lyapunov stability theory and LaSalle’s invariance principle, the controller and parameter adaptive laws are given to achieve lag synchronization and parameters identification simultaneously. Finally, numerical simulations are provided to demonstrate the effectiveness of the scheme proposed in this work.
REFERENCES
- L. M. Pecora and T. L. Carroll, “Synchronization in Chaotic Systems,” Physical Review Letters, Vol. 64, No. 8, 1990, pp. 821-824. doi:10.1103/PhysRevLett.64.821
- Z. Li and D. Xu, “A Secure Communication Scheme using Projective Chaos Synchronization,” Chaos, Solitons & Fractals, Vol. 22, No. 2, 2004, pp. 477-481. doi:10.1016/j.chaos.2004.02.019
- C. Ling, X. Wu and S. Sun, “A General Efficient Method for Chaotic Signal Estimation,” IEEE Transactions on Signal Processing, Vol. 47, No. 5, 1999, pp. 1424-1428. doi:10.1109/78.757236
- H. A. Qais and A. A. Aouda, “Image Encryption Based on the General Approach for Multiple Chaotic Systems,” Journal of Signal and Information Processing, Vol. 2, No. 3, 2011, pp. 238-244.
- F. Wang and C. Liu, “A New Criterion for Chaos and Hyperchaos Synchronization Using Linear Feedback Control,” Physics Letters A, Vol. 360, No. 2, 2006, pp. 274- 278. doi:10.1016/j.physleta.2006.08.037
- Z. Jia, J. A. Lu, and G. M. Deng, “Nonlinear State Feedback and Adaptive Synchronization of Hyperchaotic Lü Systems,” Systems Engineering and Electronics, Vol. 29, No. 4, 2007, pp. 598-600.
- M. T. Yassen, “Controlling, Synchronization and Tracking Chaotic Liu System using Active Backstepping Design,” Physics Letters A, Vol. 360, No. 4-5, 2007, pp. 582-587. doi:10.1016/j.physleta.2006.08.067
- R. Z. Luo, “Impulsive Control and Synchronization of a New Chaotic System,” Physics Letters A, Vol. 372, No. 5, 2008, pp. 648-653. doi:10.1016/j.physleta.2007.08.010
- J. Lu and J. Cao, “Adaptive Complete Synchronization of Two Identical or Different Chaotic (Hyperchaotic) Systems with Fully Unknown Parameters,” Chaos, Vol. 15, No. 4, 2005, Article ID: 043901. doi:10.1063/1.2089207
- Z. Jia, “Linear Generalized Synchronization of Chaotic Systems with Uncertain Parameters,” Journal of Systems Engineering and Electronics, Vol. 19, No. 4, 2008, pp. 779-784. doi:10.1016/S1004-4132(08)60153-X
- M. C. Ho, Y. C. Hung and C. H. Chou, “Phase and Anti-Phase Synchronization of Two Chaotic Systems by Using Active Control,” Physics Letters A, Vol. 296, No. 1, 2002, pp. 43-48. doi:10.1016/S0375-9601(02)00074-9
- Y. Chen, X. Chen and S. Chen, “Lag Synchronization of Structurally Nonequivalent Chaotic Systems with Time Delays,” Nonlinear Analysis, Vol. 66, No. 9, 2007, pp. 1929-1937. doi:10.1016/j.na.2006.02.033
- M. Hu and Z. Xu, “Nonlinear Feedback Mismatch Synchronization of Lorenz Chaotic Systems,” Systems Engineering and Electronics, Vol. 29, No. 8, 2007, pp. 1346- 1348.
- C. Li and X. Liao, “Lag Synchronization of Rössler System and Chua Circuit via a Scalar Signal,” Physics Letters A, Vol. 329, No. 4-5, 2004, pp. 301-308. doi:10.1016/j.physleta.2004.06.077
- C. Li, X. Liao and K. Wong, “Lag Synchronization of Hyperchaos with Application to Secure Communications,” Chaos, Solitons & Fractals, Vol. 23, No. 1, 2005, pp. 183-193. doi:10.1016/j.chaos.2004.04.025
- Q. J. Zhang, J. A. Lu and Z. Jia, “Global Exponential Projective Synchronization and Lag Synchronization of Hyperchaotic Lü System,” Communications in Theoretical Physics, Vol. 51, No. 4, 2009, pp. 679-683.
- E. N. Lorenz, “Deterministic Nonperiodic Flow,” Journal of the Atmospheric Sciences, Vol. 20, No. 2, 1963, pp. 130-141. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
- J. P. Lasalle, “The Extent of Asymptotic Stability,” Proceedings of the National Academy of Sciences of United States of America, Vol. 46, No. 3, 1960, pp. 363-365. dx:10.1073/pnas.46.3.363.
NOTES
*Supported by the National Natural Science Foundation of China (Grant Nos. 61164020 and 61004101), the Natural Science Foundation of Guangxi, China (Grant No. 2011GXNSFA018147) and the project of Guangxi Key Laboratory of Spatial Information and Geomatics (Grant No. Gui1103108-24).

