Applied Mathematics
Vol. 3 No. 2 (2012) , Article ID: 17393 , 11 pages DOI:10.4236/am.2012.32025
General Solution of Two Generalized Form of Burgers Equation by Using the  -Expansion Method
-Expansion Method
1Department of Mathematics, University of Mohaghegh Ardabili, Ardabil, Iran
2Department of Mathematics, Islamic Azad University, Ardabil Branch, Ardabil, Iran
Email: *borhani@uma.ac.ir, abazari-r@uma.ac.ir
Received May 11, 2011; revised June 11, 2011; accepted June 18, 2011
Keywords: 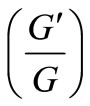 -Expansion Method; Generalized Burgers-KdV Equation; Generalized Burgers-Fisher Equation; Hyperbolic Function Solutions; Trigonometric Function Solutions
-Expansion Method; Generalized Burgers-KdV Equation; Generalized Burgers-Fisher Equation; Hyperbolic Function Solutions; Trigonometric Function Solutions
ABSTRACT
In this work, the  -expansion method is proposed for constructing more general exact solutions of two general form of Burgers type equation arising in fluid mechanics namely, Burgers-Korteweg-de Vries (Burgers-KdV) and Burger-Fisher equations. Our work is motivated by the fact that the
-expansion method is proposed for constructing more general exact solutions of two general form of Burgers type equation arising in fluid mechanics namely, Burgers-Korteweg-de Vries (Burgers-KdV) and Burger-Fisher equations. Our work is motivated by the fact that the  -expansion method provides not only more general forms of solutions but also periodic and solitary waves. If we set the parameters in the obtained wider set of solutions as special values, then some previously known solutions can be recovered. The method appears to be easier and faster by means of a symbolic computation system.
-expansion method provides not only more general forms of solutions but also periodic and solitary waves. If we set the parameters in the obtained wider set of solutions as special values, then some previously known solutions can be recovered. The method appears to be easier and faster by means of a symbolic computation system.
1. Introduction
Nonlinear evolution equations (NLEEs) have been the subject of study in various branches of mathematicalphysical sciences such as physics, biology, chemistry, etc. The analytical solutions of such equations are of fundamental importance since a lot of mathematical-physical models are described by NLEEs. Among the possible solutions to NLEEs, certain special form solutions may depend only on a single combination of variables such as traveling wave variables. In the literature, there is a wide variety of approaches to nonlinear problems for constructing traveling wave solutions. Some of these approaches are the Jacobi elliptic function method [1], inverse scattering method [2], Hirotas bilinear method [3], homogeneous balance method [4], homotopy perturbation method [5], Weierstrass function method [6], symmetry method [7], Adomian decomposition method [8], sine/cosine method [9], tanh/coth method [10], the Exp-function method [11-16] and so on. But, most of the methods may sometimes fail or can only lead to a kind of special solution and the solution procedures become very complex as the degree of nonlinearity increases.
Recently, the  -expansion method, firstly introduced by Wang et al. [17], has become widely used to search for various exact solutions of NLEEs [17-27]. The
-expansion method, firstly introduced by Wang et al. [17], has become widely used to search for various exact solutions of NLEEs [17-27]. The  -expansion method is based on the assumptions that the travelling wave solutions can be expressed by a polynomial in
-expansion method is based on the assumptions that the travelling wave solutions can be expressed by a polynomial in , and that
, and that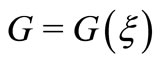 , satisfies a second order linear ordinary differential equation
, satisfies a second order linear ordinary differential equation
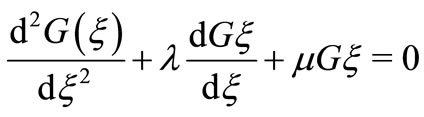 (1)
(1)
where ![]() are arbitrary constants and
are arbitrary constants and 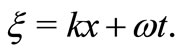
The degree of the polynomial can be determined by considering the homogeneous balance between the highest order derivative and nonlinear terms appearing in the given nonlinear evolution equations. The coefficients of the polynomial can be obtained by solving a set of algebraic equations resulted in from the process of using the method. The 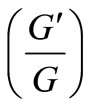 -expansion method is direct, conciseelementary and effective, and can be used for nonlinear partial differential equation involving higher-order nonlinear terms.
-expansion method is direct, conciseelementary and effective, and can be used for nonlinear partial differential equation involving higher-order nonlinear terms.
As we know, much work has been done on developing and extending the  -expansion method for solving nonlinear evolution equations (see, for example [17-27] and their references). But in generalized cases, a small amount of work has been done (see, for example [28,29]). In this paper, we restrict our attention to the study of the following generalized forms of Burgers equation,
-expansion method for solving nonlinear evolution equations (see, for example [17-27] and their references). But in generalized cases, a small amount of work has been done (see, for example [28,29]). In this paper, we restrict our attention to the study of the following generalized forms of Burgers equation,
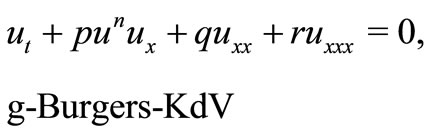 (2)
(2)
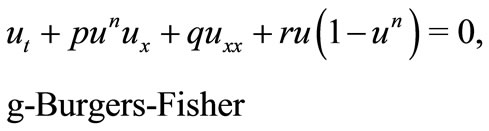 (3)
(3)
where 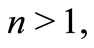 and
and  and
and  are constants. These equations are the generalized combined forms of Burgers equation
are constants. These equations are the generalized combined forms of Burgers equation
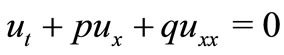 (4)
(4)
Equation (4) is the lowest order approximation for the one-dimensional propagation of weak shock waves in a fluid [30,31]. It is also used in the description of the variation in vehicle density in highway traffic [32]. It is one of the fundamental model equations in fluid mechanics. The Burgers equation demonstrates the coupling between diffusion  and the convection process
and the convection process . Burgers introduced this equation to capture some of the features of turbulent fluid in a channel caused by the interaction of the opposite effects of convection and diffusion [33]. It is also used to describe the structure of shock waves, traffic flow, and acoustic transmission [34].
. Burgers introduced this equation to capture some of the features of turbulent fluid in a channel caused by the interaction of the opposite effects of convection and diffusion [33]. It is also used to describe the structure of shock waves, traffic flow, and acoustic transmission [34].
The generalized Burgers-KdV Equation (2) are models for the propagation of waves on an elastic tube (see [28, 29,35,36] and their references). It can be regarded as a combination of the Burgers equation (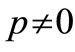 ,
, ![]() ,
,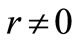 ) and the KdV equation
) and the KdV equation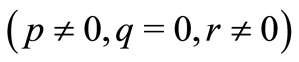 . EspeciallyIsmail Aslan in [26] applied the
. EspeciallyIsmail Aslan in [26] applied the 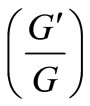 -expansion method for the Burgers-KdV equation (
-expansion method for the Burgers-KdV equation ( ) and in [36] Ahmet Bekir applied the tanh method to modified form of Burgers-KdV equation (
) and in [36] Ahmet Bekir applied the tanh method to modified form of Burgers-KdV equation (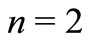 ). In addition, the generalized Burgers-Fisher Equation (3), see [37], has a wide range of applications in plasma physics, fluid physics, capillary-gravity waves, nonlinear optics and chemical physics [38].
). In addition, the generalized Burgers-Fisher Equation (3), see [37], has a wide range of applications in plasma physics, fluid physics, capillary-gravity waves, nonlinear optics and chemical physics [38].
Our first interest in the present work is in implementing the 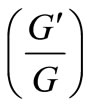 -expansion method to stress its power in handling nonlinear equations, so that one can apply it to models of various types of nonlinearity. The next interest is in the determination of exact travelling wave solutions for the generalized form of Equations (2) and (3) especially the modified form of them
-expansion method to stress its power in handling nonlinear equations, so that one can apply it to models of various types of nonlinearity. The next interest is in the determination of exact travelling wave solutions for the generalized form of Equations (2) and (3) especially the modified form of them 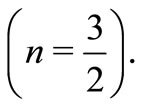 Searching for exact solutions of nonlinear problems has attracted a considerable amount of research work where computer symbolic systems facilitate the computational work.
Searching for exact solutions of nonlinear problems has attracted a considerable amount of research work where computer symbolic systems facilitate the computational work.
2. Description of the  -Expansion Method
-Expansion Method
The objective of this section is to outline the use of the 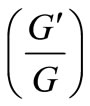 -expansion method for solving certain nonlinear partial differential equations (PDEs). Suppose we have a nonlinear PDE for
-expansion method for solving certain nonlinear partial differential equations (PDEs). Suppose we have a nonlinear PDE for 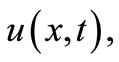 in the form
in the form
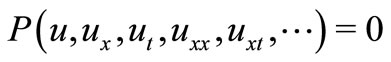 (5)
(5)
where  is a polynomial in its arguments, which includes nonlinear terms and the highest order derivatives. The transformation
is a polynomial in its arguments, which includes nonlinear terms and the highest order derivatives. The transformation 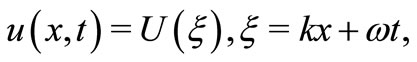 reduces Equation (5) to the ordinary differential equation (ODE)
reduces Equation (5) to the ordinary differential equation (ODE)
 (6)
(6)
where  and prime denotes derivative with respect to ξ. We assume that the solution of Equation (6)
and prime denotes derivative with respect to ξ. We assume that the solution of Equation (6)
can be expressed by a polynomial in 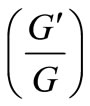 as follows:
as follows:
 (7)
(7)
where , and
, and  are constants to be determined later, and
are constants to be determined later, and 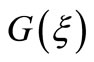 satisfies the second order linear ordinary differential Equation (1):
satisfies the second order linear ordinary differential Equation (1):
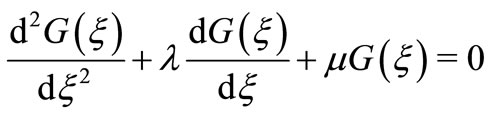 (8)
(8)
where ![]() and
and 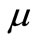 are arbitrary constants. It follows from (7) and (8), that
are arbitrary constants. It follows from (7) and (8), that
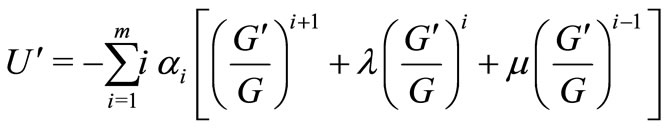 (9)
(9)
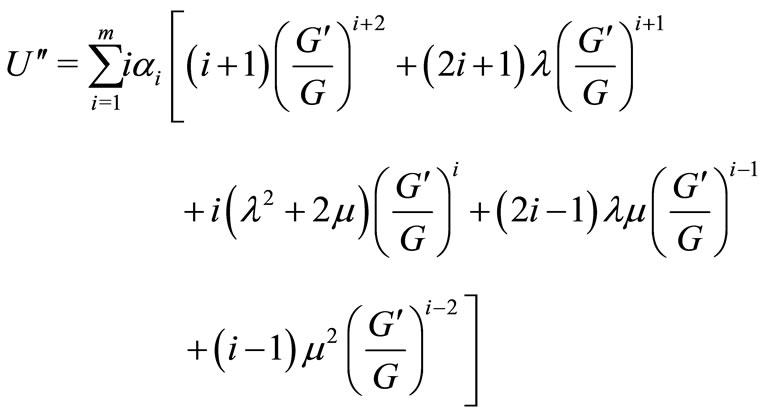 (10)
(10)
and so on, here the prime denotes the derivative with respective to .
.
To determine ![]() explicitly, we take the following three steps:
explicitly, we take the following three steps:
Step 1. Determine the integer ![]() by substituting Equation (7) into Equation (6) and balancing the highest order nonlinear term(s) and the highest order derivative.
by substituting Equation (7) into Equation (6) and balancing the highest order nonlinear term(s) and the highest order derivative.
Step 2. Substitute Equation (7) along with Equation (8) into Equation (6) and collect all terms with the same order of  together, the left-hand side of Equation (6) is converted into a polynomial in
together, the left-hand side of Equation (6) is converted into a polynomial in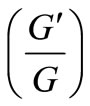 . Then set each coefficient of this polynomial to zero to derive a set of algebraic equations for
. Then set each coefficient of this polynomial to zero to derive a set of algebraic equations for  and
and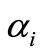 .
.
Step 3. Solve the system of algebraic equations obtained in Step 2, for  and
and  by use of Maple, along with the general solutions of Equation (8), we can have more travelling wave solutions of Equation (5).
by use of Maple, along with the general solutions of Equation (8), we can have more travelling wave solutions of Equation (5).
3. Application
In this section, we will demonstrate the  -expansion method on the generalized equations listed in (2) and (3).
-expansion method on the generalized equations listed in (2) and (3).
3.1. Generalized Burgers-KdV Equation
Considering the generalized Burgers-KdV equation with higher-order nonlinear terms
 (11)
(11)
Now,using the wave variable 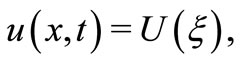
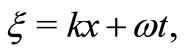 in (11) and integrating the resulting equation and neglecting the constant of integration, we find
in (11) and integrating the resulting equation and neglecting the constant of integration, we find
 (12)
(12)
To achieve our goal, we use the transformation
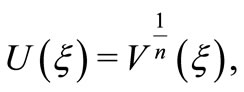 that will carry (12) into the ODE
that will carry (12) into the ODE
 (13)
(13)
According to Step 1, we get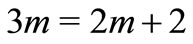 , hence
, hence 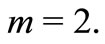 We then suppose that Equation (13) has the following formal solutions:
We then suppose that Equation (13) has the following formal solutions:
 (14)
(14)
where 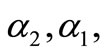 and
and 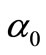 are constants which are unknown to be determined later.
are constants which are unknown to be determined later.
Substituting Equation (14) into Equation (13) and collecting all terms with the same order of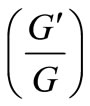 , togetherthe left-hand sides of Equation (13) are converted into a polynomial in
, togetherthe left-hand sides of Equation (13) are converted into a polynomial in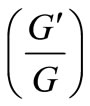 . Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for
. Setting each coefficient of each polynomial to zero, we derive a set of algebraic equations for  and
and 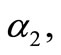 (collecting the coefficients of
(collecting the coefficients of 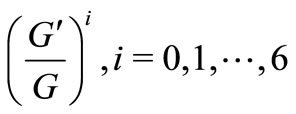 and setting it to zeroAppendix I) and solving them by use of Maple, we get the following general result:
and setting it to zeroAppendix I) and solving them by use of Maple, we get the following general result:
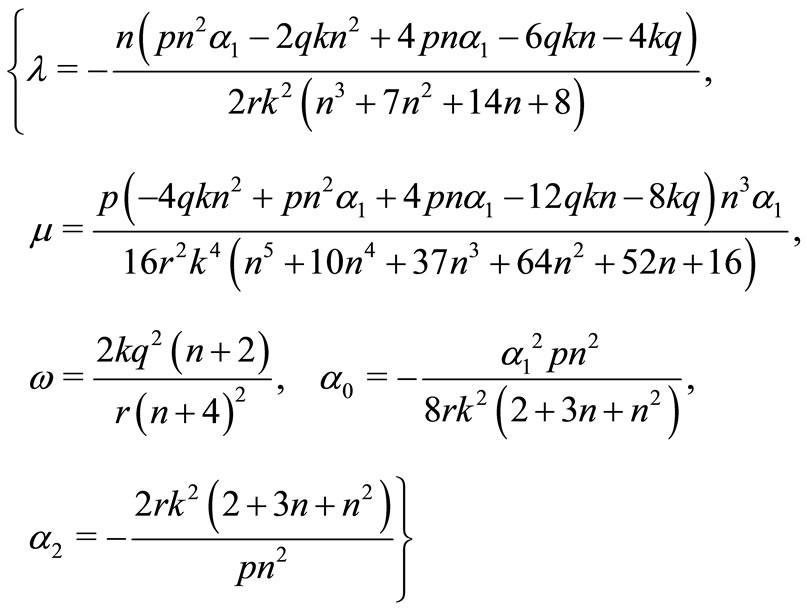 (15)
(15)
Substitute the above general case in (10), we get
 (16)
(16)
then use the transformation  the hyperbolic function solutions of Equation (11), becomes:
the hyperbolic function solutions of Equation (11), becomes:
 (17)
(17)
and the trigonometric function solutions of Equation (11), will be:
 (18)
(18)
where

and 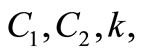 and
and 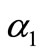 are arbitrary constants and
are arbitrary constants and 
If 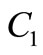 and
and 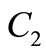 take up special values, the various known results in the literature can be rediscovered, for instance, setting
take up special values, the various known results in the literature can be rediscovered, for instance, setting 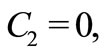 then the general solutions (17)- (18) reduces, respectively,
then the general solutions (17)- (18) reduces, respectively,
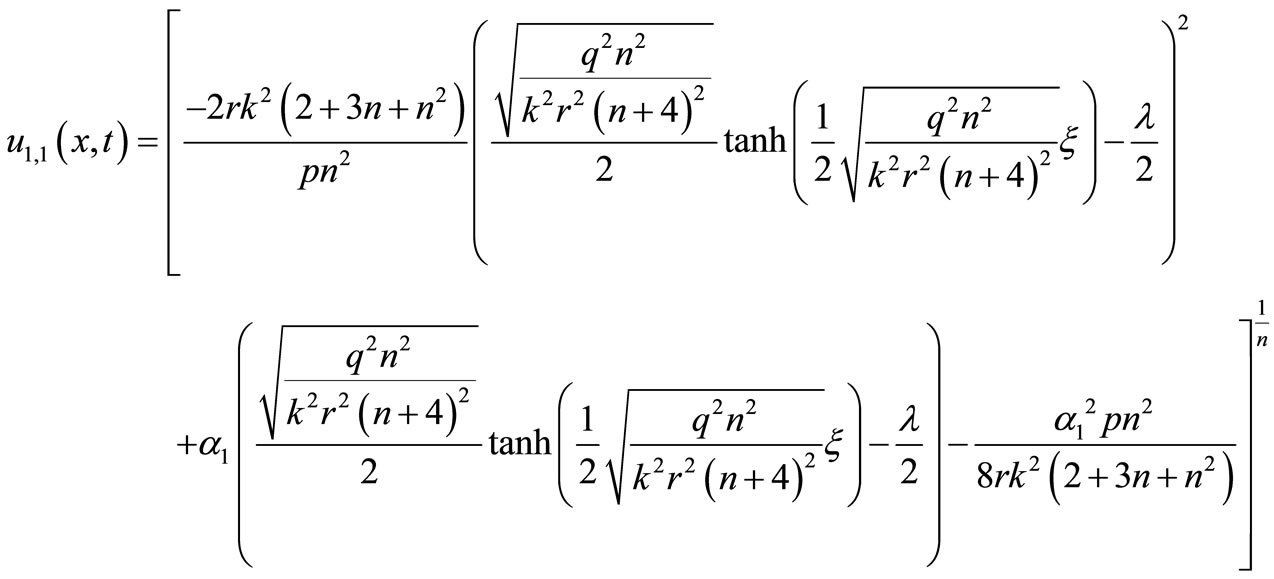 (19)
(19) 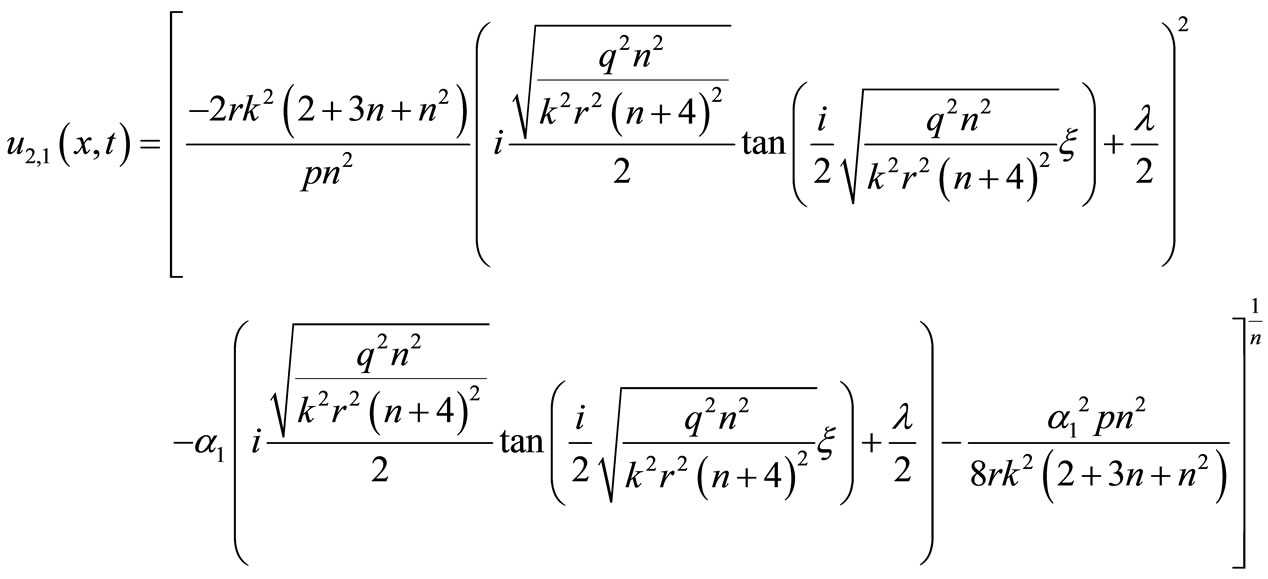 (20)
(20) and when 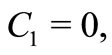 then we deduce from general solutions (17)-(18) that, respectively
then we deduce from general solutions (17)-(18) that, respectively
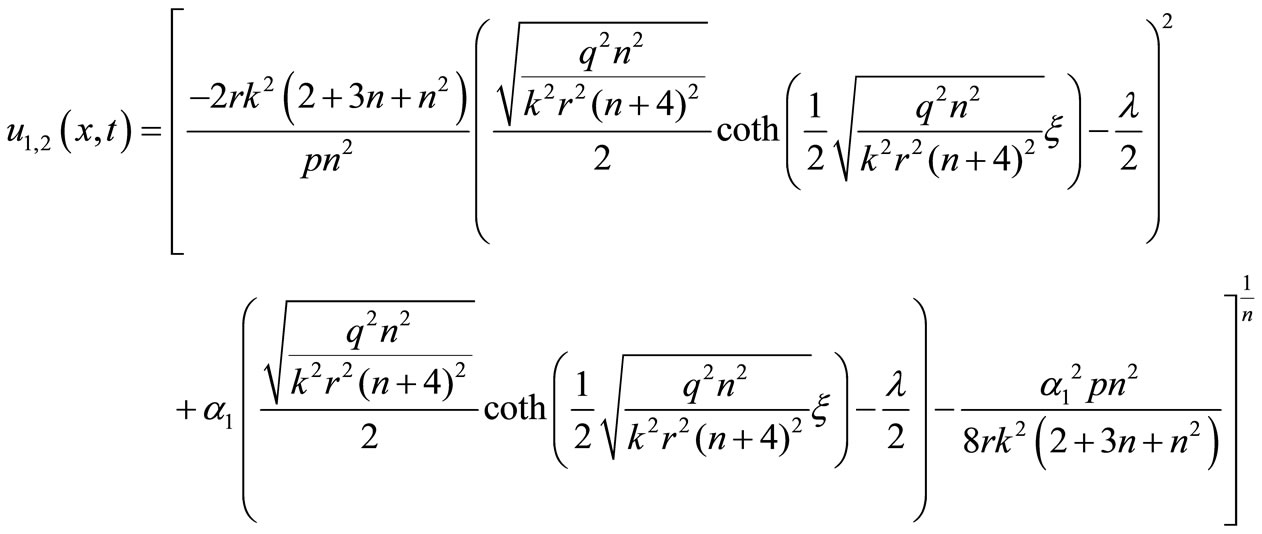 (21)
(21)  (22)
(22) where

and 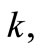 and
and 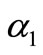 are arbitrary constants and
are arbitrary constants and 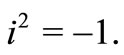
In particulars cases, if  and
and 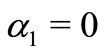 then
then
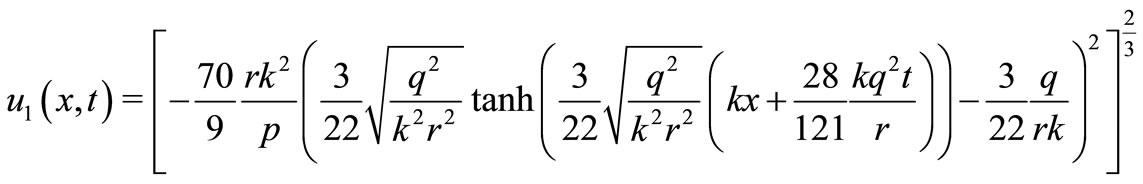
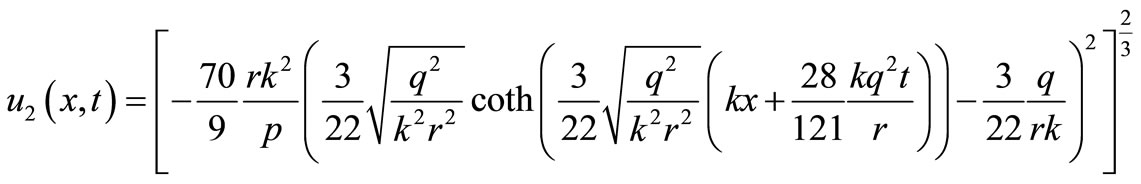
and
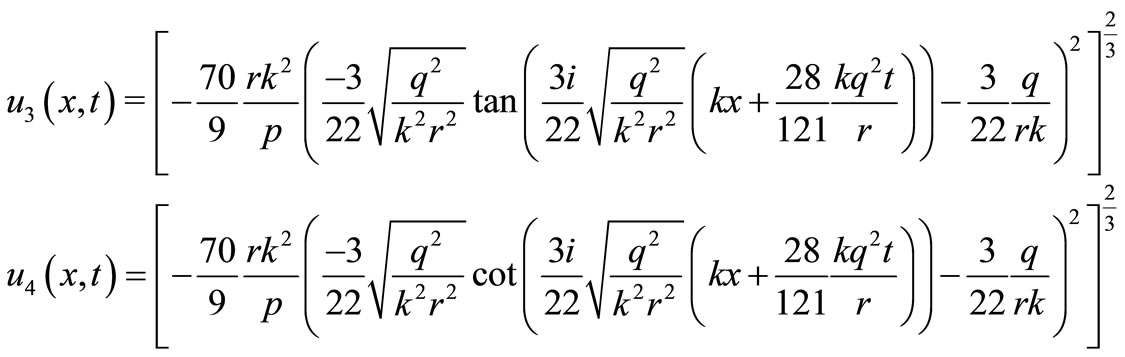
are the four solitary wave solutions of the particular Burgers-KdV equation
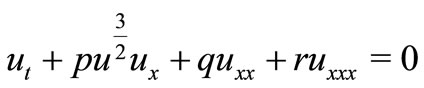 (23)
(23)
where 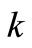 is arbitrary constant and
is arbitrary constant and 
Different real solutions of the general Burgers-KdV Equation (2) were obtained by Ahmet Bekir in [36] using the extended tanh method.
3.2. Generalized Burgers-Fisher Equation
Now considering the generalized Burgers-Fisher equation with higher-order nonlinear terms
 (24)
(24)
Using the wave variable , in (24), we find
, in (24), we find
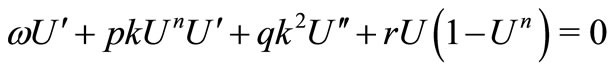 (25)
(25)
To achieve our goal, we use the transformation
 that will carry (25) into the ODE
that will carry (25) into the ODE
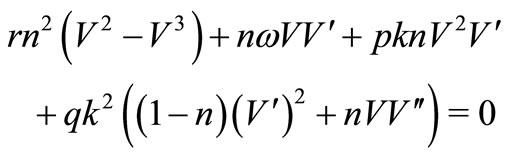 (26)
(26)
According to Step 1, we get , hence
, hence  We then suppose that Equation (26) has the following formal solutions:
We then suppose that Equation (26) has the following formal solutions:
 (27)
(27)
where 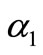 and
and  are constants which are unknown to be determined later.
are constants which are unknown to be determined later.
Similar on previous section, substituting Equation (29) into Equation (26) and collecting all terms with the same order of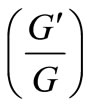 , together, we derive a set of algebraic equations for
, together, we derive a set of algebraic equations for 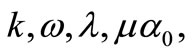 and
and 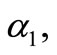 (collecting the coefficients of
(collecting the coefficients of  and setting it to zeroAppendix II) and solving them by use of Maple, we get the following general result:
and setting it to zeroAppendix II) and solving them by use of Maple, we get the following general result:
 (28)
(28) Substitute the above general case in (25), we get
 (29)
(29)
then use the transformation  the hyperbolic and the trigonometric function solutions of Equation (11), will be:
the hyperbolic and the trigonometric function solutions of Equation (11), will be:
 (30)
(30)
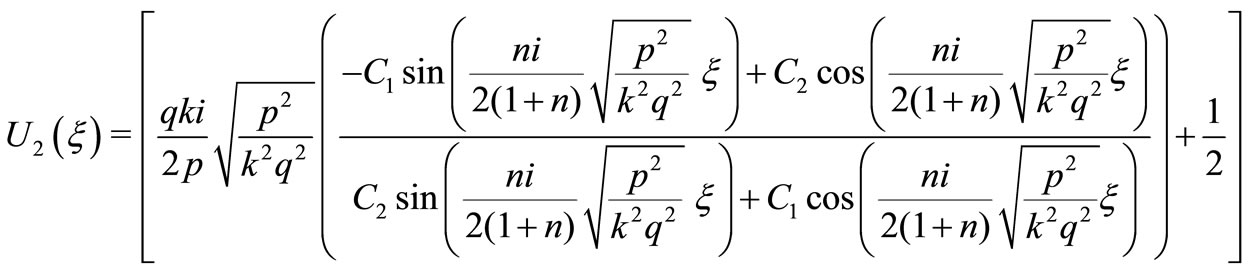 (31)
(31)
where 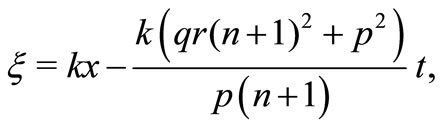 and
and  are arbitrary constants and
are arbitrary constants and .
.
If  and
and 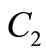 take up special values, the various known results in the literature can be rediscovered, for instance, setting
take up special values, the various known results in the literature can be rediscovered, for instance, setting  then the general solutions (30)-(31) reduces, respectively,
then the general solutions (30)-(31) reduces, respectively,
 (32)
(32)
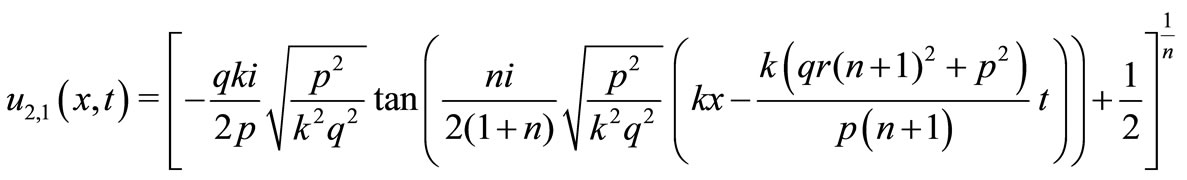 (33)
(33)
and when 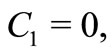 then we deduce from general solutions (30)-(31) that, respectively
then we deduce from general solutions (30)-(31) that, respectively
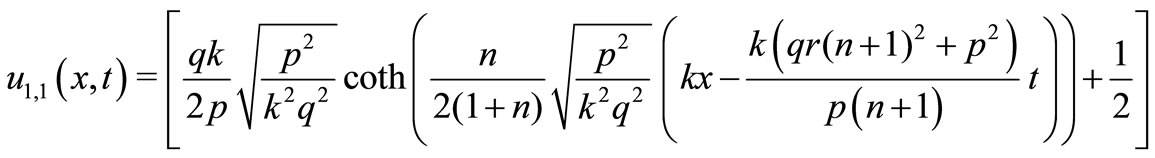 (34)
(34)
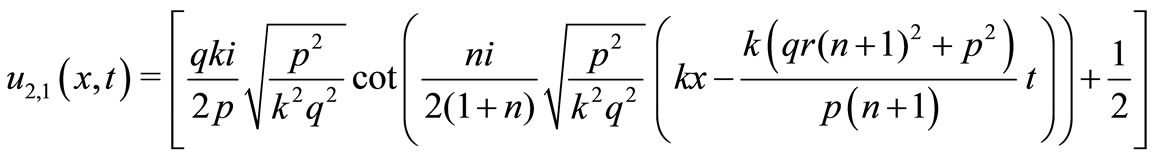 (35)
(35)
where 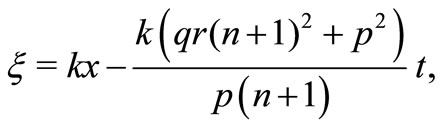
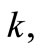 is arbitrary constant and
is arbitrary constant and .
.
In particular, if  then
then

and
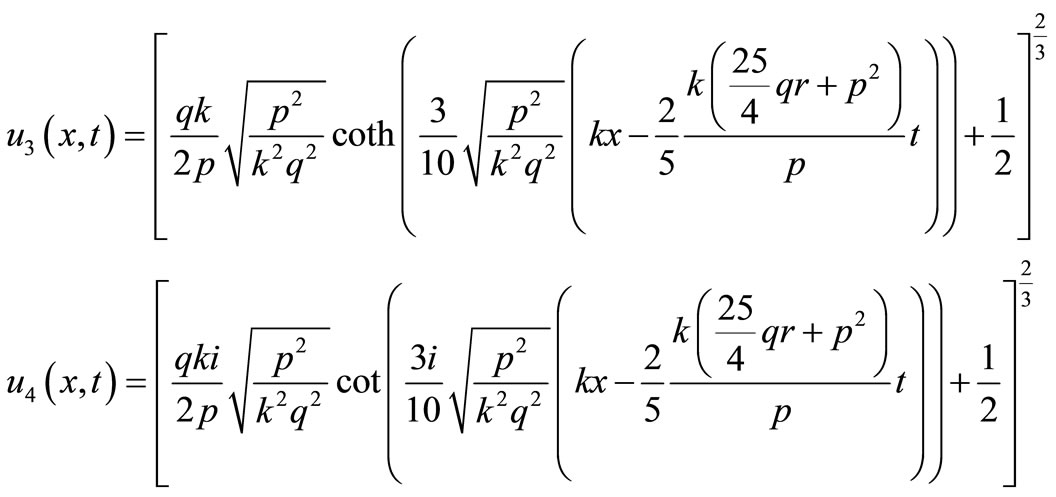
are the four solitary wave solutions of the particular Burgers-Fisher equation
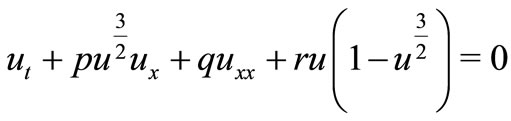 (36)
(36)
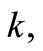 is arbitrary constant and
is arbitrary constant and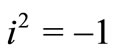 .
.
Different real solutions of the general Burgers-Fisher Equation (3) were obtained by Wazwaz in [39] using the tanh method and by El-Wakil in [38] using a modified tanh-function method and recently by Luwai Wazzan in [28] using a modified tanh-coth method.
4. Conclusions
This study shows that the  -expansion method is quite efficient and practically well suited for use in finding exact solutions for the generalized form of BurgersKorteweg-de Vries (Burgers-KdV) and Burger-Fisher equations. The results show that this method is a powerful Mathematical tool for obtaining exact solutions for the general B-Fisher and B-KdV equations. With the aid of Maple, we have assured the correctness of the obtained solutions by putting them back into the original equation. It is also a promising method to solve other nonlinear partial differential equations arising in engineering sciences.
-expansion method is quite efficient and practically well suited for use in finding exact solutions for the generalized form of BurgersKorteweg-de Vries (Burgers-KdV) and Burger-Fisher equations. The results show that this method is a powerful Mathematical tool for obtaining exact solutions for the general B-Fisher and B-KdV equations. With the aid of Maple, we have assured the correctness of the obtained solutions by putting them back into the original equation. It is also a promising method to solve other nonlinear partial differential equations arising in engineering sciences.
5. Acknowledgements
This work is partially supported by Grant-in-Aid from the university of Mohaghegh Ardabili, Ardabil, Iran.
REFERENCES
- G.T. Liu and T.Y. Fan, “New Applications of Developed Jacobi Elliptic Function Expansion Methods,” Physics Letters A, Vol. 345, No. 1-3, 2005, pp. 161-166. doi:10.1016/j.physleta.2005.07.034
- M. J. Ablowitz and H. Segur, “Solitons and Inverse Scattering Transform,” SIAM, Philadelphia, 1981. doi:10.1137/1.9781611970883
- R. Hirota, “The Direct Method in Soliton Theory,” Cambridge University Press, Cambridge, 2004.
- M. L. Wang, “Exact Solutions for a Compound KdV Burgers Equation,” Physics Letters A, Vol. 213, No. 5-6, 1996, pp. 279-287. doi:10.1016/0375-9601(96)00103-X
- J. H. He, “The Homotopy Perturbation Method for Nonlinear Oscillators with Discontinuities,” Applied Mathematics and Computation, Vol. 151, No. 1, 2004, pp. 287- 292. doi:10.1016/S0096-3003(03)00341-2
- Z. Y. Yan, “An Improved Algebra Method and Its Applications in Nonlinear Wave Equations,” Chaos, Solitons & Fractals, Vol. 21, No. 4, 2004, pp. 1013-1021. doi:10.1016/j.chaos.2003.12.042
- G. W. Bluman and S. Kumei, “Symmetries and Differential Equations,” Springer-Verlag, New York, 1989.
- G. Adomian, “Solving Frontier Problems of Physics: The Decomposition Method,” Kluwer, Boston, 1994.
- A. Borhanifar, H. Jafari and S. A. Karimi, “New Solitons and Periodic Solutions for the Kadomtsev-Petviashvili Equation,” Journal of Nonlinear Science and Applications, Vol. 1, No. 4, 2008, pp. 224-229.
- H. Jafari, A. Borhanifar and S. A. Karimi, “New Solitary Wave Solutions for the Bad Boussinesq and Good Boussinesq Equations,” Numerical Methods for Partial Differential Equations, Vol. 25, No. 5, 2009, pp. 1231-1237. doi:10.1002/num.20400.
- A. Borhanifar, M. M. Kabir and L. Maryam Vahdat, “New Periodic and Soliton Wave Solutions for the Generalized Zakharov System and (2 + 1)-Dimensional Nizhnik-Novikov-Veselov System,” Chaos, Solitons & Fractals, Vol. 42, No. 3, 2009, pp. 1646-1654. doi:10.1016/j.chaos.2009.03.064
- A. Borhanifar and M. M. Kabir, “New Periodic and Soliton Solutions by Application of Exp-Function Method for Nonlinear Evolution Equations,” Journal of Computational and Applied Mathematics, Vol. 229, No. 1, 2009, pp. 158-167. doi:10.1016/j.cam.2008.10.052
- S. A. El-Wakil, M. A. Abdou and A. Hendi, “New Periodic Wave Solutions via Exp-Function Method,” Physics Letters A, Vol. 372, No. 6, 2008, pp. 830-840. doi:10.1016/j.physleta.2007.08.033
- A. Boz and A. Bekir, “Application of Exp-Function Method for (3 + 1)-Dimensional Nonlinear Evolution Equations,” Computers & Mathematics with Applications, Vol. 56, No. 5, 2008. doi:10.1016/j.camwa.2008.02.045.
- H. Zhao and C. Bai, “New Doubly Periodic and Multiple Soliton Solutions of the Generalized (3 + 1)-Dimensional Kadomtsev-Petviashvilli Equation with Variable Coefficients,” Chaos, Solitons & Fractals, Vol. 30, No. 1, 2006, pp. 217-226. doi:10.1016/j.chaos.2005.08.148
- M. A. Abdou, “Further Improved F-Expansion and New Exact Solutions for Nonlinear Evolution Equations,” Nonlinear Dynamics, Vol. 52, No. 3, 2008, pp. 277-288. doi:10.1007/s11071-007-9277-3
- M. Wang, X. Li and J. Zhang, “The
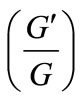 -Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics,” Physics Letters A, Vol. 372, No. 4, 2008, pp. 417-423. doi:10.1016/j.physleta.2007.07.051
-Expansion Method and Traveling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics,” Physics Letters A, Vol. 372, No. 4, 2008, pp. 417-423. doi:10.1016/j.physleta.2007.07.051 - J. Zhang, X Wei and Y. J. Lu, “A Generalized
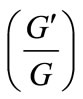 - Expansion Method and Its Applications,” Physics Letters A, Vol. 372, No. 20, 2008, pp. 3653-3658. doi:10.1016/j.physleta.2008.02.027,
- Expansion Method and Its Applications,” Physics Letters A, Vol. 372, No. 20, 2008, pp. 3653-3658. doi:10.1016/j.physleta.2008.02.027, - A. Bekir, “Application of the
 -Expansion Method for Nonlinear Evolution Equations,” Physics Letters A, Vol. 372, No. 19, 2008, pp. 3400-3406. doi:10.1016/j.physleta.2008.01.057
-Expansion Method for Nonlinear Evolution Equations,” Physics Letters A, Vol. 372, No. 19, 2008, pp. 3400-3406. doi:10.1016/j.physleta.2008.01.057 - A. Bekir and A. C. Cevikel, “New Exact Travelling Wave Solutions of Nonlinear Physical Models,” Chaos, Solitons & Fractals, Vol. 41, No. 4, 2008, pp. 1733-1739. doi:10.1016/j.chaos.2008.07.017
- E. M. E. Zayed and K. A. Gepreel, “Some Applications of the
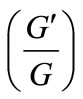 -Expansion Method to Non-Linear Partial Differential Equations,” Applied Mathematics and Computation, Vol. 212, No. 1, 2009, pp. 1-13. doi:10.1016/j.amc.2009.02.009
-Expansion Method to Non-Linear Partial Differential Equations,” Applied Mathematics and Computation, Vol. 212, No. 1, 2009, pp. 1-13. doi:10.1016/j.amc.2009.02.009 - D. D. Ganji and M. Abdollahzadeh, “Exact Traveling Solutions of Some Nonlinear Evolution Equation by
 -Expansion Method,” Journal of Mathematical Physics, Vol. 50, No. 1, 2009, p. 013519. doi:10.1063/1.3052847
-Expansion Method,” Journal of Mathematical Physics, Vol. 50, No. 1, 2009, p. 013519. doi:10.1063/1.3052847 - M. L. Wang, J. L. Zhang and X. Z. Li, “Application of the
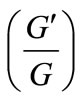 -Expansion to Travelling Wave Solutions of the BroerKaup and the Approximate Long Water Wave Equations,” Applied Mathematics and Computation, Vol. 206, No. 1, 2008, pp. 321-326. doi:10.1016/j.amc.2008.08.045
-Expansion to Travelling Wave Solutions of the BroerKaup and the Approximate Long Water Wave Equations,” Applied Mathematics and Computation, Vol. 206, No. 1, 2008, pp. 321-326. doi:10.1016/j.amc.2008.08.045 - L.-X. Li and M.-L. Wang, “The
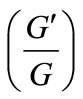 -Expansion Method and Travelling Wave Solutions for a Higher-Order Nonlinear Schrdinger Equation,” Applied Mathematics and Computation, Vol. 208, No. 2, 2009, pp. 440-445. doi:10.1016/j.amc.2008.12.005
-Expansion Method and Travelling Wave Solutions for a Higher-Order Nonlinear Schrdinger Equation,” Applied Mathematics and Computation, Vol. 208, No. 2, 2009, pp. 440-445. doi:10.1016/j.amc.2008.12.005 - E. M. E. Zayed and K. A. Gepreel, “The
 -Expansion Method for Finding Traveling Wave Solutions of Nonlinear Partial Differential Equations in Mathematical Physics,” Journal of Mathematical Physics, Vol. 50, No. 1, 2008, p. 013502. doi:10.1063/1.3033750
-Expansion Method for Finding Traveling Wave Solutions of Nonlinear Partial Differential Equations in Mathematical Physics,” Journal of Mathematical Physics, Vol. 50, No. 1, 2008, p. 013502. doi:10.1063/1.3033750 - I. Aslan, “Exact and Explicit Solutions to Some Nonlinear Evolution Equations by Utilizing the
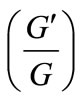 -Expansion Method,” Applied Mathematics and Computation, Vol. 215, No. 2, 2009, pp. 857-863. doi:10.1016/j.amc.2009.05.038
-Expansion Method,” Applied Mathematics and Computation, Vol. 215, No. 2, 2009, pp. 857-863. doi:10.1016/j.amc.2009.05.038 - I. Aslan and T. Ozis, “On the Validity and Reliability of the
 -Expansion Method by Using Higher-Order Nonlinear Equations,” Applied Mathematics and Computation, Vol. 211, No. 2, 2009, pp. 531-536. doi:10.1016/j.amc.2009.01.075
-Expansion Method by Using Higher-Order Nonlinear Equations,” Applied Mathematics and Computation, Vol. 211, No. 2, 2009, pp. 531-536. doi:10.1016/j.amc.2009.01.075 - L. Wazzan, “A Modified tanh-coth Method for Solving the General Burgers-Fisher and the Kuramoto-Sivashinsky Equations,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 6, 2009, pp. 2642- 2652. doi:10.1016/j.cnsns.2008.08.004
- Z.-L. Li, “Constructing of New Exact Solutions to the GKdV-mKdV Equation with Any-Order Nonlinear Terms by
 -Expansion Method,” Applied Mathematics and Computation, Vol. 217, No. 4, 2010, pp. 1398-1403. doi:10.1016/j.amc.2009.05.034
-Expansion Method,” Applied Mathematics and Computation, Vol. 217, No. 4, 2010, pp. 1398-1403. doi:10.1016/j.amc.2009.05.034 - A. Veksler and Y. Zarmi, “Wave Interactions and the Analysis of the Perturbed Burgers Equation,” Physica D: Nonlinear Phenomena, Vol. 211, No. 1-2, 2005, pp. 57- 73. doi:10.1016/j.physd.2005.08.001
- A. Veksler and Y. Zarmi, “Freedom in the Expansion and Obstacles to Integrability in Multiple-Soliton Solutions of the Perturbed KdV Equation,” Physica D: Nonlinear Phenomena, Vol. 217, No. 1, 2006, pp. 77-87. doi:10.1016/j.physd.2006.03.011
- Z.-Y. Ma, X.-F. Wu and J.-M. Zhu, “Multisoliton Excitations for the Kadomtsev-Petviashvili Equation and the Coupled Burgers Equation,” Chaos, Solitons & Fractals, Vol. 31, No. 3, 2007, pp. 648-657. doi:10.1016/j.chaos.2005.10.012
- J. M. Burgers, “The Nonlinear Diffusion Equation,” Reiedl, Dordtrecht, 1974.
- A. M. Wazwaz, “Partial Differential Equations: Methods and Applications,” Balkema Publishers, Rotterdam, 2002.
- R. S. Johnson, “A Non-Linear Equation Incorporating Damping and Dispersion,” Journal of Fluid Mechanics, Vol. 42, No. 1, 1970, pp. 49-60. doi:10.1017/S0022112070001064
- A. Bekir, “On Traveling Wave Solutions to Combined KdV-mKdV Equation and Modified Burgers-KdV Equation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 14, No. 4, 2009, pp. 1038-1042. doi:10.1016/j.cnsns.2008.03.014
- E. J. Parkes and B. R. Duffy, “An Automated tanh-Function Method for Finding Solitary Wave Solutions Nonlinear Evolution Equations,” Computer Physics Communications, Vol. 98, No. 3, 1996, pp. 288-300. doi:10.1016/0010-4655(96)00104-X
- S. A. El-Wakil and M. A. Abdou, “Modified Extended tanh-Function Method for Solving Nonlinear Partial Differential Equation,” Chaos, Soliton and Fractals, Vol. 31, No. 5, 2007, pp. 1256-1264. doi:10.1016/j.chaos.2005.10.072
- A. M. Wazwaz, “The tanh Method for Generalized Forms of Nonlinear Heat Conduction and Burgers-Fisher Equations,” Applied Mathematics and Computation, Vol. 169, No. 1, 2005, pp. 321-338. doi:10.1016/j.amc.2004.09.054
Appendix I

Appendix II
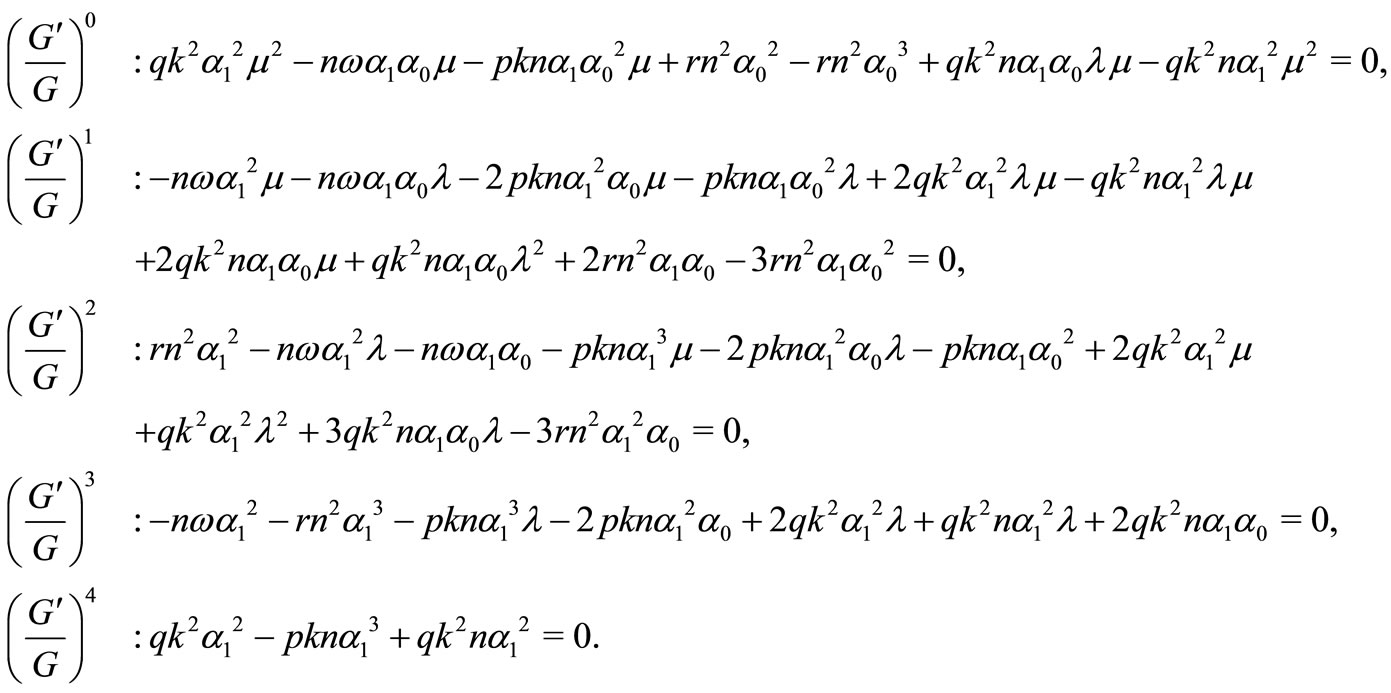
NOTES
*Corresponding author.

