Modern Economy
Vol.10 No.07(2019), Article ID:93872,12 pages
10.4236/me.2019.107115
A Reinsurance Approach in a Two-Dimensional Model with Dependent Risks
Cristina Gosio, Ester C. Lari, Marina Ravera
Department of Economics and Business Studies, University of Genoa, Genoa, Italy

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: June 11, 2019; Accepted: July 22, 2019; Published: July 25, 2019
ABSTRACT
We consider an insurer having two classes of insurance risks dependent through the number of claims of each risk in a given period of time. We assume that the insurer chooses a reinsurance strategy related to the first class of risk by means a proportional reinsurance contract; we also assume that the reinsurance strategy related to the second class of risk is of Excess of Loss reinsurance type. Within this paper, we study the possible optimal couples of proportional retention level and Excess of Loss retention limit.
Keywords:
Reinsurance, Proportional Reinsurance, Excess of Loss Reinsurance, Dependent Risks, Two Dimensional Risk Process

1. Introduction
In recent years, several authors have studied two-dimensional risk processes where an insurer has two classes of business or insurance risks and in each of these two classes there is a surplus process similar to that one of the classical model of risk theory. In [1] [2] , and [3] , it is possible to find results relating to the definition and to the determination of the ruin probability. In [4] and [5] , two-dimensional risk models are considered in the presence of two insurers and under these assumptions, models where the two insurers can be considered as an insurer and a reinsurer are studied. In the literature, further relevant models are: the model presented in [6] where the authors consider a two dimensional ruin problem for two insurance companies that divide between them both claims and premia in some specified proportions and the model presented in [7] where the authors considers two insurance companies, each one with two independent risk processes, having a mutual agreement of deficit coverage such that each company agree to cover the deficit of the other.
In this paper, we always consider only one insurer who has two classes of insurance risks; we therefore consider a two-dimensional risk model process where we assume that an insurer has two classes of insurance business. We assume that these two classes are dependent through the number of claims. The risks of the two dependent classes of insurance risks are sometimes of very different kinds (for example the risk class connected to the insurance of the current damages that can happen to the building and the class of risk connected to the insurance of damages related to an earthquake) therefore, in the insurance practice, it may be more suitable the proportional reinsurance for the first class and the Excess of Loss reinsurance for the second. Hence, we present a new model involving these two different kinds of reinsurance: we assume that the insurer reinsures each of the classes with a quota-share and with an Excess of Loss reinsurance, respectively. We address the problem of determining the proportional retention level (a) and the optimal Excess of Loss retention limit (b) that in a given period of time maximize the expected utility of the total wealth of the insurer; that is, our aim is to calculate the couple (a, b) in order to maximize the expected utility of the total terminal wealth after reinsurance. Therefore, inspired by [8] , we face in the paper a new problem. This paper can improve the reinsurance policies of the company which could thus improve its insurance offer.
The paper is organized as follows: Section 2 is devoted to the presentation of the model.
Section 3 contains the optimization problem and Section 4 presents the Theorem and resumes the results; Section 5 concludes.
2. The Model
We consider only one insurer having two classes of insurance risks dependent through the number of claims. Let be the claim size random variable for risk i, . We assume that the have the same distribution function with , and such that for . We therefore assume that:
·
·
· the moment generating functions , exist.
As done in [2] , we consider a given period of time. Let be the number of claims, for classes i, , in the given period of time considered; we assume:
(1)
where and are independent Poisson random variables with positive parameters and , respectively. Hence (N1, N2) is a bivariate Poisson distribution (see [9] ).
As usually stated, the random variables are mutually independent for each , and are independent of , .
Let be the aggregate claim amount for the risk i-th; it results that
The above risks are dependent risks since the aggregate claim amounts are correlated through the parameter .
We denote by , the value of the i-th surplus process at the end of the given period. Stating with the value of the i-th surplus process at the beginning of the given period, and with the corresponding insurance premium, it results that:
We assume that the insurer reinsures the risk of the first class with a proportional insurance contract with a retention level a, , and that he reinsures the risk of the second class with an Excess of Loss insurance contract with a retention limit b, .
After the reinsurances, the insurer is required to pay for each claim of the first class and for each claim of the second class, .
Therefore, the aggregate claims paid by the insurer are:
(2)
and
. (3)
To obtain the above reinsurance policies, the insurer pays the corresponding insurance premiums, and , respectively. The reinsurer is required to pay for each claim of the first class and for each claim of the second class. It follows that, assuming the Expected Value principle as premium calculation principle, with loading coefficients , respectively, it results:
(4)
and
(5)
Therefore, after reinsurances, the value of each reinsurer surplus, that we denote by , is:
(6)
(7)
For which, the total surplus is:
(8)
3. The Problem
As we have stated before, our goal is to maximize the expected utility of the total wealth of the insurer. According to several Authors, we assume that the insurer’s utility function, u, is defined as follows: .
We therefore aim to find the that is, remembering (2)-(7) and (8):
.
Avoiding the constant terms respect to a and b, our objective function is:
. (9)
In the following, we will consider the variables , identically distributed to and the variables and identically distributed to and , respectively. Remembering that, for assumption (1), has the bivariate Poisson distribution and therefore the moment generating function of is (see [8] and [9] ):
and therefore, if it is:
(10)
it results:
It follows that the problem (9) can be written as:
,
that is, if it is:
,
then:
. (11)
Remembering (4), (5) and (10), it results:
(12)
Finally, we observe that minimizing is equivalent to the maximizing . We therefore have the problem:
(13)
We consider the problem (13) using Kuhn-Tucker conditions and we state:
The K-T conditions are:
(14)
We observe that it results:
(15)
(16)
Let
(17)
We observe that nullifies (16) and it is decreasing when α increases.
We consider the following cases of which would be solution of the system (14).
· Case I
and .
The following conditions must be fulfilled:
and ,
that is:
(I1)
(I2)
and we observe that both (I1) and (I2) are impossible.
· Case II
and .
The following conditions must be fulfilled:
and ,
that is it must exist satisfying the conditions:
(II1)
. (II2)
We observe that it exists satisfying condition (II2); it is:
. (18)
· Case III
and .
The following conditions must be fulfilled:
and ,
that is:
(III1)
and
. (III2)
· Case IV
and .
The following conditions must be fulfilled:
and ,
that is, it must exists satisfying the following conditions:
(IV1)
and
. (IV2)
We observe that, if and only if condition (III1) is not verified, that is if and only if it results:
(19)
then, satisfying condition (IV1). Indeed, considering
it results:
, and because of (19).
· Case V
and .
The following conditions must be fulfilled:
and ,
that is, it must exists satisfying the following conditions:
(V1)
and
. (V2)
We observe that, if and only if condition (III2) is not verified, that is if and only if it results:
(20)
it exists satisfying condition (V2), it is:
(21)
· Case VI
and .
The following conditions must be fulfilled:
and ,
that is, it must exist and satisfying the following conditions:
(VI1)
and
. (VI2)
We observe that, if conditions (III1), (II1) and (IV2) are not verified, that is if (19) holds and if moreover it results:
(22)
and
(23)
then, there exist and satisfying the conditions (VI1) and (VI2). Instead, as we have observed before, from (19) it follows that it exist unique fulfilling condition (IV1). Furthermore, being (23) satisfied, it results that, for all , it is possible to find the following , fulfilling condition (VI2):
(24)
Placing:
(25)
since (22) is satisfied, it results:
while, remembering (IV1), it is:
It follows that it exists such that and therefore, there exist and , satisfying conditions (VI1) and (VI2).
Finally, we observe that if conditions (III2), (II1) and (V1) are not valid, that is if (20) and (22) hold, and if moreover it results:
(26)
then there exist and , fulfilling (VI1) and (VI2).
In fact, as we have observed before, from (20) it follows that it exists fulfilling (V2). It follows that, remembering (17), for all , it exists:
fulfilling condition (VI2).
We recall (25) and we have, since (22) is fulfilled: and since (26) is fulfilled:
As a consequence, it exists such that and therefore there exist and fulfilling (VI1) and (VI2).
4. The Results
The results obtained allow us to show the following:
Theorem
Let a Kuhn-Tucker point, solution of the system (14).
1) The following statements are hold:
1) and is impossible.
2) Let fulfilling condition (II2). If it is:
that is if condition (II1) is satisfied, it is:
and . (case (II))
In the following we suppose that condition (II1) is not satisfied, that is (22) holds and that moreover it results:
3) If it also turns out:
and
that is if (III1) and (III2) are fulfilled, it results:
and . (case (III))
4) If it also turns out:
and
that is if (III1) is not fulfilled, that is (19) holds, and (IV2) is satisfied, it results:
and . (case (IV))
5) If it also turns out:
and
that is if (III2) is not fulfilled, that is (20) holds, and (V1) is satisfied, it results:
and . (case (V))
6) F1) If it also turns out:
and
that is if (III1) and (IV2) are not satisfied, that is (19) and (23) hold, it results:
and ,
where 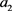 and
and 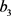 fulfill conditions (VI). (case (VI)).
fulfill conditions (VI). (case (VI)).
F2) If it also turns out:
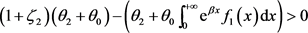
and
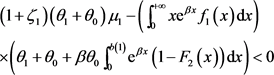
that is if (III2) and (V1) are not satisfied, that is (20) and (26) hold, it results:
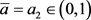 and
and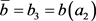 ,
,
where 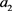 and
and 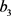 fulfill conditions (VI). (case (VI)).
fulfill conditions (VI). (case (VI)).
Proof
1), 2) and 3): see cases (I), (II) and (III) previously mentioned, respectively.
4): as proved in the case (IV), (19) ensures that exists 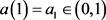 satisfying (IV1) and then, if also (IV2) is fulfilled, it is case (IV).
satisfying (IV1) and then, if also (IV2) is fulfilled, it is case (IV).
5): as proved in the case (V), (20) ensures that exists 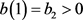 satisfying (V2) and then, if also (V1) is fulfilled, we are in the case (V).
satisfying (V2) and then, if also (V1) is fulfilled, we are in the case (V).
6): see case (VI).
5. Final Conclusions
In this paper, we presented a two dimensional risk model where the claim counting processes of the two classes of insurance business are dependent through the number of claims. We have assumed that the insurer reinsures each of the classes with a quota-share and with an excess of loss reinsurance, with a retention level a, 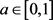 and a retention limit b,
and a retention limit b, 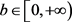 , respectively.
, respectively.
Fixed a given period of time, we have considered the expected utility of the insurer’s wealth and we have assumed that the insurer looks for the pair (a, b) that maximizes this utility. In the paper, we have constructed the model that describes the above problem and we have assumed, according with several authors, an exponential utility function and the expected value principle for the computation of the insurance premiums. We therefore have considered the possible pairs (a, b) candidates to solve the problem, deriving the conditions under which each pair exists.
We are currently dealing with the possible application of the model presented in this article to a particular case of social significance. Furthermore, as well as other authors have done in models different from the model presented in this paper, a natural development of our study could be consider more than two classes of insurance business with two or more reinsurance types.
Acknowledgements
We thank the Editor and the Referees for their comments.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Gosio, C., Lari, E.C. and Ravera, M. (2019) A Reinsurance Approach in a Two-Dimensional Model with Dependent Risks. Modern Economy, 10, 1790-1801. https://doi.org/10.4236/me.2019.107115
References
- 1. Cai, J. and Li, H. (2005) Multivariate Risk Model of Phase Type. Insurance: Mathematics and Economics, 36, 137-152. https://doi.org/10.1016/j.insmatheco.2004.11.004
- 2. Cai, J. and Li, H. (2007) Dependence Properties and Bounds for Ruin Probabilities in Multivariate Compound Risk Models. Journal of Multivariate Analysis, 98, 757-773. https://doi.org/10.1016/j.jmva.2006.06.004
- 3. Dang, L., Zhu, N. and Zhang, H. (2009). Survival Probability for a Two-Dimensional Risk Model. Insurance: Mathematics and Economics, 44, 491-496. https://doi.org/10.1016/j.insmatheco.2009.02.001
- 4. Avram, F., Palmowski, Z. and Pistorius, M. (2008) A Two-Dimensional Ruin Problem on the Positive Quadrant. Insurance: Mathematics and Economics, 42, 227-234. https://doi.org/10.1016/j.insmatheco.2007.02.004
- 5. Badescu, A.L., Cheung, E.C.K. and Rabehasaina, L. (2011) A Two-Dimensional Risk Model with Proportional Reinsurance. Journal of Applied Probability, 48, 749-765. https://doi.org/10.1239/jap/1316796912
- 6. Avram, F., Palmowski, Z. and Pistorius, M. (2008) Exit Problem of a Two-Dimensional Risk Process from the Quadrant: Exact and Asymptotic Results. The Annals of Applied Probability, 18, 2421-2449. https://doi.org/10.1214/08-AAP529
- 7. Ivanovs, J. and Boxma, O. (2015) A Bivariate Risk Model with Mutual Deficit Coverage. Insurance: Mathematics and Economics, 64, 126-134. https://doi.org/10.1016/j.insmatheco.2015.05.006
- 8. Centeno, M.L. (2005) Dependent Risks and Excess of Loss Reinsurance. Insurance: Mathematics and Economics, 37, 229-238. https://doi.org/10.1016/j.insmatheco.2004.12.001
- 9. Johnson, L., Kotz, S. and Balakrishnan (1997) Discrete Multivariate Distribution. Wiley, New York.

