Received 23 September 2015; accepted 27 October 2015; published 30 October 2015

ABSTRACT

This paper extends and surveys some basic quality-ladder models of education, innovation and trade in order to explain the dynamics of technological change and aggregate growth in developed countries. We analyze how the stochastic processes of innovation and export adaptation are affected by asymmetric factor endowments, transport costs, and barriers to entry in foreign markets. We show that the country-specific innovation rates are permanently increasing in the effectiveness of education and the countries’ relative endowment with labor. Trade liberalization leads to a temporary increase in the innovation rates but to a permanent increase in the rates of export adaptation.

Keywords:

Education, Innovation, Export Adaptation, Industry Dynamics, Economic Growth

1. Introduction

Schumpeterian growth theory is dominated by R&D-based growth models in which stochastic processes of product innovation serve as engine of growth. Grossman and Helpman [1] [2] , Aghion and Howitt [3] [4] , and Stokey [5] have been the first to explain long-run per-capita growth by intentional R & D activities of private firms. According to these first-generation quality-ladder models, technological change results from an endless sequence of vertical improvements of consumer goods. A weakness of these models is their common property of a counterfactual scale effect which predicts that larger economies grow faster and that population growth causes increasing per-capita growth rates.

In response to this theoretical shortcoming, a new class of semi-endogenous growth models has emerged (e.g. Jones [6] , Kortum [7] and Segerstrom [8] ). As a distinguishing feature, these second-generation R & D-based growth models remove the scale effect by the assumption that the difficulty of R & D increases over time, and predict that per-capita growth depends proportionally on the exogenously given population growth rate. As a consequence, constant population leads to a stationary equilibrium without innovation and growth dynamics. Due to this prediction, empirical evidence is not in favor of these semi-endogenous growth models.

We prefer the scale-invariant, fully endogenous R & D-based growth models of the third generation. As in the semi-endogenous growth theory, the scale effect is removed by an increasing difficulty of R & D, but this deterioration of technological opportunities is compensated by a continuous improvement of researchers’ human capital. Lucas [9] has been the first to emphasize the role of human-capital accumulation by education as an important source of endogenous growth. The fully endogenous growth models allow for an illuminating combination of education and innovation as the two most important in-line engines of economic growth (e.g. Arnold [10] , Strulik [11] , and Stadler [12] [13] ).

Due to the convincing explanatory power with respect to the stochastic innovation dynamics in specific industries as well as with respect to the growth dynamics in the aggregate economy, quality-ladder models of all three generations have been usefully applied to the new trade theory in order to analyze R & D-based growth and trade in the global economy. Two classes of open-economy quality-ladder models can be distinguished. A large part of these models is based on the North-South setting where the world economy consists of the developed countries (or regions) in the North on the one hand, and the developing countries (or regions) in the South on the other hand. This framework is particularly adequate to study international product cycles driven by stochastic sequences of innovations in the North and imitations in the South (e.g. the survey by Stadler [14] ).

The other class of models deals in a complementary sense with the North-North setting where the world economy consists of two developed countries (or regions). This framework is extremely appropriate to study patterns of trade between similar countries and the effects of trade restriction or liberalization. While Grossman [15] and Grossman and Helpman [1] have prominently integrated the first-generation quality-ladder model into the theory of dynamic comparative advantage, Dinopoulos and Segerstrom [16] [17] have been among the first to apply second-generation quality-ladder models to the new growth theory. Until today, however, only few quality-ladder models of the second generation and, to the best of our knowledge, no fully endogenous quality-ladder model of the third generation are discussed in this growing literature so far. The present paper aims to fill this gap. The idea is to integrate a fully endogenous quality-ladder model into a North-North trade framework in order to analyze the influence of relative factor endowments, transport costs and barriers to entry in foreign markets on the dynamics of innovation and growth.

The paper is organized as follows. Section 2 presents an asymmetric quality-ladder model of education, R & D-based growth and North-North trade. Section 3 considers the role of iceberg transport costs. Section 4 studies the role of imitation and barriers to entry in foreign markets. Section 5 summarizes and concludes.

2. Education, R & D-Based Growth, and North-North Trade

We consider a global economy consisting of two developed countries, the home (H) and the foreign (F) country. The world is populated by a fixed measure of worker-households in the home country, 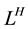, and in the foreign country,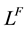. Each household is endowed with one unit of labor and can accumulate its human capital by education. Education and accumulation of human capital do not differ between the countries. However, a different initial value of households’ human capital can easily be captured by different labor endowments without loss of generality.

2.1. Households

In both countries, households maximize their discounted utility

(2.1)

where 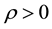is the common subjective discount rate and

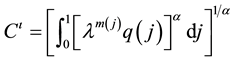(2.2)

is a quality-augmented CES consumption index, where denotes the quantity consumed of product variety j indexed on the continuous interval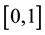, 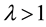is the given size of a single quality innovation, and is the number of innovations in industry 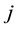realized up to the present. The parameter measures the heterogeneity of available consumer products and 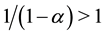is the elasticity of substitution.

At each point in time, households allocate their income

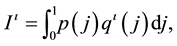
taking the product prices 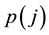as given. The solution to this across-industry maximization problem yields the individual demand functions

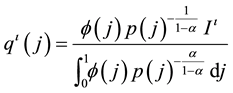(2.3)

for all product varieties j, where is a measure of product j’s quality level. The consumption index (2.2) can be expressed by definition as

(2.4)

where is the quality-adjusted price index of the consumer products.

Each household supplies human capital H to production, R & D, and education. When the share of human capital is devoted to production and R & D in exchange for a wage payment, the dynamic budget constraint reads

(2.5)

where denotes the value of asset holdings, r is the interest rate and is the wage rate for human capital where the wage rate in the foreign country is normalized to. The remaining share of human capital is devoted to education. As a consequence, human capital accumulates according to the motion equation

(2.6)

where denotes the effectiveness of the educational system and is the depreciation rate of human capital. Each household maximizes its discounted utility (2.1), given (2.4), subject to the dynamic budget constraint (2.5) and the human-capital accumulation (2.6). The solution to this dynamic maximization problem yields the well-known differential equation of consumer spending

where the country index is omitted for brevity. In addition, steady-state growth imposes

(2.7)

such that the time path of consumer spending in both countries is given by

(2.8)

Furthermore, in a steady-state equilibrium the growth rates of consumer spending and human capital must coincide. It immediately follows from (2.6) and (2.8) that and

(2.9)

Thus, the growth rates of human capital and consumer spending depend positively on the effectiveness of education but negatively on the depreciation and discount rates and. This relationship reflects the basic growth mechanism as emphasized by Lucas [9] . The larger the effectiveness of education, the more human capital is devoted to education, going along with faster growth.

2.2. The Product Markets

All consumer goods are manufactured with human capital as single input. One unit of human capital LH pro- duces one unit of output, regardless of the industry and the quality level. Therefore, each firm has a constant marginal cost which is equal to the wage rate. The price-setting behavior of the quality leaders depends on whether innovations are drastic or not. In this paper, we assume that innovations are non-drastic such that quality leaders charge the limit prices.

According to the individual demand functions (2.3), all quality leaders in the home country realize the flow of profits

(2.10)

and all quality leaders in the foreign country realize the flow of profits

(2.11)

These profits are equal only if the wage rates and, hence, the product prices in the two countries coincide.

2.3. R & D Races and the Stock Markets

The quality of consumer products is sequentially upgraded by vertical product innovations. Every industry is characterized by a symmetric quality ladder where each innovation provides a quality level, times higher than the previous one. While quality leaders have no incentive to invest in R & D targeted to the own products, challenger firms of both countries participate in stochastic R & D races and succeed in realizing the next innovation in industry j with probability. Thus the number of innovations in each industry j follows a Poisson process with the aggregate arrival rate, where the country-specific innovation rates of home and foreign firms are given by

(2.12)

They are assumed to depend proportionally on the human capital devoted to R & D in industry j. The inverse of the parameter relates the productivity of workers in R & D relative to their productivity in production. The term in the denominator indicates a negative externality of the quality level reached so far. According to (2.12), a challenger firm i which devotes units of human capital to R & D at a cost of for an infinitesimal time interval dt attains the stock-market value with prob-

ability. Stock markets are global. Each firm engaged in R & D issues equity claims

that pay nothing if the research fails but pay the flow of profits if the firm wins the R & D race. Free entry into each R & D race implies such that

(2.13)

where the quality-level index is omitted for brevity. Since the quality level is constant during every race and only jumping up to whenever an innovation occurs, it follows that the stock-market values and are also constant during each R & D race.

Absence of arbitrage opportunities implies that the expected return on equities of innovators must equal the return on an equal size investment in a riskless bond, i.e.

(2.14)

and

(2.15)

where the expected rate of return on equities of innovators consists of the dividend rate as expressed in (2.7) and the risk of losing the dividends due to another firm’s innovation, i.e. the sum of the arrival rates and.

By substituting (2.7), (2.10), (2.11), and (2.13), we obtain the no-arbitrage condition

where and. It follows that in a steady-state equilibrium,

, and such that the no-arbitrage condition simplifies to

(2.16)

Since there is a continuum of industries and the returns from participating in R & D races are independently distributed across firms and industries, each household investor minimizes risk by holding a diversified portfolio of stocks.

2.4. Product Dynamics and Quality Growth

At each point in time, a measure of H-industries has home quality leaders and a measure of F-industries has foreign quality leaders whereby. As is illustrated in Figure 1, the manufacturing of each product switches randomly across the home and foreign countries with transition probabilities depending on the Poisson arrival rates associated with the R & D investment of firms in both countries.

For the measures of and to remain constant in the steady-state equilibrium, the outflow of firms from the H-industries must be equal to the inflow, that is,. This implies

(2.17)

If the aggregate innovation rate of home firms is higher than the aggregate innovation rate of foreign firms, then the home country is characterized by a higher market share and vice versa.

The average quality of all available top-of-the-line consumer products is. The qual-

ity of each product j jumps up from to whenever an innovation occurs. Since the countries’ aggregate innovation rates are equal across industries, the time derivative of average quality is

such that the growth rate

(2.18)

depends proportionally on the aggregate innovation rate of all firms in the world.

The quality index can be decomposed into, where the aggregate quality of the home firms’ products is

and the aggregate quality of the foreign firms’ products is

The time derivatives are

and

and imply the growth rates

and

These growth rates are constant over time only if and thus

(2.19)

Dividing the quality indices by the market shares as determined in (2.17) gives

The average quality of products manufactured by the firms in both countries is equal, regardless of the factor endowment.

2.5. The Labor Markets

The labor markets of both countries are perfectly competitive. Workers can move freely across firms and sectors within each country but not across countries. As was shown above, in both countries the share of workers’ human capital is devoted to education. The remaining share of human capital is employed either in production or in R & D. It follows from the individual demand functions (2.3) that aggregate demand for human capital in the production sector is

and from (2.12) that the aggregate demand in the research sector amounts to

Thus, full employment of workers in the home country implies

(2.20)

and the full employment of workers in the foreign country implies

(2.21)

Substituting for from (2.16) yields

(2.22)

and

(2.23)

It follows from (2.22) and (2.23) that and, hence,

(2.24)

The country-specific innovation rates depend on the countries’ relative endowment with labor.

2.6. Factor Endowment, Innovation, and Growth

We are now able to solve the model for a steady-state growth path as an equilibrium time path along which all endogenous aggregate variables grow at a constant rate. We conclude from (2.9), (2.18), (2.20) and (2.21) that

The global steady-state innovation rate is therefore determined by

By substituting this expression into (2.24), we obtain the country-specific innovation rates

which depend not only on the effectiveness of education but also on the relative size of a country. This “relative scale effect” diminishes at the global level.

The country-specific consumption index (2.4) reads

and grows in both countries at the scale-invariant rate

which can be decomposed into quantity growth at rate and quality growth at rate.

In contrast to the quality-ladder models of the first and second generations, the steady-state growth rate neither depends on the worker population as in the scale-variant growth models nor on the population growth rate as in the semi-endogenous growth models. Instead, economic growth is endogenously explained in terms of educational and technological conditions. The realization of innovations becomes progressively more difficult as the quality levels climb up the ladders, but researchers compensate for this deterioration of technological opportunities by continuously raising their human capital. Education and innovation are closely related to each other and appear as in-line engines of economic growth.

3. Transport Costs and Trade Liberalization

Trade is not as free as assumed in the previous model. Instead, it is costly for firms to trade consumer goods across countries’ borders. Dinopoulos and Segerstrom [16] [17] have extended the Grossman and Helpman [1] model of North-North trade to a semi-endogenous growth model of the second generation and analyze the role of trade costs. In their model, the single driving force for innovation and growth is a positive rate of world- population growth which is not only assumed to be time-invariant, but also exogenously given and identical in both countries. Since population growth rates in most developed countries decline over time and are even negative in some countries, this growth mechanism is at least fragile. We therefore modify this approach by assuming a continuous process of workers’ skill acquisition in order to replace exogenous population growth by endogenous human-capital accumulation. We do not, however, account for heterogeneity of households, resulting in unskilled and skilled labor as two different factors of production.

3.1. The Product Markets

To keep the model simple, we use the symmetric version of the quality-ladder model as introduced in the previous section to serve a basic scenario for analyzing the influence of trade costs between the two structurally identical countries. While Dinopoulos and Segerstrom [16] [17] assume costs in terms of contingent tariffs, we follow Segerstrom [18] and replace tariffs by iceberg transport costs. An exporter needs to produce and export units of a top-of-the-line good in order for one unit to arrive at the foreign destination.

If we normalize the common wage rate to, the unit cost of a quality leader serving the home market is 1 and the unit cost of a quality leader serving the foreign market is. Since innovations are assumed to be non-drastic (i.e.), the local quality leaders charge the limit price at home. Assuming that, the exporting quality leaders charge the same price abroad1. Due to this symmetry, the individual demand functions (2.3) simplify to

(3.1)

This gives a quality leader’s flow of profit from selling at home and from selling abroad. As a whole, each quality leader realizes the profit flow

(3.2)

Trade restrictions, measured by the transport-cost parameter, reduce profits from exporting products. Conversely, trade liberalization, measured by a reduction of the transport costs, increases profits from exporting and thus provides a stronger incentive for challengers to engage in innovative activities.

3.2. The Stock and Labor Markets

The innovation rate, targeted at any industry j, is again given by

(3.3)

such that free entry into each R & D race implies that the stock-market value of a quality leader is

(3.4)

Taking into account (2.7), we obtain the no-arbitrage conditions

Substituting (3.2) and (3.4) yields

(3.5)

where.

In both countries the share of workers’ human capital is devoted to education. The remaining share of human capital is employed either in production or in research. It follows from (3.1) and the iceberg specification of transport cost that the aggregate demand for human capital in the production sector is

and from (3.3) that the aggregate demand in the research sector is

Full employment of workers in both countries implies

(3.6)

Substituting for IL from (3.5) yields

(3.7)

This condition can now be used to analyze the steady-state growth equilibrium.

3.3. The Steady-State Growth Equilibrium

In the symmetric balanced-growth equilibrium, (2.9) and (2.18) imply that

The country-specific innovation rates in each industry as well as in the aggregate are therefore determined by

(3.8)

and depend on educational and technological conditions but not on the transport costs. The consumption index grows in both countries at the scale-invariant rate

where education and innovation are again the in-line engines of economic growth.

3.4. Trade Liberalization and Innovation Dynamics

We now consider a certain point in time where a trade-liberalization measure occurs that takes the form of a permanent reduction in the transport costs. A comparative-static analysis of (3.7), given the long-run innovation rate h, shows that

Trade liberalization therefore induces an increase in the quality index. Since neither human capital LH nor the quality index can increase discontinuously, it is obvious from (3.7) that the innovation rates h have to jump up temporarily. A cluster of innovations across industries occurs since the pace of technological change in all industries accelerates. In response to the higher innovation rates, the quality index grows at a higher rate. This in turn leads to a declining adjustment path of the innovation rate which converges back to the steady-state value (3.8). We can thus conclude that a trade liberalization leads to a temporary increase in the global innovation rates in each industry and, hence, promotes technological change.

4. Barriers to Entry in Foreign Markets

Transport costs are not the only barrier to trade. There is convincing empirical evidence that some firms do export while others do not. In a seminal paper, Melitz [19] has developed a general-equilibrium model of international trade that can account for this evidence. In his model, each firm has to incur a fixed cost to enter an export market. The decision to export depends on the firms’ productivity. Only the more productive firms export, while less productive firms only produce for the home market. Haruyama and Zhao [20] have integrated the Melitz mechanism into first- and second-generation quality-ladder models of North-North trade. Recently, Segerstrom and Stepanok [21] have presented an illuminating semi-endogenous growth model of North-North trade which introduces an alternative and even more convincing explanation for the leading firms’ export behavior by pointing out the cost of export adaptation. They analyze product dynamics when firms invest not only in R & D to innovate but also to adapt export. Similar as with innovation, it takes time for firms to learn how to export. We extend a modified version of their approach to a fully endogenous quality-ladder model by replacing exogenous population growth by the demonstrated mechanism of endogenous human-capital accumulation. As a result of this modification, the pace of learning how to enter foreign markets depends on the education and qualification of the workers which are engaged in the adaptation of export.

The innovation process is modeled as before. Challenger firms participate in R & D races in order to invent higher-quality products. The first firm to succeed in developing the next higher quality product in an industry is granted a patent and takes over the local market from the previous quality leader. At the same time, competitive fringe firms in the foreign country imitate without any cost and take over the production abroad. Production by the foreign imitating firms continues until the new quality leader in the home country has learned how to export and to take over the foreign market, too.

The model is solved for a steady-state equilibrium where half of all products originate from the home and the other half from the foreign country. Home firms do not improve the quality of products originating from the foreign country and vice versa. Furthermore, it is assumed that even exporting leaders have no incentive to improve the quality of their own products.

4.1. The Product Markets

When the common wage rate is normalized to, quality leaders charge the limit price at home and abroad, whereas the imitating firms all charge the Bertrand price. It follows from the individual demand functions (2.3) that quality leaders earn the flow of profits from selling locally

(4.1)

and the flow of profits from exporting

(4.2)

Due to Bertrand competition, imitating firms realize no profits, that is.

4.2. Innovation and Export Adaptation

Following Segerstrom and Stepanok [21] we assume that there are two different types of R & D activities. First, challenger firms invest in R & D to develop higher-quality products. As before the rate of innovation, targeted at industry j, is

(4.3)

Second, quality leaders which only produce for the local market invest in R & D to learn how to export, i.e. to adapt the higher-quality products to the less familiar markets in the foreign country. Non-exporting quality leaders invest units of human capital in such an adaptation technology to become exporters with the arrival rate

(4.4)

where the inverse of is a (relative) productivity parameter and measures the degree of decreasing returns to R & D expenditures. The quality parameter in the denominator indicates that it becomes progressively more difficult to adapt a more advanced product to a foreign market.

4.3. The Stock Markets

According to (3.3), the stock-market value of a non-exporting local quality leader is

(4.5)

Using (4.1) and (4.4), the Bellman equation for non-exporting leaders can be written as

(4.6)

where is the stock-market value of an exporting quality leader. Maximization over yields the first-order condition

(4.7)

Substituting (4.7) back into (4.6) to eliminate and using (4.5) and (2.7) yields

(4.8)

where and. The Bellman equation for an exporting leader is

(4.9)

where its stock-market value can be derived from (4.5) and (4.7) as

(4.10)

Substituting (4.1), (4.2), and (4.10) into (4.9) and taking into account (2.7) gives

(4.11)

This expression can be substituted into (4.8) to obtain the no-arbitrage condition

(4.12)

which determines the export adaptation rates of quality leaders, given the long-run innovation rates.

4.4. Product Dynamics

There are four types of firms that sell the products available in a country: home leaders with a measure of HL-industries which sell their products only in the local market, home leaders with a measure of HE-industries which additionally export their products, foreign exporters with a measure of FE-industries, and home Bertrand firms with a measure of HB-industries, where. The corresponding condition for the foreign country is. Home and foreign challenger firms realize innovations with the arrival rates and, and home and foreign quality leaders succeed in adapting export to the consumers abroad with the arrival rates and. Figure 2 illustrates the dynamics in detail.

Due to the assumed symmetry across countries, the share of product varieties produced by home exporters equals the share of product varieties produced by foreign exporters, that is,. Further more, half of all product varieties are produced by home leaders at home and half of all product varieties are produced by foreign leaders abroad such that also holds. Home production covers a measure of industries, consisting of the (H)E-industries, (H)L-industries, and (H)B-industries, where the index letter H can be omitted for brevity.

For the world market shares of exporting and of non-exporting firms to remain constant in the steady-state equilibrium, the outflow of firms from the L-industries must be equal to the inflow, that is, , where and. This implies

(4.13)

An increase in the innovation rates leads to a greater market share of exporting leaders and to lower market shares of non-exporting quality leaders and imitators.

In both countries, the quality index of all available products can be decomposed into, where the aggregate quality of the exporting firms’ products is

the aggregate quality of the non-exporting domestic firms’ products is

and the aggregate quality of the domestic Bertrand firms’ products is

The time derivatives are

and

It can be shown that the growth rates of these quality indices are equal only if

and

Taking into account the market shares (4.13), this implies

indicating that the average quality of the products manufactured by non-exporting quality leaders is higher than the average quality of products manufactured by the exporting quality leaders which in turn is higher than the average quality of products manufactured by the imitating Bertrand firms.

4.5. The Labor Markets and the Steady-State Growth Equilibrium

In both countries the share of workers’ human capital is devoted to education. The remaining share of human capital is employed either in production or in R & D to innovate or in R & D to adapt export. Full employment of workers in both countries implies

(4.14)

Substituting (4.11) and taking into account that, due to the modified assumptions in this section, in (2.18), we can conclude from (2.9) and the labor-market clearing condition that balanced growth path implies

Therefore, the innovation rates in specific industries as well as in the aggregate are determined by

and thus depend again on the educational and technological conditions. As in the previous models the consumer index grows at the scale-invariant rate

with education and innovation as the two in-line engines of economic growth.

4.6. Trade Liberalization and Export Adaptation

Let us again consider a certain point in time where a trade-liberalization measure occurs that takes the form of a permanent reduction in the transport costs. Having solved for the steady-state innovation rate, we can use (4.12) to determine the export adaptation rate. A comparative-static analysis shows that

When barriers to entry in foreign markets are reduced, export becomes more profitable. Local quality leaders invest more in export adaptation such that the share of exporting firms increases.

The higher rate of export adaptation reduces the average length of an international product cycle, since the expression indicates how long, on average, a product is manufactured by imitating firms in the foreign country before being taken over by the new quality leader in the home country which has successfully learned how to export.

5. Summary and Conclusion

We present a class of quality-ladder models of education, innovation and export adaptation to explain the evolutionary dynamics of industries, economic growth, and international trade. Semi-endogenous quality-ladder models have accomplished a valuable task by removing the scale effect present in quality-ladder models of the first generation. A shortcoming of these non-scale models is, however, that the innovation and per-capita growth rates depend proportionally on population growth. Without population growth these models predict a stationary equilibrium without innovation and growth.

We offer an alternative mechanism of non-scale growth by relying on the education and human-capital accumulation of workers. Education has not only a direct effect on economic growth but also an indirect effect via an acceleration of the innovation and export adaptation processes. The effectiveness of the educational system is therefore most important for industry evolution, growth dynamics, and trade patterns. The scale effect is eliminated by the assumption that the realization of innovation and export adaptation becomes more difficult as the quality levels of products increase, but this deterioration of innovation and export opportunities is compensated by an improvement of the workers’ human capital.

The industry dynamics is generated by innovation and export adaptation. Trade liberalization leads to a temporary increase in the innovation rates and to a permanent increase in the export adaptation rates. In addition, the country-specific innovation rates are permanently increasing in a country’s relative endowment with labor.

As is well-known, Northern firms not only engage in innovation and export adaptation, but also in transferring technology into the less developed South, while Southern firms engage in imitative activities to copy the advanced technologies (e.g. Dinopoulos and Segerstrom [22] ). This evidence calls for the formulation of more general quality-ladder models being appropriate to study North-North as well as North-South trade within a single unified framework. This challenging task is left for future research.

Cite this paper

ManfredStadler, (2015) Education, Innovation and Growth in Quality-Ladder Models of North-North Trade. Modern Economy,06,1115-1128. doi: 10.4236/me.2015.610107

References