Received 18 January 2015; accepted 2 February 2015; published 5 February 2015

ABSTRACT

The Asian Steel Index (ASI) and Baltic Capsize Index (BCI)are important indices of the tramp shipping industry, where the BCI index reveals both the current tramp maritime transport fare and market status, while the ASI index is a composite index determined by the trade prices of steel. This paper first reviewed the literature of ASI and BCI indices to illustrate the current composition of the ASI index, as well as the BCI index in the present tramp maritime industry. A time-series analysis was then followed to construct the optimum model of ASI and BCI indices, and the results could be used as references for the maritime industry. According to the formulation of the multivariate time series models, the optimal mode was found to be VARMA (2,4), which meant that both the ASI and BCI indices would be affected by previous two series of data and have the error correction effect of 4 series. The results of this study confirm that ASI and BCI indices have impacts on each other, especially for the maritime zones of the BCI index, which are consistent with the status of China, a big country with high demands for raw steel material. Furthermore, this model allows the user to discover the impact multiplier of both indices. The construction of the model is hoped to help provide a reference for academics and businesses in the shipping industry.

Keywords:

BCI Index, ASI Index, Time-Series Analysis

1. Introduction

Shipping businesses can be divided into liner shipping and tramp shipping. Tramp shipping mainly focuses on delivering bulk cargo that are primarily composed of consumer goods and raw industrial materials like iron ore and coal, with no fixed schedules or timetables. The market of bulk cargo tramp shipping industry is close to a perfect competition market [1] [2] with high freight rate volatility, and the market price is dependent on the balance of supply and demand. Bulk tonnage demand is influenced by the global economic cycle, seasons, long holidays, climate and politics, while bulk tonnage supply is affected by the differences in the number of new ship orders and the breakdown of old ships. As a result, the freight rates changes as the balance of supply and demand fluctuates [3] . The difficulty of predicting and controlling the bulk cargo shipping market due to its volatility causes great risks and uncertainties for the businesses. The bulk cargo shipping industry requires a hedging trading platform, thus promotes the creation of the Baltic Dry Index (BDI).

The Baltic Freight Index (BFI), created in 1985, was the key bulk index used by the bulk cargo businesses to grasp the changes in freight rates for the bulk cargo market. It was, however, replaced by Baltic Dry Index (BDI) in 1999. Due to the differences in factors such as carrying capacity and characteristics of the maritime trade, the dry bulk shipping market is currently separated into four markets and each builds its own index, that is, Baltic Capsize Index (BCI), Baltic Panamax Index (BPI), Baltic Supermax Index (BSI) and Baltic Handy Size Index (BHSI). Each index represents different types of ships, including the market reference tariffs which are designated when signing for the shipping contracts with different routes. The economy of the bulk cargo shipping industry, there- fore, can be revealed from the changes in BDI [4] .

Steel is the main raw material required for the construction and heavy industries, and demand rises during times of economic growth, both globally and in particular regions, as reflected by fluctuations in steel price [5] . As the global economic climate continues to recover since 2003, the Chinese market has also built its reputation as an international manufacturer/world factory with annual growth in both gross domestic product and total industrial growth rate. The economic growth also brought strong demand for steel, leading to a gradual increase of iron ore imported into China [6] [7] . China’s economic growth rate rose to 9% in 2003, which meant that more raw material and energy resources were imported to support the requirements of infrastructure construction. This wave of demands for raw material continued until 2008, with both the Olympic Games and the Shanghai World Expo in 2010 contributing indirectly to its growth [8] . Furthermore, China’s investment into industries, especially the automotive industry, also generated strong demand for iron ore, reaching the peak in demand in recent years.

The prices of coal and iron ore are highly dependent on their relationship of supply and demand. Due to the rising demand of the market, China became a great importer of iron ore and coal [6] that allowed China to become a strong force in deciding the prices of coal and iron ore. This force changes with policy, production and volume of imports and exports, thus being able to control the price on the international market and make the price of steel experience stronger and more intense fluctuations. Its influence is not limited by region but also interactions with the entire Asiatic region, causing the international steel price to fluctuate along with it. Since steel price is one of the important elements in determining the global economy, many experts and academics are devoted in researching the long-term and short-term relationships in different areas [8] . The trends of the overall economy can be observed in the long-term studies, while the short-term research can reveal the investors’ concerns in dynamism. Apart from the mutual influence of different areas, furthermore, changes in policy, trade freedom or the ruling power of a region could also be factors that influence the overall changes in steel price.

This study aims to explore the relationship between BCI index and ASI index through conducting empirical research using BCI index and ASI index as variables to determine the direction of causality, their roles in influencing each other and in which way, whether the relationship is one-way or two-way, and whether there is a long-term link between the two indices. The results from the study could be used for investors as a reference to improve the effect of hedging in times of fluctuating BCI and ASI indices, and benefit the investors in making the most favorable decisions.

2. Literature Review

The demand for steel has been growing since 2000 and had brought up the demand of other raw materials along with it, especially for iron ore, coal and scrap metal. The close relationship between BCI and steel price can be seen from the BCI index of the routes and cargo. The vessels in BCI market are 172,000 DWT, not over 10 years of age and 190,000 cbm grain maximum. They principally transport iron ores and coal with a capacity of 60%, and cannot pass through the Panama Canal. The trialed route on March 1^st, 1993 was formed by seven voyage charters and four time charters. Since the release of BCI in April 26^th, 1999, it has been amended and adjusted many times, and the existing routes and weighting of BCI freight index are shown in Table 1. The main cargo for C2, C3 and C5 is iron ores with a weighting of 40%; for C4, C7 and C12, the main cargo is coal with a weighting of 20%; while C8-C11 are time charters and has a weighting of 40%. The table exhibits the high proportion of iron ores in BCI shipping (Baltic Exchange, 2011) [9] .

Affected by the rapid recovery of the global economy, the demand for steel consumption surged. China’s crude steel output continued to grow and caused the steel factories in various regions of China to rapidly increase iron ore imports [6] [7] . Due to the demand for mineral ores exceeding supply, mining companies decided to hike 90% - 100% of the contracts by nearly doubling the original price, that cause China to turn to other raw material supplying countries, such as India, Ukraine, Venezuela and Russia. These countries, however, could not meet the strong demand from China, and China had to resort to negotiating new contracts with CVRD, Riotinto, and BHP Billiton to meet its requirements. As a result, the BCI index fluctuated dramatically in this stage. The price of the ore is highly dependent on the relationship of supply and demand, and since China had a strong demand for ores due to its status as the international manufacturer/world factory, China became a strong force in deciding the prices of coal and iron ores [8] . This power changing with policy and volume of import and export has great control over the price on the international market, resulting in greater volatility in the price of steel. Its influence is not limited by region but also interactions with the entire Asiatic region [10] .

The global steel price index was lower than 80 points in 2001, and many businesses went bankrupt due to mismanagement. Some parts of the steel industry preferred to go through industrial restructuring and failed due to the poor market sentiment. With economic recovery, steel price has risen dramatically. The global steel price index had changed by 4.27 times from the lowest point of 68.5 on 11^th January 2002 to the highest point of 292.8 on 8^th August 2008. This change is especially clear in Asia [7] . Through the pulling effect of raw material demands, the BDI index had escalated to tens of thousands of points [7] . In recent years, increased volatility in steel prices is also affecting many related industries. Under the Chinese’s incessant growing demand for ores, the volume of global dry bulk cargo shipped is still high, but this is set to encounter some risks after a continually rising market over a period of time. Moreover, the shipping market is a typical cyclical industry [5] . If relationship between the freight index and steel index could be apprehended, a complete hedging strategy could be devised to reduce the risks and increase profits in the international tramp shipping market where risks and uncertainty run high.

Source: Baltic exchange (2011) [9] .

The price of coal has also undergone tremendous growth since 2000 from US $47 per ton in 2003 to US $300 per ton in 2008 [11] , with a rate of increase of 6.38 times. In October 2011, the traditional fourth season of the bulk shipping market enters its peak season. The price of iron ore imported by China was lower than the contracted price and caused increased demand of shipments from China to Australia, thus driving up the BDI index [7] . Steel refining requires a large quantity of coal and iron ores. Accordingly, the costs of obtaining the raw materials have a great influence on the final production price of steel.

In 2003, China’s economic growth rate rose to 9%. To support this wave of infrastructural needs, China had to import more raw material and energy to satisfy these demands. This surge of demand in raw material continued until the 2008 Olympics, on top of further demands for iron ore and coal from the automotive and other industries have received heavy investments. The demand for iron ore and coal from China caused the ASI steel price index jumped up to 100 - 200 points from fluctuating below 100 points from after 2003. This meant that the steel market had been driven to a new market level by the rise of the Chinese economy, and that the price of steel in China had increasingly important influence on the global steel prices. Bin [10] tried to analyze the influential relationship between the Chinese steel price and the global steel price objectively. For the two series, they would have different changes in the short term. Bin’s study discovered that in the early stages, the Chinese steel price had greater influence on itself and less influence on the global steel price; for the global steel price in the early stages, it had a long-term but small influence on itself, while greatly influencing the Chinese steel price.

Broadly speaking, the Chinese steel price has greater influential power on the global steel price, thus allowing it to become a key factor for predicting the global steel price. The global steel price, however, has less significant influence on the Chinese steel price. This is due to the global steel price indices can be branched into North American steel price index, European steel price index and the Asian steel price index, meaning that there is only an one-way relationship between the two. As for the relationship between the Chinese steel price and the Taiwanese steel price, the study by Yau et al. [12] found both to be in an endogenous structural transformation point, where the price in Taiwan from April 2001 and China from February 2002 had undergone almost identical trends. In further study with structural changes in GH (Gregory and Hansen), the research found the steel price in China and Taiwan have no long-term equilibrium relationships. This echoed the statement produced by Lin and Wu [13] , where they suggested that the time when China had successfully appointed to become an Olympic host should be used as a watershed/judging point for whether or not there was a relationship between the Chinese and Taiwanese steel price. However, the Granger causality test found that in the short-term, a two-way causal relationship of mutual feedback existed between the Chinese and Taiwanese steel prices. This also meant that both prices had mutual traction, especially on the import and export of iron ore and steel products. Accordingly, this study uses ASI and BCI index variables for analysis.

3. Methodology

Time series indicates a set of observations of the emergence of patterns in a chronological order, such as a continuous collection of data on seismic activity, rainfall, annual birth rate, and monthly sales of products [14] -[18] . This study uses BCI and ASI as series variables for analysis. In the analysis, it is not only a single variable that has to be considered, but for the interactions between multiple variables. Accordingly, it needs to construct a model for one set of time series, rather than for only a singular variable series. For example, Alizadeh [19] used a time-series model to demonstrate the relationship between crude oil futures and freights, while Papapetrou [20] used time-series model to study the connections between oil prices and real stock returns, interest rates, real economic activity and the employment rate in Greece. The relationship between variables could not be predicted during the construction of the model in terms of which was affecting the other, that is, we could not determine which the exogenous variable was and which the endogenous variable was. Therefore, it was essential to effectively construct a generalised vector time-series model, namely the Vector Autoregressive Moving-Average Model (VARMA) [16] [17] .

Time-series analysis is mainly used to help the researchers understand the causal relationships between different variables in a system. Time-series studies generally try to assess and predict the relationships between indices. As for the indices, the trends in their movement could change depending on current affairs and the economic climate. For this study, the influential relationship between ASI and BCI index is the main focus of the research.

Considering the series through the use of the Autoregressive Moving Average Model (ARMA) (Box and Jenkins, 1970), the series would likely have stable and random behaviour, thus promoting it into the VARMA model. The univariate variable used in the ARMA model is the BCI series 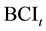(the same for Asia steel price series), and the stochastic differential equation model is shown below:

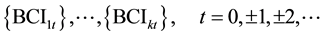
The vectors can be expressed as:

This time series can now be termed as K by K degree vectors.

Using the Baltic series univariate as, the stochastic differential equation of its ARMA 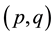model [21] would be:

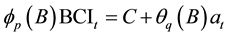
In the formula above,

B is the backward shift operator,

is the autoregressive parameter,

is the moving average parameter, and

C is the constant.

The matrix of the VARMA model can be re-written as the following formula:

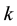B is the matrix polynomial of the backward shift operator, and are by 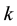matrix, 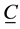is k by 1 fixed value vector, and is the random vibration vector of the normal distribution in an independent series, with an average of 0. VARMA model can be re-written as

, where.

In addition, we need to assume that the root of the polynomial determinants and fall outside of the unit circle. When the root of falls out of the unit circle, the series is stable; while when the root of falls below the unit circle, the number of series would become inversibility [16] [17] .

Assuming the final model is VARMA (1,1), could be simplified as:

, with all the elements of its matrix and vectors written as:

The parameters and can express how the -th series is influenced by series. Currently, only SAS software and Scientific Computing Associates (SCA) software can carry out the VARMA model analysis.

The Vector Autoregressive Moving Average Model (VARMA) takes all the related series to construct a dynamic model and analyze the results. Because the main aim of the time-series analysis is to understand the causal relationships between the variables, adding another related variable could make up the lack of explanation power with the pervious singular variable. VARMA can gain more understanding of the relationships between series, such as series are correlated, or a particular series could cause other series to develop, or discover their feedback relationships. Combining the ASI and BCI indices in the model reveals more information about the related series, and allows more efficiency in building the dynamic relationship between ASI and BCI indices, as well as improving the accuracy of the predictions [13] [16] [22] . To determine the VARMA model, this study uses the Smallest Canonical Correlation Analysis (SCAN) of the Partial Autoregression (PAR) matrix and Extend Cross Correlation Matrices (ECCM) [16] [22] , as proposed by Tiao and Box [21] . The SCAN graphics is used to define the best order of the VARMA model [17] [22] .

4. Empirical Analysis

4.1. Description of Data Types

This study collected data of the two variables, BCI and ASI, on a weekly basis from July 2007 to December 2011, with a total of 495 datasets. From observing the standard deviation of the two series, the degree of differences of the two variables can be assessed. BCI had a larger degree of dispersion, while ASI was less dispersed. The variable with the greater dispersion has more intense return volatility in comparison. The comparison of Figure 1 and Figure 2 revealed that the historical trends of BCI and ASI had a certain degree of relevance.

4.2. Unit Root Test

This article uses Augmented Dickey Fuller (ADF) unit root test to determine whether BCI and ASI are stationary or non-stationary series. Although many economy data such as product prices and currency supply are considered to be non-stationary series [23] . However, Granger and Newbold [15] found out when variables were in their non-stationary, the problem of Spurious Regression may occur. Accordingly, researchers using time-series analysis as a part of their studies must determine whether the variables are in a stationary. This study uses ADF unit root test to analyse BCI and ASI variables independently. The null hypothesis is that “BCI and ASI both have a unit root and are not stationary series”. Each series is independently tested from the first period, and using the smallest number of the AIC [24] as the optimal latter period. Those with more obvious trends and an intercept are chosen first, and if the ADF test value of their optimal period (lowest AIC) is no less than the critical value, their intercept would be selected to be tested. Then the ADF of the optimum period is assessed to make sure it is no less than the critical value, or the intercept would need to be removed before testing. If it remains in a non-stationary, the first-order difference is used to repeat the process above until the ADF value of the optimal period is lower than the critical value and in stationary. The hypotheses of the unit root test are as follows.

H₀: the non-stationary series has a unit root

H₁: the series is in stationary

Firstly, all the variables are made into their natural logarithm and the ADF unit root test is conducted. Table 2 and Table 3 compare the statistics and critical value of the unit root test for BDI and ASI. The ADF value for both variables, exhibited in Table 2, revealed that BCI and ASI showed no significance, thus the null hypothesis could not be rejected. Table 3 states the ADF unit root test results of the BCI and ASI indices after the first-order difference. It showed that the ADF values for both variables are less than the critical level of 1%. The results reveal that the statistical value and critical value of the Baltic capsize freight index and the Asian steel price after the first difference are both significant at the 1% significant level (statistical value is less than critical value). Therefore, the null hypothesis is rejected, which showed that the BCI and ASI series, after the first-order difference, is in stationary. That is, BCI and ASI both need to undergo the first-order differential before turning into the stationary.

4.3. The Structure of the VARMA Model

For the VARMA, the determination of the model orders is the most complicated procedure. The graphics of SCAN (Table 4) was used to determine the VARMA optimal model, and found that the VARMA (2,4) was the optimum for BCI and ASI series. VARMA (2,4) has fewer parameters than other alternative models and meet the requirements of simplicity as a model.

The aspect of model estimation is done using the Maximum Likelihood Method (MLE), and the results of VARMA (2,4) of BCI and ASI matrix are shown below.

Note: The critical values of the ADF unit root test at 1%, 5% and 10% significant level are presented as ^*, ^** and ^***, respectively.

Note: The critical values of the ADF unit root test at 1%, 5% and 10% significant level are presented as ^*, ^** and ^***, respectively.

Note: The suitable orders of the model are shown as “O”, the unsuitable orders of the model are shown as “X”.

The expansion of the ASI and BCI index matrices are shown below:

The formula above demonstrates that there is a correlation between the ASI index and BCI index. It exhibits that the current ASI is affected by the data of its past two periods as well as the second period BCI index. By adding the error correction effect of 4, such as the level of significance of 1%, we are able to discriminate between ASI and BCI indices and discover that ASI is more affected by the BCI index than being affected by itself. The current BCI is affected by its second period data. In this paper, there is empirical proof that ASI and BCI do have influence over each other. Examining the expanded matrix of the BCI and ASI indices at the 1% significant level, it is clear that the BCI index leads the ASI index, thus the causal relationship shows that the BCI index is the cause and the ASI is the effect.

5. Conclusions and Recommendations

The VARMA model was used by this study to understand the structure of the causal relationship between the ASI index and the BCI index. The results could be used to construct BCI freight cost interpretation and explanation for maritime shipping businesses and the model can be eventually used to estimate future tariffs. Overall, the results of this study are as follows.

1) According the hypothesis stated for this study, the results of the structural formula for the ASI index and BCI index showed that the ASI index is two periods ahead the BCI index and is leading towards a long-term equilibrium, making the BCI index the leading indicators of the ASI index.

2) From the analysis of the VARMA model at the 1% significant level, the ASI index had no significant relationship with some of the BCI parameters. Therefore, the BCI index is only affected by the unilateral feedback relationship caused by its lagging second period.

3) The VARMA theory demonstrated that the BCI index is the leading indicator of the ASI. Therefore, for the shipping companies or related investors, this study recommends using the BCI index to predict and interpret future steel rates. It is hoped that the results of this study would be able to provide investors and liner shipping companies a grasp of the relative relationship between the ASI index and the BCI index. Furthermore, when the liner shipping market is affected by seasonal fluctuations or poor market conditions, the BCI index could be used to predict the conditions of the shipping costs to develop investment strategies and avoid potential risks for shipping companies.

Whether the focus is on the theory or in practice, the use of the ASI index and BCI index for interpreting the freight costs is an important guide worthy of attention for the maritime shipping industry. The study also faced several limitations during the research process, but working with appropriate assumptions, the VARMA model could still be operated and produce useful reference values of the BCI index for the shipping companies. The limitations and difficulties faced by the study during its operation, as well as its corresponding solutions, are summarized as follows.

a) In reality, the composition of the shipping freight is not limited to the ASI index and the BCI index, but this study had only set ASI index and BIC index as the reference indices for the research. Other influential elements, such as oil prices, shipping company unions, and economic crisis could also influence the shipping freights. Presently, Asia is still the biggest importer of iron ores. With factors such as China being the second biggest economy in the world, the reference value of ASI would greatly increase in the future.

b) The data type used in this study for correlation analysis and estimations using the VARMA model has not considered the effects of seasonality. In order to overcome this problem, future research may consider the changes brought by seasonality, and the inclusion of this factor could improve the accuracy and rationality of the VARMA model.

c) Existing literature on the ASI index and the BCI index data base is still rare. Therefore, we would recommend associated academics and experts to participate in related research to improve the references and basis for future use.

d) This research only used two indices as research variables and used their causal behaviour to create estimations. Future research on related topics could also include other different indices for more dynamic assessments, and use their varied effects to explore and search for the common principles.

The results of this research is hoped to help investors and shipping companies to grasp the different possible outcomes and be able to be ahead in the shipping market, recognize the market freight cost fluctuations in advance, and develop investment strategies to avoid potential risks.

Acknowledgements

The author gratefully acknowledges the helpful comments and suggestions of the reviewers, which have improved the presentation. This research work was partially supported by the Ministry of Science and Technology of Taiwan, under the project number of 102-2410-H-309-013-.

References

NOTES

^*Corresponding author.