Wireless Engineering and Technology
Vol.2 No.3(2011), Article ID:5828,10 pages DOI:10.4236/wet.2011.23024
Speed-Sensitive Weighting Algorithm for Digital Beamforming of Adaptive Antenna Arrays
![]()
1Digital Communications Signal Processing Research Laboratory, Faculty of Electrical and Computer Engineering, Shahid Rajaee Teacher Training University, Tehran, Iran; 2Telecommunication Laboratory, School of Electrical and Information, University of Sydney, Sydney, Australia.
Email: sh_shirvani@srttu.edu, mahyar.shirvanimoghaddam@sydney.edu.au
Received March 1st, 2011; revised April 5th, 2011; accepted April 23rd, 2011.
Keywords: Beamforming, Adaptive Antenna Array, LMS, CM, Training-Based, Blind
ABSTRACT
One of the main objectives of adaptive antenna array processing is reducing the computational complexity and convergence time in a joint state. This article proposes a speed-sensitive adaptive algorithm for estimating the weights of smart antenna systems based on least mean squares (LMS) or constant modulus (CM) algorithms. According to the next estimated location as well as the source velocity, this novel proposed weighting algorithm selects those weights that have a higher effect on the radiation pattern and will then form the antenna pattern by only changing these weights. In this research, 3 versions of the new algorithm named as: Not-zero (Leaves half number of weights as it is the other half), Zero (Sets half number of weights to be zero and estimates other half), and Updating (Leaves half of weights unchanged and estimates other half in one phase and updates all weights in the next phase) are proposed. Through simulation of these 3 versions of speed-sensitive algorithms and comparing among conventional full weight LMS and CM algorithms, new LMS-based and CM-based algorithms have been finally proposed that offer reduced complexity and acceptable performance at different signal to noise ratios (SNRs). In this investigation, three channel scenarios are simulated which are as follows: pure noisy channel, channel with one interferer and channel with two interferers. In accordance with the simulation results, an appropriate algorithm based on weighting half number of array elements and updating all existing weights between two consecutive times to avoid error propagation effect has been proposed.
1. Introduction
In most communication systems, designers are faced with issues such as capacity shortage and increase of interferences in a joint state. Applying smart antennas in wireless communication systems can decrease these problems. Smart antenna systems use an antenna array with the ability to process the digital signal in the receiver port as well as the transmitter port based on an adaptive manner [1,2]. These systems have three major types; switched beam, fixed-beam, and adaptive array. In switched beam antenna array systems, some fixed radiation patterns with high resolution at specific predetermined directions are created. The essential goal of fixed beam methods is to locate the main lobe of the radiation pattern in the signal direction and set the radiation pattern to zero in the direction of interference signals [3]. In fixed-beam methods, statistically optimum weight vectors for beamforming can be calculated by Wiener’s solution. However, the asymptotic second-order statistics of the signal and the interference-plus-noise should be known, a priori. These statistics are usually not known but can be estimated from the available data via the ergodicity assumption, where time average equals ensemble average. For timevariant signal environments, such as wireless cellular communication systems, statistics change with time as the source and interferers move around the cell. As for time-variant signal propagation environments, a recursive update of the weight vector is required to track a moving mobile such that spatial filtering adaptively steers the main beam to the target mobile’s time-varying DOA, thus resulting in optimal transmission/reception of the desired signal. To solve the problem of time-varying statistics, weight vectors are typically determined by adaptive algorithms which adapt to the changing environment [4,5].
By changing the weights of an adaptive array, the radiation pattern can be formed and steered in the desired direction. There are two different types of adaptive weighting algorithm which are based on training sequences and blind estimation. Training based methods do not need to know the location of the source signal and will converge faster than blind algorithms. On the contrary, in blind methods, only the direction of arrival (DOA) of the main signal (source) is required and other information should be obtained from the received signal [6-9].
Reviewing recent research works on digital beamforming shows that the effect of the direction and velocity of the source has not been considered seriously. However, in cases where it has been used; calculations and computational complexity in the weighting step have increased.
Authors in [10] show that using an adaptive beamforming technique based on maximum likelihood estimation (MLE) can increase the robustness of algorithms against the effects of incorrect DOA estimation. The practical design of a smart antenna system based on DOA estimation and adaptive beamforming is the subject of [11]. In this paper, DOA estimation is based on multiple signal classification (MUSIC) algorithms and adaptive beamforming is achieved by using the LMS algorithm.
In [12], the performance of LMS and recursive least square (RLS) algorithms for smart antennas in a wideband of code division multiple access (W-CDMA) mobile communication environments are discussed. Furthermore, beamforming algorithms based on Normalized least mean square (NLMS) and matrix inversion (MI) are processed in [13]. In [14], a matrix inversion normalized least mean square (MI-NLMS) adaptive beamforming algorithm is described. Simulation results of this method show that the bit error rate (BER) improvement to be proportional to the number of antenna elements employed in the antenna array. The performance of constant modulus (CM), LMS, and RLS algorithms are discussed in [15] and a systematic comparison between them is obtained. In [16,17], the performance of blind adaptive beamforming algorithms for smart antennas in realistic environments with a constrained constant modulus (CCM) design criterion is described and used for deriving a RLS type optimization algorithm. In [18] the performance of different CCM-based adaptive beamforming algorithms has been compared.
In the present article, by using LMS and CM algorithms, a new method has been proposed that predicts the direction and velocity of source in a simple way. Compared to other algorithms and also previous research work being done relatively, it decreases the computational complexity.
The rest of this paper is organized as follows. In Section 2, some important notes about adaptive antenna array systems are illustrated and two well-known algorithms, LMS and CM, are discussed in detail. Section 3 introduces the new proposed speed-sensitive algorithm which is based on prediction of the next location of the source and reducing the complexity of weighting process about 50%. In addition to simulation assumptions and related flowcharts, simulation results of conventional LMS and CM as well as proposed ones are described in Section 4. Finally, Section 5 concludes this article.
2. Adaptive Antenna Array Systems
The main feature of antenna array is the ability to separate signals in space. Signal separation in space means adjusting the main lobe of the antenna in the direction of desired signal and its nulls in the direction of undesired signals [3]. Several adaptive algorithms can be used in such way that the weight vector adapts to the time-varying environment at each sample. As depicted in Figure 1, there are two major types of adaptive weighting algorithms, i.e., training-based methods and blind methods. In training-based methods, such as, LMS and RLS, one reference signal is required. In contrast, in blind methods, such as, CM, least squares (LS), decision directed (DD), and conjugate gradient (CG), only the DOA of the main signal is required and other information should be obtained from the received signal [19,20]. In this investigation, LMS and CM algorithms are considered to evaluate the performance of the new speed-sensitive beamforming proposed.
2.1. LMS Algorithm
LMS algorithm uses minimum mean square error (MMSE) criterion for weight estimation. In MMSE, if 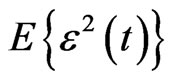 is considered as a function of w, then it has only one minimum. This minimum can be determined by solving the Wyner’s optimization equation. The most common method to solve this problem is the steepestdescent scheme that can be summarized as follows:
is considered as a function of w, then it has only one minimum. This minimum can be determined by solving the Wyner’s optimization equation. The most common method to solve this problem is the steepestdescent scheme that can be summarized as follows:
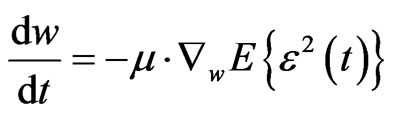 (1)
(1)
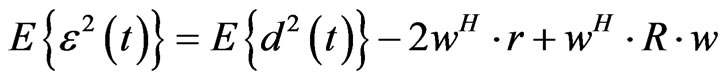 (2)
(2)
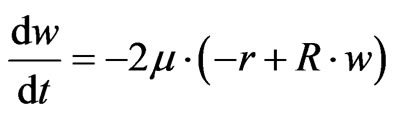 (3)
(3)
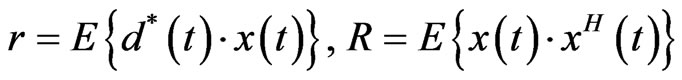 (4)
(4)
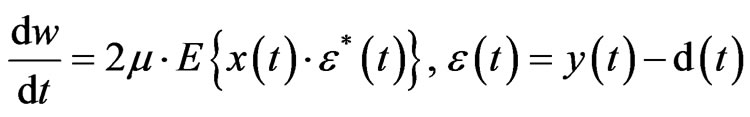 (5)
(5)
where 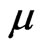 is a coefficient that determines the convergence speed of the algorithm,
is a coefficient that determines the convergence speed of the algorithm, 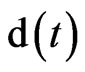 represents the reference signal, and H indicates Hermitian conjugate.
represents the reference signal, and H indicates Hermitian conjugate.

Figure 1. Adaptive array processing algorithms [3].
In (5), we use the real-time value instead of the average value. This simplification is shown in (6).
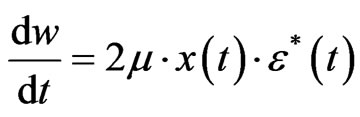 (6)
(6)
For discrete-time case, derivation can be substituted with subtraction as follows:
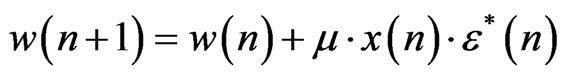 (7)
(7)
Equation (7) shows that using real-time approximation instead of expected value can lead to an iterative algorithm with simpler implementation. However, some notes should be considered about convergence speed [21]. In this research, considering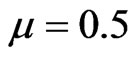 , when the temporal mean value of
, when the temporal mean value of 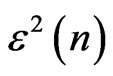 that is equal to
that is equal to 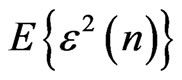 converges, the proper weights can be used for beamforming.
converges, the proper weights can be used for beamforming.
2.2. CM Algorithm
The CM algorithm uses a constant envelope feature of frequency and phase modulated signals such as frequency shift keying (FSK) or phase shift keying (PSK). By calculating this envelope, adaptive beamforming algorithm can be managed. CM algorithm uses a cost function, named as diffraction function of order p, and after minimization, its optimum weights can be obtained. The Godard’s cost function is shown in (8).
 (8)
(8)
where 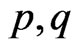 are equal to 1 or 2. Godard showed that if
are equal to 1 or 2. Godard showed that if 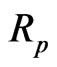 is defined as in (9), the slope of the cost function will be zero.
is defined as in (9), the slope of the cost function will be zero.
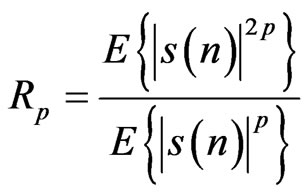 (9)
(9)
where 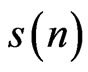 is the memoryless estimation of
is the memoryless estimation of 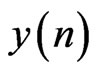 and then the estimation error is:
and then the estimation error is:
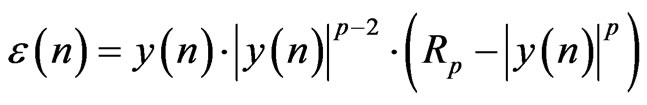 (10)
(10)
If we assume that , the cost function has the form as in (11):
, the cost function has the form as in (11):
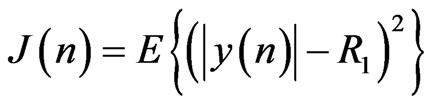 (11)
(11)
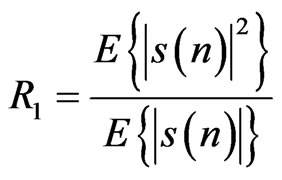 (12)
(12)
By rewriting the error signal in (10), (13) can be derived.
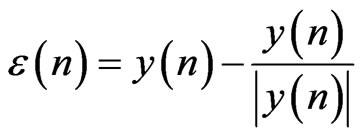 (13)
(13)
By updating the equation of weights we have the following updating equation:
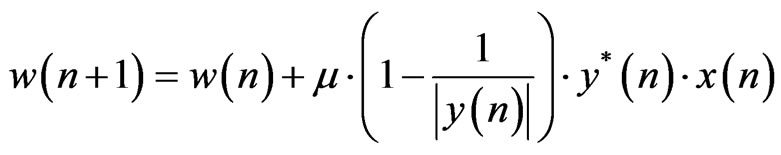 (14)
(14)
As mentioned in the LMS algorithm, in the CM algorithm with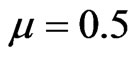 , when the temporal mean value of
, when the temporal mean value of 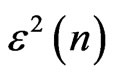 converges and has small variations, the proper weights can be used for beamforming.
converges and has small variations, the proper weights can be used for beamforming.
Despite slow convergence, CM algorithm is converged in most cases. It has been shown that the fastest convergence is obtained by using  [22].
[22].
3. New Proposed Speed-Sensitive Weighting Method
In our proposed algorithm, according to the direction and the velocity of the main source signal, the new location of user will be estimated. Then, instead of estimating all of the weights of the array antenna, some of them, in this investigation half of them will be calculated. In addition, according to the estimation of the new position of the source, the array weights will be changed and updated. By this simple estimation we can also speed up the DOA algorithm. The essential goals of these algorithms are to reduce the computational complexity and to speed up the weighting algorithm. Figure 2 shows the flowchart of the proposed new LMS-based/CM-based algorithm. After
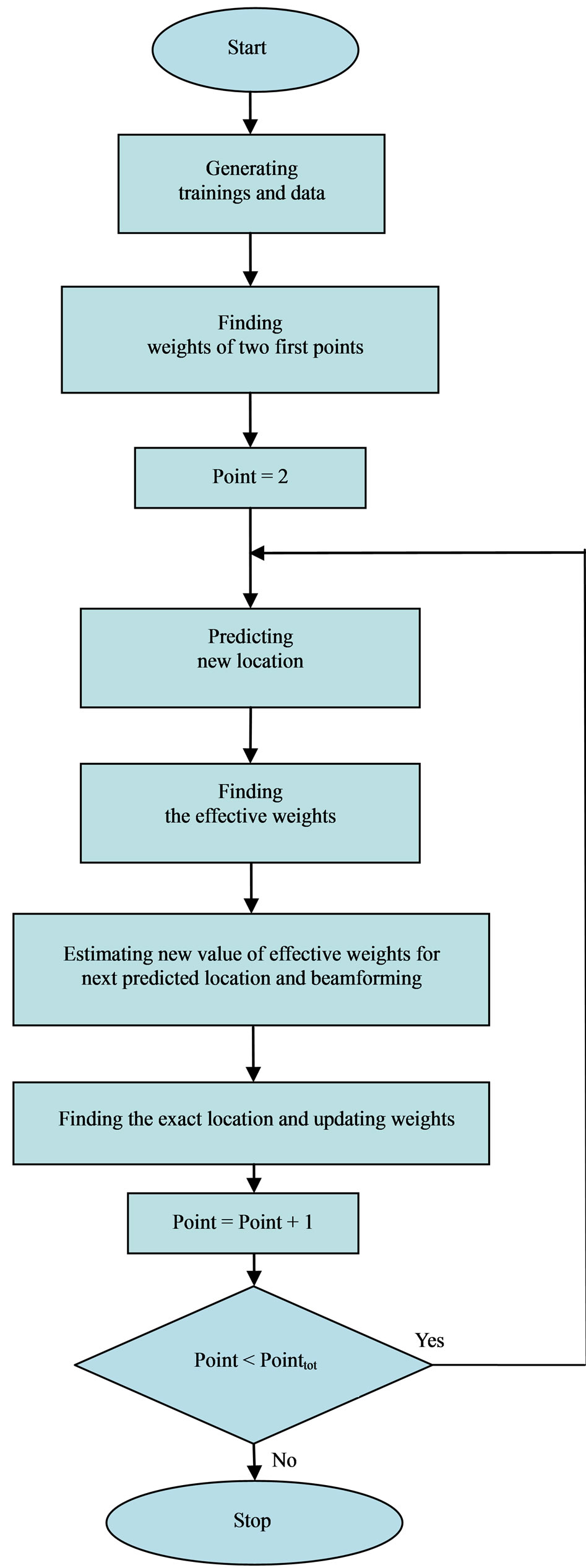
Figure 2. Flowchart of proposed speed-sensitive weighting algorithm.
obtaining the output signal, array weights should be updated. This updating is essential for error propagation avoidance and increasing the accuracy of the proposed method.
For weighting a uniform 8-element linear array (ULA), considered in this investigation, three versions of new method are provided as follows:
1) Changing 4 important weights but fixing 4 other ones (4W-Notzero);
2) Changing 4 important weights but setting 4 other ones to zero (4W-Zero);
3) Changing 4 important weights but updating all weights between two sampling point (4W-Updating).
Details of the steps of new proposed algorithm are illustrated below:
1) At first, the weighting algorithm (LMS or CM) is applied for the first two points and the direction of arrival in two points 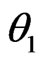 and
and 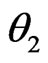 is determined and also proper weights are obtained. For example, in an 8-element uniform linear array,
is determined and also proper weights are obtained. For example, in an 8-element uniform linear array, 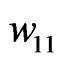 ,
, 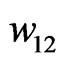 ,
, 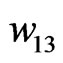 ,
, 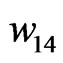 ,
, 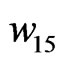 ,
, 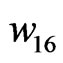 ,
,  ,
, 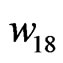 , and
, and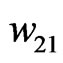 ,
, 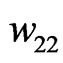 ,
, 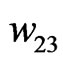 ,
, 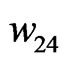 ,
, 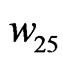 ,
, 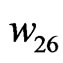 ,
, 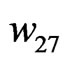 ,
, 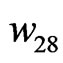 , are obtained.
, are obtained.
2) The next location of the source is predicted (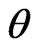 or
or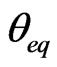 ) by using the previous locations of the source. The relative velocity has some effects on the value of the angular locations 1 and 2. In this research the direction of the source motion has been considered in the simulations. Figure 3 shows the two cases. If the source moves in parallel with the main axis of the array, according to (15) the new angular location can be found.
) by using the previous locations of the source. The relative velocity has some effects on the value of the angular locations 1 and 2. In this research the direction of the source motion has been considered in the simulations. Figure 3 shows the two cases. If the source moves in parallel with the main axis of the array, according to (15) the new angular location can be found.
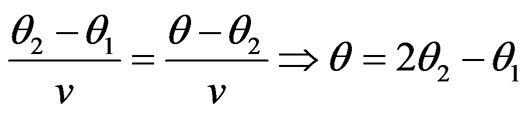 (15)
(15)
3) The effective weights are found and also the value of effective weights for the next predicted location of source are estimated.
4) The radiation pattern is formed according to the estimated weights in step 3.
5) The exact angular location (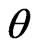 or
or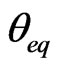 ) is found by using the LMS or CM algorithm and the weights are updated to avoid error propagation. The exact location is and new relative velocity of the source then determined.
) is found by using the LMS or CM algorithm and the weights are updated to avoid error propagation. The exact location is and new relative velocity of the source then determined.
6) Going to step 2 and doing the steps 2 to 6.
4. Simulation Results
In this section the numerical results of LMS and CM algorithms at different SNRs are proposed. For each method, the following scenarios are considered: noisy channel, channel with one interference signal in 0 degree, and channel with two interference signals in 0 and –40 degrees in both conventional and new proposed beamformers are shown.
Here, the accuracy of source angle detection, root mean square error (RMSE) and output signal to noise
 (a)
(a)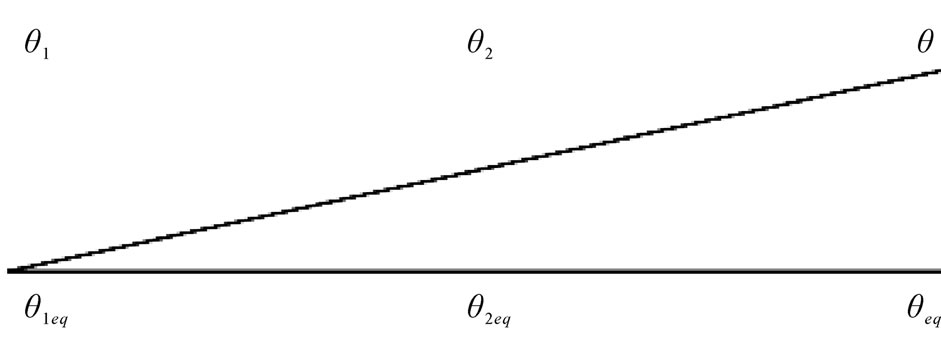 (b)
(b)
Figure 3. Movement path of the source respect to main axis of the array. (a) Parallel; (b) With nonzero angle.
plus interference ratio (SNIR) are the performance metrics. Different simulations have been done by a change in the angle of the source signal in the interval of [–80˚, 80˚]. The following three paths are considered: parallel to array, in the direction of nonzero angle with array, and random walk with constant velocity. In all simulations, the antenna array is an 8-element ULA, the average relative angular velocity is less than 5 degrees in a second and signals are modulated using minimum shift keying (MSK) constant envelope method. All simulations are done in MATLAB 7.5 package. As depicted in Figure 4, the number of iterations to access acceptable results is 1000.
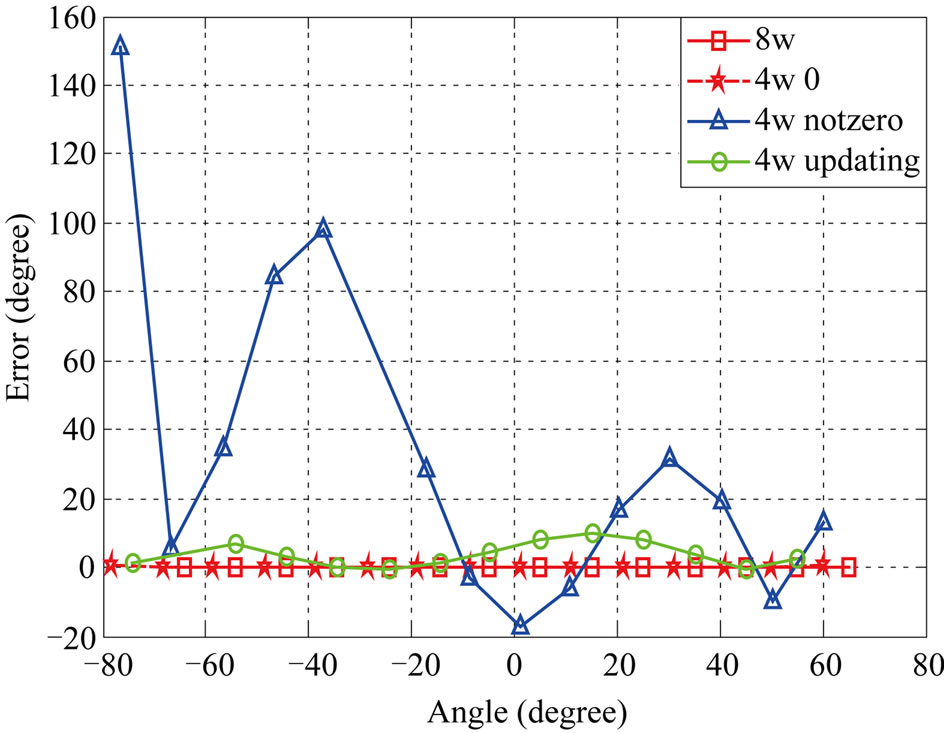
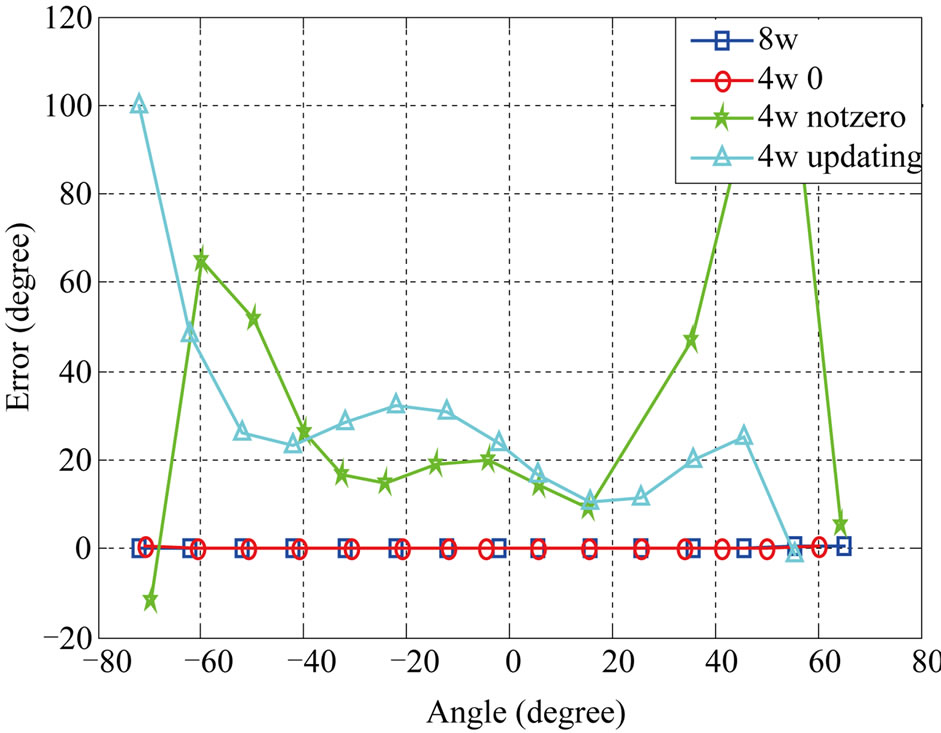
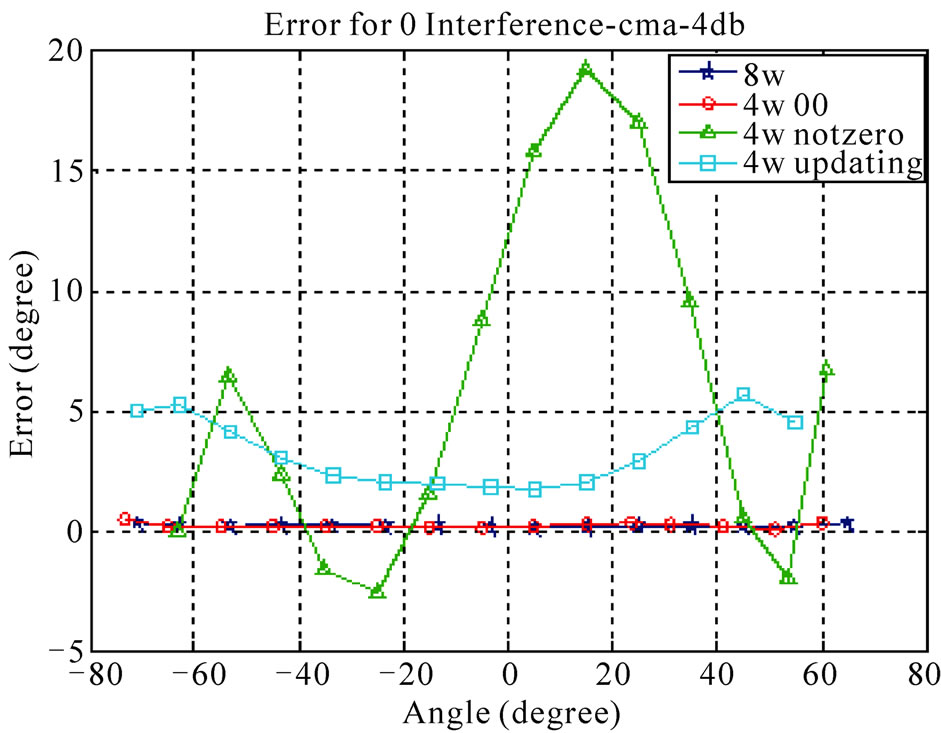
Simulation results show that the angular error of the proposed method is close to the ones of the conventional methods and acceptable SNIR will be obtained. Via an increase in the number of interferers the performance of both conventional and new LMS-based/CM-based algorithms is decreased. Figures 5-8 show the angular error of the proposed methods for 3 scenarios at low and high SNRs compared to conventional LMS-based and CMbased, respectively. As depicted in these figures, increasing the number of interference signals is a reason for decreasing the performance of these algorithms. It is also seen that the performance of 4W-Updating algorithm that updates their weights is close to the conventional LMS and CM performance. This can be seen well in low SNRs with higher interference signals.
Tables 1 and 2 show the average output SNIR and angular error for proposed algorithms. According to the numerical results, 4W-Updating speed-sensitive LMSbased and CM-based algorithms offer higher performance with respect to other ones.
The number of iterations for weighting algorithms in each case for conventional and new proposed ones is the same. Prediction of the new location is very simple and computational complexity to do this function can be ignored with respect to required iterative weight updating
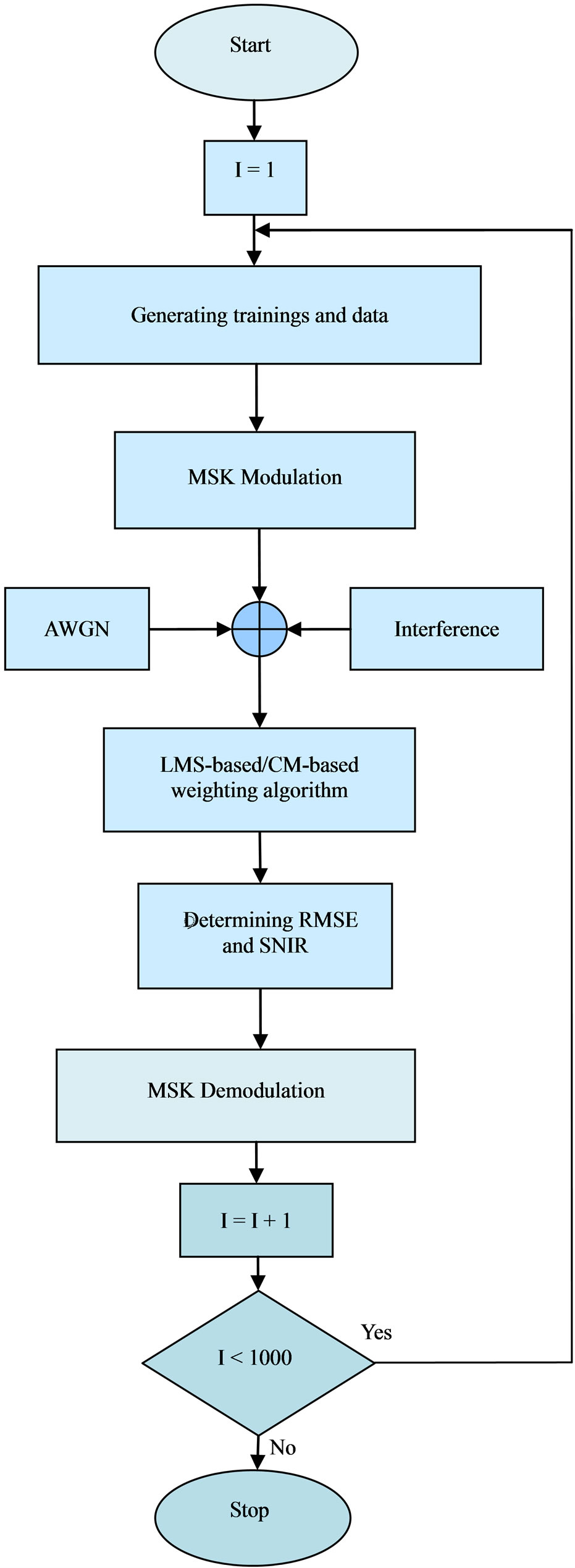
Figure 4. Simulation flowchart of conventional and proposed LMS-based/CM-based beamformers.
 (a)
(a)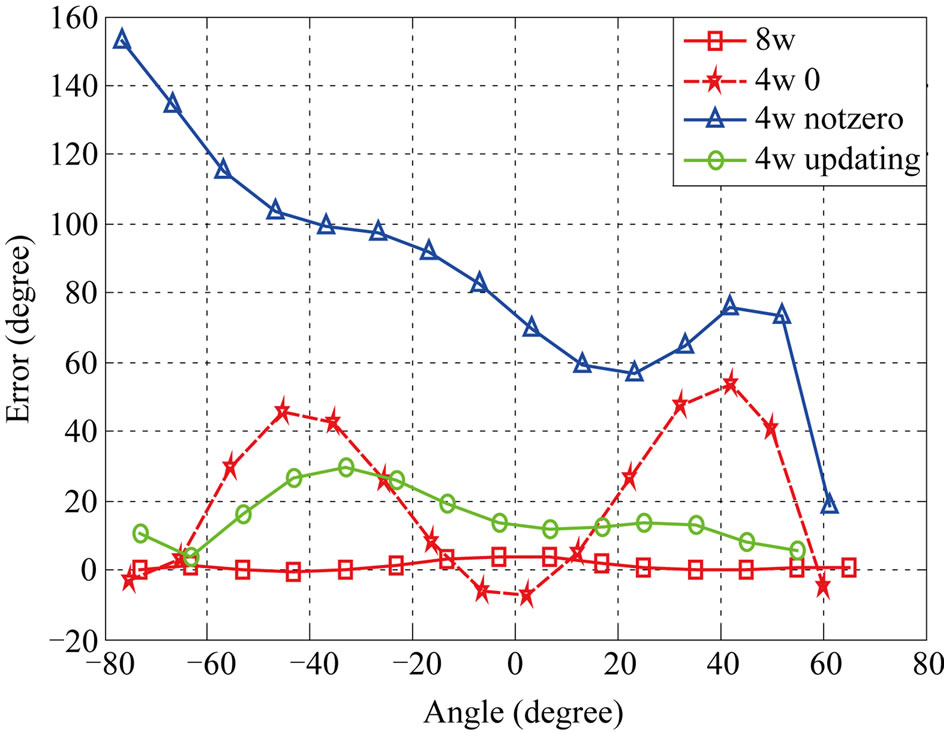 (b)
(b)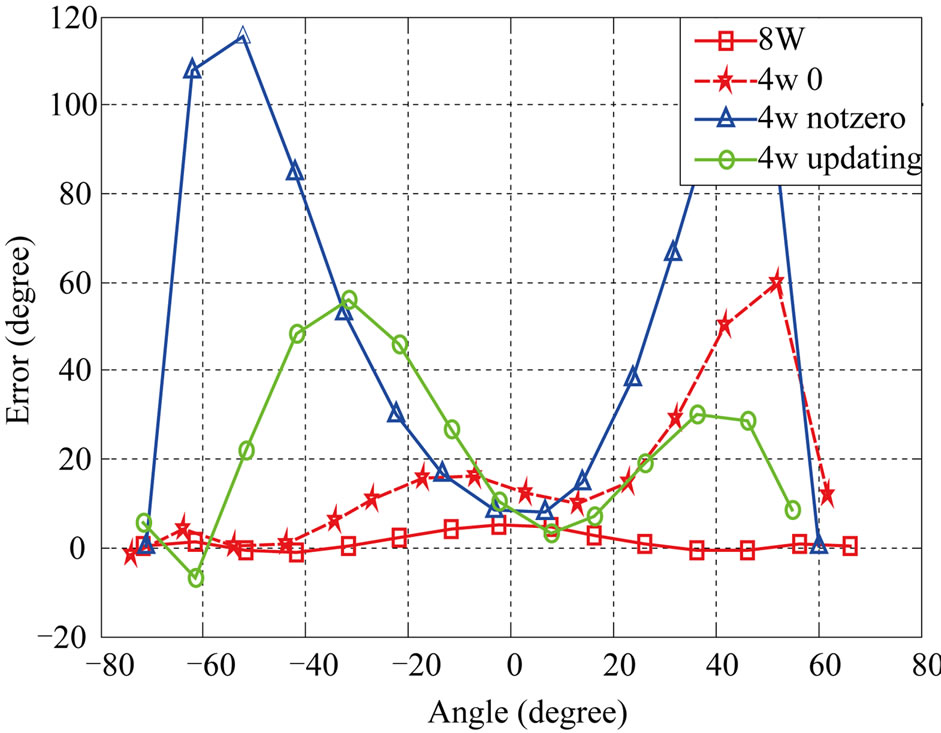 (c)
(c)
Figure 5. Comparison of the proposed and conventional LMS-based algorithms at SNR = 40 dB. (a) Noisy channel; (b) Channel with one interference signal; (c) Channel with two interference signals.
 (a)
(a)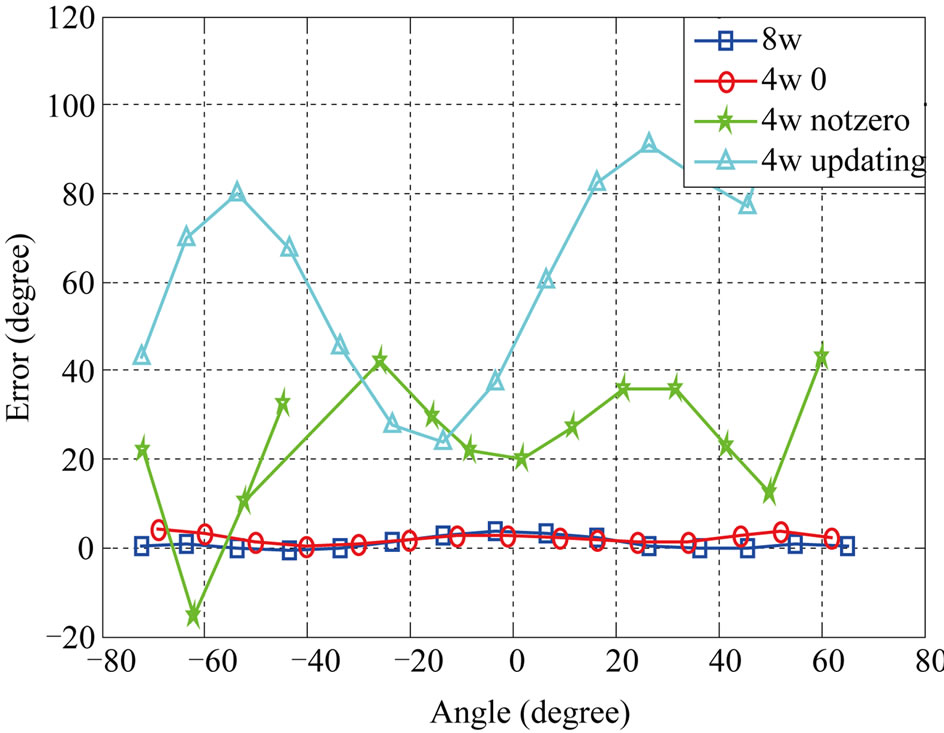 (b)
(b)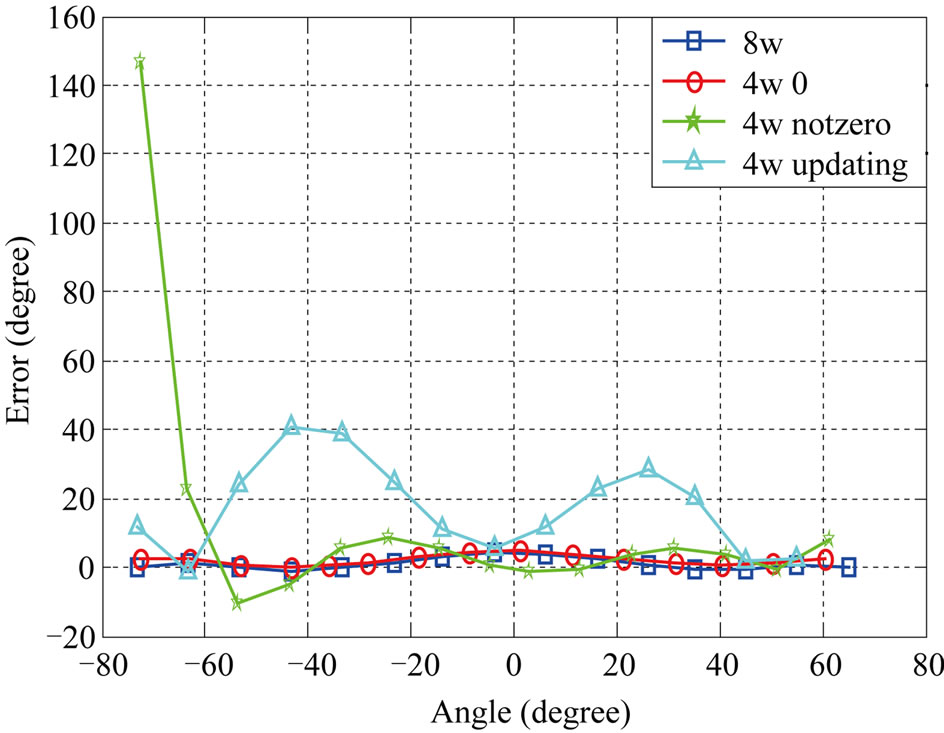 (c)
(c)
Figure 6. Comparison of the proposed and conventional LMS-based algorithms at SNR = 4 dB. (a) Noisy channel; (b) Channel with one interference signal; (c) Channel with two interference signals.
 (a)
(a)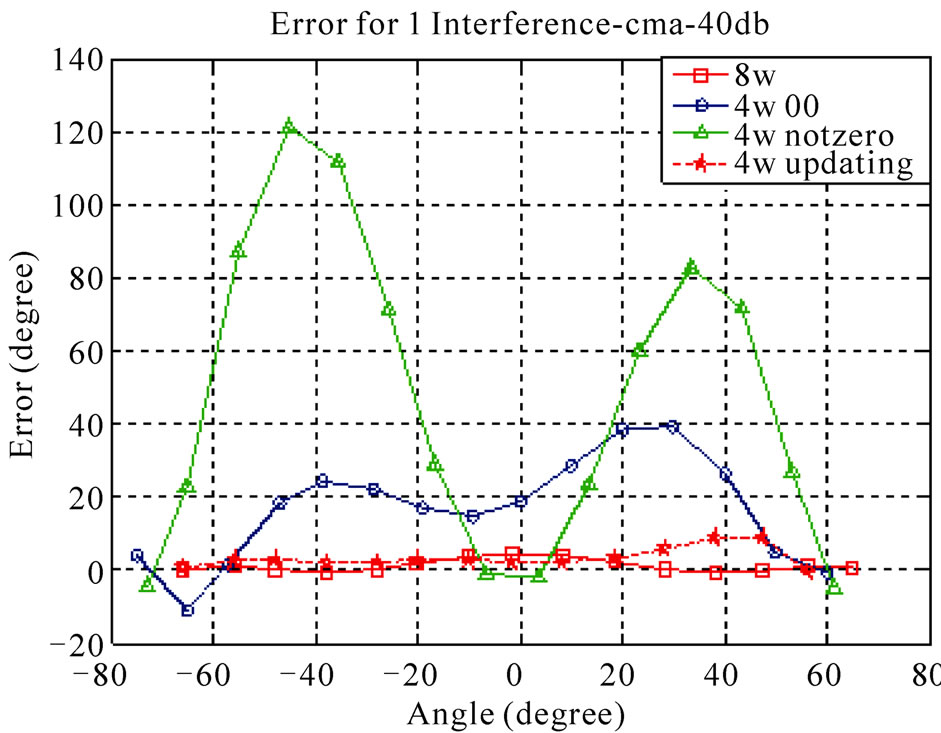 (b)
(b)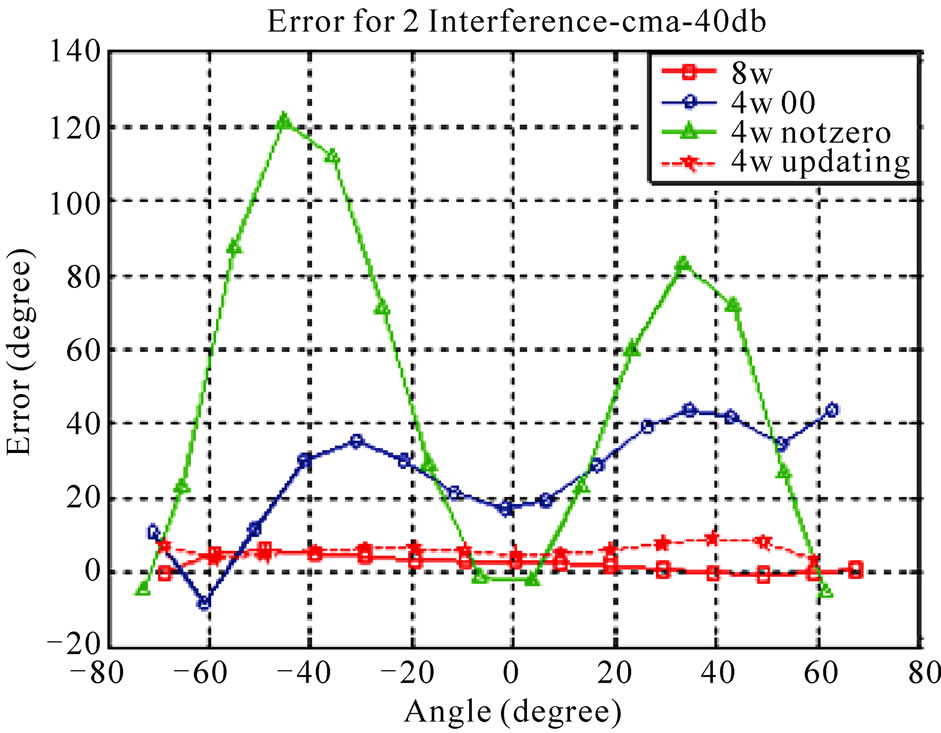 (c)
(c)
Figure 7. Comparison of the proposed and conventional CM-based algorithms at SNR = 40 dB. (a) Noisy channel; (b) Channel with one interference signal; (c) Channel with two interference signals.
 (a)
(a)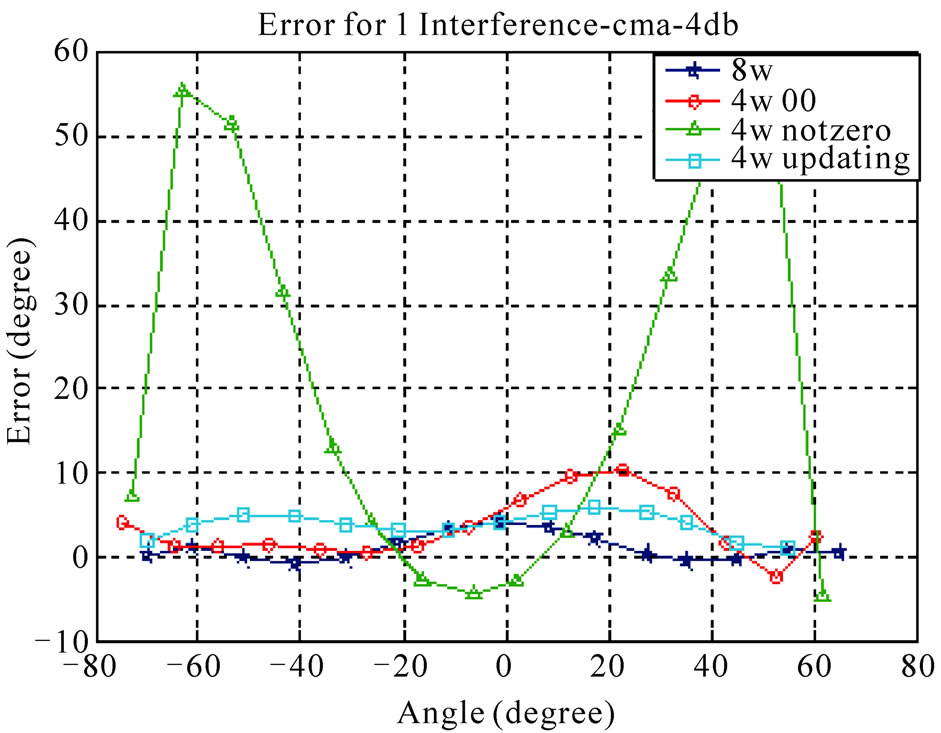 (b)
(b)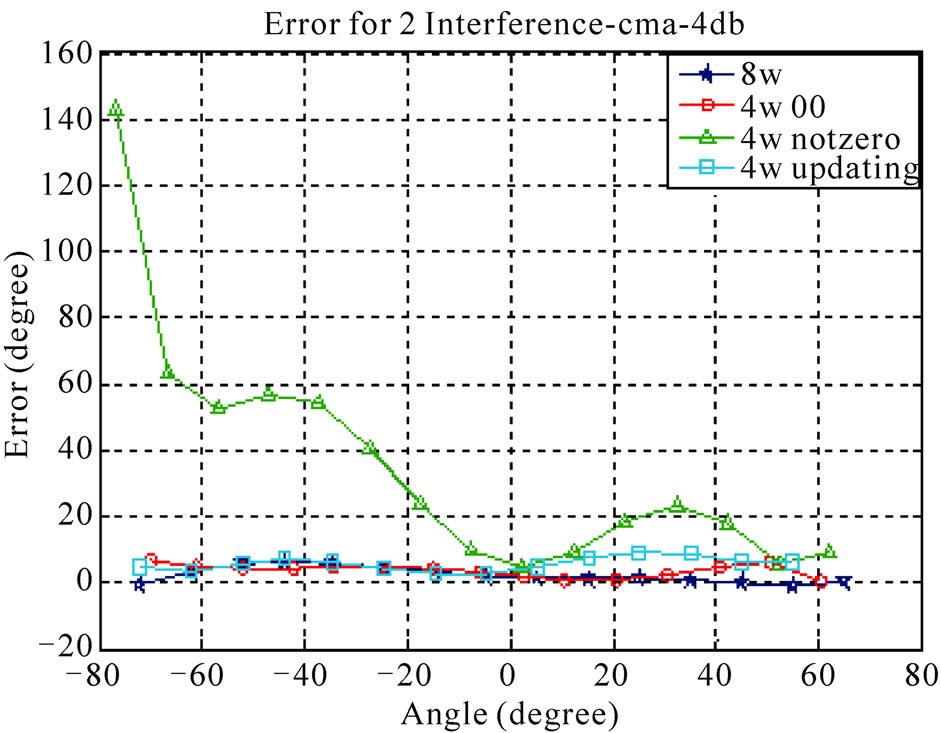 (c)
(c)
Figure 8. Comparison of proposed and conventional CMbased algorithms at SNR=4 dB. (a) Noisy channel; (b) Channel with one interference signal; (c) Channel with two interference signals.
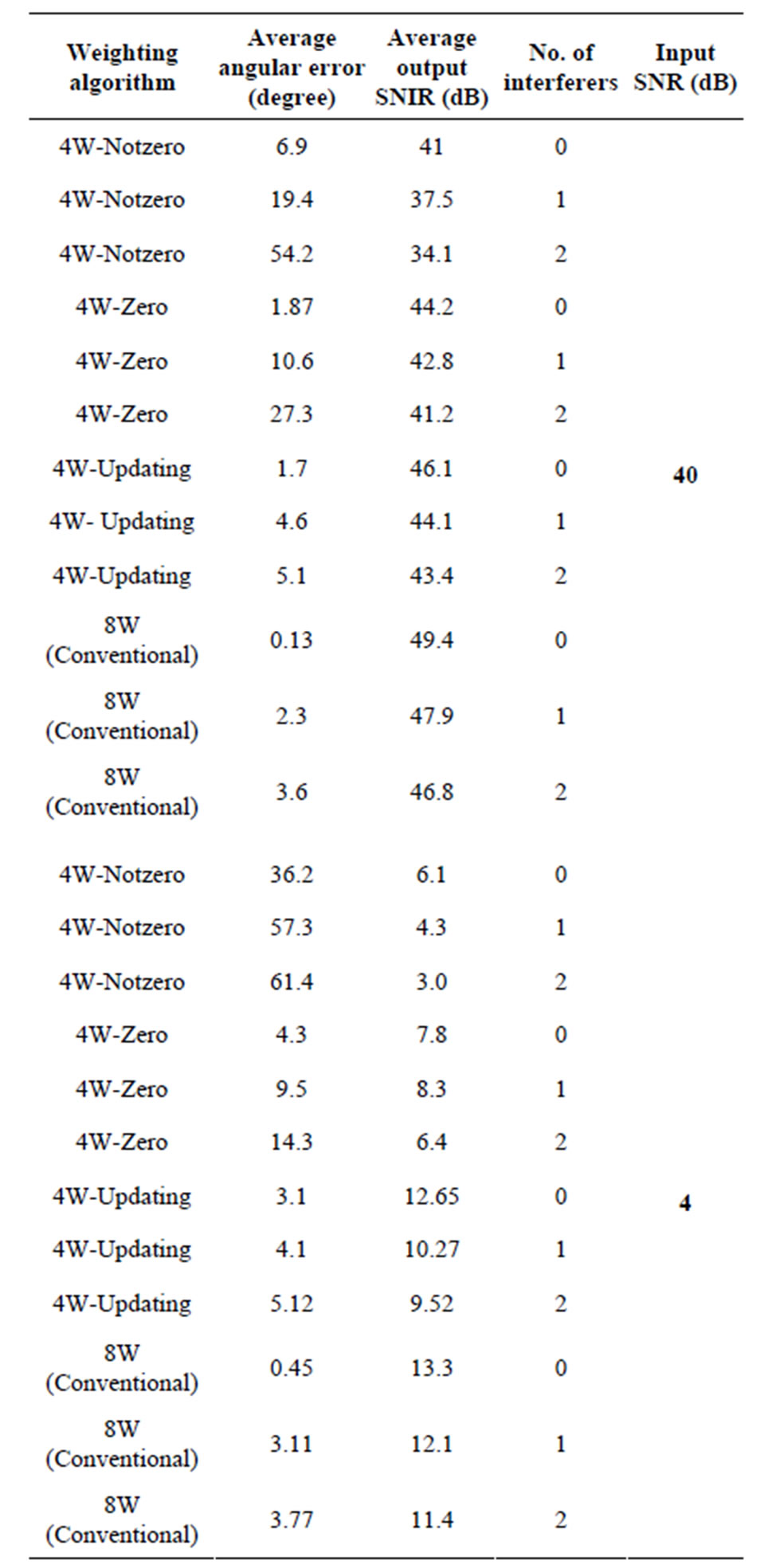
Table 1. Average performance of conventional and proposed LMS-based beamforming for an 8-element ULA.
algorithms. It means to compare the processing time of each method which equals the (Iteration × (Number of additions/subtractions and multiplications/divisions)) someone can compare the number of these instructions.
Tables 3 and 4 show the required number of additions/ subtractions and multiplications/divisions in the conventional and proposed 4W-Updating LMS-based and CMbased 8-element array algorithms, respectively. It shows lower complexity by a factor of 2.
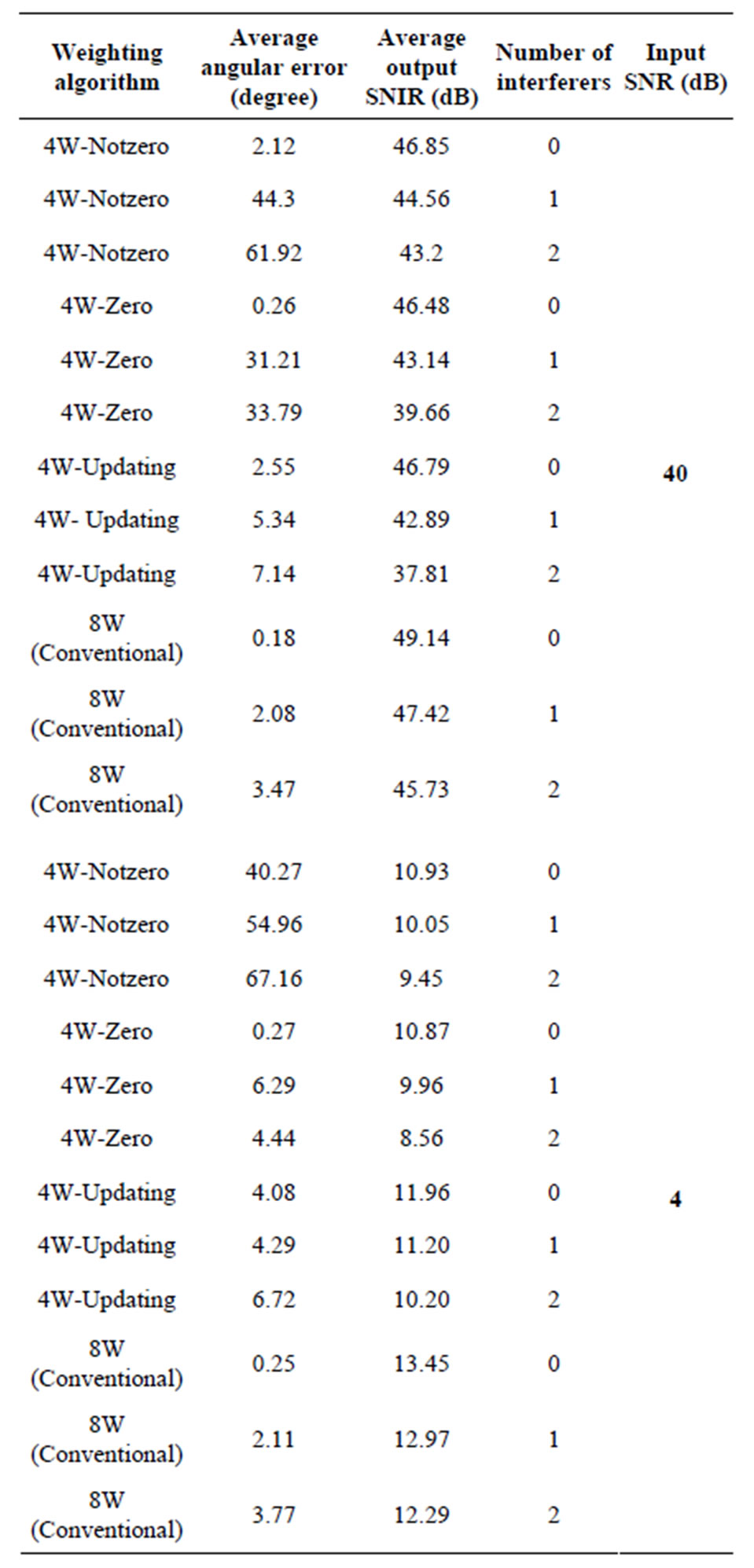
Table 2. Average performance of conventional and proposed CM-based beamforming for an 8-element ULA.
It should be noted that these simulations can be extended to other number of array elements and array configurations. It means there is no additional calculation for determining the array weights and so, new beamforming method offers lower complexity in weighting time.
5. Conclusions
In this paper a novel LMS-based/CM-based beamforming is proposed in order to estimate the weights of adaptive

Table 3. Required number of additions and multiplications in each iteration of the LMS-based algorithms for an 8-element ULA.

Table 4. Required number of additions/subtractions and multiplications/divisions in each iteration of the CM-based algorithms for an 8-element ULA.
antenna array. According to these new beamforming schemes, the direction and the relative velocity of the source will be estimated based on the two previous points; hence, the new location of the source will be predicted. According to the predicted location, those weights that have higher effects on antenna pattern will be found.
Simulation results at different SNRs show that the proposed speed-sensitive algorithms reduce the required processing time compared to the conventional methods. To prevent the error propagation, all the weights are updated in the time intervals between two consecutive points in an offline manner. Furthermore, it has been shown that the performance of 4W-Updating algorithm that updates only four of their weights is close to the conventional ones and has lower complexity and convergence time than the conventional LMS and CM algorithms.
6. Acknowledgements
We would like to thank Mrs. Samaneh Movassaghi (University of Technology, Sydney) for the great help she provided. Also, the authors would like to thank the WET editor and reviewers for their very helpful comments and suggestions which have improved the presentation of the paper.
REFERENCES
- S. Ravishankar, H. V. Kumaraswamy and B. D. Satish, “Comparative Analysis of Direction of Arrival Estimation and Beamforming Techniques in Smart Antennas,” Proceedings of ObCom Conference on Mobile, Ubiquitous & Pervasive Computing, Tamil Nadu, Vol. 2, 18-19 December 2006, pp. 39-45
- I. Stevanovic, A. Skrivervik and J. R. Mosig, “Smart Antenna Systems for Mobile Communications,” Ecole Polytechnique Federale De Lausanne, Technical Report, January 2003.
- S. S. Moghaddam and M. S. Moghaddam, “A Comprehensive Survey on Antenna Array Signal Processing,” Trends in Applied Sciences Research, Vol. 6, No. 6, 2011, pp. 507-536. doi:10.3923/tasr.2011.507.536
- J. Fuhl and E. Bonek, “Temporal Reference Algorithms versus Spatial Reference Algorithms for Smart Antennas,” Wireless Personal Communications, Vol. 9, No. 3, 1998, pp. 271-293. doi:10.1023/A:1018332029467
- S. Haykin, “Adaptive Filter Theory,” Prentice Hall, New York, 1996.
- T. K. Sarkar, M. C. Wicks, M. Salazar-Palma and R. J. Bonneau, “Smart Antennas,” John Wiley and Sons, New York, 2003. doi:10.1002/0471722839
- C. Sun, J. Cheng and T. Ohira, “Handbook on Advancements in Smart Antenna Technologies for Wireless Networks,” Idea Group Inc., Hershey, 2009.
- A. Bouacha, F. Debbat and F. T. Bendimerad, “Modified Blind Beamforming Algorithm for Smart Antenna System,” Journal of Radio Electronics, No. 1, 2008.
- P. C. Parini, D. X. Chen, D. J. Bigham, P. I. Liewellyn, D. L. Samuel, D. L. Ho and B. Collins, “Final Report on Semi-Smart Antenna Technology Project,” BSC Association Ltd., Kent, 2006.
- X. Sun, X. Lian and J. Zhou, “Robust Adaptive Beamforming Based on Maximum Likelihood Estimation,” Proceedings of International Conference on Microwave and Millimeter Wave Technology, Nanjing, 21-24 April 2008, pp. 1137-1140.
- R. M. Shubair, M. A. Al-Qutayri and J. M. Sa, “A Setup for the Evaluation of MUSIC and LMS Algorithms for a Smart Antenna System,” Journal of Communications, Vol. 2, No. 4, 2007, pp. 71-77.
- C. S. Rani, P. V. Subbaiah, K. C. Reddy and S. S. Rani, “LMS and RLS Algorithms for Smart Antennas in a W-CDMA Mobile Communication Environment,” ARPN Journal of Engineering and Applied Sciences, Vol. 4, No. 6, 2009, pp. 77-88.
- M. Islam, Z. Rashid, “MI-NLMS Adaptive Beamforming Algorithm for Smart Antenna System Applications,” Journal of Zhejiang University Science A, Vol. 7, No. 10, 2006, pp. 1709-1716. doi:10.1631/jzus.2006.A1709
- M. T. Islam and N. Misran, “MI-NLMS Adaptive Beamforming Algorithm with Tracking Ability,” Journal of Applied Sciences, Vol. 9, No. 12, 2009, pp. 2335-2339. doi:10.3923/jas.2009.2335.2339
- S. F. Shaukat, M. Hassan, R. Farooq, H. U. Saeed and Z. Saleem, “Sequential Studies of Beamforming Algorithms for Smart Antenna Systems,” World Applied Sciences Journal, Vol. 6, No. 6, 2009, pp. 754-758.
- L. Wang, R. C. Lamare and Y. L. Cai, “Low-Complexity Adaptive Step Size Constrained Constant Modulus SG Algorithms for Adaptive Beamforming,” Elsevier Signal Processing, Vol. 89, 2009, pp. 2503-2513.
- L. Wang and R. C. Lamare, “Constrained Constant Modulus RLS-Based Blind Adaptive Beamforming Algorithm for Smart Antennas,” Proceedings of the 4th International Symposium on Wireless Communication Systems, Trondheim, 17-19 October, 2007, pp. 657-661. doi:10.1109/ISWCS.2007.4392422
- H. Sadeghi, S. S. Moghaddam and V. T. Vakili, “Appropriate CCM-Based Algorithm for Adaptive Antenna Array Beamforming,” Proceedings of 5th International Symposium on Telecommunications, Tehran, 4-6 December 2010, pp. 69-75.
- L. C. Godara, “Smart Antenna,” CRC Press, New York, 2004. doi:10.1201/9780203496770
- F. B. Gross, “Smart Antenna for Wireless Communication with MATLAB,” McGraw-Hill, New York, 2005.
- S. S. Moghaddam, M. S. Moghaddam and R. K. Rad, “A Novel Adaptive LMS-Based Algorithm Considering Relative Velocity of Source,” Proceedings of the 7th International Symposium on Communication Systems, Networks and Digital Signal Processing, New Castel, July 2010, pp. 10-14.
- S. S. Moghaddam, M. S. Moghaddam and R. K. Rad, “CMA-Based Adaptive Antenna Array Digital Beamforming with Reduced Complexity,” Proceedings of the 7th International Symposium on Communication Systems, Networks and Digital Signal Processing, New Castel, 21- 23 July 2010, pp. 375-379.

