Journal of Environmental Protection
Vol. 3 No. 8A (2012) , Article ID: 21779 , 8 pages DOI:10.4236/jep.2012.328101
Sensitivity Analysis of Parameters in Water Quality Models and Water Environment Management
![]()
School of Economics and Management, Beihang University, Beijing, China.
Email: *laueastking3168@163.com
Received June 15th, 2012; revised July 10th, 2012; accepted August 9th, 2012
Keywords: Water quality model; Reclaimed water; Sensitivity analysis; Degradation coefficient; Stochastic factors
ABSTRACT
The impacts of changes of various parameters and stochastic factors on water quality models were studied. The impact of deviation of the degradation coefficient on the model results was investigated. The degradation coefficient was decomposed into the exact part and the deviation part, and the relationship between the errors of the water quality model results and the deviation of the degradation coefficient was derived. The impact of changes in the initial concentration on the model results was discussed. A linear relationship between the initial concentration changes and errors in the model results was obtained, and relevant recommendations to the water quality management were made based on the results. The impacts of stochastic factors in the water environment on the water quality model were analyzed. A variety of random factors which may affect the water quality conditions were attributed to one stochastic factor and it was further assumed to be the white noise. The solutions to the water quality model including the stochastic process were obtained by solving the stochastic differential equation. Simulation results showed that the decay trend of the concentration of the solute would not be changed, and that the results would fluctuate around the expectation centered at each corresponding displacement x.
1. Introduction
With the development of economies and the improvement of living standards, our environment, especially natural water, is constantly being polluted. Natural water plays an important role in a watershed in carrying off municipal and industrial wastewater and run-off from farm land. In recent years, water pollution and water shortages are two of the most serious and widespread environmental problems [1]. The application of reclaimed water is of great importance to ease the water shortage and reduce further pollution by sewage. The use of reclaimed water as an unconventional supply for rivers with water shortages has become a common and international trend [2]. The recycled water comes from urban sewage which has been extensively treated in sewage treatment plants. Although it may meet certain water quality standards, it is still urban sewage and carries some risk when used to recharge rivers. Therefore, study of the analysis and management of the water quality of rivers recharged with reclaimed water has high theoretical and practical significance [3].
The theoretical study of water quality management has the goal of developing mathematical models based on real water quality. Conclusions and information on water quality changes have been obtained by discussing and analyzing these models [4]. The history of study on water quality models can be divided into three stages according to the complexity and perfection of the models.
The first stage was from the 1920s to the early 1970s, when the models were simple oxygen balance models. This stage was the early stage of development of surface water quality models [5]. The models during this phase mainly focused on the study of the oxygen balance, but also involved some non-ozone-depleting substances. The starting point of this research phase was the BOD (Biochemical Oxygen Demand)-DO (Dissolved Oxygen) coupled equation which was proposed by Streeter and Phelps in 1925, designated the S-P equation [6]. In the next few decades, there were scientists who proposed an amendment to the S-P equation. Theriault (1927) [7] and Fair (1939) [8] summarized the methods for estimating the model’s parameters. To account for the removal through sedimentation of the settleable BOD, Streeter (1935) [9] realized its consideration; Thomas (1937, 1948) [10,11] considered (though less elegantly) this effect through use of a “lag-time”. In 1961, O’Conner insisted that BOD should be divided into two parts, namely CBOD at the carbonation stage and NBOD at the nitrification stage, and that the reduction of DO should also be the sum of these two parts. Thus the model was modified based on the S-P equation, after considering the impact of the nitrification process on the changes of DO [12]. Clark and Viessman (1965) [13] pointed out that second-order rather than first-order reactions frequently describe the stabilization of waste-waters. Braun and Berthouex (1970) [14] proposed a Michaelis-Menton expression to describe the BOD decay reaction and its impact on the DO concentration in a river. The S-P equation and its modified model are still widely used.
The second stage was the mid-1970s to the 1990s, when comprehensive water quality models rapidly developed [15]. With in-depth study on the environmental behavior of pollutants in water, the traditional oxygen balance model was found lacking and could not meet the actual needs. Other pollutants began to be considered in water quality models. The environmental behavior and ecological benefits of different forms of pollutants, as well as the distribution of pollutants in the air, water, soil and vegetation in a variety of environmental media, became research subjects. Therefore, river water quality needed to be described comprehensively, and it was necessary to study the link between aquatic ecosystems and water quality components; then comprehensive water quality models could be built [16]. Due to the development of computer science, a huge amount of computing had become possible at this stage. Models were developing from one-dimensional to multi-dimensional, and they were closer to real systems.
The United States started the research on the comprehensive water quality models in the early 1970s, and the QUAL model system was first proposed [17]. The QUAL-I model was developed by the Texas Water Development Board with Frank D. Masch and Associates during 1970 to 1971 [18]. In June 1972, the United States Environmental Protection Agency awarded Water Resources Engineers, Inc. (now Camp Dresser & McKee) a contract to modify QUAL-I for application to the Chattahoochee-Flint River, the Upper Mississippi River, the Iowa-Cedar River, and the Santee River. The modified version of QUAL-I was known as QUAL-II [19]. The QUAL model system has been continually developed since then. In 1985, EPA’s Center for Water Quality Modeling sponsored a National Council of the Paper Industry for Air and Stream Improvement (NCASI) review of other versions of QUAL-II and incorporated certain features of these versions into a program called QUAL2E [20]. QUAL2E is currently the best available stream model that has been adapted for use on a personal computer. The model is numerically accurate and includes an updated kinetic structure for most conventional pollutants. The QUAL2E model was widely used. In 2000, the model underwent further refinement and upgrade, and the QUAL2K version was introduced. This version could be loaded into Excel in the form of macros, and the model interface was also very user-friendly.
The third stage was the mid-1990s to the present, when surface water quality models were continuously deepened, improved and widely used. The water quality models had the following characteristics in this stage. Firstly, with increasing emphasis on non-point source pollution problems, the combination of the surface water quality model and non-point source pollution model began to be considered. Secondly, the reliability and evaluation capacity of the models were strengthened, and more importance was attached to the models’ uncertainty. Furthermore, many modern mathematical methods were introduced into the research on water quality models, such as stochastic mathematics [21], fuzzy mathematics [22], artificial neural networks [23], genetic algorithms [24], expert systems [25], etc. Lastly, with the development of computer technology, 3S technology, that is, GIS [26] (Geographic Information System), RS [27] (Remote Sensing), and GPS [28] (Global Positioning System)) was introduced into the study on water quality models, which greatly promoted the development of model studies.
In the current study, sensitivity analysis of the parameters in water quality models was carried out. The influence of various parameters on the equation results were analyzed and discussed. The impact of changes in the parameters and random factors on the errors of the model results were investigated. The relationship between these factors was verified by simulation results, and rational suggestions for water quality management were proposed.
2. Sensitivity Analysis of Water Quality Model
2.1. Water Quality Model
A one-dimensional river flow dispersion equation for a pollutant was set as [29]:
 . (1)
. (1)
where ks is the dispersion coefficient, k is the pollutant degradation coefficient, C is the BOD concentration in water, x is the distance between the monitoring point and the source of pollution, and u is the flow rate.
River water quality at steady-state was considered. Uniform river section steady-state sewage conditions were the velocity and flow of cross sections that did not change with the time, that is, where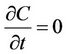 . Then Equation (1) was transformed into Equation (2):
. Then Equation (1) was transformed into Equation (2):
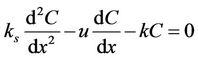 . (2)
. (2)
Sensitivity analysis of the parameters in Equation (2) is discussed below.
2.2. Degradation Coefficient
When the dispersion effect is not considered, that is, ks = 0, Equation (2) transforms to Equation (3):
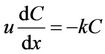 . (3)
. (3)
The initial condition is:
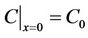 .
.
The degradation process of remaining BOD is:
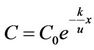 . (4)
. (4)
We decomposed k in Equation (4) into two parts:
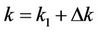 . (5)
. (5)
where k is the degradation coefficient, in d−1; k1 is the exact part of k, in d−1; Δk is the deviation of k, in d−1, and Δk could be caused by measurement errors and uncertain factors.
We substituted Equation (5) into Equation (4), then
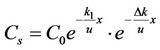 . (6)
. (6)
We expanded the power series of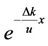 :
:
 .
.
We substituted the first two terms on the right side of the equation into Equation (6), then
 . (7)
. (7)
From Equation (7), the errors in the model results caused by Δk would be:
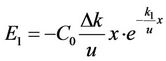 . (8)
. (8)
The impact of changes in the degradation coefficient on solute concentrations in water was investigated through the analysis of influence of Δk on E1, which was the sensitivity analysis of the degradation coefficient. After theoretical analysis, we used the data in a simulation to verify the model. The basic parameters of some rivers are shown in Table 1, from reference [30].
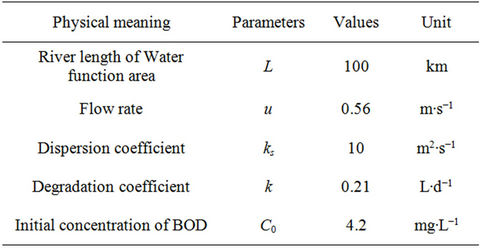
Table 1. Basic parameters of the river.
We substituted the water parameters in Table 1 into Equation (7), and obtained the variation of the concentration error E1 with the displacement x. We set Δk = 0.01 L∙d−1, Δk = 0.005 L∙d−1, Δk = 0.001 L∙d−1 and Δk = −0.005 L∙d−1 respectively, and plotted the variation of the error E1 with the displacement of x when Δk was set at different values, as shown in Figure 1.
From Figure 1 we can see that the concentration error E1 decreased with increasing deviation of the degradation coefficient Δk. Considering absolute values, when 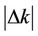 increased,
increased, 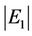 also increased. The signs of Δk and E1 were opposite. When Δk > 0, E1 < 0, and the value of Cs would decrease from Equation (7); when Δk < 0, E1 > 0, and the value of Cs would increase from Equation (7).
also increased. The signs of Δk and E1 were opposite. When Δk > 0, E1 < 0, and the value of Cs would decrease from Equation (7); when Δk < 0, E1 > 0, and the value of Cs would increase from Equation (7).
We investigated the specific values of Δk and E1 at x = 4.0 km. According to Equation (8), when the degradation coefficient had increased 0.001 L∙d−1, that is, Δk = 0.001 L∙d−1, E1 would decrease 0.0029 mg∙L−1. This was equivalent to a situation where a 1% change in the degradation coefficient would cause about 0.15% error in the solute concentration. In addition, E1 was differentiated with respect to x and we calculated the derivative values. In the river length within functional areas, that was, x ≦ 100 km, the derivative values were all less than 0. Thus we obtained the conclusion that E1 showed a monotonically decreasing trend. When x increased, E1 would decrease, and then Cs also decreased. Therefore, the impacts of Δk on E1 decreased gradually with increasing x.
2.3. Initial Concentration
In this section the impact of changes in the initial concentration on the model results are discussed.
We solve Equation (2), then
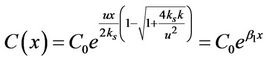 . (9)
. (9)
where
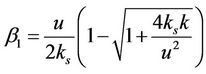 .
.
We decomposed C0 in Equation (9) into two parts:
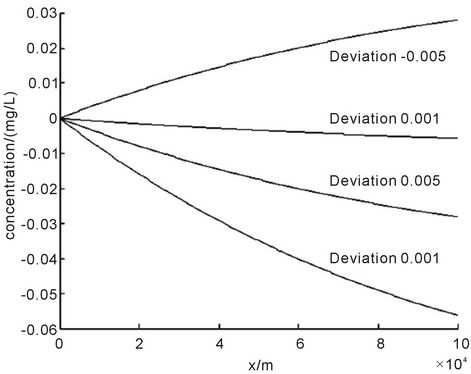
Figure 1. Sensitivity analysis of degradation coefficient.
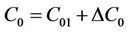 . (10)
. (10)
We substituted Equation (10) into Equation (9), then
 .
.
Therefore, the error caused by the deviation of the initial concentration ΔC0 was
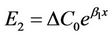 . (11)
. (11)
The impact of changes in the initial concentration on model results was investigated through the analysis of influence of ΔC0 on E2, which was the sensitivity analysis of the initial concentration. After theoretical analysis, we again used the data for simulation to validate the model. Simulation parameters were the same as the ones used in Section 2.2.
We substituted the parameters into Equation (11), and obtained the numerical relationship between E2 and ΔC0:
 .
.
We plotted the functional relationship between the error E2 and the deviation ΔC0, as shown in Figure 2.
It was clear that there was a positive linear correlation between E2 and ΔC0. When ΔC0 increased, E2 also increased at the corresponding displacement x. This was because ΔC0 is the coefficient of E2 in Equation (11). Similarly, in Equation (8), C0 is the coefficient of C(x). There was also a positive linear correlation between C(x) and C0. When C0 increased, C(x) also increased at the corresponding displacement x.
On the other hand, according to the Water Quality Standards [31], a BOD concentration of 4.2 mg/L corresponds to Class III. For natural water, it is difficult to meet water quality requirements for this initial concentration. The concentration is officially required to decay back to 3 mg/L, which corresponds to Class I, by the self-purification of the river itself. The pollutant process satisfied Equation (8), so that at least a 75 km distance would be needed if the water pollution began to decay from the initial concentration of 4.2 mg/L. The decay processes in the river are shown in Figure 3.
From Figure 3 we can see, if “3 mg/L”, which was the limiting value for Class I in Water Quality Standards, was actually required at a distance of 40 km from a pollution source, the water quality situation at present would not meet the requirements, and the concentration could not decay from the initial concentration of 4.2 mg/L to 3 mg/L at the 40 km. That means the water quality would need to be managed effectively. Reduction of the initial concentration at the pollution source is the most common and effective way to manage water quality. We implemented a reduction of the concentration at the pollution source, such that the initial concentration would be reduced to 3.5 mg/L within 40 km. Thus “4.2 mg/L” was reduced by ΔC0 = 0.7 mg/L, and now the water quality
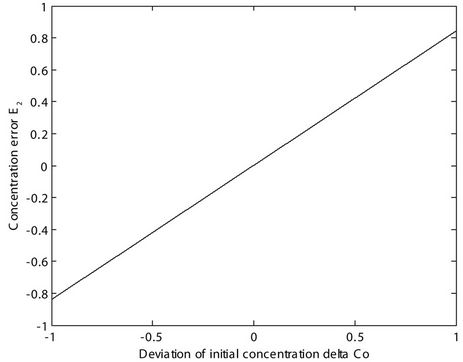
Figure 2. Concentration error and deviation of initial concentration.

Figure 3. Decay processes for different initial concentrations in the river.
began to change from an initial concentration of 3.5 mg/L. The concentration at the distance of 40 km could decay to the requirement of 3 mg/L though the river self-purification process, and its decay processes in the river are also shown in Figure 3. We calculated the initial concentration which could meet the requirement that concentration should decay to 3 mg/L at the 40 km distance from the pollution source according to Equation (9). The result was 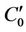 = 3.5687 mg/L.
= 3.5687 mg/L.
2.4. Stochastic Factors
In this section the impact of stochastic factors in the water environment on the water quality model are discussed. The stochastic factors in the water environment included: External or anthropogenic factors on the water environment, uncertain measurement of parameters in the water quality model, the interaction and chemical reaction of the solutes, precipitation and drought and other climatic factors, etc. [32]. As we knew, when the dispersion effect was not considered, Equation (2) was transformed into Equation (3). We took stochastic factors into account in the water quality model. The integrity of the stochastic factors was seen as one factor, and we mainly considered the impact of this factor on the model [33]. Thus a stochastic factor “S” was added into the equation. Then Equation (3) was transformed:
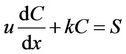 .
.
The stochastic factor “S” was assumed to be white noise with variance of σ2 [34], and “S” was represented by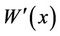 . Then the water quality model was transferred into a first-order constant coefficient linear stochastic differential equation (12):
. Then the water quality model was transferred into a first-order constant coefficient linear stochastic differential equation (12):
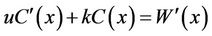 . (12)
. (12)
White noise could not be used as a stochastic process with a sample function in the usual sense, so Equation (12) was not determinate [35]. However, because 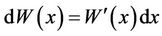 , Equation (12) was transferred into Equation (13):
, Equation (12) was transferred into Equation (13):
 . (13)
. (13)
We integrated both sides of Equation (13), and obtained
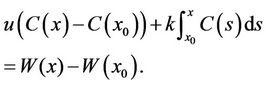 (14)
(14)
Equation (14) was a stochastic integral equation, and was determinate, because for each ω Î Ω, the sample function of the Brownian Motion W(x) = W(x, w) was a defined continuous function. C(x) was set in the interval I, x0 Î I, and C(x0) was the known stochastic variable. Then we named the stochastic process “C”, which satisfied Equation (14) and had continuous sample functions, and was the solution of the stochastic differential model Equation (13) in the interval I.
We used the constant variation method to solve the first-order non-homogeneous differential Equation (13). The general solution to the homogeneous equation corresponding to Equation (13) was
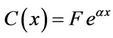 .
.
where a = −k/u. We set F = F(x), then
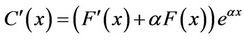 .
.
We substituted this into Equation (13), and obtained
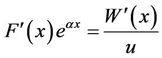 .
.
That is,
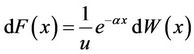 .
.
We integrated both sides of the upper equation from x0 to x, and obtained

Because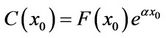 , we had
, we had 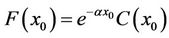 . We substituted this into the upper equation and simplified the results, and obtained
. We substituted this into the upper equation and simplified the results, and obtained
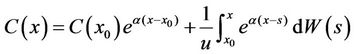 . (15)
. (15)
This was consistent with the structure of a typical differential equation. General solution of Equation (13) was equal to general solution of the corresponding homogeneous equation coupled with a special solution of Equation (13). The difference was that C(x0) here was a stochastic variable, but not necessarily constant.
We set x0 = 0, and C(x) was the solution of Equation (13) in the interval of [0, ∞], which satisfied the initial conditions C(0) = c0. Thus we had
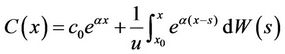 . (16)
. (16)
This was a Gaussian process. Since the expectation of the integral of the white noise was 0, the expectation of C(x) was:
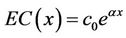 . (17)
. (17)
The covariance of C(x) was:
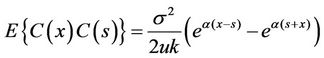 .
.
That is,
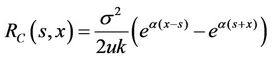 . (18)
. (18)
Specifically, we set s = x, and we obtained the variance of C(x) which was
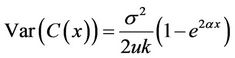 .
.
After theoretical analysis, we used the data for simulation to investigate the impact of stochastic factors in the water environment on the water quality model. Simulation parameters were the same as the ones used in Section 2.2. We substituted the simulation parameters into Equation (16), and obtained the solution of the water quality model with stochastic process.
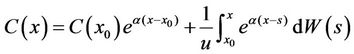 .
.
Furthermore, we substituted the simulation parameters into Equations (17) and (18), and the expectation and covariance of C(x) would be obtained.
Stochastic factors were considered in the water quality model, so determinate solutions could not be given. Solutions could only be represented in the form of the stochastic process. We plotted the solutions with the stochastic process, as shown in Figure 4. In this study the stochastic process was the white noise process with variance σ2 = 0.75.
From Figure 4 we can see that the water concentration still showed an attenuated trend, while the concentration would fluctuate around the expectation centered at each corresponding displacement x. The fluctuations had a certain range, with variance of σ2 = 0.75. The impact of
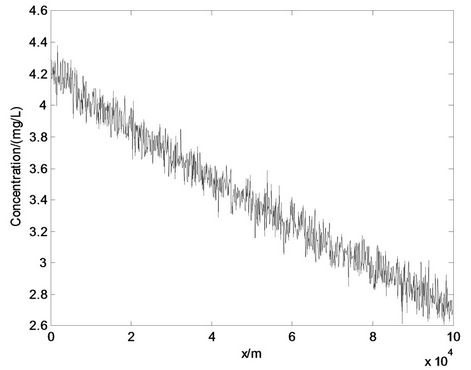
Figure 4. Solutions of water quality model with stochastic process.
stochastic factors on the water quality was uncertain, and it was difficult to describe it exactly and numerically. However, we made some reasonable assumptions for stochastic factors and dealt with them using some mathematical tools. Thus we could obtain solutions with a stochastic process.
3. Conclusions
The impacts of changes of various parameters and stochastic factors on the water quality model were analyzed and discussed. Preliminary conclusions were obtained as follows.
1) The values of Δk and E1 had the opposite sign. When the deviation of the degradation coefficient Δk increased, the concentration error E1 decreased numerically at the corresponding displacement x. When Δk > 0, E1 < 0, and the value of Cs would decrease; when Δk < 0, E1 > 0, and the value of Cs would increase. A 1% change in the degradation coefficient would cause about 0.15% error in the solute concentration. The impacts of Δk on E1 decreased with increasing x.
2) When the deviation of initial concentration “ΔC0” increased, the error of the model “E2” also increased at the corresponding displacement x. There was a positive linear correlation between E2 and ΔC0. To reduce the initial concentration at the pollution source is the most common and effective way to manage water quality. By reducing the initial concentration, the requirements of water quality could be achieved through the self-purification ability of the river itself.
3) Stochastic factors did not significantly affect the attenuation trend of water quality. However, because of the stochastic interference, the concentration of the solute would fluctuate around the expectation centered at each corresponding displacement x.
4. Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 41071322, 71031001).
REFERENCES
- R. Noori, M. S. Sabahi, A. R. Karbassi and A. Baghvand, “Multivariate Statistical Analysis of Surface Water Quality Based on Correlations and Variations in the Data Set,” Desalination, Vol. 260, No. 1-3, 2010, pp. 129-136. doi:10.1016/j.desal.2010.04.053
- H. Furumai, “Rainwater and Reclaimed Wastewater for Sustainable Urban Water Use,” Physics and Chemistry of the Earth, Vol. 33, 2008, pp. 340-346. doi:10.1016/j.pce.2008.02.029
- E. Taigbenu and M. Ncube, “Reclaimed Water as an Alternative Source of Water for the City of Bulawayo, Zimbabwe,” Physics and Chemistry of the Earth, Parts A/B/C, Vol. 30, No. 11-16, 2005, pp. 762-766.
- Y. Z. Tao and L. Jiang, “Influence of Groundwater Discharge on Decay Process of Contamination Concentration in River Flow,” Journal of Hydraulic Engineering, Vol. 39, No. 2, 2008, pp. 245-249.
- D. D. Adrian and T. G. Sanders, “Oxygen Sag Equation for Second-Order BOD Decay,” Water Research, Vol. 32, No. 3, 1998, pp. 840-848. doi:10.1016/S0043-1354(97)00259-5
- H. W. Streeter and E. B. Phelps, “A Study of the Pollution and Natural Purification of the Ohio River,” Public Health Service, Bulletin No. 146, Washington DC, 1925.
- E. J. Theriault, “The Dissolved Oxygen Demand of Polluted Waters,” Public Health Service, Bulletin 173, Washington DC, 1927.
- G. M. Fair, “The Dissolved Oxygen Sag—An Analysis,” Sewage Works Journal, Vol. 11, 1939, p. 445.
- H. W. Streeter, “Measures of NATURAL Oxidation in polluted Streams. I. The Oxygen Demand Factor,” Sewage Works Journal, Vol. 7, No. 2, 1935, p. 251.
- H. A. Thomas, “The Slope Method for Evaluating the Constants of the First-Stage Biochemical Oxygen Demand Curve,” Sewage Works Journal, Vol. 9, 1937, pp. 425-430.
- H. A. Thomas, “The Pollution Load Capacity of Streams,” Water Sewage Work, Vol. 95, No. 11, 1948, p. 409.
- D. J. O’Connor, “Oxygen Balance of an Estuary,” Transactions, ASCE, Vol. 126, 1961, pp. 556-611.
- J. W. Clark and W. Viessman, “Water Supply and Pollution Control,” International Textbook Company, 1965, pp. 387-390.
- H. B. Braun and P. M. Berthouex, “Analysis of Lag Phase BOD Curves Using the Monod Equations,” Water Resources Research, Vol. 6, 1970, pp. 838-844. doi:10.1029/WR006i003p00838
- L. Somlyody, M. Henze, L. Koncsos, W. Rauch, P. Reichert, P. Shanahan and P. Vanrolleghem, “River Quality Modelling: III. Future of the Art,” Water Science and Technology, Vol. 38, No. 11, 1998, pp. 253-260. doi:10.1016/S0273-1223(98)00662-3
- A. Drolc and J. Z. Koncan, “Calibration of QUAL2E Model for the Sava River (Slovenia),” Water Science and Technology, Vol. 40, No. 10, 1999, pp. 111-118. doi:10.1016/S0273-1223(99)00681-2
- S. Cammara and C. W. Randall, “The Qual II Model,” Journal of Environmental Engineering, Vol. 110, No. 5, 1984, p. 993. doi:10.1061/(ASCE)0733-9372(1984)110:5(993)
- F. D. Masch and Associates, “QUAL-I Simulation of Water Quality in Stream and Canals, Program Documentation and User’s Manual,” Texas Water Development Board. 1970.
- Water Resources Engineers, Inc., “Computer Program Documentation for the Stream Quality Model QUAL-II. Prepared for US Environmental Protection Agency,” System Analysis Branch, Washington DC, 1973.
- L. C. Brow and T. O. Barnwell, “Computer Program Documentation for the Enhanced Stream Water Quality Model QUAL2E,” US Environmental Protection Agency, Athens, GA, EPA/600/3-85/065, 1985.
- R. Portielje, T. H. Jacobsen and K. S. Jensen, “Risk Analysis Using Stochastic Reliability Methods Applied to Two Cases of Deterministic Water Quality Models,” Water Research, Vol. 34, No. 1, 2000, pp.153-170. doi:10.1016/S0043-1354(99)00131-1
- Y. Icaga, “Fuzzy Evaluation of Water Quality Classification,” Ecological Indicators, Vol. 7, No. 3, 2007, pp. 710- 718. doi:10.1016/j.ecolind.2006.08.002
- P. S. Kunwar, A. Basant, A. Malik and G. Jain, “Artificial Neural Network Modeling of the River Water Quality—A Case Study,” Ecological Modeling, Vol. 220, No. 6, 2009, pp. 888-895.
- H. Cho, K. S. Sung and S. R. Ha, “A River Water Quality Management Model for Optimizing Regional Wastewater Treatment Using a Genetic Algorithm,” Journal of Environmental Management, Vol. 73, No. 3, 2004, pp. 229- 242. doi:10.1016/j.jenvman.2004.07.004
- H. G. Cheng, Z. F. Yang and C. W. Chan, “An Expert System for Decision Support of Municipal Water Pollution Control,” Engineering Applications of Artificial Intelligence, Vol. 16, No. 2, 2003, pp. 159-166. doi:10.1016/S0952-1976(03)00055-1
- H. H. Liao and U. S. Tim, “Interactive Water Quality Modeling within a GIS Environment. Computer,” Environment, and Urban Systems, Vol. 18, 1994, pp. 343-363. doi:10.1016/0198-9715(94)90016-7
- X. W. Zhang, F. Qin and J. F. Liu, “Method of Monitoring Surface Water Quality Based on Remote Sensing in Miyun reservoir,” Proceedings Bioinformatics and Biomedical Engineering 3rd International Conference, Beijing, 2009, pp. 1-4.
- H. Apel, N.G. Hung, H. Thoss and T. Schöne, “GPS Buoys for Stage Monitoring of Large Rivers,” Journal of Hydrology, Vol. 412-413, 2012, pp. 182-192. doi:10.1016/j.jhydrol.2011.07.043
- M. Q. Feng, B. M. Zheng and X. D. Zhou, “Water Environment Simulation and Prediction,” Science Press, Beijing, 2009, 181-197.
- Z. Z. Peng, T. X. Yang and X. J. Liang, “Mathematical Model of Water Environment and Its Application,” Chemical Industry Press, Beijing, 2007, pp. 98-103.
- State Environmental Protection Administration of China, General Administration of Quality Supervision, Inspection and Quarantine of China (GB38382-2002), “Environmental Quality Standards for Surface Water,” Environmental Science Press, Beijing, 2002.
- F. Boano, R. Revelli and L. Ridolfi, “Stochastic Modeling of DO and BOD Components in a Stream with Random Inputs,” Advances in Water Resources, Vol. 29, No. 9, 2006, pp. 1341-1350. doi:10.1016/j.advwatres.2005.10.007
- R. Revelli and L. Ridolfi, “Stochastic Dynamics of BOD in a Stream with Random Inputs,” Advances in Water Resources, Vol. 27, No. 9, 2004, pp. 943-952. doi:10.1016/j.advwatres.2004.05.009
- W. Li and Z. Shi, “Robust Estimation of Water Quality Model Parameters under Random Noise Disturbance,” Journal of Hydraulic Engineering, Vol. 37, No. 6, 2006, pp. 687-693.
- Z. B. Fang and B. Q. Miao, “Stochastic Process,” 2nd Edition, Science Press, Beijing, 2004, pp. 121-134.
NOTES
*Corresponding author.

