Smart Grid and Renewable Energy
Vol.2 No.4(2011), Article ID:8275,8 pages DOI:10.4236/sgre.2011.24042
Study of Solar Radiation in View of Photovoltaic Systems Optimization
![]()
1Mentouri University, Constantine, Algeria; 2Catholic University, Louvain la Neuve, Belgium; 3Renewable Energy Unit Research, Ghardaia, Algeria.
Email: *rachid.chenni@gmx.fr
Received December 10th, 2010; revised May 25th, 2011; accepted June 2nd, 2011.
Keywords: Photovoltaic, Sun Radiation, Sun Position, Turbidity Factor, Circumsolar Diffuse Radiation, Albedo
ABSTRACT
The meteorological data concerning solar radiation are generally not sufficient to allow quantifying all the phenomena which occur when a photovoltaic panel receives solar light. It is therefore, necessary to supplement these data by using astronomical calculation for the sun position and modelling the atmosphere. A simple method to calculate global, diffuse and direct irradiance on vertical and tilted surfaces for all uniform sky conditions (clear sky and overcast sky), developed in Constantine (Algeria) and Louvain-la-neuve (Belgium), has been compared with experimental data obtained at Ghardaia (Algeria). In spite of its simplicity, the method furnishes reasonably good predictions, in comparison with experimental data, and can be proposed as a simplified tool for design purposes. This method relies on the fact that we can calculate the irradiance on a plane with arbitrary orientation and inclination, based on the measurement of a single irradiance value on a reference plane.
1. Introduction
Solar energy is a sustainable and abundant energy resource. Estimating solar irradiation incident on inclined surfaces of various orientations is necessary to calculate the electric power generated by photovoltaic (PV) [1], to design solar systems and to evaluate their long-term average performance. Despite the fact that many meteorological/radiometric stations measure global and diffuse irradiation received on horizontal surfaces, the data on inclined surfaces are not available and are thus estimated with different models from those measured on horizontal surfaces.
Global radiation incident on a tilted plane consists of two components: direct radiation and diffuse radiation [2]. Perez et al. [3,4] developed two new and more accurate but considerably simpler versions of the original Perez diffuse irradiance model [5]. The original version has been used worldwide to estimate with a short time step (hourly or less) the irradiance on tilted surfaces based on global and direct (or diffuse) irradiances measured on a horizontal surface. Li and Lam [6] evaluated the anisotropic models of Klucher [7]; Hay [8] and Perez et al. models were applied to two-years of measured data in Hong Kong (1996-1997). All three models produced large errors for north-facing surfaces.
Predictions for south-facing surfaces showed reasonably good agreement with measured data. Kamali et al. [9] evaluated eight diffuse models to estimate solar irradiation on tilted surfaces using daily measured solar irradiation data in Iran and recommended the Reindl et al. [10] model for estimating solar irradiation on tilted surfaces. Notton et al. [11] evaluated the combination of some well-known models to estimate the hourly global solar irradiation on a tilted surface from those on a horizontal surface. They recommended the Klucher model separately or in combination with other models to estimate diffuse solar irradiation on surfaces tilted towards the equator.
All above mentioned authors worked on models requiring the experimental values of several radiation components, for example both global and diffuse values on a horizontal plane. However, in many cases, only one component of the irradiance is measured. Often, meteorological stations include global irradiation measurements on horizontal plane. On the other hand, in PV experimental plants, often global irradiance on the PV plane is measured.
Our paper shows that, from global irradiance measurements, we can quantify the various components solar radiation at the place considered. Then, it is possible to compute global irradiance or the effect of each irradiance component on a photovoltaic field of arbitrary orientation and inclination.
This paper describes a model which makes possible this decomposition.
2. Basic Assumptions for Splitting the Irradiance in Various Components
In practice, measurements on the ground allow for quantification of global radiation on a plant and it is almost impossible to have at a given place experimental data for all incident directions simultaneously. However, using some models, it is possible to split the measured radiation at a place in a number of components with simple directional distributions.
A first subdivision is to distinguish direct sunlight and diffuse radiation. The first component reaches a given place without having undergone absorption or diffusion from the atmosphere or reflection from the ground. The second is known as diffuse radiation, i.e. the one that comes to that place after having suffered one or more changes of direction; several components are involved.
The model first separates sky diffuse from ground diffuse as the direction is pointing to the sky or toward the ground. The sky diffuse will be seen as the sum of three components: an isotropic term, a circumsolar term and a horizon circle term. The ground diffuse, less important, is normally treated as a single isotropic component.
3. Definition of Used References
3.1. Plane Orientation and Inclination, and Sun Position, in Horizontal Coordinates
The processing of solar data requires the definition of several references. Their specific use is justified in the following. The orientation and inclination of a plane are characterized by variables a and b shown in Figure 1, where  is the vector perpendicular to the plane.
is the vector perpendicular to the plane.
The sun position at any moment is given by the azimuth of the sun a and its elevation h as shown in Figure 2.

Figure 1. Orientation a and inclination b.
The incidence angle on the considered plane is then given by
 (1)
(1)
3.2. Calculation of Sun Position and Angle of Incidence from Sun Time Coordinates
We can express the azimuth a, the elevation h and the angle of incidence against the hour angle H and solar declination δ, i.e. the time (equatorial) coordinates defined as shown in Figure 3. Angle d is defined by the direction of the sun with respect to the equatorial plane of the earth.
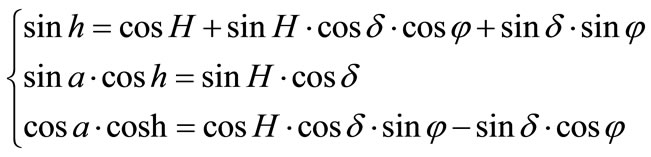 (2)
(2)
4. Determination of the Sun Position
4.1. Sun Time Coordinates
The declination d varies during the year between two extrema respectively equal to the ecliptic obliquity and its opposite. We can reference the approximate declination d (N), depending on the day of the year N, by:
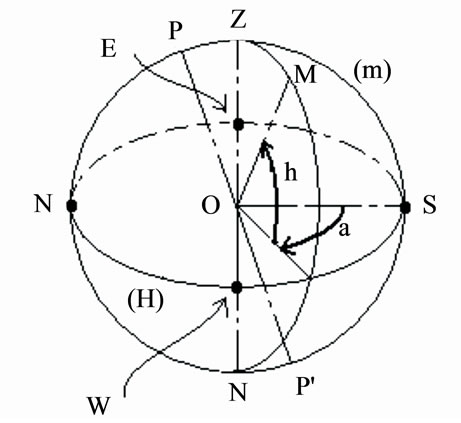
Figure 2. Horizontal coordinates.
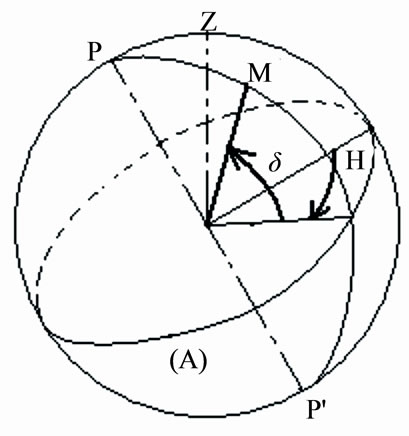
Figure 3. Time coordinates.
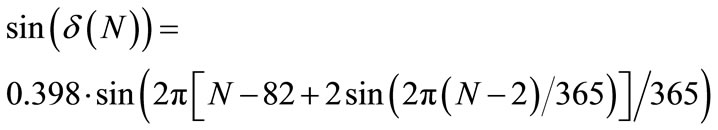 (3)
(3)
On the other hand, the angle H (in) is related to the local true solar time TSV (in hours) by the formula
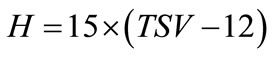 (4)
(4)
owing to the fact that a rotation of 360 of the earth take place in 24 hours.
4.2. Example
The hour angle H, the declination d, the azimuth a and the elevation h as a function of true solar time, can be observed in Figure 4 for Constantine latitude and six different dates in the year.
5. Sky Model
5.1. Extraterrestrial Irradiance
Outside atmosphere, global radiation has only one direct component. At a distance from the sun corresponding to
 (a)
(a) (b)
(b)
Figure 4. (a) Time coordinates H and d; (b) Horizontal coordinates a and h versus TSV (in hours).
the mean distance between earth and sun, the intensity of this radiation is:
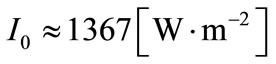 (5)
(5)
The variation of the earth-sun distance in one year alters the intensity of radiation actually received by the earth (outside atmosphere). It is therefore necessary to assign at the value of I0 a correction factor C(N) which could be calculated using Kepler’s laws, where N is the number of days of the year.
 (6)
(6)
where 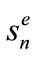 and
and 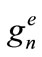 are the direct and global irradiation outside atmosphere.
are the direct and global irradiation outside atmosphere.
An approximate expression is:
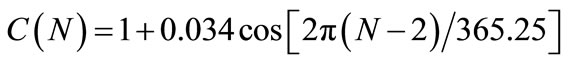 (7)
(7)
This leads to:
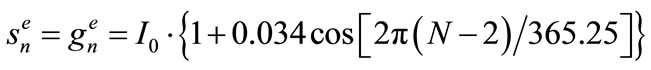 (8)
(8)
Extraterrestrial radiation received by the earth will vary as follows:
5.2. Attenuation of Radiation by Atmosphere
In the atmosphere, two phenomena will affect the radiation. A phenomenon of absorption and a phenomenon of diffusion will influence the radiation during its travel through the atmosphere.
In first approximation, the intensity of direct radiation decays exponentially in function of the relative atmospheric mass m
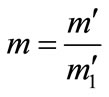 (9)
(9)
where m’ is the absolute atmospheric mass defined as the integral of air density along a solar ray

Figure 5. Variation of the global radiation outside atmosphere during the year.
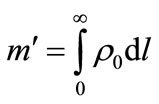 (10)
(10)
and m’1 the integral of standard air density in the vertical direction taken from the sea level.
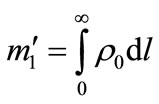 (11)
(11)
Transmission of monochromatic radiation through the atmosphere obeys Beer’s law, so that
 (12)
(12)
where I0λ is the incident radiation intensity of wavelength λ outside atmosphere, Iλ is the transmitted radiation intensity and m is the air mass in the path of radiation.
5.2.1. Reference Atmosphere
To characterize any atmosphere, it is compared to a known reference atmosphere which is defined as containing only gas (clean and dry atmosphere), including a given quantity of ozone, and being of uniform composition. [12]
For the total spectrum, one defines a mean factor k0 by
 (13)
(13)
5.2.2. Linke’s Turbidity Factor
For irradiance on a real atmosphere, it remains to introduce a factor T called total Linke’s turbidity factor as below:
 (14)
(14)
For reference atmosphere, it is obviously clear that T equal 1. This formula also shows that the irradiance will tend to 0 when T will tend to infinity.
5.2.3. Absorption and Diffusion Turbidity Factors
One admits that the Linke’s turbidity factor T can be split into an Linke’s absorption turbidity factor Tabs and a Linke’s diffusion turbidity factor T’, thus
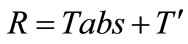 (15)
(15)
As an approximation, we assume [13] that Tabs depends only of the variable gas, i.e. the ozone layer thickness e (in mm) and of the water vapour contents w (in g/cm²). These quantities can be obtained from meteorological data or computed using local mean seasonal values.
One defines an absorption coefficient a by:
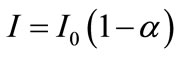 (16)
(16)
where I0 is the intensity of the light beam before it has passed through an absorbent medium and its intensity I output of it. The absorption coefficient due to ozone and water vapor will be aa1,w and is approximately
 (17)
(17)
Comparing this expression to the definition of the turbidity factor equation (14), taking into account only the component of the absorption turbidity factor, the following analogy may be observed at first order:
 (18)
(18)
This leads to the following relationship linking aa1,w to Tabs:
 (19)
(19)
It is thus possible to calculate the atmospheric absorption turbidity factor.
This graph raises some questions about the accuracy of the model used here. Indeed, the absorbing turbidity factor is supposed to be a characteristic parameter of the atmosphere. This quantity should be independent of the elevation h. So the dependence on h of the following expression should exist only through the concept of relative atmospheric mass. [14-16]
6. Radiation Components
Knowing the theoretical extraterrestrial radiation, it is possible to determine the different radiation components for each value of the Linke’s diffusion turbidity factor T’.
6.1. Direct Radiation
The Equation (13) gives the value of direct radiation on a normal surface. For a tilted surface, apparent intensity of direct radiation will be equal to:
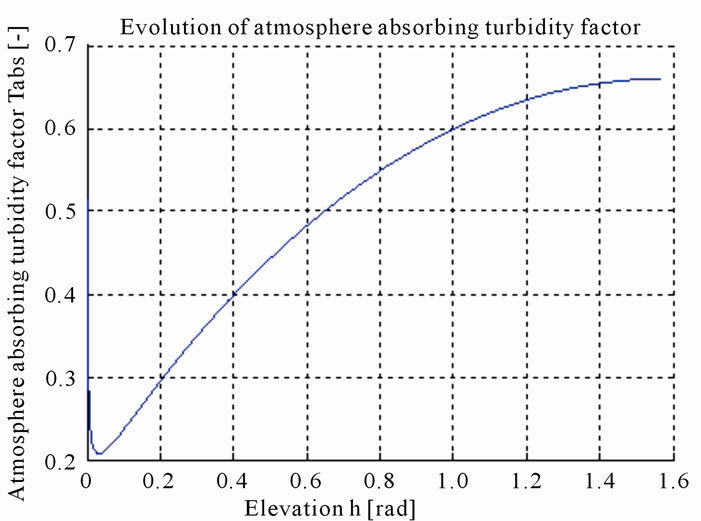
Figure 6. Atmosphere absorption turbidity factor.
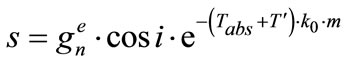 (20)
(20)
6.2. Diffuse Radiation:
6.2.1. Circumsolar Diffuse Radiation
The unidirectional component of the radiation is obtained by summing the direct radiation, and the circumsolar diffuse component dd , which leads to the expression:
 (21)
(21)
dd can be estimated by the following empirical formula:
 (22)
(22)
where:
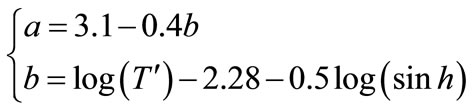 (23)
(23)
6.2.2. Diffuse Isotropic Radiation
The diffuse isotropic radiation consists of rays that reach the plane after one or several successive reflections. Some of the reflections take place on the ground so that the intensity of diffuse isotropic radiation depends on the ground reflectance, called albedo.
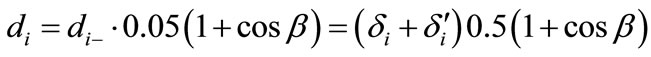 (24)
(24)
A semi-empirical expression of di is obtained by the difference
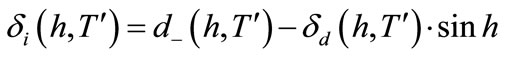 (25)
(25)
where:
 (26)
(26)
with:
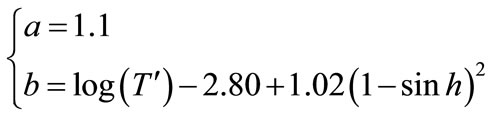 (27)
(27)
And a semi empirical expression for di' is:
 (28)
(28)
where Aregsoil the regional ground albedo and g- is the global irradiance on a horizontal plane. This component is:
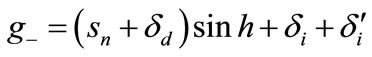 (29)
(29)
6.2.3. Diffuse Horizon Circle Radiation
The diffuse circle horizon radiation can be estimated by the expression (for a regional albedo 0.2):
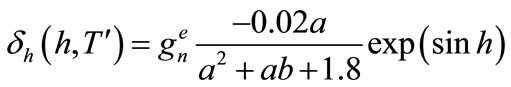 (30)
(30)
with:
 (31)
(31)
6.2.4. Ground Diffuse Radiation
An expression used to estimate this component is as follows:
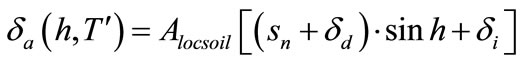 (32)
(32)
where Alocsoil the local soil albedo.
Finally, the diffuse radiation is written in the form of 4 components:
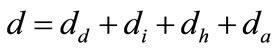 (33)
(33)
 (34)
(34)
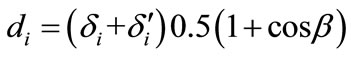 (35)
(35)
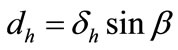 (36)
(36)
 (37)
(37)
6.3. Global Radiation
The intensity of global radiation incident at a given moment, on any surface characterized by angles (α,b) is
 (38)
(38)
6.4. Evolution of the Radiation against T'
The graph below shows the general evolution of the components of global radiation based on the Linke’s diffusion turbidity factor.
The graph below shows the general evolution of the components of global radiation based on the diffusion turbidity factor for the 12th hour throughout the year.
The following graph shows the evolution of radiation and its components for all hours of the day As we can see from this graph, the evolution of global radiation depends on time of day. Indeed, it is easy to understand that if the PV panels are not oriented towards the sun, the proportion of diffuse radiation is larger than in case they are oriented towards the sun. And as the intensity of the diffuse component from zero, passes through a maximum for a value of T’ different from zero.
6.5. Determination of the Linke’s Diffuse Turbidity Factor T'
If a measurement of the direct irradiance is available, the diffuse turbidity factor T' can be easily obtained by (14) (15) using a computed value of Tabs.
If only a measurement of the global irradiance is available, T' can be obtained by iteration in order to obtain by calculation the measured value. In some cases, as shown in Figures 7 to 9, the problem has two solutions. However, the ambiguity can generally be avoided considering the historical evolution of T'.
7. Data
The measuring station was located on the Applied Research Unit of Renewable Energy, Ghardaia (32.23°N, 3.81°E, elevation 450 m). The radiometric Ghardaia station using a three-dimensional system (Sun-Tracker) has two parts:
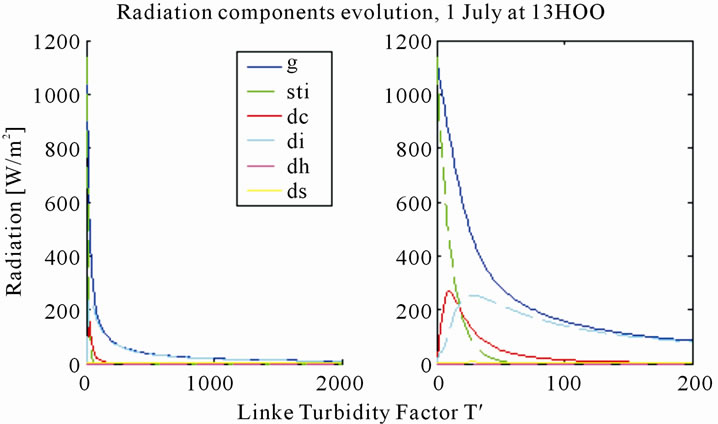
Figure 7. Radiation components evolution depending on linke’s diffusion turbidity factor.
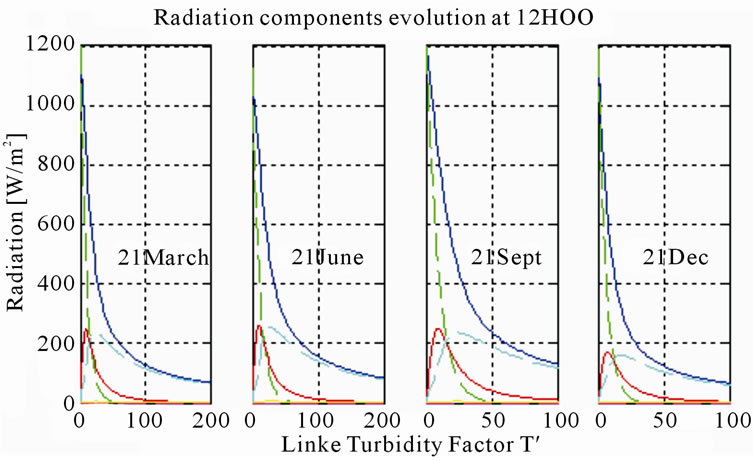
Figure 8. Radiation components evolution depending on linke’s turbidity factor t’ throughout the year.
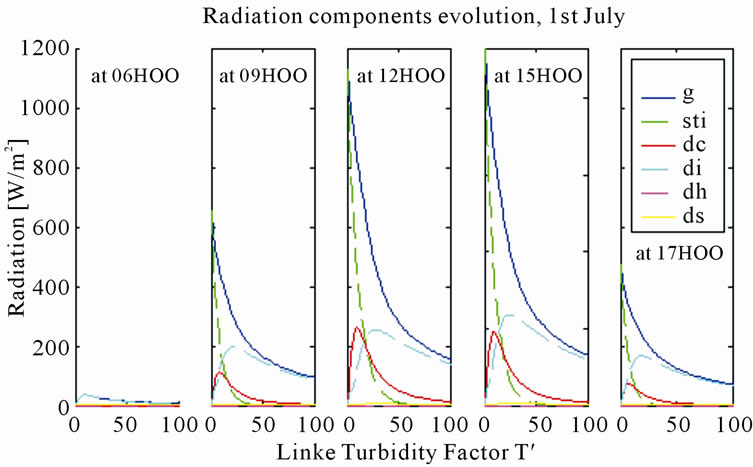
Figure 9. Variation of radiation different components depending on linke’s turbidity factor T'.

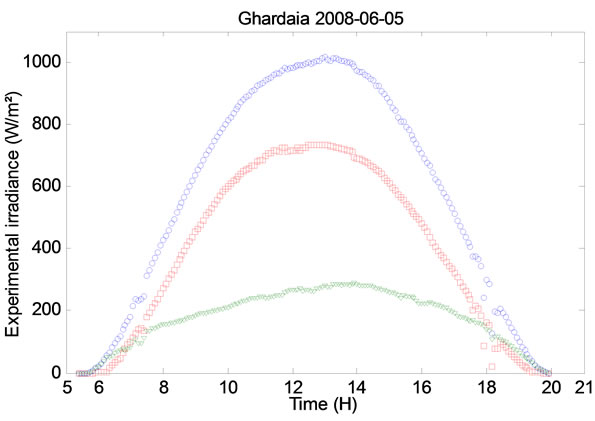
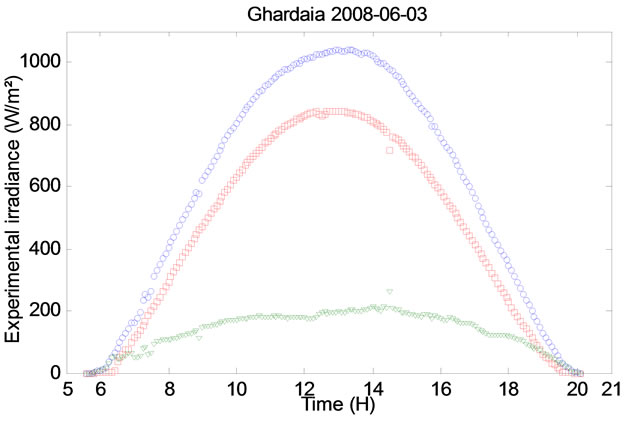
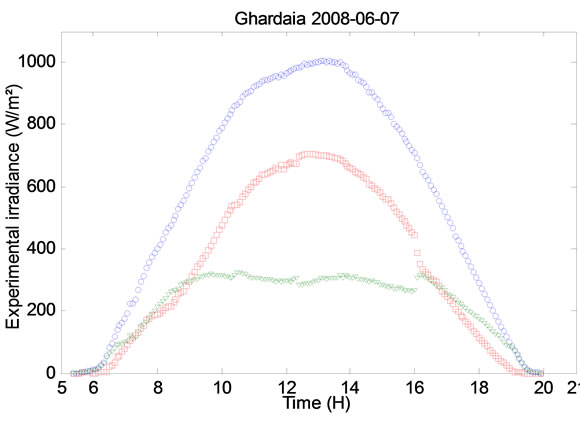
Figure 10. Experimental irradiance (1st, 3rd, 5th and 7th of June 2008).
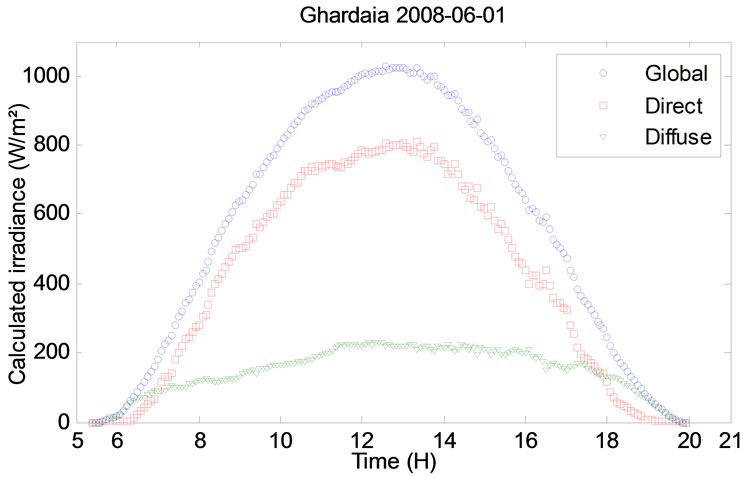
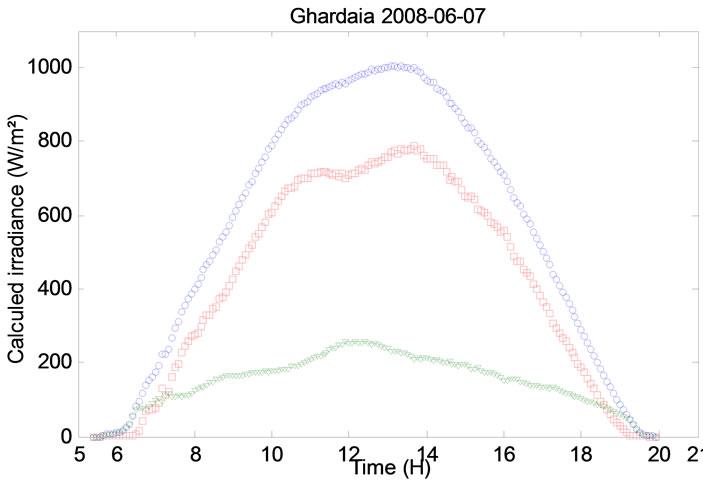
Figure 11. Calculated irradiance (1st and 7th of June 2008).

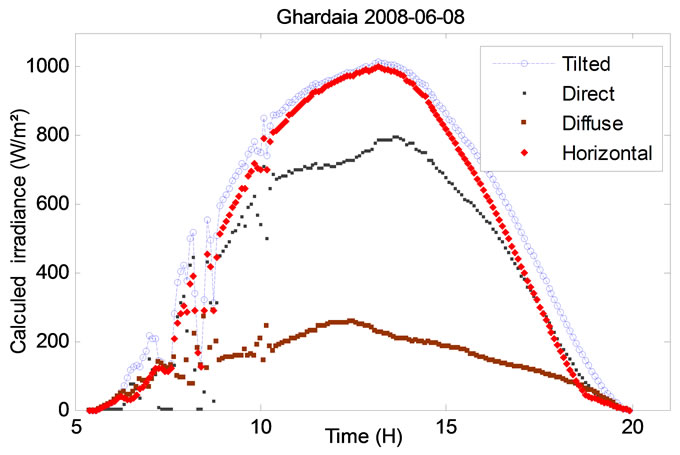
Figure 12. Experimental and calculated irradiance on Horizontal and tilted surface (8th of June 2008).
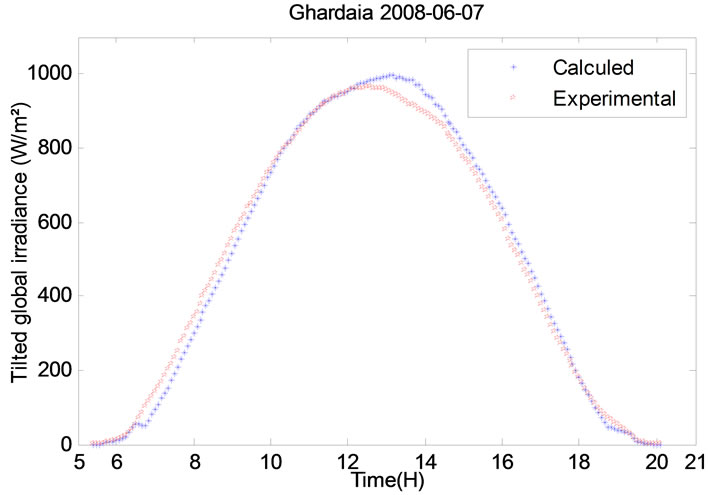
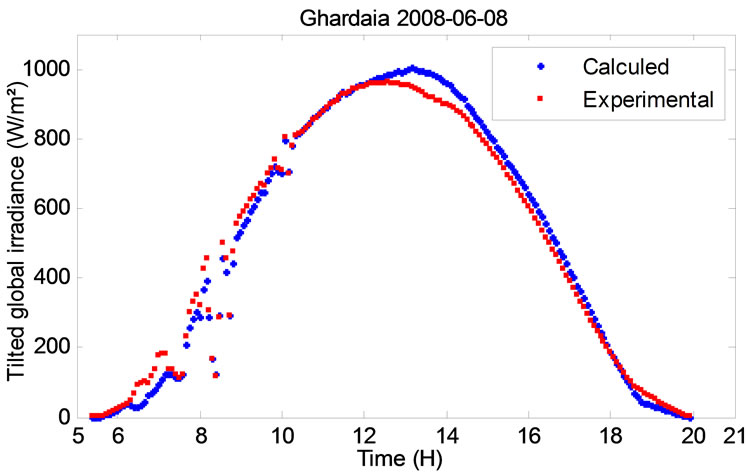
Figure 13. Experimental and calculated tilted global irradiance (7th and 8th of June 2008).
A fixed part which is EKO pyranometer for the measurement of global radiation received on a horizontal plane, thermohygrometer TECNOEL for measuring temperature and humidity, and a solarimeter. A movable part that is capable of following the path of the sun from sunrise to sunset. This part has a pyrheliometer which is pointed toward the solar disk, for measuring the normal direct solar radiation integrated over all wavelengths (between 0.2 μm and 0.4 μm) received and EKO pyranometer for the measurement of diffuse irradiance on a horizontal plane with a spherical ball to hide the radiative flux coming directly from the solar disk.
All devices listed above are linked to acquisition Campbell Scientific Cr10x. The data logger is connected to a PC via RS232 for data storage.
The solar radiation data measured by one of the authors, during the first 8 days of June 2008, were used in this study. Each consisted of 5 minutes, direct, diffuse and global solar radiation, on horizontal and tilted surface (32.23˚ south-facing).
8. Results
Shown in Figures 10-13.
9. Conclusions
This paper has provided a model that allows, only on knowledge of global radiation on one plane, determining the different directional components of sunlight. This model is not free of defects, as shown by the first numerical results. Nevertheless, it will allow us to determine the effectiveness of radiation. This efficiency is dependent on several phenomena of reflection, refraction and absorption. Even if there are errors in the calculation of these components, this model still allows us to develop a computer code that takes into account the directional properties of the irradiance.
REFERENCES
- C. L. Cheng and C. Y. Chan, “An Empirical Approach to Estimating Monthly Radiation on South-Facing Tilted Planes for Building Application,” Energy, Vol. 31, No. 14, 2006, pp. 2940-2957. doi:10.1016/j.energy.2005.11.015
- S. Burlon, S. Bivona and C. Leone, “Instantaneous Hourly and Daily Radiation on Tilted Surfaces,” Solar Energy, Vol. 47, No. 2, 1991, pp. 83-89. doi:10.1016/0038-092X(91)90038-X
- R. Perez, P. Ineichen and R. Seals, “Modelling Daylight Availability and Irradiance Components from Direct and Global Irradiance,” Solar Energy, Vol. 44, No. 5, 1990, pp. 271-289. doi:10.1016/0038-092X(90)90055-H
- R. Perez, R. Seals, P. Ineichen, P. Stewart and D. Menicucci, “A New Simplified Version of the Perez Diffuse Irradiance Model for Tilted Surfaces,” Solar Energy, Vol. 39, No. 3, 1987, pp. 221-223. doi:10.1016/S0038-092X(87)80031-2
- R. Perez, R. Stewart, C. Arbogast, R. Seals and J. Scott, “An Anisotropic Hourly Diffuse Radiation Model for Sloping Surfaces, Description, Performance Validation, Site Dependency Evaluation,” Solar Energy, Vol. 36, No. 6, 1986, pp. 481-497. doi:10.1016/0038-092X(86)90013-7
- D. H. W. Li and J. C. Lam, “Evaluation of Slope Irradiance and Illuminance Models Against Measured Hong Kong Data,” Build Environ, Vol. 35, No. 6, 2000, pp. 501-509. doi:10.1016/S0360-1323(99)00043-8
- T. M. Klucher, “Evaluation of Models to Predict Insolation on Tilted Surfaces,” Solar Energy, Vol. 23, No. 2, 1979, pp. 111-114. doi:10.1016/0038-092X(79)90110-5
- J. E. Hay, “Calculation of Monthly Mean Solar Radiation for Horizontal and Inclined Surfaces,” Solar Energy, Vol. 23, No. 4, 1979, pp. 301-30. doi:10.1016/0038-092X(79)90123-3
- G. A. Kamali, I. Moradi and A. Khalili, “Estimating Solar Radiation on Tilted Surfaces with Various Orientations: A Study Case in Karaj (Iran),” Theoretical and Applied Climatology, Vol. 84, No. 4, 2006, pp. 235-241. doi:10.1007/s00704-005-0171-y
- D. T. Reindl, W. A. Beckman and J. A. Duffie, “Evaluation of Hourly Tilted Surface Radiation Models,” Solar Energy, Vol. 45, No. 1, 1990, pp. 9-17. doi:10.1016/0038-092X(90)90061-G
- G. Notton, P. Poggi and C. Cristofari, “Predicting Hourly Solar Irradiations on Inclined Surfaces Based on the Horizontal Measurements: Performances of the Association of Well-Known Mathematical Models,” Energy Convers Manage, Vol. 47, No. 13-14, 2006, pp. 1816-1829. doi:10.1016/j.enconman.2005.10.009
- F. Kasten and A. T. Young, “Revised Optical Air Mass Tables and Approximation Formula,” Applied Optics, Vol. 28, No. 22, 1989, pp. 4735-4738. doi:10.1364/AO.28.004735
- M. Capderou, “Atlas Solaire De L’Algerie, Office Des Publications Universitaires,” University Publications Office, Algiers, 1988.
- Q. Wang, “Estimation of Total, Direct and Diffuse PAR under Clear Skies in Complex Alpine Terrain of the National Park Berchtesgaden Germany,” Ecological Modelling, Vol. 196, No. 1-2, 2006, pp. 149-162. doi:10.1016/j.ecolmodel.2006.02.005
- B. Y. H. Liu and R. C. Jordan, “The Interrelationship and Characteristic Distribution of direct, Diffuse and total Radiation,” Solar Energy, Vol. 4, No. 3, July 1960, pp. 1-19. doi:10.1016/0038-092X(60)90062-1
- S. A. Klein, “Calculation of Monthly Average Insolations on Tilted Surfaces,” Solar Energy, Vol. 19, No. 4, 1977, pp. 325-329. doi:10.1016/0038-092X(77)90001-9

