Creative Education
Vol.06 No.12(2015), Article ID:57807,9 pages
10.4236/ce.2015.612130
Understanding of Number Concepts and Number Operations through Games in Early Mathematics Education
Lu Chung Chin, Effandi Zakaria
Department of Teaching and Learning Innovation, Faculty of Education, Universiti Kebangsaan Malaysia, Bangi, Malaysia
Email: effandi@ukm.edu.my
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2015; accepted 5 July 2015; published 8 July 2015
ABSTRACT
Games Based Learning Module (GBLM) in this study has been designed and adapted by the researcher by referring to the National Pre-school Standard Curriculum (NPSC) and local context. The games were developed to test the effectiveness toward the mastery of number concepts and number operations comprehension. In this research, number concepts cover the skills of counting and comparing. Both these skills are basic mathematics that must be mastered by children before they could pursue advanced mathematics learning. Number operations include the skills of addition and subtraction. This research used quasi-experimental design with non-equivalent control group pretest/posttest research design. The experimental group consisted of 23 pre-school pupils while the control group comprised of 24 pre-school pupils. The experimental group used the GBLM module while the control group used the traditional methods. Research data was analyzed using SPANOVA (Split Plot ANOVA Test). The results show that there is significant main effect of pre-posttest and interaction effect of pre-post and group. The results also show that there is no significant main effect of group.
Keywords:
Games, Number Concepts, Number Operations, Mathematics Education

1. Introduction
Early education plays an important role in the development of children’s and can help reduce current learning problems and achievement. The Ministry of Education of Malaysia has included preschool education in the National Education System under the provisions of the Education Act 1996. The formulation of the National Preschool Curriculum (NPC) in the year 2003 became the turning point in the structure of curriculum innovation for preschool education. NPC that was implemented until the end of 2009 was to nurture the potential of pupils in all aspects in terms of development, basic skills and cultivation of positive attitudes as a preparation to enter primary school (Kementerian Pelajaran Malaysia, 2003) . The formation of the National Preschool Standard Curriculum (NPSC) replaced the NPC beginning from 2010 to achieve the objectives in physical, emotional, spiritual, intellectual and social aspects (JERI) (Kementerian Pelajaran Malaysia, 2009). NPSC stresses on learning through play because play is important in fostering comprehensive development and needs to be combined with all the things that children do (Nor Hashimah & Yahya, 2003) . This is because play is life and is the highest level in the development of children as stated by Froebel (Azizah, 2002) .
Numerical skills are considered as a skill that enables an individual to control his or her daily life more effectively (Kementerian Pelajaran Malaysia, 2011) . However, Malaysian students’ performance in the subject of Mathematics is still low at the international level and showed a decline in Trends of International Mathematics and Science Study (TIMSS) from the year 1999 to 2011. The average score of mathematics for Malaysian students in grade 8 (Form 2) declined from the year 1999 (519), year 2003 (508), year 2007 (474) and year 2011 (440). Apart from that, mathematics performance of Malaysian students in the Programme for International Student Assessment (PISA) in the year 2010 was also less satisfactory. They only managed to accumulate an average score of 404 (Walker, 2011) . This shows that nearly 60% of our students of 15 years of age who participated in PISA failed to achieve the minimum level in mathematics (Kementerian Pelajaran Malaysia, 2012) . At the national level, the results of the Primary School Evaluation Test (UPSR) for the subject of mathematics are still of concern. Every year, there are still a large number of pupils obtaining grade D or E for the subject of mathematics (Lembaga Peperiksaan Kementerian Pelajaran Malaysia, 2008, 2009, 2010, 2011, 2012) .
Mastery of mathematics at the early stage of schooling, which is preschool, is really crucial and becomes the indicator of achievement and mastery of advanced mathematics (Sarama, Lange, Clements, & Wolfe, 2012) . Literature review shows that mastery of number concepts at the preschool stage plays an important role in the development of mathematics achievement in year one, two, three, four, five, eight and at the secondary level (Jordan, Kaplan, Ramineni, & Locuniak, 2009; Locuniak & Jordan, 2008) . This is due to the process of learning mathematics that is hierarchical in nature in which higher level skills can only be mastered after the lower level skills have been mastered and involves combination of understanding in terms of concept and procedure (Aunola, Leskinen, Lerkkanen, & Nurmi, 2004) .
Teaching and learning with the games approach at the early mathematics stage is one of the strategies that have been recommended by researchers and child education experts. Literature review shows that problems of number concept and number operation mastery at the early mathematics stage can be overcome with organized games’ activities (Clark & Roche, 2010; Siegler & Ramani, 2008; Yong, 2008) . This is in line with the views and efforts of several children’s education experts such as Froebel (1782-1852), Margaret McMillan (1860-1931) and Susan Isaacs (1885-1948). They believe that playing is children’s preferred activity and the activity of playing provides an enjoyable environment for effective learning (Bruce & Meggitt, 2007) . In addition, the integration of play in children’s early curriculum is also emphasized in the National Association for Education of Young Children (National Association for the Education of Young Children, 2009) . In Malaysia, learning through play also emphasized in the National Preschool Standard Curriculum (Kementerian Pelajaran Malaysia, 2009) . This is because the approach of playing is suited to the nature and development of children (National Association for the Education of Young Children, 2009; Salma, 2010) . However, we are encountered with many challenges and problems in implementing the approach in the preschools. The studies found that most of the Malaysia’s preschool teachers are facing difficulties to implement game-based approach, due to the lack of knowledge and skills (Saayah, 2005; Sharifah & Aliza, 2012) . Needs analysis of the research, which was conducted by the researcher on 20 preschool teachers from the state of Sarawak showed that 100% of the preschool teachers agreed that there is a need for developing a module as a guideline to implement game-based teaching and learning in early mathematics.
Many studies on the effectiveness of game approaches on mathematics education were implemented in urban schools. At the same time, game-based approaches which involve the use of advanced technologies such as digital games or video games become the focus of many researchers. These studies focus on children from low-income backgrounds and medium enterprises (Ramani & Siegler, 2011) . Studies related to the game-based approach in teaching and learning is rarely done in rural schools especially for preschool. This is due to the lack of advanced technologies infrastructures and the vulnerability of rural locations (Adam, Kassim, & Salleh, 2009) especially in Sarawak. The game-based approach for this study emphasizes on the manipulative games. The materials used in this study are easily available in rural areas. There are few studies about the impact of using the teaching and learning module based on hands-on manipulatives games. Therefore, this study can be an example for educators to teach young children number concepts and number operations using structured and organized plans in the form of module to achieve teaching and learning objectives.
The main objective of this research is to compare the effectiveness of the use of GBLM in the mastery of preschool number concepts and number operations. The detailed objectives of the research are to:
1) Identify the trend of mathematics achievement scores of students across three testing time (pre, post 1, post 2).
2) Identify the effectiveness of GBLM in developing pupils’ comprehension of number concepts (counting and comparing) and number operations (addition and subtraction).
2. Conceptual Framework
Constructivism theory supports the Games Based Learning Module (GBLM). According to Jean Piaget, development of children of the age of 5 - 6 years old goes through cognitive development at the pre-operational phase. Children at this stage require concrete materials to help in the learning process. Games approach in manipulative form is suitable for children of this age level. Games approach is also supported by the Social Interaction Theory pioneered by Vygotsky (1978) . While playing, children will interact with their peers. At the same time, the scaffolding process occurs when peers provide help to others in the games. Even though GBLM emphasizes student centered activity, scaffolding will also be provided by the class teacher from time to time. In this study, both the dimensions of knowledge and cognitive process dimensions of Bloom Taxonomy used in GBLM. Learning Standards are organized according to level of difficulty from easy to difficult. In terms of the game, the difficulty level is also determined not to be too easy or too difficult for children. Morrison, Ross & Kemp (MRK) instructional design model was used for the development of GBLM module which provides a series of steps that should be followed exactly in order to produce effective teaching material and enables more efficient, more effective and less difficult learning (Morrison, Ross, Kalman, & Kemp, 2013) . The 5E learning cycle means that the class T & L cycle is organized beginning from the engagement stage, exploration stage, explanation stage, elaboration stage and evaluation stage (Bybee et al., 2006) . Games are used in the elaboration stage. In this phase, children will be applying knowledge of number concepts and number operations in the prepared games activities. This means that children have early knowledge of a number concept or number operation that is exposed by the teacher at the explanation stage. Therefore, the outcome expected at the end of this research is improvement and enhancement in the children’s skills of counting, comparing, addition and subtraction.
3. Game Approach in GBLM
Games approach in GBLM involves manipulative games that have been designed or adapted by the researcher. All the games are in accordance with learning standard of 5 year old children. Number concepts and number operations from 1 to 20 are emphasized as outlined in the National Preschool Standard Curriculum (NPSC). All these games start with rules that can be easily understood and followed by children. Rules are flexible and can be changed as needed. The context of the games is local in nature and specific for preschool in rural primary schools. The materials used in the construction of the play set consist of materials that can be easily found such as mineral bottle caps, stones, egg cartons or containers, rubber bands and many others.
Children learn number concepts and number operations through game activities that have many possibilities and in varying conditions. Each step or movement in the game is a problem solution. As an example, in the game “WHO IS BIG, LET’S EAT”, there are different token arrangements each time the game starts through the process of “cleaning”. There are many possibilities of encounters of red colored tokens (1 to 10) and green colored tokens (1 to 10). This means that children will be exposed to a situation that is very different from drill and practice that involves fixed and written questions. At the same time, children are mutually correcting the movement steps of the game, reminding peers of their turn to play, sharing ideas or thoughts in addition to learning social skills such as cooperation.
The following discussion is related to the game ‘WHO IS BIG, LET’S EAT’ that has been specifically created to integrate skills of counting objects and comparing the magnitude of numbers from 1 to 10.
The followings are the rules for this game:
1) This game consists of ten pieces of tokens numbered 1 to 10 in red and ten pieces of tokens numbered 1 to 10 in green. All the numbered tokens are placed on the table with the face lying down.
2) Suitable to be played by 2 players with the choice of red or green colored tokens respectively.
3) The first player will open a piece of numbered token followed by the second player.
4) Players are free to open the numbered tokens. When there are two pieces of numbered tokens next to each other, the player that opens the numbered token then needs to determine whether he or she can ‘eat’ the opponent’s numbered token or be ‘eaten’ by the opponent.
5) The player with the token that has a bigger number than the opponents can ‘eat’ the opponent’s token by taking out the token and making it his or hers.
6) The game is played until all the opponent’s tokens have been ‘eaten’. Players can move their tokens one square at a time in any direction (up, down, left or right) to look for their prey.
7) The winner is the player that has more tokens at the end of the game.
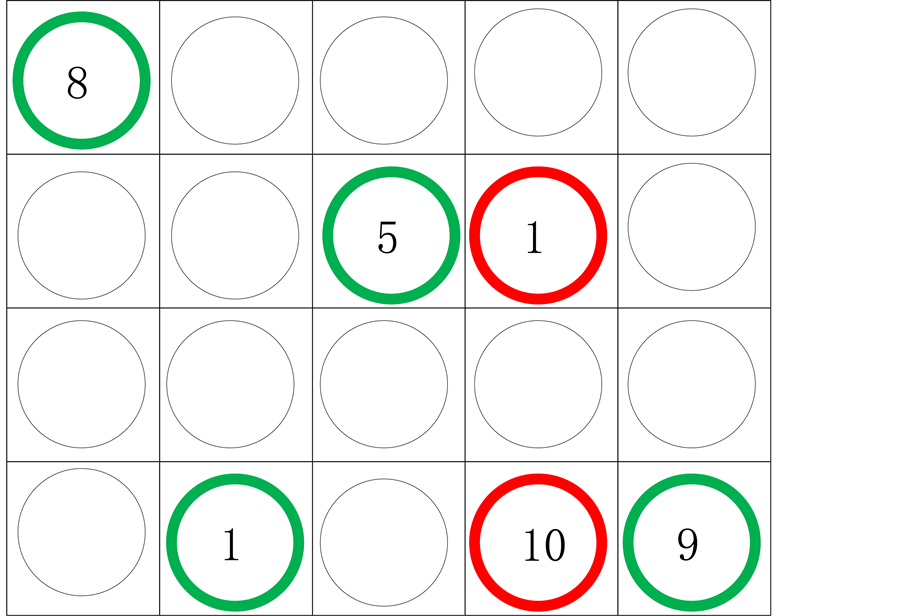
Explanation for Figure 1:
All tokens are placed faced down.
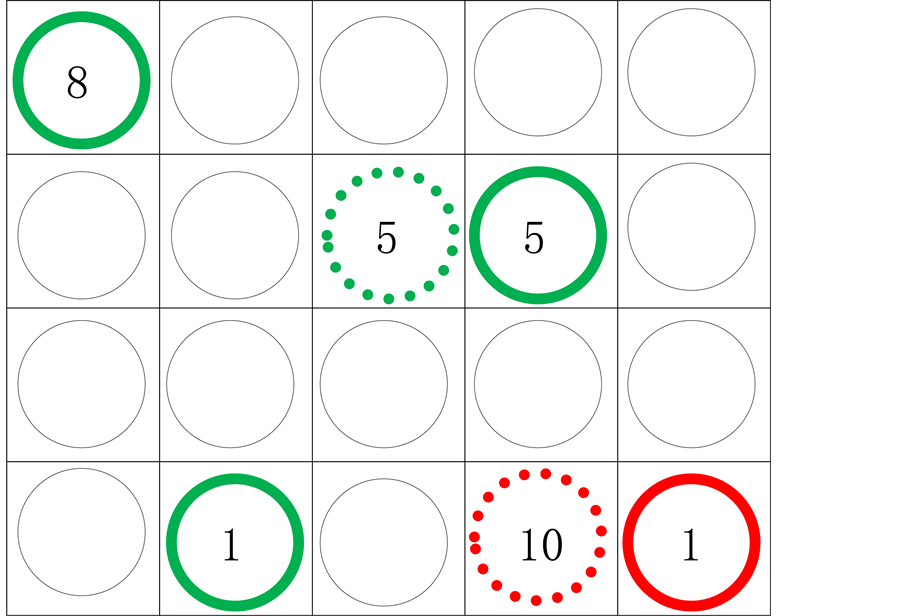
Explanation for Figure 2:
1) Player A (green) and player B (red).
2) Player A opens the “5” green token, followed by player B who opens “9” green token.
3) Player A opens “1” green token, followed by player B who opens “9” green token.
4) Player A opens “5” green token. As “5” is bigger than “1”, therefore player A (green) can “eat” the “1” red token by taking it out of the grid.
5) The game is continued with player B opening “10” red token. As “10” is bigger than “9”, therefore player B (red) can “eat” the “9” green token by taking it out of the grid.
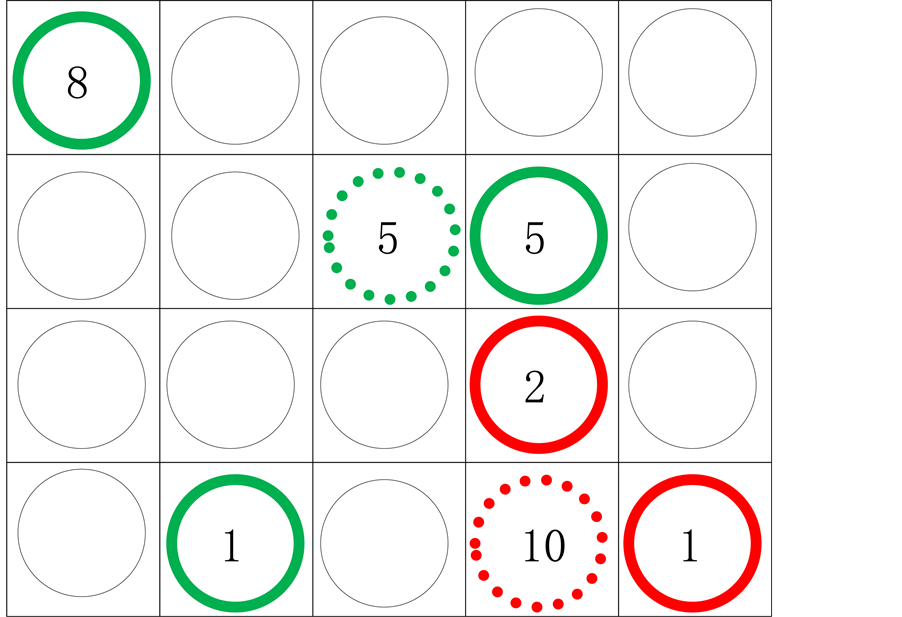
Explanation for Figure 3:
1) Token numbered “1” red is “eaten” by the opponent who is numbered “5” green.
2) The token numbered “9” green is “eaten” by the opponent’s token numbered “10” red.
3) The game continues.
Explanation for Figure 4:
Player A opens the “2” red token. Since the red token is not owned by player A, therefore there is nothing that can be done next by player A. It is the turn of player B to continue the game.
Figure 1. Step 1 of “Who Is Big, Let’s Eat”.
Figure 2. Step 2 of “Who Is Big, Let’s Eat”.
Figure 3. Step 3 of “Who Is Big, Let’s Eat”.
Figure 4. Step 4 of “Who Is Big, Let’s Eat”.
4. Methodology
This research used quasi-experimental design with non-equivalent control group pre-test/post-test research design. The experimental group consisted of 23 pre-school pupils while the control group comprised of 24 pre- school pupils. The experimental group used the GBLM module while the control group used the traditional methods. Pupils’ achievement was measured using Mathematics Achievement Test that has been developed by the researcher. Achievement test comprises of 45 questions (25 questions of number concepts and 20 questions of number operations) with a full mark of 45.
5. Findings
Table 1 shows the results of descriptive statistics between pretest and posttest of the experimental group and the control group.
In the pretest, the lowest score for the experimental group math achievement score was 0 and the highest was 40, based on 45 points. Mean score was 15.26 (s.d = 13.35). For the control group, the lowest score for math achievement was 0 and the highest score was 45. Mean score was 22.79 (s.d = 14.49).
In the posttest 1, the lowest score for the mathematics achievement of the experimental group was 5 and highest score of 45, based on 45 points. Mean score was 34.17 (s.d = 13.72). For the control group, the lowest score for math achievement was 0 and the highest score was 45.Mean score was 25.08 (s.d = 14.16).
In the posttest 2, the lowest score for the mathematics achievement of the experimental group was 7 and the highest score was 45, based on 45 points. Mean score was 33.35 (s.d = 10.75). For the control group, the lowest score for math achievement was 4 and the highest score was 45, by 45 points. Mean score was 31.54 (s.d = 12.47).
Research data was analyzed using SPANOVA (Split Plot ANOVA Test). Here are the hypotheses testing for math achievement:
H01: There were no significant differences in mathematics achievement scores of pupils across three testing time (pre, post 1, post 2).
Table 1. Descriptive Statistics of Mathematics Achievement Test.
Table 2 shows the results of the variance analysis for comparison between pretest and posttest of the experimental group and the control group. H01is rejected, [F (2, 44) = 33.94, p < 0.05]. There was main effect of pre-posttest for mean score in mathematics achievement.
Pillai’s Trace value of Pre-Post Test was 0.607 with significant value 0.000 (p < 0.05) showed that there were significant effects in terms of Pre-Post Test. This indicates that there was a change of mathematics achievement scores cross the three testing time of pre-test, posttest 1 and posttest 2. Effect across the testing time was significant. According to Cohen (1988) , the effect size is small if the η2 = 0.01, medium if the η2 = 0.06 and very large if the η2 = 0.14. From the analysis, the effect sizes of Pre-Posttest was very large with the Partial Eta Squared, η2 = 0.607 which means 60.7% of power. Thus, theresearcherrejectH01andreported that there were significant differences in mathematics achievement scores of students across three testing time (pre, post 1, post 2).
H02: There were no significant differences in mathematics achievement scores between the experimental group and the control group.
Table 3 shows the results of between-subjects effect for main effect of group. There was no main effect of group for the mean score in mathematics achievement between experimental group and control group.
Results showed that the mean math scores for both experimental and control groups did not differ significantly [F (1, 45) = 0.106, p > 0.05]. From the analysis, the effect sizes for group was small with the Partial Eta Squared, η2 = 0.002 which has a power of 0.2%. Thus, the researcher failed to reject H02. There were no significant differences in mathematics achievement scores between the experimental group pupils with a control group.
The graph in Figure 5 clearly shows that there was interaction effect of math scores between the experimental group and the control group across all three tests, in which the mean math scores for the experimental group (using GBLM) increases linearly from pre-test (test 1) to post-test 1 (test 2) and decreased slightly in the post-test 2 (test 3), while the mean math scores for the control group (traditional method) increases linearly from pre-test (test 1) to post-test 2 (test 3). However, the math scores of the experimental group was lower compared to the control group at an early stage (pretest), but the math scores of the experimental group surpassed the mean math scores for the control group across the post-test 1 and post-test 2. Findings related to achievement in the pre-test and post-test show that participants (experimental group) who followed GBLM showed higher increase in their number concepts and number operations understanding compared to the control group who received traditional mathematics activity (refer to Figure 5). These findings show that the games approach was able to increase the learners’ number concepts and number operations achievement.
6. Discussion
The pretest and post test results show that the children in the experimental group demonstrated better achievement in comparison to the children in the control group. The use of GBLM significantly influenced the results of number concepts and number operations from the pretest score to the posttest score especially for the experimental group.
・ Number Concepts
The research conducted on children’s comprehension in counting skills gave focus on 3 key concepts to enable meaningful calculation (Gelman & Gallistel, 1986) :
1) One to one: each object should have one unique number word.
2) Stable order: order of number word should be maintained each time counting process is made such as one, two, three, four…
Figure 5. Graph of mathematics achievement scores.
Table 2. SPANOVA result for mathematics achievement.
Table 3. Between-subjects effect for main effect of group.
3) Cardinality: the last number word counted represents the total of objects in the set.
Children in the experimental group had many experiences of counting and comparing such as counting the number of dots in the game “We’re the Same”, counting the number of tokens at the end of the game “Who’s Big, Let’s Eat”, comparing the magnitude of numbers throughout the game “Who’s Big, Let’s Eat”. All these games included the three principles above. Besides, most of the games in the GBLM are linearly arranged with equal-size spaces. This is important which provide multiple cues to both the order of numbers and numbers’ magnitudes as noted by Siegler and Booth (2004) that in such games, the greater the number in a square, the greater a) the distance that the child has moved the token, b) the number of discrete moves the child has made, c) the number of number names the child has spoken, d) the number of number names the child has heard, and e) the amount of time since the game began. Therefore, the researchers made the hypothesis that the experimental group will be able to demonstrate a far better achievement of number concepts and number operations than the control group. Recent research by Ramani and Siegler (2008) indicates that the positive effects of playing numerical board games improve the counting, number identification and numerical magnitude comparisons skills of preschoolers from low-income families. Ramani (2005) also indicates that card games and board games helped the participants develop their counting skills although there was no significant difference between the experimental group and control group. Thus, the use of GBLM helped the participants of the experimental group in developing counting and comparing skills.
・ Number Operations.
The result also showed that various games involving addition and subtraction activities help children in the posttest achievement. Children are capable of building number relationship and expanding arithmetic because all numbers are the repeated addition of one. In this study, children of the experimental group were exposed to various games involving addition and subtraction such as “Rambutan oh Rambutan”, “Burger”, and “Who’s Quick”. Therefore, GBLM significantly influenced learning of number operations (1 to 10) of the experimental group children compared to the traditional mathematics activities of the control group. This result in line with the research by Ramani (2005) which indicates that card games and board games significantly affected young children’s learning of addition (under 10 objects) in experimental group compared to the traditional activity (the control group). Recent research by Wang and Hung (2010) indicates that experimental group children (using teacher-designed board game) did better than contrast group children especially in addition-subtraction test. Children from both groups scored 58.3% at Addition-subtraction in the pretest; but the experimental group children managed to achieve 93.7% in the posttest, compared with 72.9% from their counterparts. Research by Bjorklund and Rosenblum (2001) indicates that children showed significantly greater speed and accuracy when adding numbers during the game activities than in the math problems that followed. Thus, the use of GBLM helped the participants of the experimental group in developing addition and subtraction skills.
7. Conclusion
The use of GBLM significantly influenced the results of number concepts and number operations from the pretest score to the posttest score. Early mathematics understanding by pre-school children is crucial to mathematics learning. Mastery of number concepts is the basis of mastery of number competence and further mathematics system. The effort of instilling pupils’ interest and enhancing their motivation level toward learning of mathematics should be emphasized from early on so that they will not be afraid or prejudiced of this subject later on at a higher level. Learning through play is one of the approaches that could nurture interest of mathematics learning among children. As children invest time and energy in play, there are opportunities for learning when they do play. Besides, verbal reinforcement from the teacher during games play may build students’ self-confidence, competence, and self-esteem.
References
- Adam, Z., Kassim, F., & Salleh, M. J. (2009). Memperkasakan pendidikan luar bandar. Paper presented at the PersidanganKebangsaan Pendidikan Luar Bandar 2009, Kota Kinabalu.
- Aunola, K., Leskinen, E., Lerkkanen, M.-K., &Nurmi, J.-E. (2004). Developmental Dynamics of Math Performance from Preschool to Grade 2. Journal of Educational Psychology, 96, 699-713. http://dx.doi.org/10.1037/0022-0663.96.4.699
- Azizah, L. N. (2002). Pendidikan Awal Kanak-kanak: Teoridan Amali. Kuala Lumpur: PenerbitUniversiti Malaya.
- Bjorklund, D. F., & Rosenblum, K. E. (2001). Children’s Use of Multiple and Variable Addition Strategies in a Game Context. Development Science, 4, 184-194. http://dx.doi.org/10.1111/1467-7687.00164
- Bruce, T., & Meggitt, C. (2007). Child Care and Education. London: Hodder Headline Group.
- Bybee, R. W., Taylor, J. A., Gardner, A., Van Scotter, P., Carlson Powell, J., Westbrook, A., & Landes, N. (2006). The BSCS 5E Instructional Model: Origins and Effectiveness. Colorado Springs, CO: BSCS.
- Clark, D., & Roche, A. (2010). The Power of Single Game to Address a Range of Important Ideas in Fraction Learning. Australian Primary Mathematics Classroom, 15, 18-24.
- Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences (Ed. Ke-2 ed.). New York: Lawrence Erlbaum Associates.
- Gelman, R., & Gallistel, C. R. (1986). The Child’s Understanding of Number. Cambridge: Havard University Press.
- Jordan, N. C., Kaplan, D., Ramineni, C., & Locuniak, M. N. (2009). Early Math Matters: Kindergarten Number Competence and Later Mathematics Outcomes. Dev Psycho, 45, 850-867. http://dx.doi.org/10.1037/a0014939
- Kementerian Pelajaran Malaysia (2003). Huraian Kurikulum Prasekolah Kebangsaan. Kuala Lumpur: Dewan Bahasa Dan Pustaka.
- Kementerian Pelajaran Malaysia (2009). Kurikulum Standard Prasekolah Kebangsaan. Putrajaya: Bahagian Pembangunan Kurikulum.
- Kementerian Pelajaran Malaysia (2011). Laporan kajian program LINUS: Faktor murid tidak menguasai kemahiran asas literasi dan numerasi. Putrajaya: Bahagian Perancangan dan Penyelidikan Dasar Pendidikan.
- Kementerian Pelajaran Malaysia (2012). Laporan Awal―Ringkasan Eksekutif Laporan Awal Pelan Pembangunan Pendidikan 2013-2025.
- Lembaga Peperiksaan Kementerian Pelajaran Malaysia (2008). Pengumuman Keputusan Ujian Pencapaian Sekolah Rendah Tahun 2008.
- Lembaga Peperiksaan Kementerian Pelajaran Malaysia (2009). Pengumuman Keputusan Ujian Pencapaian Sekolah Rendah Tahun 2009.
- Lembaga Peperiksaan Kementerian Pelajaran Malaysia (2010). Pengumuman Keputusan Ujian Pencapaian Sekolah Rendah Tahun 2010.
- Lembaga Peperiksaan Kementerian Pelajaran Malaysia (2011). Pengumuman Keputusan Ujian Pencapaian Sekolah Rendah Tahun 2011.
- Lembaga Peperiksaan Kementerian Pelajaran Malaysia (2012). Pengumuman Keputusan Ujian Pencapaian Sekolah Rendah Tahun 2012.
- Locuniak, M. N., & Jordan, N. C. (2008). Using Kindergarten Number Sense to Predict Calculation Fluency in Second Grade. Journal of Learning Disabilities, 41, 451-459. http://dx.doi.org/10.1177/0022219408321126
- Morrison, G. R., Ross, S. M., Kalman, H. K., & Kemp, J. E. (2013). Designing Effective Instruction (7th ed.). Hoboken, NJ: John Wiley & Sons, Inc.
- National Association for the Education of Young Children (2009). Developmentally Appropriate Practice in Early Childhood Programs Serving Children from Birth through Age 8. Washington DC: National Association for the Education of Young Children.
- Nor Hashimah, H., & Yahya, C. L. (2003). Panduan Pendidikan Prasekolah. Bentong: PTS Publications & Distributor Sdn. Bhd.
- Ramani, G. B. (2005). Cooperative Play and Problem Solving in Preschool Children. Master’s Thesis, Pittsburgh, PA: University of Pittsburgh.
- Ramani, G. B., & Siegler, R. S. (2008). Promoting Broad and Stable Improvements in Low-Income Children’s Numerical Knowledge through Playing Number Board Games. Child Development, 79, 375-394. http://dx.doi.org/10.1111/j.1467-8624.2007.01131.x
- Ramani, G. B., & Siegler, R. S. (2011). Reducing the Gap in Numerical Knowledge between Low- and Middle-Income Preschoolers. Journal of Applied Developmental Psychology, 32, 146-159. http://dx.doi.org/10.1016/j.appdev.2011.02.005
- Saayah, A. (2005). Pelaksanaan Aktiviti Belajar Melalui Bermain Di Tadika-Tadika Kawasan Melaka Tengah Melaka (pp. 83-120). Oleh: Saayah Binti Abu dari Jabatan Ilmu Pendidikan, Maktab Perguruan Islam.
- Salma, I. (2010). Bermaindan Hubungan Rakan Sebaya Dalam Perkembangan Kanak-Kanak. In H. A. Hilma, & M. S. Zarina (Eds.), Penilaian Psikososial Kanak-kanak: Isu-isu Kebajikan Dan Perkembangan (pp. 185-199). Sintok: Universiti Utara Malaysia.
- Sarama, J., Lange, A. A., Clements, D. H., & Wolfe, C. B. (2012). The Impacts of an Early Mathematics Curriculum on Oral Language and Literacy. Early Childhood Research Quarterly, 27, 489-502. http://dx.doi.org/10.1016/j.ecresq.2011.12.002
- Sharifah, N. P., & Aliza, A. (2012). Persepsi guru terhadap penggunaan kurikulum berasaskan bermain bagi aspek pekembangan bahasa dan literasi murid prasekolah. Jurnal Pendidikan Bahasa Melayu, 2, 141-159.
- Siegler, R. S., & Booth, J. L. (2004). Development of Numerical Estimation in Young Children. Child Development, 75, 428-444. http://dx.doi.org/10.1111/j.1467-8624.2004.00684.x
- Siegler, R. S., & Ramani, G. B. (2008). Playing Linear Numerical Board Games Promotes Low-Income Children’s Numerical Development. Development Science, 11, 655-661. http://dx.doi.org/10.1111/j.1467-7687.2008.00714.x
- Vygotsky, L. S. (1978). Mind in Society: The Development of Higher Psychological Process. Cambridge, MA: Harvard University Press.
- Walker, M. (2011). PISA 2009 plus Results: Performance of 15-Year-Old in Reading, Mathematics and Science for 10 Additional Participants. www.acerpress.com.au
- Wang, Z., & Hung, L. M. (2010). Kindergarten Children’s Number Sense Development through Board Game Number Sense. http://libir1.ied.edu.hk/pubdata/ir/link/pub/number%20sense-submission.pdf
- Yong, J. P. (2008). Using Teacher-Made Games to Support Young Children’s Learning of Number Concepts: Combining Hands-On Manipulative and Computer Software. Master’s Thesis, Buffalo, NY: The State University of New York.