Energy and Power Engineering
Vol. 5 No. 2A (2013) , Article ID: 30677 , 21 pages DOI:10.4236/epe.2013.52A008
Discrimination and Estimation of the Maximum Cost Performance of Proton Exchange Membrane Fuel Cell Power Generation with Seven Constants
State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing, China
Email: zhfsbqq@sohu.com, pchpei@tsinghua.edu.cn
Copyright © 2013 H. F. Zhang, P. C. Pei. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 31, 2013; revised February 28, 2013; accepted March 15, 2013
Keywords: Fuel Cell; Working Zone; Economic Viability; Commercialization; Cost Performance; Operation Optimization
ABSTRACT
This paper is dedicated to analytical expression of the maximum electricity-cost ratio (M-ECR) point of the proton exchange membrane (PEM) fuel cell power generation as the function of cell constants and cost constants. That is to formulize the maximum cost performance (MCP) magnitude and the optimal final operating (OFO) location in the working zone based on the five-constant ideal cell model and the two-constant cost model. The issues are well resolved by introducing the concepts of economic voltage and cost factor and describing the movement of the M-ECR point with cost factor. According to mathematical derivations, the movement can be described in the form of MCP and OFO curves. The derivations lead to a complete set of discriminants and criteria of the M-ECR point of PEM fuel cells that theoretically cover all of cell specialties and all of cost specialties. The discriminants and criteria may act as a general tool for the operation optimization of a diversity of PEM fuel cells and the economic viability estimation of the power generation.
1. Introduction
As one of well-known green power generation devices, PEM fuel cells have been confronted with the successful commercialization. Behind the matter are the cost-performance-oriented operation optimization of the cells in existence and the quantitative estimation of their economic viability, among others. Currently, the optimization may be free of theoretical guideline and the estimation may be short of direct mathematical formulae. Thus an advanced solution seems highly in need to serve the double purpose, and it is just our goal in this work.
The present task is up against an intricate problem, since all kinds of cell specialties and cost specialties need to be covered and the contributions of related factors to cost performance of PEM fuel cells need to be reflected. Thus it seems feasible to perform the task under new ideologies that allow of some simplifications. The requisite ideologies have been established. One is the ideal cell model [1] on which real cells can be regularized and the other is the user-based power generation cost model [2] that supports simple classification of cost items and good fusion of cost specialties and cell specialties.
The ideal cell model was advanced to uniformly describe cell specialty with five cell constants and the userbased power generation cost model was developed to uniformly describe cost specialty with two cost constants. Naturally, this work is planned to express the M-ECR point of PEM fuel cells directly with the seven constants. Thereout, the OFO point in the working zone and the MCP magnitude can be so formulized with the seven constants that the economic viability of any cell is fast calculated and the needed operating conditions are well specified.
Based on the two ideologies, this work is essentially of a mathematical derivation. Although so, it also needs appropriate methodologies taking the great complicity of the problem into account. These methodologies are adopted mainly to deal with the deductive logic and to represent the movement of the M-ECR point with related constants. The use of the methodologies may be accompanied with quite a few new concepts and terms, and many of them are given a long name. More advice is looked forward to for the better names.
2. Principle and Discussion
2.1. Basis and Methodologies
2.1.1. The Fundamental Premise
1) The ECR basic expression According to the definition, the ECR of PEM fuel cell power generation refers to the ratio of the total electrical energy supplied by the cells to the total cost needed over the total operating time. ECR basic expression depends on operating regime and cost classification related to electricity supply path. According to our latest work [2], in the constant-power mode by the user-self-supply path, the ECR of PEM fuel cell power generation can be expressed as Formula (1). As once named the ECR first basic expression, it is one of the basis on which this work is done.
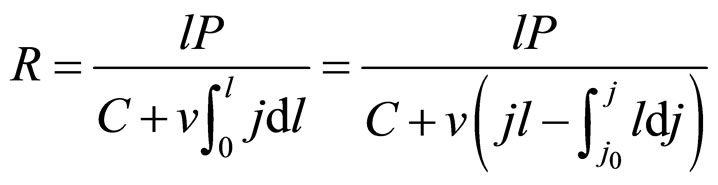 (1)
(1)
In Formula (1), R, P, l, C, v and j are the ECR of the power generation, the load power density (or cell power density), the operating time, the constant cost measured in unit active area of the cell, the variable cost coefficient based on charge quantity and the operating current density of the cell, respectively. j0 is the initial current density under power density P. Both C and v are known as cost constant. See our lasted work [2] for detailed explanations of them.
2) Time-current relationship During the cell operation, current density keeps changing with operating time, and the relationship is determined jointly by cell characteristic and load characteristic. According to the assumptions of linear cell characteristic (Formula (2)) and constant-power load characteristic (Formula (3)) in the ideal cell model, the relationship between current density and operating time can be gained as shown in Formula (4):
 (2)
(2)
 (3)
(3)
 (4)
(4)
In Formulae (2)-(4), α, λ, β and μ are all characteristic constants, known as cell constants; as the initial steadystate polarization (SSP) constants, α and λ are separately the slope and intercept of the linear part of the cell initial SSP curve; as the degradation constants, β and μ are separately the changing rates of α and λ with operating time. These constants originate from the ideal cell model. See our recent works [1,3] for details.
3) Restrictions on the extraction As stated in our recent works [1,3], in order to meet load requirement, PEM fuel cells should operate in a certain range of current and voltage. Termed the working zone of the cells, the range is determined jointly by cell characteristic, load characteristic and cell absolute lifetime (the fifth cell constant, denoted by La). In the U-j plane, the working zone presents itself as an enclosed region by the cell initial SSP curve (Formula (5)), the absolute lifetime end-curve or finial SSP curve (Formula (6)), the relative lifetime end-curve (Formula (7)) and the j = 0 line.
 (5)
(5)
 (6)
(6)
 (7)
(7)
The initial SSP curve is the assembly of the initial operating points under all load power densities that the cells can afford, and the initial current density under each load power density (Formula (8)) constitutes the lower limit to the operating current density under the corresponding load magnitude.
 (8)
(8)
The absolute lifetime end-curve and relative lifetime end-curve are separately the assembly of the absolute lifetime end-points and relative lifetime end-points. The lifetime end-points are the upper limit to the operating current density, and this limit is divided into two parts by the critical load power density as shown in Formulae (9) and (10). Under the critical load power density, the cell lifetime is both absolute and relative.
I f ,
,
 (9)
(9)
If  ,
,
 (10)
(10)
2.1.2. Methodologies
1) Overall extraction strategy As known from Formula (1), the ECR of PEM fuel cell power generation presents itself as a bivariate function of load power and current density or operating time under the conditions of given cell specialty and cost specialty, so in principle the M-ECR point can be gained by means of the maximum formula of bivariate function. However, such a formula is actually hard to use because of the complex restriction conditions on the M-ECR point extraction. Thus another strategy should be taken for the extraction.
There surely exists a M-ECR point at any given power density that the cell can provide, and this point is called the load M-ECR point under the load magnitude. It may be known the cell M-ECR point is among the load MECR points. So, an extraction strategy can be adopted: first of all to determine the load M-ECR point for each power density and this is to regard ECR only as a onevariable function with current density or operating time as the independent variable, and then to extract the cell M-ECR point by comparing load M-ECR magnitudes.
2) Zoning in the extraction Because of the restriction of cell operating points by the working zone, there are three categories of locations of load M-ECR points under any given set of cell constants and cost constants. They are either in the interior of the working zone, or on the absolute lifetime endcurve and or on the relative lifetime end-curve, depending on different load power density ranges. Thus there are three load power density ranges determined by the shapes of working zone, and there is surely one load M-ECR point whose ECR value is the maximal in each load power density range. Such a load M-ECR point is called the leading candidate for the cell M-ECR point of the load power density range.
In some cases, the leading candidate of one range can be located in its joint with others, and even the leading candidates of two or three ranges fall on the same one joint to a tee. In the extraction of the cell M-ECR point, we are to firstly find the leading candidate of each power density range in singles, then in the finial treatment, if the leading candidates of different ranges share one joint, these special leading candidates will be merged into one.
3) Expressions of extraction results Formula (1) can be transformed into Formula (11):
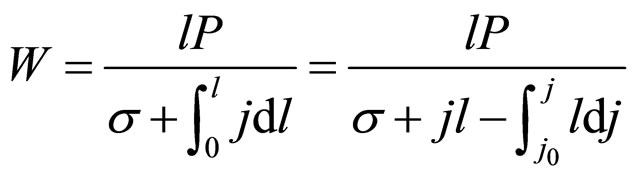 (11)
(11)
In Formula (11),
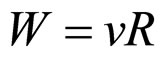 (12)
(12)
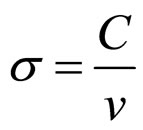 (13)
(13)
In Formulae (11)-(13), W possesses the same dimension with cell voltage. As an important parameter of the power generation in direct proportion to ECR, it is termed economic voltage for the moment. σ reflects the comprehensive cost characteristic of the power generation. It has the dimension of charge density and is termed cost factor.
The introduction of economic voltage may make for straight representation of the cell and load M-ECR points. Since economic voltage has the voltage dimension, U-j and W-j relationships can be constructed and displayed in the same one reference frame. Both M-ECR points have two properties to be known: their location and ECR magnitude. It is known the location can be geometrically described as point (j,U). Now, the ECR magnitude can be done in the form of point (j,W). The points (j,U) and (j,W) corresponding to the M-ECR point are separately called the OFO point and the MCP point before more proper names are given.
The introduction of cost factor may help systematically describe the movement of the load or cell M-ECR point with cost constants. The location and ECR magnitude of the load or cell M-ECR point may keep changing with cost constants. With the help of cost factor, the changes can be straight described in the forms of the OFO curve and the MCP curve. They are separately the loci of the OFO and MCP points of the cell or load MECR point. They are of equal cost factor if marked with load and of changing cost factor if marked with cell. As will be known, a whole load or cell MCP curve may be composed of two or three parts in different load power density ranges.
2.2. Cell Interior OFO and MCP Curves
2.2.1. Diagrammatic Representation
Figures 1-3 display the process and results of determining the cell interior OFO and MCP curves for three cell degradation characteristics. The two curves are superposed on each other point by point, given as bold dash curve. The bold solid curves ab, bc, cd and da are separately (the linear part of) the initial SSP curve, the relative lifetime end-curve, the absolute lifetime end-curve (or the final SSP curve) and the j = 0 line with a, b, c and d denoting the points of intersection. The thin solid curves are a series of load interior MCP curves of equal cost factor. The bold dashdotted curve ae is the cell precise unconditional interior MCP curve and the bold dash curve af is the cell approximate unconditional interior MCP curve. The thin dotted curves are the load characteristic curves at intervals of 50 mW∙cm−2. The thin dash curves are the fictitious part of the initial SSP curve in the low current density region. Points e and f are the points of intersection of the cell precise unconditional interior MCP curve separately with the relative lifetime end-curve and the absolute lifetime end-curve, and points  and
and 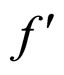 are the points of intersection of the cell approximate unconditional interior MCP curve separately
are the points of intersection of the cell approximate unconditional interior MCP curve separately

Figure 1. Diagrammatic representation of process and results of determining the cell interior OFO and MCP curves in the case of μ = 0 and β ≠ 0. The bold dash curve stands for both the resultant cell interior MCP and OFO curves, and the thin solid curves stand for a series of both load interior MCP and OFO curves of equal economic factor. The economic factor values are given with 106 C∙cm−2 as the unit. See Section 2.2.1 for more details.
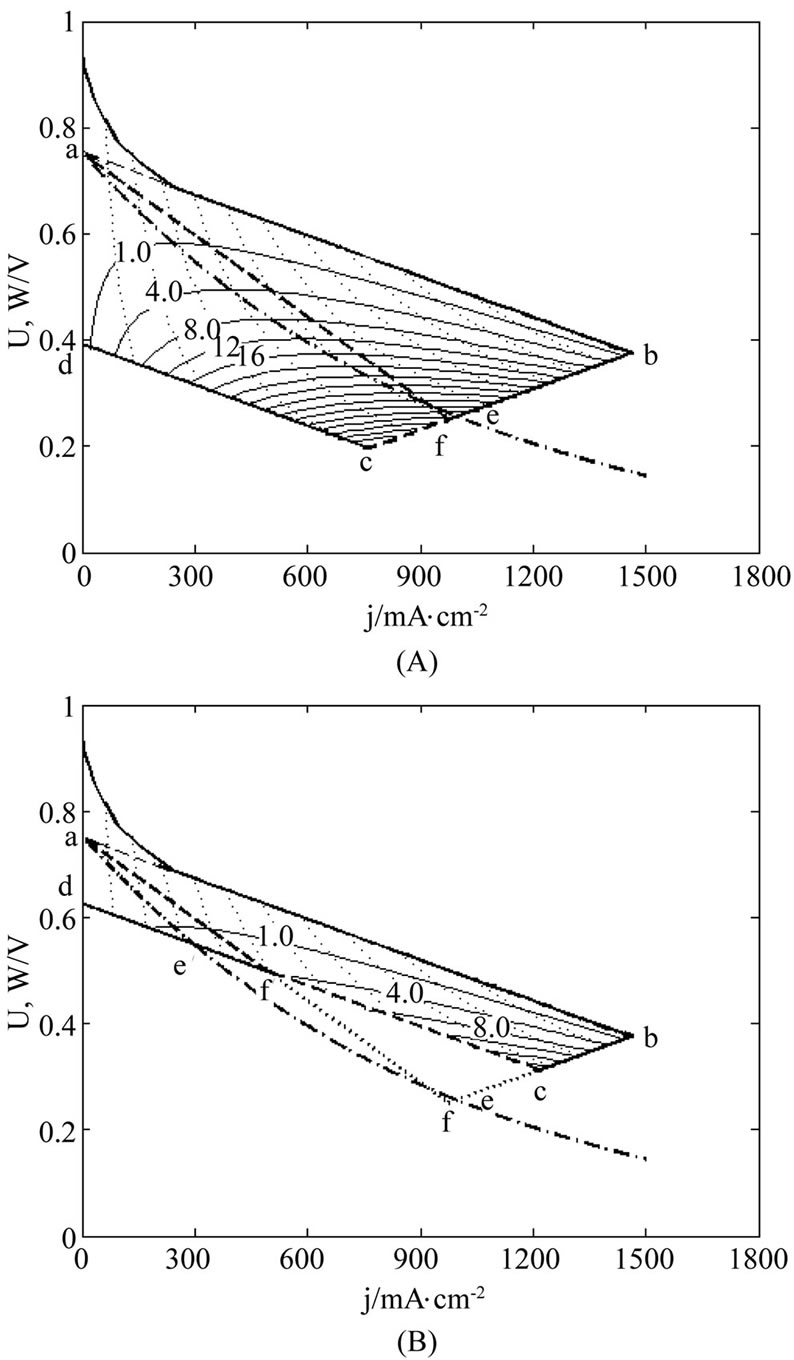
Figure 2. Diagrammatic representation of process and results of determining the cell interior OFO and MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β = 0. See Figure 1 for part annotations and see Section 2.2.1 for more details.
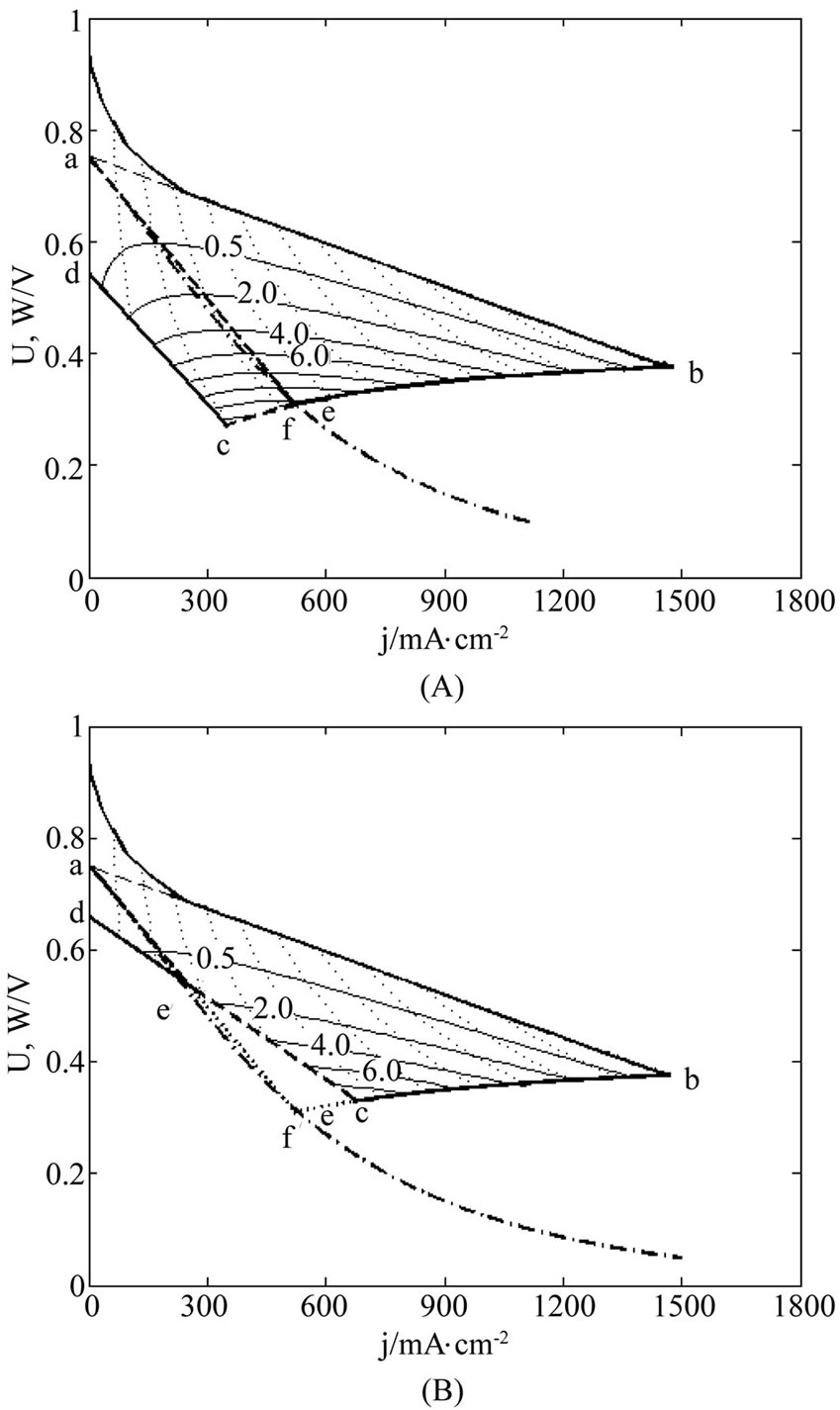
Figure 3. Diagrammatic representation of process and results of determining the cell interior OFO and MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β ≠ 0. See Figure 1 for part annotations and see Section 2.2.1 for more details.
with the relative lifetime end-curve and the absolute lifetime end-curve. See the following discussions for the detailed implications of the related terms.
The values of cell constants for illustration in Figures 1-3 are given in Table 1. The values are also used for the figures in other sections.
2.2.2. Load Interior OPO and MCP Curves
According to Formula (1) or (11), in the interior of the working zone, the ECR of the PEM fuel cell power generation is the one-variable differentiable function of current density under the condition of any given load power density. Thus the condition for the load interior MCP point is:
 (14)
(14)
Substitute Formula (4) into Formula (14), then Formula (14) can be unfolded to give the load interior OFO equa-

Table 1. Cell constant values for illustrations.
tion. The load interior OFO equation has three expressions in total depending on different degradation characteristics, as shown in Formulae (15)-(17).
when  and
and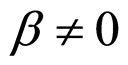 ,
,
 (15)
(15)
when 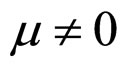 and
and ,
,
 (16)
(16)
when  and
and ,
,
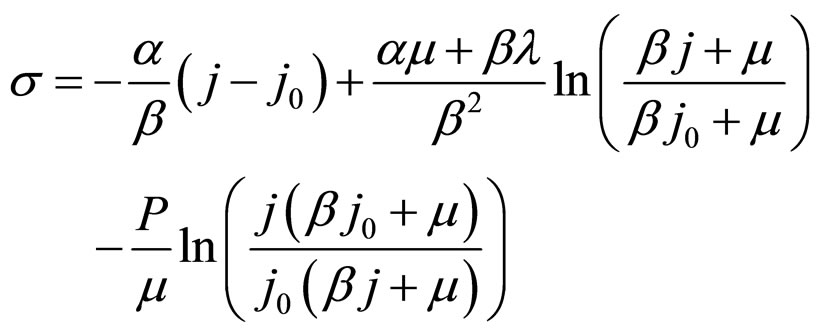 (17)
(17)
Substituting P = Uj into Formulae (15)-(17) turns the load interior OFO equation into their second form given as:
when 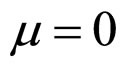 and
and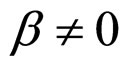 ,
,
 (18*)
(18*)
when 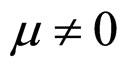 and
and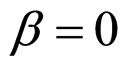 ,
,
 (19*)
(19*)
when  and
and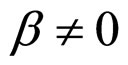 ,
,
 (20*)
(20*)
In Formulae (18*)-(20*),
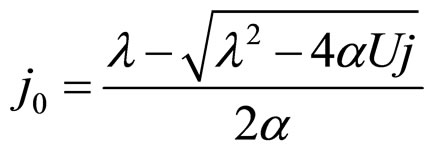 (21*)
(21*)
In U-j plane, Formulae (18*)-(20*) present themselves as a curve at any cost factor. Termed as the load interior OFO curve, the curve is composed of the OFO points under the conditions of the same economic factor but different load power densities in the interior of the working zone. Thus with a series of cost factor values, Formulae (18*)-(21*) separately turn into a contour plot, a group of thin solid curve as shown in Figures 1-3.
Because the load interior OFO equation is valid only in the interior of the working zone, the cost factor at the intersection point of the relative and absolute lifetime end-curves may be the upper limit to the application of the equations. As seen from Figures 1-3, the contour curve gradually moves down as cost factor increases. Moreover, the equation does not always apply to the whole load power density range even if cost factor is smaller than the upper limit, which can be clearly seen from Figures 1-3.
Substituting P = Uj and Formula (14) into Formula (11) gives Formula (22). It reveals the completely equal relationship between economic voltage and operating voltage regardless of cell degradation characteristic. Accordingly, Formulae (18*)-(20*) can be directly changed into those for the load interior MCP point only by substituting W for U in them, and then they are called the load interior MCP equation and present themselves as a curve in W-j plane called the load interior MCP curve. It is obvious that the load interior OFO and MCP curves are of pointto-point correspondence and superposed on each other.
 (22)
(22)
The existence of the relationship like Formula (22) may mean one set of formulae may be enough to represent the evolution of the cell interior MCP and OFO points. The complete superposition of the load interior OFO and MCP curves may naturally lead to that of the cell interior OFO and MCP curves. Since W and U can be interchanged, it is certain the two cell interior curves share a set of formulae. This is why the symbol * is given after the formula sequence numbers. The same practice will be followed in Sections 2.2.3 and 2.2.4 where the cell OFO curve is not given discussion any more. And when the formulae marked with the symbol * are mentioned in the final treatment, their implications should be understood in context.
2.2.3. Cell Unconditional Interior MCP Curve
Make dW/dj in Formulae (18*)-(20*) equal to zero, then Formulae (23*)-(25*) can be derived. j0 in Formulae (24*) and (25*) is shown in Formula (21*).
when 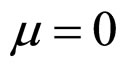 and
and ,
,
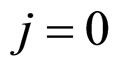 (23*)
(23*)
when  and
and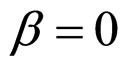 ,
,
 (24*)
(24*)
when  and
and ,
,
 (25*)
(25*)
Formulae (23*)-(25*) all are called the cell precise unconditional interior MCP equation, and this is to distinguish it from the cell approximate unconditional interior MCP equation derived latter on. Unconditional means the infinity of the relative and absolute lifetimes, and precise should be understood in a relative sense as the equation is always based on the ideal cell model. In W-j plane, each of Formulae (23*)-(25*) present itself as a curve, the bold dashdotted curve as separately shown in Figures 1-3. As the assembly of the cell interior MCP points under different economic factors, the curve is called the cell precise unconditional interior MCP curve.
The Equations (24*) and (25*) look as if they were simple, but they are very complicated actually. Then Formulae (26*) and (27*) can be used as substitutes for them.
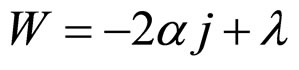 (26*)
(26*)
 (27*)
(27*)
Formulae (26*) and (27*) are called the cell approximate unconditional interior MCP equation. They actually present themselves as a straight line, af, as shown in Figures 2 and 3. The cell approximate unconditional interior MCP curve has the same starting point but different intersection point with the relative lifetime end-curve from the cell precise unconditional interior MCP curve. In fact, the cell approximate unconditional interior MCP curve is decided jointly by the cell precise unconditional interior MCP curve, the cell approximate unconditional relative lifetime boundary MCP curve and the relative lifetime end-curve. See Section 2.4 for details on this aspect.
Due to simplicity and small error, the following discussions about the latter two degradation characteristics ( and
and ,
,  and
and ) will be developed around the cell approximate unconditional interior MCP curve. And the term the cell unconditional interior MCP curve used in the following discussions for the two degradation characteristics exactly refers to the cell approximate unconditional interior MCP curve, unless otherwise stated. For the first degradation characteristic,
) will be developed around the cell approximate unconditional interior MCP curve. And the term the cell unconditional interior MCP curve used in the following discussions for the two degradation characteristics exactly refers to the cell approximate unconditional interior MCP curve, unless otherwise stated. For the first degradation characteristic,  and
and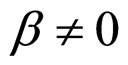 , there are no terms the cell approximate unconditional interior MCP curve and equation. Thus the term the cell precise unconditional interior MCP curve is now changed into the cell unconditional interior MCP curve that will be used in the following discussions.
, there are no terms the cell approximate unconditional interior MCP curve and equation. Thus the term the cell precise unconditional interior MCP curve is now changed into the cell unconditional interior MCP curve that will be used in the following discussions.
2.2.4. Cell Conditional Interior MCP Curve
Considering the finity of the relative and absolute lifetimes, the cell unconditional interior MCP curve turns into the cell conditional interior MCP curve. Here there are three cases in total corresponding to the three degradation characteristics.
1) Case of  and
and 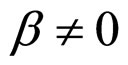
As shown in Figure 1, in the case of 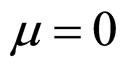 and
and , the cell unconditional interior MCP curve is always located outside of the working zone however long the absolute lifetime is. It is the very zero current density line, and this means the load interior MCP keeps monotonously decreasing with the increase of load power density under any cost factor. So nothing but the absolute lifetime end-curve, the straight line segment ac, can act as the cell conditional interior MCP curve under this first degradation characteristic.
, the cell unconditional interior MCP curve is always located outside of the working zone however long the absolute lifetime is. It is the very zero current density line, and this means the load interior MCP keeps monotonously decreasing with the increase of load power density under any cost factor. So nothing but the absolute lifetime end-curve, the straight line segment ac, can act as the cell conditional interior MCP curve under this first degradation characteristic.
2) Case of  and
and 
In the case of 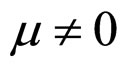 and
and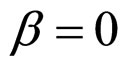 , both the cell unconditional interior MCP curve is a straight line only determined by the initial SSP constants α and λ independent of the degradation constant μ. As shown in Figures 2(A) and 2(B), the straight line passes through the working zone and intersects with the relative lifetime end-curve at point f for a long cell absolute lifetime, or intersects with the absolute lifetime end-curve at point
, both the cell unconditional interior MCP curve is a straight line only determined by the initial SSP constants α and λ independent of the degradation constant μ. As shown in Figures 2(A) and 2(B), the straight line passes through the working zone and intersects with the relative lifetime end-curve at point f for a long cell absolute lifetime, or intersects with the absolute lifetime end-curve at point 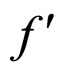 and suppositionally does with the relative lifetime end-curve at point f for a short cell absolute lifetime. Here, the criterion to judge the absolute lifetime is short or long is the length of the absolute lifetime at point f. Such a length is critical and thus called the critical absolute lifetime, denoted by La,f, as shown in Formula (28). As seen from Formula (28), for the second degradation characteristic, the critical absolute lifetime of the cell is determined only by μ and λ and has no relation with other cell constants.
and suppositionally does with the relative lifetime end-curve at point f for a short cell absolute lifetime. Here, the criterion to judge the absolute lifetime is short or long is the length of the absolute lifetime at point f. Such a length is critical and thus called the critical absolute lifetime, denoted by La,f, as shown in Formula (28). As seen from Formula (28), for the second degradation characteristic, the critical absolute lifetime of the cell is determined only by μ and λ and has no relation with other cell constants.
 (28)
(28)
In this second degradation case, the cell interior MCP curve is composed of two straight line segments: one is the cell unconditional interior MCP curve and the other is the cell conditional interior MCP curve. The cell unconditional interior MCP curve here exactly refers to its part in the interior of the working zone, and this conceptual renewal applies henceforward. As shown in Figure 2(A), when , the cell unconditional interior MCP curve is the straight line segment af, and the cell conditional interior MCP curve is one part of the relative lifetime end-curve, the straight line segment fc. As shown in Figure 2(B), when
, the cell unconditional interior MCP curve is the straight line segment af, and the cell conditional interior MCP curve is one part of the relative lifetime end-curve, the straight line segment fc. As shown in Figure 2(B), when , the cell unconditional interior MCP curve is the straight line segment
, the cell unconditional interior MCP curve is the straight line segment , and the cell conditional interior MCP curve is one part of the absolute lifetime end-curve, the straight line segment
, and the cell conditional interior MCP curve is one part of the absolute lifetime end-curve, the straight line segment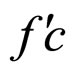 .
.
3) Case of 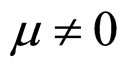 and
and 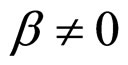
The structure of the cell interior MCP curve in this third case is similar to that in the second case. However, there are two major differences. One is that the critical absolute lifetime is determined jointly by four cell constants, α, λ, β and μ, as shown in Formula (29). The other is that, when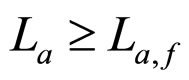 , the cell conditional interior MCP curve (fc) presents itself as a curve segment as it is one part of the relative lifetime end-curve
, the cell conditional interior MCP curve (fc) presents itself as a curve segment as it is one part of the relative lifetime end-curve
 (29)
(29)
2.2.5. Applicable Cost Factor Range of Cell Interior MCP Curves
The applicable cost factor ranges of the load interior MCP equation is just those of the cell interior MCP curve. However, the range needs to be further decomposed because of the various configurations of the cell interior MCP curves. And there are three cases in total corresponding to the three degradation characteristics.
1) Case of 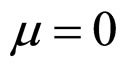 and
and 
In this first case, determined by the finity of the cell absolute lifetime, nothing but the cell conditional interior MCP curve is the very cell interior MCP curve. And the applicable cost factor range is  (
( denotes the cost factor magnitude at operating point x).
denotes the cost factor magnitude at operating point x).  can be gained by substituting the coordinates of operating point c into Formula (18*). The coordinates of operating point c are:
can be gained by substituting the coordinates of operating point c into Formula (18*). The coordinates of operating point c are:
 (30*)
(30*)
2) Case of  and
and 
In this second case, the applicable cost factor range depends on the magnitude of the cell absolute lifetime.
If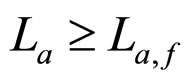 , the cell interior MCP curve, the bold dash curve shown in Figure 2(A), is composed of the straight curve segments af and fc. Their applicable cost factor ranges are
, the cell interior MCP curve, the bold dash curve shown in Figure 2(A), is composed of the straight curve segments af and fc. Their applicable cost factor ranges are  and
and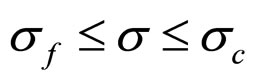 , respectively.
, respectively.  and
and  can be gained by substituting the coordinates of the coordinates of operating points f and c, respectively, into Formula (19*). They are given in Formulae (31*) and (32*).
can be gained by substituting the coordinates of the coordinates of operating points f and c, respectively, into Formula (19*). They are given in Formulae (31*) and (32*).
 (31*)
(31*)
 (32*)
(32*)
If , the cell interior MCP curve, the bold dash curve shown in Figure 2(B), is composed of the straight curve segments
, the cell interior MCP curve, the bold dash curve shown in Figure 2(B), is composed of the straight curve segments  and
and . Their applicable cost factor ranges are
. Their applicable cost factor ranges are 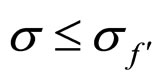 and
and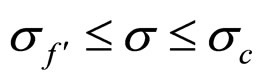 , respectively.
, respectively.  and
and 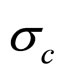 can be gained by substituting the coordinates of the coordinates of operating points
can be gained by substituting the coordinates of the coordinates of operating points  and c, respectively, into Formula (19*). The coordinates of operating point c is shown in Formula (32*), and those of operating point
and c, respectively, into Formula (19*). The coordinates of operating point c is shown in Formula (32*), and those of operating point 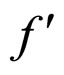 are given in Formula (33*).
are given in Formula (33*).
 (33*)
(33*)
In the case of this second degradation characteristic, the cell precise unconditional interior MCP curve (the curve ae) is a curve determined only by the initial SSP constants α and λ independent of the degradation constant μ, as shown in Figures 2(A) and (B). It intersects the relative lifetime end-curve at point e whose coordinates are given in Formula (34*).
 (34*)
(34*)
As known from Formulae (31*) and (34*), operating points f and e are highly close to each other. As seen from Figures 2(A) and 2(B), it may be rational and convenient to substitute the cell precise unconditional interior MCP curve with the cell approximate unconditional interior MCP curve, and a major error may not be produced. It can be proved that the cell precise unconditional interior M-ECR curve does not get tangental to the absolute lifetime end-curve in the interior of the working zone however long the absolute lifetime is. This is also an important reason to treat the cell unconditional interior curve as a straight line.
3) Case of  and
and 
In terms of the applicable cost factor range, this third case is similar to the second case. And the dividing cost factor magnitudes can be gained by substituting the coordinates of the related operating points as given in Formulae (35*)-(37*) into Formula (20).
 (35*)
(35*)
 (36*)
(36*)
 (37*)
(37*)
As seen from Figures 3(A) and (B), in this third case, the intersection point e of the cell precise unconditional interior MCP curve with the relative lifetime end-curve may likewise be close to the point f. So it may be rational and of little error to approximately treat the cell unconditional interior MCP curve as a straight line. We fail to find the analytical expressions of the coordinates of the point e, but it can be validated that the cell precise unconditional interior MCP curve does not get tangental to the absolute lifetime end-curve in the interior of the working zone however long the absolute lifetime is.
2.3. Cell Relative Lifetime Boundary MCP Curve
2.3.1. Diagrammatic Representation
Figures 4-6 display the process and results of determining the cell relative lifetime boundary MCP curve (the bold dash curve) for the three degradation characteristics. In these figures, the thin solid curves are a series of load relative lifetime boundary cost performance (CP) curves of equal cost factor with 106 C∙cm−2 as the unit of charge density. The bold dashdotted curve is the cell precise unconditional interior MCP curve; fh is the cell approximate unconditional interior MCP curve; cg is the cell conditional relative lifetime boundary MCP curve; af is the cell unconditional interior MCP curve; the bold dotted curve, the thin dotted curve and the thin solid curves all play auxiliary roles. Point g is the intersection point of curve cg and line W = 0, and point f is the intersection point of curve eh, curve fh and line W = 0. See Section 2.2 for the implications of bold solid curves ab, bc, cd, da and points a, b, c, d, e, f,  and
and . See the following discussions for the detailed implications of the related terms.
. See the following discussions for the detailed implications of the related terms.
2.3.2. Load Relative Lifetime Boundary CP Curve
When cell operating time gets as long as relative lifetime Lr under load power density P, the operating point arrives at the relative lifetime boundary end-curve. Here, the economic voltage can be expressed as:
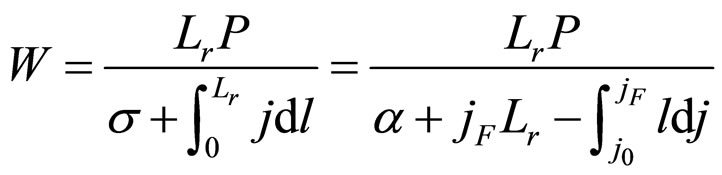 (38)
(38)
Substitute Formula (4) into Formula (38), then the relationship between economic voltage and power density

Figure 4. Diagrammatic representation of process and results of determining the cell relative lifetime boundary MCP curve in the case of μ = 0 and β ≠ 0. The bold dash curve stands for the resultant cell relative lifetime boundary MCP curve, and the thin solid curves stand for a series of load relative lifetime boundary CP curves of equal economic factor. The economic factor values are given with 106 C∙cm−2 as the unit. See Section 2.3.1 for more details. See Section 2.2.1 for more details.

Figure 5. Diagrammatic representation of process and results of determining the cell relative lifetime boundary MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β = 0. See Figure 4 for part annotations and see Section 2.3.1 for more details.

Figure 6. Diagrammatic representation of process and results of determining the cell relative lifetime boundary MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β ≠ 0. See Figure 4 for part annotations and see Section 2.3.1 for more details.
can be derived. Called the load relative lifetime boundary (cost performance) CP equation, the relationship present itself as three analytical expressions as shown in Formulae 39 - 41 depending on the three degradation characteristics. j0 and jF in Formulae (39)-(41) are given in Formulae (11) and (13), respectively.
when  and
and ,
,
 (39)
(39)
when 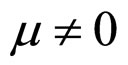 and
and ,
,
 (40)
(40)
when  and
and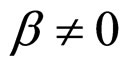 According to our recent works, the relative lifetime can be expressed with Formulae (42)-(44) under load power density P for the three degradation characteristics.
According to our recent works, the relative lifetime can be expressed with Formulae (42)-(44) under load power density P for the three degradation characteristics.
when 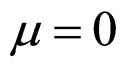 and
and ,
,
 (42)
(42)
when  and
and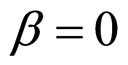 ,
,
 (43)
(43)
when 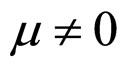 and
and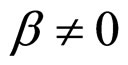 ,
,
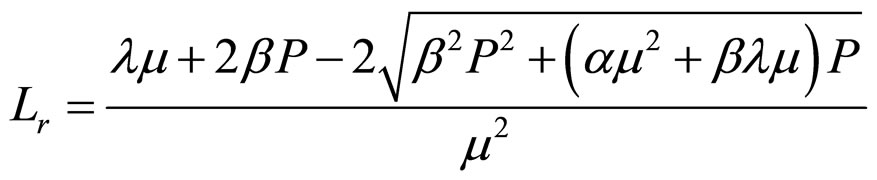 (44)
(44)
When the relative lifetime end comes under load power density P, the relationship between load power density P and current density jr is given in Formulae (45) - (47).
when 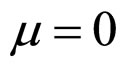 and
and ,
,
 (45)
(45)
when  and
and ,
,
 (46)
(46)
when 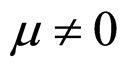 and
and ,
,
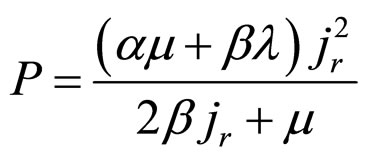 (47)
(47)
Separately substitute Formulae (42) and (45) into Formula (39), Formulae (43) and (46) into Formula (40) and Formulae (44) and (47) into Formula (41), then the second form of the load relative lifetime boundary CP equation can be obtained for the three degradation characteristics, as shown in Formulae (48)-(50).
when  and
and ,
,
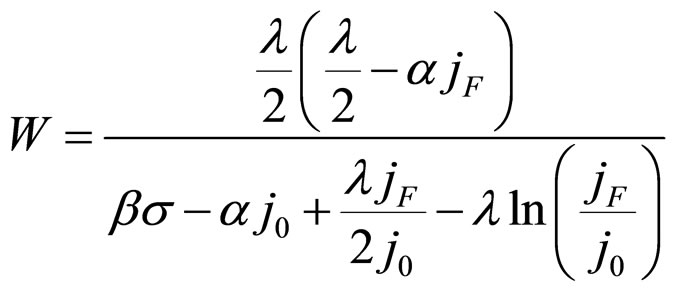 (48)
(48)
 (41)
(41)
when  and
and ,
,
 (49)
(49)
when 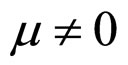 and
and ,
,
 (50)
(50)
Initial current densities j0 in Formulae (48)-(50) are given in Formulae (51)-(53), respectively.
 (51)
(51)
 (52)
(52)
 (53)
(53)
Under any cost factor, each of Formulae (48)-(50) presents itself as a curve in W-j plane. It is called the load relative lifetime boundary CP curve as it is composed of the CP points under different load power densities at the relative lifetime boundary. For a series of cost factors, each of Formulae (48)-(50) gives a group of load relative lifetime boundary CP curves with different cost factors, as shown in Figures 4-6.
Although the load relative lifetime boundary CP curve moves with cost factor, the load relative lifetime boundary final operating (FO) curve keeps unchanged, and it is the very relative lifetime end-curve. The load relative lifetime boundary CP and FO curves are of point-to-point correspondence, but they are not superposed.
3.3.3. Cell Unconditional Relative Boundary MCP Curve
Make dW/djF in Formulae (48)-(50) equal to zero and get rid of σ by using Formulae (48)-(50), then Formulae (54)-(56) can be obtained. Initial current densities j0 in Formulae (55) and (56) are given in Formulae (52) and (53), respectively when 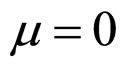 and
and ,
,
 (54)
(54)
when 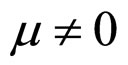 and
and ,
,
 (55)
(55)
when  and
and ,
,
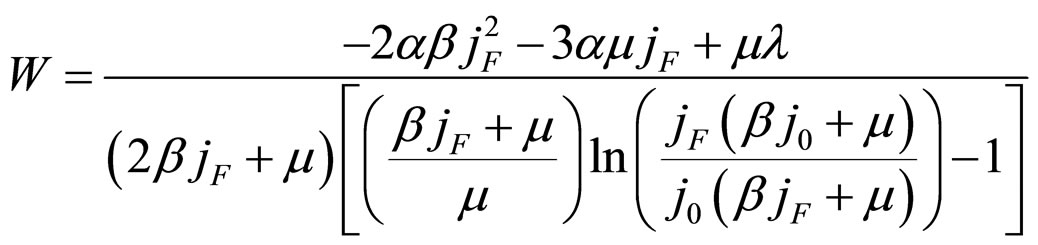 (56)
(56)
Formulae (54)-(56) all are called the cell precise unconditional relative lifetime boundary MCP equation. This is to distinguish it from the cell approximate unconditional relative lifetime boundary MCP equation derived latter on. Unconditional refers to the infinitely long absolute lifetime. In W-j plane, each of Formulae (54)-(56) presents itself as a curve, the bold dashdotted curve as separately shown in Figures 6-10. The curve is called cell precise unconditional relative lifetime boundary MCP curve, as it is the assembly of the cell precise unconditional relative lifetime boundary MCP points under different cost factors. The intersection point of the cell precise unconditional relative lifetime boundary MCP curve and the corresponding load relative lifetime boundary CP curve is just the cell precise unconditional relative lifetime boundary MCP point under a given cost factor.
Formulae (55) and (56) look as if they were simple, but they are very complicated actually. The cell precise unconditional relative lifetime boundary MCP curve corresponding to Formula (55) or (56) is only in a small current density range as shown in Figure 4 or 5, so, it may be substituted with a constant current density line that passes through its intersection point with the line W = 0. The corresponding mathematical expressions are given as Formula (57) or (58).
 (57)
(57)
 (58)
(58)
Formulae (57) and (58) both are called the cell approximate unconditional relative lifetime boundary MCP equation. Because both of them stand for a constant current density line, so they are also called the cell approximate unconditional relative lifetime boundary MCP

Figure 7. Diagrammatic representation of process and results of determining the cell absolute lifetime boundary MCP curve in the case of μ = 0 and β ≠ 0. The bold dash curve stands for the resultant cell absolute lifetime boundary MCP curve, and the thin solid curves stand for a series of load absolute lifetime boundary CP curves of equal economic factor at regular intervals of economic factor. The economic factor values are given with 106 C∙cm−2 as the unit. See Section 2.4.1 for more details.

Figure 8. Diagrammatic representation of process and results of determining the cell absolute lifetime boundary MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β = 0. See Figure 7 for part annotations and see Section 2.4.1 for more details.

Figure 9. Diagrammatic representation of process and results of determining the cell absolute lifetime boundary MCP curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β ≠ 0. See Figure 7 for part annotations and see Section 2.4.1 for more details.
curve. The cell precise and approximate unconditional relative lifetime boundary MCP curves have the same starting point and different intersection points with the relative lifetime end-curve in both cases.
In the case of  and
and , the cell precise unconditional relative lifetime boundary MCP curve, the cell precise unconditional interior MCP curve and the relative lifetime end-curve intersect at point e. So a straight line can be defined with the intersection point of the cell precise unconditional interior MCP curve and the line j = 0 as one point and with the intersection point of the cell approximate unconditional relative lifetime boundary MCP curve and the relative lifetime end-curve as the other. Such a straight line, af, is just the cell approximate unconditional interior MCP curve, as shown in Figure 5. This principle also applies to the construction of the cell approximate unconditional interior MCP curve in the case of
, the cell precise unconditional relative lifetime boundary MCP curve, the cell precise unconditional interior MCP curve and the relative lifetime end-curve intersect at point e. So a straight line can be defined with the intersection point of the cell precise unconditional interior MCP curve and the line j = 0 as one point and with the intersection point of the cell approximate unconditional relative lifetime boundary MCP curve and the relative lifetime end-curve as the other. Such a straight line, af, is just the cell approximate unconditional interior MCP curve, as shown in Figure 5. This principle also applies to the construction of the cell approximate unconditional interior MCP curve in the case of 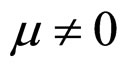 and
and  as shown in Figure 6.
as shown in Figure 6.

Figure 10. The composition of the cell MCP and OFO curves for (A) long and (B) short cell absolute lifetimes in the case of μ = 0 and β ≠ 0. See text for more details.
Due to simplicity and small error, the following discussions about the two degradation characteristics,  and
and ,
,  and
and , will be developed around the cell approximate unconditional relative lifetime boundary MCP curve. And the term the cell unconditional relative lifetime boundary MCP curve used in the following discussions for the two degradation characteristics exactly refers to the cell approximate unconditional relative lifetime boundary MCP curve, unless otherwise stated. Correspondingly, the term the cell conditional relative lifetime boundary MCP curve refers to the cell approximate conditional relative lifetime boundary MCP curve. For the first degradation characteristic,
, will be developed around the cell approximate unconditional relative lifetime boundary MCP curve. And the term the cell unconditional relative lifetime boundary MCP curve used in the following discussions for the two degradation characteristics exactly refers to the cell approximate unconditional relative lifetime boundary MCP curve, unless otherwise stated. Correspondingly, the term the cell conditional relative lifetime boundary MCP curve refers to the cell approximate conditional relative lifetime boundary MCP curve. For the first degradation characteristic, 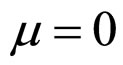 and
and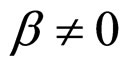 , there are no term the cell approximate unconditional relative lifetime boundary MCP curve or equation. Thus the term the cell precise unconditional relative lifetime boundary MCP curve is now changed into the cell unconditional relative lifetime boundary MCP curve that will be used in the following discussions.
, there are no term the cell approximate unconditional relative lifetime boundary MCP curve or equation. Thus the term the cell precise unconditional relative lifetime boundary MCP curve is now changed into the cell unconditional relative lifetime boundary MCP curve that will be used in the following discussions.
Under any degradation characteristic, although the cell unconditional relative lifetime boundary MCP point moves with cost factor and thus forms the cell unconditional relative lifetime boundary MCP curve, the cell unconditional OFO point keeps unmoved. That is to say, the whole cell unconditional relative lifetime boundary MCP curve belongs to one cell OFO point in the relative lifetime end-curve. Here, there is no concept like the cell unconditional relative boundary OFO curve.
3.3.4. Cell Conditional Relative Lifetime Boundary MCP Curve
Considering the finity of the cell absolute lifetime, the cell unconditional relative lifetime boundary MCP curve turns into the cell conditional relative lifetime boundary MCP curve.
In the case of  and
and , as shown in Figure 4, the line j = 0 is just the cell unconditional relative lifetime boundary MCP curve. This means the monotonous decrease of the load relative lifetime boundary CP as the increase of current density under any cost factor. So, nothing but the constant current density line (cg) passing through the intersection point of the absolute and lifetime end-curves (c) acts as the cell relative lifetime boundary MCP curve, because of the finity of the cell absolute lifetime. It is the cell conditional relative lifetime boundary MCP curve whose mathematical expression is given as Formula (59).
, as shown in Figure 4, the line j = 0 is just the cell unconditional relative lifetime boundary MCP curve. This means the monotonous decrease of the load relative lifetime boundary CP as the increase of current density under any cost factor. So, nothing but the constant current density line (cg) passing through the intersection point of the absolute and lifetime end-curves (c) acts as the cell relative lifetime boundary MCP curve, because of the finity of the cell absolute lifetime. It is the cell conditional relative lifetime boundary MCP curve whose mathematical expression is given as Formula (59).
 (59)
(59)
In the other two cases, as shown in Figures 5 and 6, the constant current density line fh corresponding to point f is just the cell unconditional relative lifetime boundary MCP curve. This means the monotonous increase of the load relative lifetime boundary CP as the increase of current density in the range of  and the monotonous decrease in the range of
and the monotonous decrease in the range of 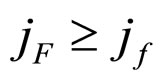 under any cost factor, if the cell absolute lifetime is infinitely long.
under any cost factor, if the cell absolute lifetime is infinitely long.
The finity of the absolute lifetime restricts the load relative lifetime boundary CP curve within the current density range of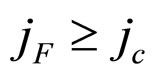 . As shown in Figures 5(A) and 6(A), when
. As shown in Figures 5(A) and 6(A), when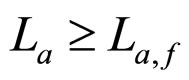 , the cell unconditional relative lifetime boundary MCP curve fh lies in the current density range of
, the cell unconditional relative lifetime boundary MCP curve fh lies in the current density range of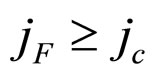 , so it is surely the cell relative lifetime boundary MCP curve. As shown in Figures 5(B) and 6(B), when
, so it is surely the cell relative lifetime boundary MCP curve. As shown in Figures 5(B) and 6(B), when , the cell unconditional relative lifetime boundary MCP curve fh does not lie in the range of
, the cell unconditional relative lifetime boundary MCP curve fh does not lie in the range of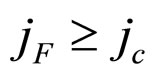 , so it can’t act as the cell relative lifetime boundary MCP curve. Here, the constant density line cg passing through point c is the veritable cell relative lifetime boundary MCP curve, and it is the cell conditional relative lifetime boundary MCP curve. Formulae (60) and (61) give the mathematical expressions of the line cf, respectively, in the case of
, so it can’t act as the cell relative lifetime boundary MCP curve. Here, the constant density line cg passing through point c is the veritable cell relative lifetime boundary MCP curve, and it is the cell conditional relative lifetime boundary MCP curve. Formulae (60) and (61) give the mathematical expressions of the line cf, respectively, in the case of 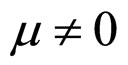 and
and  and the case of
and the case of  and
and .
.
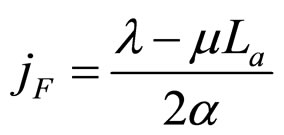 (60)
(60)
 (61)
(61)
Similar to the cell unconditional relative lifetime boundary MCP curve, the whole cell conditional relative lifetime boundary MCP curve belongs to one cell OFO point in the relative lifetime end-curve for any degradation characteristic. And likewise, there is no concept like the cell conditional relative boundary OFO curve
3.3.5. Applicable Cost Factor Range of Cell Relative Lifetime Boundary MCP Curve
As seen from Figures 4-6, the cell relative lifetime boundary MCP curve applies to the whole cost factor range from zero to infinity for any cell degradation characteristic.
3.4. Cell Absolute Lifetime Boundary MCP Curve
3.4.1. Diagrammatic Representation
Figures 7-9 display the process and results of determining the cell absolute lifetime boundary MCP curve (the bold dash curve) for the three cell degradation characteristics. In these figures, the thin solid curves are a series of load absolute lifetime boundary CP curves of equal cost factor with 106 C∙cm−2 as the unit of charge density. The bold dashdotted curve  is the cell first precise absolute lifetime boundary MCP curve.
is the cell first precise absolute lifetime boundary MCP curve.  is the cell first approximate absolute lifetime boundary MCP curve.
is the cell first approximate absolute lifetime boundary MCP curve.  is the cell second absolute lifetime boundary MCP curve. The bold dotted curve, the thin dotted curve and the thin dash curve are displayed for assistant roles. Point i is the intersection point of curves
is the cell second absolute lifetime boundary MCP curve. The bold dotted curve, the thin dotted curve and the thin dash curve are displayed for assistant roles. Point i is the intersection point of curves ,
, 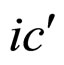 and line j = 0, and points
and line j = 0, and points  and
and 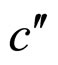 are separately the intersection points of
are separately the intersection points of  and
and 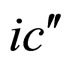 with line cg. See Section 2.2 or 2.3 for the implications of other points and curves and see the following discussions for the implications of new terms.
with line cg. See Section 2.2 or 2.3 for the implications of other points and curves and see the following discussions for the implications of new terms.
3.4.2. Load Absolute Lifetime Boundary CP Curve
When cell operating time gets as long as absolute lifetime La under load power density P, the operating point arrives at the absolute lifetime end-curve. Here, the economic voltage can be expressed as:
 (62)
(62)
Substituting Formula 4 into Formula 62 gives the relationship between economic voltage and load power density, and this is called the load absolute lifetime boundary CP equation. There are three expressions of the load absolute lifetime boundary CP equation in total depending on cell degradation characteristic, as shown in Formulae 63 - 65.
when  and
and ,
,
 (63)
(63)
when  and
and ,
,
 (64)
(64)
when  and
and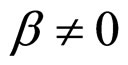 In Formulae (62)-(65), j0 and jF are given as Formulae (8) and (9), respectively.
In Formulae (62)-(65), j0 and jF are given as Formulae (8) and (9), respectively.
According to Formulae (3) and (6), when the cell operates until the absolute lifetime end-point under load power density P, the relationship between the load power density and current density are expressed as Formulae (66)-(68):
when  and
and ,
,
 (66)
(66)
when  and
and ,
,
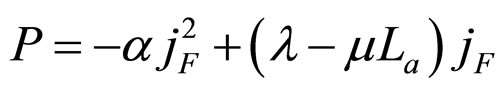 (67)
(67)
when  and
and ,
,
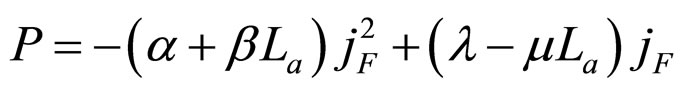 (68)
(68)
Separately substituting Formula (66) into (63), Formula (67) into Formula (64) and Formula (68) into (65) give the second form of the load absolute lifetime boundary CP equation, as shown in Formulae (69)-(71).
 (65)
(65)
when  and
and ,
,
 (69)
(69)
when 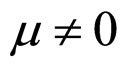 and
and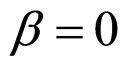 ,
,
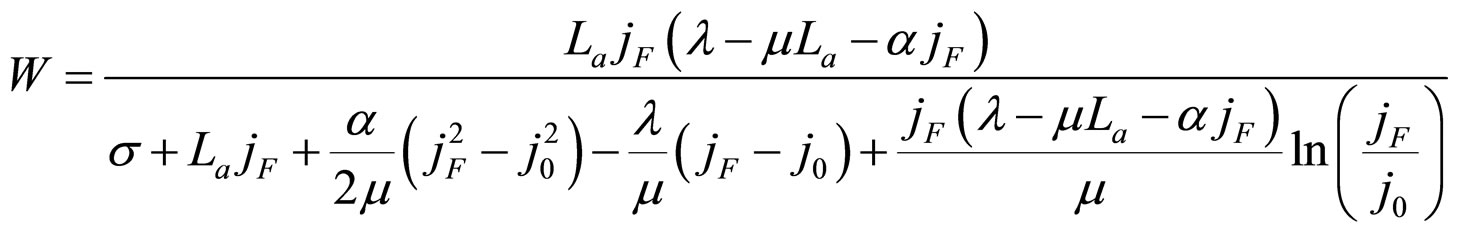 (70)
(70)
when  and
and ,
,
 (71)
(71)
In Formulae (69)-(71), initial current densities are separately given as:
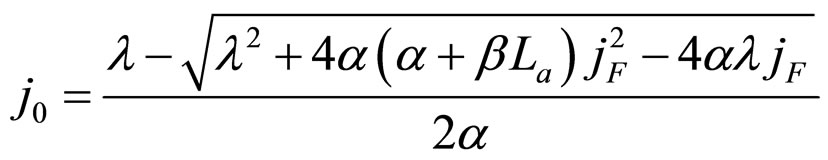 (72)
(72)
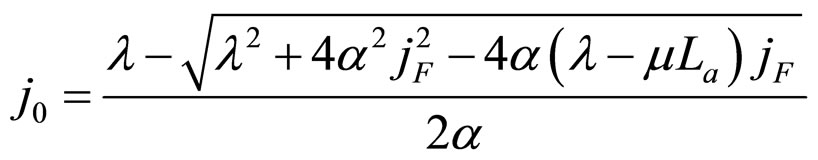 (73)
(73)
 (74)
(74)
In W-j plane, Formulae (69) and (70) all present themselves as a curve under any cost factor. The curve is composed of the load CP points under different load power densities at the absolute lifetime boundary and thus called the load absolute lifetime boundary CP curve. For a series of cost factors, each of Formulae (69)-(71) gives a group of load absolute lifetime boundary CP curves with different cost factors In order to observe the evolution of the load absolute lifetime boundary CP as economic factor, a series of load absolute lifetime boundary CP curves over the complete current density range are given in Figures 7-9, respectively, according to Formulae (69)-(71). However, owing to the restriction of the cell absolute lifetime, the load absolute lifetime boundary CP equation is valid only in the current density range of , while invalid in the range of
, while invalid in the range of . In Figures 7-9, the valid and invalid parts of the load absolute lifetime boundary CP curves are display as the thin solid curves and the dotted curves, respectively.
. In Figures 7-9, the valid and invalid parts of the load absolute lifetime boundary CP curves are display as the thin solid curves and the dotted curves, respectively.
Although the load absolute lifetime boundary CP curve moves with cost factor, the load absolute lifetime boundary FO curve keeps unchanged, and it is the very absolute lifetime end-curve. The load absolute lifetime boundary CP and FO curves are of point-to-point correspondence, but they are not superposed.
3.4.3. Cell Absolute Lifetime Boundary MCP Curve
Make dW/djF in Formulae(69)-(71) equal to zero and get rid of σ by using Formulae (69)-(71), then two solutions can be obtained for each cell degradation characteristic. The first solution is given as Formulae (75)-(77) and the second is given as Formulae (59)-(61)
when 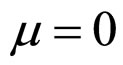 and
and ,
,
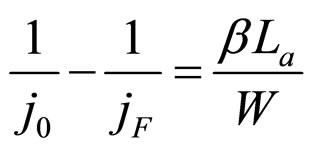 (75)
(75)
when 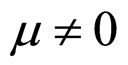 and
and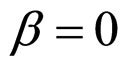 ,
,
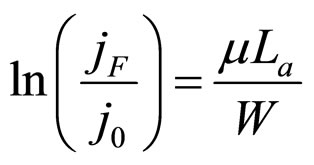 (76)
(76)
when 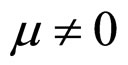 and
and ,
,
 (77)
(77)
In Formulae (75)-(77), initial current densities j0 are given separately as Formulae (72)-(74).
In W-j plane, Formulae (75)-(77) all present themselves as a curve, the bold dashdotted curve  in Figures 7-9, called the cell first precise absolute lifetime boundary MCP curve for the corresponding cell degradation characteristic. This is to distinguish it from the cell first approximate absolute lifetime boundary MCP curve that will occur latter on. Formulae (59)-(61) all present themselves as a straight line of equal current density, the straight line
in Figures 7-9, called the cell first precise absolute lifetime boundary MCP curve for the corresponding cell degradation characteristic. This is to distinguish it from the cell first approximate absolute lifetime boundary MCP curve that will occur latter on. Formulae (59)-(61) all present themselves as a straight line of equal current density, the straight line  in Figures 7-9, called the cell second absolute lifetime boundary MCP curve. As seen from Figures 7-9, the cell precise absolute lifetime boundary MCP curve is actually a devious curve composed of the cell first precise absolute lifetime boundary MCP curve in the economic voltage range of
in Figures 7-9, called the cell second absolute lifetime boundary MCP curve. As seen from Figures 7-9, the cell precise absolute lifetime boundary MCP curve is actually a devious curve composed of the cell first precise absolute lifetime boundary MCP curve in the economic voltage range of  and the cell second absolute lifetime boundary MCP curve in the range of
and the cell second absolute lifetime boundary MCP curve in the range of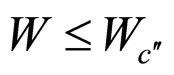 . It is the assembly of the cell MCP points at the absolute lifetime boundary over the whole cost factor range.
. It is the assembly of the cell MCP points at the absolute lifetime boundary over the whole cost factor range.
Formulae (75)-(77) look as they were simple, but they are very complicated actually. Akin to the related treatments in Sections 2.2.3 and 2.3.3, the cell first precise absolute lifetime boundary MCP curve for each cell degradation characteristic can be approximately replaced with a straight line, the line  displayed in Figures 7-9. This straight line is called the cell first approximate absolute lifetime boundary MCP curve, and its expressions are given as Formulae (78)-(80).
displayed in Figures 7-9. This straight line is called the cell first approximate absolute lifetime boundary MCP curve, and its expressions are given as Formulae (78)-(80).
when  and
and ,
,
 (78)
(78)
when 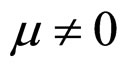 and
and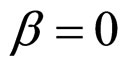 ,
,
 (79)
(79)
when  and
and ,
,
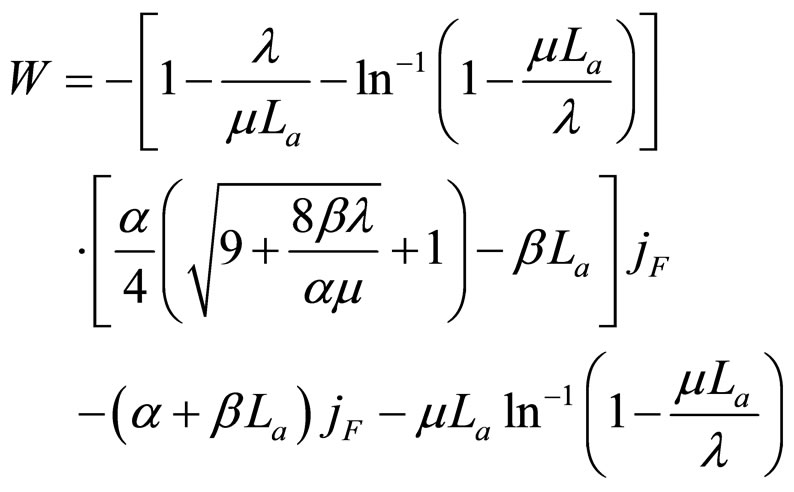 (80)
(80)
In the case of 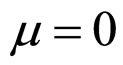 and
and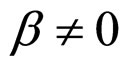 , the cell first approximate absolute lifetime boundary MCP curve
, the cell first approximate absolute lifetime boundary MCP curve 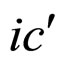 is passing by points i and
is passing by points i and . Here, points i, a and d are superposed as one and points
. Here, points i, a and d are superposed as one and points  and
and 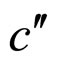 are done as the other. As seen from Figure 7, it may be acceptable to substitute curve
are done as the other. As seen from Figure 7, it may be acceptable to substitute curve  with curve
with curve  as one part of the cell absolute lifetime boundary MCP curve because of simplicity and small error.
as one part of the cell absolute lifetime boundary MCP curve because of simplicity and small error.
In the case of 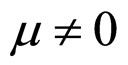 and
and , as shown in Figures 8(A) and 8(B), the cell first approximate absolute lifetime boundary MCP curve is a straight line that passes by the point i and the intersection point
, as shown in Figures 8(A) and 8(B), the cell first approximate absolute lifetime boundary MCP curve is a straight line that passes by the point i and the intersection point 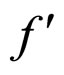 of the cell approximate unconditional interior MCP curve af with the absolute lifetime end-curve cd (or its extended part), and intersects the cell second absolute lifetime boundary MCP curve
of the cell approximate unconditional interior MCP curve af with the absolute lifetime end-curve cd (or its extended part), and intersects the cell second absolute lifetime boundary MCP curve 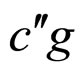 at point
at point . As seen from Figures 8(A) and 8(B), it may be allowable to replace the curve
. As seen from Figures 8(A) and 8(B), it may be allowable to replace the curve 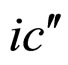 with the curve
with the curve 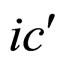 as one part of the cell absolute lifetime boundary MCP curve because of simplicity and small error. Such an approximate treatment of the cell first absolute lifetime boundary MCP equation actually originates from those of the cell unconditional interior MCP equation and the cell unconditional relative lifetime boundary MCP equation.
as one part of the cell absolute lifetime boundary MCP curve because of simplicity and small error. Such an approximate treatment of the cell first absolute lifetime boundary MCP equation actually originates from those of the cell unconditional interior MCP equation and the cell unconditional relative lifetime boundary MCP equation.
The case of  and
and  is similar to the case of
is similar to the case of 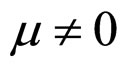 and
and 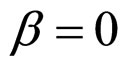 in principle in terms of the approximate treatment of the cell first absolute lifetime boundary MCP equation, so it is not discussed any more here. In the case of
in principle in terms of the approximate treatment of the cell first absolute lifetime boundary MCP equation, so it is not discussed any more here. In the case of  and
and , it should be noted that there exists an absolute lifetime value as given in Formula (81) where the cell approximate unconditional interior MCP curve is parallel to the absolute lifetime end-curve. Here, the cell first approximate absolute life-time boundary MCP curve is also parallel to both of them, but its expression is given still as Formula (80).
, it should be noted that there exists an absolute lifetime value as given in Formula (81) where the cell approximate unconditional interior MCP curve is parallel to the absolute lifetime end-curve. Here, the cell first approximate absolute life-time boundary MCP curve is also parallel to both of them, but its expression is given still as Formula (80).
 (81)
(81)
After the approximate treatment of the cell first absolute lifetime boundary MCP curve, the cell absolute lifetime boundary MCP curve becomes composed of two straight line segments,  and
and .
.
Owing to simplicity and small error, the following discussions will be opened up on the cell first approximate absolute lifetime boundary MCP curve. Moreover, the term the cell first absolute lifetime boundary MCP curve refers to the cell first approximate absolute lifetime boundary MCP curve unless otherwise stated.
3.4.4. Applicable Cost Factor Range of Cell Absolute Lifetime Boundary MCP Curve
The cell first and second absolute lifetime boundary MCP curves apply to different cost factor ranges, and their ranges can be defined by means of their intersection point. As seen from Figures 7-9, their intersection point is point , so their applicable cost factor ranges are
, so their applicable cost factor ranges are  and
and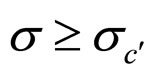 , respectively.
, respectively.
Under the three degradation characteristics,  and
and ,
, 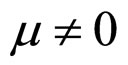 and
and  and
and 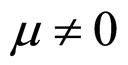 and
and , the coordinates of point c’ are given as Formula (82)-(84), respectively. Substituting Formula (82) into Formula (69), Formula (83) into Formula (70) and Formula (84) into Formula (71) separately give the value of
, the coordinates of point c’ are given as Formula (82)-(84), respectively. Substituting Formula (82) into Formula (69), Formula (83) into Formula (70) and Formula (84) into Formula (71) separately give the value of  under the three degradation characteristics.
under the three degradation characteristics.
 (82)
(82)
 (83)
(83)
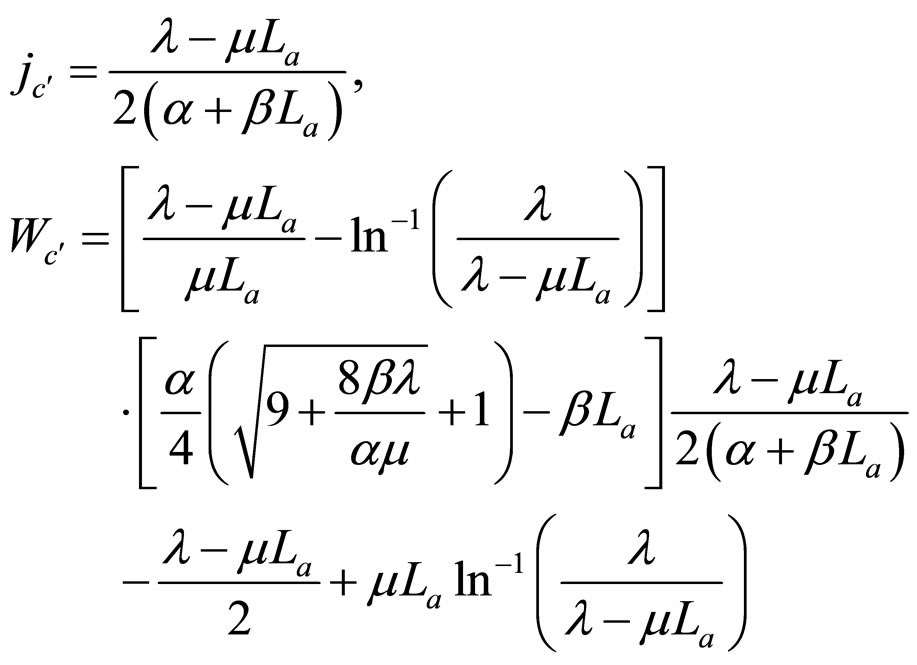 (84)
(84)
3.4.5. Cell Absolute Lifetime Boundary OFO Curve
The whole cell absolute lifetime boundary MCP curve is composed of two parts, i.e. two straight line segments in different cost factor ranges regardless of degradation characteristic. This composition may determine the corresponding cell absolute lifetime boundary OFO curve has two parts as well. Obviously, the cell first absolute lifetime boundary MCP curve corresponds to the absolute lifetime end-curve by point-to-point but they are not superposed, thus the absolute lifetime end-curve is just the first part of the cell absolute lifetime boundary OFO curve in the cost factor range of . The second part of the cell absolute lifetime boundary OFO curve seems special, as it is nothing but one point, point c. That is to say, in the cost factor range of
. The second part of the cell absolute lifetime boundary OFO curve seems special, as it is nothing but one point, point c. That is to say, in the cost factor range of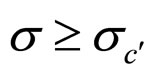 , the cell second absolute lifetime boundary MCP curve belongs to only one final operating point, point c, a special point on the absolute lifetime end-curve.
, the cell second absolute lifetime boundary MCP curve belongs to only one final operating point, point c, a special point on the absolute lifetime end-curve.
3.5. Discriminant Approach for Cell MCP Point
3.5.1. Diagrammatic Representation
Figures 10-12 display the integrative results about the evolutions of the load and cell MCP points under the three cell degradation characteristics. In these figures, the thin solid curves denote the load MCP curves of equal economic factor; the short bold dash curve is the cell MCP curve; the thin dotted curves are the load characteristic curves or constant current density curve and the short thin curves play an assistant role. See Sections 2.2, 2.3 and 2.4 for the implications of other points and curves, and see the following discussions for the implications of related terms.
3.5.2. Components of Load MCP Curves
The individual discussions on the load interior MCP curve, the load relative lifetime boundary CP curve and the load absolute lifetime boundary CP curves separately in Sections 2.2, 2.3 and 2.4 can help clarify the components of load MCP curves. The clarification is mainly to distinguish the attribute of load MCP points.
As displayed in Figures 10-12, the components of
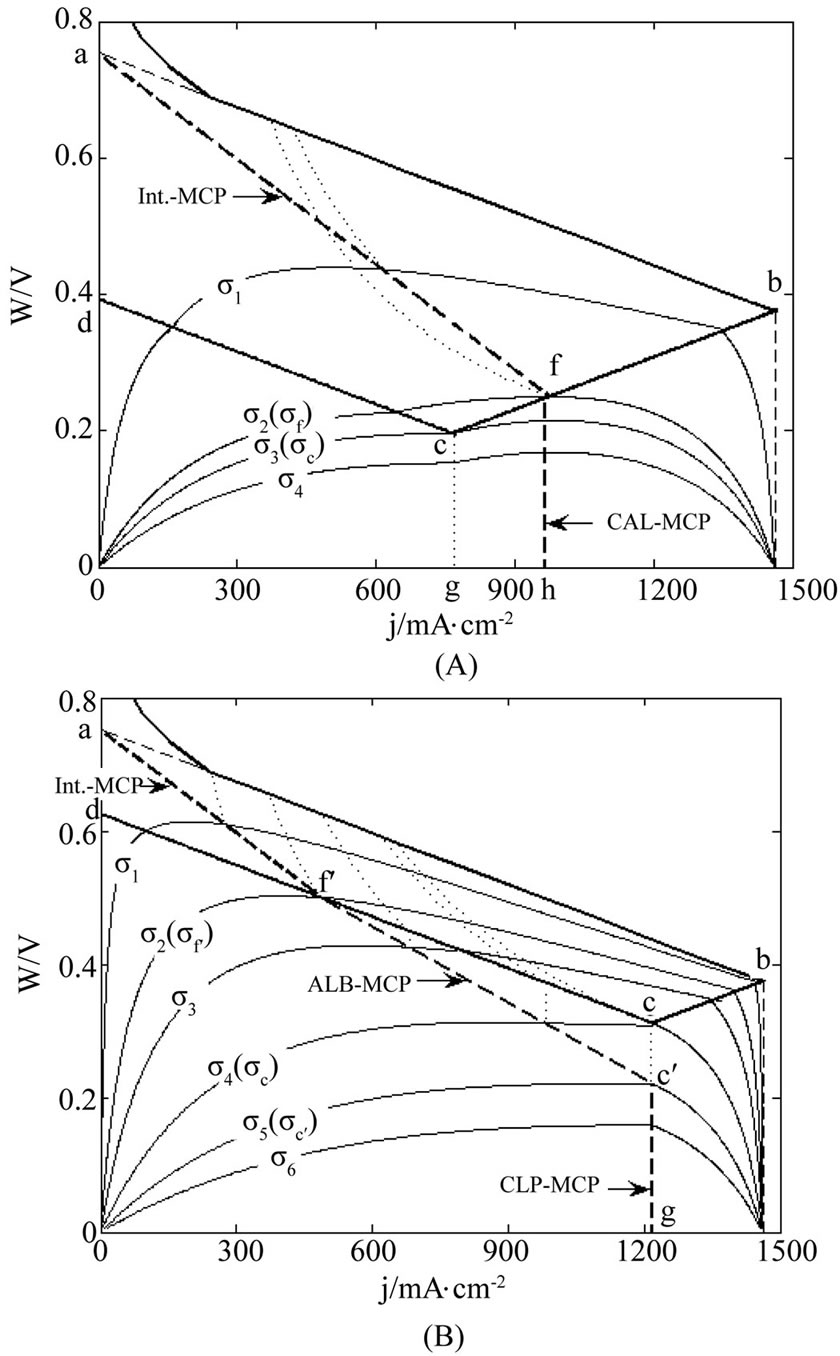
Figure 11. The composition of the cell MCP and OFO curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β = 0. See text for more details.
load M-ECR curves depend on the cost factor range where they are under any cell degradation characteristic. Here the dividing point is the cost factor value at the intersection point c of the relative and absolute lifetime end-curves. When , load M-ECR curves are made up of three attributes of points: the load absolute lifetime boundary CP point, the load interior MCP point and the load relative lifetime boundary CP point. When
, load M-ECR curves are made up of three attributes of points: the load absolute lifetime boundary CP point, the load interior MCP point and the load relative lifetime boundary CP point. When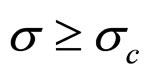 , load M-ECR curves are only made up of two attributes of points: the load absolute and relative lifetime boundary CP points.
, load M-ECR curves are only made up of two attributes of points: the load absolute and relative lifetime boundary CP points.
As seen from Figures 10-12, in W-j plane, all of load absolute lifetime boundary CP curves add up to an enclosed zone by the absolute lifetime end-curve, the j = 0 line, the W = 0 line and the j = jc line, called the load absolute lifetime boundary MCP zone. All of load relative lifetime boundary CP curves also add up to an enclosed zone by the relative lifetime end-curve, the j = jc line, the W = 0 line and the j = jh line. The working zone is just the assembly of all of load interior MCP curve, the third enclosed zone, called the load interior MCP zone.
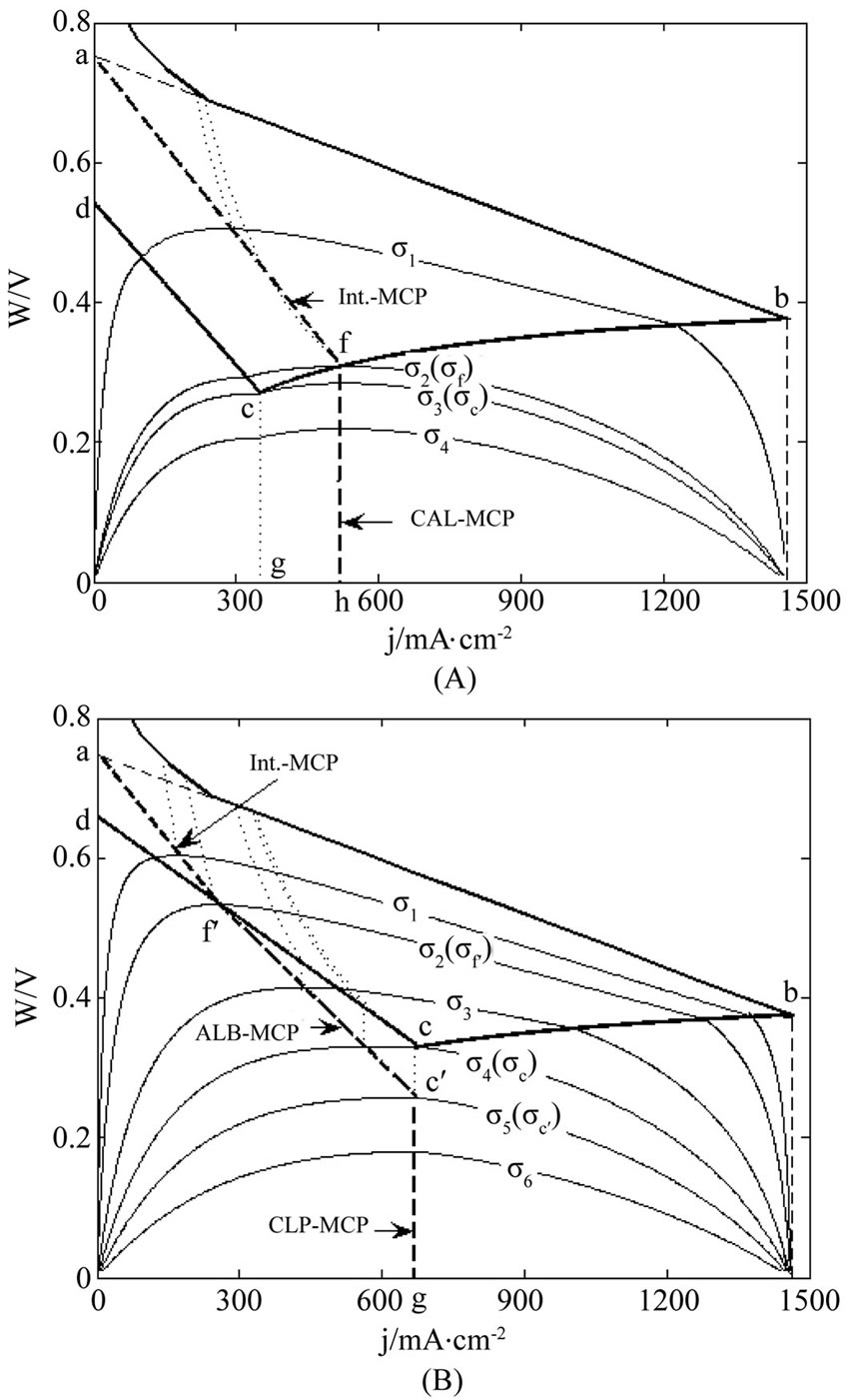
Figure 12. The composition of the cell MCP and OFO curves in the cell absolute lifetime ranges of (A) La ≥ La,f and (B) La ≤ La,f in the case of μ ≠ 0 and β ≠ 0. See text for more details.
3.5.3. Components of the Cell MCP Curve
Put together the individual results on the cell interior MCP curve, the cell relative lifetime boundary MCP curve and the cell absolute lifetime boundary MCP curve as discussed separately in Sections 2.2, 2.3 and 2.4, then the components of the cell MCP curve can be clarified. This clarification is to distinguish the attributes of different cell MCP points.
In the case of 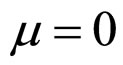 and
and , as shown in Figures 10(A) and 10(B), in W-j plane, the cell MCP curve is made up of two straight line segments,
, as shown in Figures 10(A) and 10(B), in W-j plane, the cell MCP curve is made up of two straight line segments,  and
and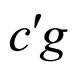 , regardless of absolute lifetime. The former is located in the load absolute lifetime boundary MCP zone, and thus it is the cell first absolute lifetime boundary MCP curve. The latter is nicely located on the boundary between the load relative and absolute lifetime boundary MCP zones, so it is the cell second absolute lifetime boundary MCP curve as well as the cell conditional relative lifetime boundary MCP curve.
, regardless of absolute lifetime. The former is located in the load absolute lifetime boundary MCP zone, and thus it is the cell first absolute lifetime boundary MCP curve. The latter is nicely located on the boundary between the load relative and absolute lifetime boundary MCP zones, so it is the cell second absolute lifetime boundary MCP curve as well as the cell conditional relative lifetime boundary MCP curve.
In the case of 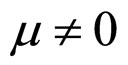 and
and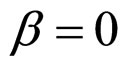 , the components of the cell MCP curve depends on the range where the cell absolute lifetime is. When
, the components of the cell MCP curve depends on the range where the cell absolute lifetime is. When , as shown in Figure 11(A), the cell MCP curve is composed of two straight line segments, af and fh. Located in the load interior MCP zone, the former is the cell unconditional interior MCP curve; located in the load relative lifetime boundary MCP zone, the latter is the cell unconditional relative lifetime boundary MCP curve. When
, as shown in Figure 11(A), the cell MCP curve is composed of two straight line segments, af and fh. Located in the load interior MCP zone, the former is the cell unconditional interior MCP curve; located in the load relative lifetime boundary MCP zone, the latter is the cell unconditional relative lifetime boundary MCP curve. When , as shown in Figure 11(B), the cell MCP curve is composed of three straight line segments,
, as shown in Figure 11(B), the cell MCP curve is composed of three straight line segments,  ,
, 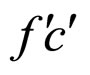 and
and . Located in the load interior MCP zone, the first is the cell unconditional interior MCP curve; located in the load absolute lifetime boundary MCP zone, the second is the cell first absolute lifetime boundary MCP curve; located on the boundary between the load relative and absolute lifetime boundary MCP zones, the third is the cell second absolute lifetime boundary MCP curve as well as the cell conditional relative lifetime boundary MCP curve.
. Located in the load interior MCP zone, the first is the cell unconditional interior MCP curve; located in the load absolute lifetime boundary MCP zone, the second is the cell first absolute lifetime boundary MCP curve; located on the boundary between the load relative and absolute lifetime boundary MCP zones, the third is the cell second absolute lifetime boundary MCP curve as well as the cell conditional relative lifetime boundary MCP curve.
The case of  and
and 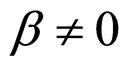 is the same with that of
is the same with that of 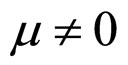 and
and 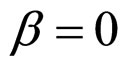 in terms of the components of the cell MCP curve, so it is not stated any more.
in terms of the components of the cell MCP curve, so it is not stated any more.
3.5.4. Simple Names of Cell MCP Curve Components
In Section 2.1, three leading candidates for the cell M-ECR point are preparatorily named after their positions. The movement of each leading candidate with cost factor is expressed in the form of cell MCP curve in the individual discussions in Sections 2.2, 2.3 and 2.4. As a result, various and multifarious names of cell MCP curve are produced. However, once the three leading candidates are integrated together, the final overall results become relatively simple. The following are a set of more simple names.
The cell MCP curve 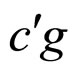 as shown in Figures 10(A), 10(B), 11(B) and 12(B) only belongs to the finial operating point c. Point c is so important that it should be given a special name, the critical load power point. Thus, the curve
as shown in Figures 10(A), 10(B), 11(B) and 12(B) only belongs to the finial operating point c. Point c is so important that it should be given a special name, the critical load power point. Thus, the curve  can be called the cell critical load power MCP curve, abbreviated to the cell CLP-MCP curve as shown in Figures 10(A), 10(B), 11(B) and 12(B).
can be called the cell critical load power MCP curve, abbreviated to the cell CLP-MCP curve as shown in Figures 10(A), 10(B), 11(B) and 12(B).
The cell MCP curve fh as shown in Figures 11(A) and 12(A) only belongs to the finial operating point f. Point f is so significant that it should be given a special name, the critical absolute lifetime point. Thus, the curve fh can be called the cell critical absolute lifetime MCP curve, abbreviated to the cell CAL-MCP curve as shown in Figures 11(A) and 12(A).
Both the curve af in Figures 11(A) and 12(A) and the curve  in Figures 11(B) and 12(B) belongs to different finial operating points in the interior of the working zone and they can still be called the cell interior MCP curve, abbreviated to the cell int.-MCP curve as shown in Figures 11(A), 11(B), 12(A) and 12(B). Compared with the names in independent analyses, the attributes unconditional and approximate are removed.
in Figures 11(B) and 12(B) belongs to different finial operating points in the interior of the working zone and they can still be called the cell interior MCP curve, abbreviated to the cell int.-MCP curve as shown in Figures 11(A), 11(B), 12(A) and 12(B). Compared with the names in independent analyses, the attributes unconditional and approximate are removed.
Both the curve  in Figures 10(A) and 10(B) and the curve
in Figures 10(A) and 10(B) and the curve  in Figures 11(B) and 12(B) belongs to different finial operating points on the absolute lifetime boundary of the working zone and they can still be called the cell absolute lifetime boundary MCP curve, abbreviated to the cell ALB-MCP curve as shown in Figures 10(A), 10(B), 11(B) and 12(B). Compared with the names in independent analyses, the attributes first and approximate are removed.
in Figures 11(B) and 12(B) belongs to different finial operating points on the absolute lifetime boundary of the working zone and they can still be called the cell absolute lifetime boundary MCP curve, abbreviated to the cell ALB-MCP curve as shown in Figures 10(A), 10(B), 11(B) and 12(B). Compared with the names in independent analyses, the attributes first and approximate are removed.
3.5.5. Discriminants and Criteria of the Cell M-ECR Point
By now a set of discriminants and criteria of the cell M-ECR point can be summarized by referring to Figures 10-12. These discriminants and criteria cover all of cell specialties and all of cost specialties, thus the OFO state and the M-ECR value of the PEM fuel cell power generation can be directly calculated however the conditions are complex. These discriminants and criteria are used to rapidly calculate the OFO current density, the OFO voltage and the maximum economic voltage (MEV).
1) The case of  and
and 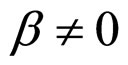
When , the cell OFO and MCP points move with cost factor separately by the absolute lifetime endcurve and the ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae (69) and 78, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6). When
, the cell OFO and MCP points move with cost factor separately by the absolute lifetime endcurve and the ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae (69) and 78, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6). When , the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula 59, and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (69) or (39). Thereinto,
, the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula 59, and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (69) or (39). Thereinto,  is gained by substituting Formula (82) into Formula (69).
is gained by substituting Formula (82) into Formula (69).
2) The case of  and
and 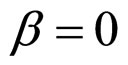
If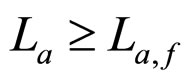 , when
, when , both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (19*) and (26*), and the MEV keeps equal to the OFO voltage; when
, both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (19*) and (26*), and the MEV keeps equal to the OFO voltage; when , the cell MCP point moves by the cell CAL-MCP curve with the OFO point fixed at the cell critical absolute lifetime point, the OFO current density is given as Formula (57), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (7) and (49). Thereinto,
, the cell MCP point moves by the cell CAL-MCP curve with the OFO point fixed at the cell critical absolute lifetime point, the OFO current density is given as Formula (57), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (7) and (49). Thereinto,  is gained by substituting Formula (31*) into Formula (19*), and La,f is given as Formula (28).
is gained by substituting Formula (31*) into Formula (19*), and La,f is given as Formula (28).
If , when
, when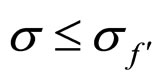 , both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (19*) and (26*), and the MEV keeps equal to the OFO voltage; when
, both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (19*) and (26*), and the MEV keeps equal to the OFO voltage; when , the cell OFO and MCP points move separately by the cell absolute lifetime end-curve and the cell ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae 70 and 79, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6); when
, the cell OFO and MCP points move separately by the cell absolute lifetime end-curve and the cell ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae 70 and 79, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6); when , the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula (60), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (70) or (40). Thereinto,
, the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula (60), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (70) or (40). Thereinto,  is gained by substituting Formula (33*) into Formula (19*),
is gained by substituting Formula (33*) into Formula (19*),  is done by substituting Formula (83) into Formula (70), and La,f is given as Formula (28).
is done by substituting Formula (83) into Formula (70), and La,f is given as Formula (28).
3) The case of  and
and 
If , when
, when , both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (20*) and (27*), and the MEV keeps equal to the OFO voltage; when
, both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (20*) and (27*), and the MEV keeps equal to the OFO voltage; when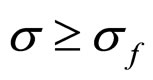 , the cell MCP point moves by the cell CAL-MCP curve with the OFO point fixed at the cell critical absolute lifetime point, the OFO current density is given as Formula (58), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (7) and (50). Thereinto,
, the cell MCP point moves by the cell CAL-MCP curve with the OFO point fixed at the cell critical absolute lifetime point, the OFO current density is given as Formula (58), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (7) and (50). Thereinto,  is gained by substituting Formula (35*) into Formula (20*), and La,f is given as Formula (29).
is gained by substituting Formula (35*) into Formula (20*), and La,f is given as Formula (29).
If , when
, when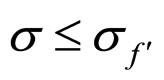 , both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (20*) and (27*), and the MEV keeps equal to the OFO voltage; when
, both the cell OFO and MCP points move by the int.-MCP curve, the OFO current density and voltage are the common solution to Formulae (20*) and (27*), and the MEV keeps equal to the OFO voltage; when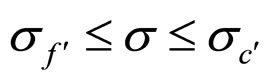 , the cell OFO and MCP points move separately by the cell absolute lifetime end-curve and the cell ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae 71 and 80, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6); when
, the cell OFO and MCP points move separately by the cell absolute lifetime end-curve and the cell ALB-MCP curve, the OFO current density and the MEV are the common solution to Formulae 71 and 80, and the OFO voltage can be calculated by substituting the OFO current density into Formula (6); when , the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula (61), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (71) or (41). Thereinto,
, the cell MCP point moves by the cell CLP-MCP curve with the OFO point fixed at the cell critical load power point, the OFO current density is given as Formula (61), and the OFO voltage and the MEV can be calculated by substituting the OFO current density separately into Formulae (6) and (71) or (41). Thereinto, 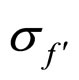 is gained by substituting Formula (37*) into Formula (20*),
is gained by substituting Formula (37*) into Formula (20*),  is done by substituting Formula (84) into Formula (71), and La,f is given as Formula (29).
is done by substituting Formula (84) into Formula (71), and La,f is given as Formula (29).
3.5.6. Ramifications of Cell M-ECR Point
There has been a lack of theory to determine the rated power and rated lifetime of PEM fuel cells for a long time. The determination of the cell M-ECR point may help solve this problem. The operating time and power density at the cell M-ECR point may be the OFO time and the optimal power density of the cells. These two parameters may be easy to calculate once the cell M-ECR point is determined. If they can be regarded as the rated lifetime and rated power of the cells, then the determination of the rated power and rated lifetime of PEM fuel cells gets free of random.
The cell M-ECR point can also be used to determine the optimal initial operating (OIO) point of PEM fuel cells. It may be certain there exists an OIO point for any cell that corresponds to the cell M-ECR point. Since it is located both on the initial SSP curve and on the load characteristic curve where the cell M-ECR point is located, the OIO point may be easily determined as well. Knowing the OIO point may be of importance for optimization of cell operation. For the purpose of the most economic use of PEM fuel cells, such an optimization is based on the combination of cell specialty and cost specialty.
3.6. Application Examples
As known from the discussions in Sections 2.5.5 and 2.5.6, the M-ECR point and the OIO point of PEM fuel cells can be determined however much cell degradation constants, cell initial polarization constants, cell absolute lifetime and cost constants are. For examples, given ,
,  ,
, 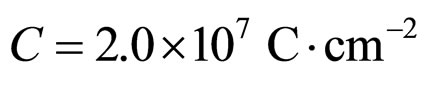 ,
,  , then the related data of the M-ECR point and the OIO point are given in Tables 2, 3 and 4 separately for three degradation constant combinations,
, then the related data of the M-ECR point and the OIO point are given in Tables 2, 3 and 4 separately for three degradation constant combinations, 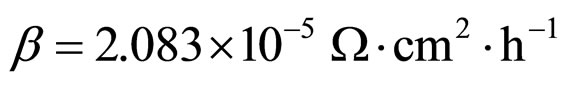 and
and ,
, 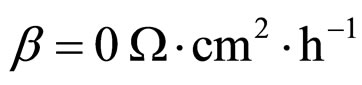 and
and ,
, 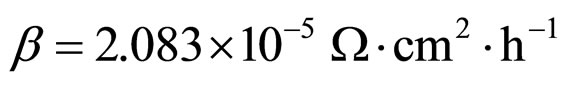 and
and . Six levels of absolute lifetime La, 2000 h, 5000 h, 10,000 h, 20,000 h, 30,000 h and 40,000 h, are given for each combination. The critical absolute lifetimes under the latter two combinations are calculated as 30,041 h and 16,076 h, respectively.
. Six levels of absolute lifetime La, 2000 h, 5000 h, 10,000 h, 20,000 h, 30,000 h and 40,000 h, are given for each combination. The critical absolute lifetimes under the latter two combinations are calculated as 30,041 h and 16,076 h, respectively.
From Tables 2-4, two important conclusions can be drawn: 1) the shorter the absolute lifetime, the smaller the OIO voltage is and the larger the optimal load power density is; 2) the achievement of high ECR does not require too long absolute lifetime of the cells with either of the latter two degradation characteristics owing to the existence of the critical absolute lifetime.
4. Conclusions
A complete set of discriminants and criteria of the maximal electricity-cost ratio (M-ECR) point of PEM fuel cells are successfully established based on the ideal cell model. They theoretically cover all of cell specialties and all of cost specialties and make the determination of

Table 2. Evolutions of the M-RCR point and the OIO point as cell absolute lifetime in the case of β = 2.083 × 10−5 Ω·cm2·h−1 and μ = 0 V·h−1.

Table 3. Evolutions of the M-RCR point and the OIO point as cell absolute lifetime in the case of β = 0 Ω·cm2·h−1 and μ = 8.333 × 10−6 V·h−1.
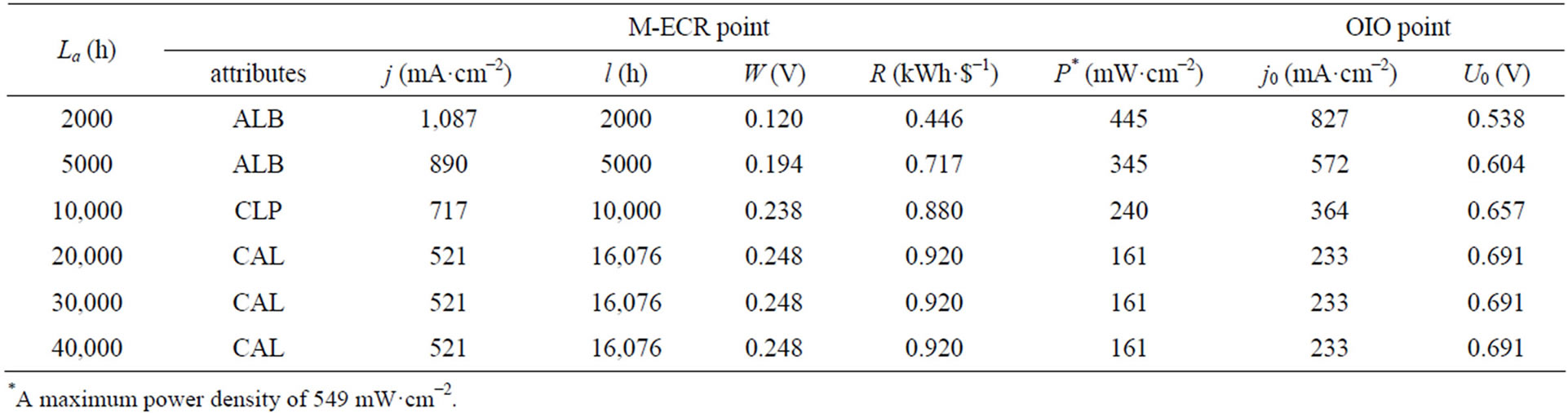
Table 4. Evolutions of the M-RCR point and the OIO point as cell absolute lifetime in the case of β = 2.083 × 10−5 Ω·cm2·h−1 and μ = 8.333 × 10−6 V·h−1.
the cell M-ECR point and the selection of the optimal load simpler, more direct and more rapid.
By means of the discriminants and criteria, the location and the ECR value of the cell M-ECR point can be directly calculated whatever the cell initial polarization constants, the cell degradation constants, the cell absolute lifetime and the cost constants of the power generation are. And the optimal initial operating point, the optimal load power and the optimal operating time of the cells can be determined together.
According to the discriminants and criteria, the movement of the M-ECR point with cell constants and cost constants forms two curves, the maximum cost performance curve and the optimal final operating curve. As the moving loca of two aspects of the M-ECR point, the latter is a straight line segment and the former is composed of two or three straight line segments in U-j plane.
From the discriminants and criteria, it is theoretically made clear that: 1) the shorter the absolute lifetime, the smaller the optimal initial operating voltage is and the larger the optimal load power density is; 2) there exists a critical absolute lifetime for some cells from the viewpoint of economics, thus the achievement of the highest ECR does not require too long absolute lifetime for these cells.
5. Acknowledgements
This work has been supported by the National 863 Program (No. 2012AA053402) and Specialized Research Fund for the Doctoral Program of Higher Education (No. 20090002110074).
REFERENCES
- H. F. Zhang, P. C. Pei, X. Yuan and X. Z. Wang, “Regularization of the Degradation Behavior and Working Zone of Proton Exchange Membrane Fuel Cells with a FiveConstant Ideal Cell as Prototype,” Energy Conversion and Management, Vol. 52, No. 10, 2011, pp. 3189-3196. doi:10.1016/j.enconman.2011.04.022
- H. F. Zhang and P. C. Pei, “The Two-Constant Cost Model and the Estimation of the Cost Performance Evolutions of the Proton Exchange Membrane Fuel Cell Power Generation,” Energy and Power Engineering, in Press.
- H. F. Zhang, P. C. Pei, M. C. Song and D. P. Zhang, “A Volt-Ampere Method to Estimate the Energy Efficiency Evolutions of Proton Exchange Membrane Fuel Cells along with Load and Time,” Energy and Power Engineering, in Press.
Nomenclature
Constants and variables
α: the slope of the linear part of the initial polarization curve;
β: the changing rate of α with operating time;
λ: the intercept of the linear part of the initial polarization curve;
μ: the changing rate of λ with operating time;
σ: cost factor, the ratio of the constant cost to the variable cost coefficient;
σx: cost factor at geometric point x;
C: the constant cost measured in unit cell active area;
v: the variable cost coefficient based on charge quantity;
l: operating time;
j: operating current density;
j0: the initial operating current density;
jF: the final operating current density;
jx: the operating current density at geometric point x;
La: the absolute lifetime;
La,f: the critical absolute lifetime;
Lr: the relative lifetime;
P: power density of cell or load;
R: electricity-cost ratio;
U: operating voltage;
U0: initial operating voltage;
W: economic voltage, the product of R and v;
Wx: the economic voltage at geometric point x.
Abbreviations
CAL: critical absolute lifetime;
CLP: critical load power;
CP: cost performance;
ECR: electricity-cost ratio;
FO: final operating;
int.: interior;
MCP: maximum cost performance;
M-ECR: maximum electricity-cost ratio;
MEV: maximum economic voltage;
OFO: optimal final operating;
OIO: optimal initial operating;
PEM: proton exchange membrane;
SSP: steady-state polarization.

