Energy and Power Engineering
Vol.4 No.5(2012), Article ID:22846,7 pages DOI:10.4236/epe.2012.45048
The Density and Momentum Distributions of 2-Dimensional Transonic Flow in an LP-Steam Turbine
Researching and Graduate Section, Applied Hydraulics and Thermal Engineering Laboratory, ESIME—Instituto Politécnico Nacional, Mexico City, Mexico
Email: mtv49@yahoo.com
Received June 5, 2012; revised July 7, 2012; accepted July 19, 2012
Keywords: Steam Turbines; Nucleation; Two Phase Flow; Erosion
ABSTRACT
Within turbine blade rows, particularly for cascades of high deflection angle, cross-channel gradients of steam properties may be appreciable. To determine the effects on spontaneous condensation of gradients of supersaturation normal to streamlines, the conservation equations can be incorporated in a two dimensional calculation procedure. With the help of program FORTRAN 90 a developed computational program of calculations is accomplished, whose results are communicated to the pressure and Mach number distribution, direction of flow and streamlines in the field and the drops distribution in the outlet of the stator blade mesh. The procedure contains a program section, which avoids difficulties in the strongly curved profile of the leading and trailing edge by a developed computational mesh construction.
1. Introduction
Basically, there are two fundamental theories for two-phase flow, namely, the macroscopic continuum mechanics theory and the microscopic kinetic theory. At present, the most accurate and efficient manner to model the interaction between the moisture and the gas phase, is within a Lagrangian frame of reference. Interaction between the phases, in the present model, is through appropriately modeled interphase source terms.
When a particle is injected into the flow (for steady-state calculations) the particle is tracked until some fate is reached, such as impacting a wall, Figure 1, passing into a periodic boundary, exiting the flow domain or reaching a stage interface. For a particular fate, a predetermined action is undertaken such as bouncing or sticking (wall), leaving the domain (outflow), translation/rotation and reinjection (periodic condition), collection/scaling and reinjection (stage interface).
The addition of two-phase effects to the three-dimensional flow field in turbomachinery increases the complexity of an already difficult problem. However, many of the features involved occur in two-dimensional flow fields and so, for simplicity, the theory presented below focuses on two-dimensional methods.
Before embarking on a multi-dimensional two phase flow calculation, it is important to establish a consistent set of conservation equations. Steam in the vapour phase is not a perfect gas and it is important to model the imperfections as accurately as possible in order to reduce the sources of error when comparing theoretical with experimental measurements.

Figure 1. Drop (pink line) leaving the trailing edge of a stator blade and reaching the leading edge of a rotor blade in a steam turbine. Blue lines are streamlines.
When the codes combine Eulerian-Lagrangian frame of reference it means that the main flow equations are solved in an Eulerian framework (the program uses a conventional H-mesh) but the wetness calculation follow individual fluid particles through the cascades. For steadyflow, this involves identifying the true streamlines through the cascades in order to interpolate the pressure time variation required for the wetness calculation.
The ultimate objective is to develop a computer model of a wet steam turbine which will provide estimates for all the main effects of wetness including changes in the flow aerodynamics, the wetness loss distribution and even the potential for erosion damage.
2. Methodology
2.1. Two Phase Flow: Fog Droplet Deposition and Coarse Water Formation
What we known about the formation and movement of coarse water in steam turbines (and its effect on turbine efficiency), is that the mechanism responsible for fog droplet deposition onto the turbine blading is originated essentially by two methods: inertial impaction in which fog droplets are transported to the blade surfaces and is a laminar flow phenomenon caused by the inability of the droplets to follow precisely the vapour stream lines during their passage through a blade row. The second is deposition by turbulent diffusion and occurs because very small droplets have a tendency to be transported through a turbulent boundary layer to a solid surface.
Coarse water appears as a result of the accumulation of fog droplets that come into contact with, and adhere to, the blade/casing surfaces. This coarse water flow continues to build-up in passing through the machine as the steam continues to expand to lower pressures, at increased “equilibrium” wetness level, with more fog production and deposition. The effects of wetness, resulting from water formation and distribution, on both fluid dynamics and plant thermodynamics includes: the worsening of stage efficiencies and the degrading effect on overall cycle performance.
Wetness loss, affecting both stage efficiency and turbine performance, is considered to be caused by several effects, initially by supersaturation and nucleation, followed by the moisture losses of droplet drag and incidence/centrifuging on rotor blades The total wetness fraction, at a point between blade rows in a turbine, can be considered to be the sum of contributions from fog (undeposited) droplets, coarse droplets and coarse water flowing on hub or casing surfaces. The coarse droplet contribution can be measured by capture on absorbent material in suitably designed probes, with collection efficiencies greater than 90 percent for droplets larger than about 10 µm [1].
Erosion at the tip-inlet region of LP (Low Pressure) moving blades is seen as the major mechanical problem of steam turbine operation in wet-steam. In essence, steam expanding in a LP turbine into the wet region, initially contains a fog of sub-micron drops. Some of the fog is deposited on fixed and moving blade surfaces and a high proportion of the resultant water is successively re-entrained and deposited downstream, while further deposition of fog droplets occurs on later stages. The water deposited on the moving blades is centrifuged towards the outer casing, whereas that deposited on the fixed blades moves across and along their surfaces under the action of steam forces. Water eventually leaves the trailing edges of the fixed blades to form a distribution of drops typically up to 350 µm in diameter. These are only slowly accelerated by the steam and therefore impinge onto the leadingedge of the moving blade at an off-design incident trajectory-angle, and higher relative velocity, than the steam [2].
This in general, causes the familiar erosion of LP blades at the tip where relative velocities are high and water is concentrated by centrifugal effects.
In detail, the continuous impact of water drops onto the surface of the blade at high speed, causing impact pressure, leads to cracking of the grain structure of the blade material, followed by grains being removed leaving a roughened surface sometimes, as in Figure 2, displaying sharp peaks/pinnacles and deep pits. Eventually, the eroded surface takes on a familiar pitted appearance and, in extreme cases, with wholesale removal of material, changing the shape of the blade-nose and altering the blade structural properties (cutting-back towards lacing-holes, causing eccentric CF bending and producing change in blade natural frequencies/engine order resonance).
Impact erosion is characterized by individual particles contacting the surface with a velocity (V) and angle of impact (α) as shown in Figure 3. Removal of material over time occurs through small scale deformation, fatigue cracking or a combination of the above depending upon the properties of both the wear surface and the eroding particle.

Figure 2. Severe erosion on suction side of steam turbine blades.
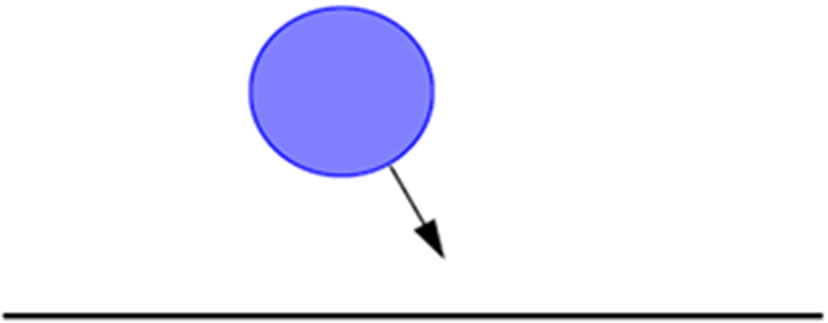
Figure 3. Oblique impact of a drop on a solid surface.
Important though this may be, erosion is only one consequence of the presence of water in steam. Very serious also are the problem caused by local departures of the system from thermodynamic equilibrium. This is because the release of latent heat, associated with a return to equilibrium, to the parent compressible vapour can have serious aerodynamic consequences, of which chocking mass flowrates through turbine stages and flow patterns round blades are examples.
Much progress has been made in the development of numerical methods for twoand three-dimensional flows in other contexts and such treatments can be extended to two-phase flows with some modifications. Condensing flows can be regarded as a special case of compressible fluid flow with heat addition in which the source is the latent energy released by phase change. Other two-phase effects include change in the specific volume of the fluid upon condensation and the drag and deposition of the liquid droplets, but due to the large enthalpy of phase change it is the heat release effect that dominates [3].
2.2. Numerical Method
For any multi-dimensional two phase flow calculation, it is important to establish a consistent set of conservation equation. If these equations are applied to the gas field alone, then the liquid phase equations serve to provide source terms of heat and mass. Alternatively, if the conservation equations are applied to the mixture as a whole, then the liquid phase equations must be integrated in order to compute mixture quantities (such as specific enthalpy and density) via the wetness fraction.
Clearly, the addition of two-phase effects to the threedimensional flow field in turbomachinery increases the complexity of an already difficult problem. However, many of the features involved occur in two-dimensional flow fields and so, for simplicity, the theory presented below focuses on two-dimensional methods.
Generally, the three physics laws of conservation, namely: mass conservation law, momentum conservation law and energy conservation law, must be followed in fluid calculation. According to the characteristics and nature of the flow, other constraint equations could be included, such as: viscosity, transport equation, fraction conservation equation, etc. [4].
The sequence in which variables are updated is as follows: the density is updated from the continuity equation, the internal energy is updated from the energy equation, and in combination with new values of density, is used to update pressure and temperature. The velocity components are updated from the momentum equations, using upwinded values of the newly calculated pressures.
At present CFD methods for modelling dispersed twophase flows fall into two categories, either an Eulerian/Lagrangian or an Eulerian/Eulerian representation of the phases. A 2D Eulerian/Eulerian approach, in the simplest cases involving heat transfer and one representative droplet size requires solving and additional four equations for the dispersed phase.
These equations are the first four moments of the droplet size distribution. The conservation equations are thus supplemented by droplet number conservation (the zeroth moment), liquid surface area conservation (the second moment), and liquid volume conservation (the third moment); the first has no obvious physical interpretation.
In combination with the conservation equations, the preceding equations describe two-phase and wet steam flows. With the ultimate aim being application to turbine flows, an important consideration is that flows round turbine blading are generally transonic with appreciable supersonic zones. The mathematical behaviour of the governing equations differs in subsonic, transonic, and supersonic regimes due to the change in direction of propagated waves and ideally the method of treatment should be applicable to all such regimes and have good shock capturing capabilities.
Other methods for the comprehensive investigation of water drop presence in LP turbines are: experimental and numerical simulations, where the first step is to obtain the two-phase flow field and relevant impact statistics of the water drops, and the second step is to explore the fundamental liquid-solid impact problem, and to obtain damage characteristics. Both experimental and numerical simulations may be used to track the motion of water drops in the wet steam.
2.3. Validation of Numerical Model
For the developed problem-specific algorithm, it was found that mesh-independent enthalpy solutions were obtained when 73 nodes are used in the x and 32 nodes in the y Cartesian mesh directions. The approach of the results of calculation to the stationary solution was effectuated several times. After 1200 steps the result depends hardly of the time. An examination of the mass flow densities showed deviations after 2200 steps.
Other two-dimensional treatments using time marching scheme are used for comparisons. For the most part, the methods have been applied to blade-to-blade flows. Calculations in the meridional plane have also been undertaken, however, using a time marching method, and using streamline curvature.
For the quantitative examination of the calculation the representation of the total enthalpy is used. The comparison between calculated and isentropic total enthalpy shows that the arithmetic procedures in the leading edge of the profile have a better agreement than in the trailing edge. The control of the transonic flow calculation was accomplished also by the comparison of the inlet and outlet mass flows. The difference in the comparison of the inlet and outlet mass flows was accomplished. The difference is small as seen in Figure 4.
2.4. Processing of Results
For the representation of the calculation procedure, the dimensionless formulation was introduced and, on the basis of U, V and σ, the temporal derivatives were calculated at each point in the mesh by:
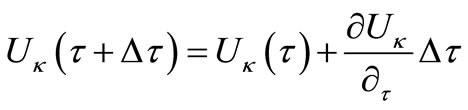 (1)
(1)
 (2)
(2)
 (3)
(3)
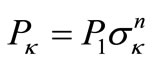 (4)
(4)
the magnitude of Uk, Vk, sk in the time t + Dt and the Equation (4) are associated to Pk.
The edges were treated as the upper and lower delimitations of the blade profile. Here the condition of periodicity was fulfilled. It demands that the values int he place (i, js) are equal to those in the place (i, jp), as in Figure 5.
3. Results
The governing equations for mass and momentum are solved in a coupled manner, and for the present model can be shown in tensor form as
 (5)
(5)
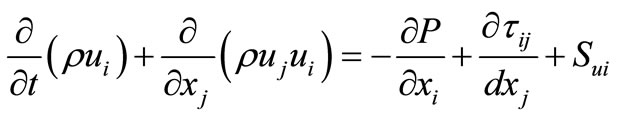 (6)
(6)
where the source terms, Sm and Sui, contain sources representing mass and momentum exchange between the water droplets and the surrounding gas. The source term Sui, in a rotating frame of reference, also includes appropriate

Figure 4. Comparison of inlet and outlet mass flow for control of the transonic flow calculation.

Figure 5. Stagnation points and periodicity condition.
contributions to represent Coriolas and centripetal forces.
The conservation of total energy, H, in the domain is governed by the conservation equation
 (7)
(7)
where

The solutions based on these equations for two-phase flows when used in combination with H-grids, show some smearing pressure rises but by using a more orthogonal grid the problems can be minimized. The use of higher order schemes and more sophisticated grids reduce the problems still further. Consequently, the use of these methods in the examination of two phase flows in turbines can be recommended with some confidence.
Numerical results demonstrate that wet steam flows occurring in turbine passages exhibit features which are absent in single phase. The dominant effect of phase change in high speed condensing flows is the local departures from thermodynamic equilibrium and sudden release of heat when the system subsequently recovers it.
The approach of the results from the calculation of the stationary solution was effectuated several times and examined. After 1200 steps the results depends on the time. An examination of the mass flow showed deviation after 2200 steps. For the mesh presented in Figure 6 an example of calculation is accomplished.
Submicron-sized fog droplets are deposited on blade surfaces: in low-pressure turbines, deposition on the final stage stator blades is particularly relevant, but the penultimate stage will normally also operate in wet steam. The resulting surface water films are stripped from the trailing edge (centrifuged to the rip region in the case of penultimate stage rotor blades) and broken up by aerodynamic forces into large secondary or coarse droplets in the 10 - 100 µm, see Figure 7. These large droplets fail to accelerate to vapour speed before impact with rotor blade leading edges on the suction side.
For the quantitative examination of the calculation the representation of the total enthalpy was achieved. The comparison between the calculated and isentropic total enthalpy shows that the arithmetic procedures in the leading edge of the profile have a better agreement than in the trailing edge.
IsoMach numbers are indicated in Figure 8 and the isobars in Figure 9. There is a clear difference between suction and pressure lateral velocity. Originally, substantial problems came up along the blade profiles in the case of the evaluation of pressure and Mach numbers process due to the inaccurate treatment of the zone of flow within the range of the blade points that are found. These difficulties are avoided with the improvement of the mesh organization.
The sharp curvature of the profile outline, particularly in the trailing edge, leads to difficulties in the calculation. For the necessary adjustment of the mesh organization in this point a special section in the program was developed.

Figure 6. Mesh profile and example of calculation.

Figure 7. Inlet and outlet Mach numbers in the channel of stator blade.

Figure 8. IsoMach number.

Figure 9. Isobars for the stator blade channel with wet steam.
The lattice geometry and the mesh organization of the computation are given. An estimated initial distribution of the searched flow parameters σ, P, U and V must be entered. With the progress in time, the initial distribution, with constant boundary conditions, is iterated close to the stationary solution of the flow. If the difference of the flow functions is successively under a barrier which can be given, the approach to the stationary final state is ended. Then, the velocities fields are corrected in the suction and pressure side of the blade surface.
In addition, the solution functions σ, P, U and V of the iterated final state, were converted to quantities of ρ, p, cx, cy. The first parameter ρ1 was selected in such way that the pressure P1 fulfilled the turbine design. Inlet and outlet Mach number and the exit angle resulted from the calculation. At the same overall pressure ratio, the outlet Mach number, flow angle, and fluid properties differ substantially between superheated and wet steam flows. For the same pressure ratio, the wet steam flow has a lower exit Mach number than dry flows.
4. Conclusions
The quality of agreement between the theoretical and numerical results is very good demonstrating that twodimensional wet steam flows in blading can be treated satisfactorily by the time step method. For an appropriate mesh interpretation of the grade of saturated steam is essential the knowledge of the influence of the mesh geometry as well as the steam condition in the stator blade channel. The saturated steam stream in turbine stages connects the flow losses as well as the drop impact erosion of the blades. Both features are produced by the expansion, which partially in the stator blade surface is deposited as a fine fog and finally a water film is formed becoming in secondary drops in the trailing edge.
On the basis of the conservation law for mass, impulse and total enthalpy the calculation of the stationary, frictionless, two-dimensional, transonic flow in the turbine cascade was compiled, according to the method of the finite volume. The direction of flow and streamlines in the field and the drops distribution in the outlet of the stator blade were also found. With the help of FORTRAN language a computational program was developed. Results were shown as the pressure and Mach number distribution.
REFERENCES
- R. I. Crane, “Droplet Deposition in Steam Turbines,” Proceedings of the Institute of Mechanical Engineer Sciences, Vol. 218, No. 8, 2004, pp. 859-870.
- J. A. Hesketh and P. J. Walker, “Effects of Wetness in Steam Turbines,” Proceedings of the Institution of Mechanical Engineers Science, Vol. 219, No. 12, 2005, pp. 1301-1314.
- F. Bakhtar, A. J. White and H. Mashmoushy, “Theoretical Treatments of Two-Dimensional Two-Phase Flows of Steam and Comparison with Cascade Measurement,” Proceedings of the Institution of Mechanical Engineering Science, Vol. 219, No. 12, 2005, pp. 1335-1336. doi:10.1243/095440605X31454
- D. Xie, X. Yu, W. Li, Y. Hou, y. Shi and S. Cai, “Numerical Simulation of Water Droplets Deposition on the Last Stage Stationary Blade of Steam Turbine,” Energy and Power Engineering, vol. 2, No. 4, 2010. pp. 248-249. doi:10.4236/epe.2010.24036
Nomenclature


