Communications and Network
Vol.5 No.4(2013), Article ID:39760,9 pages DOI:10.4236/cn.2013.54041
Probabilistic Selection of QoS Paths for Improving Survivability in MPLS Networks
1Computer Science and Engineering, Jaypee University of Engineering and Technology, Guna, India
2Computer Science and Engineering, Indian Institute of Technology Indore, Indore, India
3Computer Applications, Samrat Ashok Technological Institute, Vidisha, India
Email: singh.ravindrakumar@gmail.com, nsc183@gmail.com, kanak.saxena@gmail.com
Copyright © 2013 Ravindra Kumar Singh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 21, 2013; revised October 28, 2013; accepted November 5, 2013
Keywords: MPLS; Label Switched Paths; Fault Tolerance; Survivability
ABSTRACT
Many applications do not fit well with the traditional best effort packet delivery policy of the Internet. These include applications such as Internet telephony and video conferencing which require voice and bulky graphical images transfer. Therefore, the policies of assigning traffic to various service classes and providing service as per the service level agreement of the user with the network provider came into existence. Multi-protocol Label Switching is the backbone of fast switching technology that helps the network service providers to implement these policies. It provides Quality of service oriented reserved paths from the source to the destination for the user’s traffic. Selection of these paths is a cumbersome task, especially when the traffic forecast is totally unknown. Furthermore, nodes and link failures in the Internet worsen the situation. This paper addresses the issue of selecting Label Switched Paths (LSPs) for various traffic demands in the network so that the resultant network has the characteristics like high failure resistance, low LSP demand blocking probability, low impact from the node or link failure, load balancing and low over-all resource utilization. By extensive simulations, the proposed cost function has been compared with the various cost functions mentioned in the literature and it was found to score over them in major aspects.
1. Introduction
The drastic growth of Internet and the use of computer networks have encouraged service providers to offer high priority Internet applications. These applications require continuous bandwidth and high availability of the network resources. Since the resources like bandwidth are limited and it is not always feasible to enhance them, it is necessary that they are used efficiently. Multiprotocollabel switching (MPLS) was essentially proposed for fast forwarding the packets over the Internet [1]. However it has other capabilities which are used for the traffic engineering and efficient resource utilization. It also facilitates source routing by using the pre-signaled path known as Label switched path (LSP). Optimized routing of these LSPs is very important which in turn is done by using the major building block, Constraint-Based Routing (CBR) [2]. These paths are signaled with the help of Resource reservation protocol-Traffic engineering (RSVPTE) which is the enhancement of Resource reservation protocol (RSVP). Figure 1 illustrates the MPLS network with two LSPs. Similarly, there can be more than one LSP between a pair of nodes. Selection of these paths should comply with the service level agreement between the end user and service provider. In addition, these paths should also reduce the cost of the network resources to increase the revenue of service provider. Moreover, the network resources are subject to failure which could hamper the service level agreement, so fault tolerance should also be considered while routing the LSPs. Internet engineering task force (IETF) [1] proposed two methods namely protection switching and rerouting for coping with the failure of links and nodes in the Internet. Protection switching is the end to end establishment of the backup path for every primary LSP whereas rerouting is the local recovery path bypassing the failed node or link. Both these techniques have their own set of advantages and disadvantages. Protection switching leads to inefficient utilization of resources since the backup path is not used until the primary path fails. Moreover, the
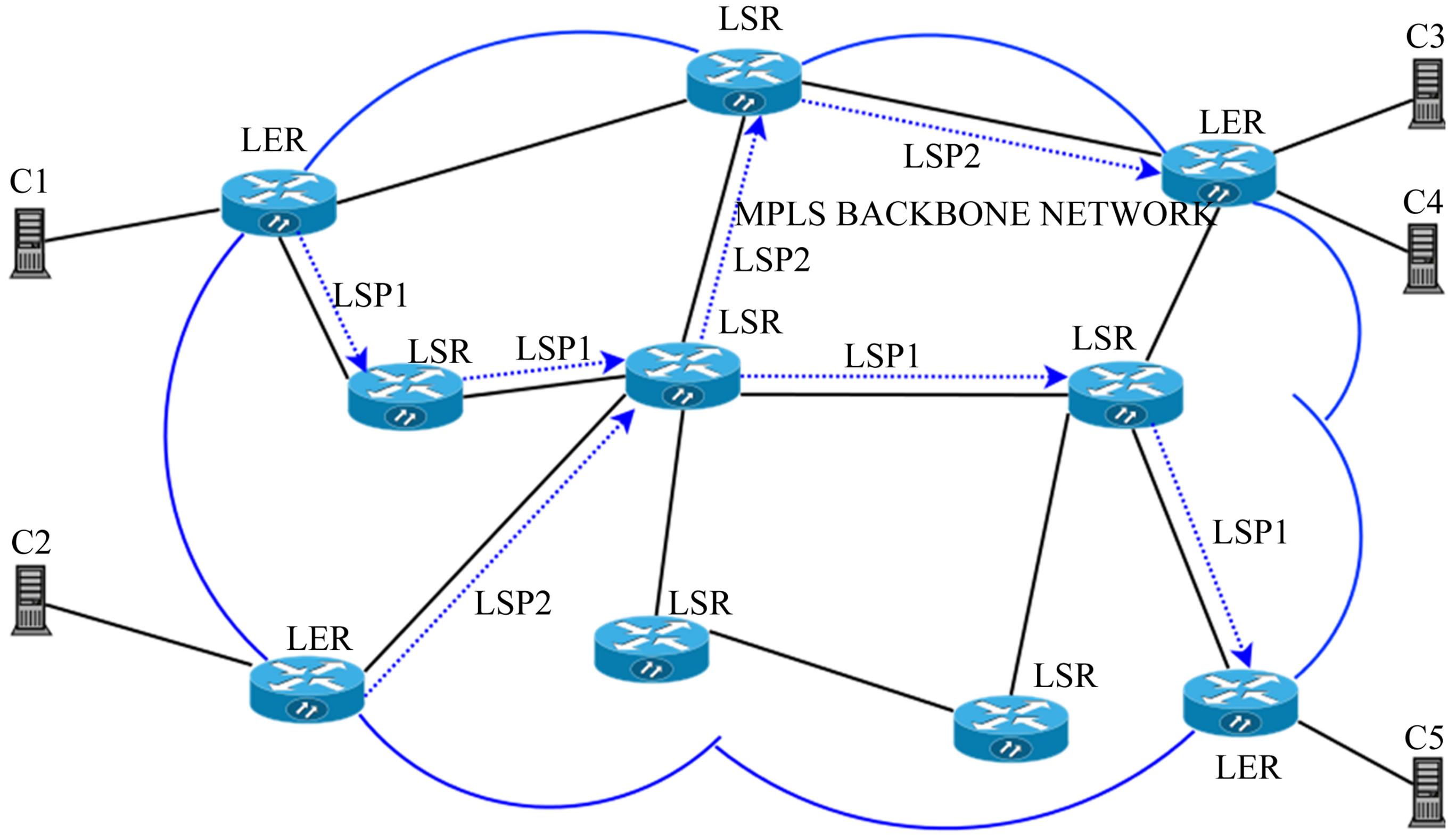
Figure 1. MPLS Network with two LSPs signaled.
Failure information signal (FIS) has to travel to the source node to initiate the switching of traffic to the recovery path which leads to the packet loss. This is because the source keeps on transmitting the packets in the mean time. Rerouting has the disadvantage of high network restoration time since the new routes are established only after the node or link fails.
Failure in the network cannot be fully avoided but it can be reduced if some consideration is paid to the failure history of the link during its selection [3]. This paper proposes a model for selection of paths with the lowest cost functions. A comparison between various cost functions suggested in the literature has been done with the proposed cost function which overcomes the limitations of traditional cost functions.
The rest of the paper is organized as follows. Section 2 discusses related work on the efficient path selection. Section 3 describes the model formulation. Section 4 provides the details of various cost functions used. Section 5 describes simulation results and performance analysis. Finally, the conclusion and the scope for future work are provided in Section 6.
2. Related Work
Pertaining to the issues discussed in Section 1, many authors have proposed various solutions for the efficient selection of the LSP in MPLS networks. This section discusses the proposals related to the work put forward in this paper.
Paper [4] suggests an algorithm to control the admission of traffic from the edges of the network using the threshold characteristics like bandwidth of the network state. The paper essentially states that for efficient admission control, emphasis should be given on consideration of the network state with the state of flow in the network. These network states are computed by the shortest path algorithms run beforehand in the background. Paper [5] performs comparative study of four LSP selection methods i.e. Minimim Hop (MinHop) [6], Load balancing, MinimumLength (MinLength) and Minimum Interface routing algorithm (MIRA) [7]. MinHop algorithm selects the LSPs considering the path length which is the number of intermediate hops. Load balancing tries to distribute the traffic demands into the entire network by balancing the load as per the residue bandwidth of the link. Minimum length algorithm engineers the traffic on the basis of physical length of the link. MIRA defines the critical link as the link which can result in affecting the MaxFlow [8] between the node pairs. MIRA delivers the best performance but has very high complexity since it computes the MaxFlow frequently [5]. The paper proposes an integrated solution by combining load balancing, MIRA and MinHop. Although it states that MIRA is computationally complex yet, it has been utilized more number of times than that in the original MIRA algorithm [7]. The paper [3] proposes a probabilistic algorithm for improving survivability of the selected paths for the traffic demands in the network. It proposes four cost functions and computes their performance by sequentially implementing the cost functions in the algorithms. Results vary with the sequence of the cost function deployed in the algorithms since there are trade-offs between cost functions. If the paths are selected on the basis of their failure probability history then load balancing gets affected i.e. the network is secured at the cost of resource consumption. Authors in [9] propose a model for link and node disjoint loop free path selection for 1:1 backup path protected network. They consider number of labels and maximum path length as the constraints to eliminate the splitting of traffic across any node and to prevent the formation of loops. Authors in [10] update the methods proposed by various authors on fault tolerance in MPLS networks. Recommendations of the transmission of traffic of failed LSP by one of more failure free LSPs have been made. Following issues and their solutions have been considered:
1) How to distribute the affected traffic to the failure free working LSPs?
Solution: The paper reflects the use of minimum cost flow solution for this problem by establishing a simple graph.
2) How to redirect the affected traffic to the failurefree working LSPs?
Solution: Changing the routing tables of the IP Access Network before MPLS networks for redirecting the traffic to new LSPs.
3) How to forward the affected traffic along the route of a failure-free working LSP?
Solution: Using IP tunneling mechanism.
4) How to solve packet loss and disorder?
Solution: Transferring the sequence number of the unsent packet to the source and thereafter all the packets starting from that number are transmitted by working LSPs.
There are certain issues that have not been addressed in this paper:
1) The paper does not mention how to select the failure free LSPs from that particular source to destination? If the backup LSP is selected simultaneously with the selection of active LSP then following problems can arise:
• Convergence will take considerable time since failure signals will have to travel to source router.
• We cannot predict whether the LSPs will be free when needed since they are allowed to carry other traffic also.
On the other hand, if the LSPs are selected in real time then the specific load balancing algorithm having the same effect as the minimum cost flow approach to transmit the failed LSPs traffic to failure free LSPs should have been mentioned. In minimum cost flow, the LSP having the minimum number of routers will be selected to transmit maximum packets. An instance described in the paper is to transmit 10 Mbps by balancing the load between LSP1 and LSP2. LSP2 is having cost 2 and residual bandwidth 8 whereas LSP3 is having cost 3 and residual bandwidth 10. The algorithm proposed to transmits 8 Mbps by LSP2 and 2 Mbps by LSP3 which does not solve the purpose since the aim is to have the packets in order. The speed with which the packet reaches will be the speed of the slower LSP having 3 as the cost. And more over it is not a good idea to use all the residual bandwidth of a LSP since it will limit its further usage when required.
2) In the permission token approach, the proposal hands over the token to the egress routers of the failure free LSPs. The router which possesses the token will forward the packets. Until then it will keep the packets in its buffer. The buffer size of the router is limited and there will be packet loss if the buffer gets overflow awaiting the permission token in the absence of flow control method.
In paper [11] authors have proposed an integrated solution by using the different selection algorithms depending on the load in the network. Authors in paper [12] present the model for problem of embedding the virtual network onto the physical substrate network. This has been done by selecting the appropriate path keeping in consideration the CPU capacity and bandwidth of the virtual network. The problem is then relaxed by reducing the restriction of integer constraints. In paper [13] this problem is further elaborated and solved by assuming that the substrate network is not fault resistant. Authors propose the algorithm for survivable virtual network embedding on the substrate network.
In the above works authors except that of paper [3] did not consider the link failure probability as the cost function. Authors in paper [3] differentiate the links into high availability and low availability links based on the threshold of the link failure probability and then establish the paths comprising of high availability links. For the low availability links they propose backup paths. As discussed above, due to the tradeoff between the cost functions, applying the cost function on the output of previous cost function do not give the optimized output. This problem is the motivation of the present work which for the best of our knowledge, is the first proposal to have considered the following three cost functions i.e. link failure probability history, distance of link from the source and the residual bandwidth encapsulated in a single cost function.
3. Proposed Model
Model: G = (V, E) is a directed graph representing the network in which:
V is the set of LSR (Label switched routers) and E is the set of edges Action: Determine the optimal set of binary variables a(e) and b(e) that:
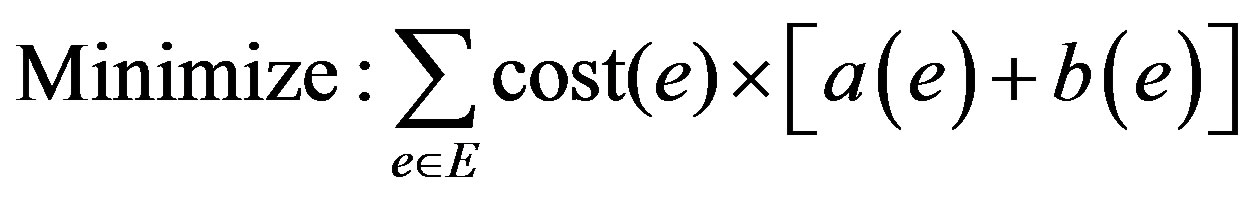 (1)
(1)
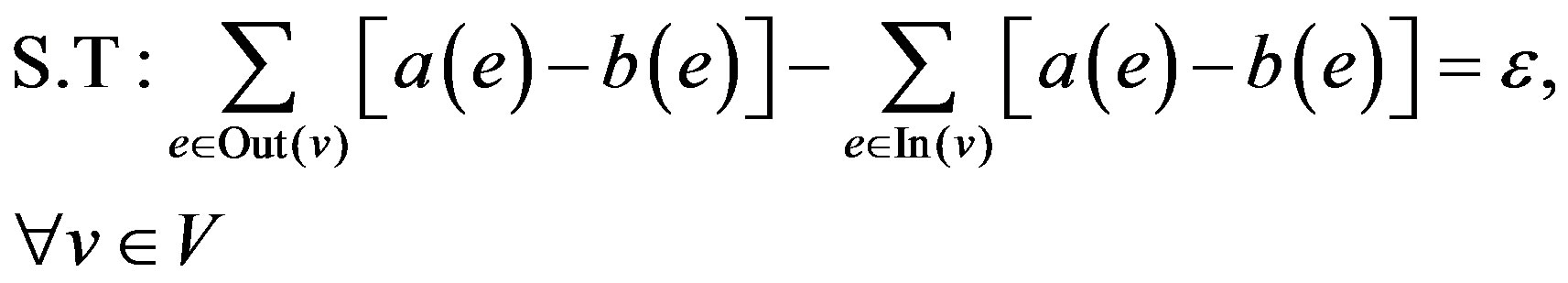 (2)
(2)
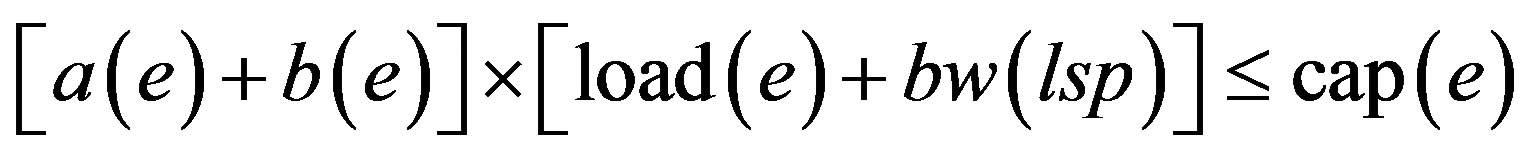 (3)
(3)
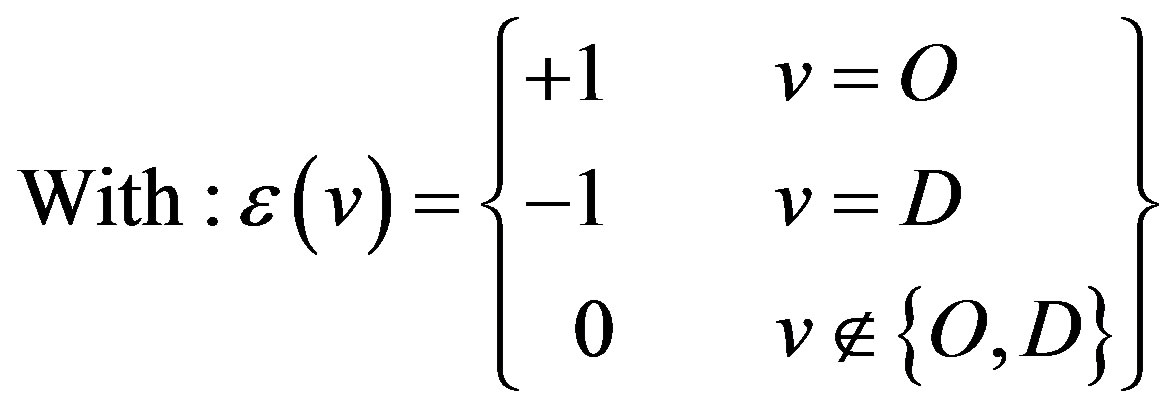 (4)
(4)
 (5)
(5)
Equation (1) is the objective of the model which calculates the minimum summation of the cost of the LSP calculated by the model. Binary variables a(e) and b(e) have the values 1 and 0 depending on whether the edge e is included in the LSP or not. Equations (2) and (4) are the flow conservation constraints which impose the condition that the total flow entering the node should be equal to the total flow leaving the node for every node which is not source or destination. For the source (destination) the incoming (outgoing) flow should be zero. Equation (3) applies the constraint that the sum of used bandwidth of a link and the bandwidth demand of a LSP should not be greater than the capacity of the edge. Equation (5) which is the base of this model defines the cost calculating functions. In this paper various cost functions are calculated by MinHop, load balancing, Residual Bandwidth, Link Cost, MIRA, and Proposed Algorithm.
4. Details of Cost Functions
Shortest path in the network is calculated by the famous Dijkstra’s algorithm [14] which calculates the shortest path by considering the weight of each edge of the network. This paper implements important cost functions in the literature.
4.1. MinHop
In the MinHop cost function, every link is given a unit weight. Shortest path algorithm selects the path which has minimum number of links. Therefore, same links are selected every time whenever there is a demand between the set of nodes. Consequently this causes rapid congestion of the links which leads to a scenario in which a part of network is heavily loaded while the remaining part is left underutilized.
4.2. Load Balancing
Load balancing refers to the distribution of load so that the network under consideration is uniformly loaded. In order to do this the cost of every link is given by:
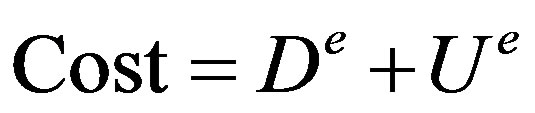 (6)
(6)
where D is the various queuing and the propagation delay experienced by the packets traversing the link and U is the load on the link due to the current passing by traffic.
4.3. Residual Bandwidth
Cost function for every link using this technique is calculated as:
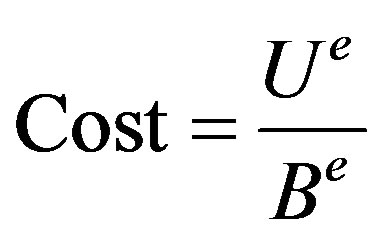 (7)
(7)
where U and B in Equation (7) are load of the present traffic and bandwidth of the link respectively.
4.4. Link Cost
In the Link Cost function every link is assigned a cost as shown in Equation (8):
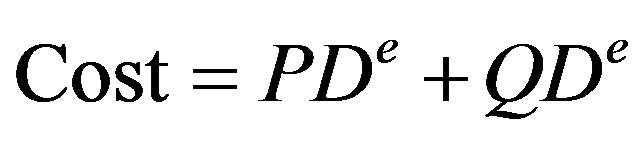 (8)
(8)
where, PD is the delay induced while propagation of packet through link and QD is average delay of the packets while waiting in the queue
4.5. MIRA
In MIRA the critical links are calculated on the basis of MaxFlow between source and destination. Cost of the link is then assigned as:
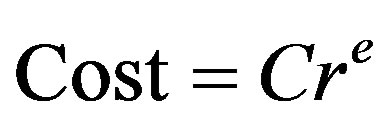 (9)
(9)
Criticality of a link in Equation (9), denoted by Cr is the numerical value incremented whenever the MaxFlow crosses a link. Thus, cost is directly proportional to the criticality of the link.
4.6. Proposed Cost Function
This paper implements the major cost functions and compares them with the proposed novel cost function to calculate the cost of a link based on three factors namely Link capacity, Link survival probability and Link Distance from source as:
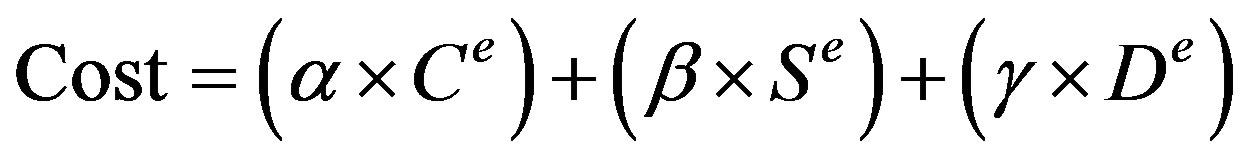 (10)
(10)
where C, S and D in Equation (10) are capacity, survival probability and distance of link from the source respectively. Distance of link from the source is calculated by all pair shortest path algorithm. Constants α, β and γ are used for assigning relative weightage to the three metrics.
5. Performance
Extensive simulations are performed on the proposed model in Section 3. This paper generates the topology by using BRITE [15] topology generator. Waxmann model with 10 nodes and 38 directed edges are used in the network topology. Bandwidth is uniformly distributed between 10 to 1050 MB. AMPL [16] is used for coding the model with various cost functions. Integer linear equations of Section 3 are solved by CPLEX [16] solver. Various network metrics have been compared for all the six cost functions of the proposed model in Section 3. These are illustrated in the following subsections.
5.1. Network Protection Degree
Network Protection Degree (NPD) of a network is computed as:
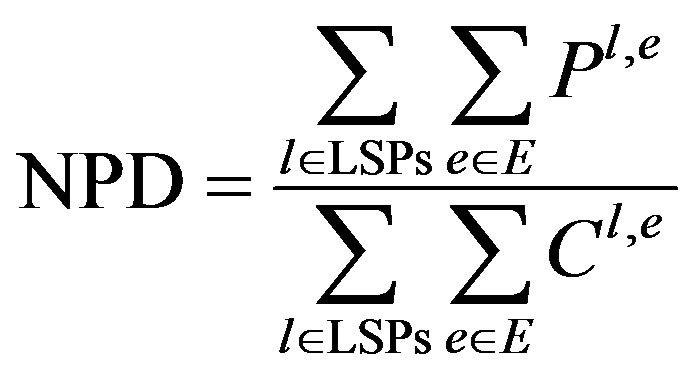 (11)
(11)
In Equation (11) P is the survival probability of link e and C is the count variable which is denotes the total number of edges in all the LSPs. A plot of number of LSPs with Network Protection Degree in Figure 2 depicts that the proposed algorithm performs better than rest of the algorithms in most of the cases. Standard deviation of the values of NPD plotted in Figure 3 states that the proposed algorithm does not vary considerably with the input.
5.2. Failure Impact Degree
Failure Impact Degree (FID) is the impact of the failure on the network. Impact of the failure is the amount of packet loss and packet disorder due to the link failure.
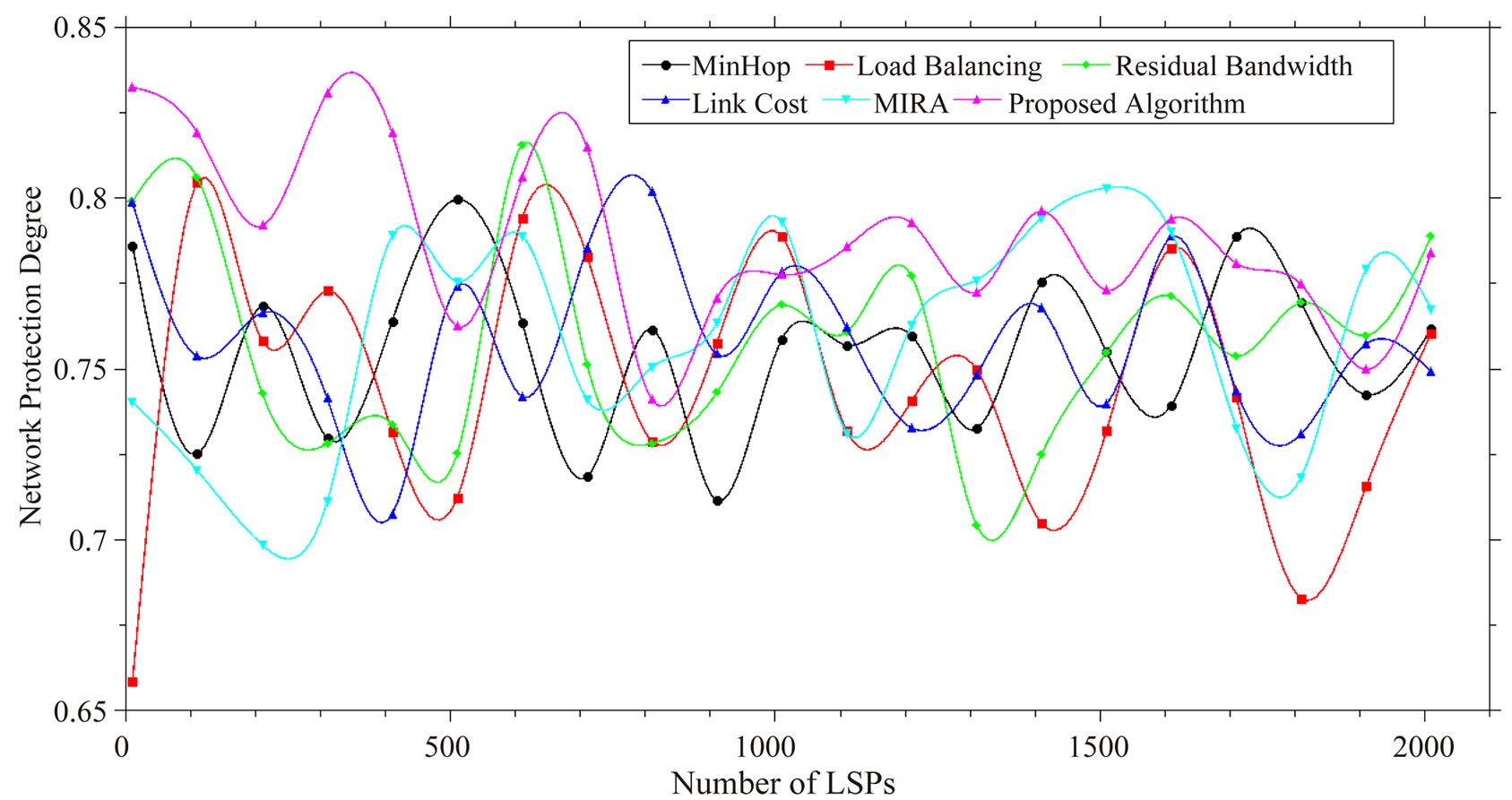
Figure 2. Network protection degree.
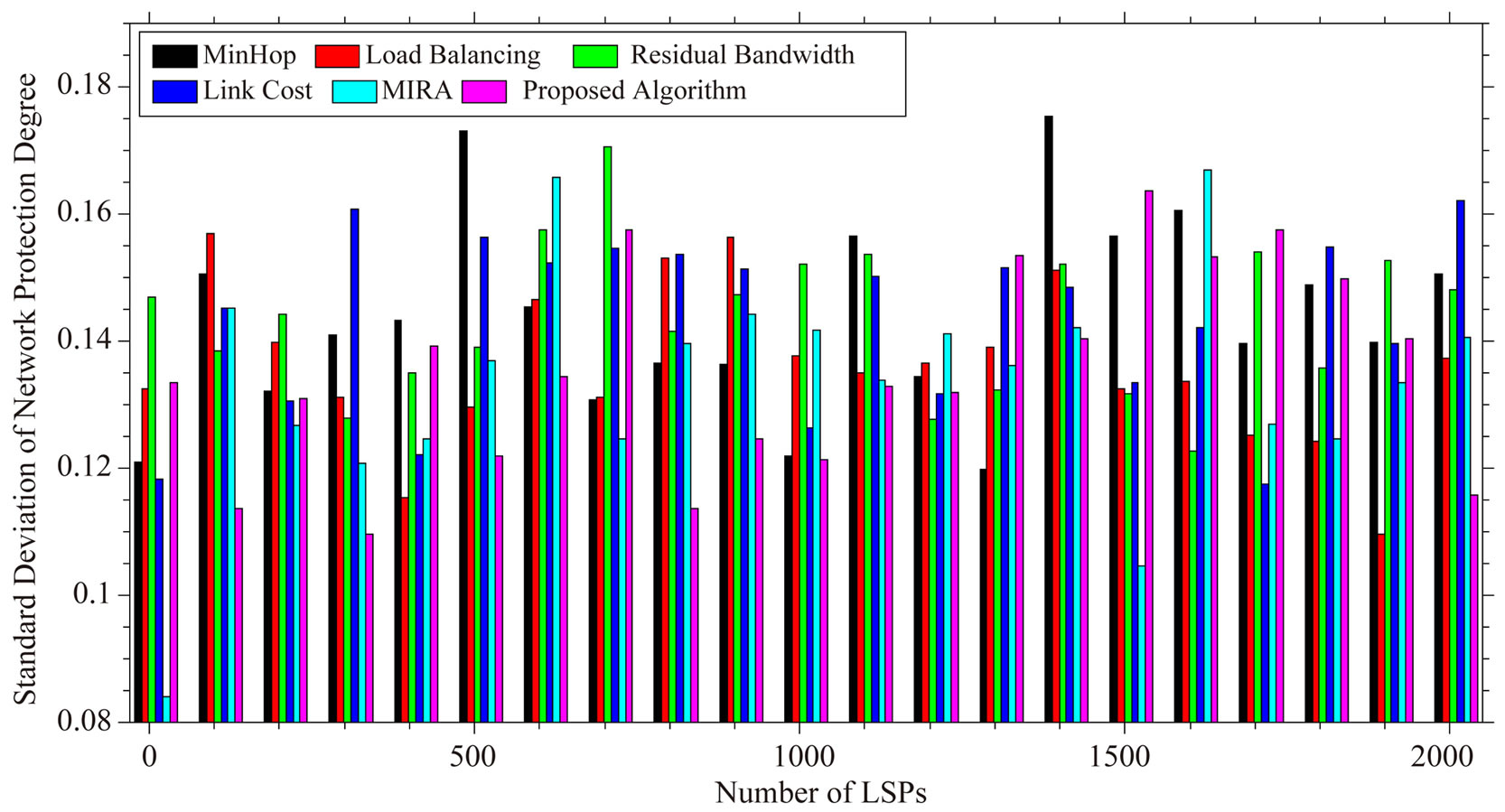
Figure 3. Standard deviation of network protection degree.
Most probably the link with low survival probability will fail and as suggested in this paper, this type of link has high cost function and therefore would not be considered in minimum cost path. But other proposals do not consider this metric. FID is calculated as:
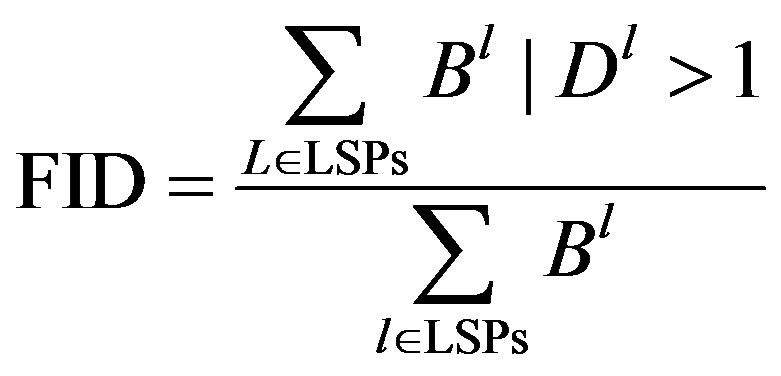 (12)
(12)
In Equation (12), B is the bandwidth of LSP l and D is the distance of low survival probability link from the source. The links with low survival probability having distance more than one hop from the source are selected. The sum of such is divided with the total number of paths. Plot the FID is illustrated in Figure 4. The proposed algorithm has low FID among all algorithms.
5.3. Number of Links to Be Protected (NLP)
NLP is calculated as:
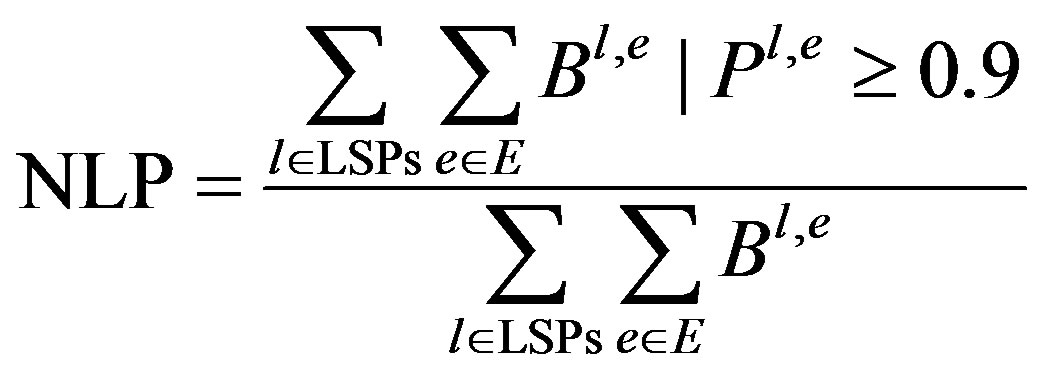 (13)
(13)
In Equation (13), B in the numerator denotes the bandwidth of edge of a LSP having probability more than or equal to 0.9 whereas in the denominator, B is the total bandwidth of all the edges. Figure 5 depicts that proposed algorithm has lower NLP in most of the case studies.
5.4. Blocked Request
Blocked request is the number of LSP requests blocked
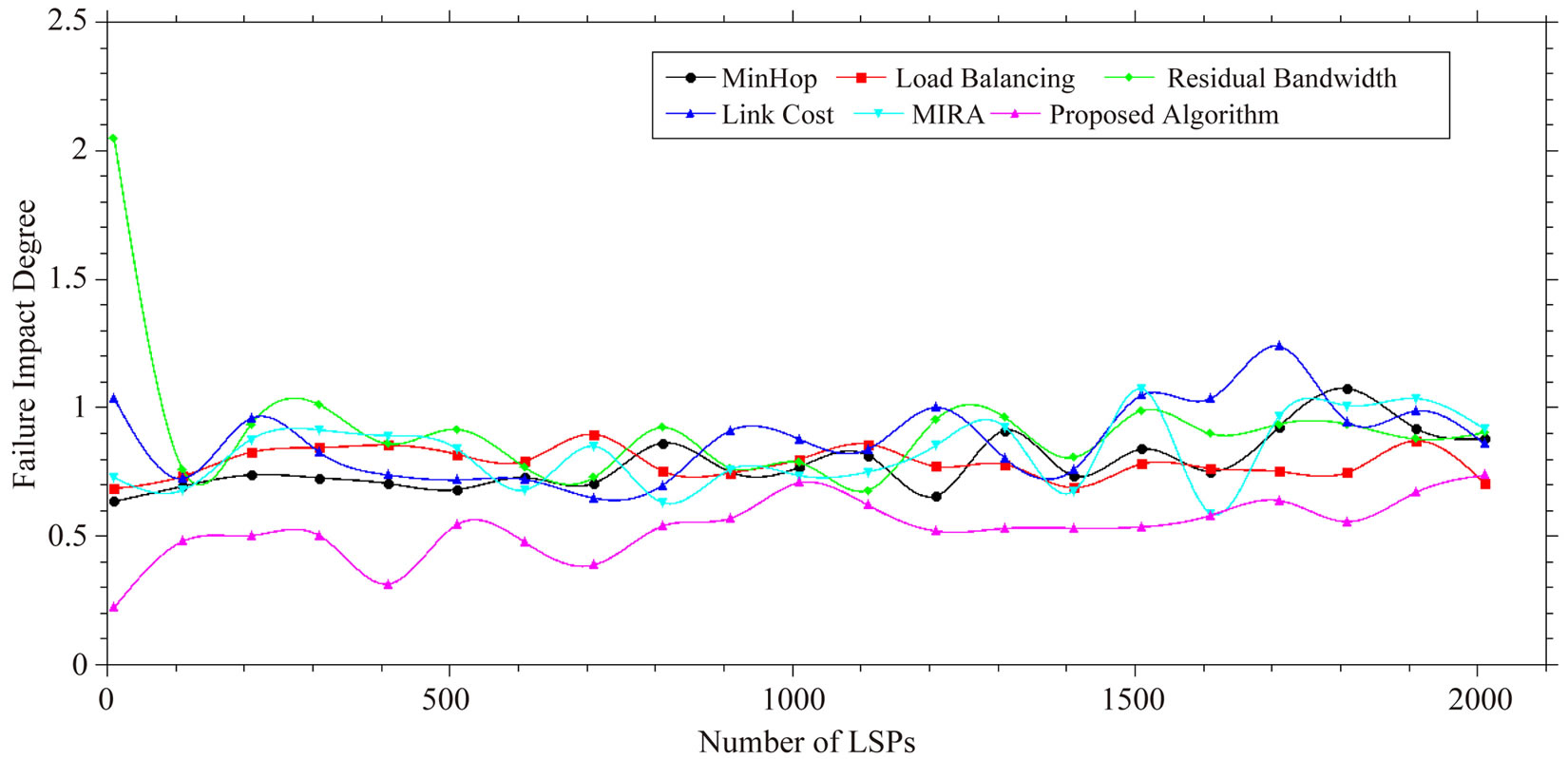
Figure 4. Failure Impact Degree (FID).
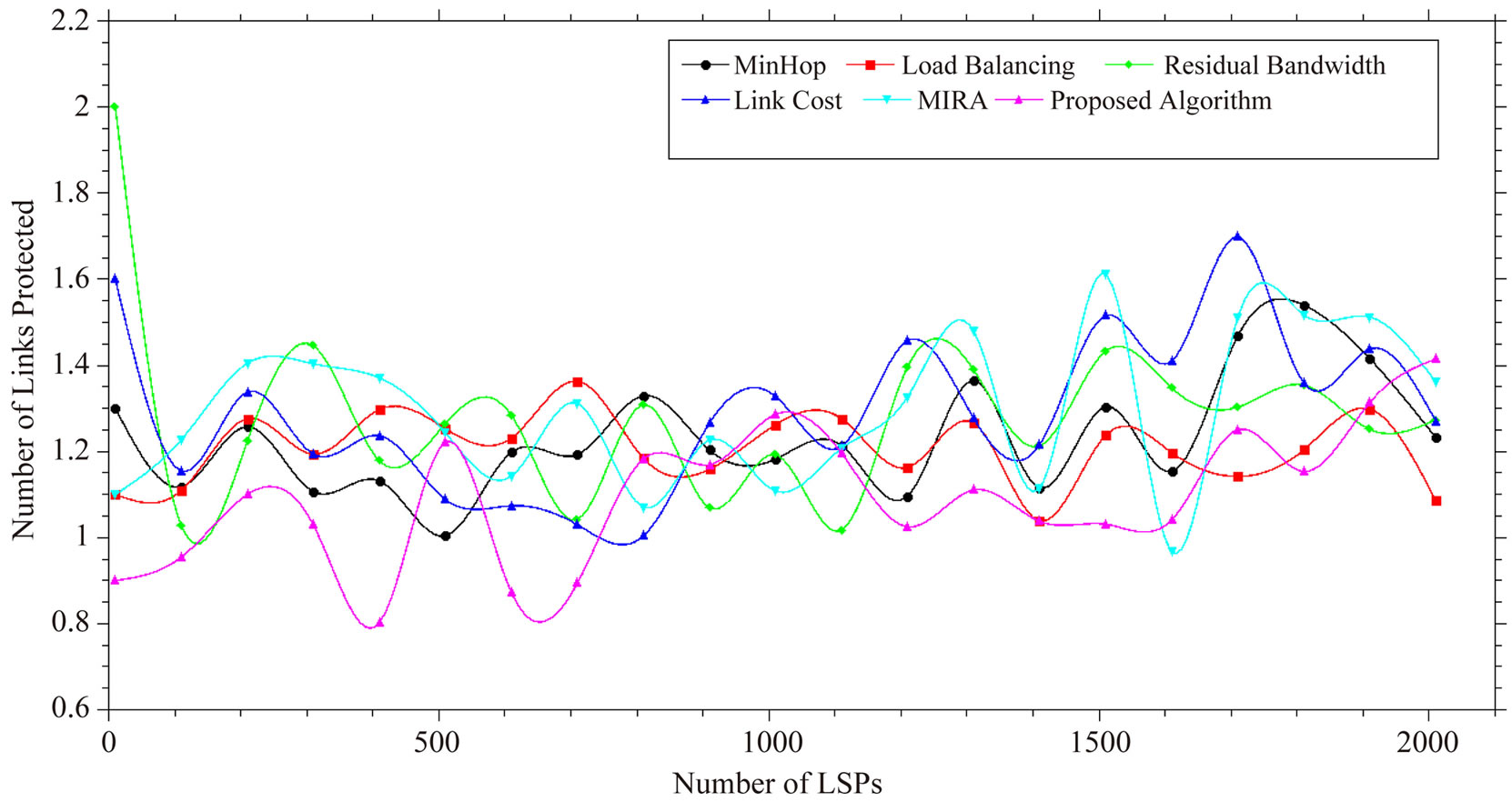
Figure 5. Number of links to be protected (NLP).
by the model. When plotted with total number of LSPs requested in Figure 6 illustrates that our algorithm performs better than all other algorithms except the residual bandwidth algorithm. The reason being the residual bandwidth algorithm does not try to consume the bandwidth of a link fully. Instead, it distributes the traffic among all the links in order to keep the bandwidth spare for the future requests. Load balancing is the worst performer in the blocked request.
5.5. Average Load on the Network
Average load on the network is calculated as:
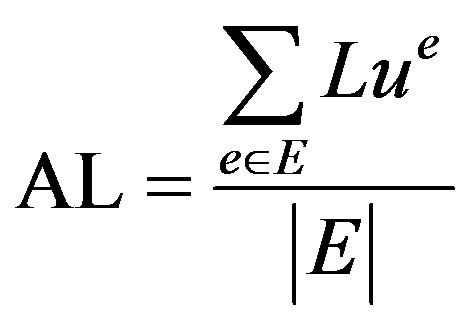 (14)
(14)
In Equation (14) Lu is the link usage. As shown in Figure 7, it is found that proposed algorithm has the second lowest average load. Load balancing has the lowest average load since it rejects many requests and therefore has less traffic to pass on. Figure 8 depicts the standard deviation of the average load value of all algorithms. Proposed algorithm again has the second lowest value for the same reason as above.
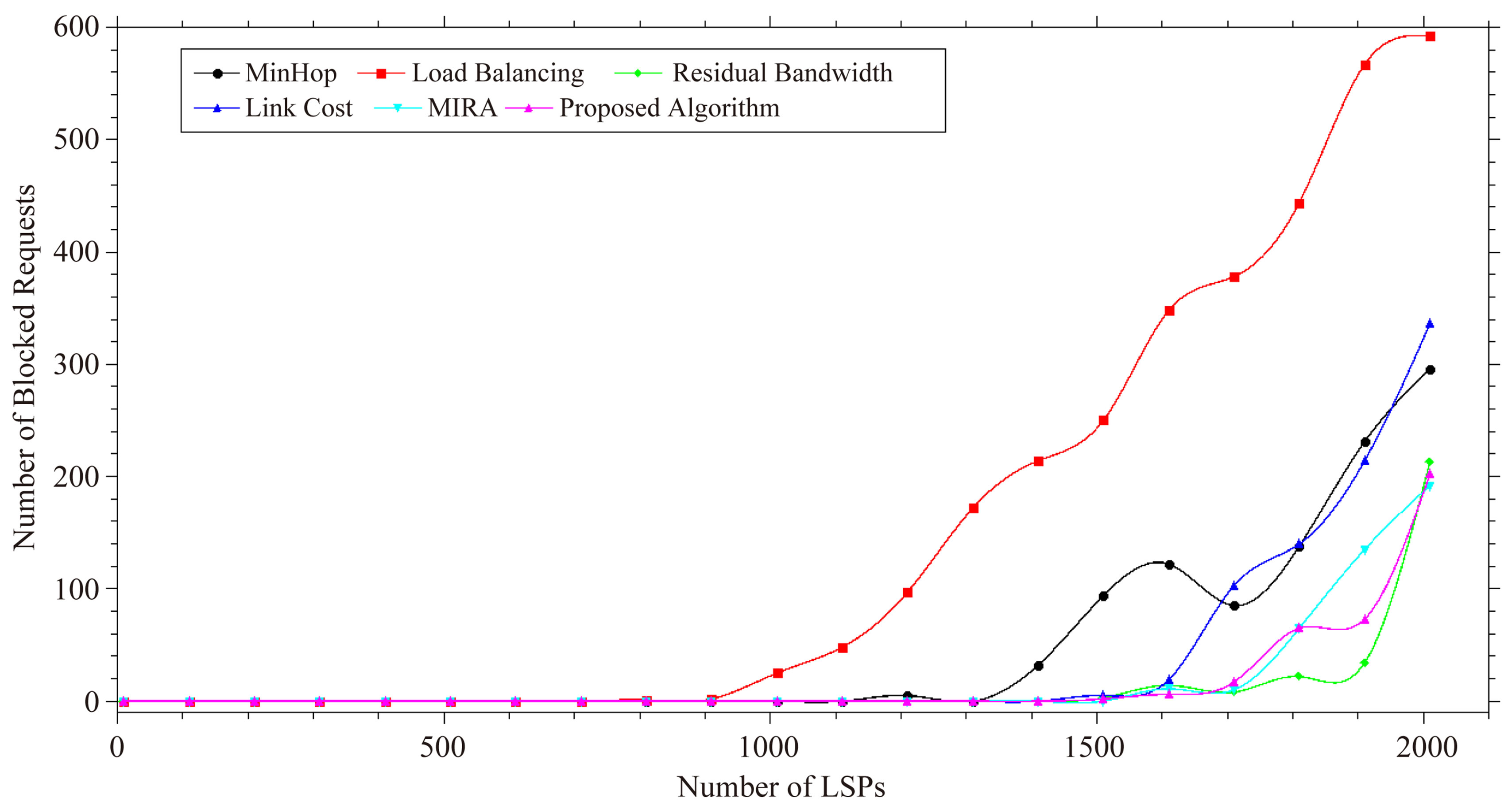
Figure 6. Blocked requests.
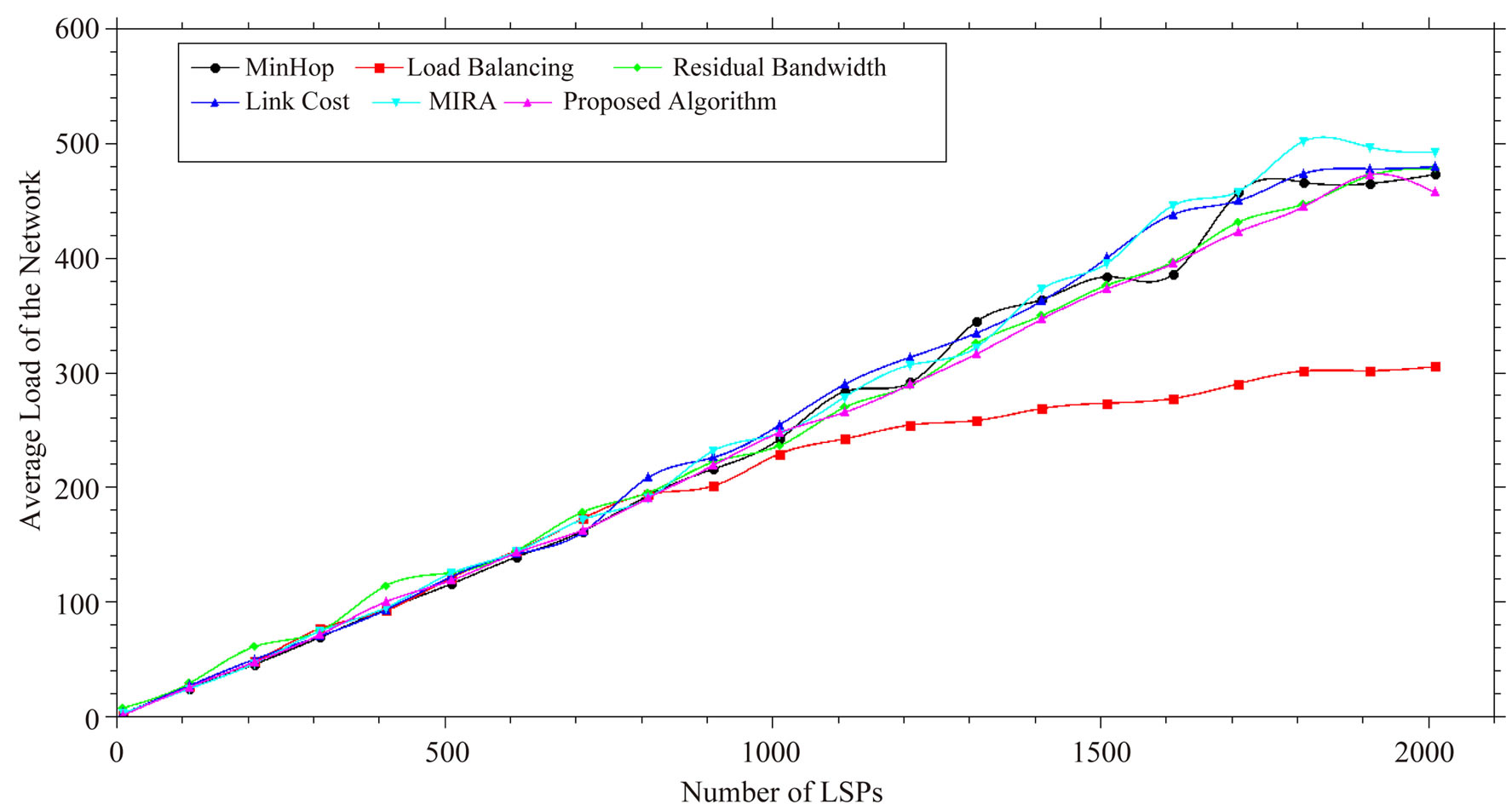
Figure 7. Average load on the network.
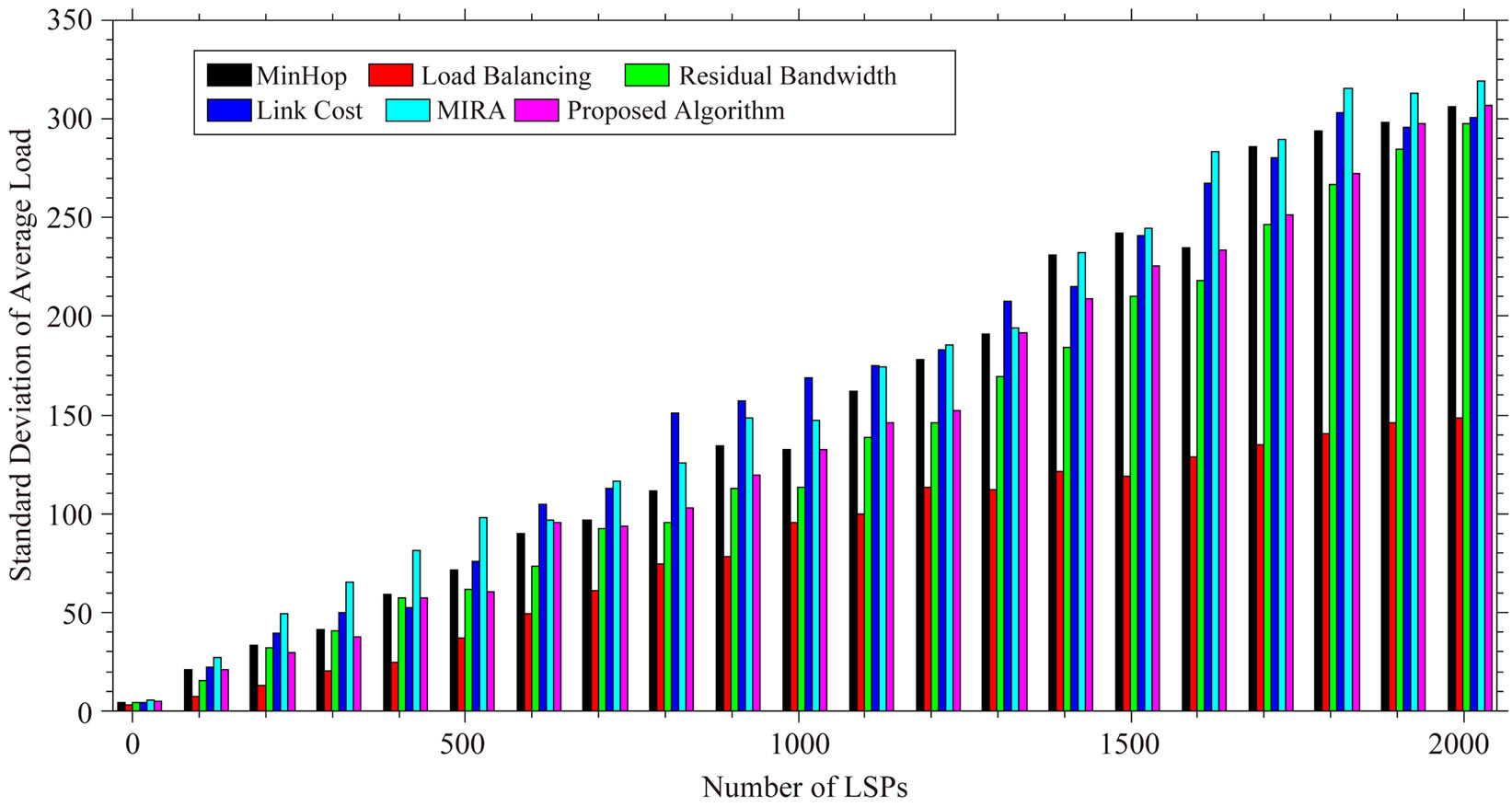
Figure 8. Standard deviation of the average load on the network.
6. Conclusion and Future Direction
This paper presents a model for path allocation for dynamic LSP request in a MPLS network. A novel cost function with three metrics is proposed. Proposed cost function has been simulated and was found to increase the survivability of network considerably when compared with five other algorithms mentioned in the literature. For the future, the present work can be extended and models for efficient backup path can be devised and compared with other traffic protection techniques proposed in this realm.
7. Acknowledgements
This work has been made possible by extensive support from Jaypee University of Engineering and Technology, Guna. Authors also acknowledge the software provided by www.ampl.com and IBM for academic research.
REFERENCES
- E. Rosen, A. Viswanathan and R. Callon, “Multiprotocol Label Switching Architecture,” IETF RFC 3031, January 2001.
- D. Awduche, J. Malcolm, J. Agogbua, M. O’Dell and J. McManuz, “Requirement of Traffic Engineering over MPLS,” IETF RFC 2702, September 1999.
- M. Amin, K. H. Ho, G. Pavlou and M. Howarth, “Improving Survivability through Traffic Engineering in MPLS Networks,” Proceeding of the 10th IEEE Symposium on Computers and Communications (ISCC 2005), Murcia, Cartagena, 27-30 June 2005, pp. 758-763.
- A. Bosco, R. Mameli, E. Manconi and F. Ubaldi, “Edge Distributed Admission Control in MPLS Networks,” IEEE Communications Letters, Vol. 7, No. 2, 2003, pp. 88-90. http://dx.doi.org/10.1109/LCOMM.2002.808379
- S. Lahoud, G. Texier and L. Toutain, “Classification and Evaluation of Constraint-Based Routing Algorithms for MPLS Traffic Engineering,” French Sixth Meetings on Algorithmic Aspects of Telecommunications (AlgoTel 2004), Batz-sur-Mer, France, 2004.
- J. Moy, “OSPF: Anatomy of an Internet Routing Protocol,” Addison-Wesley, New York, 1998.
- K. Kar, M. Kodialam and T. V. Lakshman, “Minimum Interference Routing of Bandwidth Guaranteed Tunnels with MPLS Traffic Engineering Applications,” IEEE Journal on Selected Areas in Communications, Vol. 18, No. 12, 2000, pp. 2566-2579. http://dx.doi.org/10.1109/49.898737
- R. K. Ahuja, T. L. Magnanti and J. B. Orlin, “Network Flows: Theory, Algorithms, and Applications,” PrenticeHall, Englewood Cliffs, 1993.
- M. Naraghi-Pour and V. Desai, “Loop-Free Traffic Engineering with Pathprotection in MPLS VPNs,” Computer Networks, Vol. 52, No. 12, 2008, pp. 2360-2372. http://dx.doi.org/10.1016/j.comnet.2008.04.015
- J.-W. Lin and H.-Y. Liu, “Redirection Based Recovery for MPLS Network Systems,” The Journal of Systems and Software, Vol. 83, No. 4, 2010, pp. 609-620. http://dx.doi.org/10.1016/j.jss.2009.10.043
- R. K. Singh and N. S. Chaudhari, “Integrated Load Balancing Approach for Fault Tolerance in MPLS Networks,” International Conference on Communication Systems and Network Technologies (CSNT), Gwalior, 6-8 April 2013, pp. 295-298,
- M. Chowdhury, M. R. Rahman and R. Baoutaba, “ViNEYard: “Virtual Network Embedding Algorithms with Coordinated Node and Link Mapping,” IEEE/ACM Transactions on Networking, Vol. 20, No. 1, 2012, pp. 206- 219. http://dx.doi.org/10.1109/TNET.2011.2159308
- M. R. Rahman and R. Baoutaba, “SVNE: Survivable virtual Network Enbedding Algorithms for Network Virtulization,” IEEE/ACM Transactionson Network and Service Management, Vol. 10, No. 2, 2013, pp. 105-118.
- E. W. Dijkstra, “A Note on Two Problems in Connection with Graphs,” Numerische Mathematik, Vol. 1, No. 1, 1959, pp. 269-271. http://dx.doi.org/10.1007/BF01386390
- A. Medina, A. Lakhina, I. Matta and J. Byers, “BRITE: An Approach to Universal Topology Generation,” Proceedings of the 9th International Symposium on Modeling, Analysis and Simulation of Computer and Telecommunication Systems (MASCOTS’01), Cincinnati, 15-18 August 2001, p. 346.
- “A Modeling Language for Mathematical Programming,” 2013. www.ampl.com

