Communications and Network
Vol. 5 No. 1 (2013) , Article ID: 28242 , 9 pages DOI:10.4236/cn.2013.51008
Buffer Occupancy of Double-Buffer Traffic Shaper in Real-Time Multimedia Applications across Slow-Speed Links
Comnetlab, Network Utility Maximisation Sub-Group, Computer Science and Engineering, Obafemi Awolowo University, Ile-Ife, Nigeria
Email: aoluwato@oauife.edu.ng
Received October 17, 2012; revised November 19, 2012; accepted December 21, 2012
Keywords: Multimedia Application; Slow-Speed Link; TCP; Buffer Occupancy; QoS
ABSTRACT
In this paper, a double-buffer traffic shaper was investigated to adjust video frame rate inflow into the TCP sender-buffer of a multimedia application source across a slow-speed link. In order to guarantee QoS across a slow-speed link (i.e. < 1 MBPS), the double-buffer traffic shaper was developed. In this paper, the buffer size dynamics of double-buffer was investigated. The arrival and departure of frames were modeled as a stochastic process. The transition matrix for the process was generated and the stationary probability computed. A simulation program was written in Matlab 7.0 to monitor the buffer fullness of the second buffer when a 3600 seconds H.263 encoder trace data was used as test data. In the second buffer, it was discovered that over 90% of the play-time, the buffer occupancy was upper bounded at 300 frames per second and utilization maintained below 30%.
1. Introduction
Over the years, there has been an unimaginable growth in the usage of the Internet across the globe. However, the range of applications being deployed across the Internet today is far broader than it was a few years back [1]. As it can be observed, traditional applications such as bulk file transfer (e.g. E-mail), and static websites are no longer sufficient for today’s Internet requirement, hence the need for the deployment of wider spectrum of applications. Applications that rely on the real-time delivery of data, such as video conferencing tools, Internet telephony, as well as video and audio streaming (referred to as multimedia applications) are fast gaining prominence in the Internet application space [1,2]. Video streaming, a multimedia application enables simultaneous delivery and playback of the video which overcomes the problems associated with file download since users do not have to wait for the entire video to be received before viewing it [3]. There are two types of streaming applications depending on whether the video is pre-encoded and stored for later viewing, or it is captured and encoded for real-time communication [4]. These new applications (real-time multimedia streaming, video-on-demand etc.) have diverse quality of service (QoS) requirements that are significantly different from traditional best effort service. QoS means that delays, transmission rates, error rates and other characteristics can be measured, improved upon, and to some extent, guaranteed in some advance [5]. Users consider delays larger than 300 ms not suitable for interactive conversation [6]. Therefore concerted effort has to be made to keep within this range. Since the Internet is a best-effort network and does not guarantee quality of service [7], several problems have to be solved before low delay streaming, suitable for inter-active communication via the Internet can be widely deployed. These problems include: Bandwidth variation, Packet loss, Bit (Packet) errors, Packet delay variation (PDV). Though non-real time applications can still adapt to these challenges [8], they are however responsible for the poor quality delivery in real-time multimedia transmission which should ensure smooth playout rate and hence highly interactive [9,10]. Employing the Internet as a medium of transmission of real-time interactive video is a challenging task especially in a slow-speed link environment. Slow-Speed link is defined as data transmission speed of at most 4 Megabits per second (Mbps), downstream (from the Internet to the user’s computer) and 1 Mbit/s upstream (from the user’s computer to the Internet) according to the United States (US) Federal Communications Commission [11]. Any speed less than 4 Mbits/s downstream and 1Mbit/s upstream is considered slow and may not be suitable for real-time multimedia traffics transmission. Heterogeneity in Internet access and dynamic variability in network conditions have brought about the need to design network-adaptive video applications [12]. Frame rate adaptor is a traffic shaping scheme that enhances the transmission of multimedia applications across the network. It automatically regulates the video frames rates according to network congestion level [13]. Traffic shaper represents a complete system that provides high interactivity while adapting to a poor network condition [14]. This is achieved by adjusting transmission rate and controlling the quality of the received streams. Token bucket and Leaky bucket are techniques used to implement the double-buffer traffic shaper [15].
2. Relative Works
Real-time multimedia application transmission has been an active area of research. [16] studied an efficient delay distribution scheme that allocates the end-to-end delay bound into the end-station shaper and the network. They reviewed the effect of switch delay and shaping on network performance based on the empirical envelope traffic model, and analyzed the impact of shaping via computer simulations [1] offered a system design and implementation that ameliorates some of the important problems with video streaming over the Internet. He leveraged the characteristics of MPEG-4 to selectively retransmit the most important data in order to limit the propagation of errors. [5] presented an implementation of an end-to-end application for streaming stored MPEG-4 Fine-Grained Scalable (FGS) videos over the best-effort Internet. There scheme adapts the coding rate of the streaming video to the variations of the available bandwidth for the connection, while smoothing changes in image quality between consecutive video scenes. Ioan and Niculescu in [17] proposed two mathematical models of an algorithm named Leaky bucket mechanism used for the parameter usage of connection control in multimedia networks.Bajic et al., in [18] addressed the issue of robust and efficient scalable video communication by integrating an end-to-end buffer management and congestion control at the source with the frame rate playout adjustment mechanism at the receiver. Lam et al., in [19] addressed the challenge of the lack of end-to-end quality of service support in the current Internet which caused significant difficulties to ensuring playback continuity in video streaming applications by investigating a new adaptation algorithm to adjust the bit-rate of video data in response to the network bandwidth available to improve playback continuity. In [20], Dubious and Chiustudied statistical multiplexing of VBR video in ATM networks. ATM promises to provide high speed real-time multipoint to central video transmission for telemedicine applications in rural hospitals and in emergency medical services. The ramifications of this technology are clear: speed, reliability (lower loss rate and jitter), and increased capacity in video transmission for telemedicine. [3] studied the buffering schemes for the VBR video streaming in heterogeneous wireless networks. The proposed adaptive rate control algorithms provide significantly improved streaming quality compared with the non-control policy. [13] asserted that the great endto-end delays are the major factor influencing the visual quality of real-time video across the Internet using TCP as transport layer protocol. Xiong et al. in [21] again pointed the requirement for transmitting real-time video with acceptable playing performance via TCP and presented a stochastic prediction model which can predict the sending delays of video frames.
However, these available frame rate adaptation techniques are not suited for slow speed network environment. It is therefore imperative to develop a new technique that will meet this challenge. Double buffer traffic shaper is thus presented.
3. The Proposed Scheme (DBTS) Description
3.1. Video Transmission over the Internet
As described in our earlier paper, the first step in the transmission of video is compression of the raw video using encoding coder-decoder scheme (CODEC) such as H.263, H.264, etc. at the sender-end [22,23]. The compressed video is passed to the sender-buffer within the application layer, thereafter passed to the TCP senderbuffer wherein they are fragmented into TCP data packets. From within the TCP sender-buffer the fragmented video frames are moved into the network. The video frames are later received into a TCP receiver-buffer wherein they are defragmented and decompressed. The decompressed video frames are then sent into the receiver playout-buffer. Figure 1 depicts the stage by stage transmission of video frames from the sender to the receiver across the internet.
3.2. The Double-Buffer Traffic Shaper (DBTS)
Because of the bursty nature of video frames traffics when released from the sender buffer [24], a network of two buffers in tandem is being introduced to model the Double-Buffer Traffic Shaper (DBTS) being proposed. A network of buffers is a collection of service centers which represent the server of the buffer and the customers which represent video frames being transmitted [25]. As shown in Figure 2, the first queue models the dynamics of first queue as an “M/D/1/K” and the other, models the dynamics of the second queue as a “D/D/1/K” while the service discipline for the two buffers is FIFO (First-In-First Out). The two buffers are in an open queu-

Figure 1. Stages involved in the transmission of video frames from the sender to the receiver across the internet.
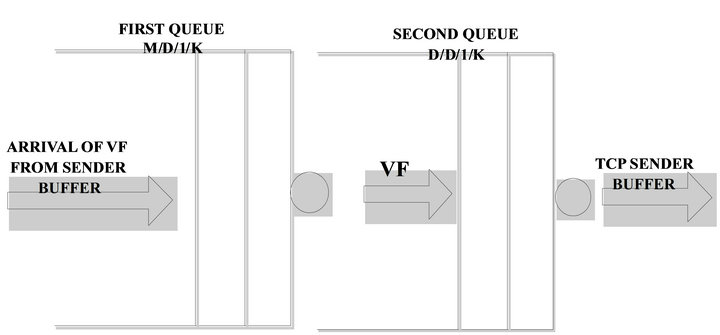
Figure 2. Network of queues modeling of the proposed model.
ing network where jobs enter and depart from the network. “M/D/1/K” is interpreted as the arrival rate being markovian [26] and the departure rate is deterministic at the feeding the second buffer, thereby ensuring that frame out flow from the second buffer is maintained at a constant rate. Video frames thereafter are sent into sender’s TCP-buffer, hence achieving rate-adaptation. The frames flow dynamics can be expressed as a birth and death process. The transition is precipitated on H.263 encoder which sends an average of 10 frames per second [25,26]. The arrival rate into the queue is Poisson, which implies that frames arrive in bursts (irregular spurts). The service rate is deterministic with mean departure rate, 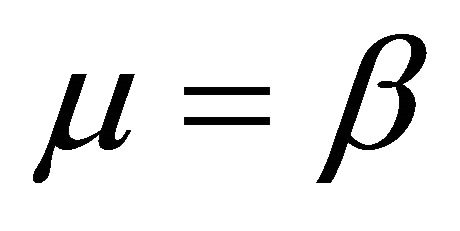 frames per second depending on the size of the queue. The inter-arrival rate in second queue of Figure 2 is inherited from the departure rate of the previous queue. There is a direct relationship between the two because the frame outflow of the M/D/1/K queue forms the inflow into the D/D/1/K queue.
frames per second depending on the size of the queue. The inter-arrival rate in second queue of Figure 2 is inherited from the departure rate of the previous queue. There is a direct relationship between the two because the frame outflow of the M/D/1/K queue forms the inflow into the D/D/1/K queue.
3.3. Stochastic Processes
Formally, a stochastic model is one represented as a stochastic process. A stochastic process is a set of random variables where
where ![]() is the index of set and taken to represent time.
is the index of set and taken to represent time.
The above stochastic process has the following properties:
1)  is a Markov process. This implies that
is a Markov process. This implies that  has the Markov or memoryless property: given the value of
has the Markov or memoryless property: given the value of 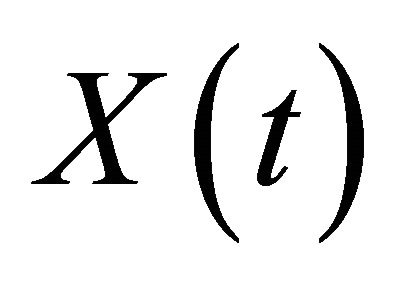 at some time
at some time , the future path
, the future path 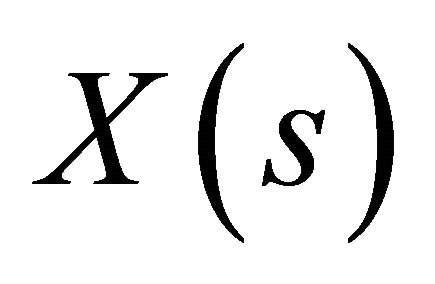 for
for  does not depend on the knowledge of the past history
does not depend on the knowledge of the past history 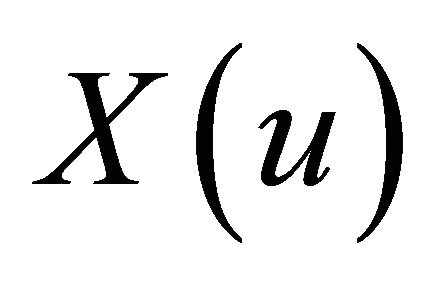 for
for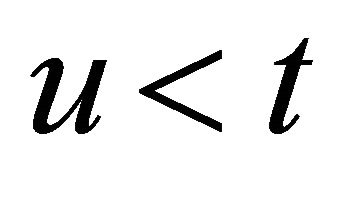 , i.e. for
, i.e. for 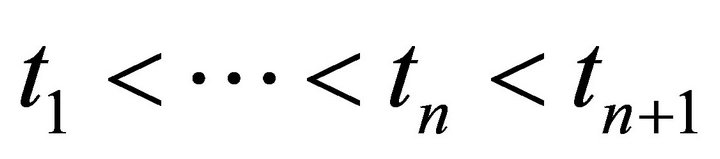 ,
,
 (1)
(1)
2) 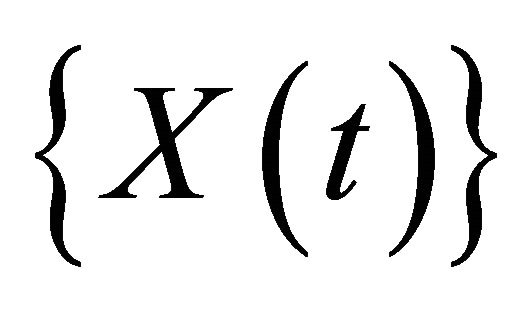 is irreducible. This implies that all states in the state space,
is irreducible. This implies that all states in the state space, ![]() , can be reached from all other states by following the transitions of the process.
, can be reached from all other states by following the transitions of the process.
3) 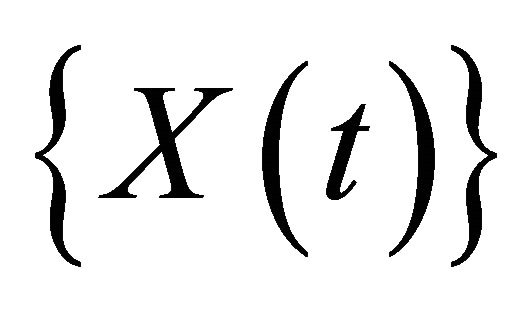 is stationary: for any
is stationary: for any
 .
.
Then the process’s joint distributions are unaffected by the change in the time axis and so,
![]() (2)
(2)
4) 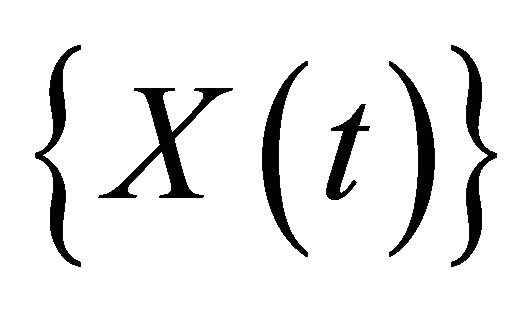 is time homogenous: the behavior of the system does not depend on time when it is observed. In particular, the transition rates between states are independent of the time at which the transition occurs. Thus for all
is time homogenous: the behavior of the system does not depend on time when it is observed. In particular, the transition rates between states are independent of the time at which the transition occurs. Thus for all , it follows that
, it follows that
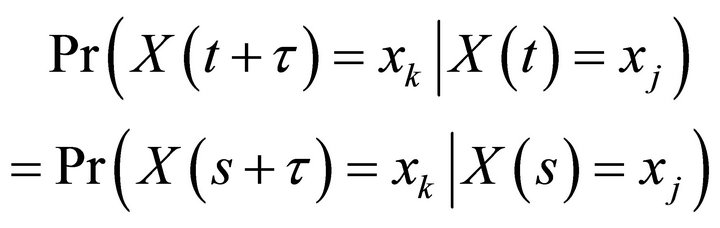 (3)
(3)
3.4. Transition Rate Diagrams of Double-Buffer Traffic Shaper
For Markov processes, the simplest way to represent the process is often in terms of its transition rate diagram. In this diagram, each state of the process is represented as a node in a graph. The arcs in the graph represent possible transitions between states of the processes. Since every transition is assumed to be governed by an exponential distribution, the rate of the transition becomes the parameter of the distribution. In this paper, H.263 encoder transmits frame at an uneven rate. The range however is within 0 frames per second and 12 frames per second as shown in Figure 3. This also depicts the state space which is {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}. Any of the states could be the initial number of frames; and the state can transmit to any other state per unit time. This is because the arrival pattern is Markovian. A current state can be maintained for more than a unit time if that is the rate being sent out by the H.263 encoder. Figure 3

Figure 3. Transition rate diagram for M/D/1/K queue when α =1.
represents when the initial state is 1; it assumes that the first frame released by the encoder is 1.The service rate in Figure 3 is deterministic, so the queue serves a fixed number of frames per unit time. However, the service rate in Figures 3 and 4 which model the first queue if α = 1, 2 in Figure 2 has to be regulated because it determines the fullness of the second queue. Therefore, when the fullness of the second queue reaches a certain threshold, it informs the first queue to either decrease the frame rate to 3 frames per second or increase it to 9 frames per second. This informs the transition pattern that is observed in Figure 5. The initial state is state 6; but it can transit to either state 3 or state 9 per second. The service rate of the first queue translates to the arrival rate of the second queue because they are connected together in series. Since the essence of DBFR is to obtain a constant bit rate, the server in the second queue serves only 6 frames per second which has been experimented to be suitable for a slow-speed of network that is <<< 1 Mbps. The parameters of distribution used in this paper are 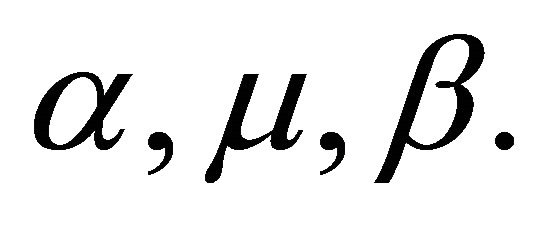 They stand for the arrival rate of the first queue, service rate of the first queue and service rate of the second queue respectively.
They stand for the arrival rate of the first queue, service rate of the first queue and service rate of the second queue respectively.
3.5. Algorithm
Case 1: When current first queue size, 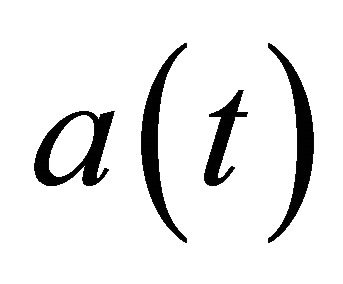 , approaches and above 75% capacity utilization, then current first queue outflow rate
, approaches and above 75% capacity utilization, then current first queue outflow rate , where
, where ![]() belongs to the set of positive real numbers.
belongs to the set of positive real numbers.
If 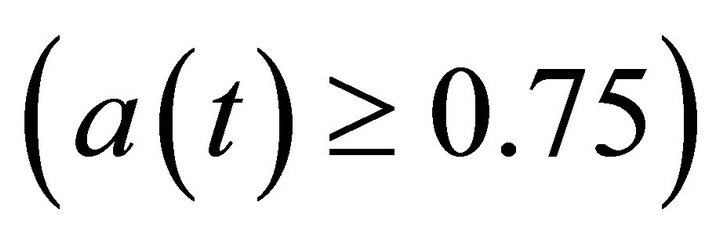 then
then
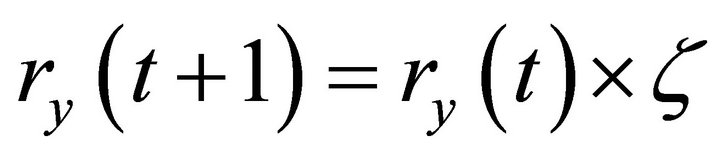
Case 2: When current first queue size, a(t), operates below 25% capacity utilization, then current first queue outflow rate is halved i.e. , such that
, such that 
Case 3: Otherwise, the flow rate is set at the default.
Assumptions:
Video frames inflow into First queue is Markovian utilizing the H.263 Standard. Second queue size is assumed larger than the First queue i.e. .
.
List of terms:
 —number of frames in first queue at time
—number of frames in first queue at time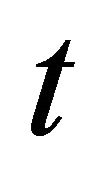 ,
,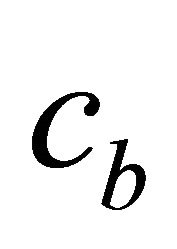 —number of frames in second queue at time
—number of frames in second queue at time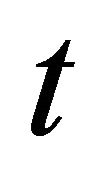 ,
,![]() : rate of Inflow to first queue,
: rate of Inflow to first queue,![]() : rate of Inflow to second queue,
: rate of Inflow to second queue,![]() : rate of Inflow to the TCP sender buffer,
: rate of Inflow to the TCP sender buffer,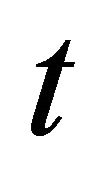 : time(s) a: size of first queue (number of video frames),
: time(s) a: size of first queue (number of video frames), : size of Second queue (number of video frames).
: size of Second queue (number of video frames).
Input: uneven arrival of video frames; Output: even departure of video framesInitialization: ca, cb, ry, rx, out: array [1,…,n].
rx ← H.263 trace data.
begin:
ca(i+1) = ca(i) + rx(i);
if (ca(i) > 0.75 × a).
ry(i + 1)= ry(i) × ζ;
else if (ca(i)< 0.25× a).

Figure 4. Transition rate diagram for M/D/1/K queue when α = 2.

Figure 5. Transition rate diagram for D/D/1/K queue.
ry(i + 1)= ry(i) × γ;
else ry(i + 1) = 10;
end if (ca(i + 1) > 0).
ca(i + 1) = ca(i + 1) − ry(i + 1);
end cb(i +1) = cb(i) + ry(i + 1);
if (cb(i + 1) > rz)
out(i) = rz;
cb(i + 1) = cb(i + 1) − rz;
end.
end.
4. Derivation of Performance Measure— Utilization
A Markov process with ![]() states can be characterized by its
states can be characterized by its . Matrix Q’s entry in the
. Matrix Q’s entry in the 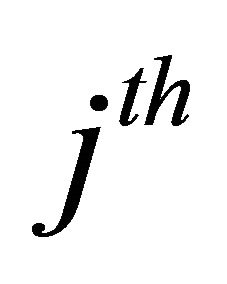 column of the
column of the  row of the matrix
row of the matrix  is
is 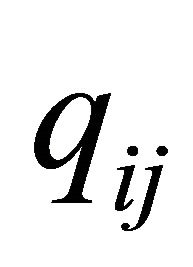 being the instantaneous transition rate.
being the instantaneous transition rate. 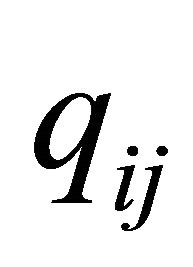 is the sum of the parameters labeling arcs connecting states
is the sum of the parameters labeling arcs connecting states  and
and  in the transition rate diagram. The diagonal elements are chosen to ensure that the sum of the elements in every row is zero, i.e.
in the transition rate diagram. The diagonal elements are chosen to ensure that the sum of the elements in every row is zero, i.e.
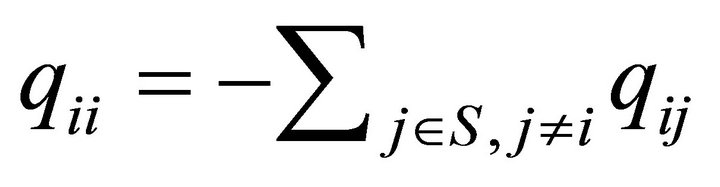 (4)
(4)
The infinitesimal generator matrix for the transition rate diagram of the M/D/1/K queue of Figure 3 is shown in Equation (5). It is a  matrix, meaning that it has 13 states. The values for the parameters
matrix, meaning that it has 13 states. The values for the parameters

expressed in Equation (3.4) were obtained from the transitions from one state to another. Therefore,

In solving the matrix Equation , in equation 5, the parameter values were inserted. The whole equation is thereafter transposed. i.e.
, in equation 5, the parameter values were inserted. The whole equation is thereafter transposed. i.e.  becomes
becomes . This enabled the right hand side to be converted to column vector of zeros rather than the initial row vector.
. This enabled the right hand side to be converted to column vector of zeros rather than the initial row vector.
In other to resolve the problem of redundancy amongst the global balance equation, one of the global balance equations was replaced by the normalization condition. In the transposed matrix, this corresponds to replacing one row (last row) by a row of 1’s and also change the solution vector, which was all zeros to be a column vector with 1 in the last row, and zero everywhere else. This vector is denoted by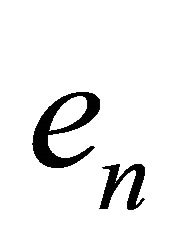 , and the modified matrix is denoted by
, and the modified matrix is denoted by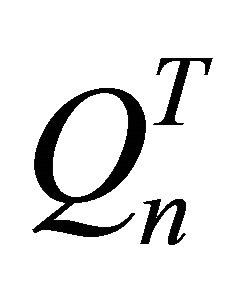 . It then becomes
. It then becomes
 (6)
(6)
When Equation (7) was solved, the stationary probabilities were obtained as presented in (8). The state based performance measures are those which clearly correspond to the probability that the model is in a state, or a subset of states which satisfy some condition. Therefore, utilization in the proposed model corresponds to those states in which service took place (states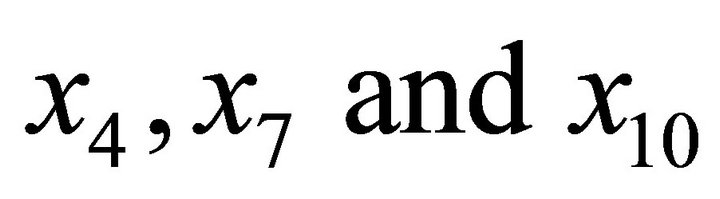 ) on M/D/1/K Queue. i.e
) on M/D/1/K Queue. i.e
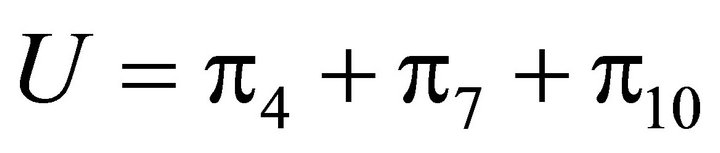

The analytical utilization of M/D/1/K queue is about 23.08%.
5. Results and Discussion
Matlab 7.0 was used in simulating the proposed algorithm. H.263 trace data obtained from Verbose Jurassic standard data set was used as the test data. The data file is a one-hour video session, and it is composed of 25,432 frames. Frame rate arrival into the first buffer was set  according to the principle of H.263 encoder. Arrival rate into the second buffer is obtained from the operation of the algorithm introduced at the server of the first queue.
according to the principle of H.263 encoder. Arrival rate into the second buffer is obtained from the operation of the algorithm introduced at the server of the first queue.
The volume of frames in the buffer is obtained from the accumulation of frames as a result of delay experienced by the frames. As shown in Figure 6, the initial 400 seconds of the video session shows a steady increase in the number of video frames to around 230 frames. The quantity however steadily reduced to zero within the proceeding 500 seconds. The volume rose to 250 frames at 1600 seconds and lingered at that point for 200 seconds. It thereafter dropped to less than 40 video frames for about 25% of the simulation period. It however peaked to 370 video frames towards the last 200 seconds of the simulation of the video session.
Again when the proposed scheme was compared with the existing scheme in terms of buffer occupancy, it was observed that the existing scheme outperformed the proposed scheme in most part of the simulation duration as can be seen in Figure 7. This performance is evident in the overall quantity of frames in the buffer per unit time. Throughout the duration of the simulation, the quantity of frames in the existing scheme was constantly below 100 frames; it was highly bounded, while that of the proposed DBFR scheme hovered between 0 and 300 frames for more than 95% of the simulation duration.
For closer observation of the interesting points and disparities of the buffer fullness of the existing and proposed schemes, the simulation period was divided into six epochs.

Figure 6. Showing fullness of second buffer of DBTS.

Figure 7. Comparison of DBFR and VFSM schemes.
Figure 8 compares the two schemes for the first 200 seconds, it was noticed that for during the first 160 seconds, the proposed scheme performed excellently by maintaining a buffer fullness lower than the existing scheme. Figure 9 represents the buffer fullness between 200 - 700 seconds. This shows that the buffer fullness in the proposed scheme increased steadily to about 300 frames while the existing scheme did not exceed 100 frames. The two schemes later reduced the buffer fullness during which the existing scheme crashed to as low as 3 to 10 frames for almost 50% of the time duration, the proposed scheme reduced buffer fullness to as low as 50 frames. In the third epoch shown in Figure 10, the two schemes’ performance was very close. They both maintained a fullness of about 50 frames throughout the duration (701 and 1100) seconds. Between 1101 and 2000 seconds, there was a remarkable difference in the performance of the two schemes as seen in Figure 11.
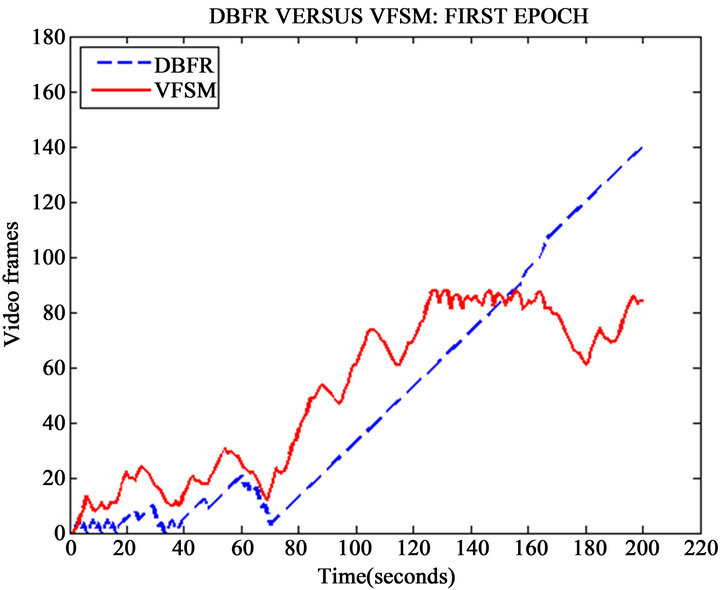
Figure 8. The first epoch of the comparison of DBFR and VFSM schemes.

Figure 9. The second epoch of the comparison of DBFR and VFSM schemes.
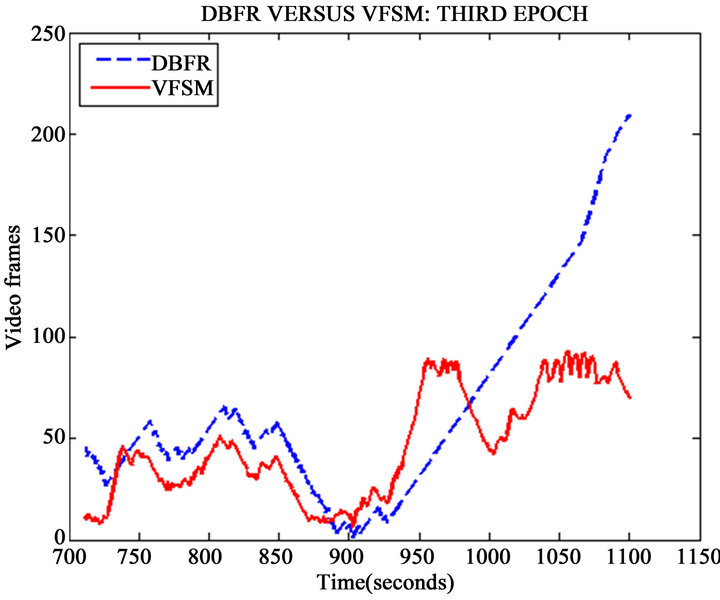
Figure 10. The third epoch of the comparison of DBFR and VFSM schemes.
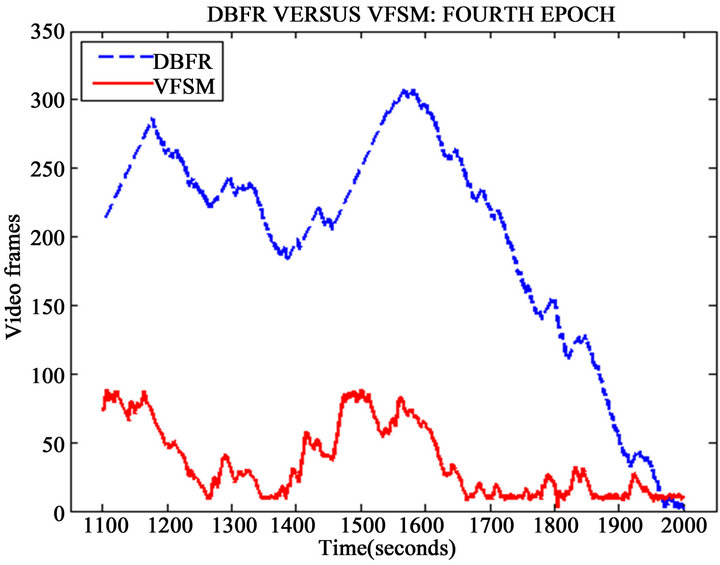
Figure 11. The fourth epoch of the comparison of DBFR and VFSM schemes

Figure 12. The fifth epoch of the comparison of DBFR and VFSM schemes
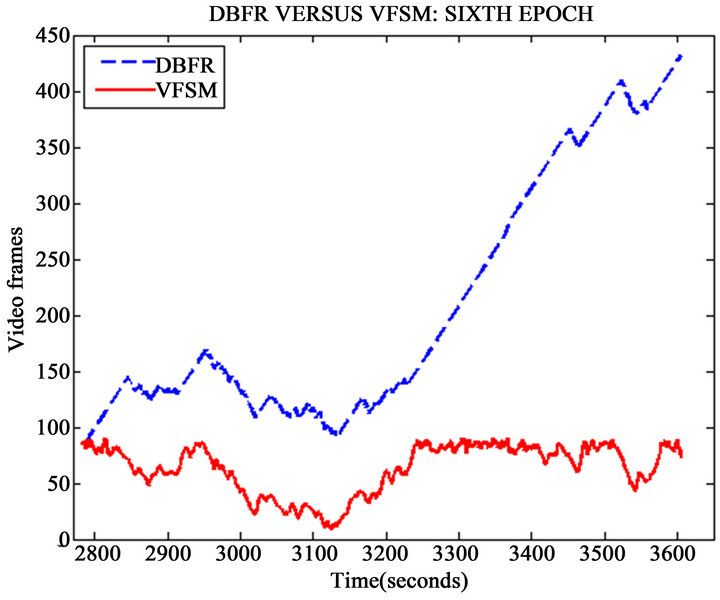
Figure 13. The sixth epoch of the comparison of DBFR and VFSM schemes.
The proposed scheme hovered between 100 frames and 300 frames for about 80% of the time in this epoch. The fifth epoch saw the two schemes returning to a close performance. Interestingly, the two schemes had less than 100 frames throughout the duration simulation which was between 2001 and 2780. In fact, for the first 20% of this fifth epoch, there were less than 30 frames in the two schemes as noticed in Figure 12. The last epoch, shown in Figure 13 lasted between 2781 and 3605. For the first 50%, the fullness in the proposed scheme was less than 160 frames. It however increased steadily to about 450 frames towards the end of the simulation, this experience lasted for less than 5% of the whole simulation duration.
Unfortunately, according to Little’s law, volume of frames in queue is equal to the product of arrival rate and means waiting time. This implies that the quantity of frames in the queue is directly proportional to the delay experienced by the frames in the queue. The delay that is experienced in the proposed scheme is expected to be greater than what is expected to be experienced in the existing scheme. Though the proposed scheme was able to achieve the purpose of its development, it is however being challenged with buffer fullness and packet delay being unbounded. The implication of this is that the infrastructure provider would require more capital in providing memory space. The user however only gets a better and improved video streaming quality.
6. Conclusion
In conclusion, it is evident that the proposed scheme was bounded to maximum of 300 frames per unit time for over 90% of the simulation time. This value is high when compared with the existing scheme (VFSM) which was bounded at less than 100 frames per unit time throughout the simulation time. However, the tripling value is justifiable because, it is opportunity cost for maintaining QoS along a slow-speed link for real-time multimedia application deployment across the Internet.
REFERENCES
- N. Feamster, “Adaptive Delivery of Real-Time Streaming Video,” Master’s Thesis, Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, 2001.
- L. Tilley, “Computing Studies Multimedia Applications,” Number 1, Germany, 2005.
- G. Ji, “VBR Video Streaming over Wireless Networks,” Master’s Thesis, Department of Electrical and Computer Engineering, University of Toronto, Toronto, 2009, pp. 10-22.
- C. Huang, J. Li and K. W. Ross, “Can Internet Videoon-Demand Be Profitable?” ACM SIGCOMM Computer Communication Review, Vol. 37, No. 4, 2007, pp. 133- 144.
- M. Karakas, “Determination of Network Delay Distribution of Network over the Internet,” Master’s Thesis, Middle East Technical University, The Graduate School of Natural and Applied Sciences, Ankara, 2003.
- M. Salomoni and M. Bonfigle, “A Software Audio Terminal for Interactive Communications in Web-Based Educational Environments over the Internet,” In Booktitle, 1999. http://www.cineca.it/nume03/Papers/IECON99/iecon2.htm
- S.-J. Yang and H.-C. Chou, “Adaptive QoS Parameters Approach to Modeling Internet Performance,” International Journal of Network Management, Vol. 13, No. 1, 2003, pp. 69-82. doi:10.1002/nem.460
- C. Dinesh, H. Zhang and D. Ferrari, “Delay Jitter Control for Real-Time Communication in a Packet Switching Network,” IEEE Conference on Communications Software, “Communications for Distributed Applications and Systems”, 18-19 April 1991, Chapel Hill, pp. 35-43. http://trace.kom.aau.dk/trace/tut/html
- D. Austerberry, “The Technology of Video and Audio Streaming,” 2nd Edition, Focal Press, Burlington, 2005.
- J. Apostolopoulos, W. Tan and S. Wee, “Video Streaming: Concepts, Algorithms and Systems,” Technical Report, Mobile and Media Systems Laboratory, HP Laboratories, Palo Alto, 2002.
- FCC, “Sixth Broadband Deployment Report,” Technical Report, Federal Communications Commission, 2010. http://www.fcc.gov/Daily-Releases/Daily-Busi-ness/2010/db0720/FCC-10129A1.pdf
- P. de Cuetos, P. Guillote, K. Ross and D. Thoreau, “Implementation of Adaptive Streaming of Stored MPEG4 FGS Video over TCP,” IEEE International Conference on Multimedia and Expo, Vol. 1, 2002, pp. 405-408. doi:10.1109/ICME.2002.1035804
- Y. Xiong, M. Wu and W. Jia, “Efficient Frame Schedule Scheme for Real-Time Video Transmission across the Internet Using TCP,” Journal of Networks, Vol. 4, No. 3, 2009, pp. 216-223. doi:10.4304/jnw.4.3.216-223
- K. Ibrahim, “TCP Traffic Shaping in ATM Networks,” Department of Electronics, Faculty of Engineering and Architecture, Uludağ University, Bursa, 2000.
- B. A. Farouzan, “Data Communications and Networking,” 4th Edition, McGraw-Hill, New York, 2007.
- Lee, B., Lim, H., Kang, H., and Kim, C. “A Study on Efficient Delay Distribution Methods for Real-Time VBR Traffic Transfer,” Technical Report, Department of Computer Science, Seoul National University, Korea Institute of Advanced Engineering, Seoul, 1997.
- L. Ioan and G. Niculescu, “Two Mathematical Models fo Performance Evaluation of Leaky-Bucket Algorithm,” Revue Roumaine des Sciences Techniques Serie Electrotechnique et Energetique, Vol. 50, No. 3, 2005, pp. 357- 372.
- O. Tickoo, A. Balan, S. Kalyanaraman and J. W. Woods, “Integrated End-to-End Buffer Management and Congestion Control for Scalable Video Communications,” International Conference on Image Processing, Barcelona, 14-17 September 2003, pp. 257-260.
- L. Lam, Y. Jack, B. Lee, S. Liew and W. Wang, “A Transparent Rate Adaptation Algorithm for Streaming Video over the Internet,” Department of Information Engineering, The Chinese University of Hong Kong, Shatin, 2005.
- J. Dubious and H. Chiu, “High Speed Video Transmission for Telemedicine Using ATM Technology,” Proceedings of World Academy of Science, Engineering and Technology, Vol. 7, 2005, pp. 357-361.
- Y. Xiong, M. Wu and W. Jia, “Delay Prediction for Real-Time Video Adaptive Transmission over TCP,” Journal of multimedia, Vol. 5, No. 3, 2010, pp. 216-222. doi:10.4304/jmm.5.3.216-223
- J. Doggen and F. Van der Schueren, “Design and Simulation of a H.264 AVC Video Streaming Model,” Department of Applied Engineering, University College of Antwerp, Antwerp, 2008.
- L. Arne and K. Jirka, “Evalvid-RA: Trace Driven Simulation of Rate Adaptive MPEG-4 VBR Video,” Department of Communication Systems, Technical University of Berlin, Berlin, 2007.
- Y. Won and B. Shim, “Empirical Study of VBR traffic Smoothing in Wireless Environment,” Division of Electrical and Computer Engineering Hanyang University, Seoul, 2002.
- X. Li, “Simulation: Queuing Models,” Technical Report, University of Tennessee, Knoxville, 2009.
- S. Balsamo, “A Tool for the Numerical Solution of Cooperating Markov Chains in Product-Form,” 2010, pp. 311-324.

