Communications and Network
Vol. 4 No. 4 (2012) , Article ID: 25125 , 10 pages DOI:10.4236/cn.2012.44038
Network Connectivity Probability of Linear Vehicular Ad-Hoc Networks on Two-Way Street
Department of Electronics and Communication Engineering, National Institute of Technology, Calicut, India
Email: neelakantan_pc@nitc.ac.in, babu@nitc.ac.in
Received August 8, 2012; revised September 7, 2012; accepted October 12, 2012
Keywords: Two-Way Connectivity; Nakagami Fading; Vehicular Ad-Hoc Network
ABSTRACT
In this paper, we present an analytical model to determine the network connectivity probability of a linear vehicular adhoc network (VANET) formed by communication equipped vehicles on a two-way street scenario. We consider the highway to be consisting of two lanes with vehicles moving in both directions on these lanes and focus on the probability of being able to convey messages from a source vehicle to a destination vehicle, which may be multiple hops away. Closed form analytical expression is obtained for the network connectivity probability in the presence of Nakagami fading channel. In our model, the transmission range of each vehicle is modeled as a random variable due to channel fading. The analytical results are validated by extensive simulations.
1. Introduction
Vehicular Ad-Hoc Networks (VANETs), which allow vehicles equipped with wireless communications devices to form a self-organized network without the requirement of permanent infrastructures, are highly mobile wireless ad-hoc networks envisioned to provide support for passenger safety, traffic management and entertainment applications by enabling both vehicle-to-vehicle (V2V) as well as vehicle-to-infrastructure (V2I) communications [1]. The Dedicated Short Range Communications (DSRC) has been proposed as the emerging technology that supports vehicular communications. The Federal Communication Commission (FCC) in USA has approved 75 MHz of spectrum between 5850 and 5925 MHz for DSRC to enhance safety and productivity of the transportation systems. The Task Group known as IEEE 802.11 p has recently proposed an amendment to the 802.11 standard to support communications in vehicular environments [1]. The IEEE working group 1609 has been formed to specify additional layers of the protocol stack. The combination of IEEE 802.11 p and the IEEE 1609 protocol suite is designated as WAVE (Wireless Access in Vehicular Environments). The overall WAVE architecture includes IEEE standards 1609.1 to 1609.4 (for resource management, security architecture, networking services, and multichannel operation, respectively), and IEEE 802.11 p (for MAC and PHY) [1-3].
Network connectivity is a fundamental requirement in VANETs, i.e., all vehicles on a highway segment should be able to communicate with each other directly, or via multiple hops between intermediate vehicles. To ensure that a time critical message from a source vehicle is conveyed to another (destination) vehicle which may be multiple hops away, the highway segment should have a certain number of vehicles equipped with wireless communication devices. It is the task of a network designer to determine the minimum number of vehicles (or minimum vehicle density) necessary to form a fully connected network. Moreover, characterizing the connectivity of VANETs when the vehicle density is low and the speed of the vehicles and the flow are independent, i.e. in free-flow phase, is a crucial research challenge for realizing commercial VANET applications.
In the literature, several attempts have been made to analyze the connectivity properties of VANETs (e.g. [4-15]). The connectivity analysis of VANETs in [4] advocates a dynamic transmission range for each vehicle to adapt to the frequent topology changes. In [5], network connectivity of one-dimensional VANET has been analyzed using a queuing theoretic approach. In [6], authors present a technique to improve the connectivity in VANET by adding extra nodes known as mobile base stations. The connectivity properties of a mobile linear network with high speed mobile nodes and strict delay constraints are investigated in [7]. In [8], VANET connectivity has been analyzed based on a comprehensive mobility model. A new analytical model for VANET connectivity based on product-form queuing networks has been proposed in [9]. Authors of [10] presented connectivity analysis of both one way and two way highway scenarios assuming that all vehicles maintain a constant speed. In [11], authors analyzed the connectivity of message propagation in a two-dimensional VANET, for highway and city scenarios. In [12], authors address the effects of intersections and two-dimensional road topology on the connectivity of VANETs in urban areas. An analytical model to investigate the impact of vehicle speed on VANET connectivity has been presented in [13] assuming vehicles’ transmission range to be deterministic. In [14], authors present an analytical model to compute the network connectivity probability of VANET on one-way street in the presence of channel fading. In [15], authors analyze connectivity properties of one-dimensional VANET from a queuing theoretic perspective to find the average connectivity distance and average cluster size, in the presence of fading.
In this paper, differently from the above, our aim is to develop an analytical model to find the network connectivity probability of a VANET on a two-way street scenario shown in Figure 1. In this case, we consider the highway to be consisting of two lanes (say, lower lane and upper lane), with vehicles moving in both directions on these lanes. If the connectivity probability on a specific lane (say, lower lane), is less than 1, then the network formed by vehicles on this lane may consists of more than one cluster, (where a cluster is defined as a unit of connected vehicles), between which no communication is possible. If the connectivity probability is low, then the chance of having multiple clusters is high and vice versa. To ensure that a time critical message from a source vehicle is conveyed to another vehicle which may be multiple hops away, all the vehicles on the lane segment should be able to communicate with each other directly, or via multiple hops between intermediate vehicles, to meet this requirement, the network must consist of only one connected cluster.
To improve the probability of connectivity on a typical lane (say, lower lane), and to ensure that the network on this lane consists of only one cluster, it may be possible to take advantage of vehicles moving in the opposite direction on the second lane (say, upper lane). This means

Figure 1. Vehicles on a typical two-lane highway.
that, if there is a link failure on the lower lane, the link connectivity can be restored with the help of opposing vehicles on the other (upper) lane. Let us consider a specific scenario shown in Figure 1, where there is a twoway street (say, lower lane and upper lane), and where a packet is being relayed from the left end of a road segment (vehicle A) to the right end of the segment on the lower lane (vehicle B). Assume that along the multi-hop route from A to B, the packet from a vehicle 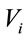 cannot be forwarded to another vehicle
cannot be forwarded to another vehicle  on the same lane because the inter-vehicle distance
on the same lane because the inter-vehicle distance , is greater than the vehicle’s transmission range. Thus the connectivity on the lower lane will be lost at this point. However, it is possible to take advantage of the vehicles on the second lane. Note that, in this case, if there is a vehicle S on the upper lane, that is within the transmission range of the vehicle
, is greater than the vehicle’s transmission range. Thus the connectivity on the lower lane will be lost at this point. However, it is possible to take advantage of the vehicles on the second lane. Note that, in this case, if there is a vehicle S on the upper lane, that is within the transmission range of the vehicle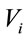 , vehicle
, vehicle  can first forward the packet to S, and when S gets closer to
can first forward the packet to S, and when S gets closer to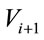 , it can then forward the packet further to
, it can then forward the packet further to . With this forwarding strategy, the network connectivity on the lower lane can be restored. This forwarding strategy is usually referred to as storecarry-forward routing, and is suitable only for delay tolerant applications.
. With this forwarding strategy, the network connectivity on the lower lane can be restored. This forwarding strategy is usually referred to as storecarry-forward routing, and is suitable only for delay tolerant applications.
In this paper, we present an analytical model to find the network connectivity probability of a VANET for the two-way street scenario with store-carry-forward approach. In our model, the effect of fading is also considered and the transmission range of each vehicle is modeled as a random variable. The random transmission range model is relevant for the connectivity analysis because it can account for variability in the communication links caused by fading, and thus will be able to accurately estimate the connectivity. The highway and the vehicle mobility model that we employ for the analysis is based on the work presented in [5,6,13]. We consider one-dimensional linear VANET formed by vehicles on a two-way highway operating in the free flow state, in which the vehicle density on the highway is very low and the vehicle speed and traffic flow are independent; thus drivers can drive as fast as they want (subject to a limit on maximum speed known as freeway velocity) and overtaking is allowed [5,6]. The free flow traffic state has been assumed for the analysis since the connectivity of the network is very low in this state. Further the vehicle speed is assumed to be a Gaussian random variable. This particular model for highway and vehicle mobility represents a realistic VANET scenario for uninterrupted highways and similar model has been used in many papers [5-7,13-15]. The proposed analysis does not consider the effects of the underlying MAC protocol. It is assumed that an ideal MAC protocol is employed that can resolve contention effectively. Further, since our focus is on VANETs used for dissemination of broadcast information related to traffic safety, we do not consider the effects of specific unicast routing scheme [5-15]. We employ Nakagami fading for our connectivity analysis since recent studies have shown that Nakagami fading can be used to describe statistical characteristics of small scale fading in a V2V channel [16-18]. A distance dependent power law model is used for the path loss since recent empirical and analytical modeling studies have shown that, for highway, urban, and suburban scenarios, a classical power law model is suitable to describe the V2V path loss [19,20]. The validity of our theoretical analysis is verified by extensive simulation studies. To the best of these authors’ knowledge, analytical models to determine the impact of physical layer dependent parameters on VANET connectivity on a two-way street have not appeared in the literature so far. Rest of this paper is organized as follows: Section 2 describes the system model. In Section 3, analytical models are presented for the connectivity. In Section 4, we present the analytical and simulation results. The paper is concluded in Section 5.
2. System Model
The system model used for the connectivity analysis, which includes models for highway and vehicle mobility, is similar to that of [5] and is briefly described as follows: Assume that an observer stands at an arbitrary point of an uninterrupted highway (i.e., without traffic lights, etc.). Empirical studies have shown that Poisson distribution provides an excellent model for vehicle arrival process in free flow state [21]. Accordingly, assume that the number of vehicles passing the observer per unit time is a Poisson process with rate 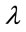 veh/hr. Thus the inter-arrival times are exponentially distributed with parameter
veh/hr. Thus the inter-arrival times are exponentially distributed with parameter . Further, assume that there are M discrete levels of constant speed
. Further, assume that there are M discrete levels of constant speed 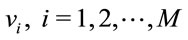 where the speeds are i.i.d., and independent of the inter-arrival times. Let the arrival process of vehicles with speed
where the speeds are i.i.d., and independent of the inter-arrival times. Let the arrival process of vehicles with speed  be Poisson with rate
be Poisson with rate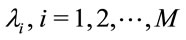 , and let
, and let
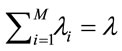 .
.
These arrival processes are independent and the probability of occurrence of each speed is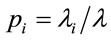 . Let
. Let  be the random variable representing the distance between
be the random variable representing the distance between 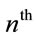 closest vehicle
closest vehicle  to the observer and
to the observer and 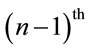 closest vehicle,
closest vehicle,  to the observer. It has been proved in [5] that the inter-vehicle distances (IVD’s) are i.i.d., and exponentially distributed with parameter
to the observer. It has been proved in [5] that the inter-vehicle distances (IVD’s) are i.i.d., and exponentially distributed with parameter
 .
.
Empirical studies have shown that the vehicle speed V in free flow state follows a Gaussian probability distribution [21]. To avoid dealing with negative speeds or speeds close to zero, two limits are defined for the speed, i.e., 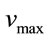 and
and 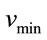 for the maximum and minimum levels of vehicle speed, respectively. For this, a truncated Gaussian PDF is used given by [5].
for the maximum and minimum levels of vehicle speed, respectively. For this, a truncated Gaussian PDF is used given by [5].
 (1)
(1)
where
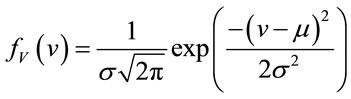
is the Gaussian PDF, μ = average speed, σ-standard deviation of the vehicle speed, 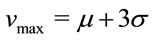 is the maximum speed,
is the maximum speed,  is the minimum speed. Substituting for
is the minimum speed. Substituting for  in (1), the truncated Gaussian PDF
in (1), the truncated Gaussian PDF  is given by [5]:
is given by [5]:
 (2)
(2)
where 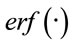 is the error function. With this model, the cumulative distribution function (CDF) of inter-vehicle distance
is the error function. With this model, the cumulative distribution function (CDF) of inter-vehicle distance  is given by
is given by , where
, where
 .
.
Here 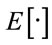 is the expectation operator and
is the expectation operator and 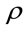 represents the average vehicle density (veh/km). When the vehicle speed follows truncated Gaussian PDF, the average vehicle density
represents the average vehicle density (veh/km). When the vehicle speed follows truncated Gaussian PDF, the average vehicle density  is computed as follows [5]:
is computed as follows [5]:
 (3)
(3)
It may be noted that the average vehicle density given in (3) does not have a closed form solution, but has to be evaluated by numerical integration. Since each vehicle enters the highway with random speed, the number of vehicles on the highway segment of length L is a random variable. The average number of vehicles on the highway segment, in the steady state is then given by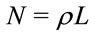 .
.
3. Analysis of Network Connectivity
Consider the two-way street (consisting of lower and upper lanes) shown in Figure 1. Assume that vehicles are moving from right to left on the lower lane (referred to as main lane); and from left to right on the upper lane. Let 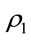 and
and  respectively represent the average vehicle densities on the lower and the upper lanes; and let N1 and N2 respectively represent the average number of vehicles on these lanes. Further, assume V1 and V2 to be the random variables representing vehicle speed and
respectively represent the average vehicle densities on the lower and the upper lanes; and let N1 and N2 respectively represent the average number of vehicles on these lanes. Further, assume V1 and V2 to be the random variables representing vehicle speed and  and
and  respectively represent the vehicle arrival rates on these lanes. Assume that
respectively represent the vehicle arrival rates on these lanes. Assume that  and
and  respectively be the mean and the standard deviation of vehicle speed on these lanes. Then, we have
respectively be the mean and the standard deviation of vehicle speed on these lanes. Then, we have 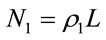 and
and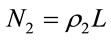 , where L is the highway length;
, where L is the highway length;  and
and 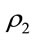 are computed according to (3). It is assumed that packets are relayed from the left to the right of the road segment on the lower lane, which means that packets are relayed in the opposite direction of vehicle movement. This is a reasonable assumption because traffic information such as safety warning, is usually relayed from the source vehicle to the vehicles following it. We now proceed to derive an analytical expression for the network connectivity on one-way street (lower lane), and use this expression to find network connectivity on two-way street.
are computed according to (3). It is assumed that packets are relayed from the left to the right of the road segment on the lower lane, which means that packets are relayed in the opposite direction of vehicle movement. This is a reasonable assumption because traffic information such as safety warning, is usually relayed from the source vehicle to the vehicles following it. We now proceed to derive an analytical expression for the network connectivity on one-way street (lower lane), and use this expression to find network connectivity on two-way street.
3.1. Network Connectivity on One-Way Street
Consider the network formed by vehicles on the main (lower) lane, where the average number of vehicles is equal to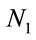 , that corresponds to
, that corresponds to  links on the street. Two consecutive vehicles in the network will be connected if the inter-vehicle distance between them is smaller than vehicle’s transmission range R. Accordingly, the probability that two consecutive vehicles
links on the street. Two consecutive vehicles in the network will be connected if the inter-vehicle distance between them is smaller than vehicle’s transmission range R. Accordingly, the probability that two consecutive vehicles 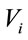 and
and  are connected is given by
are connected is given by , where Xi is the inter-vehicle distance. The network will be connected if there is a path connecting any pair of vehicles. More precisely, it is required that the inter-vehicle distances
, where Xi is the inter-vehicle distance. The network will be connected if there is a path connecting any pair of vehicles. More precisely, it is required that the inter-vehicle distances . Let the vehicle transmission range be a random variable with CDF
. Let the vehicle transmission range be a random variable with CDF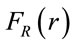 . Let
. Let  be the probability that a pair of consecutive vehicles in the network are connected (link connectivity probability). As mentioned before, this probability is computed as
be the probability that a pair of consecutive vehicles in the network are connected (link connectivity probability). As mentioned before, this probability is computed as . It may be noted that both Xi and R are independent random variables. Accordingly, we find this probability as follows:
. It may be noted that both Xi and R are independent random variables. Accordingly, we find this probability as follows:
 (4)
(4)
where  is the PDF of the inter-vehicle distance (IVD), Xi. Let
is the PDF of the inter-vehicle distance (IVD), Xi. Let  be the probability that the network is connected. It follows that
be the probability that the network is connected. It follows that
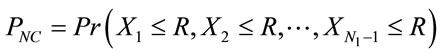 .
.
Note that  are i.i.d. random variables [5]. Hence the network connectivity probability of one-way street (
are i.i.d. random variables [5]. Hence the network connectivity probability of one-way street (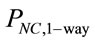 ) is computed as follows:
) is computed as follows:
 (5)
(5)
To compute the connectivity probabilities, the CDF of the transmission range,  must be known. Next, we find
must be known. Next, we find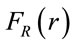 , assuming that V2V channels exhibit Nakagami fading characteristics, and then derive expression for network connectivity probability.
, assuming that V2V channels exhibit Nakagami fading characteristics, and then derive expression for network connectivity probability.
Consider the Nakagami fading channel with the assumption that the fading is constant over the transmission of a frame and subsequent fading states are i.i.d. The received signal to noise power at a distance d away from transmitter in a fading channel is written as 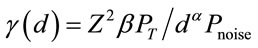 where Z is the fading coefficient,
where Z is the fading coefficient,  is a constant associated with path loss model,
is a constant associated with path loss model, 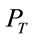 is the transmit power,
is the transmit power,  is the path loss exponent, and
is the path loss exponent, and  is the total additive noise power. Here
is the total additive noise power. Here , where
, where  and
and  respectively represent the transmit and receive antenna gains, c is the speed of light and
respectively represent the transmit and receive antenna gains, c is the speed of light and  is the carrier frequency [22]. Now
is the carrier frequency [22]. Now  is determined by assuming
is determined by assuming  and fo = 5.9 GHz [2]. The thermal noise power is given by
and fo = 5.9 GHz [2]. The thermal noise power is given by 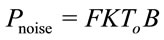 where F is the receiver Noise Figure, K is the Boltzmann constant,
where F is the receiver Noise Figure, K is the Boltzmann constant,  is the room temperature and B is the bandwidth. Now
is the room temperature and B is the bandwidth. Now 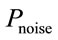 is determined by assuming that
is determined by assuming that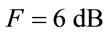 , K = 1.38 × 10−23 J/Kelvin, To = 300˚ Kelvin and
, K = 1.38 × 10−23 J/Kelvin, To = 300˚ Kelvin and 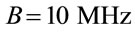 for 802.11 p [2]. Assuming that
for 802.11 p [2]. Assuming that , the average SNR can be written as
, the average SNR can be written as
 . The PDF of the received SNR under Nakagami-m fading is given by [22]:
. The PDF of the received SNR under Nakagami-m fading is given by [22]:
 (6)
(6)
where  is the average SNR, m is the Nakagami fading parameter
is the average SNR, m is the Nakagami fading parameter , and
, and 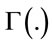 is the Gamma function. The probability that a transmitted message is correctly received at a distance d is given by,
is the Gamma function. The probability that a transmitted message is correctly received at a distance d is given by,
 (7)
(7)
where  and
and  is the upper incomplete Gamma function [23]. The CDF of the transmission range can be computed as follows:
is the upper incomplete Gamma function [23]. The CDF of the transmission range can be computed as follows:
 (8)
(8)
where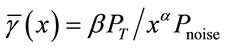 . As mentioned in Section 2, the IVDs are i.i.d., and exponential with PDF
. As mentioned in Section 2, the IVDs are i.i.d., and exponential with PDF  , the link connectivity probability,
, the link connectivity probability, 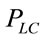 is determined by combining (4) and (8) and is given by
is determined by combining (4) and (8) and is given by
 (9)
(9)
The network connectivity probability is computed by combining (5) and (9) as:
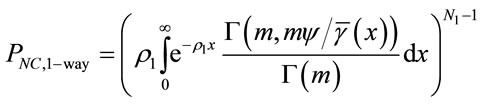 (10)
(10)
For integer values of s,  can be written as
can be written as
 and
and 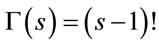 [23]. Accordingly, for integer values of m, (9) becomes:
[23]. Accordingly, for integer values of m, (9) becomes:
 (11)
(11)
To evaluate the integral in (11), we use the following result reported in [24]:
 (12)
(12)
Note that (12) is valid for positive integer values of r and  is the Meijer’s G function [24]. Accordingly, when
is the Meijer’s G function [24]. Accordingly, when 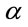 is a positive integer, the integral in (11) can be written in terms of Meijer’s G function based on (12). Thus
is a positive integer, the integral in (11) can be written in terms of Meijer’s G function based on (12). Thus 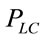 is computed as follows:
is computed as follows:
 (13)
(13)
For integer values of  and m, the network connectivity probability on one-way street can be written as,
and m, the network connectivity probability on one-way street can be written as,
 (14)
(14)
For non-integer values of , (11) has no closed-form solution and hence both
, (11) has no closed-form solution and hence both 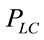 and
and  have to be evaluated by numerical techniques using (9) and (10) respectively.
have to be evaluated by numerical techniques using (9) and (10) respectively.
3.2. Network Connectivity for the Two-Way Street
In this section, we present the connectivity analysis for the two-way street scenario. Consider the two-way street scenario shown in Figure 1, where vehicles on the lower lane relay packets opposite to their direction of motion and store-carry-forward routing is used when there is a broken link on the lower lane. With this approach, network connectivity on the lower lane can be restored with the help of vehicles that move in the opposite direction on the upper lane. Let 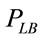 be the probability that connectivity on a specific link is lost (i.e., the link is broken) on the lower lane. This happens when the IVD between a pair of vehicles becomes greater than the transmission range. Accordingly,
be the probability that connectivity on a specific link is lost (i.e., the link is broken) on the lower lane. This happens when the IVD between a pair of vehicles becomes greater than the transmission range. Accordingly,  is equal to the complement of the link connectivity probability
is equal to the complement of the link connectivity probability , the analysis of which was conducted in Section 3.1. Thus we have,
, the analysis of which was conducted in Section 3.1. Thus we have,
 (15)
(15)
where  is computed using (9). Out of a total of (N1 – 1) links on the lower lane, the probability that J of these links will be broken, is given by:
is computed using (9). Out of a total of (N1 – 1) links on the lower lane, the probability that J of these links will be broken, is given by:
 (16)
(16)
If all of the broken links on the lower lane are fixable with the help of vehicles on the upper lane, the network connectivity on the lower lane can be restored. Consider the broken link between vehicles  and
and 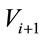 shown in Figure 1. In this case
shown in Figure 1. In this case  has a packet to be sent to
has a packet to be sent to . This broken link is fixable if there is at least one vehicle on the upper lane in the interval of length 2R centered around
. This broken link is fixable if there is at least one vehicle on the upper lane in the interval of length 2R centered around .
.
Let U be a random variable denoting the number of vehicles that are present in the interval of 2R on the upper lane. According to the system model described in Section 2, the IVDs on the lower as well as the upper lanes are i.i.d. exponential with parameters ρ1 and ρ2 respectively. Hence the number of vehicles on the lower and upper lanes is Poisson with parameters ρ1 and ρ2 respectively. Accordingly U is also Poisson with probability mass function given as follows:
 (17)
(17)
A broken link on the lower lane is not fixable if there are no vehicles in the interval of 2R on the upper lane. Thus the conditional probability that broken link is not fixable is computed as . Unconditioning, the probability that a broken link is not fixable (
. Unconditioning, the probability that a broken link is not fixable ( ) is calculated as follows:
) is calculated as follows:
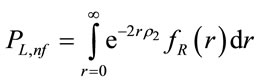 (18)
(18)
where  is the PDF of R. For Nakagami fading,
is the PDF of R. For Nakagami fading, 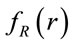 is given by the following expression (Proof given in Appendix A).
is given by the following expression (Proof given in Appendix A).
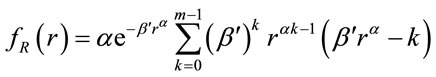 (19)
(19)
where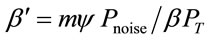 . Substituting (19) in (18), the following expression can be obtained for
. Substituting (19) in (18), the following expression can be obtained for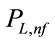 : (Proof given in Appendix B) (see formula (21) below).
: (Proof given in Appendix B) (see formula (21) below).
Let  be the conditional network connectivity probability given that there are J broken links. Since the probability that each broken link is fixable is equal to
be the conditional network connectivity probability given that there are J broken links. Since the probability that each broken link is fixable is equal to ,
, 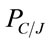 is computed as follows:
is computed as follows:
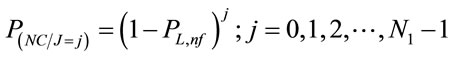 (21)
(21)
The network connectivity probability on the two-way street is then computed as follows:
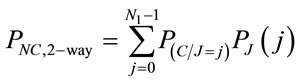 (22)
(22)
It may be noted that, to compute 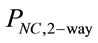 according to (22), Equations (9), (15), (16), (20) and (21) must be used.
according to (22), Equations (9), (15), (16), (20) and (21) must be used.
4. Analytical and Simulation Results
In this section, we present results for the network connectivity. Both the analytical as well as simulation results are obtained using MATLAB. As mentioned before, in the free flow state, the vehicle speed and the traffic flow are independent and hence there are no significant interactions between individual vehicles. Therefore, generating vehicle traffic arrival process is possible without using commercial traffic or network simulators [5]. Hence MATLAB is used to simulate an uninterrupted highway. The vehicle arrival model and the mobility model of Section 2 are implemented using an event driven simulation using MATLAB. The effect of fading is introduced into the simulation using Monte-Carlo techniques. We consider a highway of length L = 10 km and the vehicles are generated from a Poisson process with rate λ veh/sec. Each vehicle is assigned a random speed chosen from a truncated Gaussian distribution. Table 1 shows typical values for the mean (μ km/hr) and standard deviation (σ km/hr) of the vehicle speed on the highway [5]. To find the network connectivity, we fix λ1 = 0.1 veh/sec. The vehicle speed follows a truncated gaussian random variable with mean μ = 70 km/hr and standard deviation σ = 21 km/hr. These values of λ, μ and σ correspond to average vehicle density 5.8 veh/km on the lower lane. Further, the transmit power is fixed as PT = 33.3 dBm according to DSRC and IEEE 802.11 p specifications [2] and receive SNR threshold is selected as .
.
The snap shot of the highway at the arrival instant of each vehicle is observed and the inter-vehicle distance values are determined. For each link, the average SNR 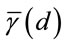 is determined corresponding to the measured value of inter-vehicle distance, d of that link. Assuming Nakagami fading environment, we then generate a random variable representing the received SNR over that link with average value
is determined corresponding to the measured value of inter-vehicle distance, d of that link. Assuming Nakagami fading environment, we then generate a random variable representing the received SNR over that link with average value . If the received SNR is greater than the threshold value
. If the received SNR is greater than the threshold value , the link is considered to be connected. The procedure is repeated for all the
, the link is considered to be connected. The procedure is repeated for all the 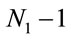 links with their corresponding inter-vehicle distance values. If all the links in a snap shot are connected, the network is considered to be connected. The connectivity evaluation process is then repeated 10,000 times. The network connectivity probability is calculated from these 10,000 sample values.
links with their corresponding inter-vehicle distance values. If all the links in a snap shot are connected, the network is considered to be connected. The connectivity evaluation process is then repeated 10,000 times. The network connectivity probability is calculated from these 10,000 sample values.
Figure 2 shows the network connectivity probability of one-way street and two-way street (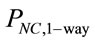 and
and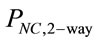 ) plotted against path loss exponent (
) plotted against path loss exponent ( ), for a
), for a

Table 1. Normal-vehicle speed statistics [5].
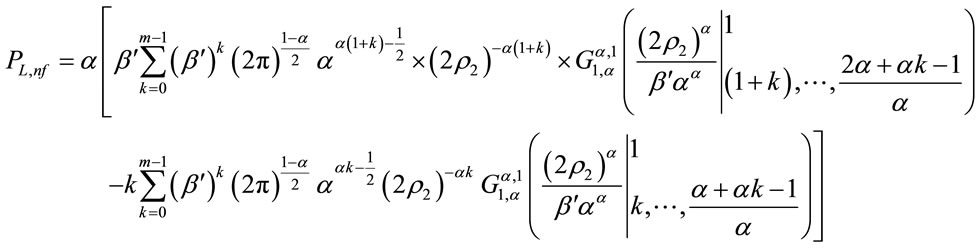 (20)
(20)
fixed average vehicle density. To determine the two-way street connectivity, the average vehicle density on the upper and the lower lanes are assumed to be equal (i.e.,  =
= ). In Figures 3 and 4, network connectivity probabilities on both one-way as well as two-way streets are plotted against average vehicle density (
). In Figures 3 and 4, network connectivity probabilities on both one-way as well as two-way streets are plotted against average vehicle density (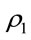 ) for
) for  = 1.8 and 3.5 respectively. In this case, to find two-way street connectivity probability,
= 1.8 and 3.5 respectively. In this case, to find two-way street connectivity probability, 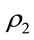 is set equal to 15 veh/km. The results show that the connectivity on two-way street is always greater than that of the one-way street case. Further, both Nakagami factor (m) and path loss exponent (
is set equal to 15 veh/km. The results show that the connectivity on two-way street is always greater than that of the one-way street case. Further, both Nakagami factor (m) and path loss exponent ( ) have strong influence on the connectivity. As
) have strong influence on the connectivity. As  increases both
increases both 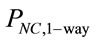 and
and  decays very rapidly. Depending on the value of m, the network gets almost disconnected when
decays very rapidly. Depending on the value of m, the network gets almost disconnected when 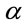 becomes more than 3. Further, the network connectivity probability gets degraded when the Nakagami parameter m goes below 0.5 (lower most plot in Figure 3), and gets improved when m > 0.5. As expected, the connectivity probability increases as average vehicle density increases. Moreover, it can be observed that, the average vehicle density (
becomes more than 3. Further, the network connectivity probability gets degraded when the Nakagami parameter m goes below 0.5 (lower most plot in Figure 3), and gets improved when m > 0.5. As expected, the connectivity probability increases as average vehicle density increases. Moreover, it can be observed that, the average vehicle density ( ), corresponding to the lower lane, required to
), corresponding to the lower lane, required to
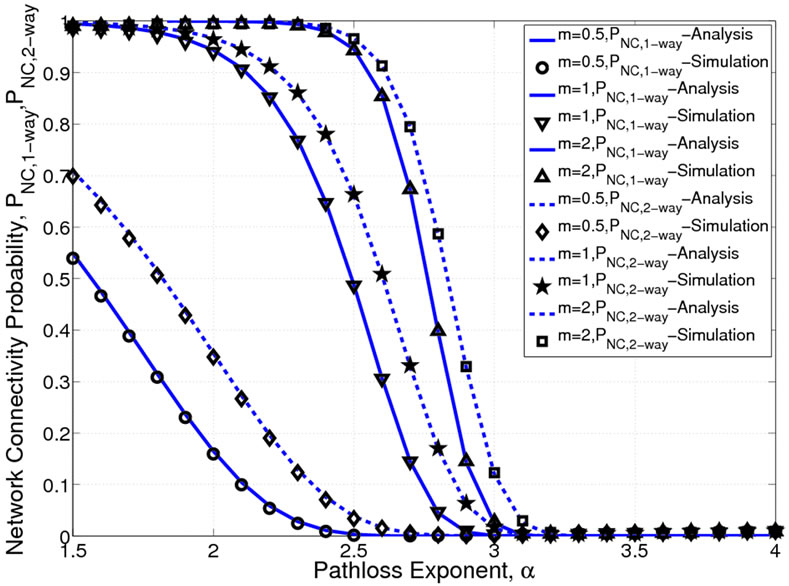
Figure 2. Network connectivity probability (one-way and two-way) versus Pathloss exponent (PT = 33 dBm, L = 10 km, λ1 = λ2 = 0.3 veh/sec, μ1 = μ2 = 70 km/hr, σ1 = σ2 = 21 km/hr).
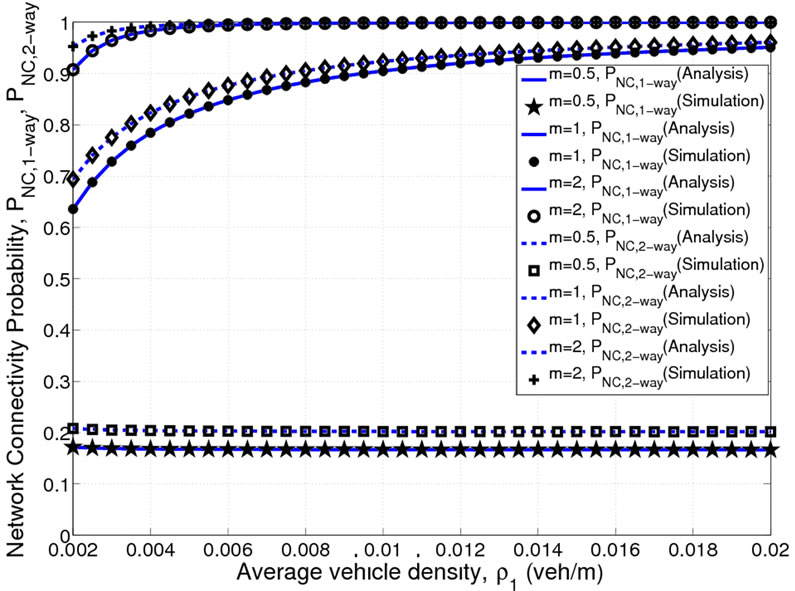
Figure 3. Network connectivity probability (one-way and two-way) versus average vehicle density (PT = 33 dBm, α = 1.8, L = 10 km, ρ2 = 0.015 veh/m).
satisfy a target value for the network connectivity probability, decreases when the pathloss exponent decreases. Figure 5 shows the two-way network connectivity probability plotted against average vehicle density  for two different values of
for two different values of , average vehicle density on the upper lane, and for a fixed path loss exponent
, average vehicle density on the upper lane, and for a fixed path loss exponent . Results show that as
. Results show that as 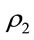 increases, the two-way connectivity probability increases, which means that deploying more vehicles on the upper lane can improve the connectivity of the lower lane.
increases, the two-way connectivity probability increases, which means that deploying more vehicles on the upper lane can improve the connectivity of the lower lane.
The analytical model and the results of this paper would be useful for developing a self organizing VANET for intelligent transport applications. The presented model gives a unique framework for analyzing the impact of traffic related and channel dependent parameters on network connectivity on two-way street. The significance of the model is that it can be used as a tool to find the minimum average vehicle density required to satisfy a certain connectivity probability. Given a certain kind of traffic flow, the model may be of help to determine whether a fully connected network can be formed. Message routing is a challenging problem in VANETs due to the inherent high degree of mobility of the vehicles in the network. Due to the dynamic nature of the traffic and the environment, individual communication links are shortlived and the routing paths that rely on such links are highly vulnerable to connection disruptions. A multi-hop route established between two vehicles may get disrupted due to mobility of the source, the destination, or the intermediate vehicles, causing route failures to occur. Further, when vehicle density varies considerably, the traditional multi-hop forwarding approach for unicast routing fails since locating a vehicle for forwarding a message becomes difficult. Instead, a carry-and-forward technique

Figure 4. Network connectivity probability (one-way and two-way) versus average vehicle density (PT = 33 dBm, α = 3.5, L = 10 km, ρ2 = 0.015 veh/m).

Figure 5. Two-way network connectivity probability versus average vehicle density on the lower lane, ρ1 (PT = 33 dBm, α = 1.8, L = 10 km, m = 1).
can be used where a vehicle carries the data packet until a new vehicle moves into its vicinity and then forwards the packet. As far as routing of messages is concerned, it is critical to select routes that have maximum connectivity probability. The presented analytical model would be an important step towards the design of such connectivity aware routing protocols for VANETs.
5. Conclusion
In this paper, we derived closed form expression for the network connectivity probability of a linear VANET on a two-way street, in the presence of Nakagami fading. Initially, we presented a model to find the network connectivity on one-way street. We then extended the model to find network connectivity on a two-way street scenario. Through extensive analytical and simulation studies, we established that, the network connectivity on a specific lane can be significantly improved with the help of opposing vehicles on the other lane. Our analytical model is unique in the sense that it can be used to find the dependence of various parameters such as average vehicle density, vehicle speed, highway length and significant physical layer parameters such as path loss exponent, Nakagami fading factor etc., on network connectivity on a two-way street.
REFERENCES
- S. Yousefi, M. Mousavi and M. Fathy, “Vehicular AdHoc Networks (VANETs): Challenges and Perspectives,” Proceedings of International Conference on Intelligent Transportation System Telecommunication, Chengdu, June 2006, pp. 761-766.
- IEEE 802.11p Draft Amendment, “Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications,” Wireless Access in Vehicular Environments (WAVE), July 2010.
- G. Karagiannis, O. Altintas, E. Ekici, G. Heijenk, B. Jarupan, K. Lin and T. Weil, “Vehicular Networking: A Survey and Tutorial on Requirements, Architectures, Challenges, Standards and Solutions,” IEEE Communications Surveys & Tutorials, Vol. 13, No. 4, 2011, pp. 584- 616. doi:10.1109/SURV.2011.061411.00019
- M. Artimy, W. Phillips and W. Robertson, “Connectivity with Static Transmission Range in Vehicular Ad-Hoc Networks,” Proceedings of the 3rd Annual IEEE Communication Networks and Services Research Conference, Nova Scotia, 16-18 May 2005, pp. 237-242. doi:10.1109/CNSR.2005.29
- S. Yousefi, E. Altman, R. El-Azouzi and M. Fathy, “Analytical Model for Connectivity in Vehicular Ad-Hoc Networks,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 6, 2008, pp. 3341-3356. doi:10.1109/TVT.2008.2002957
- S. Yousefi, E. Altman, R. El Azouzi and M. Fathy, “Improving Connectivity in Vehicular Ad-Hoc Networks: An Analytical Study,” Elsevier Computer Communications, Vol. 31, No. 9, 2008, pp. 1653-1659.
- J. Wu, “Connectivity of Mobile Linear Networks with Dynamic Node Population and Delay Constraint,” IEEE Journal on Selected Areas in Communications, Vol. 27, No. 7, 2009, pp. 1218-1225. doi:10.1109/JSAC.2009.090917
- M. Khabazian and M. Ali, “A Performance Modeling of Connectivity in Vehicular Ad-Hoc Networks,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 4, 2008, pp. 2440-2450. doi:10.1109/TVT.2007.912161
- G. Mohimani, F. Ashtiani, A. Javanmard and M. Hamdi, “Mobility Modeling, Spatial Traffic Distribution, and Probability of Connectivity for Sparse and Dense Vehicular Ad-Hoc Networks,” IEEE Transactions on Vehicular Technology, Vol. 58, No. 4, 2009, pp. 1998-2007. doi:10.1109/TVT.2008.2004266
- S. Panichpapiboon and W. Pattara-Atikom, “Connectivity Requirements for Self-Organizing Traffic Information Systems,” IEEE Transactions on Vehicular Technology, Vol. 57, No. 6, 2008, pp. 3333-3340. doi:10.1109/TVT.2008.929067
- Y. Zhuang, J. Pan and L. Cai, “A Probabilistic Model for Message Propagation in Two-Dimensional Vehicular AdHoc Networks,” Proceedings of the 7th ACM International Workshop on Vehicular Internetworking, Chicago (USA), July 2010, pp. 31-40. doi:10.1145/1860058.1860064
- W. Viriyasitavat, O. Tonguz and F. Bai, “Network Connectivity of VANETs in Urban Areas,” Proceedings of the 6th Annual IEEE Communications Society Conference on Sensor Mesh and Ad-Hoc Communications and Networks (SECON), Boston (USA), 22-26 June 2009, pp. 1-9.
- V. K. M. Ajeer, P. C. Neelakantan and A. V. Babu, “Network Connectivity of One-Dimensional Vehicular Ad-Hoc Network,” Proceedings of IEEE International Conference on Communications and Signal Processing (ICCSP), Calicut (India), 10-12 February 2011, pp. 241- 245.
- A. V. Babu and V. K. M. Ajeer, “Analytical Model for Connectivity of Vehicular Ad-Hoc Networks in the Presence of Channel Randomness,” Wiley International Journal of Communication Systems, 2011. doi:10.1002/dac.1379
- P. C. Neelakantan and A. V. Babu, “Connectivity Analysis of One-Dimensional Vehicular Ad-Hoc Networks in Fading Channels,” EURASIP Journal on Wireless Communications and Networking, 2012. doi:10.1186/1687-1499-2012-1
- J. Maurer, T. Fugen and W. Wiesbeck, “Narrow-Band Measurement and Analysis of the Inter-Vehicle Transmission Channelat 5.2 GHz,” IEEE 55th Vehicular Technology Conference (VTC Spring), Alabama (USA), Vol. 3, May 2002, pp. 1274-1278.
- L. Cheng, B. Henty, D. Stancil, F. Bai and P. Mudalige, “Mobile Vehicle-to-Vehicle Narrow-Band Channel Measurement and Characterization of the 5.9 GHz Dedicated Short Range Communication (DSRC) Frequency Band,” IEEE Journal on Selected Areas in Communications, Vol. 25, No. 8, 2007, pp. 1501-1516. doi:10.1109/JSAC.2007.071002
- I. Sen and D. Matolak, “Vehicle-Vehicle Channel Models for the 5-GHz Band,” IEEE Transactions on Intelligent Transportation Systems, Vol. 9, No. 2, 2008, pp. 235-245. doi:10.1109/TITS.2008.922881
- J. Karedal, N. Czink, A. Paier, F. Tufvesson and A. Molisch, “Pathloss Modeling for Vehicle-to-Vehicle Communications,” IEEE Transactions on Vehicular Technology, Vol. 60, No. 1, 2011, pp. 323-328.
- J. Kunisch and J. Pamp, “Wideband Car-to-Car Radio Channel Measurements and Model at 5.9 GHz,” IEEE 68th Vehicular Technology Conference (VTC Fall), Calgary (Canada), September 2008, pp. 1-5.
- W. McShane and R. Roess, “Traffic Engineering,” 3rd Edition, Pearson Prentice Hall, Upper Saddle River, 2004.
- A. Goldsmith, “Wireless Communications,” Cambridge University Press, Cambridge, 2005.
- I. Gradshtein, I. Ryzhik and A. Jeffrey, “Table of Integrals, Series, and Products,” Academic Press, Waltham, 2000.
- J. Cheng, C. Tellambura and N. Beaulieu, “Performance of Digital Linear Modulations on Weibull Slow-Fading Channels,” IEEE Transactions on Communications, Vol. 52, No. 8, 2004, pp. 1265-1268. doi:10.1109/TCOMM.2004.833015
Appendix A
Derivation of (19):
To find the PDF of R , we use the CDF expression given by (8). When
, we use the CDF expression given by (8). When 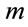 is an integer,
is an integer,

[23], where . Accordingly, the CDF given by (8) can be simplified to get the following expression:
. Accordingly, the CDF given by (8) can be simplified to get the following expression:
 (A.1)
(A.1)
where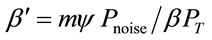 . Now
. Now 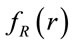 is obtained by differentiating (A.1) and is given by (19).
is obtained by differentiating (A.1) and is given by (19).
Appendix B
Derivation of (20):
To prove (20), we substitute (19) in (18) and rewrite the integral as follows:
To evaluate the first integral expression in (B.1), we use (12). When 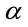 is a positive integer, the first integral in (B.1) can be written in terms of Meijer’s G function based on (12) to get the following expression:
is a positive integer, the first integral in (B.1) can be written in terms of Meijer’s G function based on (12) to get the following expression:
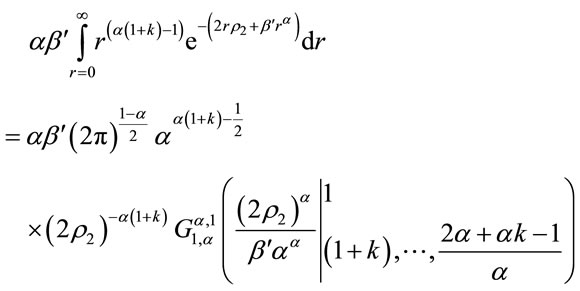 (B.2)
(B.2)
Using a similar approach, the second integral in (B.1) can be evaluated to get the following expression:
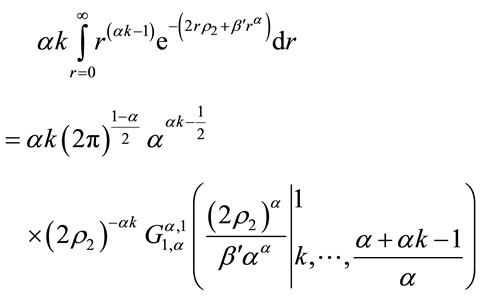 (B.3)
(B.3)
Substituting (B.2) and (B.3) in (B.1) we get (20).
 (B.1)
(B.1)

