Communications and Network
Vol. 4 No. 1 (2012) , Article ID: 17499 , 7 pages DOI:10.4236/cn.2012.41008
Training Based Channel Estimation in MIMO-OFDM Systems
Electrical Engineering Department, Shahed University, Tehran, Iran
Email: mimani@shahed.ac.ir
Received November 14, 2011; revised December 18, 2011; accepted December 31, 2011
Keywords: training symbol; channel estimation; MIMO; OFDM; LS
ABSTRACT
OFDM combined with the MIMO technique has become a core and attractive technology in future wireless communication systems and can be used to both improve capacity and quality of mobile wireless systems. Accurate and efficient channel estimation plays a key role in MIMO-OFDM communication systems, which is typically realized by using pilot or training sequences by virtue of low complexity and considerable performance. In this paper, we discuss some methods for channel estimation based training symbols in MIMO-OFDM systems. The results confirm the superiority of the represented methods over the existing ones in terms of bandwidth efficiency and estimation error.
1. Introduction
Future mobile wireless communication systems will require high-bit-rate technologies. Orthogonal frequency division multiplexing (OFDM) is a novel technique that divides entire channel into many narrow parallel subchannels, so that it improves data rate and avoids intersymbol interference (ISI) caused by multi-path propagation. Multi-input multi output (MIMO) system uses multiple antennas at both sides to increase capacity of wireless channel without the need of extra bandwidth. The MIMO-OFDM system is an attractive candidate for high data rate wireless applications. Various channel estimation methods including two major methods LS and MMSE [1,2], have been widely used for MIMO-OFDM channel estimation. Also, Different types like Pilot aided/ Training based estimation schemes are frequently used for different systems under different channel environments like Fast fading and Flat fading.
In [3], the training sequence design for MIMO-OFDM systems under the minimum mean square error (MMSE) criterion is addressed. Authors present a necessary and sufficient condition for the optimal training sequence, and reformulate the training design problem as a convex optimization problem whose optimal solution is efficiently solved. In addition, tight upper bounds for MMSE and resulting low complexity iterative algorithms with the closed-form expression in iterations to find the optimum training sequence are derived. In [3], authors consider the broadband MIMO channels together with the use of OFDM modulation. Although OFDM techniques can transform the broadband frequency-selective fading channels into a set of parallel flat fading sub-channels, the channel estimation of MIMO-OFDM systems is more challenging as compared to that of narrowband MIMO systems. One reason is that the number of channel parameters to be estimated are proportional to the channel delay spread and the number of antennas. Another reason is that each received signal depends on multiple channel parameters. Authors in [3] focus on the optimal design of time-division multiplexed (TDM) training sequences for channel estimation. Authors focus on the optimal design of training sequences for MIMO-OFDM systems with the general case of spatial correlations. To formulate the optimization problem of the training sequence design, they adopt the minimum mean square error (MMSE) criterion subject to the power constraint.
In this paper, we study some novel methods for channel estimation based training symbols in MIMO-OFDM systems.
Notation: Boldface letters will be used for matrices and column vectors. Superscript ,
, 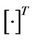 and
and  denote the conjugate, transpose and Hermitian, respectively.
denote the conjugate, transpose and Hermitian, respectively. 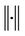 denotes the Euclidean norm of a vector. We will reserve
denotes the Euclidean norm of a vector. We will reserve  for the Kronecker product.
for the Kronecker product.  is used to represent the statistical expectation while
is used to represent the statistical expectation while  denotes a circularly symmetric complex Gaussian random variable. Operator
denotes a circularly symmetric complex Gaussian random variable. Operator  stacks the columns of a matrix into a column vector. Finally, the
stacks the columns of a matrix into a column vector. Finally, the 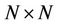 identity matrix is represented by
identity matrix is represented by .
.
2. Superimposed Training Based Channel Estimation
Superimposed training (ST) based channel estimation techniques have been proposed in [4,5]. In this section, a novel method consisting of a technique to refine the channel estimate at the transmitter in a ST based closed loop MIMO-OFDM system is proposed. This method is represented in [6] completely. The estimate is refined at the transmitter by making use of the previous data that was transmitted. This significantly reduces the data interference in the channel estimate and hence improves performance. Two factors in general affect all transmitter side techniques that make use of the fed back channel coefficients. One is the quantization error affecting the channel estimate. The other is the channel variations that may render the fed back channel coefficients outdated for further use. The effect of these factors on the proposed refined channel estimation scheme is discussed.
Consider a MIMO-OFDM system with  transmitting antennas and
transmitting antennas and  receiving antennas having
receiving antennas having  subcarriers and an OFDM symbol duration
subcarriers and an OFDM symbol duration . Let
. Let  be a vector of data symbols associated with the
be a vector of data symbols associated with the  th OFDM symbol of the
th OFDM symbol of the  th transmitting antenna. Superimposed training (ST) sequences are added to the data symbols for the purpose of channel estimation. Let the training sequence
th transmitting antenna. Superimposed training (ST) sequences are added to the data symbols for the purpose of channel estimation. Let the training sequence  be algebraically added to IDFT output with a specific data to pilot power ratio, to get
be algebraically added to IDFT output with a specific data to pilot power ratio, to get
 (1)
(1)
We make the following assumptions for the present formulation and study.
1) The channel is wide sense stationary with uncorrelated scattering (WSSUS); 2) The data symbols are uncorrelated with each other and have zero mean; 3) The data is uncorrelated with the superimposed training sequence; 4) The noise is additive white Gaussian with mean zero; 5) We also assume perfect synchronization and a zero dc offset at the baseband receiver.
The equivalent baseband vectors at the rth receive antenna obtained after guard removal from the OFDM symbols may then be expressed as:
 (2)
(2)
The estimate of the channel impulse response for each transmit-receive antenna pair at the rth received antenna can be determined by minimizing the least squares difference between the received signal and the sum of the outputs of the ST sequences passed through the channel estimators.
The estimate is given by:
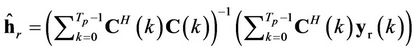 (3)
(3)
where 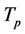 denotes coherent time of the channel.
denotes coherent time of the channel.
In closed loop systems the channel state information is feedback to the transmitter. In this case, we consider the case wherein the channel coefficients are quantized and fed back to the transmitter. The quantized composite channel estimation vector 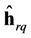 is now given by
is now given by
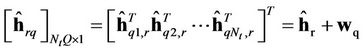 (4)
(4)
Here 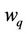 represents the quantization noise or error and
represents the quantization noise or error and  are the corresponding quantized versions of the channel estimates associated with all the transmit antennas and the rth receive antenna. We assume that the quantized channel coefficients are reliably received at the transmitter through the feedback channel.
are the corresponding quantized versions of the channel estimates associated with all the transmit antennas and the rth receive antenna. We assume that the quantized channel coefficients are reliably received at the transmitter through the feedback channel.
The composite channel vector of the refined channel estimation coefficients 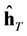 is given by
is given by
 (5)
(5)
where the vectors  are the refined channel estimates associated with the transmit antennas and the rth receive antenna.
are the refined channel estimates associated with the transmit antennas and the rth receive antenna.
The channel estimation performance in ST based methods is severely affected by the data interference. Interestingly closed loop ST based systems provide scope to improve the performance by canceling the data interference at the transmitter by making use of the previous data that was transmitted.
It can be revealed that the effective data interference on the channel estimate is a pre-multiplication by , where
, where
 . Hencethe way to remove this effective interference is by a pre-multiplication of
. Hencethe way to remove this effective interference is by a pre-multiplication of 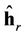 by the inverse of this term. Let
by the inverse of this term. Let  be defined as the inverse of this term given by
be defined as the inverse of this term given by
 (6)
(6)
The estimation accuracy may be improved by premultiplying the fed back channel estimate by the matrix . Therefore, it is proposed to pre-multiply
. Therefore, it is proposed to pre-multiply  at the transmitter by
at the transmitter by  to obtain
to obtain , as a new method to reduce the effect of the data interference on the channel estimate at the transmitter of an ST based MIMO-OFDM system. The proposed refined channel estimate is given by
, as a new method to reduce the effect of the data interference on the channel estimate at the transmitter of an ST based MIMO-OFDM system. The proposed refined channel estimate is given by
 (7)
(7)
Figure 1 illustrates the impact of the quantization error on the MSEE performance. The objective of the designer is to use the minimum number of bits to quantize the channel without significantly affecting performance. From Figure 1 we see that, the MSEE performance is
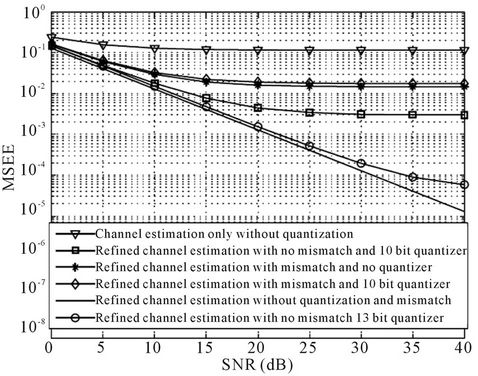
Figure 1. Simulated MSEE as a function of SNR for the proposed channel estimation scheme employing 10 bit and 13 bit channel quantizers [6].
nearly identical to the lower bound for SNRs below 30 dB when a 13 bit quantizer is used. In comparison, the 10 bit quantizer results in an inferior performance. However, when the 10 bit quantizer is used in scenarios with a channel mismatch arising from a Doppler bandwidth of 30 Hz, the performance is nearly the same as seen from the figure. Hence a 10 bit quantizer is good enough in such scenarios (for more details about this section, see [6]).
3. A Simplified Training Pattern
In MIMO-OFDM systems, channel state information is required for space-time decoding. In [7], the low complexity channel estimation based on STBC training sequences was proposed. However, if too much training blocks are used, the efficiency of system will be decreased. A simplified training pattern which can reduce the waste of resources was proposed in [8] and we describe it in this section. When the STBC training pattern applied in systems with four transmitting antennas, the training block is given by
 (8)
(8)
Hence, eight OFDM periods will be needed to transmit training sequences, and assume that the channel is quasifixed over eight OFDM periods. More resources are wasted for transmitting training sequences, and the assumption is not reasonable. We can transmit training blocks according to the following pattern shown in Figure 2. At training time , transmitting antennas
, transmitting antennas  and
and 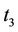 transmit the first group of training sequence
transmit the first group of training sequence  and
and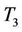 , the transmitting antennas
, the transmitting antennas  and
and 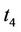 do not transmit any data. At the time
do not transmit any data. At the time ,
,  and
and 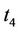 transmit the first group of training sequence
transmit the first group of training sequence 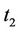 and
and ,
, 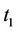 and
and  do not transmit any data. Then at time
do not transmit any data. Then at time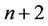 ,
, 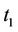 and
and  transmit the second group of training sequence
transmit the second group of training sequence 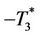 and
and ,
,  and
and  do not transmit any data. At the last training time
do not transmit any data. At the last training time ,
, 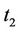 and
and  transmit the second group of training sequence
transmit the second group of training sequence  and
and ,
,  and
and 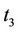 do not transmit any data. The received signal can be expressed as
do not transmit any data. The received signal can be expressed as
 (9)
(9)
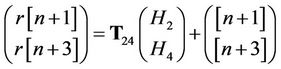 (10)
(10)
where
 (11)
(11)
Figure 3 shows the MSE of channel estimator with the old pattern and the simplified training pattern proposed here under typical urban (TU) delay profile respectively. From the simulation results we can see that the MSE of estimator with simplified transmitting pattern of training blocks is almost equal to that of estimator with old pattern under low SNR. With the rise of SNR, the performance of estimator with simplified pattern gets better than the old one. And note that the estimator with simplified pattern can save four OFOM periods for transmitting training blocks, and the complexity of estimator can also be reduced. The efficiency of the estimator with simplified pattern is higher than the old one (for more details about this section, see [8]).
4. Optimal Pilot Sequences for Correlated Fading Channels
In practical wireless communications, channel parame-

Figure 2. Simplified transmitting pattern of training blocks [8].
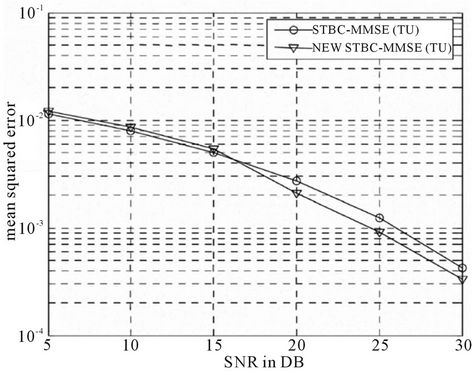
Figure 3. MSE of channel estimators under TU delay profile [8].
ters can be estimated by sending training sequences to the receiver. In general, the accuracy of channel estimation highly relies on the design of training sequences. Some pilot designs for MIMO-OFDM systems were addressed in [9,10].
In this section, the optimal pilot sequences are designed by maximizing the mutual information (carried by pilot tones) between the channel and the received sequences during the training over multiple OFDM symbols. The complete description of this design is represented in [11].
After removing the CP and performing FFT, the received signal in frequency at the kth subcarrier of the nth OFDM symbol can be modeled as
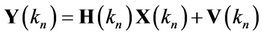 (12)
(12)
where 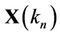 and
and 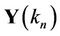 are respectively transmitted and received signal vector,
are respectively transmitted and received signal vector,  is noise vector,
is noise vector,  is the channel matrix of frequency response. The channel has L paths. We can write each of the taps as the sum of a fixed (possibly line-of-sight) component
is the channel matrix of frequency response. The channel has L paths. We can write each of the taps as the sum of a fixed (possibly line-of-sight) component  and a variable (or scattered) component
and a variable (or scattered) component  as
as
 (13)
(13)
Let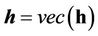 , we would take the spatial correlation (include receive correlation and transmit correlation) and tap gain correlation into account, so the covariance matrix of
, we would take the spatial correlation (include receive correlation and transmit correlation) and tap gain correlation into account, so the covariance matrix of  can be expressed as
can be expressed as
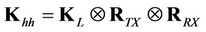 (14)
(14)
where  and
and 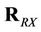 are respectively the transmit correlation matrix and the receive correlation matrix,
are respectively the transmit correlation matrix and the receive correlation matrix, 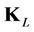 is the tap gain covariance matrix, and can be written as
is the tap gain covariance matrix, and can be written as
 (15)
(15)
where ,
,
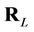 is the tap gain correlation matrix,
is the tap gain correlation matrix,  and
and  are the power and Rice factor of the lth tap, respectively.
are the power and Rice factor of the lth tap, respectively.
Assuming the MIMO channel obeys block fading, that is, the channel is constant during the consecutive multiple symbols. e.g., over the time indices 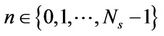 , the receive matrix at the
, the receive matrix at the  pilot tone of the nth OFDM symbol during the pilot symbols scheme can be described as
pilot tone of the nth OFDM symbol during the pilot symbols scheme can be described as
 (16)
(16)
where  is the total number of the pilot tones of the nth OFDM symbol, such that
is the total number of the pilot tones of the nth OFDM symbol, such that . So we can have
. So we can have
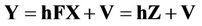 (17)
(17)
where  is FFT matrix and
is FFT matrix and  .
.
Our goal for pilot sequences design here is to find  in order to maximize the channel mutual information (CMI) with a fixed power
in order to maximize the channel mutual information (CMI) with a fixed power  during the pilot symbols scheme. And the pilot sequences
during the pilot symbols scheme. And the pilot sequences  is only determined by
is only determined by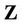 . So the optimization problem of pilot sequences can be expressed as
. So the optimization problem of pilot sequences can be expressed as
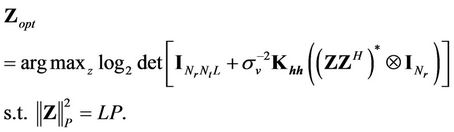 (18)
(18)
 and
and  are defined as the spatial correlation coefficient at the transmitter and the spatial correlation coefficient at the receiver, respectively.
are defined as the spatial correlation coefficient at the transmitter and the spatial correlation coefficient at the receiver, respectively.  is defined as the tap gain correlation coefficient. From Figure 4 we can see that the stronger the
is defined as the tap gain correlation coefficient. From Figure 4 we can see that the stronger the  is, the greater the CMI gap between the optimum pilot sequences and orthogonal pilot sequences is. It can be seen that the smaller correlation is not helpful to increase the CMI gap (for more details about this section, see [11]).
is, the greater the CMI gap between the optimum pilot sequences and orthogonal pilot sequences is. It can be seen that the smaller correlation is not helpful to increase the CMI gap (for more details about this section, see [11]).
5. QR-RLS Channel Estimator
Adaptive channel estimator was suggested for channel tracking [12]. In this section, a novel method for OFDMMIMO channel estimation using QR-RLS (Square RootRecursive Least Square) estimator is presented. Preamble aided channel estimation is performed in time-domain, estimated channel is then used for data detection during data transmission within that frame. This method is completely represented in [13].
Each transmitter transmits Preamble as first OFDM
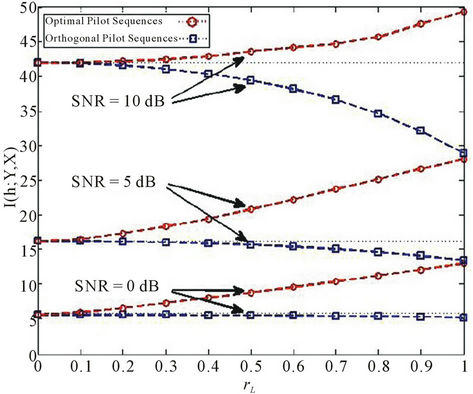
Figure 4. CMI versus 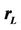 without transmit correlation and receive correlation [11].
without transmit correlation and receive correlation [11].
symbol. Channel is estimated during this training period, where estimated channel is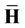 . Consider the received signal at qth receive antenna represented in matrix form as
. Consider the received signal at qth receive antenna represented in matrix form as
 (19)
(19)
where matrix  is prewindowed matrix of
is prewindowed matrix of  having
having  data symbols from each transmit antenna at time instant n. Estimated channel with least square (LS) criteria is calculated as follows:
data symbols from each transmit antenna at time instant n. Estimated channel with least square (LS) criteria is calculated as follows:
 (20)
(20)
where  is the autocorrelation matrix of the Preamble signal, and
is the autocorrelation matrix of the Preamble signal, and  is the cross correlation matrix between received signal and the preamble signal at time n. Above Equation (20) involves inverse of a matrix which is solved using woolbury identity in Standard-RLS based MIMO channel estimation. In different environment channel conditions like low noise, highly correlated channel etc, the Correlation matrix becomes singular. In such cases the Standard-RLS channel estimation method either build up roundup errors or become susceptible to instability. To overcome these effects Square root based estimation is used as it involves QR factorization of the correlation matrix and inverse of a triangle matrix, thus escapes the rounding errors.
is the cross correlation matrix between received signal and the preamble signal at time n. Above Equation (20) involves inverse of a matrix which is solved using woolbury identity in Standard-RLS based MIMO channel estimation. In different environment channel conditions like low noise, highly correlated channel etc, the Correlation matrix becomes singular. In such cases the Standard-RLS channel estimation method either build up roundup errors or become susceptible to instability. To overcome these effects Square root based estimation is used as it involves QR factorization of the correlation matrix and inverse of a triangle matrix, thus escapes the rounding errors.
Here QR factorization using givens rotation is applied on Equation (20) which can be written as
 (21)
(21)
Decomposition of matrix  is given by
is given by
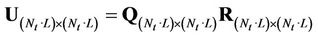
where  is orthogonal matrix and
is orthogonal matrix and 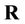 is upper triangle matrix. Substituting this into Equation (21) results in
is upper triangle matrix. Substituting this into Equation (21) results in
 (22)
(22)
Updated/estimated vector at time 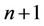 is
is
 (23)
(23)
where . Figure 5 illustrares MMSE error for
. Figure 5 illustrares MMSE error for  MIMO system. Note that the channel is considered approx. constant for OFDM symbol duration and First Symbol of each subframe is Preamble symbol (for more details about this section, see [13]).
MIMO system. Note that the channel is considered approx. constant for OFDM symbol duration and First Symbol of each subframe is Preamble symbol (for more details about this section, see [13]).
6. 3D Pilot Design
In this section the deployment specific correlations in time, frequency and space are exploited for the design of a bandwidth efficient three dimensional (3D) pilot grid. The associated channel estimation procedure is based on the principle of channel estimation by interpolation in three dimensions time, frequency and space. The complete description of this subject and the proposed method can be found in [14].
To facilitate coherent detection, reference symbols (pilots) known to the receiver are commonly used. For pilot aided channel estimation (PACE) pilots subsample the transmitted signal stream. If pilots are spaced sufficiently close to satisfy the sampling theorem, the channel response of the entire data sequence can be reconstructed by means of interpolation. Applied to OFDM, PACE is extended by scattered placement of pilots in time and frequency, giving rise to two dimensional (2D) channel estimation by interpolation. Due to its favorable trade-off between achieved channel estimation accuracy and required pilot overhead, 2D-PACE has been selected for a

Figure 5. MMSE error for 2 × 2 MIMO system [13].
wide range of wireless communication standards. Considering MIMO-OFDM, the principle of channel estimation by interpolation can be extended to the spatial domain, in case transmit antenna elements are spatially correlated, giving rise to three dimensional (3D) PACE.
3D PACE is an effective means to substantially improve bandwidth efficiency, as it overcomes the proportional increase of pilot overhead with the number of transmit antennas.
Unfortunately, 3D PACE strictly requires spatially correlated channels; when transmit antennas are mutually uncorrelated, interpolation in space is not possible. On a MIMO-OFDM downlink where the base station transmitter is mounted above rooftop, measurement campaigns suggest that the angles of departing rays are contained within a narrow angular spread. So that the assumption of spatially correlated transmit antennas is justified. In an indoor environment, however, spatial correlation tends to be low, so that 3D PACE may only improve the channel estimation accuracy, but cannot reduce the pilot overhead.
Typically, a robust pilot design needs to be dimensioned based on worst case channel conditions; in the context of 3D PACE this translates to worst case propagation delays, Doppler frequencies and angular spreads. However, in deployment scenarios where propagation delays and Doppler frequencies tend to be high, angular spreads are likely to be low, as observed in outdoor macro-cells. For local area deployments, such as indoor office environments, the opposite is true; spatial correlation is diminishing, while low mobility and small cell sizes result in substantially higher correlation in time and frequency. In this paper these reversal correlation properties, i.e. high spatial correlation occurs in conjunction with low time-frequency correlations and vice versa, are exploited by an appropriately dimensioned 3D pilot grid. If complemented by an adaptive, scenario dependent 3D channel estimation unit, a unified and bandwidth efficient 3D pilot design is established that fits diverse deployment scenarios. The basic structure of the proposed 3D pilot design is shown in Figure 6; adjacent pilots alternate between odd and even transmit antennas. In case the channel is spatially correlated, pilots located on odd transmit antennas are able support channel estimation on even antennas, and vice versa, which effectively allows for increased frequency selectivity and/or higher mobile velocities; or alternatively, for improved channel estimation accuracy. Otherwise, when spatial correlation diminishes, as typically encountered in local area scenarios, only pilots located at the same transmit antenna can be used for interpolation in the time-frequency plane. As in this case time and frequency correlations are high, reliable channel estimation is still feasible (for more

Figure 6. Three dimensional (3D) pilot grid for MIMOOFDM [14].
details about this section, see [14]).
7. Conclusion
In this paper, we have considered the training based channel estimation for MIMO-OFDM systems. It is seen that there is ample scope for performance improvement even in the presence of the channel mismatch error and the channel quantization error using superimposed training based channel estimation with quantized feedback. The simplified training pattern saves four OFDM periods to transmitting training blocks, and improves the efficiency of the system. We have discussed the design of the optimum pilot sequences using maximizing the channel mutual information. Simulation results show that QRRLS based channel estimation guarantees better estimation compared to standard-RLS based estimation. A bandwidth efficient 3D pilot design has been represented that reduces the necessary pilot overhead. As compared to the previously known methods, presented methods have more efficient.
REFERENCES
- J.-J. van de Beek, O. Edfors, M. Sandell, S. K. Wilson and P. O. Borjesson, “On Channel Estimation in OFDM Systems,” Vehicular Technology Conference, Chicago, 25-28 July 1995, pp. 815-819.
- G. J. Foschini and M. J. Gans, “On Limits of Wireless Communications in a Fading Environment When Using Multiple Antennas,” Wireless Personal Communications, Vol. 6, No. 3, 1998, pp. 311-335. doi:10.1023/A:1008889222784
- H. D. Taun, H. H. Kha, H. H. Nguyen and V.-J. Luong, “Optimized Training Sequences for Spatially Correlated MIMO-OFDM,” IEEE Transaction on Wireless Communications, Vol. 9, No. 9, 2010, pp. 2768-2778.
- K. Josiam and D. Rajan, “Bandwidth Efficient Channel Estimation Using Super-Imposed Pilots in OFDM Systems,” IEEE Transaction on Wireless Communications, Vol. 6, No. 6, 2007, pp. 2234-2245. doi:10.1109/TWC.2007.05787
- S. He, J. K. Tugnait and X. H. Meng, “On Superimposed Training for MIMO Channel Estimation and Symbol Detection,” IEEE Transactions on Signal Processing, Vol. 55, No. 56, 2007, pp. 3007-3021. doi:10.1109/TSP.2007.893941
- J. P. Nair and R. V. R. Kumar, “Improved Superimposed Training Based Channel Estimation for MIMO-OFDM Systems with Quantized Feedback,” International Conference on Signal Processing and Communications, Bangalore, 18-21 July 2010, pp. 1-5.
- Y. Gong and K. B. Letaief, “Low Complexity Channel Estimation for Space-Time Coded Wideband OFDM Systems,” IEEE Transaction on Wireless Communications, Vol. 2, No. 5, 2003, pp. 876-882. doi:10.1109/TWC.2003.816797
- W. Zhe, B. Fan and J. Zhanjun, “A Simplified Training Pattern for MIMO-OFDM Channel Estimation Technology,” International Conference on Computer Application and System Modeling, Taiyuan, Vol. 5, 2010, pp. 385- 388.
- Q. Huang, M. Ghogho and S. Freear, “Pilot Design for MIMO OFDM Systems with Virtual Carriers,” IEEE Transactions on Signal Processing, Vol. 57, No. 5, 2009, pp. 2024-2029. doi:10.1109/TSP.2008.2011824
- Y. Li and H. Minn, “Robust and Consistent Pilot Designs for Frequency Offset Estimation in MIMO OFDM Systems,” IEEE Transactions on Communications, Vol. 56, No. 10, 2008, pp. 1737-1747. doi:10.1109/TCOMM.2008.060522
- X. Geng, H. Hu, W. Cui and M. Wang, “Optimal Pilot Sequences for Correlated Fading Channels in MIMOOFDM System,” International Conference on Wireless Communications Networking and Mobile Computing, Chengdu, 23-25 September 2010, pp. 1-4.
- S. Haykin, A. H. Sayed, J. R. Zeidler, P. Yee and P. C. Wei, “Adaptive Tracking of Linear Time-Variant Systems by Extended RLS Algorithms,” IEEE Transactions on Signal Processing, Vol. 45, No. 5, 1997, pp. 1118- 1128. doi:10.1109/78.575687
- D. Rawal, P. Y. Ok and C. Vijaykumar, “A Novel Training Based QR-RLS Channel Estimator for MIMO OFDM Systems,” Conference on Wireless Advanced, London, 27-29 June 2010, pp. 1-4.
- G. Auer, “Bandwidth Efficient 3D Pilot Design for MIMOOFDM,” Wireless Conference (EW), Lucca, 12-15 April 2010, pp. 701-705. doi:10.1109/EW.2010.5483487

