Modern Mechanical Engineering
Vol.3 No.1(2013), Article ID:28261,3 pages DOI:10.4236/mme.2013.31008
Lever-Loading System Analysis and Application
Beijing Institute of Space Mechanics & Electricity, Beijing, China
Email: emptyzb@gmail.com
Received July 6, 2012; revised September 7, 2012; accepted September 21, 2012
Keywords: Component; Static Test; Lever; Loading Beams
ABSTRACT
In order to prove the rationality of structural design and carrying capacity, reasonable design of lever-loading system to apply loadings to some loading-points was needed in spacecraft structural mechanics static test. Lever-loading system design affects the carrying capacity of test piece. This paper describes the application of different section loading beams. Optimizing and analysis the different models of loading beams, and verification the feasibility of combination beams.
1. Introduction
Structural design is one of important contents of the overall design of the spacecraft [1]. Comprehensive design and analysis of structures is needed, based on the test load. Finally, through experiments to further optimize the structure of the original design and verify the reasonableness of design. Ensure the reliability of the spacecraft loading bearing structure. In spacecraft structural mechanics static test, loadings need to be assigned to some loading points on test piece. The widely used method is designed multistage lever-loading system to apply loadings. Design and implementation of leverloading system are as shown in Figure 1.
Structure static loading test check the carrying capacity of test piece. It requires loading system satisfies the loading conditions, and transfer loadings to the loading points, therefore, the design of lever-loading system are very important in static test [2]. The method of leverloading system has many advantages such as it can be applied simultaneously, synchronization, high installation precision, convenient installation and easy control. Lever-loading system composition by different lengths

Figure 1. Lever-loading system.
and loads loading beams based on actual working conditions. Commonly used loading beams such as rectangular beam is made by welding from single hot-rolled steel channel and web, I beam is welded by two hot-rolled steel channels and two webs, and special shaped beam is designed by the actual working conditions, as Figure 2.
2. Theoretical Basis of Mechanics
Lever-loading system is composed of loading beams which are regarded as the basic units of the lever-loading system. Mechanical analysis can be simplified as a concentrated force applied on the two-end simply supported beam. The loading position of concentrated force was determined by mechanical characteristics of lever. In multistage lever-loading system, the main deformation of member is plane bending, the effect of superposed deformation is performed on loading equipment stroke and loading precision. Simplified model of lever and concentrated force are shown in Figure 3 [3].
The length of lever based on test piece dimension and multistage lever-loading system, According to the test load, the stress analysis and strength check of lever section types and dimension is an important composition of lever design. According to the knowledge of material mechanics, under central concentrated load, the equation

Figure 2. Rectangular section and I beam section.
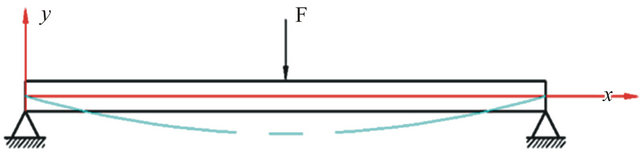
Figure 3. Simplified model of lever.
of simple beams’ deflection as follows [3]:
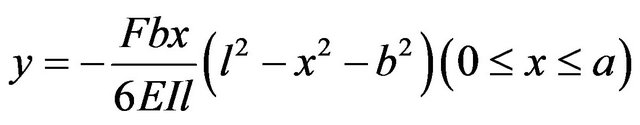 (1)
(1)
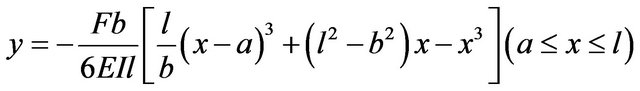 (2)
(2)
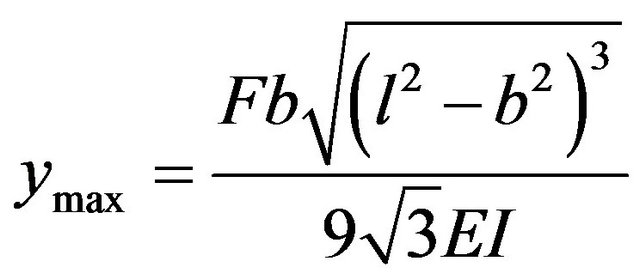 (3)
(3)
l is beam length, a is long side of beam length, b is short side of beam length. As can be seen from the equations, reduce the beam deflection need to increase the curved surfaces’ moment of inertia. The moment of inertia is proportional to section width and section height h2. Therefore, under the premise of stability and safety margin, compared with increase the section width, increase the section height h is more cost efficiency to reduce the deflection.
3. Design Case and Application Analysis of Heavy-Loading Beam
The design way of rectangular beam has advantage such as simple, light weight and can meet the requirement usually under the action of light loading. There are some problems about design of loading beam under heavy loading (as bearing of single lever over 1000 KN) such as overweight and installation difficulty.
A typical design case of lever: length 1400 mm, intermediate concentrated loading 700 KN.
The lever loaded through three points was designed based on simplified model as shown as Figure 3. The structure is welded by two No. 14a hot-rolled steel channels and two 12 mm thick, 160 mm wide webs, Cross section as Figure 2.
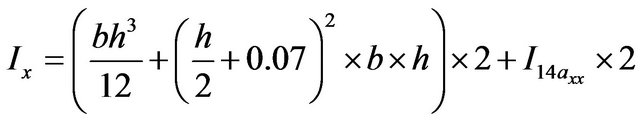 (4)
(4)
Result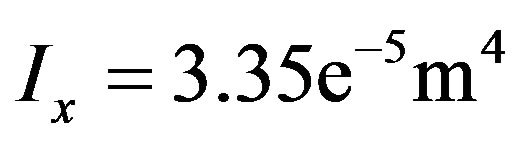 .
.
Finite element analysis results are as shown in Figure 4.
The weight of this lever is 85 kg, maximum deflection 5.7 mm. According to the results, this design of beam can meet the requirement. But in practical operation, the operational space for installers is limited, overweight of beams which brought difficulty to install lever-loading system and keep precision. Consider to optimize to reduce the lever’s weight on the basis of force analysis and real condition [4]. Using the combination beams composed of three points loading beam and four points loading beam, as Figure 5.
Programming the software compiled on MATLAB platforms to search best solution of combination beams loading method [5]. Three points loading beam length L1, deflection Y1, four points loading beam length L2 = 1400 mm, deflection Y2. Optimization constraints:
1)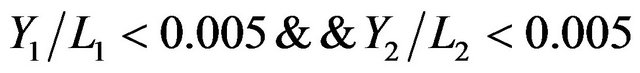 ;
;
2)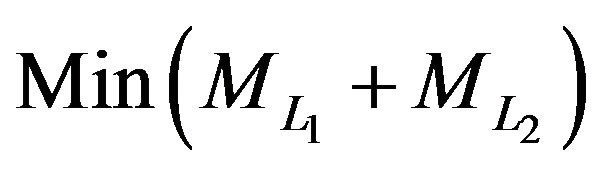 .
.
Solving result, 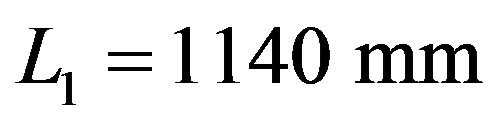 , No. 12.6 hot-rolled steel channel, weight about 50 kg.
, No. 12.6 hot-rolled steel channel, weight about 50 kg. , No. 10 hot-rolled steel channel, weight about 60 kg. Maximum deflection of two loading beams about 3 mm. Finite element analysis results are as shown in Figures 6 and 7.
, No. 10 hot-rolled steel channel, weight about 60 kg. Maximum deflection of two loading beams about 3 mm. Finite element analysis results are as shown in Figures 6 and 7.
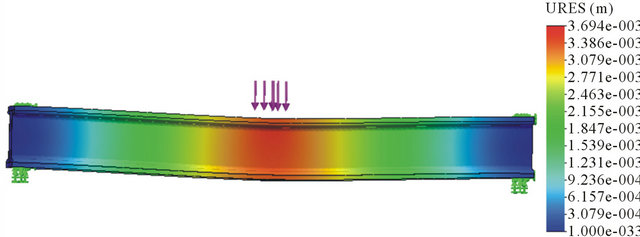
Figure 4. Finite element analysis results.

Figure 5. Combination beams loading method.
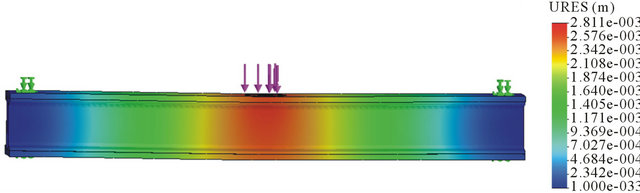
Figure 6. Three points loading beam finite element analysis results.

Figure 7. Four points loading beam finite element analysis results
Finite element analysis results and verification by experiment showed that, combination beams loading method reduce the single lever’s weight, improve the installability, safety factor and installation precision of leverloading system.
4. Summary
1) Multistage lever-loading system has many advantages as follows; can be applied simultaneously, synchronization, high installation precision, convenient installation and easy control, which was further verified by cite case and analysis results in this paper.
2) According to the literature data [6], section types of lever which satisfied strength of normal stress, rectangular beam’s carrying capacity is similar to I beam, and can meet the requirement usually under the action of light loading.
3) Overweight of beams which brought difficulty to installation under heavy loading (as bearing of single lever over 1000 KN). Combination beams loading method inherits the advantages of multistage lever-loading system, reduce the single lever’s weight, improve the installability, safety factor and installation precision of lever-loading system to some extent.
4) Additional loads of loading frock need to be counteracted in test load. Combination beams loading method provides the further optimization foundation for multipoint loading method.
REFERENCES
- Z. H. He, “Design of Preliminary Scheme on the Static Test of Fuselage Handing a New Object,” Northwestern Polytechnical University, Xi’an, 2007.
- G. G. Yang, W. G. Jiang, W. W. Wang and X. Zhao, “The Application of Helicopter Static-Test Load-CoefficientMethod in Calculate of Add Weight of Lever,” The 25th National Annual Meeting of Helicopter, Jiangxi, August 2009, pp. 500-504. (in Chinese)
- W. X. Gou, “Mechanics of Materials,” Science Press, Beijing, 2005.
- J. G. Sun, “Analysis and Experiment of Folding Girders,” Mechanics in Engineering, Vol. 26, No. 4, 2004, pp. 74- 76.
- G. H. Xu and B. P. Zhao, “Application of Uniform Designs in Aircraft Static Test,” Uniform Experimental Design Symposium, Beijing, August 2007, pp. 184-188. (in Chinese)
- J. H. Lin, “The Stress Analysis and Experiment on Three Section Beams,” Henan Sciences, Vol. 27, No. 3, 2009, pp. 343-345.

