ABSTRACT

Independent sets play an important role in matroid theory. In this paper, the definitions of pre-independent fuzzy set system and independent fuzzy set system in L-fuzzy setting are presented. Independent M-fuzzifying set system is introduced and some of its properties are discussed. Further independent (L,M)-fuzzy set system is given and some of its properties are obtained. The relations of these independent set systems in the setting of fuzzy vector spaces and fuzzy graphs are showed.

Keywords:

Pre-Independent L-Fuzzy Set System, Independent L-Fuzzy Set System, Independent M-Fuzzifying Set System, Independent (L,M)-Fuzzy Set System

1. Introduction

As a generalization of both graphs and matrices, matroids were introduced by Whitney in 1935. It plays an important role in mathematics, especially in applied mathematics. Matroids are precisely the structures for which the simple and efficient greedy algorithm works.

In 1988, the concept of fuzzy matroids was introduced by R. Goetschel and W. Voxman [1] . Subsequently Goetschel-Voxman fuzzy matroids were researched by many scholars (see [2] [3] [4] [5] , etc.). Recently, a new approach to fuzzification of matroids was introduced by Shi [6] , namely M-fuzzifying matroids. In the study an M-fuzzifying matroid was defined as a mapping satisfying three axioms. The approach to the fuzzification of matroids preserves many basic properties of crisp matroids, and an M-fuzzifying matroid and its fuzzy rank function are one-to-one corresponding. Further the concept of (L,M)-fuzzy matroid was presented by Shi [7] , it is a wider generalization of M-fuzzifying matroids.

Independent set systems play an important role in matroids theory. In this paper, firstly, the pre-independent fuzzy set system, independent fuzzy set system to L-fuzzy setting, independent M-fuzzifying set system, and independent (L,M)-fuzzy set system are presented. Secondly, the properties of these independent set systems are discussed. Finally, the relevance of these independent set systems in the setting of fuzzy vector spaces and fuzzy graphs are given.

2. Preliminaries

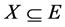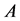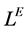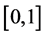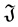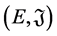Let E be a non-empty finite set. We denote the power set of E by and the cardinality of by for any. Let L be a lattice, an L -fuzzy set on E is a mapping, we denote the family of L -fuzzy sets by, -fuzzy sets are called fuzzy sets for short, denote. If is a non-empty subset of, then the pair is called a (crisp) set system. Use insteads of, where 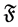is non-empty subsets of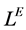, then the pairs 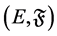is called an L-fuzzy set system, a -fuzzy set system is called a fuzzy set system for short.

A set system is called an independent set system if satisfies the following statement:

(H) and, if, then.

Use fuzzy sets on instead of crisp sets, Novak [4] obtained the definition of independent fuzzy set systems as follows.

Definition 2.1. Let be a finite set and be a fuzzy subset family on. If satisfies the following condition:

(FH) and, if, then,

then the pairs is called an independent fuzzy set system.

Throughout this paper, let be a finite set, both and denote completely distributive lattices. The smallest element and the largest element in are denoted by and, respectively. We often do not distinguish a crisp subset of and its characteristic function.

An element in is called a prime element if implies or. in is called co-prime if implies or [8] . The set of non-unit prime elements in is denoted by. The set of non-zero co-prime elements in is denoted by.

The binary relation. in is defined as follows: for, if and only if for every subset, the relation always implies the existence of with [9] . is called the greatest minimal family of in the sense of [10] , denoted by, and. Moreover, for, we define and. In a completely distri- butive lattice L, there exist and for each, and (see [10] ).

In [10] , Wang thought that and. In fact, it should be that and.

Definition 2.2 ( [7] ) Let and. Define

Some properties of these cut sets can be found in [7] [11] [12] .

Let and. We denote

Similarly, , we denote

Let and, define by

3. Independent L-Fuzzy Set Systems and Theirs Properties

There is not a method such that we immediately believe which way of fuzzification of a crisp structure is more natural than others. Nevertheless, it seems to be widely accepted that any fuzzifying structures have an analogous crisp structures as theirs levels. Consequently, an L-fuzzy set system is a pre-independent L-fuzzy set system if and only if is an independent set system for each, when, a pre-independent -fuzzy set system is an fuzzy pre-independent set system [4] . In this section, we introduce the concept of independent L-fuzzy set system and discuss theirs properties.

Definition 3.1. Let be a finite set. If a mapping satisfies the following condition:

(LH), , if, then

then the pair is called an independent L -fuzzy set system. An independent -fuzzy set system is precise a fuzzy independent set system [4] .

Theorem 3.2. Let be an independent L-fuzzy set system. Then is an independent set system for each.

For each, we show that is an independent set system as follows., , if, there is such that. Since sa- tisfies the condition (LH), then. We have since, this implies. Thus Therefore is an inde- pendent set system.

By Theorem 3.2, it is easy to obtain the following.

Corollary 3.3. Let be an independent L-fuzzy set system. Then be a pre-independent L-fuzzy set system.

Conversely, given a family of independent set systems, we can obtain an independent L-fuzzy set system.

Theorem 3.4. Let be a finite set and. If is an independent set system for each, we define

then is an independent L-fuzzy set system.

Proof. Since is an independent set system for each, we have. We show that satisfies the property (LH) as follows., , if, it means for each. Since, we have for each. Because satisfies the condition (H), then for each. Thus. Therefore is an independent L-fuzzy set system.

By Theorem 3.2, we get a family of independent set systems by an independent - fuzzy set system. Subsequently, Theorem 3.4 tells us the family of independent set systems can induce an independent L-fuzzy set system. In general, is not true.

In the following, we will prove when satisfies the condition (which will be given in Theorem 3.5), we have.

Theorem 3.5. Let be a finite set and be an independent L-fuzzy set system. We suppose that satisfies the statement:

(s), if for each, then

Define

then.

Proof. Obviously. We show that as follows., this implies for each. Since is an independent L-fuzzy set system, then for each. By the condition, then Thus

We call is strong if it satisfies the condition (LH) and , then the pair is called a strong independent L-fuzzy set system. Fuzzy matroids which are introduced by Goerschel and Voxman [1] are a subclass of strong independent L-fuzzy set systems.

For a strong independent L-fuzzy set system, we can obtain an equivalent description as follows.

Theorem 3.6. Let be an independent L-fuzzy set system. Then is strong if and only if, if for each, then

Proof. is an independent L-fuzzy set system. If is strong, , we suppose that for each, since is an independent L- fuzzy set system, we have for each. Thus. Conversely, , if for each, since, then.

In Theorem 3.6, when, the strong independent -fuzzy set systems are the perfect independent set systems which are defined by Novak [4] .

Lemma 3.7 ( [13] ). If is a finite L-fuzzy set and for, then there exists such that and

Theorem 3.8. Let be a finite set and be an independent L-fuzzy set system. For each, we have then is an independent set system.

Proof. For each, we show that is an independent set system as follows., , if, there is such that. By Lemma 3.7, there exists such that and Since satisfies the condition (LH), then. Hence

This implies. Thus Therefore is an in- dependent set system.

4. Independent M-Fuzzifying Set Systems

In crisp independent set system, we can regard as a mapping satisfies the property (H). Use fuzzy sets instead of crisp sets, Novak [4] presented an approach to the fuzzification of independent set systems, which is called fuzzy in- dependent set system. In fact, we may consider such a mapping satisfies some conditions.

Definition 4.1. Let be a finite set. A mapping satisfies and the following statement:

(MH), if, then

then the pair is called an independent M-fuzzifying set system. Specially, when an independent -fuzzifying set system is also called an independent fuzzifying set system for short.

Theorem 4.2. Let be a mapping. Then the following statements are equivalent:

(i) is an independent M-fuzzifying set system;

(ii) For each, is an independent set system;

(iii) For each, is an independent set system;

(iv) For each, is an independent set system;

(v) For each, is an independent set system;

(vi) For each, is an independent set system.

Proof. For each, , , if, it means. Since satisfies (MH), then. Thus, i.e. satisfies (H). Therefore is an independent set system.

, , let, then. Since satisfies (H), we have, it implies that. Thus is an independent M-fuzzifying set system on E.

For each, , , if, it means . Since satisfies (MH), then. Thus is an inde- pendent set system.

, , let, then for any . Since satisfies the condition (H), we have for any, it implies that for any. Then

For each, , , if, it means. We have since, it implies.

, , let, then for each we have. Since is an independent set system we have for each, i.e. for each. Then Therefore is an independent M-fuzzifying set system on.

We can similarly prove the remainder statements are also equivalent.

Corollary 4.3. Let be a mapping. Then the following statements are equivalent:

(i) is an independent M-fuzzifying set system;

(ii) For each, is an independent set system;

(iii) For each, is an independent set system.

Remark 4.4. In Proposition 2 of [4] , Novak has illuminated that when, a closed fuzzy independent set system is equivalent with an independent fuzzifying set system. M-fuzzifying matroids [13] are precise a subclass of the independent M- fuzzifying set system.

5. Independent (L,M)-Fuzzy Set Systems

In this section, we obtain the definition of independent M-fuzzifying set systems and discuss theirs properties.

Definition 5.1. Let be a finite set and L,M be lattices. A mapping satisfies the following statement:

(LMH), if, we have

then the pair is called an independent (L,M)-fuzzy set system.

Obviously, an independent (2,M)-fuzzy set system can be viewed as an independent M-fuzzifying set system, where. Moreover, an independent (L,2)-fuzzy set system is called an independent L-fuzzy set system. An crisp independent set system can be regarded as an independent (2,2)-fuzzy set system.

Theorem 5.2. Let be a finite set and be a mapping. Then the following statements are equivalent:

(i) is an independent (L,M) -fuzzy set system;

(ii) For each, is an independent L-fuzzy set system;

(iii) For each, is an independent L-fuzzy set system;

(iv) For each, is an independent L-fuzzy set system;

(v) For each, is an independent L-fuzzy set system.

The prove is trivial and omitted.

Corollary 5.3. Let be a finite set and be a mapping. Then the following conditions are equivalent:

(i) is an independent -fuzzy set system;

(ii), is an independent fuzzy set system;

(ii), is an independent fuzzy set system.

6. Some Examples of Independent (L,M)-Fuzzy Set Systems

Example 6.1. Let be a fuzzy graph, where. We define a mapping by

then the pair is an independent fuzzifying set system.

Obviously,., if, it is easy to obtain.

Example 6.2. Let be a fuzzy graph, where. We define a subfamily of by

then the pair is an independent fuzzy set system.

The prove is trivial and omitted.

Similarly, we can obtain easily the followings.

Example 6.3. Let be a fuzzy vector space. If is a subset of, we define a mapping by

then the pair is an independent fuzzifying set system.

Example 6.4. Let be a fuzzy vector space. If is a subset of, we define a subfamily of by

then the pair is an independent fuzzy set system.

7. Conclusion

In this paper, pre-independent fuzzy set system and independent fuzzy set system to L-fuzzy setting are defined. Independent M-fuzzifying set system is introduced and obtained its some properties. Further the definition of independent M-fuzzifying set system is generalized to independent (L,M)-fuzzy set system, and its some properties are proved. Finally, the relevance of generalized independent set systems are presented in the setting of fuzzy vector spaces and fuzzy graphs.

Funds

The project is supported by the Science & Technology Program of Beijing Municipal Commission of Education (KM201611417007, KM201511417012), the NNSF of China (11371002), the academic youth backbone project of Heilongjiang Education Department (1251G3036), and the foundation of Heilongjiang Province (A201209).

Cite this paper

Huang, C.-E., Liu, Z.L., Song, Y. and Wang, X.R. (2016) The Study on the (L,M)-Fuzzy Independent Set Systems. Advances in Pure Mathematics, 6, 1057-1064. http://dx.doi.org/10.4236/apm.2016.613078

References

NOTES

*Corresponding author.