ABSTRACT

The aim of this work is to study the existence of a periodic solution for some neutral partial functional differential equations. Our approach is based on the R-boundedness of linear operators L^p-multipliers and UMD-spaces.

Keywords:

Neutral Partial Functional Differential Equations, Periodic Solutions, R-Boundedness, L^p-Multipliers, UMD Spaces

1. Introduction

Motivated by the fact that neutral functional differential equations (abbreviated, NFDE) with finite delay arise in many areas of applied mathematics, this type of equations has received much attention in recent years. In particular, the problem of existence of periodic solutions has been considered by several authors. We refer the readers to papers [1] - [8] and the references listed therein for information on this subject.

In this work, we study the existence of periodic solutions for the following neutral partial functional differential equations of the following form

(1)

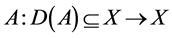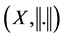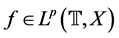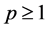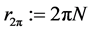where is a linear closed operator on Banach space and for all. For (some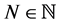) L and G are in is the space of all bounded linear operators and 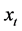is an element of 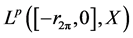which is defined as follows

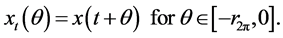
In [4] , Ezzinbi et al. established the existence of periodic solutions for the following partial functional differential equation:

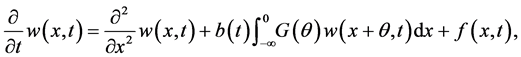
where 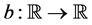is a continuous w-periodic function, 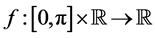is a con- tinuous function w-in t, periodic and G is a positive function.

In [1] , Arendt gave necessary and sufficient conditions for the existence of periodic solutions of the following evolution equation.

where A is a closed linear operator on an UMD-space Y.

In [2] , C. Lizama established results on the existence of periodic solutions of Equation (1) when 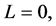namely, for the following partial functional differential equation

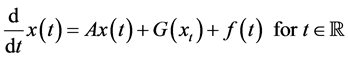
where 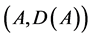is a linear operator on an UMD-space X.

In [3] , Hernan et al., studied the existence of periodic solution for the class of linear abstract neutral functional differential equation described in the following form:

where and are closed linear operator such that

and.

The organisation of this work is as follows: In Section 2, we present preliminary results on UMD spaces. In Section 3, we study the existence of periodic strong solution for Equation (1) with finite delay and we discuss the existence of mild solutions of Equation (1). In Section 4, we give the main abstract result [Theorem 4.1] of this work, and some important consequence when A generates a -semigroup [Theorem 4.2]. The last section is devoted to some examples.

2. UMD Spaces

Let X be a Banach space. Firstly, we denote By the group defined as the quotient. There is an identification between functions on and 2p-periodic func- tions on. We consider the interval as a model for.

Given, we denote by the space of 2p-periodic locally p-inte- grable functions from into X, with the norm:

For, we denote by, the k-th Fourier coefficient of f that is defined by:

Definition 2.1 Let and. Define the operator by: for all

if exists in Then, is called the Hilbert transform of f on.

Definition 2.2 [2]

A Banach space X is said to be UMD space if the Hilbert transform is bounded on for all.

Example 2.1 [9] 1) Any Hilbert space is an UMD space.

2) (0.1) are UMD spaces for every.

3) Any closed subspace of UMD space is an UMD space.

R-Bounded and L^p-Multipliers

Let X and Y be Banach spaces. Then denotes the space of bounded linear ope- rators from X to Y.

Definition 2.3 [1]

A family of operators is called R-bounded (Rademacher bounded or randomized bounded), if there is a constant and such that for each, and for all independent, symmetric, -va- lued random variables on a probability space the inequality

is valid. The smallest C is called R-bounded of and it is denoted by.

Lemma 2.1 ( [2] , Remark 2.2)

1) If is R-bounded then it is uniformly bounded, with

2) The definition of R-boundedness is independent of

Definition 2.4 [1] For, a sequence is said to be an -multiplier if for each, there exists such that

for all.

Proposition 2.1 ( [1] , Proposition 1.11) Let X be a Banach space and be an -multiplier, where. Then the set is R-bounded.

Theorem 2.1 (Marcinkiewicz operator-valud multiplier Theorem).

Let X, Y be UMD spaces and. If the sets and

are R-bounded, then is an -multiplier for.

Theorem 2.2 [2] Let. Then

in where

with.

Theorem 2.3 (Neumann Expansion) Let, where X is a Banach space.

If then is invertible, moreover

3. Periodic Solutions for Equation (1)

Lemma 3.1 Let. If and. Then

Proof. Let. Then by applying the Fourier transform, we obtain that

Integration by parts we obtain that

The proof is complete.

Lemma 3.2 [1] Let and. Then the following assertions are equivalent:

1) and there exists such that

2) for any.

Let

By a Lemma 3.2 we obtain that

():such that and there exists with

Definition 3.1 [2] . For, we say that a sequence is an -multiplier, if for each there exists such that

Lemma 3.3 [2] Let and (is the set of all boun- ded linear operators from X to X). Then the following assertions are equivalent:

1) is an -multiplier.

2) is an -multiplier.

3.1. Existence of Strong Solutions for Equation (2)

Let.

Then the Equation (1) is equivalent:

(2)

Denote by; and for all. We define

We begin by establishing our concept of strong solution for Equation (2).

Definition 3.2 Let. A function is said to be a 2p- periodic strong -solution of Equation (2) if for all and Equation (2) holds almost every where.

Lemma 3.4 Let be a bounded linear operateur. Then

Proof. Let. Then

Moreover

It follows

Since G is bounded, then

Then

Lemma 3.5 [1] Let X be a Banach space, independent, symmetric, -valued random variables on a probability space, and such that, for each. Then

Proposition 3.1 Let A be a closed linear operator defined on an UMD space X. Suppose that. Then the following assertions are equivalent:

1) is an -multiplier for

2) is R-bounded.

Proof. 1) Þ 2) As a consequence of Proposition 2.1

2) Þ 1) We claim first that the set is R-bounded. In fact, for we have:

Since

Then

By Lemma 3.4, we obtain that

We conclude that

.

Next define, where. By Theorem 2.1 it is su- fficient to prove that the set is R-bounded. Since

we have

Therefore

Since products and sums of R-bounded sequences is R-bounded [10. Remark 2.2]. Then the proof is complete.

Lemma 3.6 Let. Suppose that and that for every

there exists a 2p-periodic strong -solution x of Equation (2). Then, x is the unique 2p-periodic strong -solution.

Proof. Suppose that and two strong -solution of Equation (2) then

is a strong -solution of Equation (2) corresponding to. Taking Fourier transform in (2), we obtain that

Then

It follows that for every and therefore. Then.

Theorem 3.1 Let X be a Banach space. Suppose that for every there exists a unique strong solution of Equation (2) for. Then

1) for every the operator has bounded inverse

2) is R-bounded.

Before to give the proof of Theorem 3.1, we need the following Lemma.

Lemma 3.7 if for all, then is a 2p-periodic strong -solution of the following equation

Proof of Lemma 3.7.

Then

We have and

Proof of Theorem 3.1: 1) Let and. Then for, there exists such that:

Taking Fourier transform, G and D are bounded. We have

by Lemma 3.2 and Lemma 3.4 , we deduce that:

Consequently, we have

is surjective.

If, then by Lemma 3.7, is a 2p-periodic strong -solution of Equation (2) corresponing to the function Hence and then is injective.

2) Let. By hypothesis, there exists a unique such that the Equation (2) is valid. Taking Fourier transforms, we deduce that

Hence

Since then there exists such that

Then is an -multiplier and is R-bounded.

3.2. Periodic Mild Solutions of Equation (2) When A Generates a C₀-Semigroup

It is well known that in many important applications the operator A can be the infini- tesimal generator of -semigroup on the space X.

Definition 3.3 Assume that A generates a -semigroup on X. A func- tion x is called a mild solution of Equation (2) if:

Remark 3.1 ( [3] , Remark 4.2) Let be the -semigroup generated by A.

If is a continuous function, then and

Lemma 3.8 [3] Assume that A generates a -semigroup on X, if x is a mild solution then

Theorem 3.2 Assume that A generates a -semigroup on X and

. For some; if x is a mild solution of Equation (2). Then

Proof. Let x be a mild solution of Equation (2). Then by Lemma 3.8, we have

For, we have

Since:, then

which shows that the assertion holds for.

Now, define and by Lemma 3.1 We have:

Then

Corollary 3.1 Assume that A generates a -semigroup on X and let and x be a mild solution of Equation (2). If

has a bounded inverse. Then

Proof. From Theorem (3.2), we have that

Our main result in this work is to establish that the converse of Theorem 3.1 and Corollary 3.1 are true, provided X is an UMD space.

Theorem 3.3 Let X be an UMD space and be an closed linear operator. Then the following assertions are equivalent for.

1) for every there exists a unique 2p-periodic strong -solution of Equation (2).

2) and is R-bounded.

Lemma 3.9 [1] Let. If and for all Then

Proof of Theorem 3.3:

1) Þ 2) see Theorem 3.1

1) Ü 2) Let. Define.

By proposition 3.1, the family is an -multiplier it is equivalent to the family is an -multiplier that maps into, namely

there exists such that

(3)

In particular, and there exists such that

(4)

By Theorem 2.2, we have

Hence in, we obtain that

Since G is bounded, then

Using now (3) and (4) we have:

Since A is closed, then [Lemma 4.1] and from the uniqueness theorem of Fourier coefficients, that Equation (2) is valid.

Theorem 3.4 Let. Assume that A generates a -semigroup on X. If and is an -multiplier Then there exists a unique mild periodic solution of Equation (2).

Proof. For, we define

By Theorem 2.2 we can assert that as for the norm in.

We have is an -multiplier then there exists such that

let

Using again Theorem 2.2, we obtain that and is strong - solution of Equation (2) and verified

let. Then

(5)

For, we obtain that

From which we infer that the sequence is convergent to some element y as

. Moreover, y satisfies the following condition

let n go to infinity in (5), we can write

Then, we conclude that x is a 2p-periodic mild solution of Equation (2).

4. Applications

Example 5.1: Let A be a closed linear operator on a Hilbert space H and suppose that

and.

If then for every there exists a unique strong -

solution of Equation (2).

From the identity

it follows that is invertible whenever [Theo-

rem 2.3], we observe that.

Hence,

Then and by Theorem 2.3 we deduce that

Moreovery

and

We conclude that there exists a unique strong -solution of Equation (2). Using Corollary 3.8 in [2] .

Example 5.2:

Let A be a closed linear operator and X be a Hilbert space such that and. Suppose that. Then using Lemma 2.1

(1), we obtain that

From the identity it follows that is invertible whenever

Observe that.

Hence

Then and by Theorem 2.3, we have

Finaly

This proves that is R-bounded and by Theorem 3.3, we get that there exists a unique strong -solution of (2).

Acknowledgements

The authors would like to thank the referee for his remarks to improve the original version.

Cite this paper

Bahloul, R., Ezzinbi, K. and Sidki, O. (2016) Periodic Solutions in UMD Spaces for Some Neutral Partial Functional Differential Equations. Advances in Pure Mathematics, 6, 713-726. http://dx.doi.org/10.4236/apm.2016.610058

References