Advances in Pure Mathematics
Vol.4 No.6(2014), Article
ID:47281,7
pages
DOI:10.4236/apm.2014.46037
Existence and Uniqueness of Positive Solution for Third-Order Three-Point Boundary Value Problems
Tongchun Hu1, Yongping Sun2*
1Department of Public Teaching, Hangzhou Polytechnic, Hangzhou, China
2College of Electron and Information, Zhejiang University of Media and Communications, Hangzhou, China
Email: hutongchun888@126.com, sunyongping@126.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 March 2014; revised 14 April 2014; accepted 1 May 2014
ABSTRACT
This paper is devoted to the study of the existence and uniqueness of the positive solution for a type of the nonlinear third-order three-point boundary value problem. Our results are based on an iterative method and the Leray-Schauder fixed point theorem.
Keywords:Positive Solution, Uniqueness and Existence, Third-Order Three-Point BVPs

1. Introduction
In this paper, we consider the uniqueness and existence of the positive solution for the following third-order differential equation
 (1)
(1)
or
 (2)
(2)
with the following three-point boundary conditions
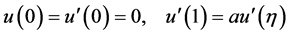 . (3)
. (3)
Throughout this paper, we assume that 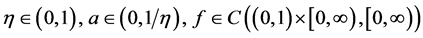 may be singular at
may be singular at ![]() and/or
and/or ![]() and
and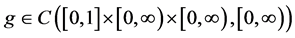 . Here, the solution
. Here, the solution 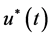 of the BVP (1)-(3) (or the BVP (2)-(3)) is called positive if
of the BVP (1)-(3) (or the BVP (2)-(3)) is called positive if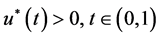 .
.
In the past few years, because of the extensive applications in mechanics and engineering, the existence of solutions or positive solutions for nonlinear singular or nonsingular three-point boundary value problems for third-order ordinary differential equations has been studied extensively in the literature (see [1] -[13] and references therein). For example, in the case of 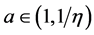 and
and 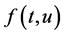 is nonsingular at
is nonsingular at ![]() and
and![]() , Guo et al. [1] [2] established some existence results of at least one and at least three positive solutions for the BVP (1)- (3) by using the well-known Krasnosel’skii fixed point theorem and the Leggett-Williams fixed point theorem, respectively. By using the upper and lower solutions and the maximum principle, Yao and Feng in [14] and Feng and Liu in [15] studied the existence of solutions for the BVP (1)-(3) and BVP (2)-(3) with
, Guo et al. [1] [2] established some existence results of at least one and at least three positive solutions for the BVP (1)- (3) by using the well-known Krasnosel’skii fixed point theorem and the Leggett-Williams fixed point theorem, respectively. By using the upper and lower solutions and the maximum principle, Yao and Feng in [14] and Feng and Liu in [15] studied the existence of solutions for the BVP (1)-(3) and BVP (2)-(3) with![]() , respectively.
, respectively.
Motivated mainly by the papers mentioned above, in this paper we will consider the uniqueness of the positive solution, the iteration and the rate of the convergence by the iteration for the nonlinear singular third-order three-point BVP (1)-(3). We study the existence of the positive solution for the nonlinear third-order three-point BVP (2)-(3) by using the Leray-Schauder fixed point theorem.
The rest of this paper is organized as follows. After this section, we present some notations and lemmas that will be used to prove our main results in Section 2. We discuss the uniqueness in Section 3. Finally, we discuss the existence in Section 4.
2. Preliminaries
In this section, we introduce definitions and preliminary facts which are used throughout this paper.
Definition 1 Let 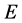 be a real Banach space. A nonempty closed convex set
be a real Banach space. A nonempty closed convex set 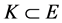 is called a cone of
is called a cone of 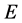 if it satisfies the following two conditions:
if it satisfies the following two conditions:
1) 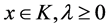 implies
implies![]() ;
;
2)  implies
implies![]() .
.
Definition 2 An operator is called completely continuous if it is continuous and maps bounded sets into precompact sets.
The following lemma plays a pivotal role in the forthcoming analysis.
Lemma 3 [9] Suppose that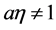 ,
, 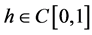 , then the unique solution of the following equation
, then the unique solution of the following equation
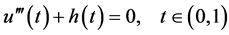 (4)
(4)
with boundary conditions (3) is given by
 (5)
(5)
where
 (6)
(6)
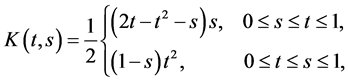 (7)
(7)
and
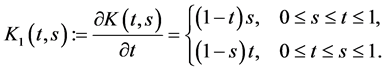
We need some properties of functions 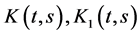 and
and 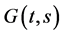 in order to establish the existence and uniqueness of positive solutions.
in order to establish the existence and uniqueness of positive solutions.
Lemma 4 For all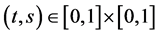 , we have
, we have

Proof The conclusion is obvious. The proof is completed.
Lemma 5 For all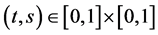 , we have
, we have
 (8)
(8)
Proof For all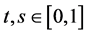 , if
, if![]() , it follows from (7) that
, it follows from (7) that

and
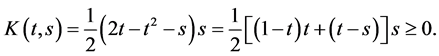
If![]() , then from (7) we have
, then from (7) we have
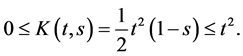
The proof is completed.
Lemma 6 The Green’s function 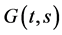 has the following properties:
has the following properties:
 (9)
(9)
 (10)
(10)
Proof After direct computations, we easily get
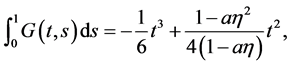 (11)
(11)
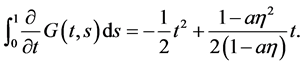 (12)
(12)
From (11) and (12) we can get (9) and (10) respectively. The proof is completed.
3. Uniqueness
We shall consider the Banach space  equipped with norm
equipped with norm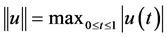 .
.
Theorem 7 Suppose that
(H1) 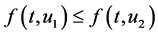 for any
for any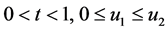 ;
;
(H2) There exist 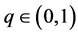 such that
such that
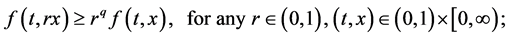
(H3) 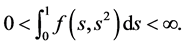
Then the BVP (1)-(3) has an unique positive, nondecreasing solution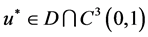 , here
, here
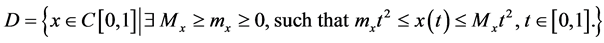 . (13)
. (13)
Constructing successively the sequence of functions
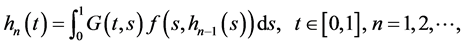 (14)
(14)
for any initial function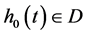 , then
, then  must converge to
must converge to  uniformly on [0, 1] and the rate of convergence is
uniformly on [0, 1] and the rate of convergence is
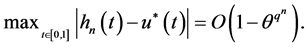 (15)
(15)
where![]() , which depends on the initial function
, which depends on the initial function .
.
Proof Obviously, from (H1) we obtain
 (16)
(16)
Let

In view of Lemma 3, we define an operator T as
 . (17)
. (17)
By (H1) it is easy to see that the operator 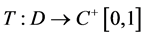 is increasing. Observe that the BVP (1)-(3) has a solution if and only if the operator T has a fixed point.
is increasing. Observe that the BVP (1)-(3) has a solution if and only if the operator T has a fixed point.
In what follows, we first prove ![]() In fact, for any
In fact, for any 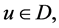 there exist positive numbers
there exist positive numbers 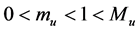 such that
such that

It follows from (H2) and (16) that
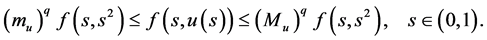 (18)
(18)
Using (17), (18), (8) and the condition (H1), we obtain
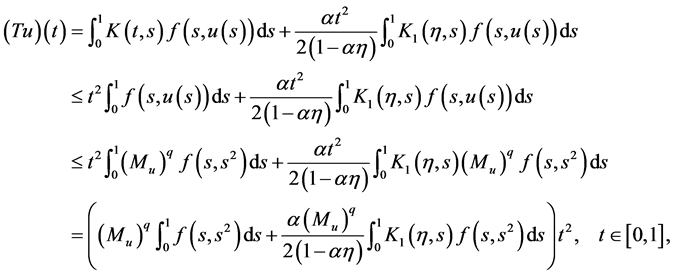 (19)
(19)
and
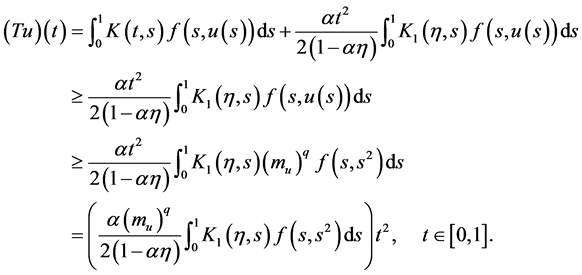 (20)
(20)
Equations (19), (20) and (H5) imply that![]() .
.
For any , we let
, we let
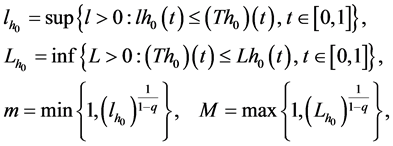 (21)
(21)
and
 (22)
(22)
Since the operator 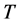 is increasing, (H1), (H2), (21) and (22) imply that
is increasing, (H1), (H2), (21) and (22) imply that
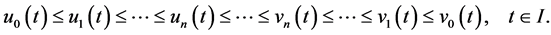 (23)
(23)
For , from (H1), (17) and (22), it can obtained by induction that
, from (H1), (17) and (22), it can obtained by induction that
 (24)
(24)
From (23) and (24) we know that
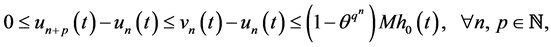 (25)
(25)
so that there exists a function  such that
such that
 (26)
(26)
and
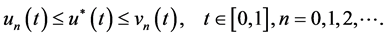 (27)
(27)
From (H1) and (22) we have
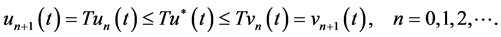
This together with (26) and uniqueness of the limit imply that u* satisfy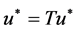 , thus
, thus  is a solution of the BVP (1)-(3).
is a solution of the BVP (1)-(3).
Form (22), (23) and (H1), we obtain
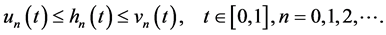 (28)
(28)
It follows from (26), (27) and (28) that
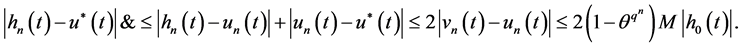
Therefore,

So that (15) holds. Since 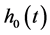 is arbitrary in D we know that
is arbitrary in D we know that 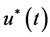 is the unique solution of the BVP (1)-(3) in D.
is the unique solution of the BVP (1)-(3) in D.
Remark If  is continuous on
is continuous on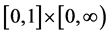 , then it is quite evident that the condition (H3) holds. Hence the unique solution
, then it is quite evident that the condition (H3) holds. Hence the unique solution 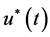 is in
is in .
.
4. Existence
Now we are ready to discuss the existence of positive solutions for the BVP (2)-(3).
Theorem 8 Suppose that
(H4) 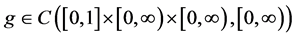 and
and 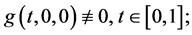
(H5) There exists positive number 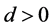 such that
such that
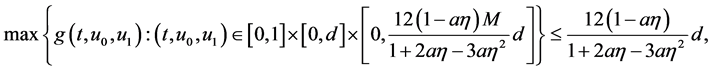 (29)
(29)
where M is defined by (11).
Then the BVP (2)-(3) has at least one positive solution 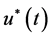 such that
such that
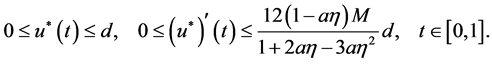 (30)
(30)
Proof We consider the Banach space  equipped with the norm
equipped with the norm
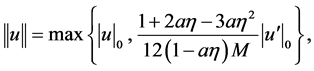 (31)
(31)
where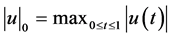 .
.
For![]() , define the operator S by
, define the operator S by
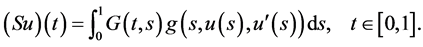 (32)
(32)
By Ascoli-Arzela Theorem, it is easy to known that the operator ![]() is a completely continuous operator. The BVP (2)-(3) has a solution
is a completely continuous operator. The BVP (2)-(3) has a solution 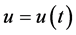 if and only if
if and only if  is a fixed point of operator S defined by (32).
is a fixed point of operator S defined by (32).
Let
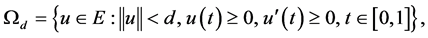
then 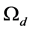 is a bounded closed convex set of E. We show that
is a bounded closed convex set of E. We show that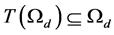 . For
. For , by (31) we have
, by (31) we have
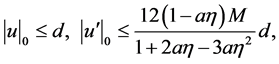
which implies that
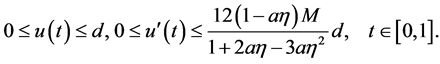
Therefore, by (9), (10), (29) and (32) we get
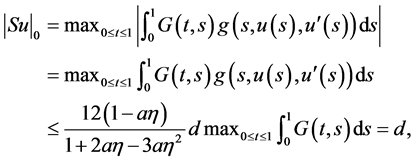 (33)
(33)
and
 (34)
(34)
Then (33) and (34) show that
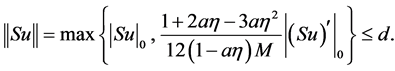
i.e.,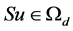 . Thus, by Leray-Schauder fixed point theorem, S has a fixed point
. Thus, by Leray-Schauder fixed point theorem, S has a fixed point , which implies that BVP (2)-(3) has at least one positive solution
, which implies that BVP (2)-(3) has at least one positive solution ![]() satisfying (30). This completes the proof.
satisfying (30). This completes the proof.
Acknowledgements
The authors thank the referee for her/his careful reading of the paper and useful suggestions. This work is supported by Hangzhou Polytechnic (KZYZ-2009-2) and the Natural Science Foundation of Zhejiang Province of China (LY12A01012).
References
- Guo, L., Sun, J. and Zhao, Y. (2007) Multiple Positive Solutions for Nonlinear Third-Order Three-Point Boundary-Value Problems. Electronic Journal of Differential Equations, 112, 1-7.
- Guo, L., Sun, J. and Zhao, Y. (2008) Existence of Positive Solution for Nonlinear Third-Order Three-Point Boundary Value Problem. Nonlinear Analysis, Theory, Methods and Applications, 68, 3151-3158.
- Anderson, D. (1998) Multiple Positive Solutions for a Three-Point Boundary Value Problem. Mathematical and Computer Modelling, 27, 49-57. http://dx.doi.org/10.1016/S0895-7177(98)00028-4
- Graef, J.R. and Yang, B. (2005) Multiple Positive Silutions to a Three Point Third Order Boundary Value Problem. Discrete and Continuous Dynmical Systems, 1-8.
- Palamides, P.K. and Palamides, A.P. (2008) A Third-Order 3-Point BVP. Applying Krasnosel’skii’s Theorem on the Plane without a Green’s Function. Electronic Journal of Differential Equations, 14, 1-15.
- Palamides, A.P. and Stavrakakis, N.M. (2010) Existence and Uniqueness of a Positive Solution for a Third-Order Three-Point Boundary-Value Problem. Electronic Journal of Differential Equations, 155, 1-12.
- Sun, J., Ren, Q. and Zhao, Y. (2010) The Upper and Lower Solution Method for Nonlinear Third-Order Three-Point Boundary Value Problem. Electronic Journal of Qualitative Theory of Differential Equations, 26, 1-8.
- Sun, Y. (2005) Positive Solutions of Singular Third-Order Three-Point Boundary Value Problems. Journal of Mathematical Analysis and Applications, 306, 589-603. http://dx.doi.org/10.1016/j.jmaa.2004.10.029
- Sun, Y. (2009) Positive Solutions for Third-Order Three-Point Nonhomogeneous Boundary Value Problems. Applied Mathematics Letters, 22, 45-51. http://dx.doi.org/10.1016/j.aml.2008.02.002
- Sun, Y. (2008) Existence of Triple Positive Solutions for a Third-Order Three-Point Boundary Value Problem. Journal of Computational and Applied Mathematics, 221, 194-201. http://dx.doi.org/10.1016/j.cam.2007.10.064
- Torres, F.J. (2013) Positive Solutions for a Third-Order Three-Point Boundary-Value Problem. Electronic Journal of Differential Equations, 147, 1-11.
- Yao, Q. (2009) Positive Solutions of Singular Third-Order Three-Point Boundary Value Problems. Journal of Mathematical Analysis and Applications, 354, 207-212. http://dx.doi.org/10.1016/j.jmaa.2008.12.057
- Zhang, X. and Liu, L. (2008) Nontrivial Solution of Third-Order Nonlinear Eigenvalue Problems (II). Applied Mathematics and Computation, 204, 508-512. http://dx.doi.org/10.1016/j.amc.2008.06.048
- Yao, Q. and Feng, Y. (2002) The Existence of Solutions for a Third Order Two-Point Boundary Value Problem. Applied Mathematics Letters, 15, 227-232. http://dx.doi.org/10.1016/S0893-9659(01)00122-7
- Feng, Y. and Liu, S. (2005) Solvability of a Third-Order Two-Point Boundary Value Problem. Applied Mathematics Letters, 18, 1034-1040. http://dx.doi.org/10.1016/j.aml.2004.04.016
NOTES

*Corresponding author.

