Advances in Pure Mathematics
Vol. 3 No. 5 (2013) , Article ID: 36305 , 9 pages DOI:10.4236/apm.2013.35070
The Mass-Critical for the Nonlinear Schrödinger Equation in d = 2
Department of Mathematics, Faculty of Education, Kassala University, Kassala, Sudan
Email: mujahid@mail.ustc.edu.cn
Copyright © 2013 Mujahid Abd Elmjed M-Ali. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 13, 2013; revised March 16, 2013; accepted April 19, 2013
Keywords: NLS; Well Posed
ABSTRACT
This paper studies the global behavior defocusing nonlinear Schrödinger equation in dimension d = 2, and we will discuss the case 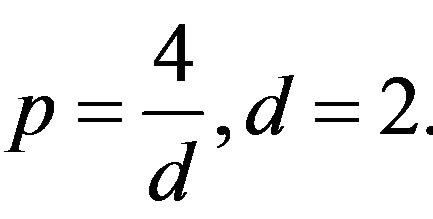 This means that the solutions
This means that the solutions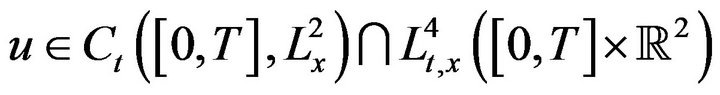 , and called critical solution. We show that u scatters forward and backward to a free solution and the solution is globally well posed.
, and called critical solution. We show that u scatters forward and backward to a free solution and the solution is globally well posed.
1. Introduction
We consider the Cauchy problem for the nonlinear Schrö- dinger equation in dimension d = 2.
 (1.1)
(1.1)
where ,
, 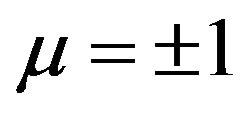 , and
, and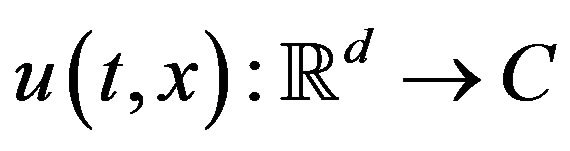 , When
, When  (1.1) is called defocusing when
(1.1) is called defocusing when 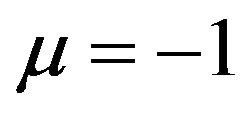 (1.1) is called focusing. In this paper we discuss the case when
(1.1) is called focusing. In this paper we discuss the case when 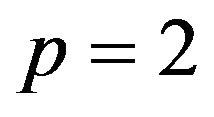 and
and 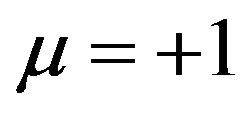 (defocusing case).
(defocusing case).
If 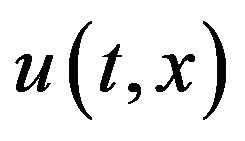 is a solution to (1.1) on a time interval
is a solution to (1.1) on a time interval  then
then
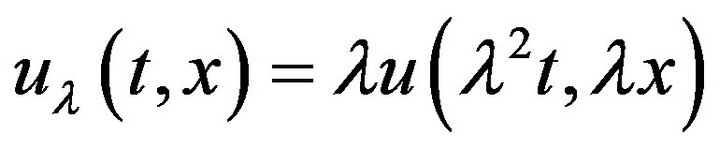 (1.2)
(1.2)
is a solution to (1.1) on 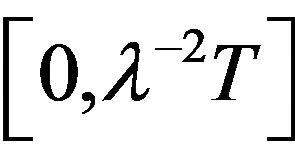 with
with .
.
This scaling saves the 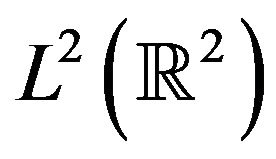 norm of u,
norm of u,
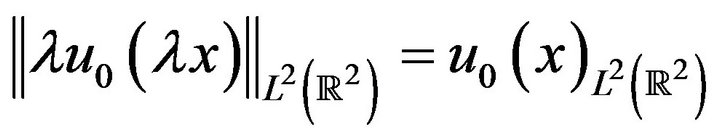 (1.3)
(1.3)
Thus (1.1) under previous hypotheses is called L2-critical or mass critical.
Proposition 1.1. Suppose that  and
and 
then, for any initial data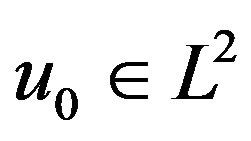 , there exist
, there exist  such that there exists a unique solution
such that there exists a unique solution

of the nonlinear Schrödinger Equation (1.1). If  then
then 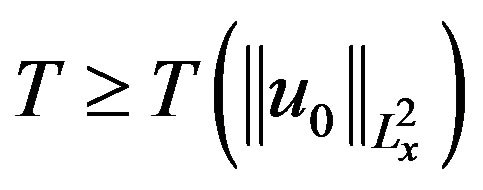 for some non-increasing, and if
for some non-increasing, and if 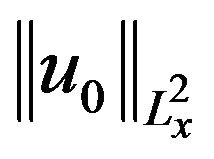 is sufficiently small u exists globally.
is sufficiently small u exists globally.
In this paper we will discuss the case, 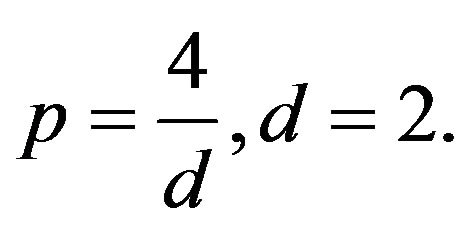
This means that a solution u
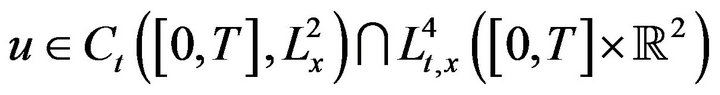 and called critical solution.
and called critical solution.
Definition 1.1. Let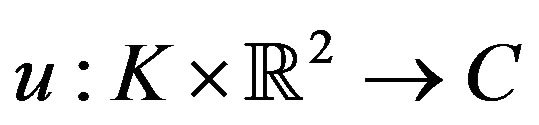 ,
,  is a solution to (1.1) if for any compact
is a solution to (1.1) if for any compact
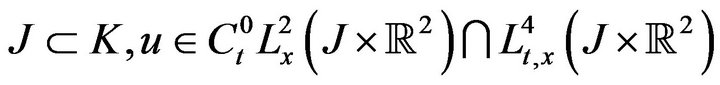
and for all 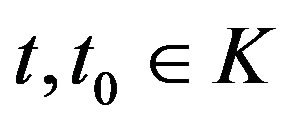
 (1.4)
(1.4)
The space 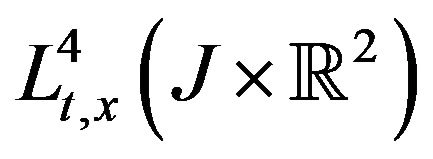 caused from strichartz estimates. This norm is invariant under the scaling (1.2).
caused from strichartz estimates. This norm is invariant under the scaling (1.2).
Definition 1.2. If there exist  a solution u to (1.1) defined on
a solution u to (1.1) defined on  blows up forward in time, such that
blows up forward in time, such that
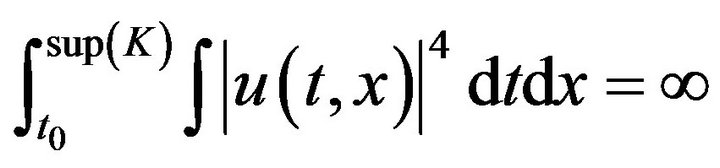 (1.5)
(1.5)
And u blows up backward in time, such that
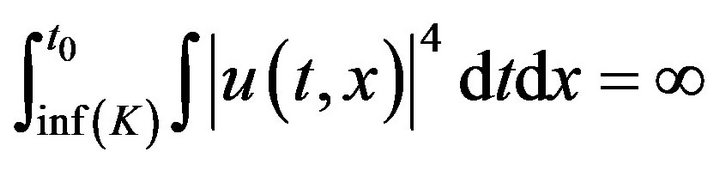 (1.6)
(1.6)
Definition 1.3. If there exist  we say that a solution u to (1.1) scatter forward in time such that,
we say that a solution u to (1.1) scatter forward in time such that,
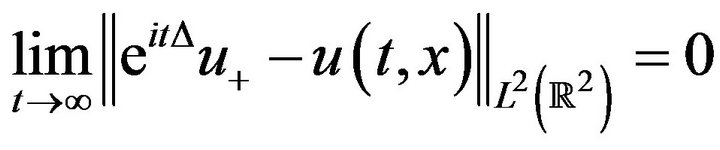 (1.7)
(1.7)
A solution is said to scatter backward in time if there exist 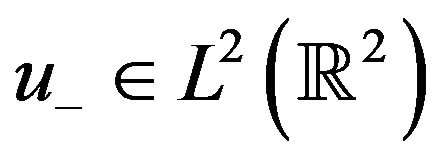
Such that,
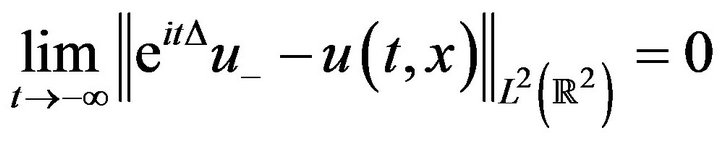 (1.8)
(1.8)
We note that the Equation (1.1) has preserved quantities, the mass
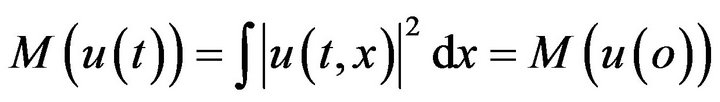 (1.9)
(1.9)
And energy
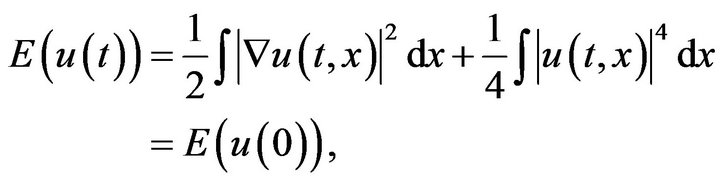 (1.10)
(1.10)
For more see [1].
Proposition 1.2. let p be the 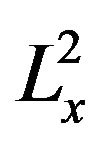 -critical exponent
-critical exponent
 , then the NLS (1.1) is locally well posed in
, then the NLS (1.1) is locally well posed in
 in the critical case. More precisely, given any
in the critical case. More precisely, given any , there exists
, there exists 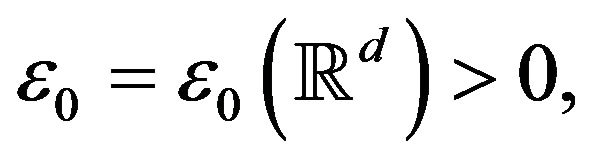 such that whenever
such that whenever 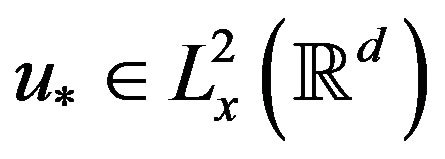 has norm at most R, and K is a time interval containing 0 such that
has norm at most R, and K is a time interval containing 0 such that

Then for any u0 in the ball

there exists a unique strong 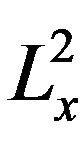 solution
solution 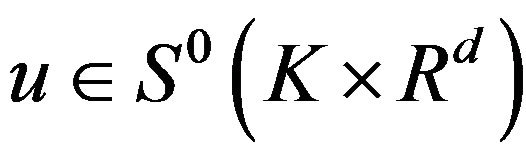 to (1.1), and moreover the map
to (1.1), and moreover the map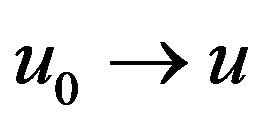 , is Lipschitz from B to
, is Lipschitz from B to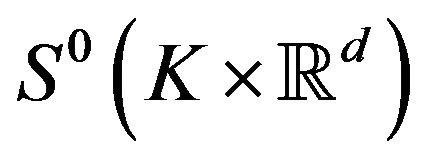 , where
, where 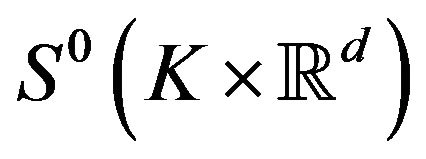 defined in Equation (2.5).
defined in Equation (2.5).
Proposition 1.3. let K be a time interval containing 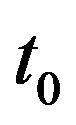 and let
and let  be two classical solutions to (1.1) with same initial datum u0 for some fixed μ and p, assume also that we have the temperate decay hypothesis
be two classical solutions to (1.1) with same initial datum u0 for some fixed μ and p, assume also that we have the temperate decay hypothesis 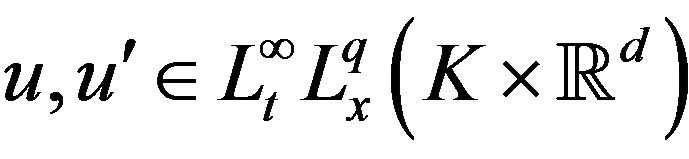 for q = 2, ∞. Then
for q = 2, ∞. Then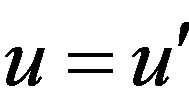 .
.
Proposition 1.4. Let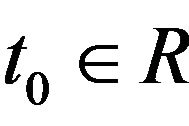 , given
, given 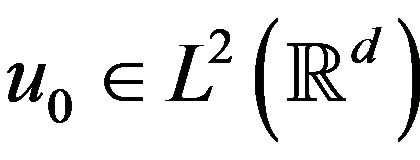 there exists a maximal lifespan solution u to (1.1) define on
there exists a maximal lifespan solution u to (1.1) define on , with
, with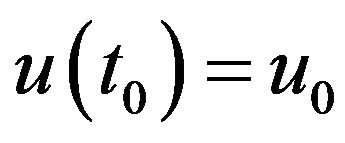 . Furthermore1) k is an open neighborhood of
. Furthermore1) k is an open neighborhood of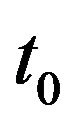 .
.
2) We say u is a blow up in the contrast direction If 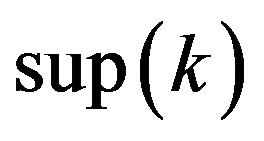 or
or  is finite.
is finite.
3) If we have compact time intervals for bounded sets of initial data, then the map that takes initial data to the corresponding solution is uniformly continuous in these intervals.
4) We say that u scatters forward to a free solution, if  and u does not blow up forward in time. And we say that u scatters backward to a free solution, if
and u does not blow up forward in time. And we say that u scatters backward to a free solution, if 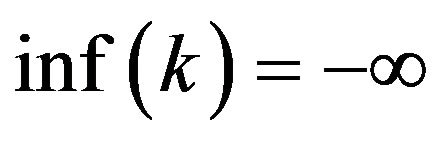 and u does not blow up backward in time.
and u does not blow up backward in time.
To Proof: see [1-3].
2. Strichartz Estimates
In this section we discuss some notation and Strichartz estimates for critical NLS (1.1) and we turn to prove Propositions 1.1 and 1.3.
2.1. Some Notation
If X, Y are nonnegative quantities, we use 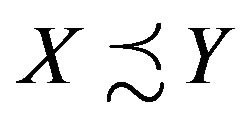 or
or , to denote the estimate
, to denote the estimate 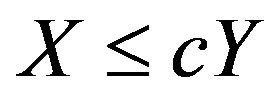 for some c and
for some c and  to denote the estimate
to denote the estimate 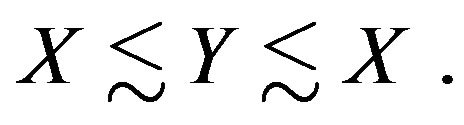
We defined the Fourier transform on  by
by
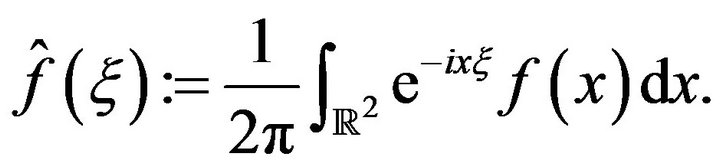
We use  to denote the Banach space for any space time slab
to denote the Banach space for any space time slab  of function
of function 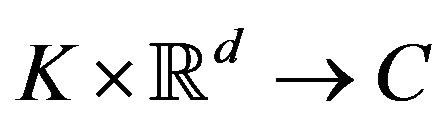 with norm is
with norm is
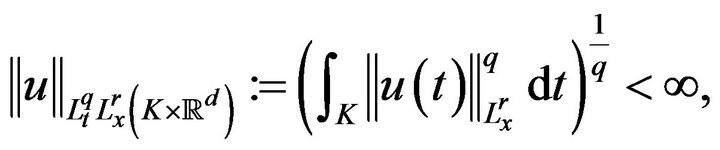
With the usual amendments when q or r is equal to infinity. When 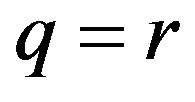 we cut short
we cut short  as
as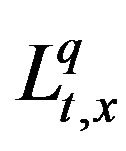 .
.
Defined the fractional differentiation operators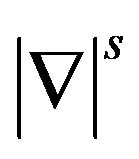 ,
, 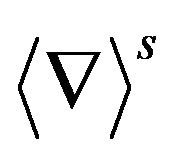 by
by
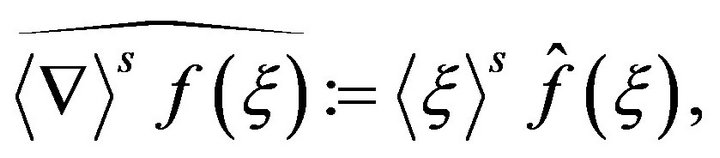
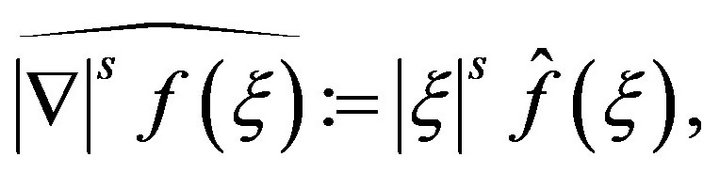
where , specially, we will use
, specially, we will use  to signify the spatial gradient
to signify the spatial gradient 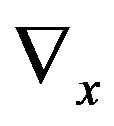 and define the Sobolev norms as
and define the Sobolev norms as
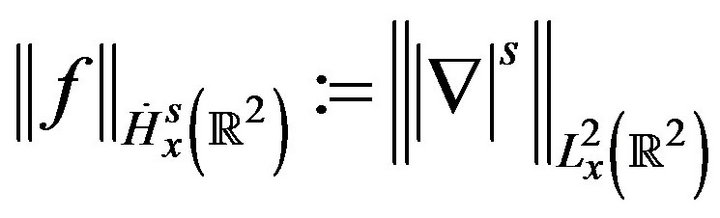
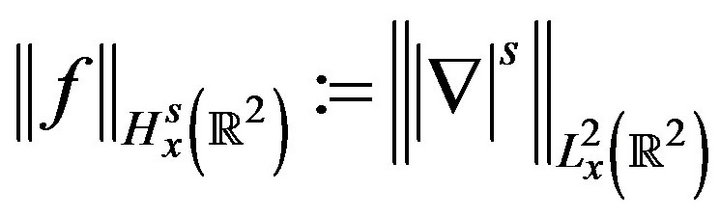
Let 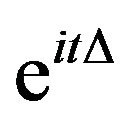 be the free Schrödinger propagator; in terms of the Fourier transform, this is given by,
be the free Schrödinger propagator; in terms of the Fourier transform, this is given by,
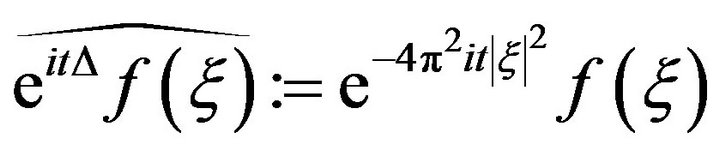 .
.
A Gagliardo-Nirenberg type inequality for Schrödinger equation the generator of the spurious conformal transformation 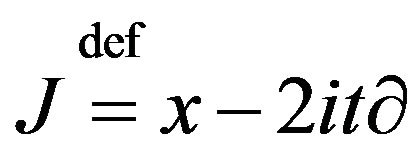 plays the role of the partial differentiation.
plays the role of the partial differentiation.
2.2. Strichartz Estimates
Let 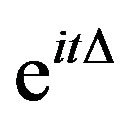 be the free Schrödinger evolution, from the explicit formula
be the free Schrödinger evolution, from the explicit formula
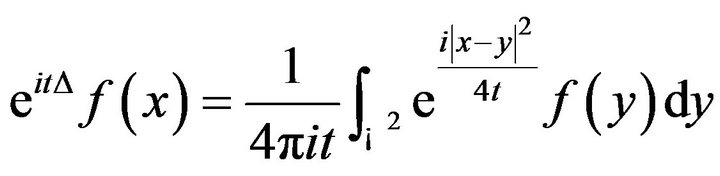 (2.1)
(2.1)
Specially, as the free propagator saves the 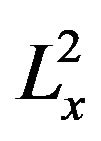 -norm,
-norm,
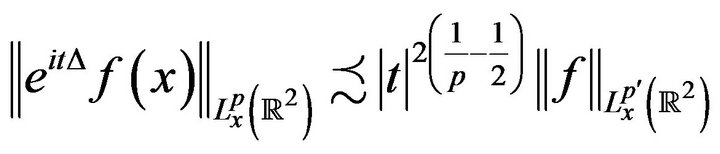
For all  and
and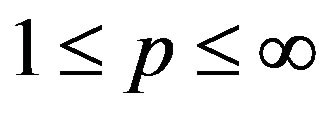 , where
, where 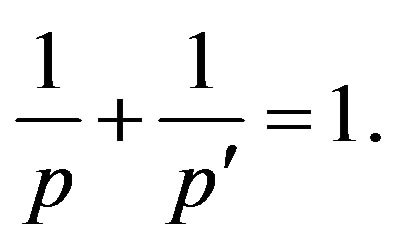
Proposition 2.1. There holds that
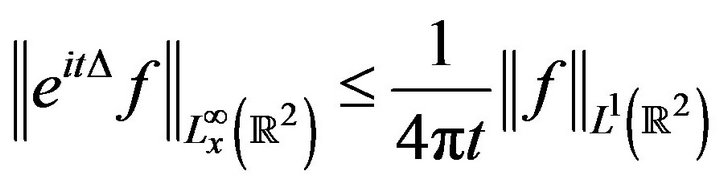 (2.2)
(2.2)
In fact, this follows directly from the formula (2.1).
Definition 2.1. Define an admissible pair to be pair
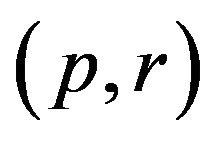 with
with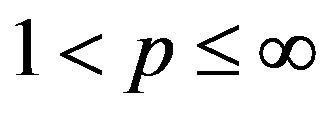 ,
, 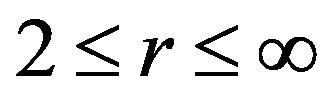 , With
, With 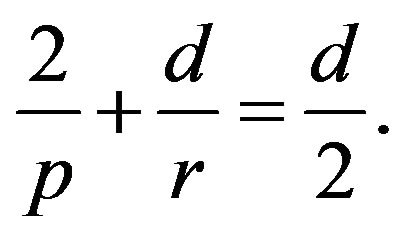
Theorem 2.2. If  solves the initial value problem
solves the initial value problem

 On an interval K, then
On an interval K, then
 (2.3)
(2.3)
For all admissible pairs ,
, .
.  denotes the Lebesgue dual
denotes the Lebesgue dual .
.
To prove: see [4,5].
Definition 2.2. Define the norm
 (2.4)
(2.4)
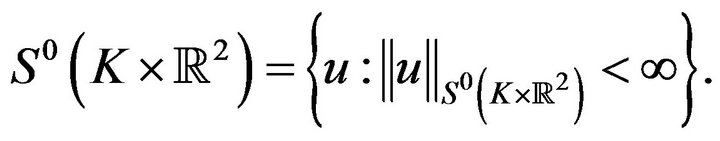 (2.5)
(2.5)
We also define the space 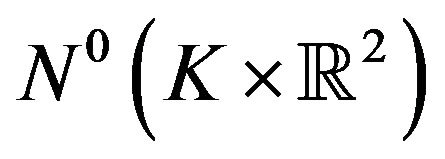 to be the space dual to
to be the space dual to  with suitable norm. By theorem.2.2,
with suitable norm. By theorem.2.2,
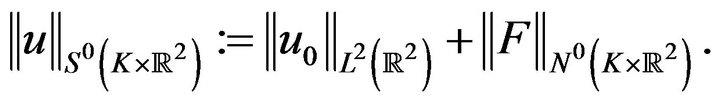 (2.6)
(2.6)
Theorem 2.3. If  is small, then (1.1) is globally well posed, for more see [6,7].
is small, then (1.1) is globally well posed, for more see [6,7].
Proof: by (2.3) and (2.6)
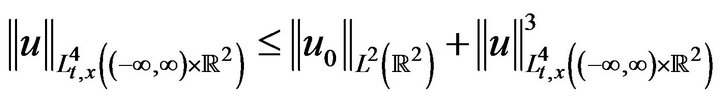 (2.7)
(2.7)
If 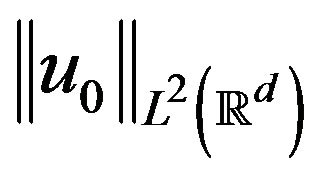 is small enough and by the continuity method, then we have global well-posedness. Furthermore, for any
is small enough and by the continuity method, then we have global well-posedness. Furthermore, for any 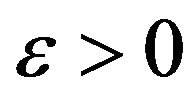 there exist
there exist 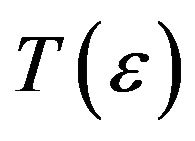 such that
such that

Then
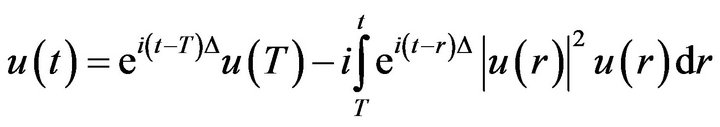 (2.8)
(2.8)
So by (2.6), when 
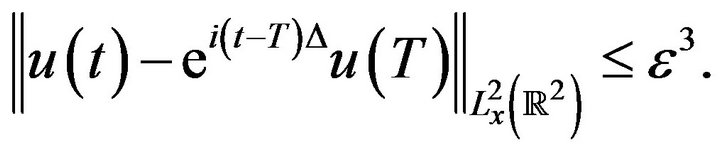 (2.9)
(2.9)
Thus, the limit
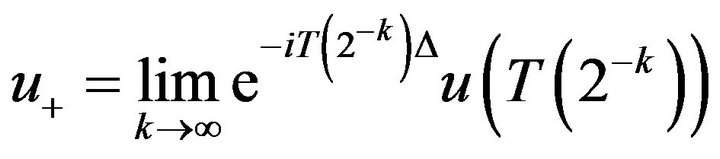 (2.10)
(2.10)
Exists, and,
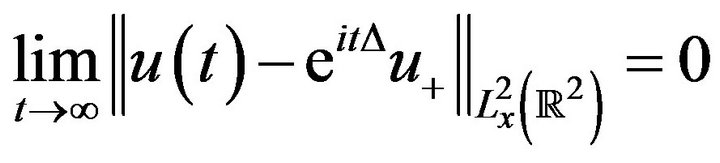 (2.11)
(2.11)
A conformable argument can be made for 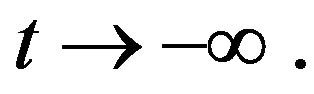
indeed, if , then
, then 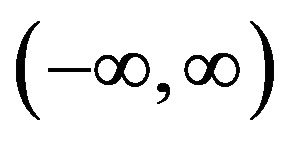 can be division into
can be division into  subintervals K with
subintervals K with 
on each subinterval. Using the Duhamel formula on each interval individually, we obtain global well-posedness and scattering. 
Now we return to prove Proposition 1.1 and Proposition 1.3.
Proof proposition 1.1:
We suppose in what follows that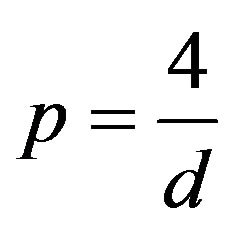 . Let
. Let
 and for some
and for some  to be chosen,
to be chosen,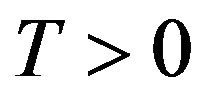 be such that
be such that
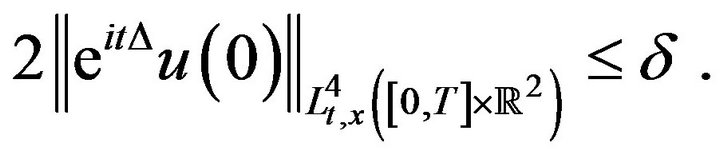 (2.12)
(2.12)
We deem the space

And the mapping,
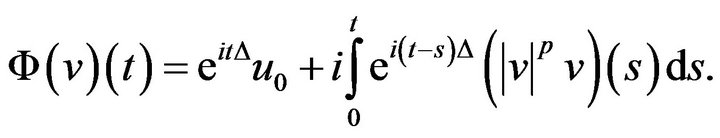 (2.13)
(2.13)
We want to prove that the δ small adequate, 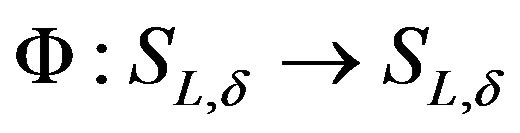 is contraction. We use first Strichartz estimates, to compute that
is contraction. We use first Strichartz estimates, to compute that
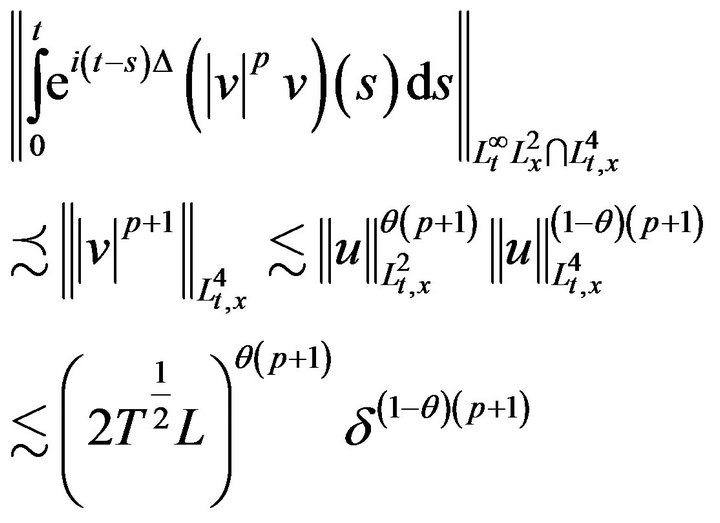
where 
Then, distinctly,
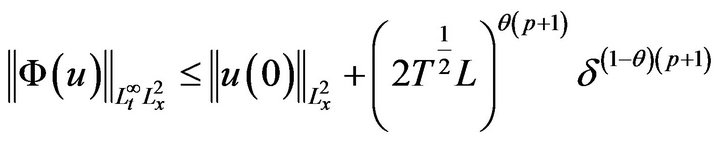
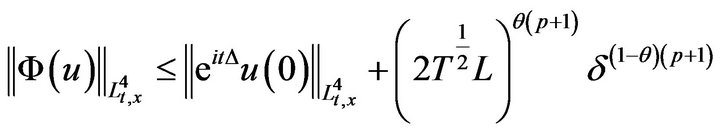
So that for 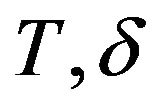 is small enough,
is small enough, 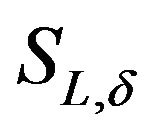 is settled under
is settled under . In addition,
. In addition,
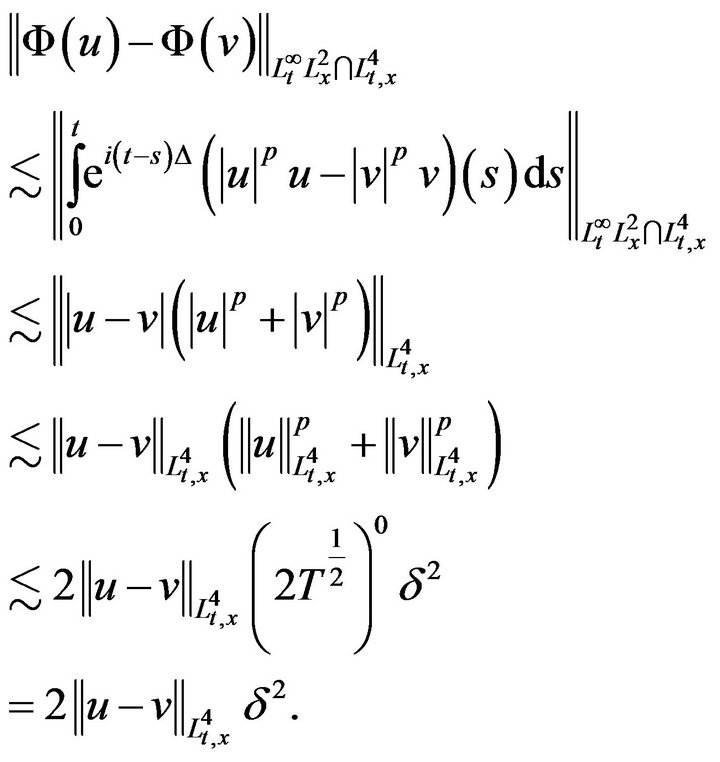
Again, decreasing may be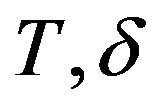 , we get a contraction.
, we get a contraction.
If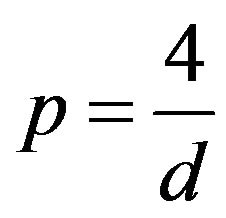 , then
, then , and from Strichartz estimateswe see that if
, and from Strichartz estimateswe see that if 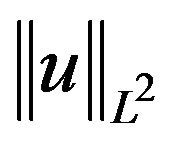 is small enough, then (2.12) is satisfied for
is small enough, then (2.12) is satisfied for 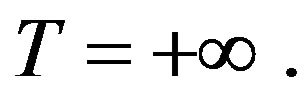

Proof Proposition 1.3: By time translation symmetry we can take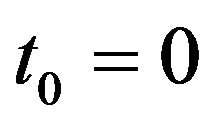 . By time reversal symmetry we may assume that K lies in the upper time axis
. By time reversal symmetry we may assume that K lies in the upper time axis . Let
. Let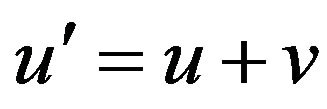 , and then,
, and then, 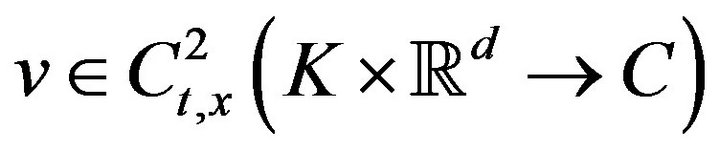 ,
,  and v obey the variance equation
and v obey the variance equation
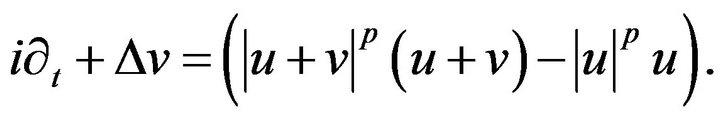
Since v and 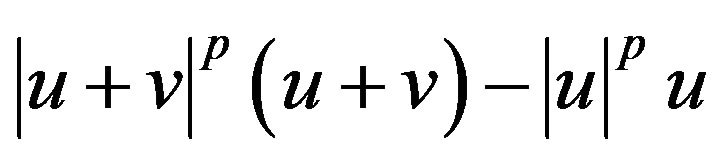 lies in the
lies in the  we may calling Duhamel’s and conclude
we may calling Duhamel’s and conclude
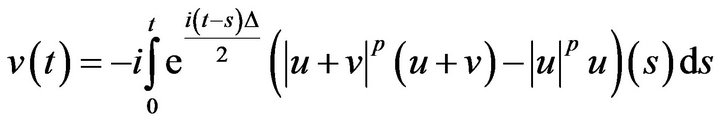
for all. By Minkowski’s inequality, and the unitarity of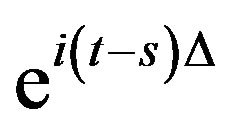 , conclude that,
, conclude that,
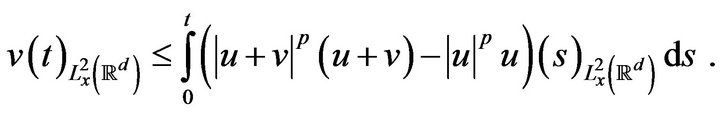
Since u and v are in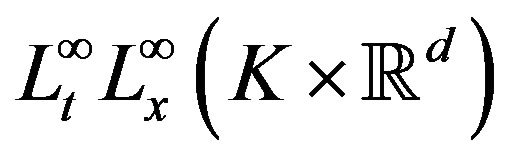 , and the function
, and the function  is locally Lipcshitz, we have the bound
is locally Lipcshitz, we have the bound

Apply Gronwall’s inequality to conclude that
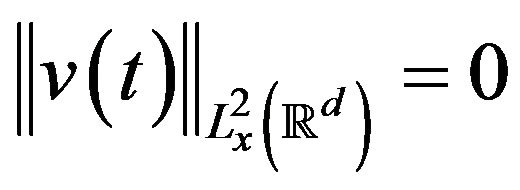 for all
for all  and hence
and hence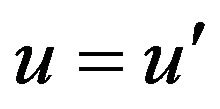 .
. 
3. Decay Estimates
Consider the defocusing nonlinear Schrödinger Equation (1.1), in , where
, where  and
and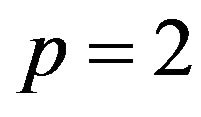 , for
, for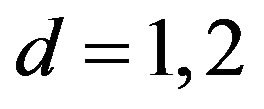 . We suppose that at
. We suppose that at 
 (3.1)
(3.1)
First we have the following result.
Theorem 3.1. Suppose that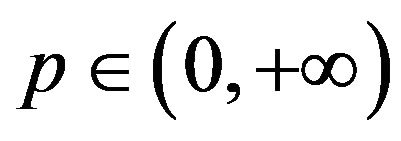 , if
, if 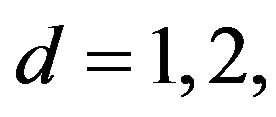 and let u be a solution to (1.1), identical to an initial data
and let u be a solution to (1.1), identical to an initial data
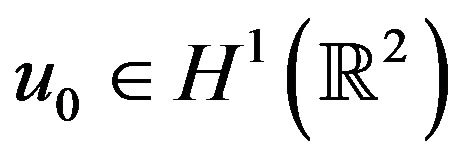 such that
such that . If d = 2let r be such that,
. If d = 2let r be such that,  , then there exists a constant c > 0 such that if R is the solution of,
, then there exists a constant c > 0 such that if R is the solution of,  , with
, with
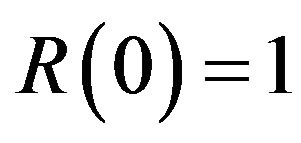
 ,
, 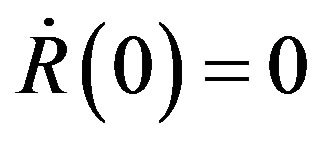 then
then
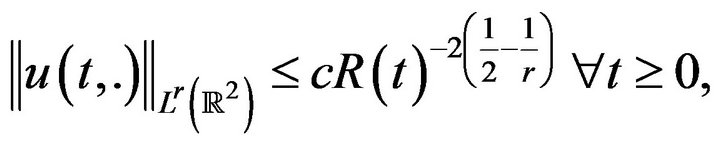
Furthermore, c depends only on d, p, r and,
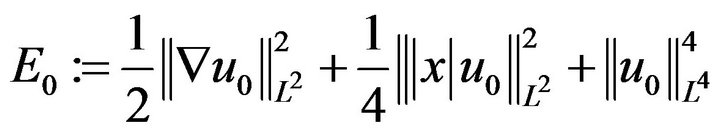 .
.
The method made up in rescheduling, by the average of a time dependent rescheduling the equation, and to use the energy of the equation, to get by interpolation decay estimates in suitable norms. The asymptotically average, is normally obtained directly by using the pseudo conformal law, the above result was in fact partially proved in [8], under a bit different point of view: look for a time dependent change of coordinates, which maintain the Galilean invariance, and the construction directly a Lyapunov functional by a suitable ansatz. This Lyapunov functional is surely the energy of the rescaled equation. Our aim here is to study with further details the rescaled wave function and its energy. Found to be the method provides rates which are seems completely new in the limiting case of the logarithmic nonlinear Schrödinger equation. Because of the reversibility of the Schrödinger equation and standard results of scattering theory, one cannot foresee the convergence of the rescaled wave function to some a intuition given limiting wave function, but found to be some convexity properties of the energy can be used to state an asymptotically stabilization result. From the general theory of Schrödinger equations, it is well known that the Cauchy problems (1.1)-(3.1) is well posed for any initial data in 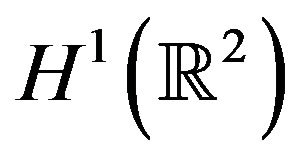 when
when , and that the solution u belongs to
, and that the solution u belongs to
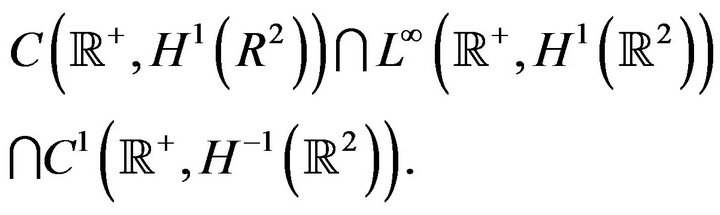
As usual for Schrödinger equations is critical when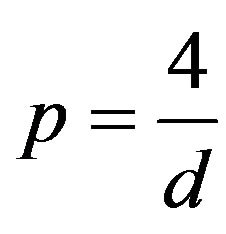 .
.
Let 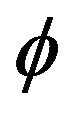 be such that
be such that
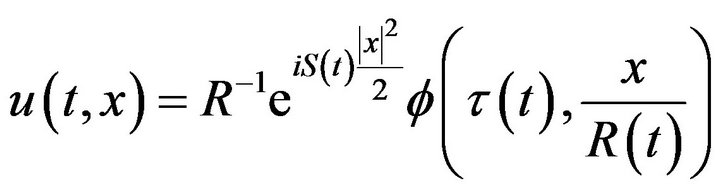 .
.
where and 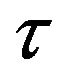 are positive derivable real functions of the time.
are positive derivable real functions of the time.
It is simple to check that with this change of coordinates, 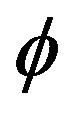 satisfies the following equation,
satisfies the following equation,
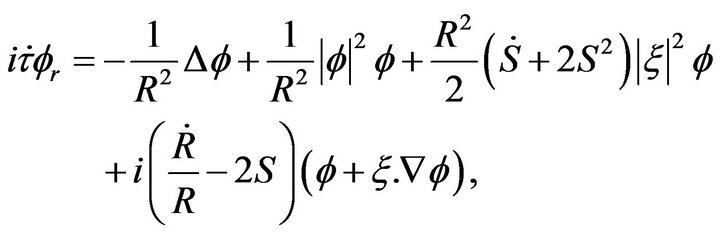
where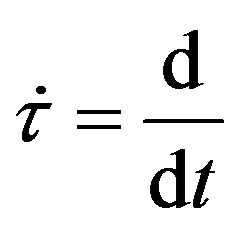 , with the choice
, with the choice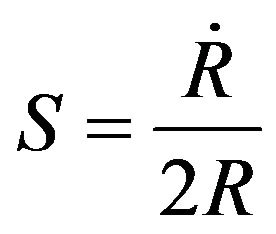 , which means that
, which means that 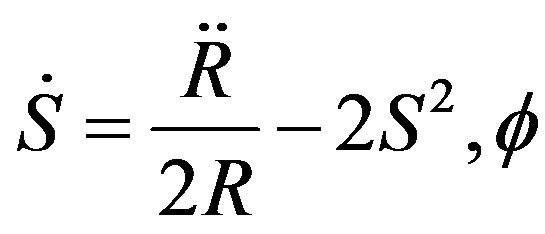 and u are linked by,
and u are linked by,
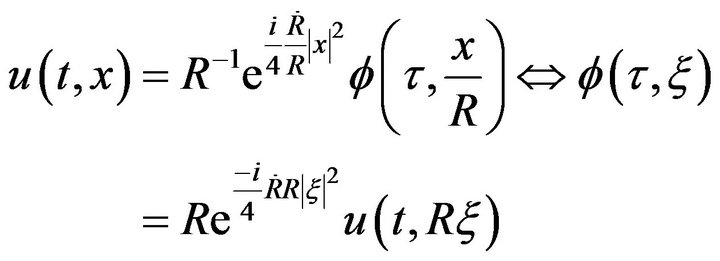 (3.2)
(3.2)
where 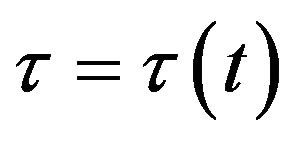 and
and  and
and 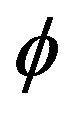 has to satisfy the following time-dependent defocusing nonlinear Schrö- dinger equation,
has to satisfy the following time-dependent defocusing nonlinear Schrö- dinger equation,
 (3.3)
(3.3)
We note that  so that
so that

for all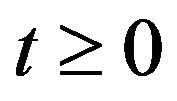 .
.
Also we note that if 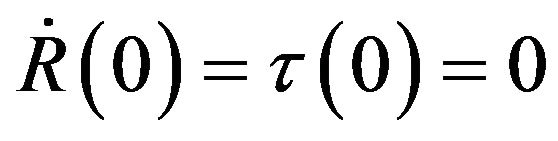 and
and  then
then
 (3.4)
(3.4)
To extract the controlling impacts as  we fix
we fix 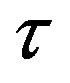 and R such that,
and R such that,
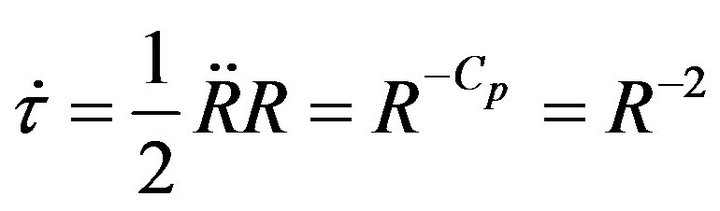
where
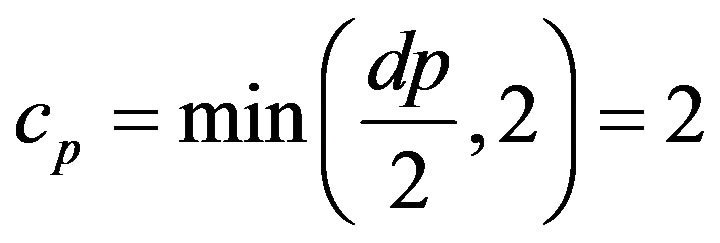 (3.5)
(3.5)
Because p is critical, this ansatz is actually the only one that sets to 1 at least three of the four coefficients in the equation for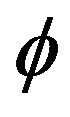 , with
, with  and
and  solves the equation,
solves the equation,
 (3.6)
(3.6)
With the choice 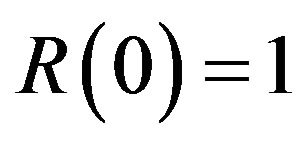 and
and , integration of (3.5) with respect to t gives
, integration of (3.5) with respect to t gives  and this is possible if, and only if,
and this is possible if, and only if,  for all
for all  thus the function
thus the function 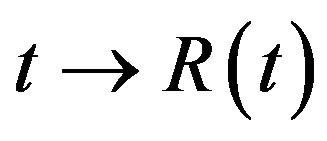 is globally defined on
is globally defined on 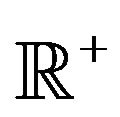 increasing,
increasing, 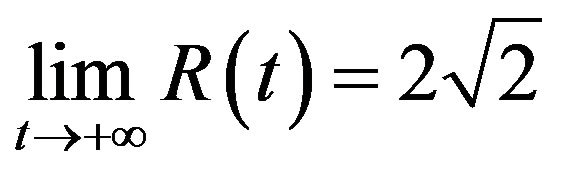 and
and  as
as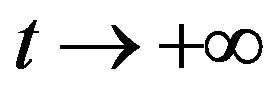 .
.
Supposing that ,
, 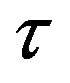 is an increasing positive function such that,
is an increasing positive function such that, 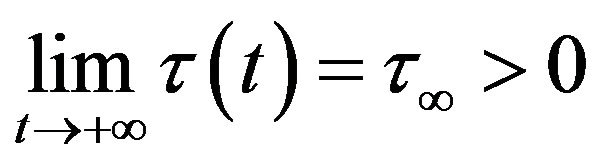 , where
, where 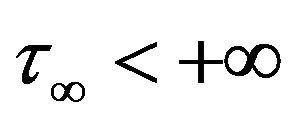 if
if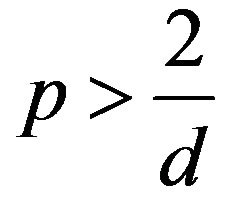 .
.
Consider now the energy functional linked to Equation (3.6)
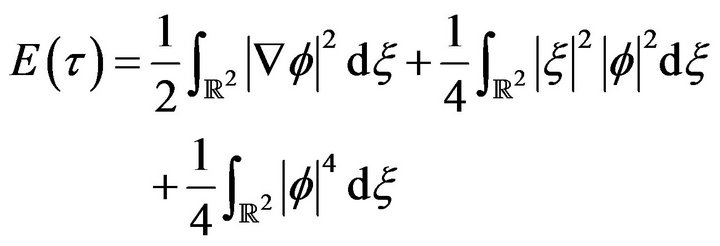 (3.7)
(3.7)
where R has to be understood as a function of.
Lemma 3.2. Suppose that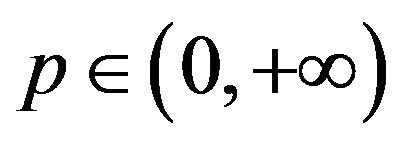 , if
, if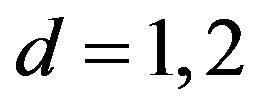 , and let u be a solution to (1.1), identical to an initial data,
, and let u be a solution to (1.1), identical to an initial data,
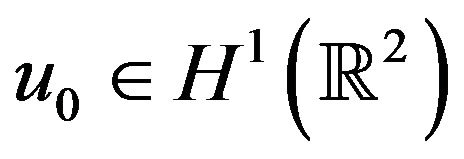 such that
such that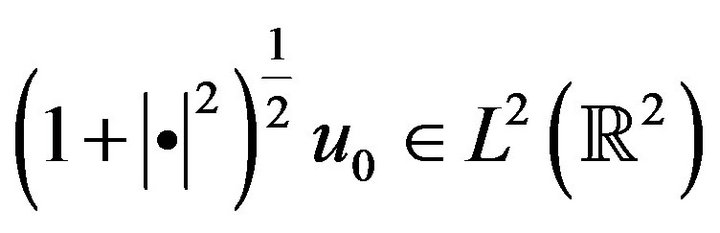 .
.
With the above notations, E is a decreasing positive functional. Thus 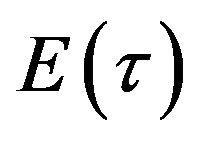 is bounded by
is bounded by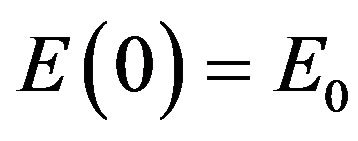 , with the notations of Theorem 3.1.
, with the notations of Theorem 3.1.
Proof: The proof follows by a direct computation.
Because of (3.6), only the coefficients of , and
, and  contribute to the decay of the energy.
contribute to the decay of the energy.
For more see [9]. 
Proof of Theorem 3.1: Suppose that p is critical. By Lemma 3.2 and pursuant to the time-dependent rescaling (3.2),
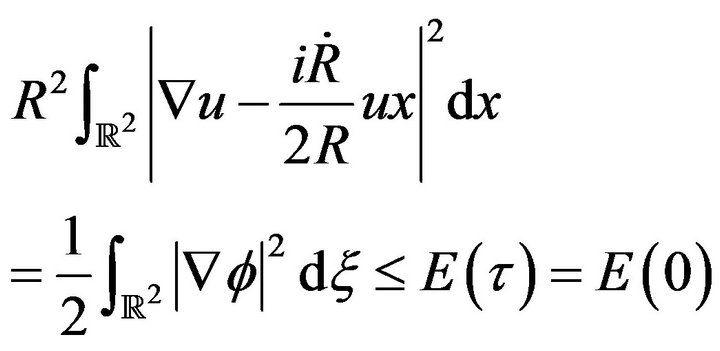
Thus
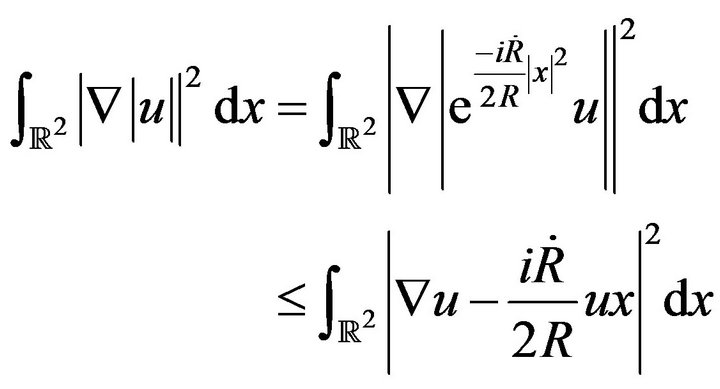
Is bounded by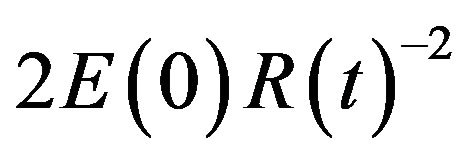 , the remainder of the proof follows the same lines that in Theorem 7.2.1 of [10], see also [11,12], using maintain the L2-norm and the Sobolev-Gagliardo-Nirenberg inequality.
, the remainder of the proof follows the same lines that in Theorem 7.2.1 of [10], see also [11,12], using maintain the L2-norm and the Sobolev-Gagliardo-Nirenberg inequality. 
Proposition 3.3. Consider the two-dimensional defocusing cubic NLS (1.1), (is 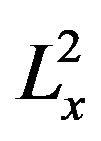 -critical). Let
-critical). Let  then there exists a global
then there exists a global 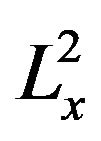 -well posed solution to (1.1), and moreover the
-well posed solution to (1.1), and moreover the 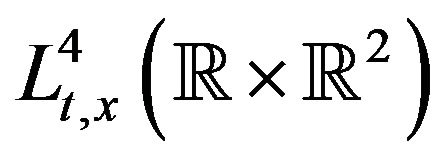 norm of u0 is finite.
norm of u0 is finite.
Proof: By time reflection symmetry and adhesion arguments we may heed attention to the time interval 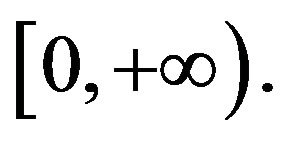 Since u0 lies in
Since u0 lies in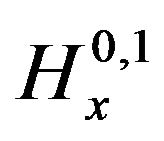 , it lies in
, it lies in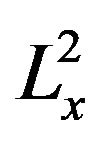 . Apply the
. Apply the 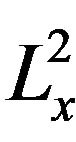 well posedness theory (Proposition 1.2) we can find an
well posedness theory (Proposition 1.2) we can find an  -well posed solution
-well posed solution , on some time interval
, on some time interval 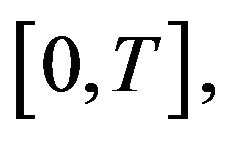 with
with 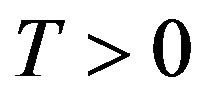 depending on the profile of u0.
depending on the profile of u0.
Specially the 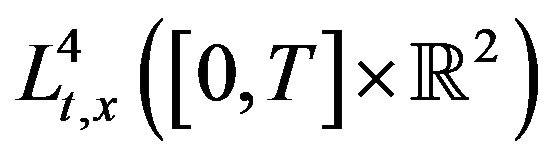 norm of u is finite. Next we apply the pseudoconformal law to deduce that,
norm of u is finite. Next we apply the pseudoconformal law to deduce that,

Since , we got a solution from t = 0 to t = T. To go to all the way to
, we got a solution from t = 0 to t = T. To go to all the way to . We apply the pseudoconformal transformation at time t = T, obtaining an initial datum
. We apply the pseudoconformal transformation at time t = T, obtaining an initial datum  at time
at time 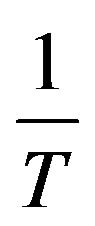 by the formula
by the formula
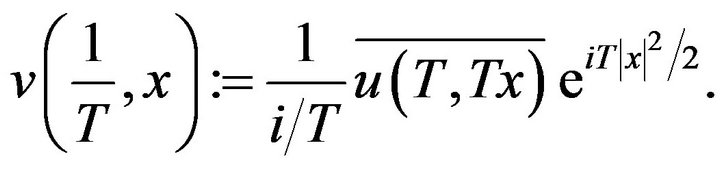
From 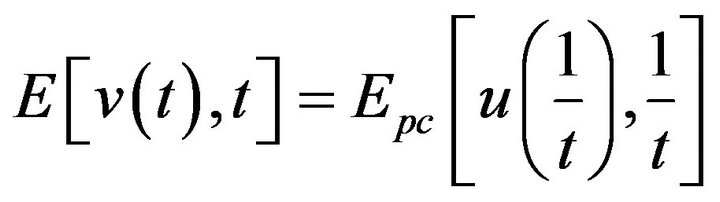 we see that v has finite energy:
we see that v has finite energy:
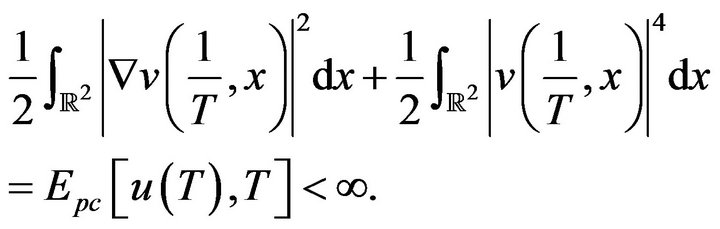
And, the pseudoconformal transformation saves mass and hence
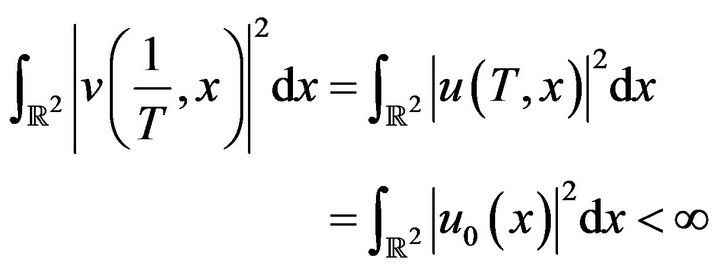
So we see that 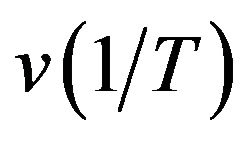 has a finite
has a finite 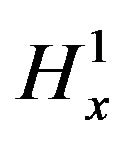 norm. Thus, we can use the global
norm. Thus, we can use the global  -well posedness theory, backwards in time to obtain an
-well posedness theory, backwards in time to obtain an  -well posed solution
-well posed solution
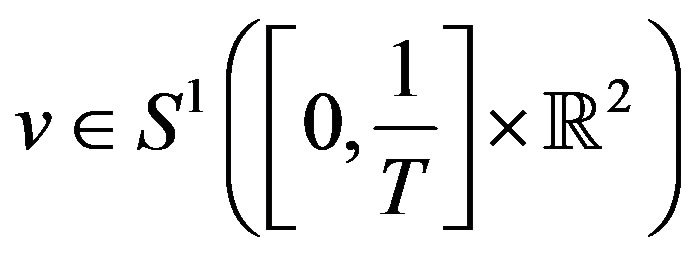 , to the equation
, to the equation  particularly,
particularly, 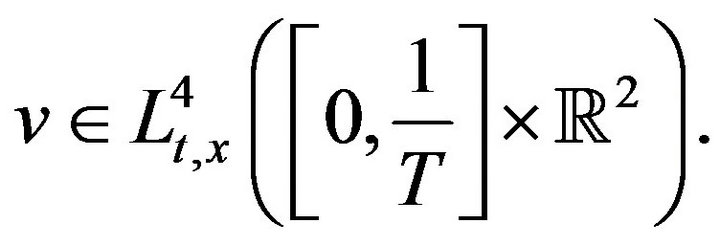
We reverse the pseudoconformal transformation, which defines the original field u on the new slab 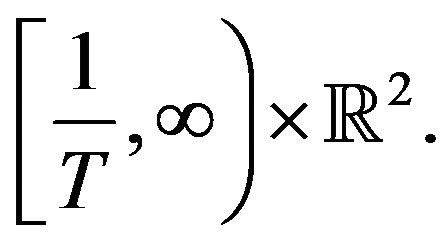
![]() We see that the
We see that the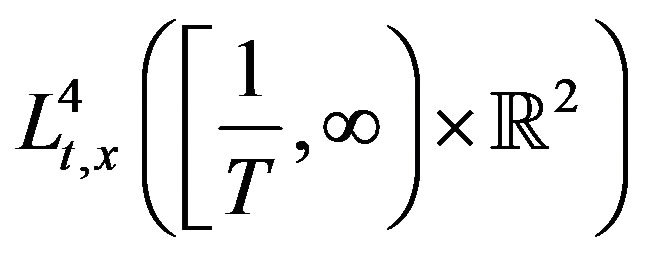 , and
, and
 norm of u are finite. This is sufficient to make u an
norm of u are finite. This is sufficient to make u an  -well posed solution to NLS on the time interval
-well posed solution to NLS on the time interval ; for v classical. And for general
; for v classical. And for general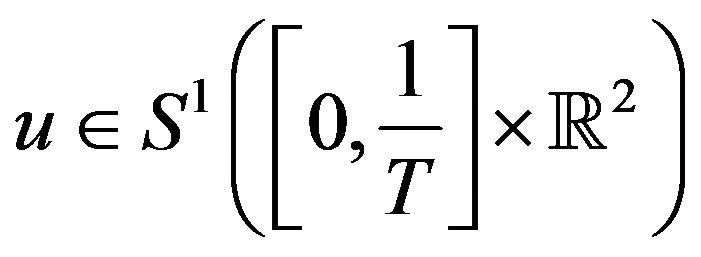 , the claim follows by a limiting argument using the
, the claim follows by a limiting argument using the 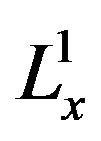 -well posedness theory. Adhesion together the two intervals
-well posedness theory. Adhesion together the two intervals  and
and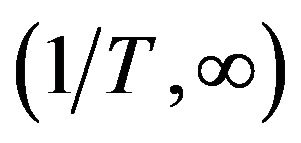 , we have obtained a global
, we have obtained a global 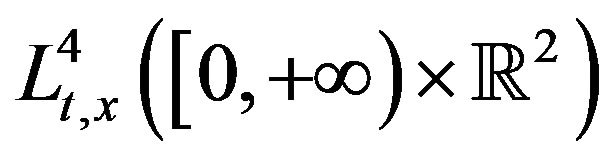 solution u to (1.1).
solution u to (1.1).
4. Some Lemma
Consider the defocusing case of the NLS (1.1) and if , the energy and mass together will control the
, the energy and mass together will control the  norm of the solution:
norm of the solution:

Conversely, energy and mass are controlled by the 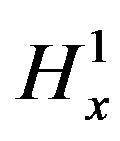 norm (the Gagliardo-Nirenberg inequality showed that):
norm (the Gagliardo-Nirenberg inequality showed that):
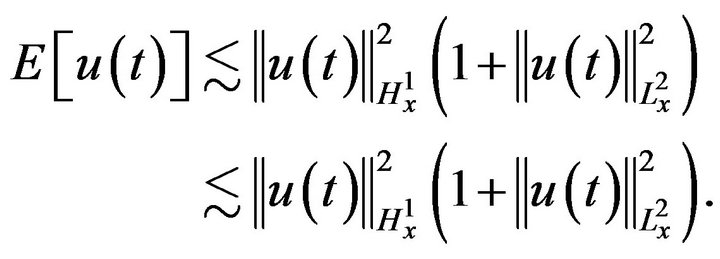
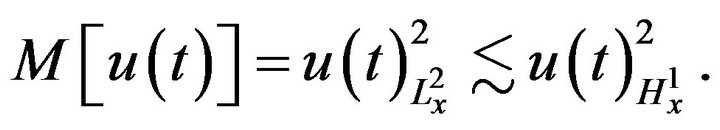
This bound and the energy conservation law and mass conservation law showed that for any 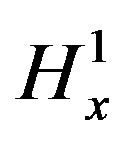 -well posed solution, the
-well posed solution, the 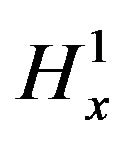 norm of the solution
norm of the solution 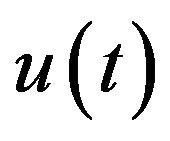 at time t is bounded by a quantity depending only on the
at time t is bounded by a quantity depending only on the 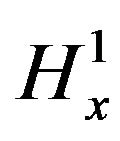 norm of the initial data.
norm of the initial data.
Proposition 4.1. The cubic NLS (1.1) with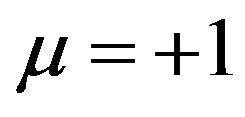 , d = 2 is globally well posed in
, d = 2 is globally well posed in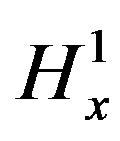 . Actually, for
. Actually, for 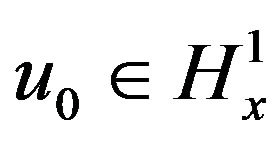 and any time interval, K the Cauchy problem (1.1) has a
and any time interval, K the Cauchy problem (1.1) has a 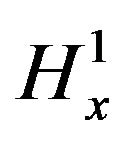 well posed solution
well posed solution
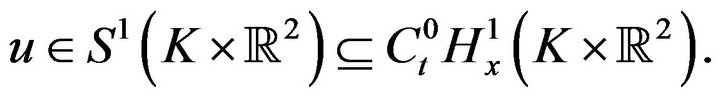
Lemma 4.2. If  the following holds:
the following holds:
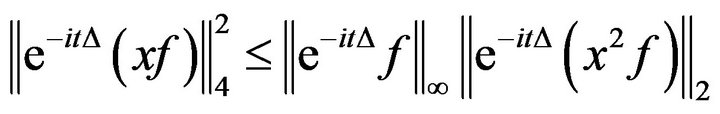 .
.
Proof: The proof depends on the noticing that;
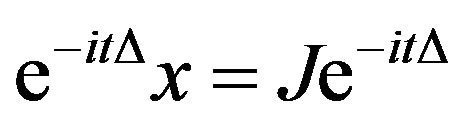 .
.
With
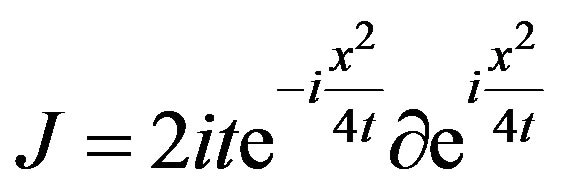
Thus
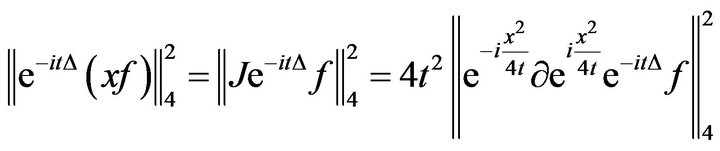
By standard Gagliardo-Nirenberg inequality,
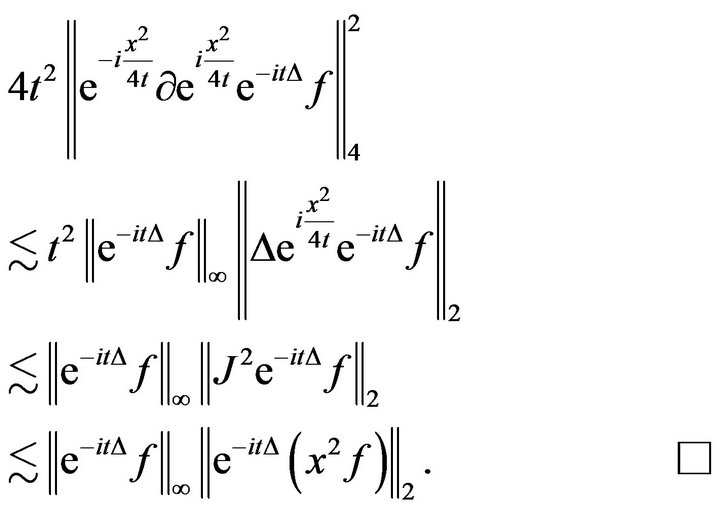
Lemma.4.3. Let . For any spacetime slab
. For any spacetime slab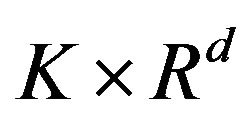 ,
, 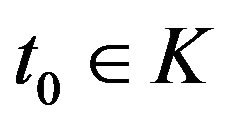 , and for any
, and for any 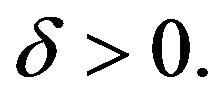
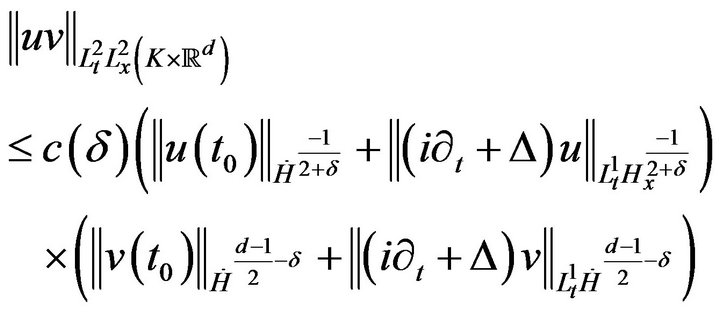 (4.1)
(4.1)
The estimate (4.1) is very helpful when u is high hesitancy and v is low hesitancy, as it moves abundance of derivatives onto the low hesitancy term. In particular, this estimate shows that there is little interaction between high and low hesitancy. This estimate is basically the repeated Strichartz estimate of Bourgain in [13]. We make the trivial remark that the 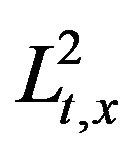 norm of uv is the same as that of
norm of uv is the same as that of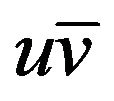 ,
, 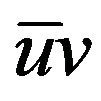 , or
, or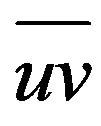 , thus the above estimate also applies to expressions of the form
, thus the above estimate also applies to expressions of the form 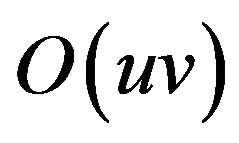
Proof: We fix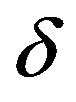 , and permit our tacit constants to depend on
, and permit our tacit constants to depend on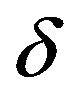 . We begin by dealing with homogeneous case, with
. We begin by dealing with homogeneous case, with 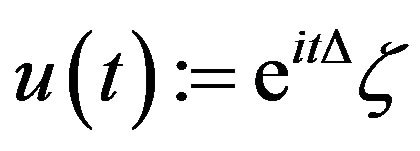 and
and , And consider the more general problem of proving,
, And consider the more general problem of proving,
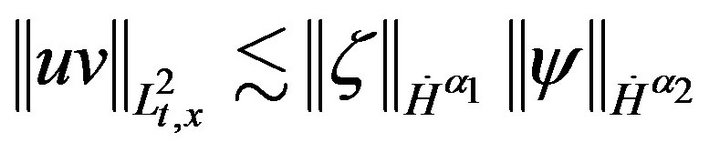 (4.2)
(4.2)
where 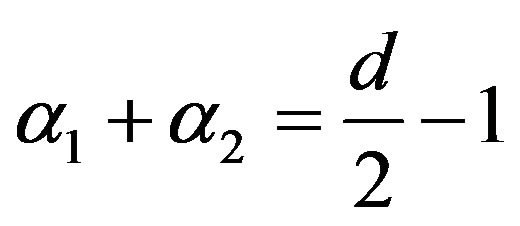 the scaling invariance of this estimate, first, our objective is to prove this for
the scaling invariance of this estimate, first, our objective is to prove this for 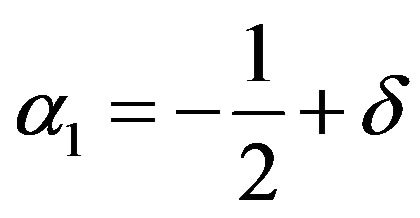 and
and .
.
May be recast (4.2) using duality and renormalization as
 (4.3)
(4.3)
Since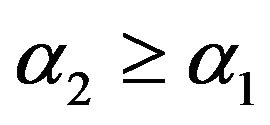 , we may restrict attention to the interactions with
, we may restrict attention to the interactions with 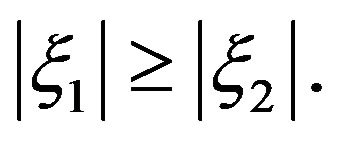
In fact, in the residual case we can multiply by
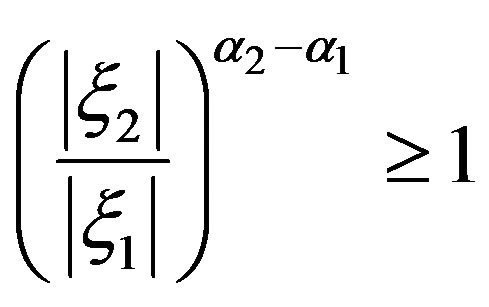 to return to the condition under discussion. In fact, we may further restrict attention to the case where
to return to the condition under discussion. In fact, we may further restrict attention to the case where  since, in the other case, we can move the frequencies between the two factors and reduce the case where
since, in the other case, we can move the frequencies between the two factors and reduce the case where , which can be dealt by
, which can be dealt by 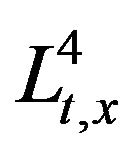 Strichartz estimates when
Strichartz estimates when 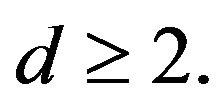 Next, we decompose
Next, we decompose  dyadically and
dyadically and 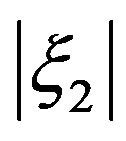 in dyadic multiples of the size of
in dyadic multiples of the size of  by rewriting the quantity to be controlled as (N,
by rewriting the quantity to be controlled as (N,  dyadic):
dyadic):
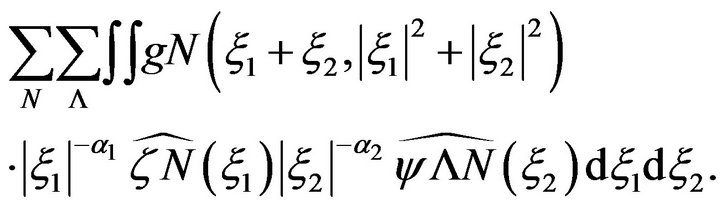
Note that subscripts on  have been inserted to invoke the localizations to
have been inserted to invoke the localizations to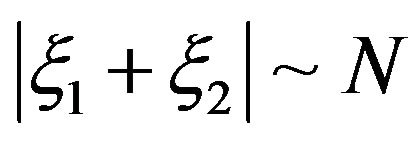 ,
,  ,
,  , consecutive. In the case
, consecutive. In the case , we have that
, we have that  and this expound, why g may be so localized. By renaming components, we may suppose that
and this expound, why g may be so localized. By renaming components, we may suppose that 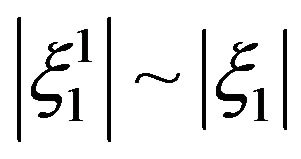 and
and .
.
Write 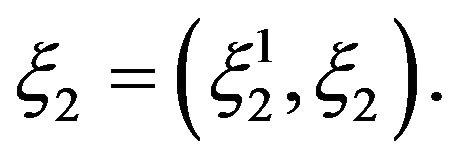 We change variables by writing
We change variables by writing

And 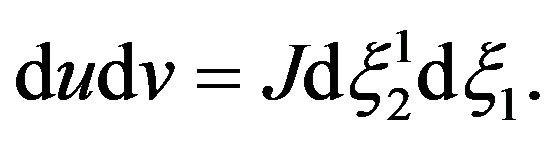
We show that by calculation

Thus, upon changing variables in the inner two integrals, we encounter

where
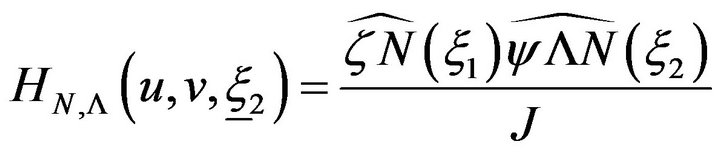
Apply the Cauchy-Schwarz on the u, v integration and change back to the original variables to obtain
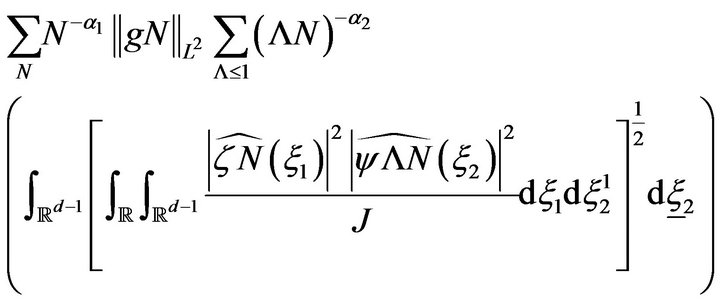
We recall that  and use Cauchy-Schwarz in the integration, taking into consideration the localization
and use Cauchy-Schwarz in the integration, taking into consideration the localization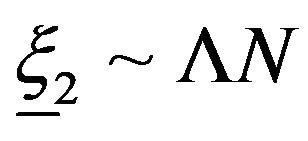 , to get
, to get
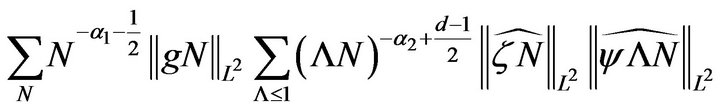
Choose  and
and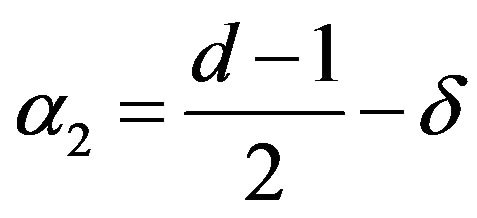 . with
. with 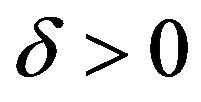 to obtain
to obtain

This summarizes to get the claimed homogeneous estimate. Now we discuss the inhomogeneous estimate (4.1). For simplicity we set,  and
and 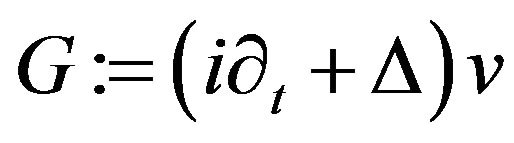 . Then we use Duhamel’s formula to write
. Then we use Duhamel’s formula to write

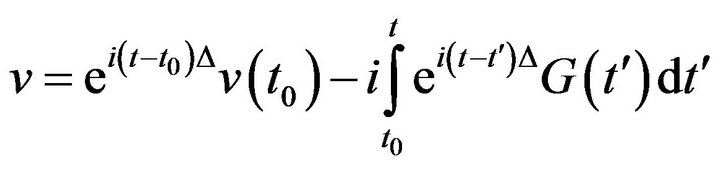
We obtain
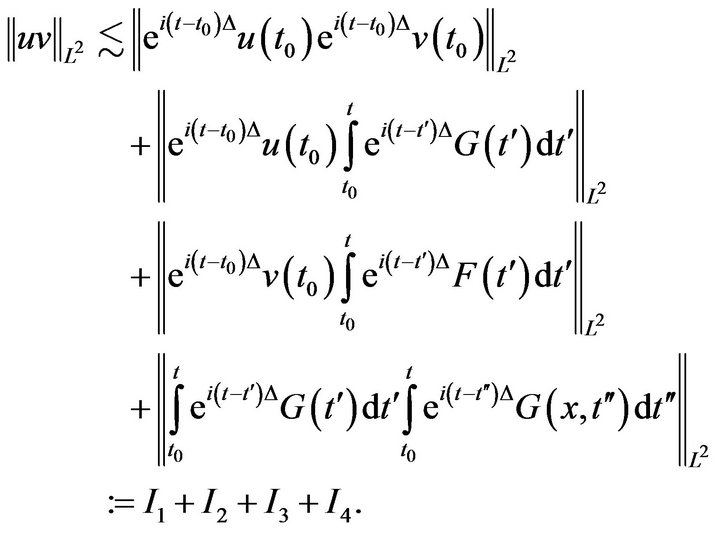
The first term was treated in the first part of the proof. The second and the third are similar and so we consider I2 only. By the Minkowski inequality,

And in this case the lemma follows from the homogeneous estimate proved above. Finally, again by Minkowski’s inequality we have

![]() And the proof follows by inserting in the integral the homogeneous estimate above.
And the proof follows by inserting in the integral the homogeneous estimate above. 
Lemma.4.4. Let 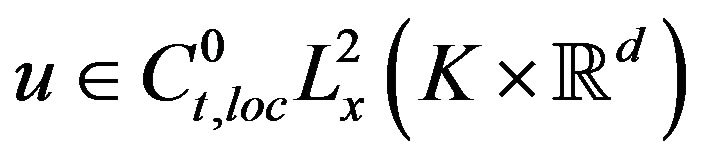 is nearly periodic modulo G. Then there exist functions
is nearly periodic modulo G. Then there exist functions ,
, 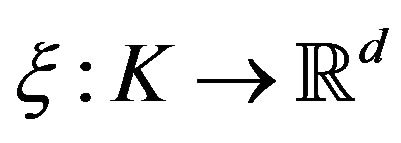 and
and , and for every
, and for every  there exists
there exists  such that we have the spatial concentration estimate,
such that we have the spatial concentration estimate,
 (4.3)
(4.3)
And hesitancy concentration estimate,
 (4.4)
(4.4)
For all 
Remark 4.5. Informally, this lemma confirms that the mass  is spatially concentrated in the ball
is spatially concentrated in the ball
 And is hesitancy concentrated in the ball
And is hesitancy concentrated in the ball
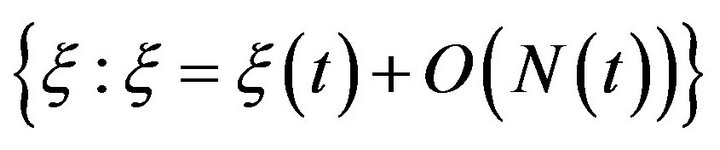 .
.
Note that we have presently no control about how ,
, 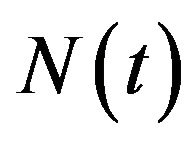 ,
, 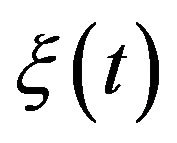 vary in time; (for more see [14- 17]).
vary in time; (for more see [14- 17]).
Proof: By hypothesis,  lay in GI for some compact subset I in
lay in GI for some compact subset I in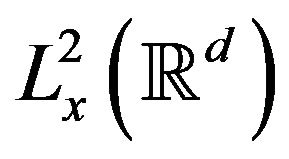 . For every
. For every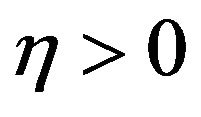 , compactness argument shows that there exists
, compactness argument shows that there exists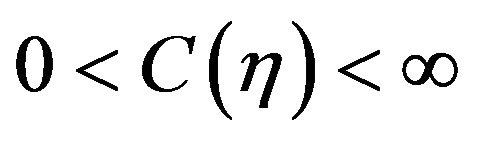 , (depending on) such that
, (depending on) such that
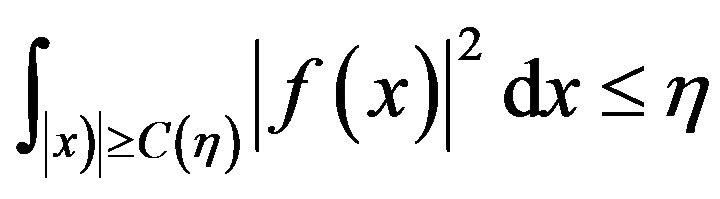
And hesitancy concentration estimate
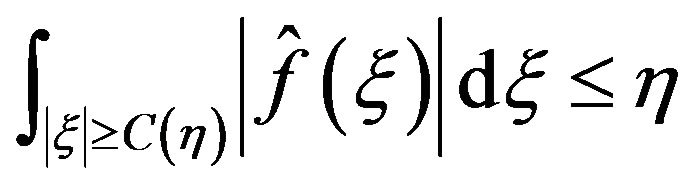
![]() For all
For all . By inspecting what the symmetry group G does to the spatial and hesitancy distribution of the mass of a function, then the claim follows.
. By inspecting what the symmetry group G does to the spatial and hesitancy distribution of the mass of a function, then the claim follows. 
Corollary 4.6. Fix 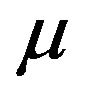 and d, and assume that m0 is finite. Then there exists a maximal-lifespan solution
and d, and assume that m0 is finite. Then there exists a maximal-lifespan solution  of mass precisely m0 which blows up both forward and backward in time, and functions,
of mass precisely m0 which blows up both forward and backward in time, and functions, 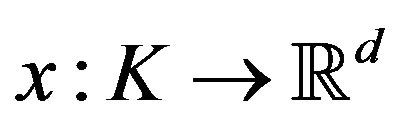 ,
, 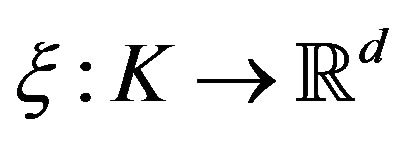 and
and , with property
, with property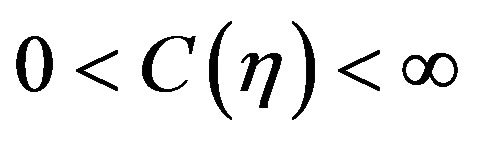 , for every
, for every  (depending on
(depending on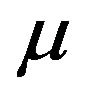 , d, m0) such that we have the concentration estimates (4.3), (4.4) For all
, d, m0) such that we have the concentration estimates (4.3), (4.4) For all 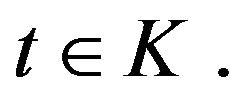
REFERENCES
- T. Cazenave and F. Weissler, “The Cauchy Problem for the Nonlinear Schrödinger Equation in H1,” Manuscripta Mathematics, Vol. 61, No. 4, 1988, pp. 477-494. doi:10.1007/BF01258601
- T. Cazenave and F. Weissler, “The Cauchy Problem for the Nonlinear Schrödinger Equation in Hs,” Nonlinear Analysis, Vol. 14, No. 10, 1990, pp. 807-836. doi:10.1016/0362-546X(90)90023-A
- Y. Tsutsumi, “L2-Solutions for Nonlinear Schrödinger Equations and Nonlinear Groups,” Funkcialaj Ekvacioj, Vol. 30, No. 1, 1987, pp. 115-125.
- T. Tao, “Nonlinear Dispersive Equations: Local and Global Analysis,” CBMS Series, 106, American Mathematical Society, Providence, RI, 2006.
- T. Tao, “Spherically Averaged Endpoint Stnchartz Estimates for the Two-Dimensional Schrödinger Equation,” Communications in Partial Differential Equations, Vol. 25, No. 7-8, 2000, pp. 1471-1485. doi:10.1080/03605300008821556
- T. Tao, M. Visan and X. Zhang, “Minimal-Mass Blow up Solutions of the Mass-Critical NLS,” Forum Mathematicum, Vol. 20, No. 5, 2008, pp. 881-919. doi:10.1515/FORUM.2008.042
- J. Bourgain, “Global Solutions of Nonlinear Schrödinger Equations,” American Mathematical Society Colloquium Publications, Vol. 46, American Mathematical Society, Providence, RI, 1999.
- J. Dolbeault and G. Rein, “Time-Dependent Rescalings and Lyapunov Functionals for the Vlasov-Poisson Ena d Euler-Poisson Systems, and for Related Models of Kinetic Equations, fluid Dynamics and Quantum Mechanics,” Mathematical Models and Methods in Applied Sciences, Vol. 11, 2001, pp. 407-432.
- J. Colliander, M. Grillakis and N. Tzirakis, “Improved Interaction Morawetz Inequalities for the Cubic Nonlinear Schrödinger Equation on R2,” International Mathematics Research Notices, No. 23, 2007, pp. 90-119.
- T. Cazenave, “An Introduction to Nonlinear Schrödinger Equations, First Edition,” Textos de Métodos Matemáticos 22, IM-UFRJ, Rio de Janeiro, 1989.
- M. Del Pino and J. Dolbeault, “Best Constants for Gagliardo-Nirenberg Inequalities and Applications to Nonlinear Diffusions,” Journal de Mathématiques Pures et Appliquées, Vol. 81, No. 9, 2002, pp. 847-875.
- M. Del Pino and J. Dolbeault, “Generalized Sobolev IneQualities and Asymptotic Behaviour in Fast Diffusion and Porous Media Problems,” Ceremade, 9905, 1999, pp. 1-45.
- J. Bourgain, “Refinements of Strichartz’ Inequality and Applications to 2D-NLS with Critical Nonlinearity,” International Mathematics Research Notices, No. 5, 1998, 253-283.
- T. Tao, M. Visan and X. Zhang, “Global Well-Posedness and Scattering for the Mass-Critical Nonlinear Schrö- dinger Equation for Radial Data in Higher Dimensions” Duke Mathematical Journal, Vol. 140, 2007, pp. 165- 202.
- T. Tho and M. Visan, “Stability of Energy-Critical Nonlinear Schrödinger Equations in High Dimensions,” Electronic Journal of Differential Equations, Vol. 2005, No. 118, 2005, pp. 1-28.
- T. Tao, M. Visan and X. Zhang, “Global Well-Posedness and Scattering for the Defocusing Mass-Critical Nonlinear Schrödinger Equation for Radial Data in High Dimensions,” Duke Mathematical Journal, Vol. 140, 2007, No. 1, pp. 165-202.
- T. Tao, M. Visan and X. Zhang, “The Nonlinear Schrö- dinger Equation with Combined Power-Type Nonlinearities,” Communications in Partial Differential Equations, Vol. 32, No. 7-9, 2007, pp. 1281-1343. doi:10.1080/03605300701588805

