Advances in Pure Mathematics
Vol.3 No.1A(2013), Article ID:27566,5 pages DOI:10.4236/apm.2013.31A028
Existence of Weak Solutions for a Class of Quasilinear Parabolic Problems in Weighted Sobolev Space*
1School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, China
2Center for Computational Geosciences, Xi’an Jiaotong University, Xi’an, China
Email: #lqmei@mail.xjtu.edu.cn
Received November 23, 2012; revised December 27, 2012; accepted January 7, 2013
Keywords: Weighted Sobolev Space; Energy Estimates; Compact Imbedding; Sobolev Interpolation Inequalities
ABSTRACT
In this paper, we investigate the existence and uniqueness of weak solutions for a new class of initial/boundary-value parabolic problems with nonlinear perturbation term in weighted Sobolev space. By building up the compact imbedding in weighted Sobolev space and extending Galerkin’s method to a new class of nonlinear problems, we drive out that there exists at least one weak solution of the nonlinear equations in the interval 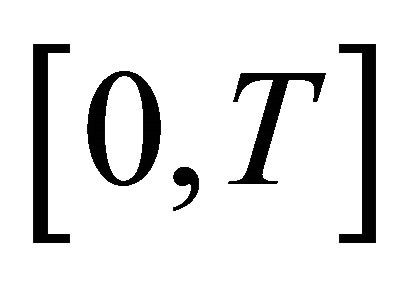 for the fixed time
for the fixed time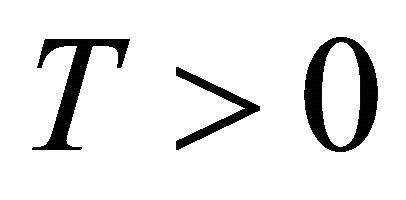 .
.
1. Introduction
Now we consider the initial/boundary-value problem [1] as following
 (1.1)
(1.1)
where ,
,  ,
, 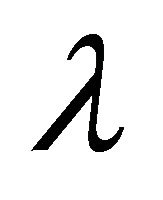 is a real positive parameter and
is a real positive parameter and  is (uniformly) parabolic,
is (uniformly) parabolic,  for some fixed time
for some fixed time ,
,  is an open bounded subset with smooth boundary in
is an open bounded subset with smooth boundary in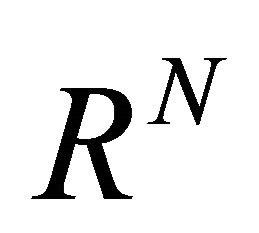 ,
, 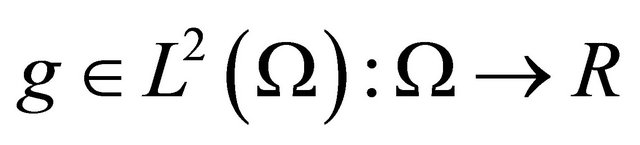 is given,
is given, 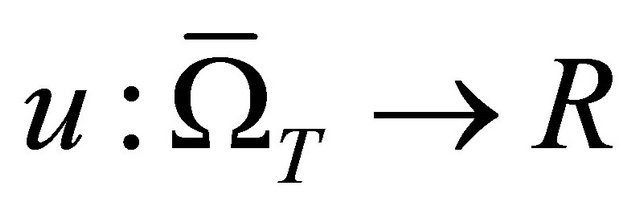 is the unknown,
is the unknown, 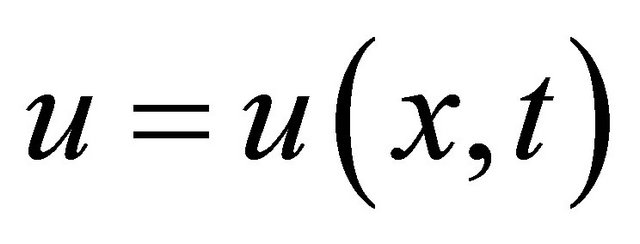 ,
, 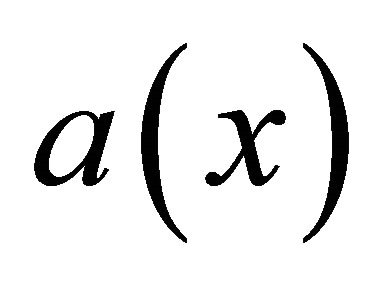 ,
, 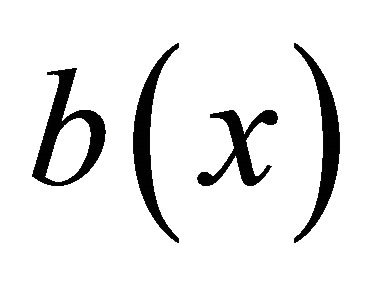 are functions satisfying some suitable conditions [2-4].
are functions satisfying some suitable conditions [2-4].
The main purpose of this paper is to establish the existence of weak solutions for the parabolic initial/boundary-value problem (1.1) in a weighted Sobolev space. For this purpose, we assume for now that
1)  is a positive measurable sufficiently smooth function2)
is a positive measurable sufficiently smooth function2) 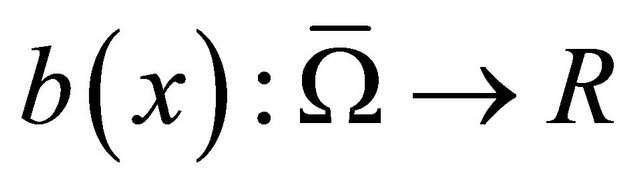 is a non-negative smooth function which may change sign3)
is a non-negative smooth function which may change sign3) 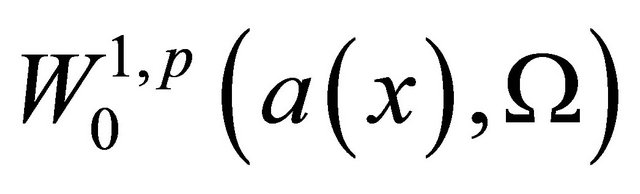 is a weighted Sobolev space [5-8] with a weight function
is a weighted Sobolev space [5-8] with a weight function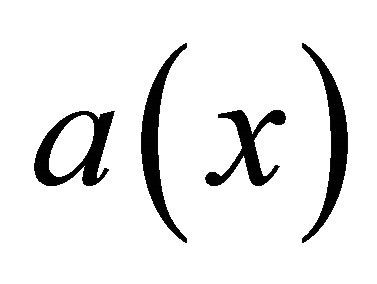 , its norm defined as
, its norm defined as
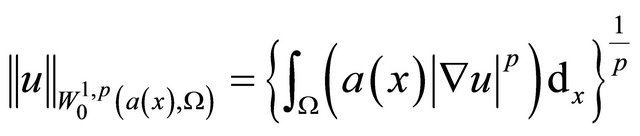 .
.
For convenience, we will denote 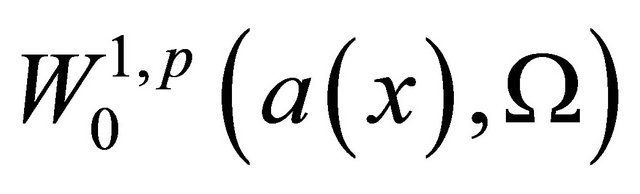 by Xnote
by Xnote  by
by , and unless otherwise statedintegrals are over
, and unless otherwise statedintegrals are over .
.
Similar problems have been studied by Evans [9], he investigated the solvability of the initial/bondary-value problem for the reaction-diffusion system
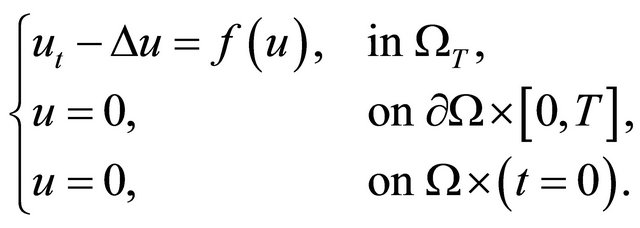 (1.2)
(1.2)
Here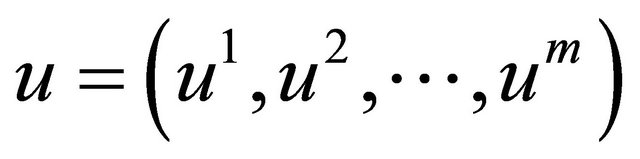 ,
, 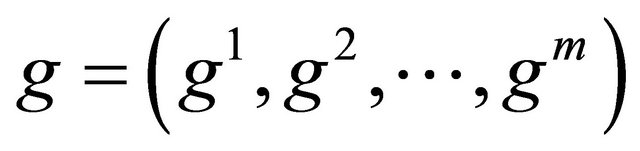 , and as usual
, and as usual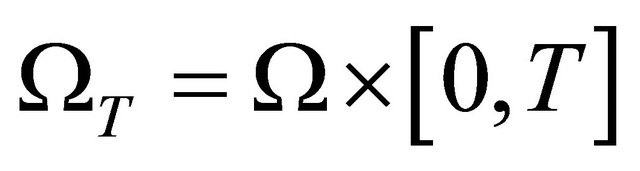 ,
,  is open and bounded with smooth boundary. Via the techniques of Banach's fixed point theorem method, he obtained the existence and uniqueness and some estimates of the weak solution under the assumer that the initial function
is open and bounded with smooth boundary. Via the techniques of Banach's fixed point theorem method, he obtained the existence and uniqueness and some estimates of the weak solution under the assumer that the initial function 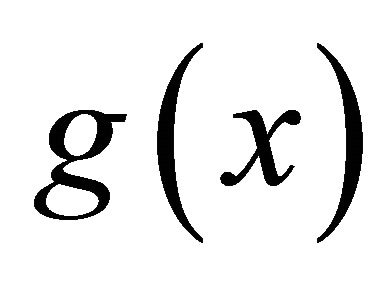 belongs to
belongs to 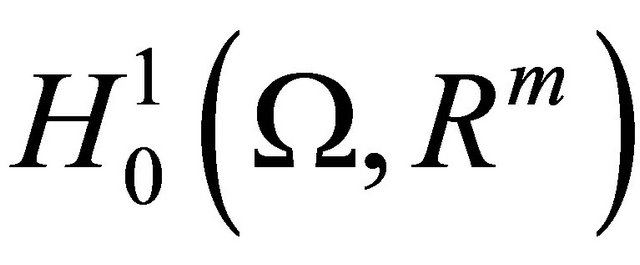 and
and  is Lipschitz continuous. He also studied the nonlinear heat equation with a simple quadratic nonlinearity
is Lipschitz continuous. He also studied the nonlinear heat equation with a simple quadratic nonlinearity
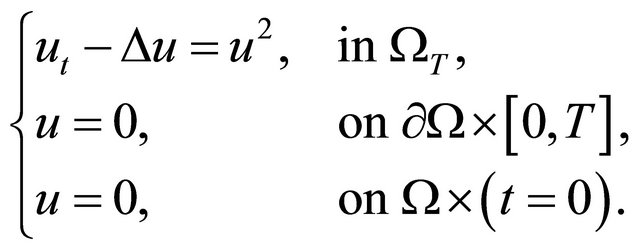 (1.3)
(1.3)
The Blow-up solution has been established under the assumer that  and
and  are large enough in an appropriate sense.
are large enough in an appropriate sense.
The main results of this paper can be stated as followsTheorem 1.1. There exists a unique weak solution of problem (1.1) on the interval 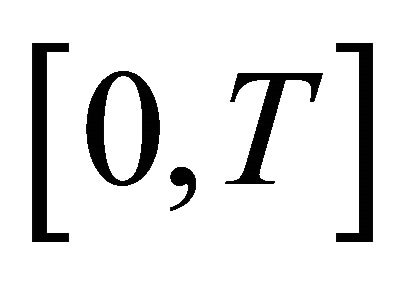 for the fixed time
for the fixed time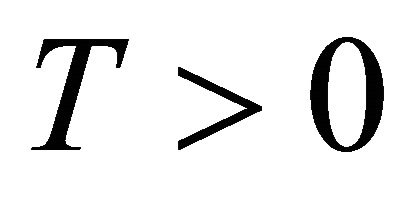 .
.
For the further argument, we need the following Lemma.
Lemma 1.1. If , then1)
, then1) 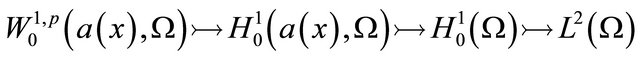 are the compact imbedding [6]2)
are the compact imbedding [6]2)  are also compact imbedding.
are also compact imbedding.
Proof. 1) Since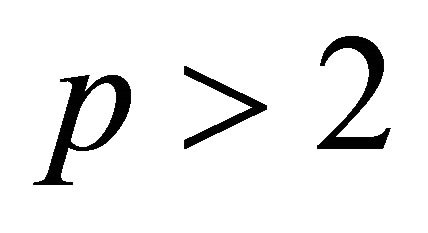 , and
, and 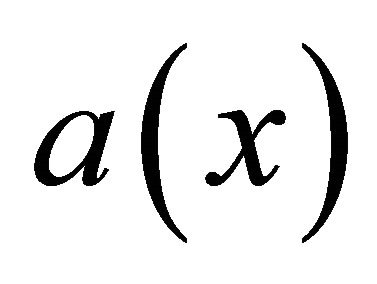 is a positive sufficiently smooth function, there exists a positive constant C, such that
is a positive sufficiently smooth function, there exists a positive constant C, such that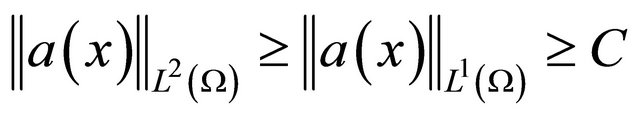 . Hence
. Hence
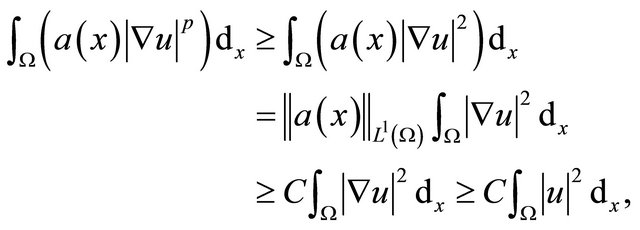
for all , and a.e. time
, and a.e. time . We used the poincare’s inequality in the last inequality above. Thus1) Holds and is compact.
. We used the poincare’s inequality in the last inequality above. Thus1) Holds and is compact.
2) The proof of 2) is almost the same as 1). This completes the proof of Lemma 1.1.
2. Weak Solutions
According to Lemma 1.1, it suffices to consider the initial/boundary-value problem (1.1) in spaces 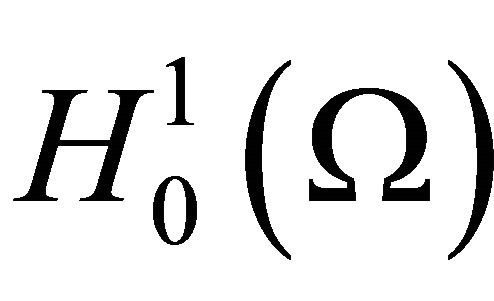 and
and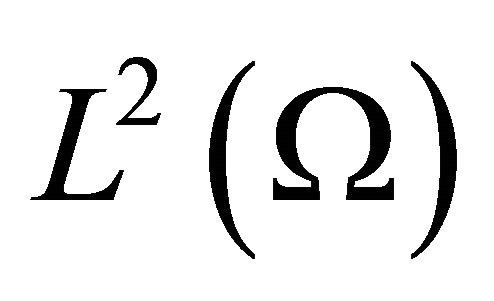 . We will employ the Galerkin’s method to prove our results.
. We will employ the Galerkin’s method to prove our results.
Definition 2.1. We say a function
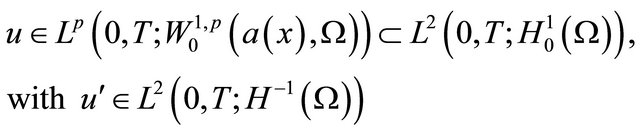
is a weak solution of the parabolic initial/boundary-value problem (1.1) provided
1)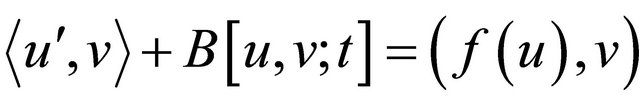 , for each
, for each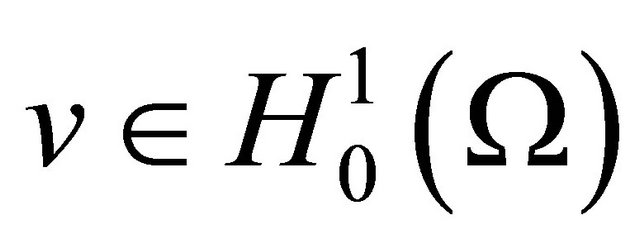 , and a.e. time
, and a.e. time , and 2)
, and 2)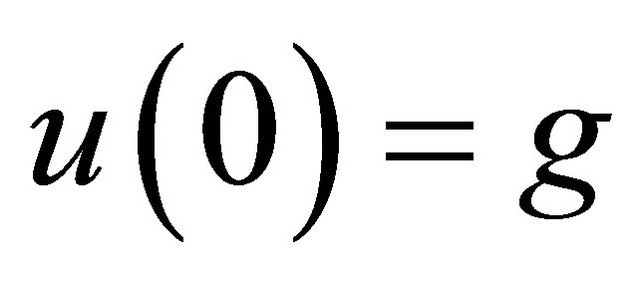 .
.
Here  denotes the time-dependent bilinear form
denotes the time-dependent bilinear form
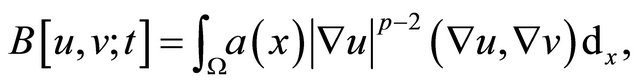
for each 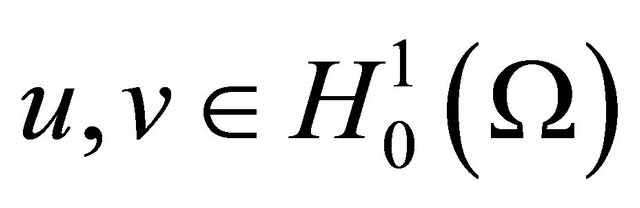 and a.e. time
and a.e. time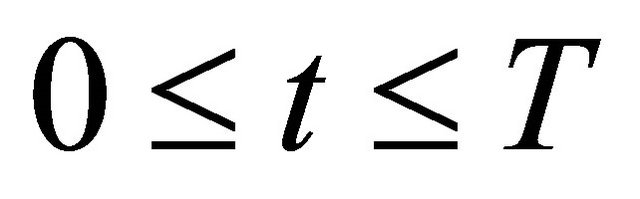 .
.
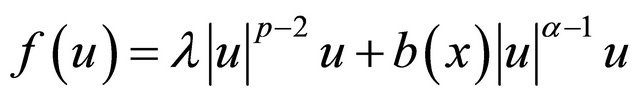 is the nonlinearity term. the pairing
is the nonlinearity term. the pairing  denoting inner product in
denoting inner product in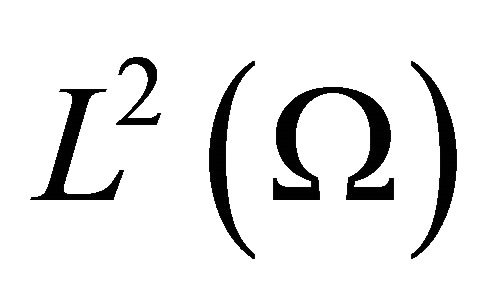 ,
,  being the pairing of
being the pairing of  and
and .
.
By the Definition 2.1, we see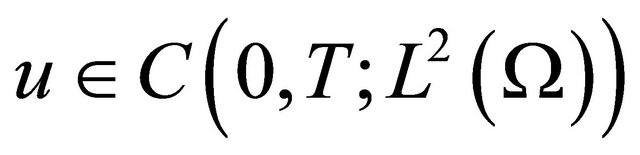 , and thus the equality 2) makes sense.
, and thus the equality 2) makes sense.
We now switch our view point, by associating with u a mapping
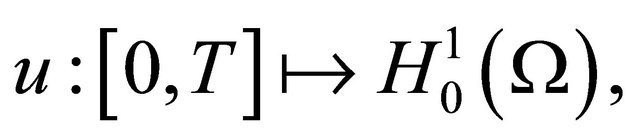
defined by
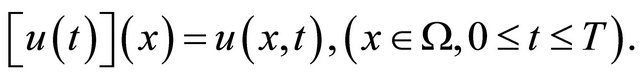
More precisely, assume that the functions 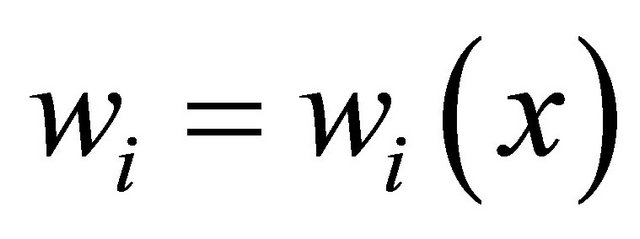
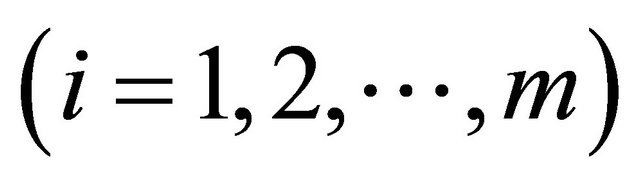 are smooth1)
are smooth1) 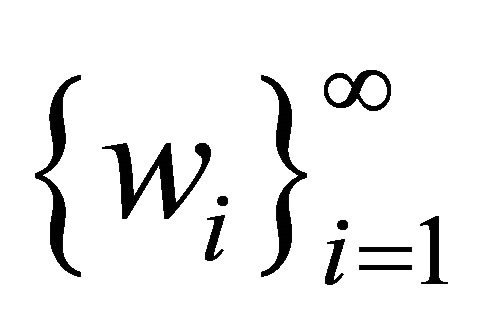 is an orthogonal basis of
is an orthogonal basis of 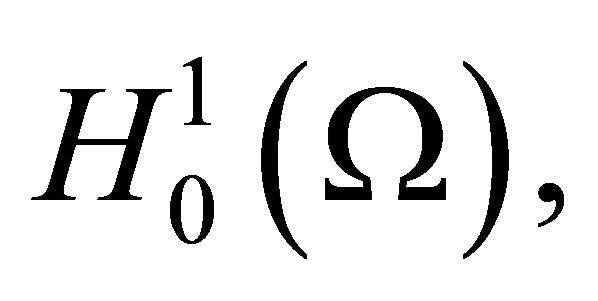 and 2)
and 2) 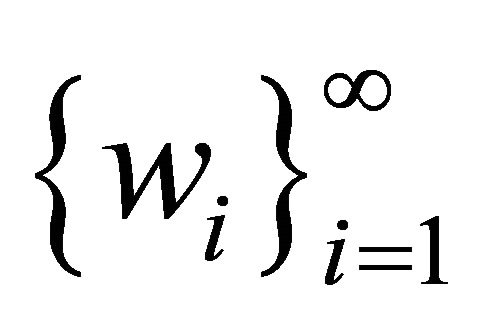 is an orthogonal basis of
is an orthogonal basis of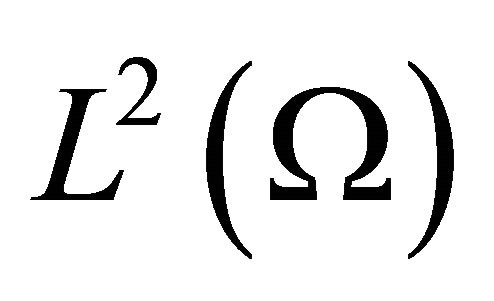 , (0 ≤ t ≤ T, i = 1, 2, ∙∙∙, m) taken with the inner product
, (0 ≤ t ≤ T, i = 1, 2, ∙∙∙, m) taken with the inner product
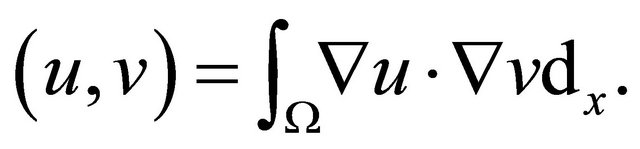 Sm is the finite dimensional subspace spanned by
Sm is the finite dimensional subspace spanned by . Fix a positive integer m, we will look for a function
. Fix a positive integer m, we will look for a function 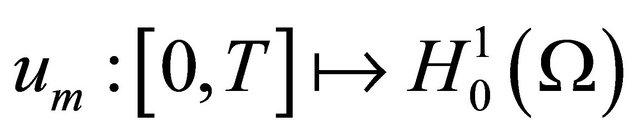 of the form
of the form
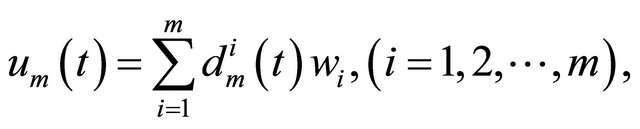 (2.1)
(2.1)
Here we hope to select the coefficients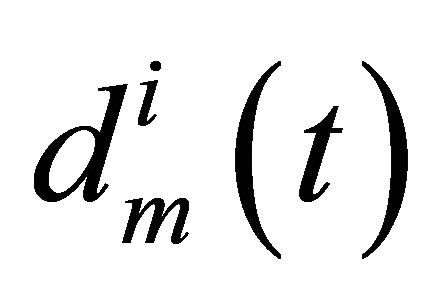 , (0 ≤ t ≤ T, i = 1, 2, ∙∙∙, m) such that
, (0 ≤ t ≤ T, i = 1, 2, ∙∙∙, m) such that
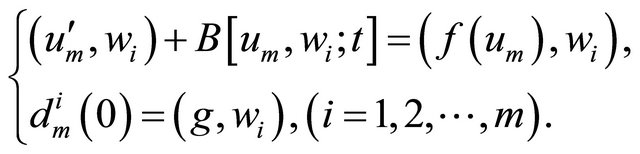 (2.2)
(2.2)
That is
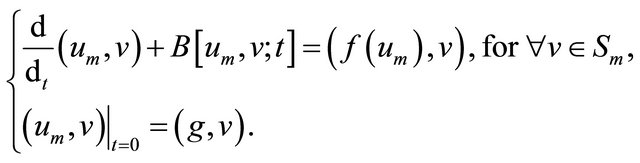 (2.3)
(2.3)
This amounts to our requiring that um solves the “projection” of problem (1.1) onto the finite dimensional subspace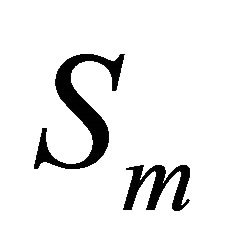 .
.
Theorem 2.1. (construction of approximate solutions)
For each integer 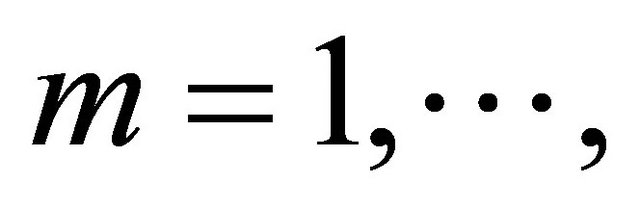 there exists a function um of the form (2.1) satisfying the identities (2.3).
there exists a function um of the form (2.1) satisfying the identities (2.3).
Proof. Taking 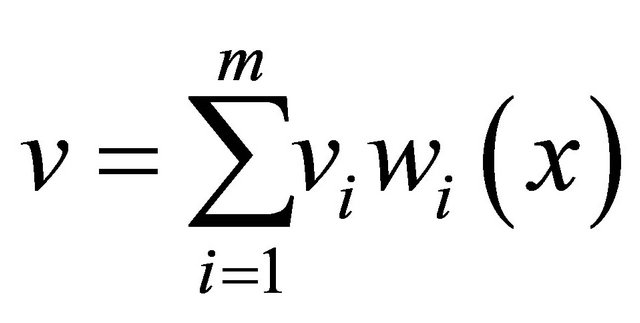 arbitrary, then
arbitrary, then
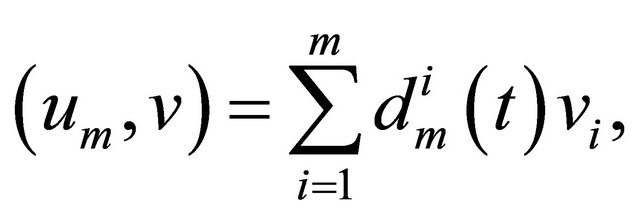

Thus, 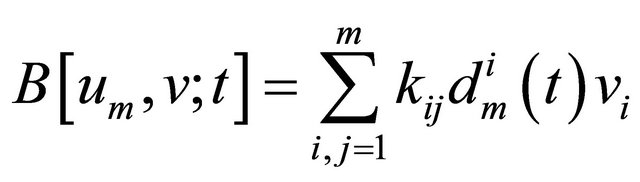 , and
, and
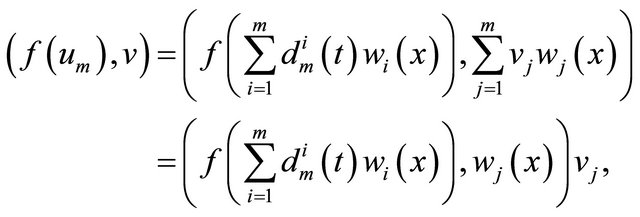
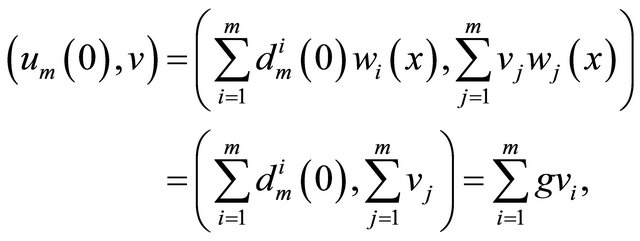
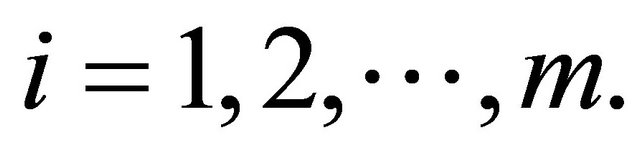 Hence,
Hence,
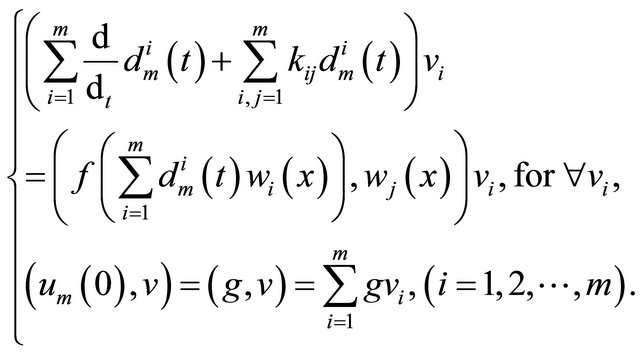 (2.4)
(2.4)
Since 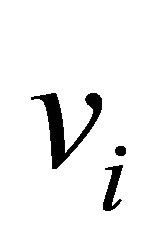 is random, therefore, system (2.4) becomes
is random, therefore, system (2.4) becomes
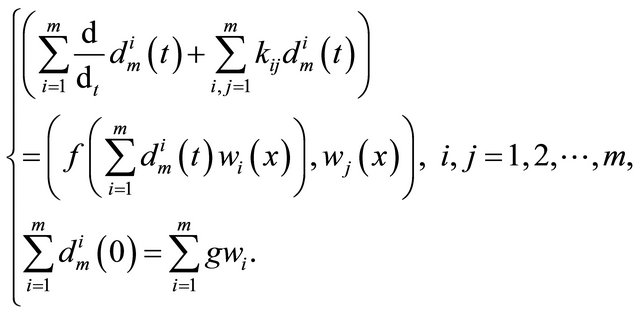 (2.5)
(2.5)
This is a nonlinear system of ordinary differential equation, according to the existence theory for nonlinear ODE, there exists a unique local solution on interval  for fixed time T > 0. That is, the initial/boundaryvalue problem (1.1) has a unique local weak solution on the interval
for fixed time T > 0. That is, the initial/boundaryvalue problem (1.1) has a unique local weak solution on the interval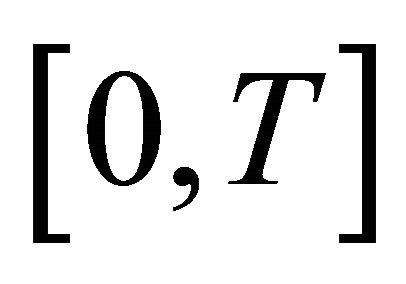 .
.
3. Energy Estimates
Theorem 3.1. There exists a constant C, depending only on 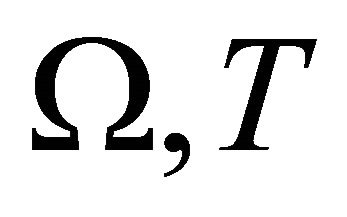 and
and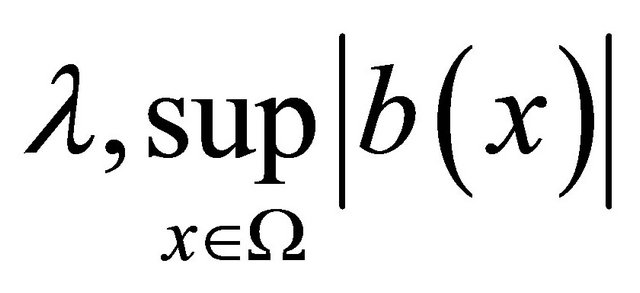 , such that
, such that
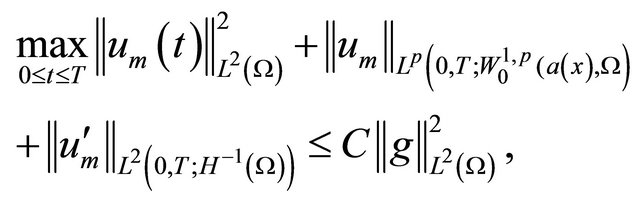 (3.1)
(3.1)
for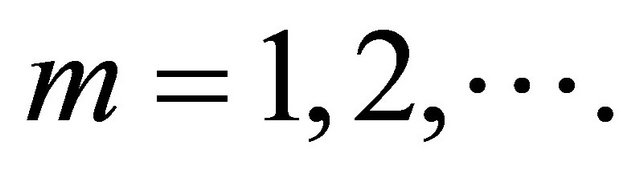
Proof. We separate this proof into 3 steps.
Step 1. Multiply equality (2.2) by  and sum for
and sum for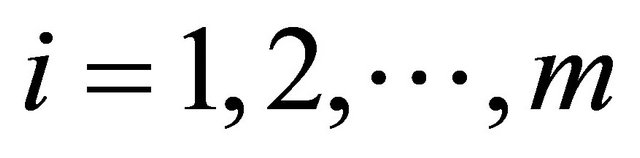 , and then recall to (2.1) to find
, and then recall to (2.1) to find
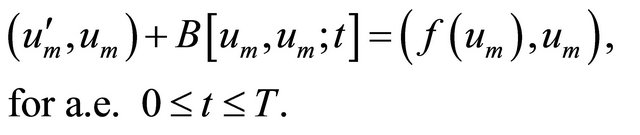 (3.2)
(3.2)
Whereas,
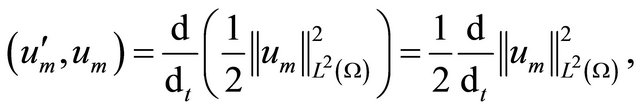

and
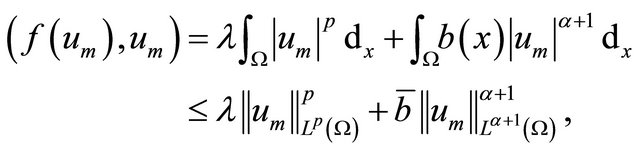
for a.e. time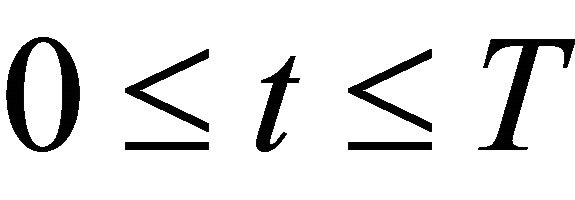 , here,
, here, 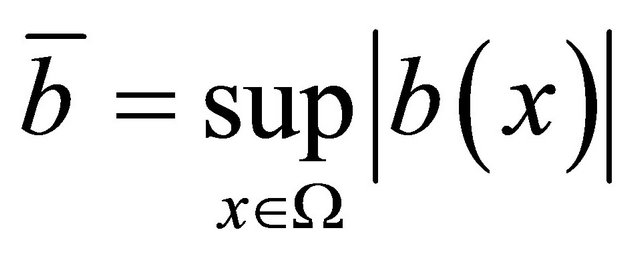 , since
, since 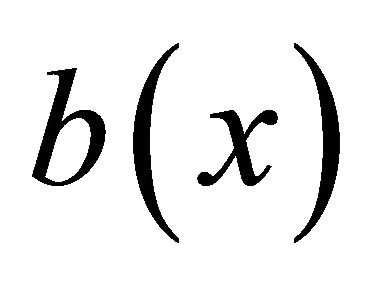 is a smooth function.
is a smooth function.
Consequently (3.2) yields the inequality
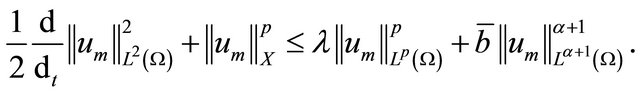 (3.3)
(3.3)
Since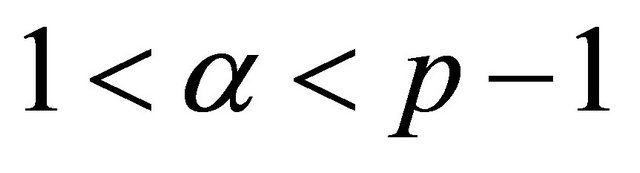 , that is
, that is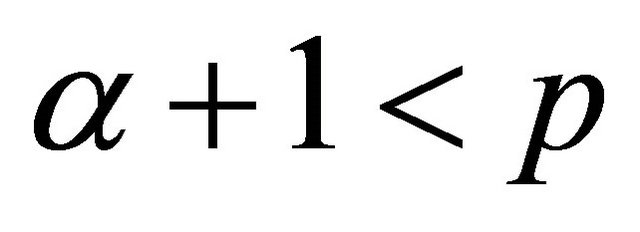 , then by Sobolev imbedding theorem, we obtain
, then by Sobolev imbedding theorem, we obtain , and moreover,
, and moreover,
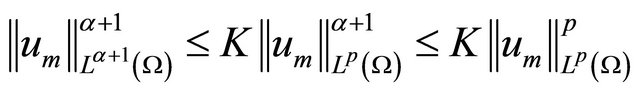 here k is the best Sobolev constant [10-13].
here k is the best Sobolev constant [10-13].
Thus, we can write inequality (3.3) as
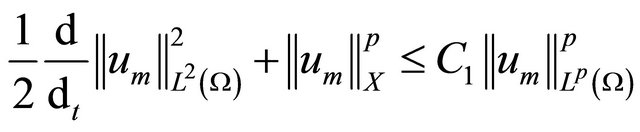 (3.4)
(3.4)
For a.e. time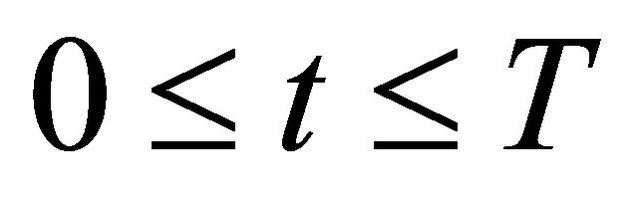 , and appropriate constant
, and appropriate constant .
.
In addition, since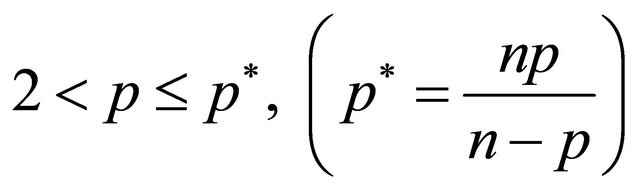 , by Sobolev interpolation inequality, we find
, by Sobolev interpolation inequality, we find

here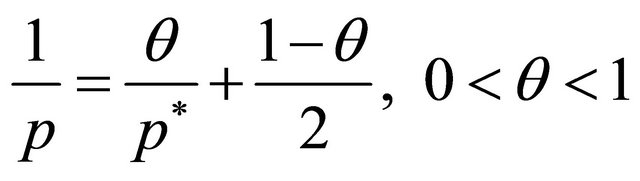 , and we have used the Young’s inequality with
, and we have used the Young’s inequality with  in the last inequality. Thus
in the last inequality. Thus
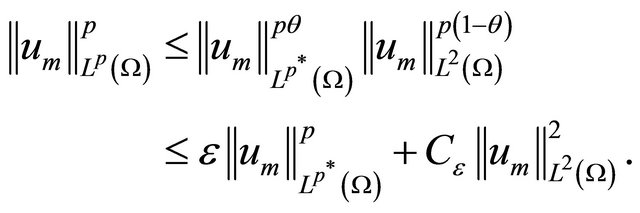 (3.5)
(3.5)
By Lemma 1.1 2) and Sobolev’s inequality, we have
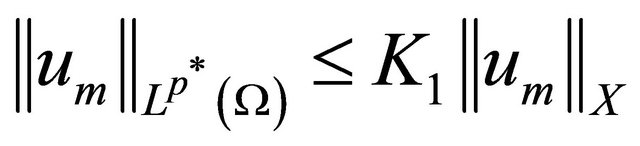 ,
, 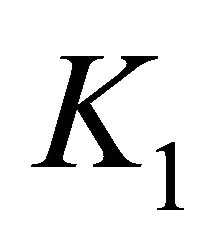 is the best Sobolev imbedding constant, insert the inequality above and (3.5) into inequality (3.4) yields
is the best Sobolev imbedding constant, insert the inequality above and (3.5) into inequality (3.4) yields
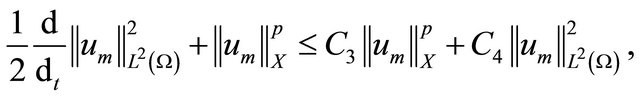 (3.6)
(3.6)
for a.e. time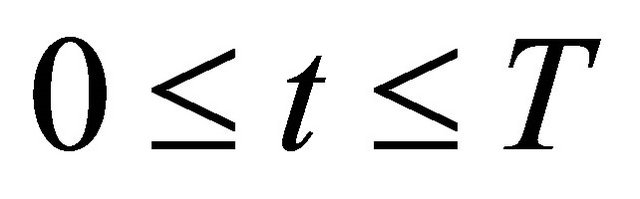 , and appropriate constants
, and appropriate constants  and
and .
.
Furthermore, we rewrite inequality (3.6) as
 (3.7)
(3.7)
for a.e. time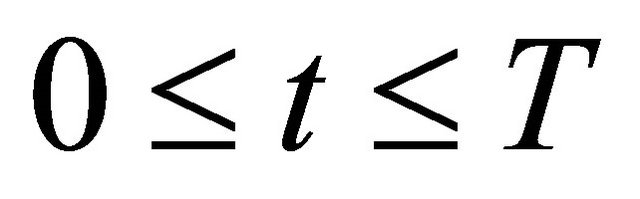 , and appropriate constants
, and appropriate constants  and
and .
.
By Gronwall’s inequality, (3.7) yields the estimate
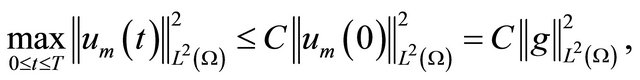 (3.8)
(3.8)
for a.e. time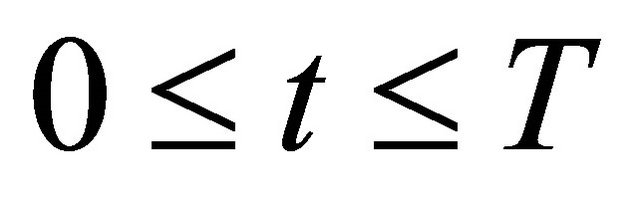 , and appropriate constant
, and appropriate constant .
.
Step 2. Returning once more to inequality (3.7), we integrate from 0 to T and employ the inequality (3.8) to obtain
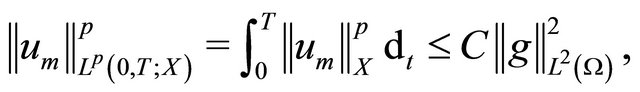 (3.9)
(3.9)
for a.e. time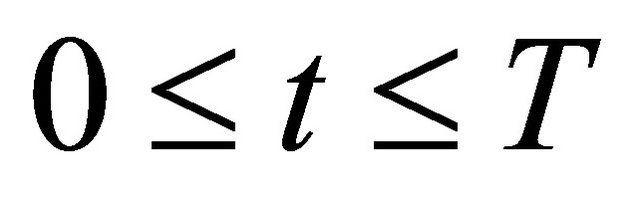 , and appropriate constant C.
, and appropriate constant C.
Step 3. Fix any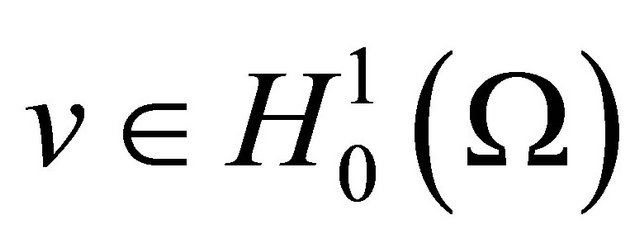 , with
, with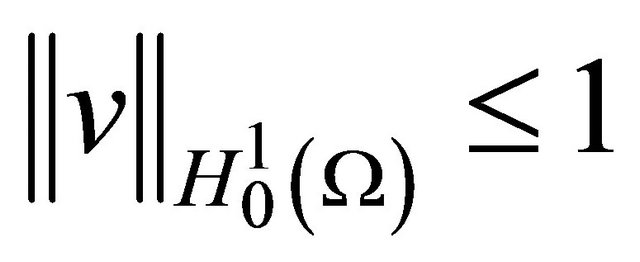 , and write
, and write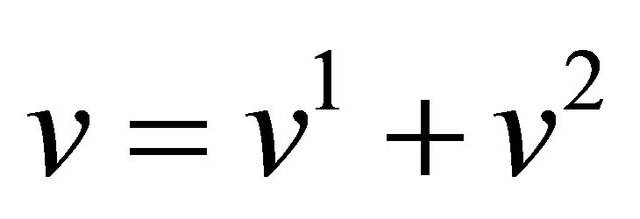 , where
, where 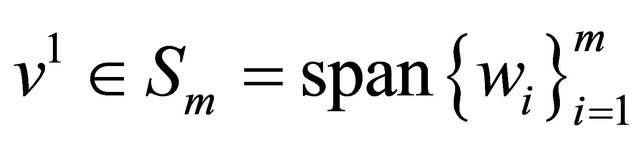 and
and
 . Since functions
. Since functions  are orthogonal in
are orthogonal in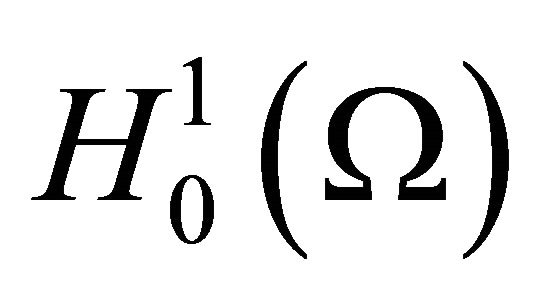 ,
,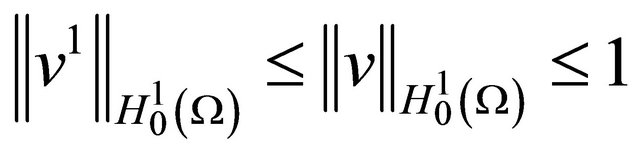 . Utilizing (2.2) we deduce for a.e. time
. Utilizing (2.2) we deduce for a.e. time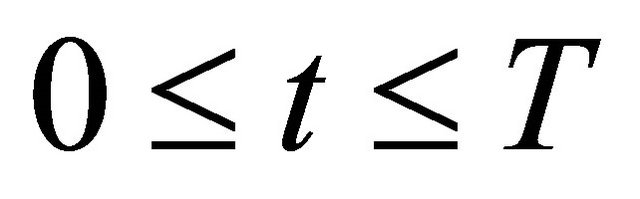 , that
, that
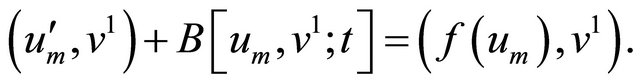
Then (2.1) implies
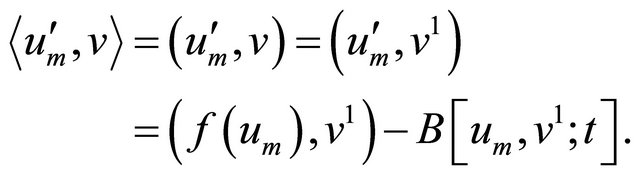
Consequently,
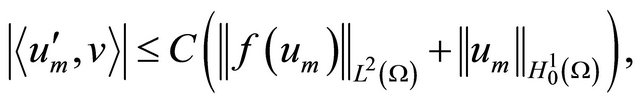
since . Thus
. Thus
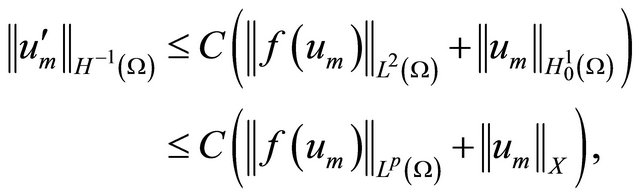
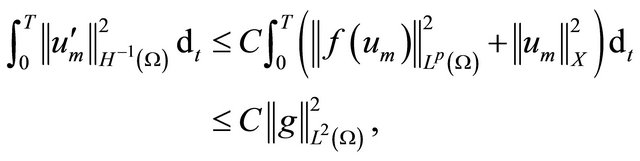 (3.10)
(3.10)
for a.e. time , and appropriate constant C.
, and appropriate constant C.
Combing (3.8), (3.9) and (3.10) we complete the proof of Theorem 3.1.
4. Existence of Weak Solutions
Next we pass to limits as , to build a weak solution of our initial/boundary-value problem (1.1).
, to build a weak solution of our initial/boundary-value problem (1.1).
Theorem 4.1. There exists a local weak solution of problem (1.1).
Proof. According to the energy estimates (3.1), we see that the sequence 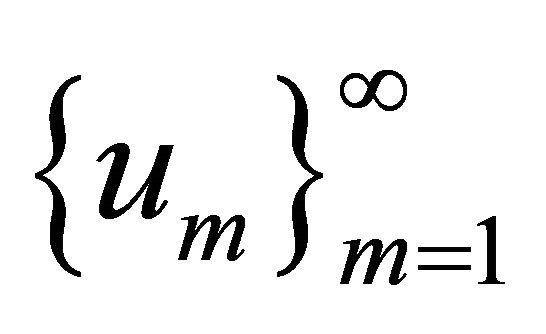 is bounded in
is bounded in
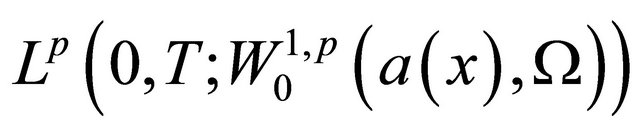 , and
, and 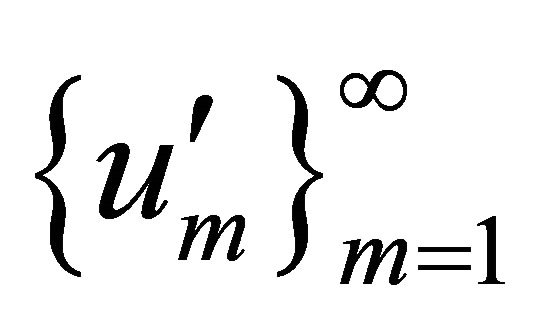 is bounded in
is bounded in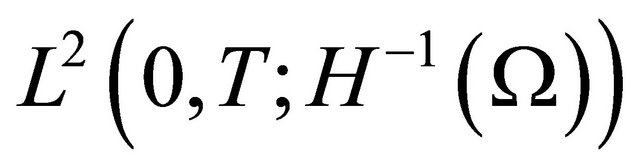 . Consequently there exists a subsequence
. Consequently there exists a subsequence 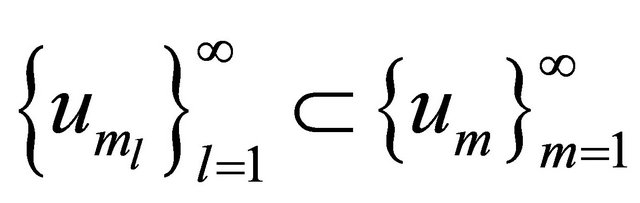 and a function
and a function
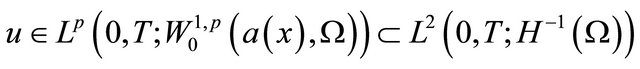
with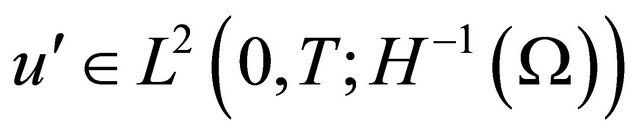 , such that
, such that
1)  weakly in
weakly in , and
, and 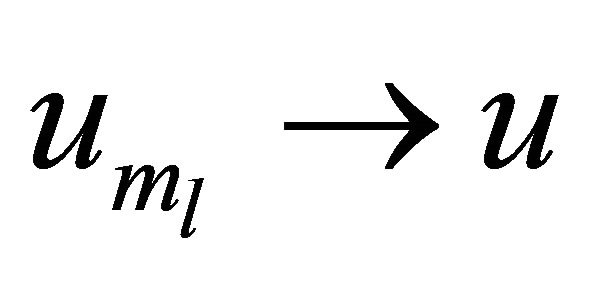 strongly in
strongly in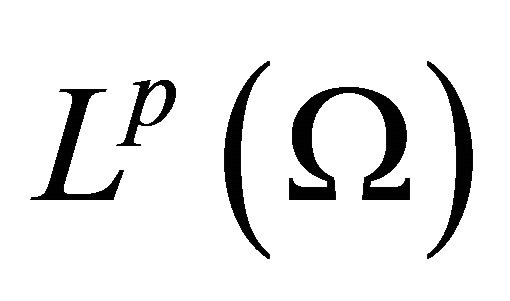 .
.
2) 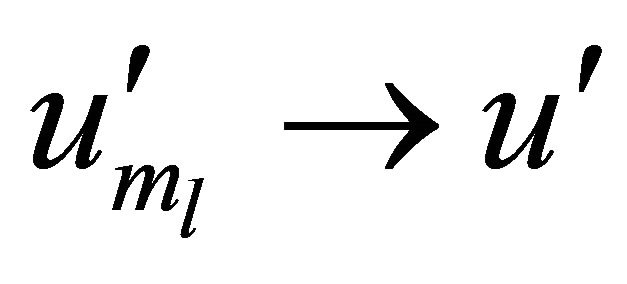 weakly in
weakly in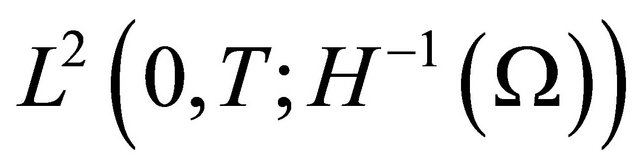 .
.
Now we fix an integer  and choose a function
and choose a function 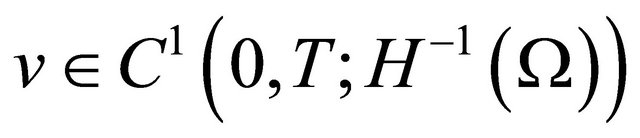 having the form
having the form
 (4.1)
(4.1)
here 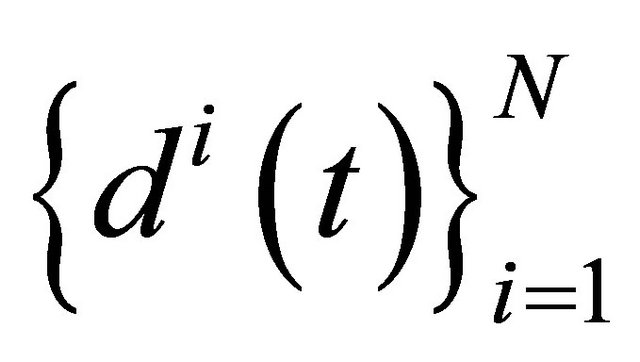 are given smooth functions. We choose
are given smooth functions. We choose
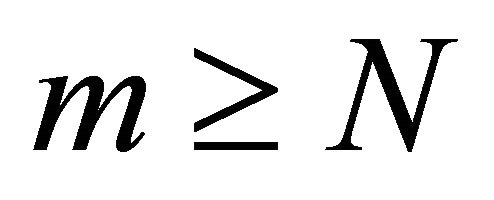 , multiply (2.2) by
, multiply (2.2) by , sum
, sum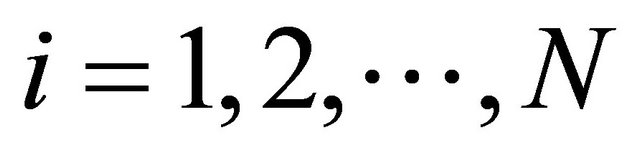 , and then integrate with respect to t, we find
, and then integrate with respect to t, we find
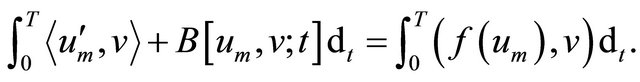 (4.2)
(4.2)
We set , and recall 1), 2) to find upon passing to weak limits that
, and recall 1), 2) to find upon passing to weak limits that
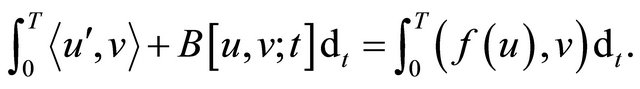 (4.3)
(4.3)
This equality then holds for all functions  , as functions of the form (4.1) are dense in this space. Hence in particular
, as functions of the form (4.1) are dense in this space. Hence in particular
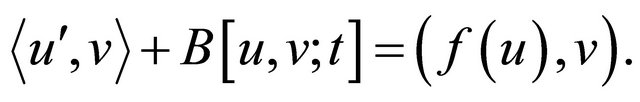 (4.4)
(4.4)
for each 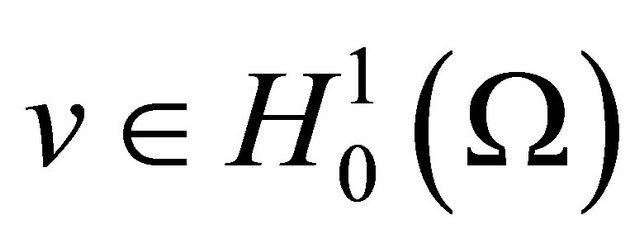 and a.e. time
and a.e. time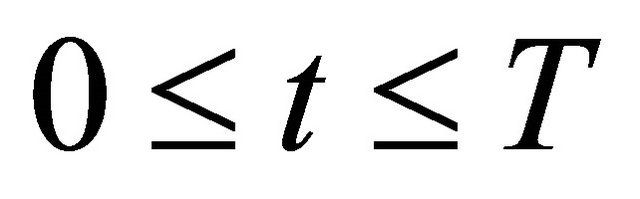 .
.
In order to prove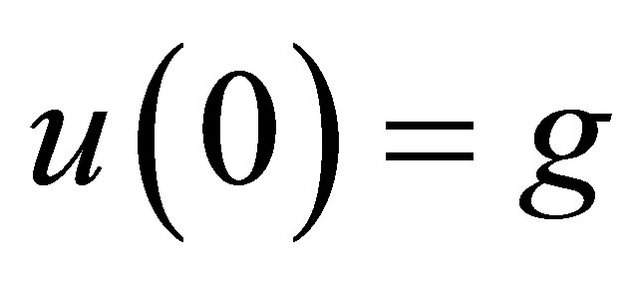 , we first note from (4.3) that
, we first note from (4.3) that
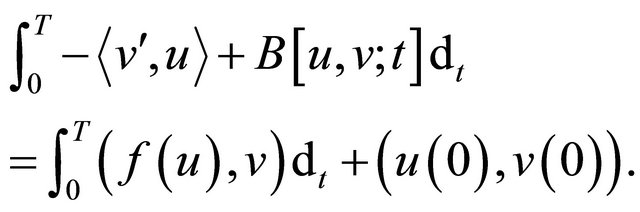 (4.5)
(4.5)
for each 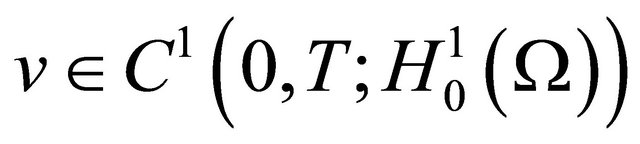 with
with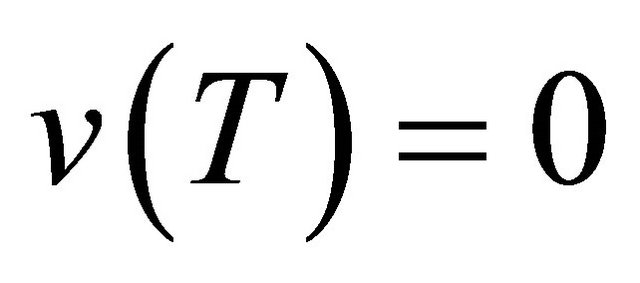 . Similarly, from (4.2) we deduce
. Similarly, from (4.2) we deduce
 (4.6)
(4.6)
We set 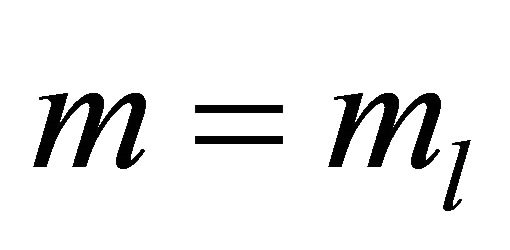 and once again employ 1), 2), we obtain
and once again employ 1), 2), we obtain
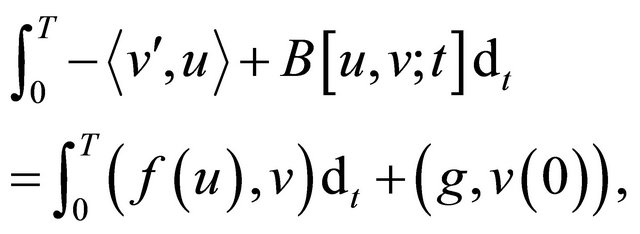 (4.7)
(4.7)
since 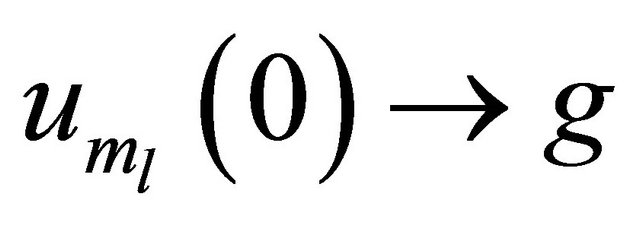 in
in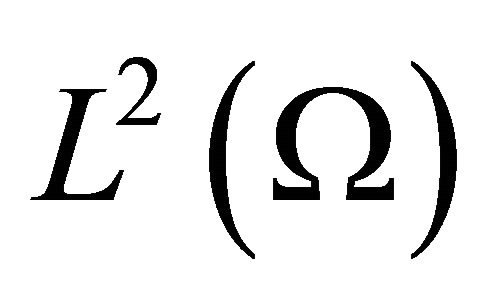 . As
. As 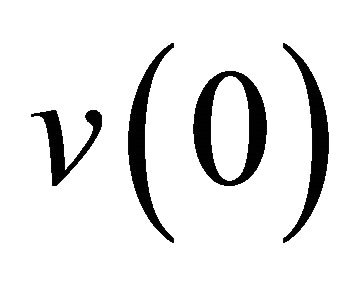 is arbitrary, comparing (4.5) and (4.7), we conclude
is arbitrary, comparing (4.5) and (4.7), we conclude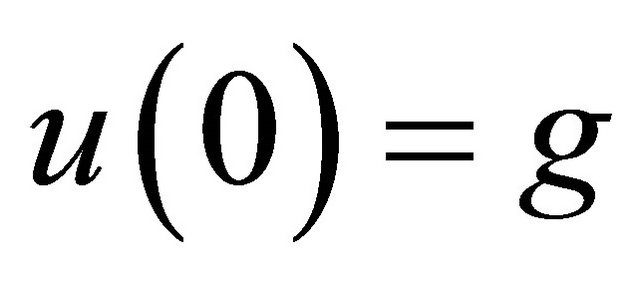 . This completes the proof of theorem 4.1.
. This completes the proof of theorem 4.1.
5. Uniqueness of Weak Solutions
In this part, we will prove Theorem 1.1.
Proof. Let 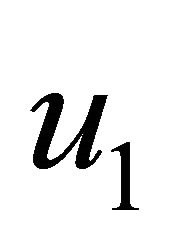 and
and 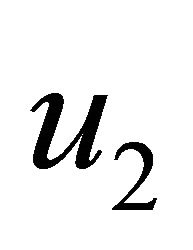 are two weak solutions for the initial/boundary-value problem, put
are two weak solutions for the initial/boundary-value problem, put , and insert it into the origin equation, we discover
, and insert it into the origin equation, we discover
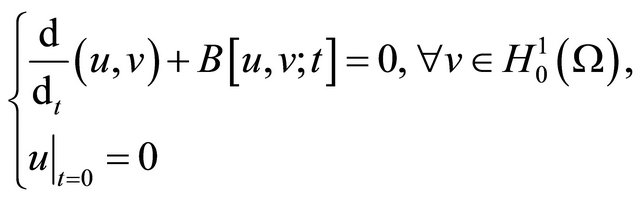
Taking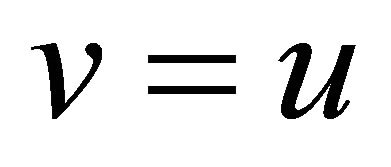 , we obtain the energy estimates inequality
, we obtain the energy estimates inequality
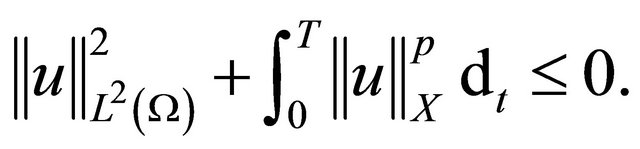
Since ,
,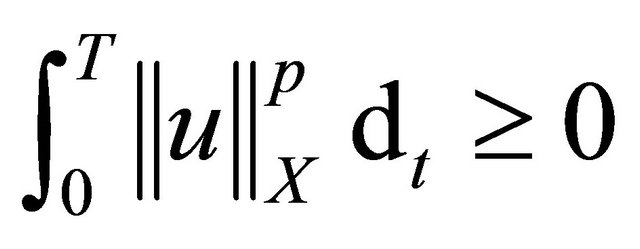 . So we have
. So we have 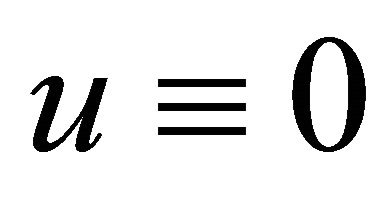
for a.e. time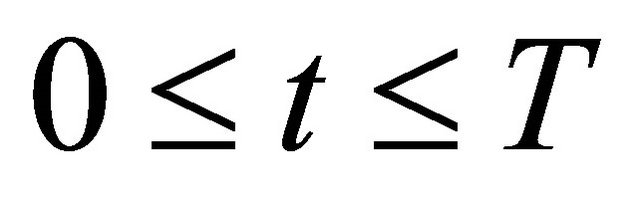 . This completes the proof of Theorem 1.1.
. This completes the proof of Theorem 1.1.
6. Conclusion
In this paper, we established the existence and uniqueness of weak solutions for initial/boundary-value parabolic problems with nonlinear perturbation term in weighted Sobolev space. First, we investigated the compact imbedding in weighted Sobolev space, which can be imbedded compactly into 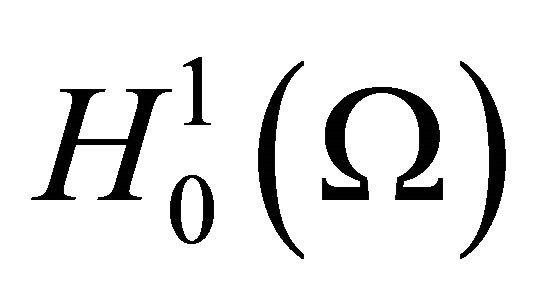 and
and 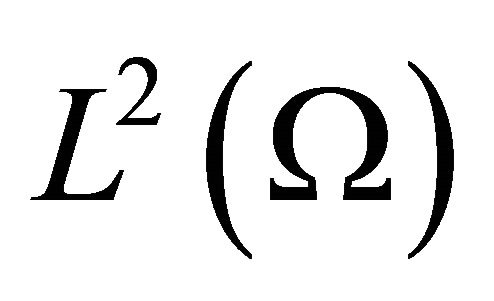 spaces. By exploiting Sobolev interpolation inequalities and extending Galerkin’s method to a new class of nonlinear problems, we proofed the energy estimates of the equations and furthermore obtained the unique weak solution of the problem.
spaces. By exploiting Sobolev interpolation inequalities and extending Galerkin’s method to a new class of nonlinear problems, we proofed the energy estimates of the equations and furthermore obtained the unique weak solution of the problem.
REFERENCES
- C. O. Alvesa and A. El Hamidib, “Nehari Manifold and Existence of Positive Solutions to a Class of Quasilinear Problems,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 60, No. 4, 2005, pp. 611-624. doi:10.1016/j.na.2004.09.039
- K. J. Brown and Y. P. Zhang, “The Nehari Manifold for a Semilinear Elliptic Problem with a Sign-Changing Weight Function,” Journal of Differential Equations, Vol. 193, No. 2, 2003, pp. 481-499. doi:10.1016/S0022-0396(03)00121-9
- J. Huang and Z. L. Pu, “The Nehari Manifold of Nonlinear Elliptic Equations,” Journal of Sichuan Normal University, Vol. 31, No. 2, 2007, pp. 18-32.
- T. Bartsch and M. Willem, “On an Elliptic Equation with Concave and Convex Nonlinearities,” Proceedings of the American Mathematical Society, Vol. 123, 1995, pp. 3555-3561. doi:10.1090/S0002-9939-1995-1301008-2
- P. Drabek, A. kufner and F. Nicolosi, “Quasilinear Elliptic Equations with Degenerations and Singularities,” Walter de Gruyter, Berlin, 1997. doi:10.1515/9783110804775
- P. A. Binding, P. Drabek and Y. X. Huang, “On Neumann Boundary Value Problems for Some Quasilinear Elliptic Equations,” Electronic Journal of Differential Equations, Vol. 1997, No. 5, 1997, pp. 1-11.
- R. A. Adams and J. F. F. John, “Sobolev Space,” Academy Press, New York, 2009.
- M. Renardy and R. Rogers, “An Introduction to Partial Differential Equations,” Springer, New York, 2004.
- L. Evans, “Partial Differential Equations,” American Mathematical Society, Providence, 1998.
- A. Antonio, “On Compact Imbedding Theorems in Weighted Sobolev Spaces,” Czechoslovak Mathematical Journal, Vol. 104, No. 29, 1979, pp. 635-648.
- T. F. Wu, “On Semilinear Elliptic Equations Involving Concave-Convex Nonlinearities and Sign-Changing Weight Function,” Journal of Mathematical Analysis and Applications, Vol. 318, No. 1, 2006, pp. 253-270. doi:10.1016/j.jmaa.2005.05.057
- M. L. Miotto and O. H. Miyagaki, “Multiple Positive Solutions for Semilinear Dirichlet Problems with SignChanging Weight Function in Infinite Strip Domains,” Nonlinear Analysis: Theory, Methods & Applications, Vol. 71, No. 7-8, 2009, pp. 3434-3447. doi:10.1016/j.na.2009.02.010
- M. A. Nielsen and I. L. Chuang, “Quantum Computation and Quantum Information,” Cambridge University Press, Cambridge, 2000.
NOTES
*The project is supported by NSF of China (10971164).
#Corresponding author.

