Advances in Pure Mathematics
Vol. 3 No. 7 (2013) , Article ID: 38607 , 4 pages DOI:10.4236/apm.2013.37085
Finite Element Analysis for Singularly Perturbed Advection-Diffusion Robin Boundary Values Problem*
School of Mathematics and Physics, Anhui University of Technology, Ma’anshan, China
Email: slchen@ahut.edu.cn, wghou@ahut.edu.cn, chaodao987@163.com
Copyright © 2013 Songlin Chen et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 14, 2012; revised December 16, 2012; accepted January 21, 2013
Keywords: Singular Perturbation; Advection-Diffusion; Robin BVP; Finite Element Method; Shishkin Mesh; Error Estimation
ABSTRACT
A singularly perturbed advection-diffusion two-point Robin boundary value problem whose solution has a single boundary layer is considered. Based on the piecewise linear polynomial approximation, the finite element method is applied to the problem. Estimation of the error between solution and the finite element approximation is given in energy norm on shishkin-type mesh.
1. Introduction
We consider the singularly perturbed advection-diffusion Robin boundary values problem
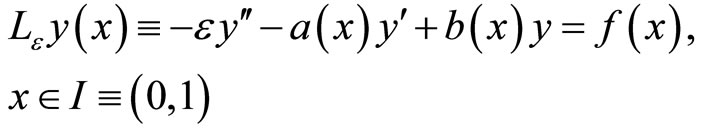 (1)
(1)
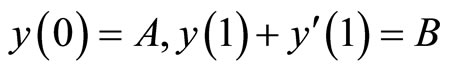 (2)
(2)
with sufficiently smooth functions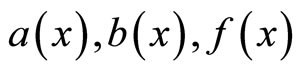 , and a small positive parameter
, and a small positive parameter . We assume that
. We assume that  be decreasing monotonously, moreover
be decreasing monotonously, moreover
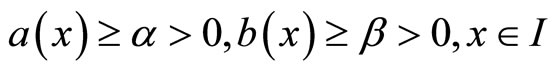 (3)
(3)
which guarantees the unique solvability of the problem. It is well known that there exists a boundary layer of width 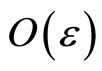 at
at 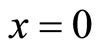 (see [1], K.W. Chang & F.A. Howes 1984). Standard numerical methods for singularly perturbed problem exhibit spurious error unless the layeradapted-mesh, such as Shishkin mesh, B-mesh(see [2-7]) are employed, for the solutions of singularly perturbed problem usually contain layers. The main objective of the paper is to use the method of singular perturbation to give the estimation of error between solution and the finite element approximation w.r.t. some energy norm on shishkin-type mesh.
(see [1], K.W. Chang & F.A. Howes 1984). Standard numerical methods for singularly perturbed problem exhibit spurious error unless the layeradapted-mesh, such as Shishkin mesh, B-mesh(see [2-7]) are employed, for the solutions of singularly perturbed problem usually contain layers. The main objective of the paper is to use the method of singular perturbation to give the estimation of error between solution and the finite element approximation w.r.t. some energy norm on shishkin-type mesh.
Throughout the paper, we shall use C to denote a generic positive constant ,that is independent of ε and mesh, while it can value differently at different places, we occasionally use a subscribed one such as C1.
2. Properties of Solution for Continuous Problem
In this section, some properties and bounds of the exact solution and its derivatives are deduced preliminarily.
Lemma 1 (Maximum principle) Let 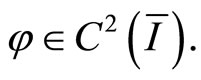 If
If
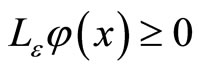 for
for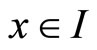 ,
, 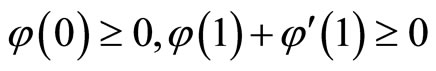 ,then
,then
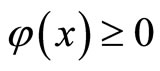 for
for 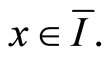
Proof. Assume that there exists 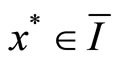 such that
such that
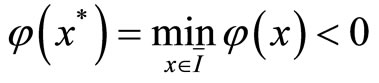
If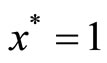 , then there holds
, then there holds  which results in a contradiction to
which results in a contradiction to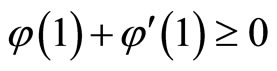 ;Thus
;Thus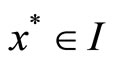 .
.
Since we have 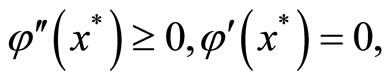 the differential operator on
the differential operator on ![]() at
at  gives
gives
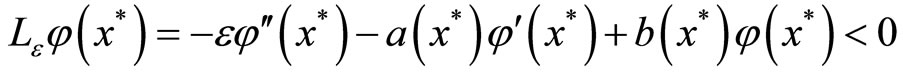
which result in a contradiction to 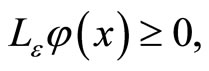 therefore we can conclude that the minimum of
therefore we can conclude that the minimum of ![]() is non-negative.
is non-negative.
Lemma 2 (Comparison principle) If 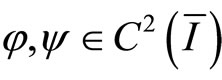 satisfy
satisfy 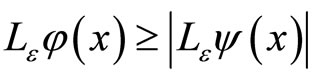 for
for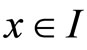 , and
, and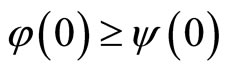 ,
,
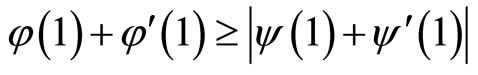 , then
, then 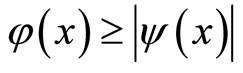 for all
for all
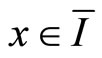 .
.
Lemma 3 (Stability result) If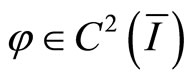 , then we have
, then we have
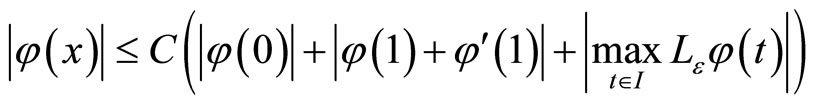
for all .
.
The Proofs of Lemma 2 and Lemma 3 are followed essentially from Lemma 1. (See [3] Roos, Stynes and Tobiska, (1996)).
Lemma 4 Let  be the solution to (1) (2). then there exists a constant C, such that for all
be the solution to (1) (2). then there exists a constant C, such that for all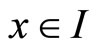 , we have the splitting
, we have the splitting
 (4)
(4)
where the regular component u(x) satisfy
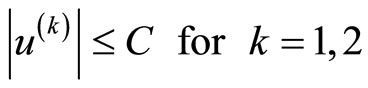 (5)
(5)
while the layer component 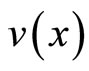 satisfy
satisfy
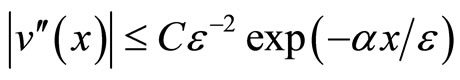 . (6)
. (6)
Proof. It is known that (see [4] Kellogg 1978, Chang & Howes 1984)

We assume  spontaneously since singular perturbation.
spontaneously since singular perturbation.
We set 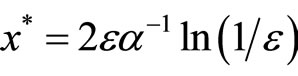 such that
such that 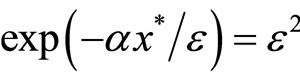
and 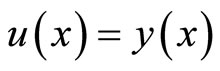 on
on 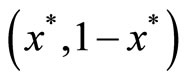 thus
thus 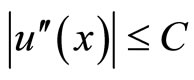 on
on
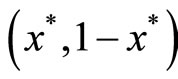 and then extended on (0,1) with
and then extended on (0,1) with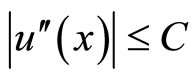 ;
;
Next let

Then considering that 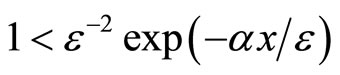 on
on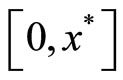 , we know that
, we know that 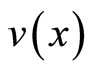 satisfy
satisfy
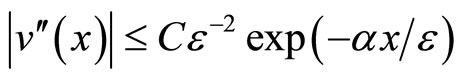 on
on 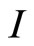
3. Simplification
For simplification of the original problem, we set a transformation
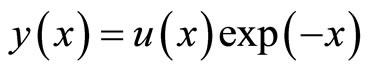
then Equation (1), (2) are transformed to
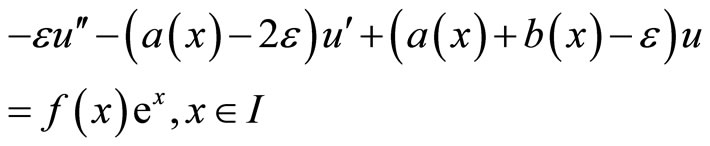

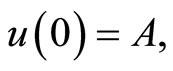
Continuing, we transform the boundary values homogeneously by

at last, the problem (1), (2) are converted to


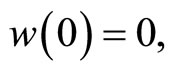
where in the 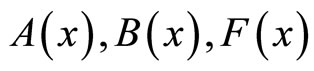 posses the same properties as
posses the same properties as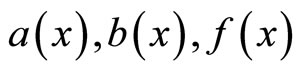 , thus we just make discussion on the simplified problem below
, thus we just make discussion on the simplified problem below
 (1’)
(1’)

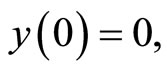 (2’)
(2’)
4. The Analysis of Finite Element Approximation
We consider the Galerkin approximation in form of Find 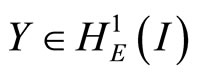 such that
such that
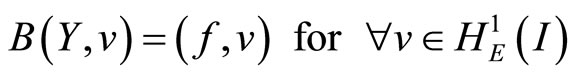 (7)
(7)
where , the bilinear form
, the bilinear form
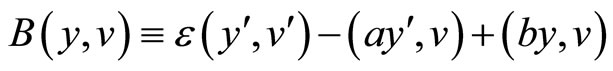
And a natural norm associated with  is chosen by
is chosen by
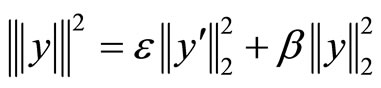
wherein

is the usual 2-norm.
It is easy to see that  is coercive with respect to
is coercive with respect to  by the assumption of the monotony of
by the assumption of the monotony of 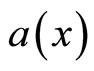 which guarantees the existence of the solution of (7) (see [8-10]). Let N be an even positive integer that denotes the number of mesh intervals.
which guarantees the existence of the solution of (7) (see [8-10]). Let N be an even positive integer that denotes the number of mesh intervals.
We consider the space of piecewise linear function denoted by 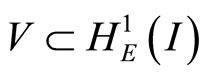 as our work space,
as our work space, 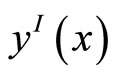 denotes the piecewise linear interpolant to
denotes the piecewise linear interpolant to  at some special mesh points on I, We’ll utmost estimate the error
at some special mesh points on I, We’ll utmost estimate the error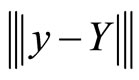 .
.
Firstly we have
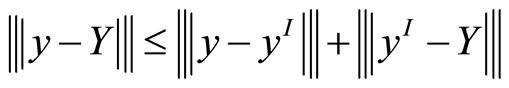 (8)
(8)
For the second term of inequality (8), we make use of the coerciveness, continuousness of  and the Galerkin orthogonality relation:
and the Galerkin orthogonality relation: 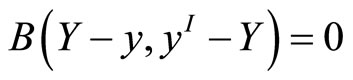 to obtain that
to obtain that

Thus
 . (9)
. (9)
Combined with (8), we just need to estimate the interpolation error bound  below.
below.
Lemma 5 The solution  of (1’), (2’) and its piecewise linear interpolant
of (1’), (2’) and its piecewise linear interpolant 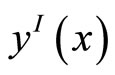 satisfy
satisfy
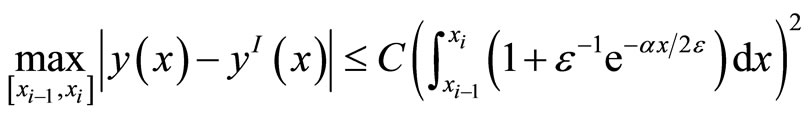
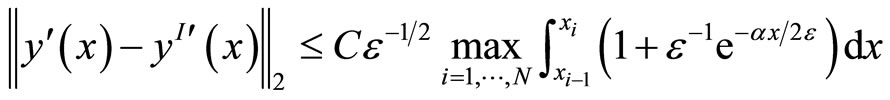
Proof. According to the splitting of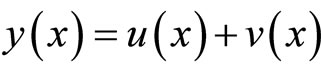 , we have correspondingly
, we have correspondingly
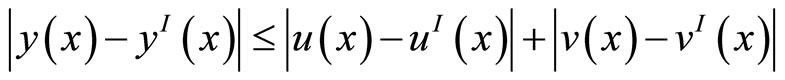
From Lemma 1 we have
 To obtain the estimation for singular component, we use a Taylor expansion
To obtain the estimation for singular component, we use a Taylor expansion
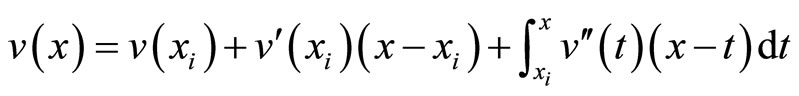
to express the error bound
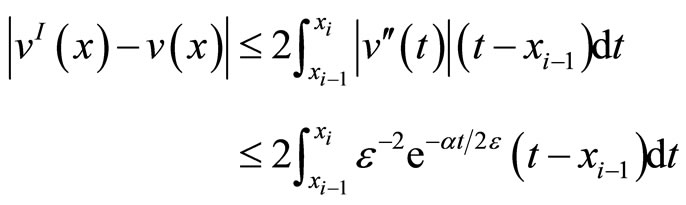
Continuously, we use the inequality involved a positive monotonically decreasing function g on 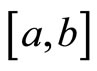

Thus we have
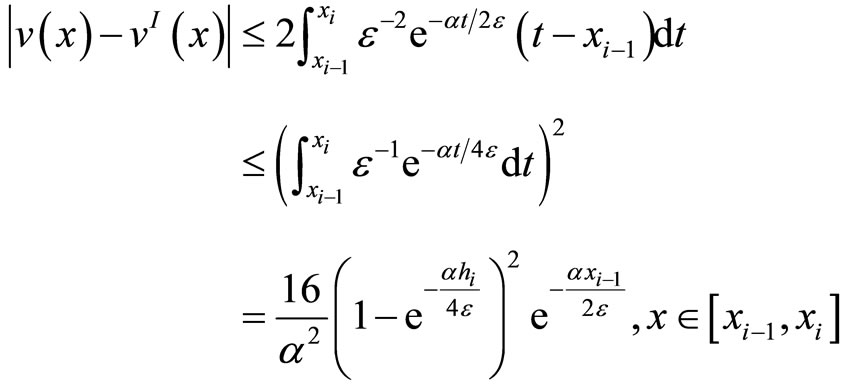
Hence
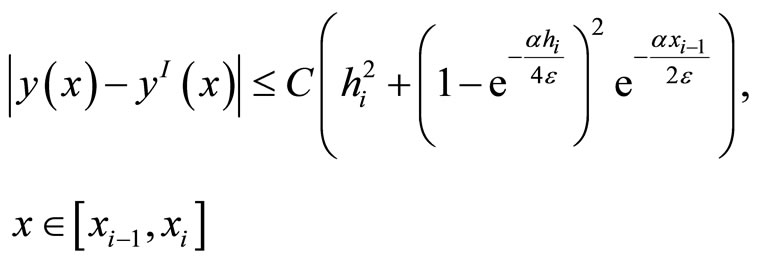
For the proof of the second statement, we have
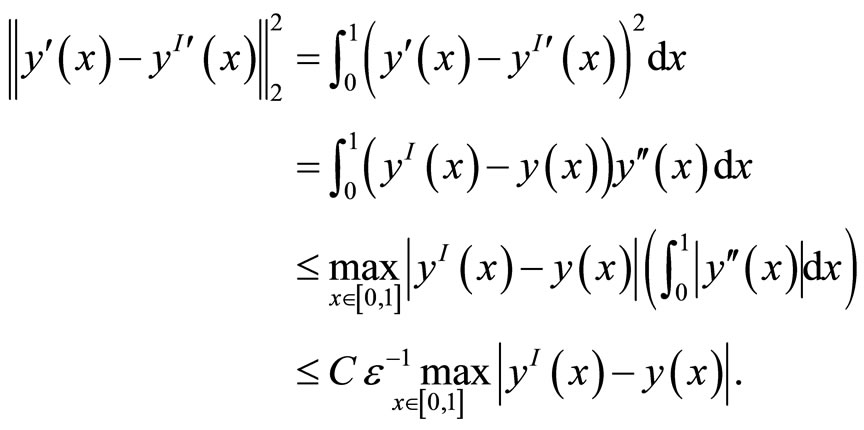
thus, lemma 5 follows.
Theorem For ,
,![]() defined before, when the Shishkin mesh are applied ,we have the parameter uniform error bound in the energy norm naturally associated with the weak formulation of (1’), (2’)
defined before, when the Shishkin mesh are applied ,we have the parameter uniform error bound in the energy norm naturally associated with the weak formulation of (1’), (2’)
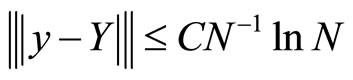 (10)
(10)
Proof. Firstly, we have by triangle inequality and (9)

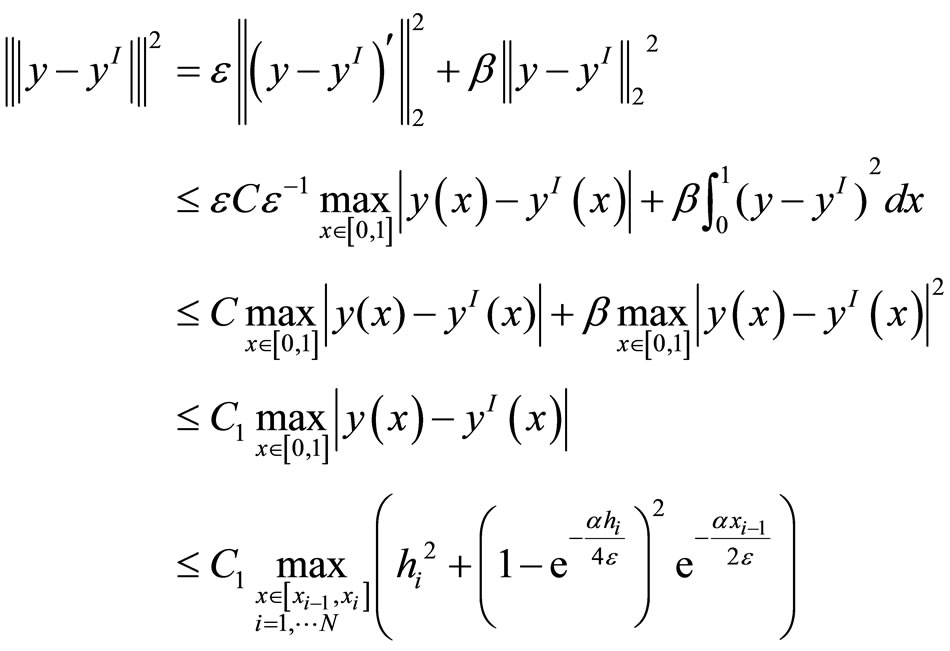
where in C’s and C1 are stated before. thus we have
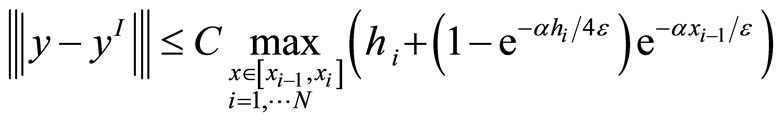
Now we use the classical Shishkin mesh (see [11-13]) by setting the mesh transition parameter defined by
 and allocate uniformly
and allocate uniformly 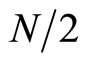
points in each of  and
and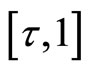 . In practice one typically has
. In practice one typically has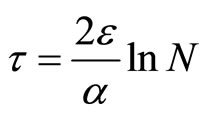 , we just acquiesce in this case thus
, we just acquiesce in this case thus
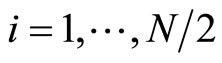
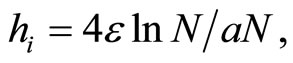
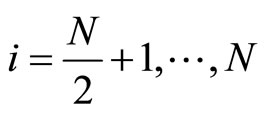
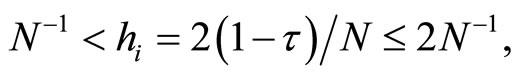
thus for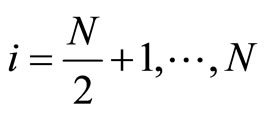 ,
,
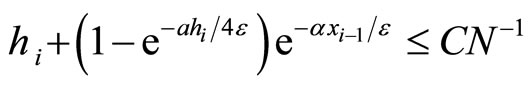
Also for 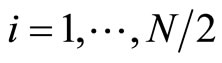
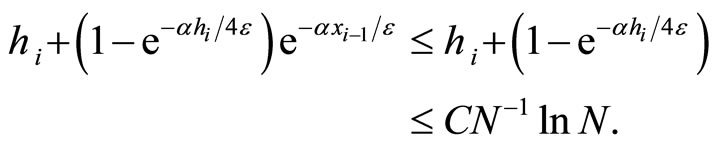
Combining the above two cases reads (10).
Remark. To obtain  estimation, the standard Aubin-Nitche dual verification skill may be involved.
estimation, the standard Aubin-Nitche dual verification skill may be involved.
The superconvergence phenomena on Shishkin mesh for the convection-diffusion problems can be discussed according to Z. Zhang (see [13,14]).
REFERENCES
- K. W. Chang and F. A. Howes, “Nonlinear Singular Perturbation Phenomena: Theory and Applications,” SpringVerlag, New York, 1984.
- S. C. Brenner and L. R. Scott, “The Mathematical Theory of Finite Element Methods,” Springer, Berlin, 1994. http://dx.doi.org/10.1007/978-1-4757-4338-8
- H. G. Roos, M. Stynes and L. Tobiska, “Numerical Methods for Singularly Perturbed Differential Equations,” Springer, Berlin, 1996. http://dx.doi.org/10.1007/978-3-662-03206-0
- R. B. Kellogg and A. Tsan, “Analysis of Some Difference Approximations for a Singular Perturbation Problem without Turning Points,” Mathematics of Computation, Vol. 32, No. 144, 1978, pp. 1025-1039. http://dx.doi.org/10.1090/S0025-5718-1978-0483484-9
- F. Brezzi, L. D. Marini and A. Russo, “On the Choice of Stabilizing Subgrid for Convection-Diffusion Problems,” Computer Methods in Applied Mechanics and Engineering, Vol. 194, No. 2-5, 2005, pp. 127-148. http://dx.doi.org/10.1016/j.cma.2004.02.022
- T. Linβ and N. Madden, “A Finite Element Analysis of Coupled System of Singularly Perturbed Reaction-Diffusion Equations,” Applied Mathematics and Computation, Vol. 148, No. 3, 2004, pp. 869-880. http://dx.doi.org/10.1016/S0096-3003(02)00955-4
- M. K. Kadalbajoo, A. S. Yadaw and D. Kumar, “Comparative Study of Singularly Perturbed Two-Point BVPs via: Fitted-Mesh Finite Difference Method, B-Spline Collocation Method and Finite Element Method,” Applied Mathematics and Computation, Vol. 204, No. 2, 2008, pp. 713-725. http://dx.doi.org/10.1016/j.amc.2008.07.014
- L. P. Franca and E. G. Dutra do Carmo, “The Galerkin Gradient Least Squares Method,” Computer Methods in Applied Mechanics and Engineering, Vol. 74, No. 1, 1989, pp. 41-54. http://dx.doi.org/10.1016/0045-7825(89)90085-6
- F. Ilinca and J.-F. Hétu, “Galerkin Gradient Least- Squares Formulations for Transient Conduction Heat Transfer,” Computer Methods in Applied Mechanics and Engineering, Vol. 191, No. 27-28, 2002, pp. 3073-3097. http://dx.doi.org/10.1016/S0045-7825(02)00242-6
- T. Linβ, “Layer-Adapted Meshes for Convection-Diffusion Problems,” Computer Methods in Applied Mechanics and Engineering, Vol. 192, No. 9-10, 2003, pp. 1061- 1105. http://dx.doi.org/10.1016/S0045-7825(02)00630-8
- M. Stynes, “Steady-State Convection-Diffusion Problems,” Acta Numerica, Vol. 14, 2005, pp. 445-508. http://dx.doi.org/10.1017/S0962492904000261
- M. Stynes and L. Tobiska, “The SDFEM for a Convection-Diffusion Problem with a Boundary Layer: Optimal Error Analysis and Enhancement of Accuracy,” SIAM Journal on Numerical Analysis, Vol. 41, No. 5, 2003, pp. 1620-1642.
- Z. Zhang, “Finite Element Superconvergence Approximation of One Dimensional Singularly Perturbed Problems,” Numerical Methods for Partial Differential Equations, Vol. 18, No. 3, 2002, pp. 374-395. http://dx.doi.org/10.1002/num.10001
- Z. Zhang, “Finite Element Super-Convergence on Shishkin Mesh for 2-d Convection-Diffusion Problems,” Mathematical and Computer Modelling, Vol. 72, No. 243, 2003, pp. 1147-1177. http://dx.doi.org/10.1090/S0025-5718-03-01486-8
NOTES
*This research was supported by the National Natural Science Foundation of China (Grant No. 50975003).

