Advances in Pure Mathematics
Vol.3 No.2(2013), Article ID:28744,10 pages DOI:10.4236/apm.2013.32040
Concircular π-Vector Fields and Special Finsler Spaces*
1Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt
2Center for Theoretical Physics (CTP), The British University in Egypt (BUE), Cairo, Egypt
3Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt
Email: nlyoussef@sci.cu.edu.eg, nlyoussef2003@yahoo.fr, amr.hassan@fsci.bu.edu.eg, amrsoleiman@yahoo.com
Received September 21, 2012; revised November 28, 2012; accepted December 12, 2012
Keywords: Finsler manifold; Cartan connection; Concurrent π-vector field; Concircular π-vector field; Special Finsler space, Recurrent Finsler space
ABSTRACT
The aim of the present paper is to investigate intrinsically the notion of a concircular π-vector field in Finsler geometry. This generalizes the concept of a concircular vector field in Riemannian geometry and the concept of concurrent vector field in Finsler geometry. Some properties of concircular π-vector fields are obtained. Different types of recurrence are discussed. The effect of the existence of a concircular π-vector field on some important special Finsler spaces is investigated. Almost all results obtained in this work are formulated in a coordinate-free form.
1. Introduction
The concept of a concurrent vector field in Riemannian geometry had been introduced and investigated by K. Yano [1]. Concurrent vector fields in Finsler geometry had been studied locally by S. Tachibana [2], M. Matsumoto and K. Eguchi [3]. In [4], we investigated intrinsically concurrent vector fields in Finsler geometry. On the other hand, the notion of a concircular vector field in Riemannian geometry has been studied by Adat and Miyazawa [5]. Concircular vector fields in Finsler geometry have been studied locally by Prasad et al. [6].
In this paper, we introduce and investigate intrinsically the notion of a concircular π-vector field in Finsler geometry, which generalizes the concept of a concircular vector field in Riemannian geometry and the concept of a concurrent vector field in Finsler geometry. Some properties of concircular π-vector fields are obtained. These properties, in turn, play a key role in obtaining other interesting results. Different types of recurrence are discussed. The effect of the existence of a concircular π-vector field on some important special Finsler spaces is investigated: Berwald, Landesberg, c-reducible, semi-creducible, quasi-c-reducible, c2-like, s3-like, p-reducible, p2-like, h-isotropic, Th-recurrent, Tv-recurrent, etc.
Global formulation of different aspects of Finsler geometry may help better understand these aspects without being trapped into the complications of indices. This is one of the motivations of the present work, where almost all results obtained are formulated in a coordinate-free form.
2. Notation and Preliminaries
In this section, we give a brief account of the basic concepts of the pullback approach to intrinsic Finsler geometry necessary for this work. For more details, we refer to [7] and [8]. We shall use the same notations of [7].
In what follows, we denote by 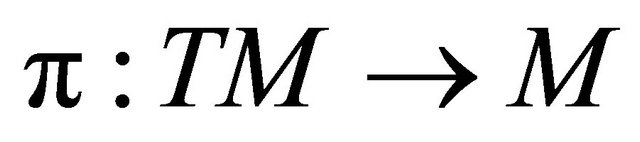 the tangent bundle to
the tangent bundle to ,
, 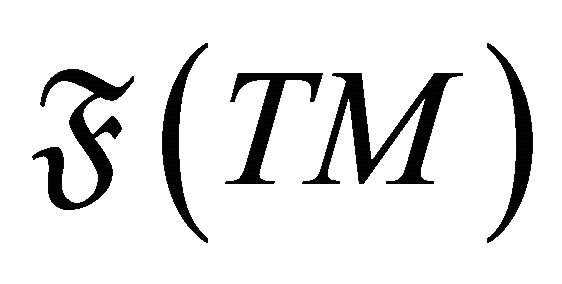 the algebra of
the algebra of  functions on
functions on ,
,  the
the 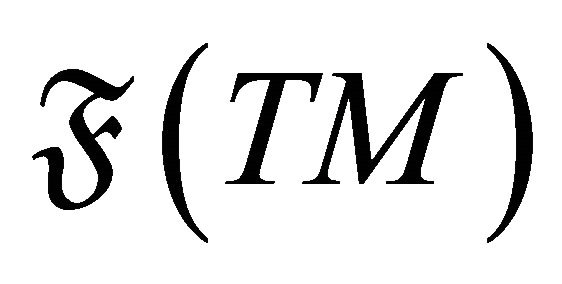 -module of differentiable sections of the pullback bundle
-module of differentiable sections of the pullback bundle . The elements of
. The elements of 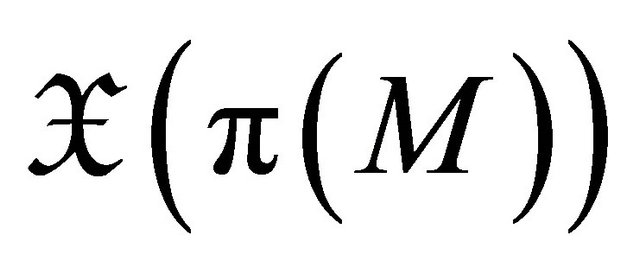 will be called
will be called  -vector fields and will be denoted by barred letters
-vector fields and will be denoted by barred letters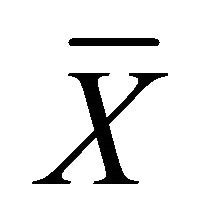 . The tensor fields on
. The tensor fields on  will be called
will be called  -tensor fields. The fundamental
-tensor fields. The fundamental  -vector field is the
-vector field is the  -vector field
-vector field 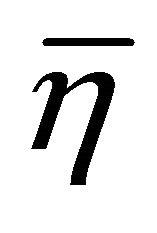 defined by
defined by 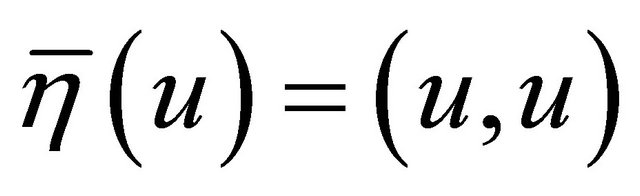 for all
for all .
.
We have the following short exact sequence of vector bundles
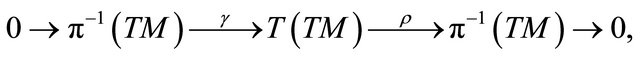
with the well known definitions of the bundle morphisms 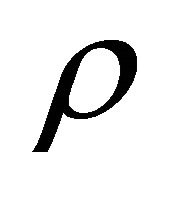 and
and . The vector space
. The vector space 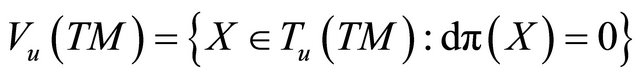 is the vertical space to
is the vertical space to  at
at .
.
Let 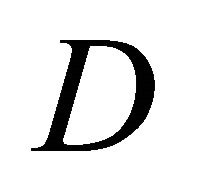 be a linear connection on the pullback bundle
be a linear connection on the pullback bundle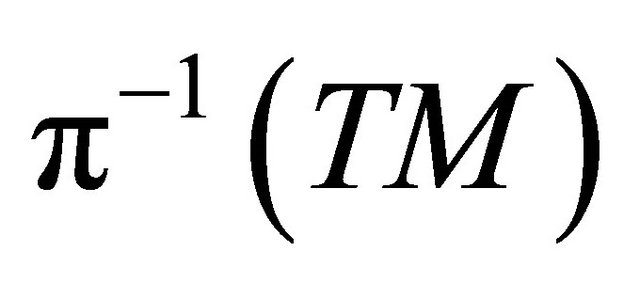 . We associate with
. We associate with 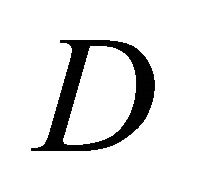 the map
the map 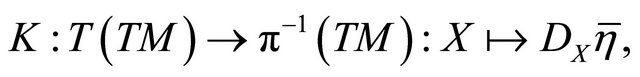 called the connection map of
called the connection map of . The vector space
. The vector space  is the horizontal space to
is the horizontal space to  at
at . The connection
. The connection  is said to be regular if
is said to be regular if
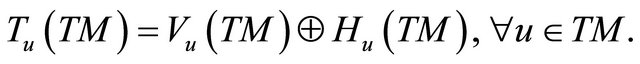
If  is endowed with a regular connection, then the vector bundle maps
is endowed with a regular connection, then the vector bundle maps 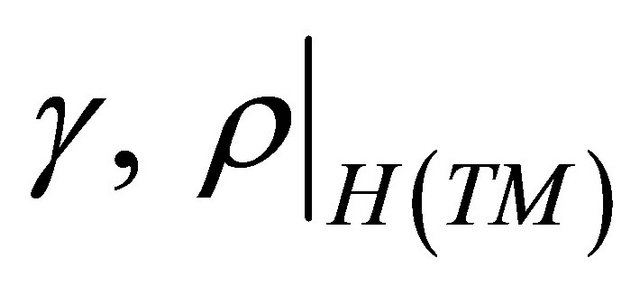 and
and  are vector bundle isomorphisms. The map
are vector bundle isomorphisms. The map 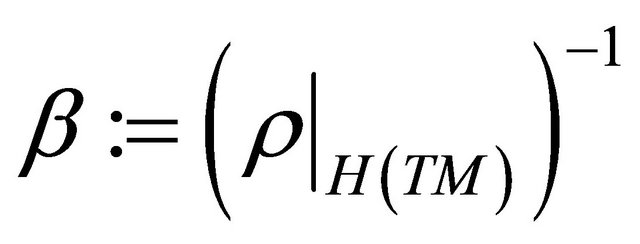 will be called the horizontal map of the connection
will be called the horizontal map of the connection . We have
. We have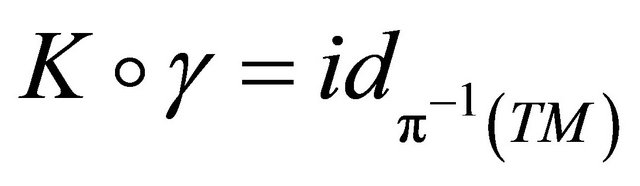 .
.
The horizontal ((h)h-) and mixed ((h)hv-) torsion tensors of , denoted by
, denoted by 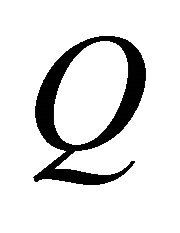 and
and 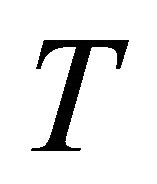 respectively, are defined by
respectively, are defined by
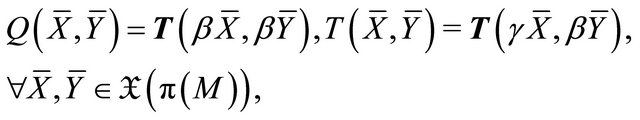
where  is the (classical) torsion tensor field associated with
is the (classical) torsion tensor field associated with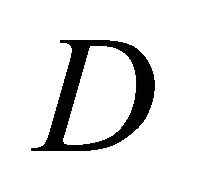 .
.
The horizontal (h-), mixed (hv-) and vertical (v-) curvature tensors of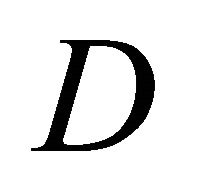 , denoted by
, denoted by 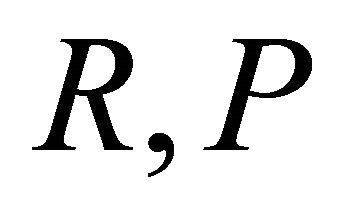 and
and 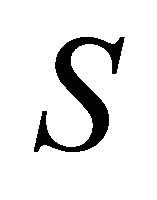 respectively, are defined by
respectively, are defined by
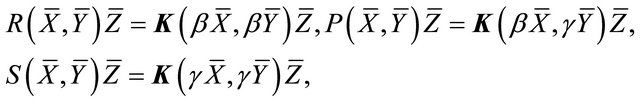 where
where 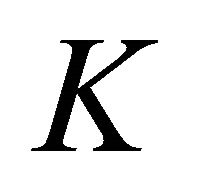 is the (classical) curvature tensor field associated with
is the (classical) curvature tensor field associated with .
.
The contracted curvature tensors of , denoted by
, denoted by 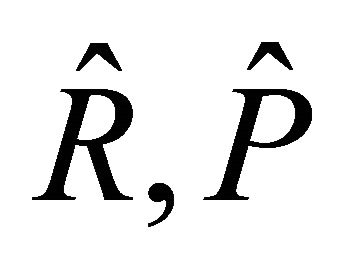 and
and  respectively, known also as the (v)h-, (v)hvand (v)v-torsion tensors, are defined by
respectively, known also as the (v)h-, (v)hvand (v)v-torsion tensors, are defined by
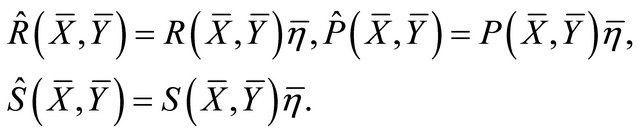
If  is endowed with a metric
is endowed with a metric 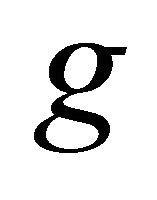 on
on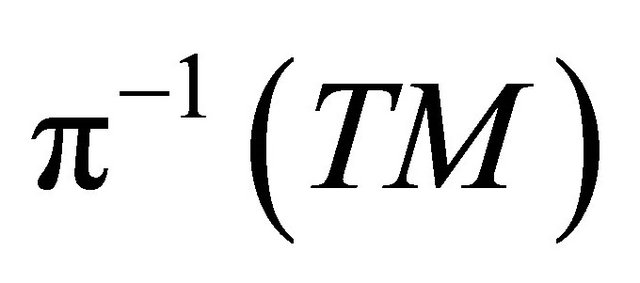 , we write
, we write
 (1)
(1)
The following theorem guarantees the existence and uniqueness of the Cartan connection on the pullback bundle.
Theorem 2.1. [9] Let 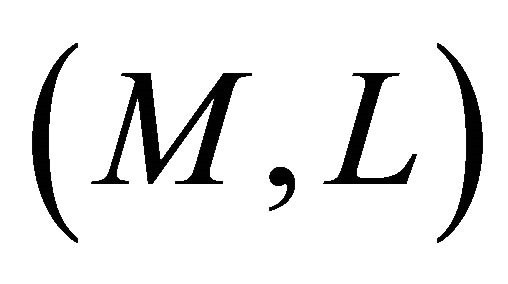 be a Finsler manifold and
be a Finsler manifold and 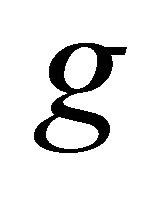 the Finsler metric defined by
the Finsler metric defined by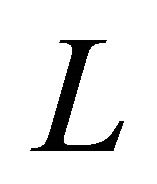 . There exists a unique regular connection
. There exists a unique regular connection  on
on 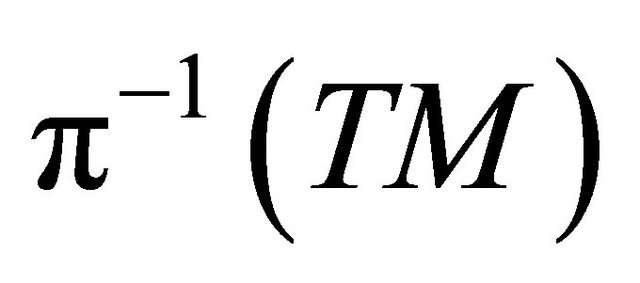 such that
such that
a)  is metric:
is metric: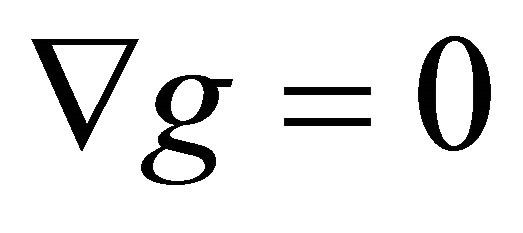 ;
;
b) The (h)h-torsion of  vanishes:
vanishes: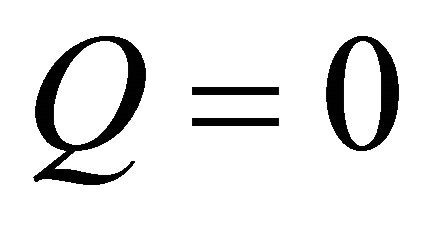 ;
;
c) The (h)hv-torsion 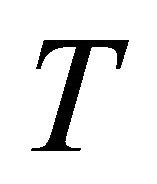 of
of  satisfies:
satisfies:
 .
.
Such a connection is called the Cartan connection associated with the Finsler manifold .
.
One can show that the (h)hv-torsion of the Cartan connection is symmetric and has the property that 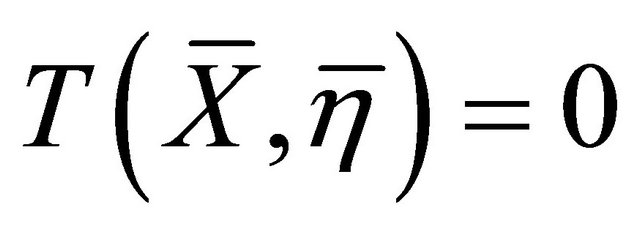 for all
for all  [9].
[9].
Concerning the Berwald connection on the pullback bundle, we have Theorem 2.2. [9] Let 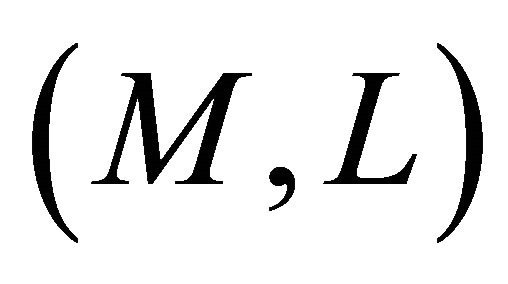 be a Finsler manifold. There exists a unique regular connection
be a Finsler manifold. There exists a unique regular connection 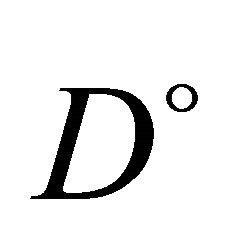 on
on  such that a)
such that a)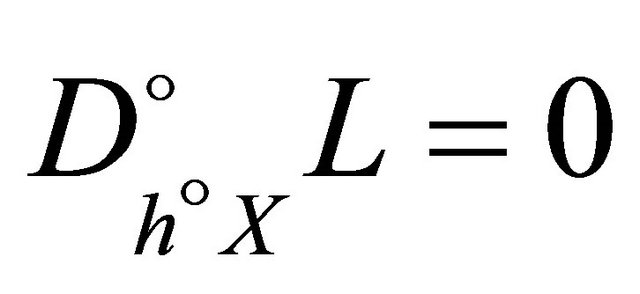 ;
;
b)  is torsion-free:
is torsion-free: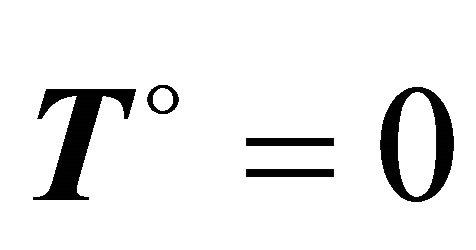 ;
;
c) The (v)hv-torsion tensor  of
of  vanishes:
vanishes:
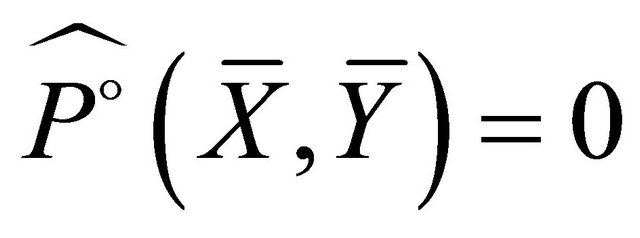 .
.
Such a connection is called the Berwald connection associated with the Finsler manifold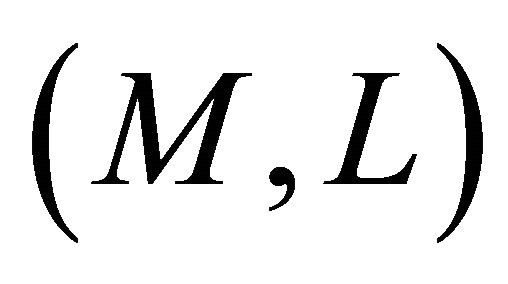 .
.
Theorem 2.3. [9] Let 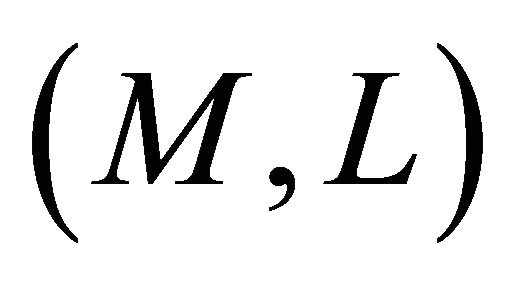 be a Finsler manifold. The Berwald connection
be a Finsler manifold. The Berwald connection  is expressed in terms of the Cartan connection
is expressed in terms of the Cartan connection  as
as

In particular, we have:
a) 
b)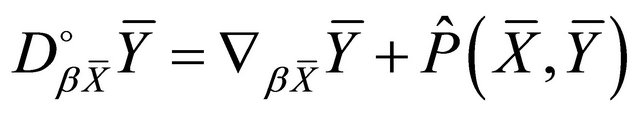 .
.
Finally, for a Finsler manifold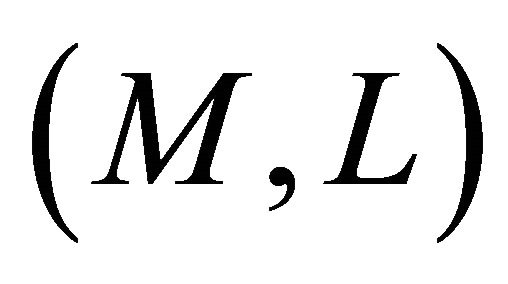 , we use the following definitions and notations:
, we use the following definitions and notations:
 ,
,
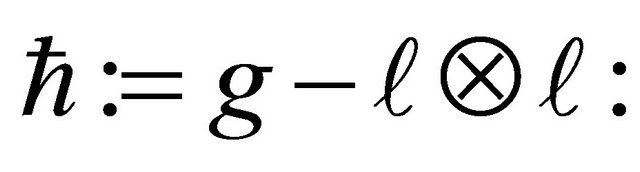 the angular metric tensor,
the angular metric tensor,
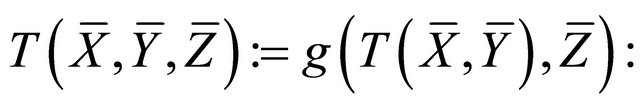 the Cartan tensor,
the Cartan tensor,
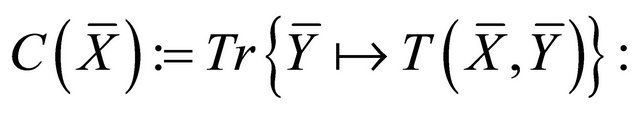 the contracted torsion,
the contracted torsion,

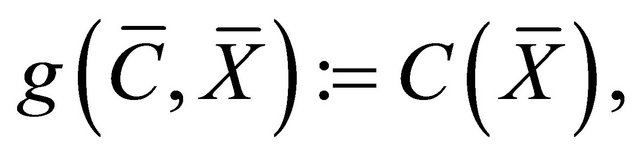 is the
is the  -vector field associated with the
-vector field associated with the  -form
-form ,
,
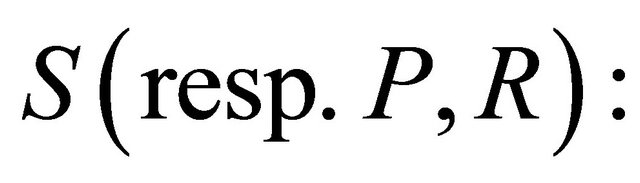 the v-curvature (hv-crvature, h-curvature) tensor of Cartan connection.
the v-curvature (hv-crvature, h-curvature) tensor of Cartan connection.
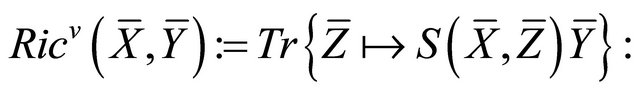 the vertical Ricci tensor,
the vertical Ricci tensor,
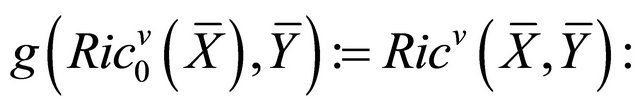 the vertical Ricci map
the vertical Ricci map 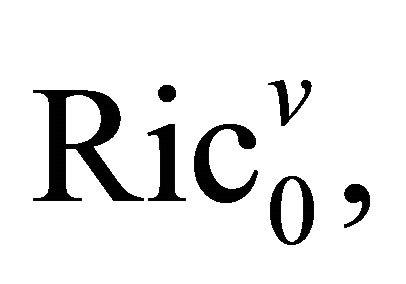
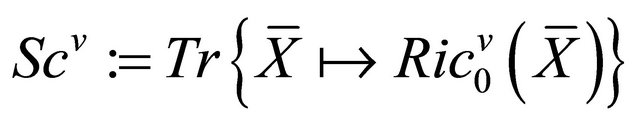 : the vertical Scalar curvature,
: the vertical Scalar curvature,
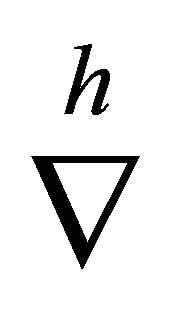 : the h-covariant derivative associated with the Cartan connection,
: the h-covariant derivative associated with the Cartan connection,
 : the v-covariant derivative associated with the Cartan connection.
: the v-covariant derivative associated with the Cartan connection.
3. Concircular π-Vector Fields on a Finsler Manifold
The notion of a concircular vector field has been studied in Riemannian geometry by Adati and Miyazawa [5]. The notion of a concurrent vector field has been investigated locally (resp. intrinsically) in Finsler geometry by Matsumoto and Eguchi [3], Tachibana [2] (resp. Youssef et al. [4]). In this section, we investigate intrinsically the notion of a concircular  -vector field in Finsler geometry, which generalizes the concept of a concircular vector field in Riemannian geometry and the concept of concurrent vector field in Finsler geometry.
-vector field in Finsler geometry, which generalizes the concept of a concircular vector field in Riemannian geometry and the concept of concurrent vector field in Finsler geometry.
Definition 3.1. Let 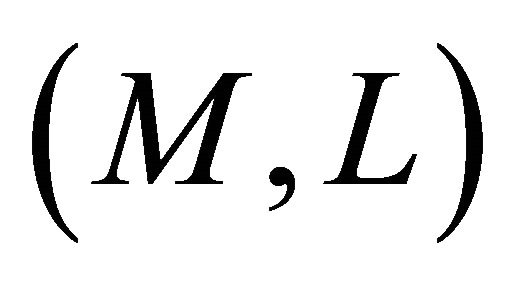 be a Finsler manifold. A π-vector field
be a Finsler manifold. A π-vector field  is called a concircular π-vector field (with respect to the Cartan connection) if it satisfies the following conditions:
is called a concircular π-vector field (with respect to the Cartan connection) if it satisfies the following conditions:
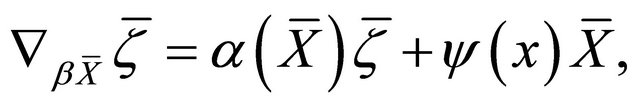 (1)
(1)
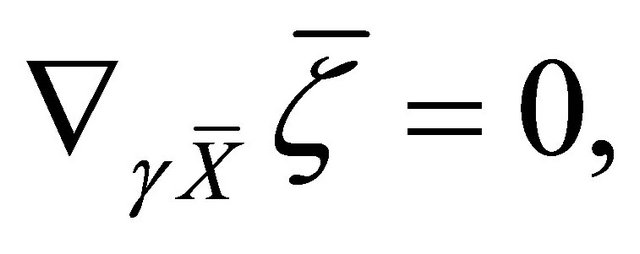 (2)
(2)
where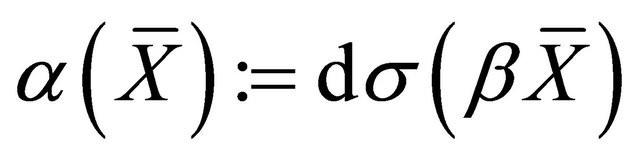 ;
; 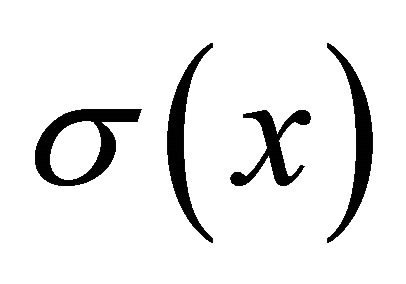 and
and 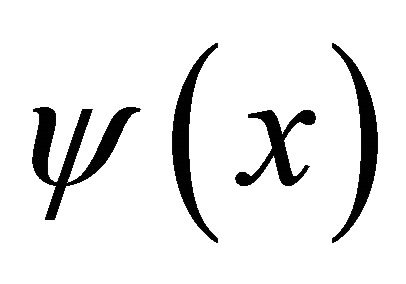 are two non-zero scalar functions on
are two non-zero scalar functions on .
.
In particular, if 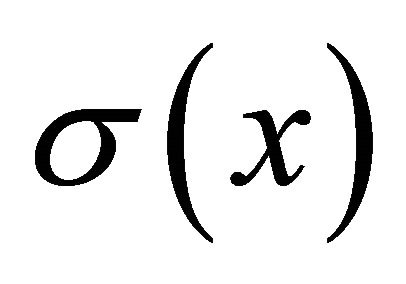 is constant and
is constant and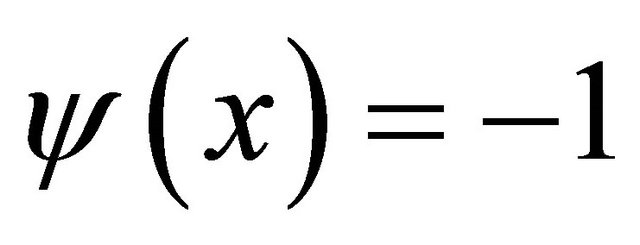 , then
, then  is a concurrent
is a concurrent  -vector field.
-vector field.
The following two Lemmas are useful for subsequent use.
Lemma 3.2. Let 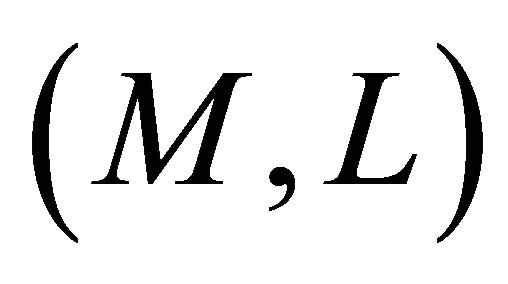 be a Finsler manifold. If
be a Finsler manifold. If 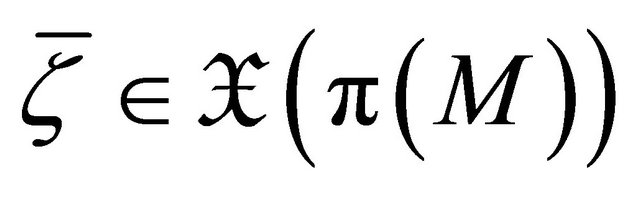 is a concircular
is a concircular  -vector field and
-vector field and 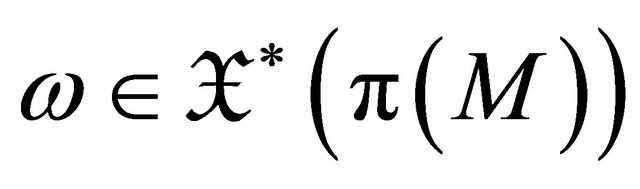 is the
is the  -form defined by
-form defined by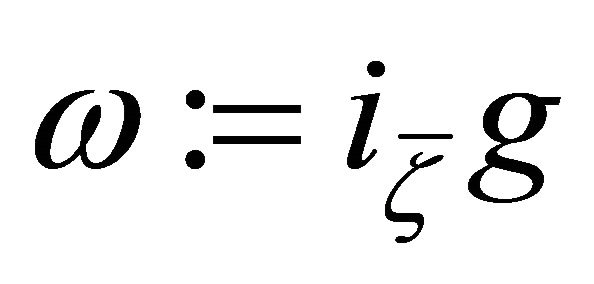 , then
, then  has the properties:
has the properties:
a)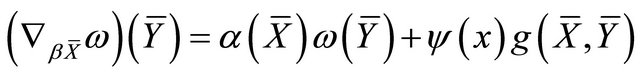 b)
b)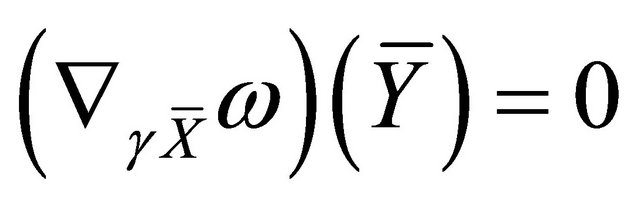 .
.
Proof.
a) Using the fact that , we have
, we have
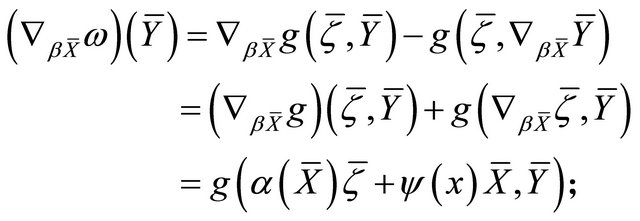
b) The proof is similar to that of (a). □
Lemma 3.3. Let 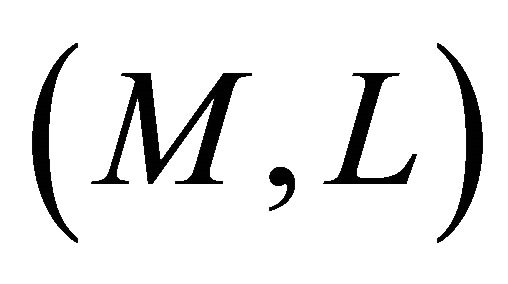 be a Finsler manifold and
be a Finsler manifold and  the Berwald connection on
the Berwald connection on . Then, we have
. Then, we have
a) A  -vector field
-vector field 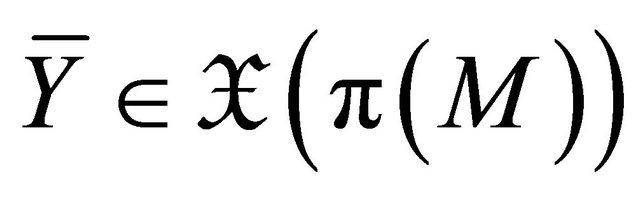 is independent of the directional argument
is independent of the directional argument 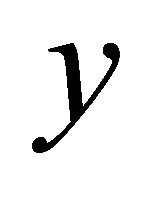 if, and only if,
if, and only if,  for all
for all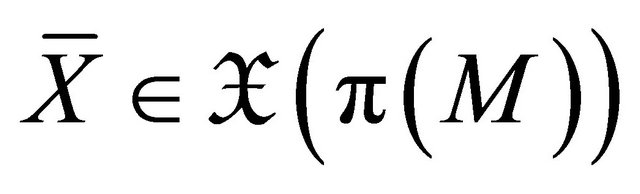 ;
;
b) A scalar (vector)  -form
-form  is independent of the directional argument
is independent of the directional argument 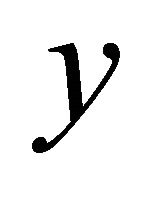 if, and only if,
if, and only if,  for all
for all .
.
Proof. We prove (a) only; the proof of (b) is similar. Let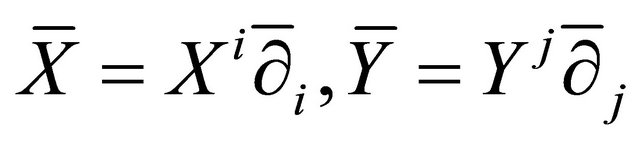 . Then,
. Then,
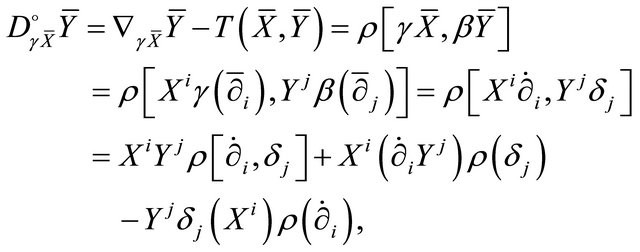
where 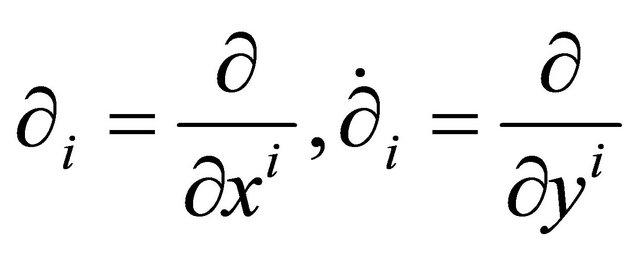 and
and 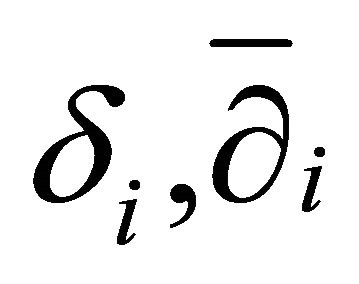 are respectively the bases of the horizontal space and the pullback fibre. As
are respectively the bases of the horizontal space and the pullback fibre. As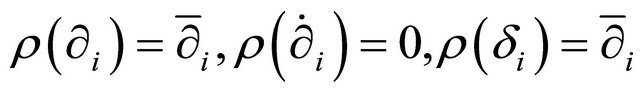 , we have
, we have 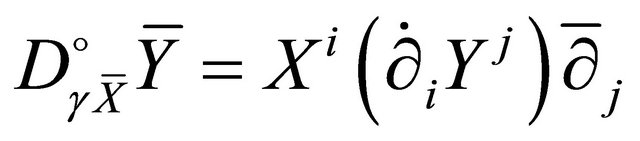 , and so
, and so
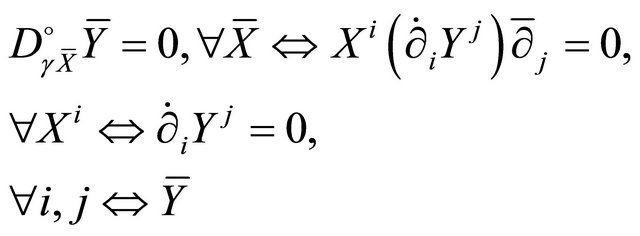
is in dependent of .□
.□
Remark 3.4. From Definition 2.1, Lemma 2.3 and Theorem 1.3, we conclude that a)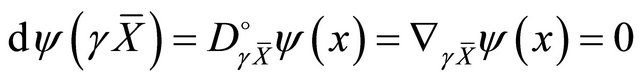 ;
;
b) ;
;
c)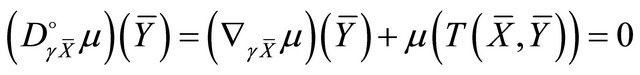 where
where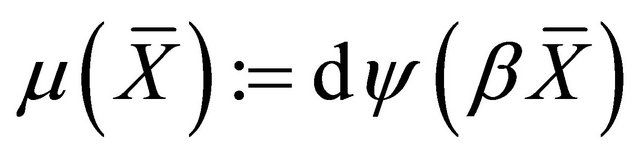 .
.
Now, we have the following
Theorem 3.5. Let 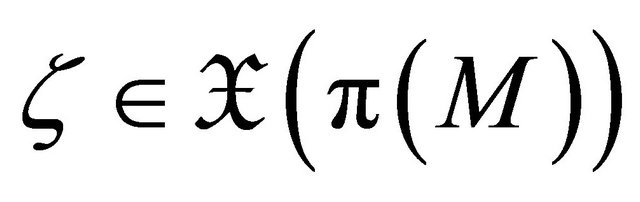 be a concircular
be a concircular  -vector field on
-vector field on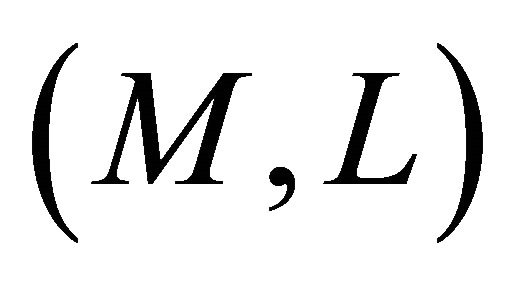 .
.
For the v-curvature tensor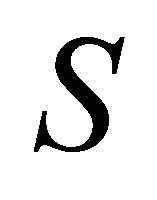 , the following relations hold1:
, the following relations hold1:
a) ;
;
b)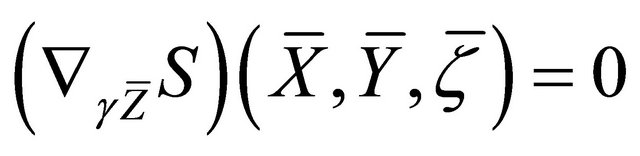 ;
;
c)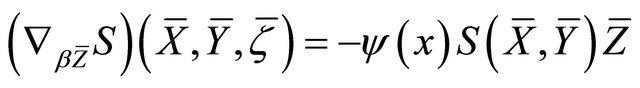 ;
;
d) 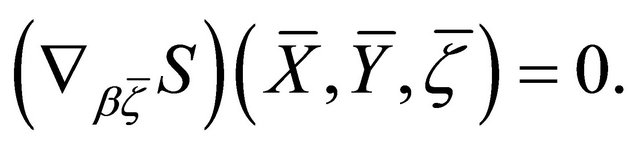
For the hv-curvature tensor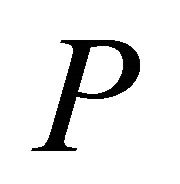 , the following relations hold:
, the following relations hold:
e)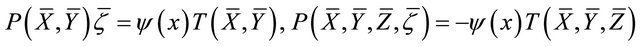 ;
;
f)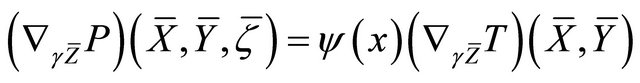 ;
;
g)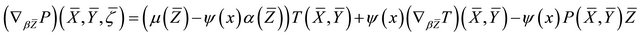 ;
;
h)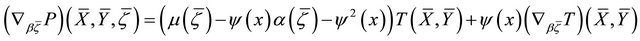 ;
;
For the h-curvature tensor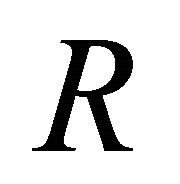 , the following relations hold1:
, the following relations hold1:
i)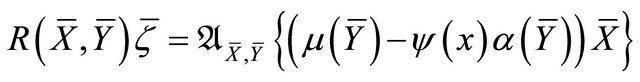 ;
;
j)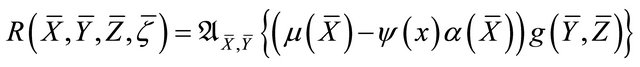 ;
;
k) ;
;
l) 
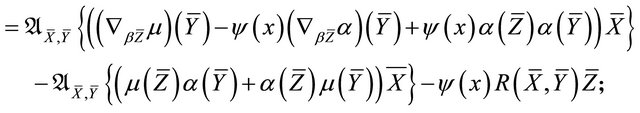
m) 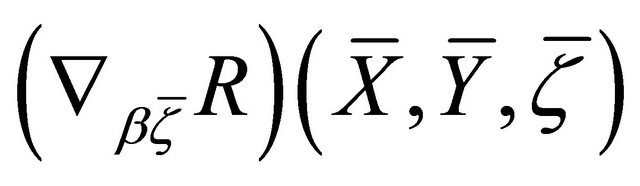

Proof. The proof follows from the properties of the curvature tensors  and
and , investigated in [10], together with Definition 2.1 and Remark 2.4, taking into account the fact that the (h)h-torsion of the Cartan connection vanishes. □
, investigated in [10], together with Definition 2.1 and Remark 2.4, taking into account the fact that the (h)h-torsion of the Cartan connection vanishes. □
In view of the above theorem, we retrieve a result of [4] concerning concurrent  -vector fields.
-vector fields.
Corollary 3.6. Let 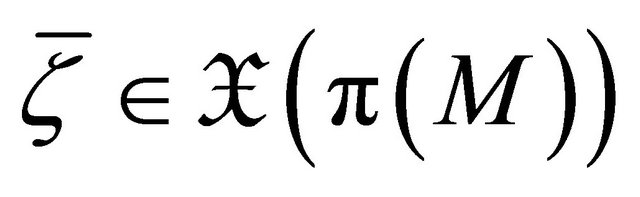 be a concurrent
be a concurrent  -vector field on
-vector field on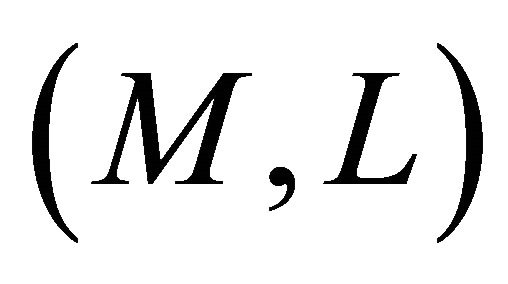 .
.
For the v-curvature tensor , the following relations hold:
, the following relations hold:
a)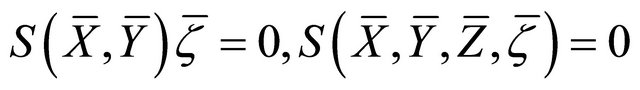 ;
;
b) 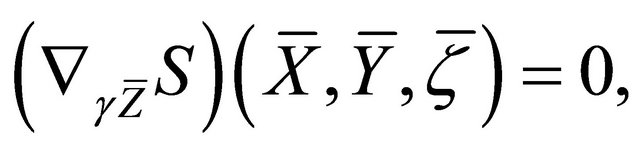
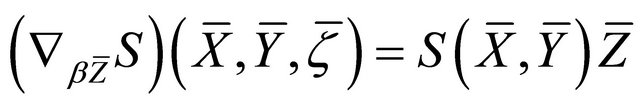 ;
;
c)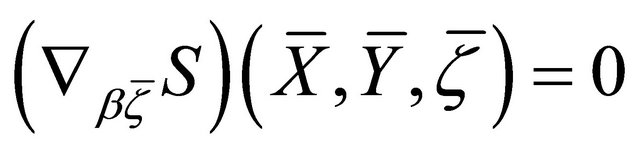 .
.
For the hv-curvature tensor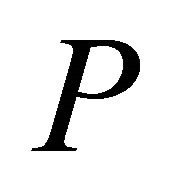 , the following relations hold:
, the following relations hold:
d) 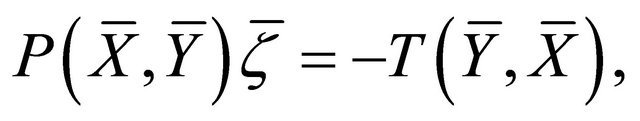
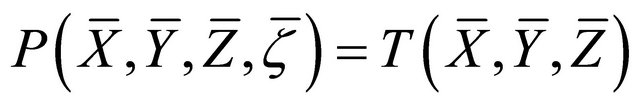 ;
;
e) 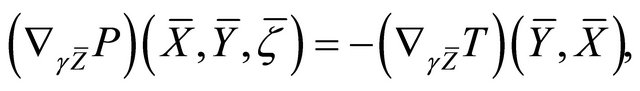
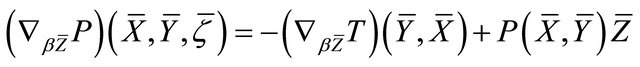 ;
;
f) .
.
For the h-curvature tensor , the following relations hold:
, the following relations hold:
g) ;
;
h) 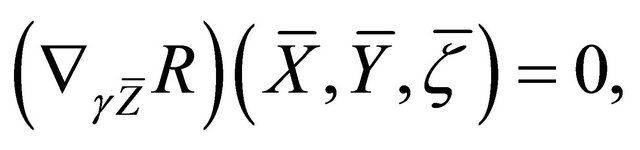
 ;
;
i) .
.
Proof. The proof follows from Theorem 2.5 by letting  be a constant function on
be a constant function on  and
and . □
. □
Proposition 3.7. Let  be a concircular
be a concircular  -vector field. For every
-vector field. For every , we have:
, we have:
a)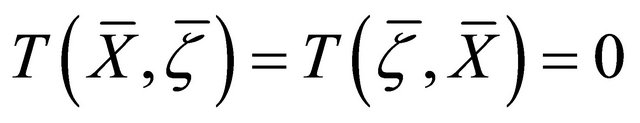 ;
;
b)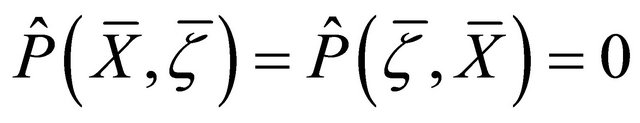 ;
;
c)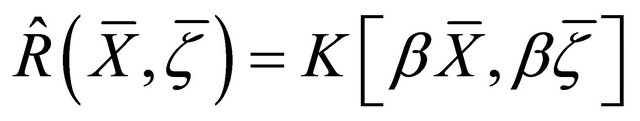 ;
;
d) ;
;
e)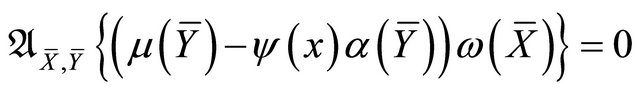 ;
;
f)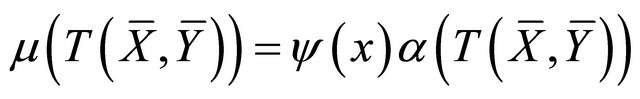 .
.
Proof.
a) From Theorem 2.5(e), by setting  and making use of the symmetry of
and making use of the symmetry of 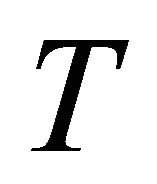 and the identity
and the identity  [10], we obtain
[10], we obtain
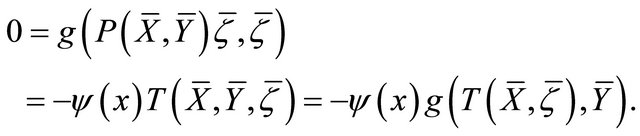
From which, since , the result follows.
, the result follows.
b) We have [10]
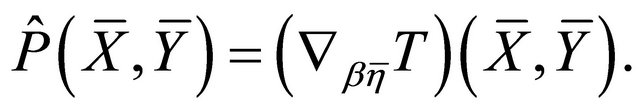
From which, setting , it follows that
, it follows that
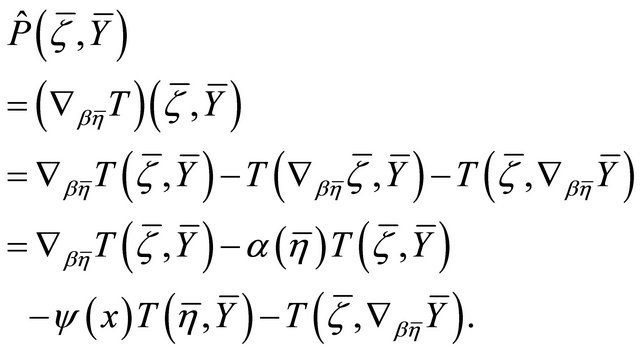
Hence, making use of (a), the symmetry of  and the fact that
and the fact that , the result follows.
, the result follows.
c) Clear.
d) We have from [10],
 (3)
(3)
From which, by setting  in (3), using (b) and the symmetry of
in (3), using (b) and the symmetry of , we conclude that
, we conclude that . Similarly, setting
. Similarly, setting 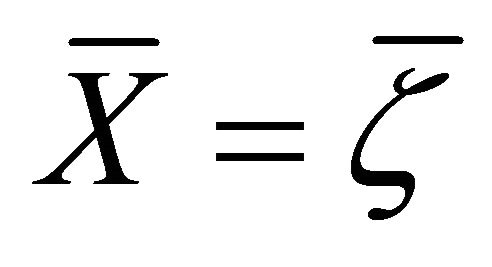 in (3), using (a) and the symmetry of
in (3), using (a) and the symmetry of , we get
, we get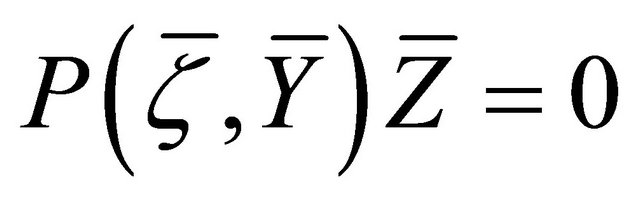 .
.
e) The proof follows from Theorem 2.5 (j) by setting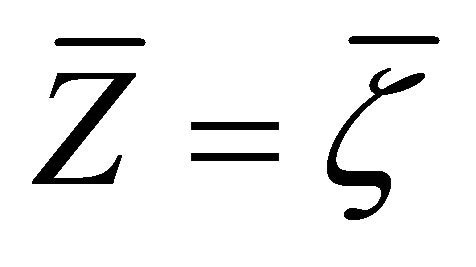 , taking into account the fact that
, taking into account the fact that 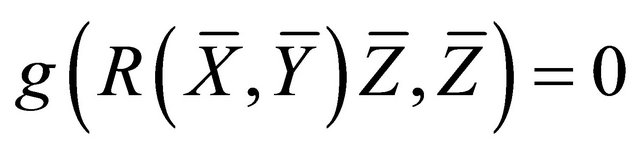 [10].
[10].
f) We have
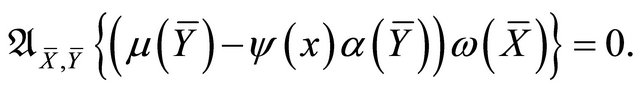
Hence, there exists a scalar function 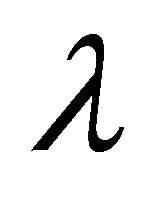 such that
such that
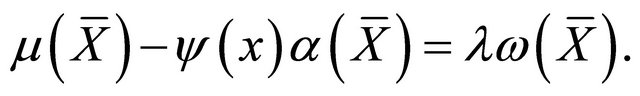
Consequently, using (a) and the symmetry of , we get
, we get
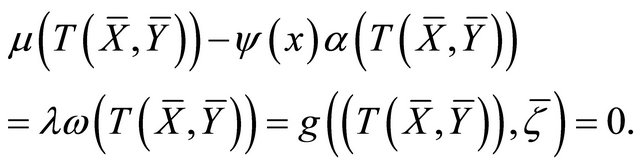
This completes the proof. □
Theorem 3.8. A concircular  -vector field
-vector field  and its associated
and its associated  -form
-form  are independent of the directional argument
are independent of the directional argument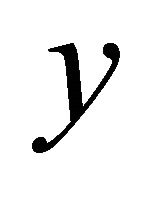 .
.
Proof. By Theorem 1.3(a), we have

From which, by setting  and taking into account (2), Proposition 2.7(a) and Lemma 2.3, we conclude that
and taking into account (2), Proposition 2.7(a) and Lemma 2.3, we conclude that  and
and  is thus independent of the directional argument
is thus independent of the directional argument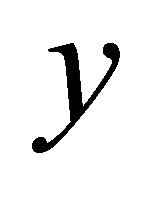 .
.
On the other hand, we have from the above relation

This, together with Lemma 2.2(b), Proposition 2.7(a) and the symmetry of , imply that
, imply that  is also independent of the directional argument
is also independent of the directional argument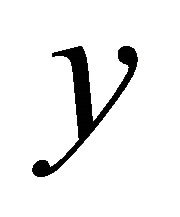 . □
. □
In view of Theorem 1.3 and Proposition 2.7, we have Theorem 3.9. A  -vector field
-vector field  on
on 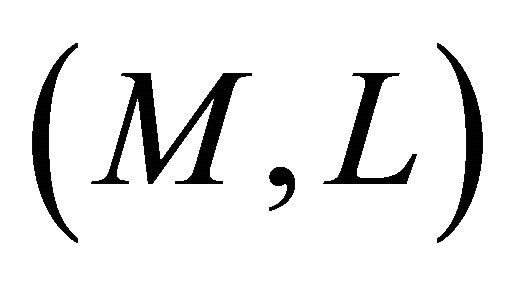 is concircular with respect to Cartan connection if, and only if, it is concircular with respect to Berwald connection.
is concircular with respect to Cartan connection if, and only if, it is concircular with respect to Berwald connection.
Remark 3.10. As a consequence of the above results, we retrieve a result of [4] concerning concurrent  - vector fields: A concurrent
- vector fields: A concurrent  -vector field
-vector field  and its associated
and its associated  -form
-form  are independent of the directional argument
are independent of the directional argument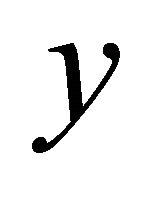 . Moreover, a
. Moreover, a  -vector field
-vector field  on
on 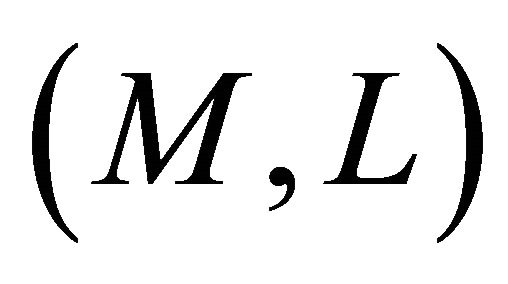 is concurrent with respect to Cartan connection if, and only if, it is concurrent with respect to Berwald connection.
is concurrent with respect to Cartan connection if, and only if, it is concurrent with respect to Berwald connection.
4. Special Finsler Spaces Admitting Concircular π-Vector Fields
Special Finsler manifolds arise by imposing extra conditions on the curvature and torsion tensors available in the space. Due to the abundance of such geometric objects in the context of Finsler geometry, special Finsler spaces are quite numerous. The study of these spaces constitutes a substantial part of research in Finsler geometry. A complete and systematic study of special Finsler spaces, from a global point of view, has been accomplished in [7].
In this section, we investigate the effect of the existence of a concircular  -vector field on some important special Finsler spaces. The intrinsic definitions of the special Finsler spaces treated here are quoted from [7].
-vector field on some important special Finsler spaces. The intrinsic definitions of the special Finsler spaces treated here are quoted from [7].
For later use, we need the following lemma.
Lemma 4.1. Let 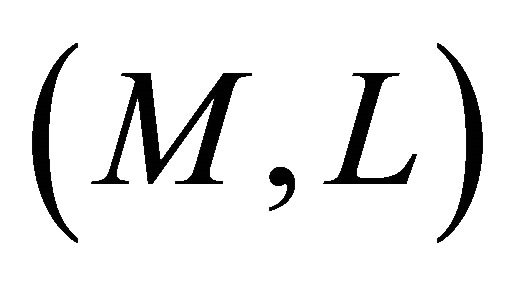 be a Finsler manifold admitting a concircular
be a Finsler manifold admitting a concircular  -vector field
-vector field . Then, we have:
. Then, we have:
a) The concircular  -vector field
-vector field  is everywhere non-zero.
is everywhere non-zero.
b) The scalar function 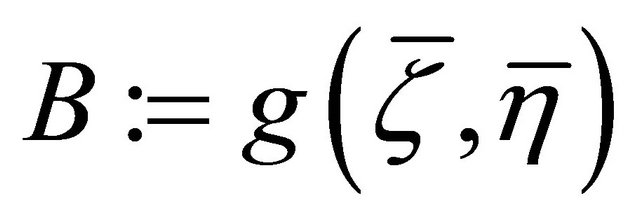 is everywhere nonzero.
is everywhere nonzero.
c) The  -vector field
-vector field 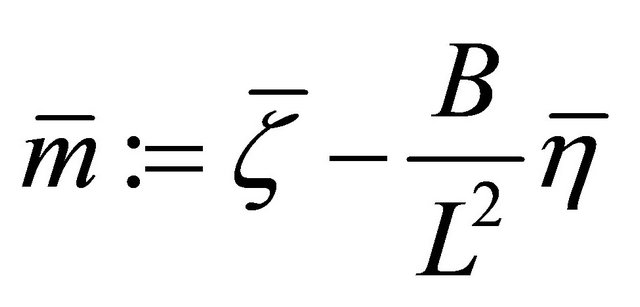 is everywhere non-zero and is orthogonal to
is everywhere non-zero and is orthogonal to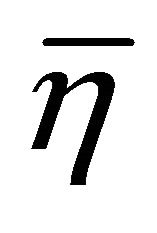 .
.
d) The  -vector fields
-vector fields 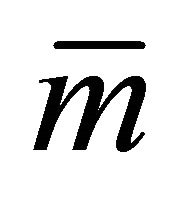 and
and  satisfy
satisfy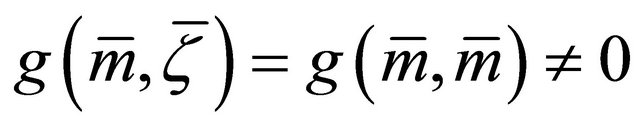 .
.
e) The scalar function 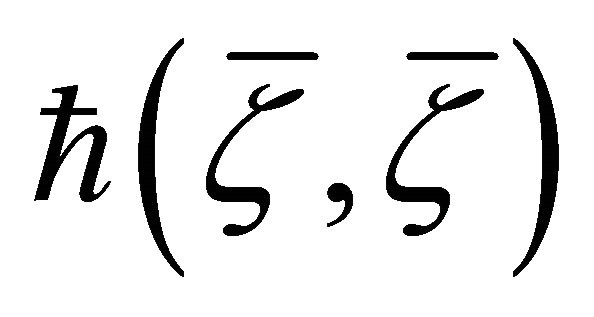 is everywhere non-zero.
is everywhere non-zero.
Proof.
a) Follows by Definition 2.1.
b) Suppose that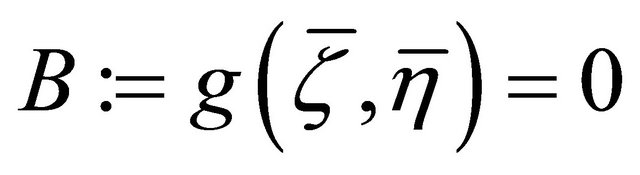 , then
, then
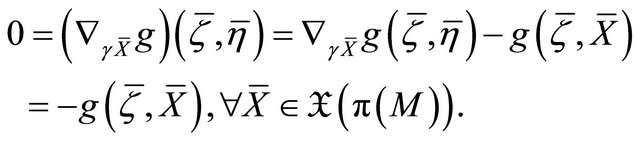
Hence, as  is nondegenerate,
is nondegenerate,  vanishes, which contradicts (a). Consequently,
vanishes, which contradicts (a). Consequently, .
.
c) If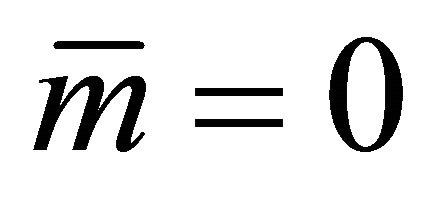 , then
, then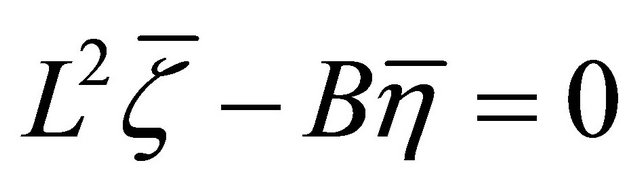 . Differentiating covariantly with respect to
. Differentiating covariantly with respect to , we get
, we get
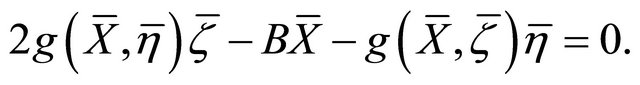 (1)
(1)
From which,
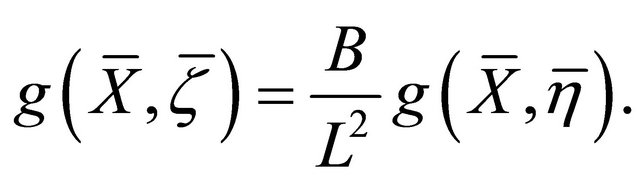 (2)
(2)
By (1), using (2), we obtain

From which, since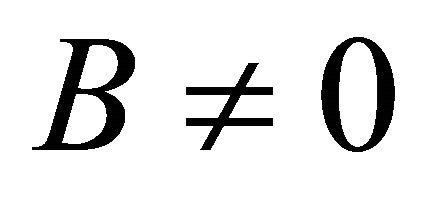 , we are led to a contradiction:
, we are led to a contradiction: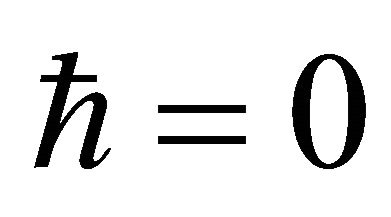 . Consequently,
. Consequently,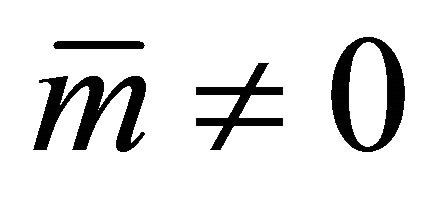 .
.
On the other hand, the orthogonality of the two  - vector fields
- vector fields  and
and 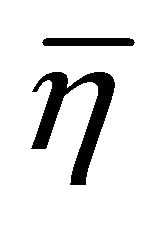 follows from the identities
follows from the identities 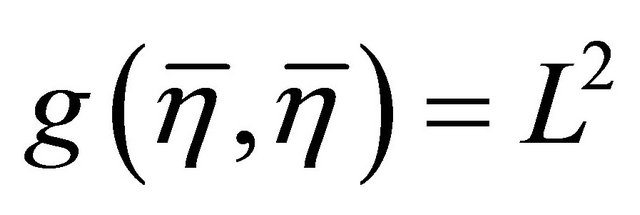 and
and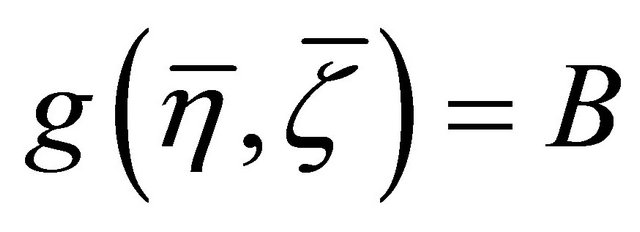 .
.
d) Follows from (c).
e) Follows from (d), (c) and the fact that 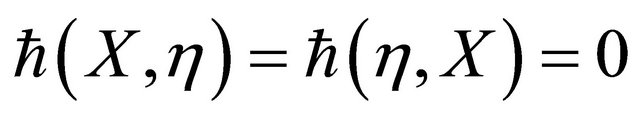 . □
. □
Definition 4.2. A Finsler manifold 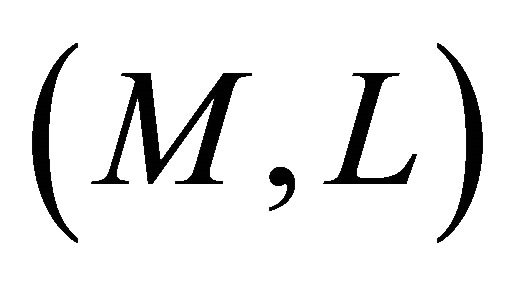 is said to be:
is said to be:
a) Riemannian if the metric tensor 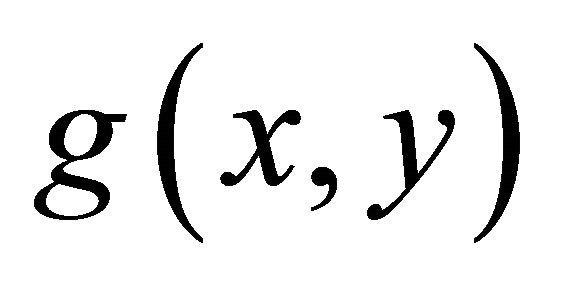 is independent of
is independent of 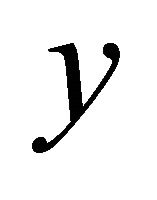 or, equivalently, if
or, equivalently, if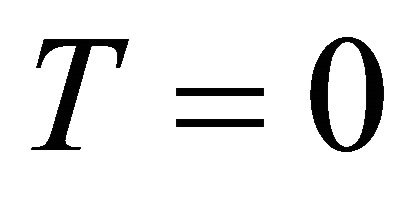 ;
;
b) Berwald if the torsion tensor 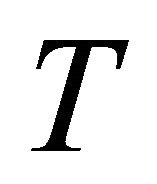 is horizontally parallel:
is horizontally parallel: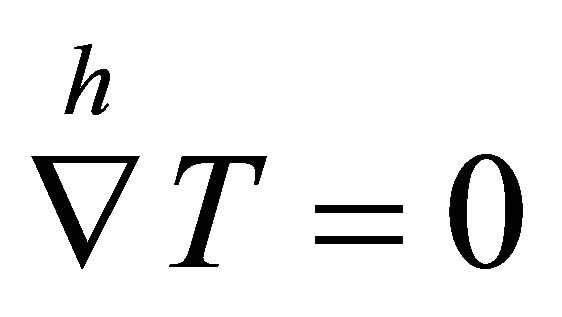 ;
;
c) Landsberg if the 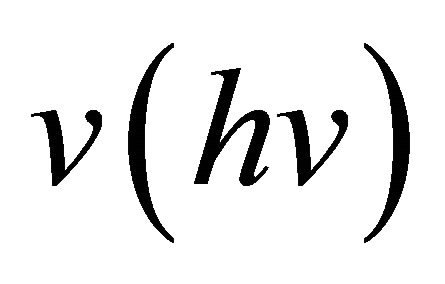 -torsion tensor
-torsion tensor 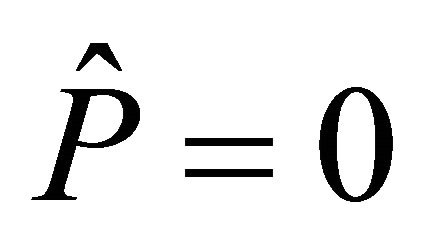 or, equivalently, if
or, equivalently, if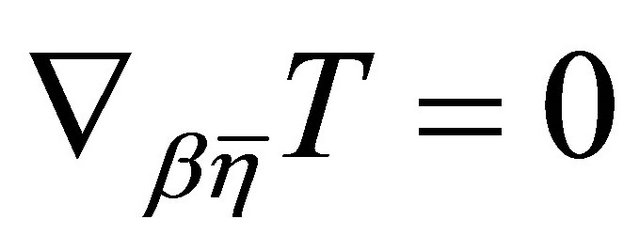 .
.
Theorem 4.3. A Landsberg manifold admitting a concircular  -vector field
-vector field  is Riemannian.
is Riemannian.
Proof. Suppose that 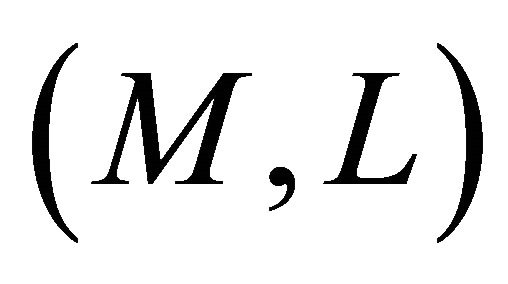 is Landsberg, then
is Landsberg, then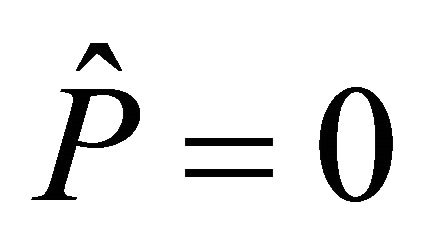 . Consequently, the hv-curvature
. Consequently, the hv-curvature 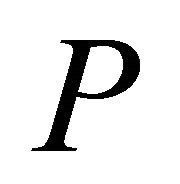 vanishes [10]. Hence, by Theorem 2.5(e),
vanishes [10]. Hence, by Theorem 2.5(e),
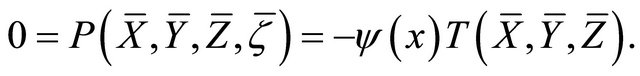
From which, taking into account the fact that 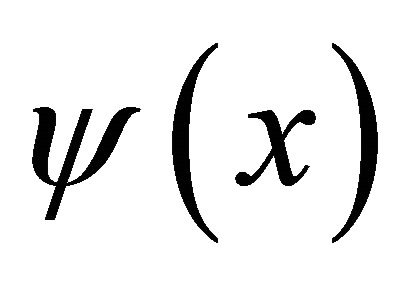 is a non-zero function, it follows that
is a non-zero function, it follows that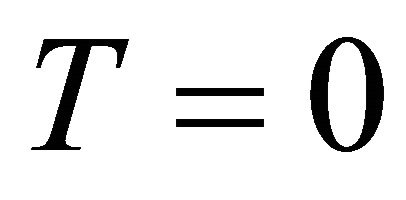 . Hence the result follows. □
. Hence the result follows. □
As a consequence of the above result, we get Corollary 4.4. The existence of a concircular  - vector field
- vector field  implies that the three notions of being Landsberg, Berwald and Riemannian coincide.
implies that the three notions of being Landsberg, Berwald and Riemannian coincide.
Definition 4.5. A Finsler manifold  is said to be:
is said to be:
a) 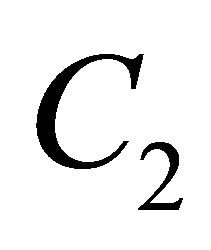 -like if
-like if 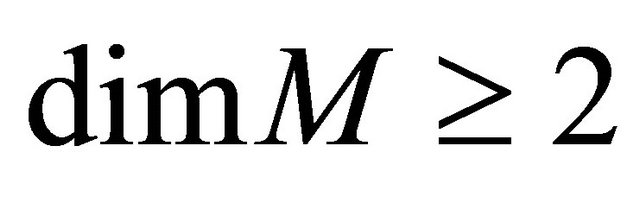 and the Cartan tensor
and the Cartan tensor  has the form
has the form
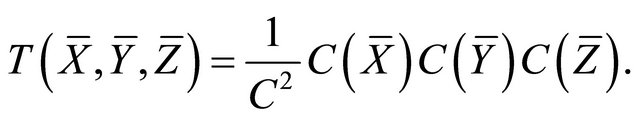
b)  -reducible if
-reducible if 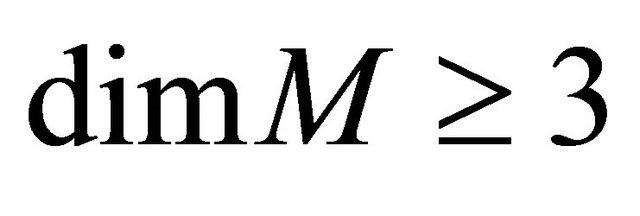 and the Cartan tensor
and the Cartan tensor 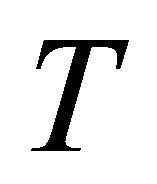 has the form2
has the form2
 (3)
(3)
c) semi- -reducible if
-reducible if  and the Cartan tensor
and the Cartan tensor  has the form
has the form
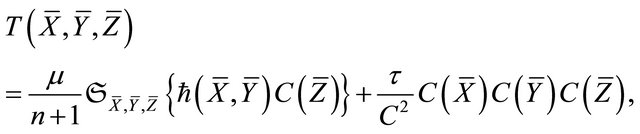 (4)
(4)
where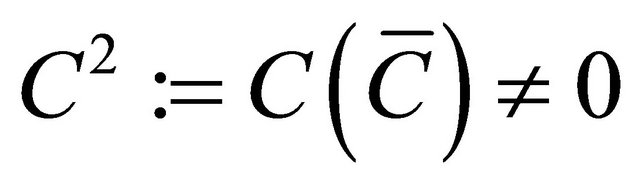 ,
,  and
and  are scalar functions satisfying
are scalar functions satisfying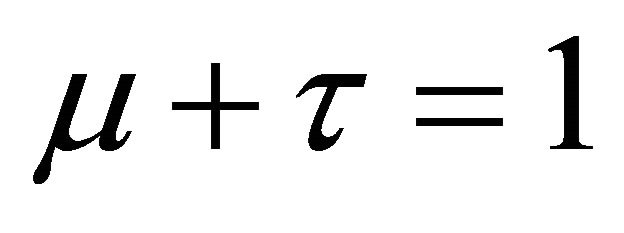 .
.
d) quasi- -reducible if
-reducible if  and the Cartan tensor
and the Cartan tensor  has the from
has the from
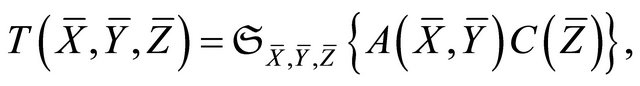
where  is a symmetric
is a symmetric  -tensor field satisfying
-tensor field satisfying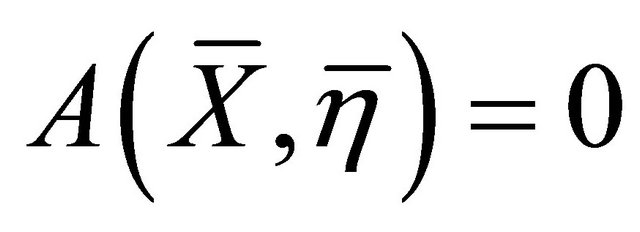 .
.
Theorem 4.6. Let 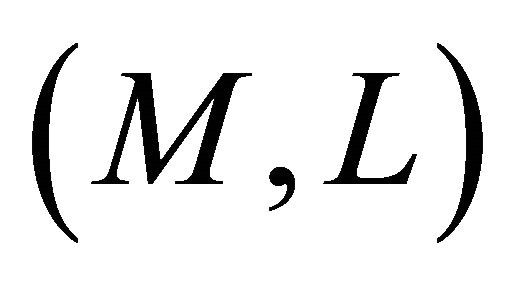 be a Finsler manifold
be a Finsler manifold 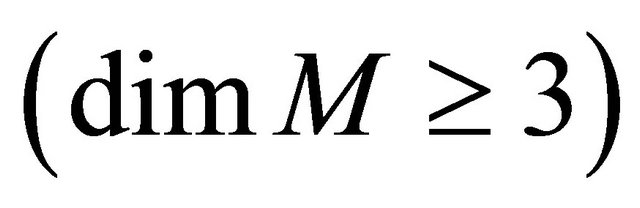 admitting a concircular
admitting a concircular  -vector field
-vector field .
.
a) If  is quasi-C-reducible, then it is Riemannian, provided that
is quasi-C-reducible, then it is Riemannian, provided that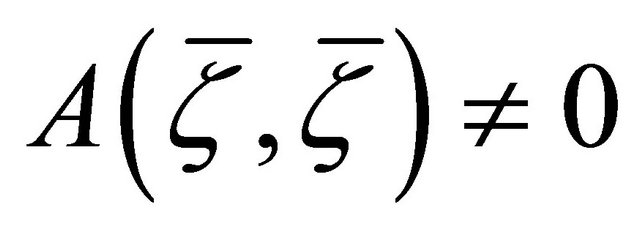 .
.
b) If 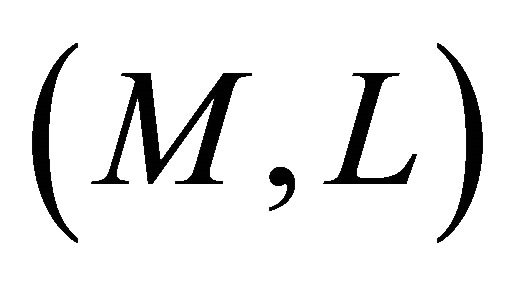 is
is  -reducible, then it is Riemannian.
-reducible, then it is Riemannian.
c) If  is semi-
is semi- -reducible, then it is
-reducible, then it is 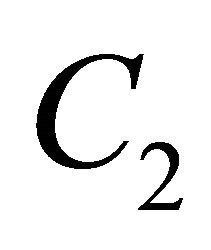 -like.
-like.
Proof.
a) Follows from the defining property of quasi-Creducibility by setting  and using the fact that
and using the fact that  and the given assumption
and the given assumption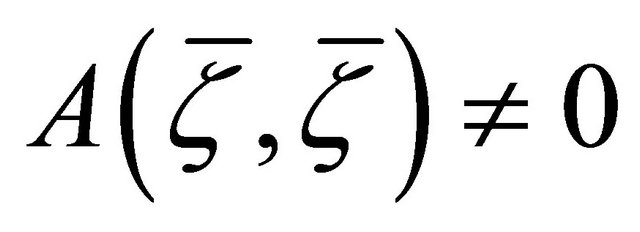 ;
;
b) Setting 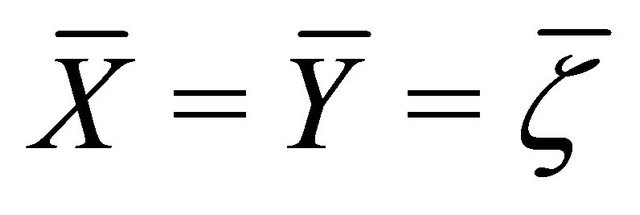 in (3.3), taking into account Proposition 2.7(a), Lemma 3.1(e) and
in (3.3), taking into account Proposition 2.7(a), Lemma 3.1(e) and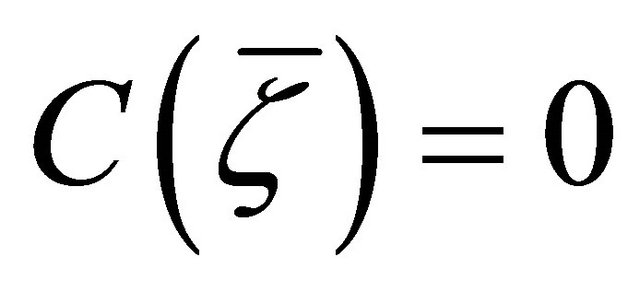 , it follows that
, it follows that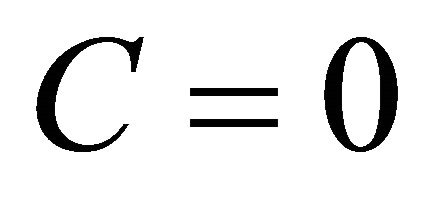 , which is equivalent to
, which is equivalent to  (Deicke theorem [11]);
(Deicke theorem [11]);
c) Let 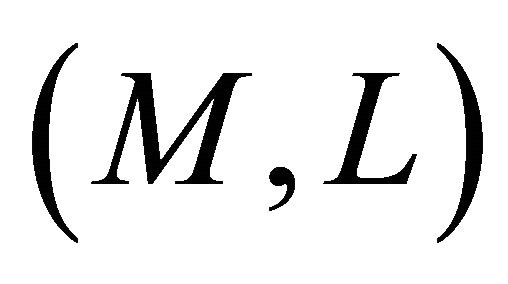 be semi-
be semi- -reducible. Setting
-reducible. Setting 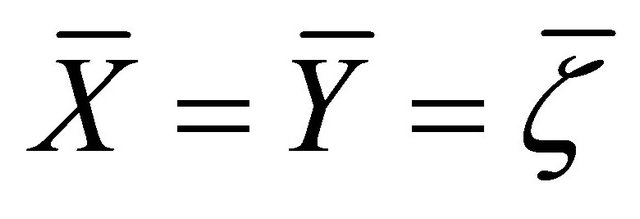 and
and 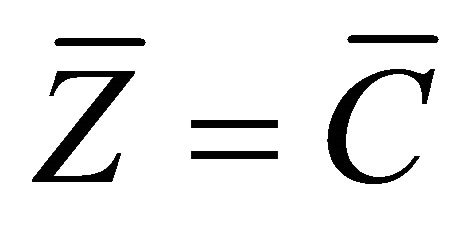 in (3.4), taking into account Proposition 2.7(a) and
in (3.4), taking into account Proposition 2.7(a) and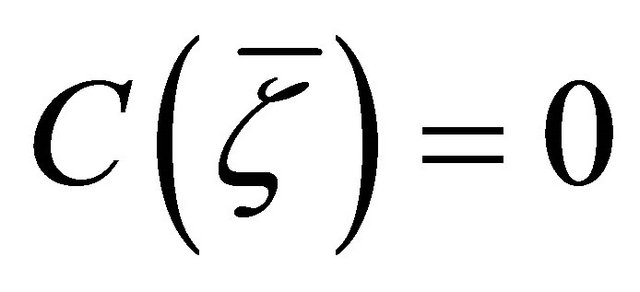 , we get
, we get
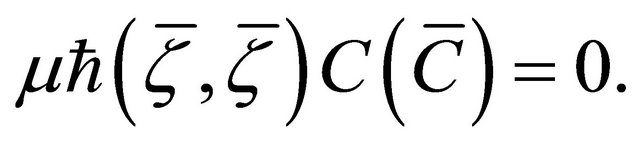
From which, since 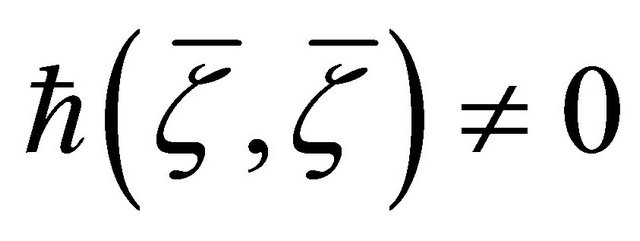 (Lemma 3.1(e)) and
(Lemma 3.1(e)) and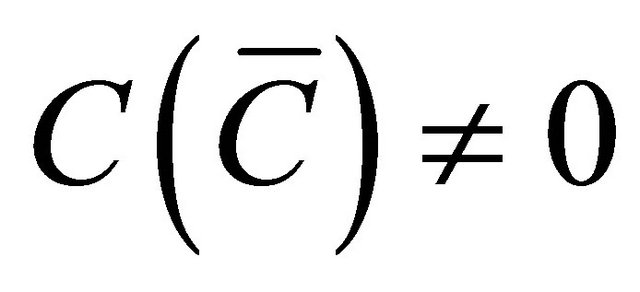 , it follows that
, it follows that .
.
Consequently, 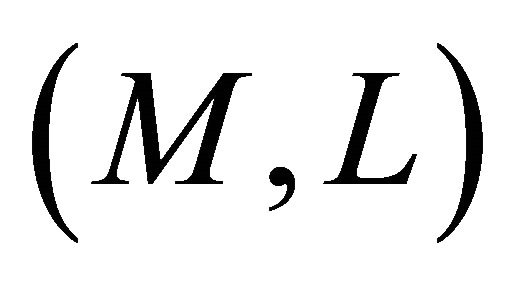 is
is  -like. □
-like. □
Definition 4.7. A Finsler manifold 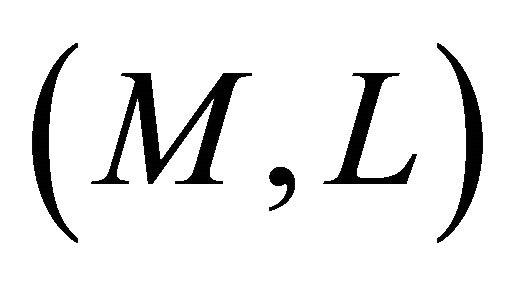 is said to be
is said to be 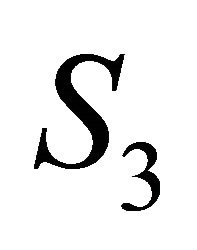 -like if
-like if  and the v-curvature tensor
and the v-curvature tensor 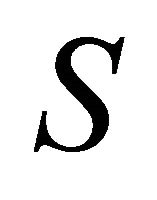 has the form:
has the form:
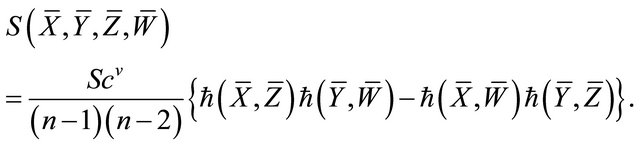 (5)
(5)
Theorem 4.8. If an  -like manifold admits a concircular
-like manifold admits a concircular  -vector field
-vector field , then the v-curvature tensor
, then the v-curvature tensor  vanishes.
vanishes.
Proof. Setting 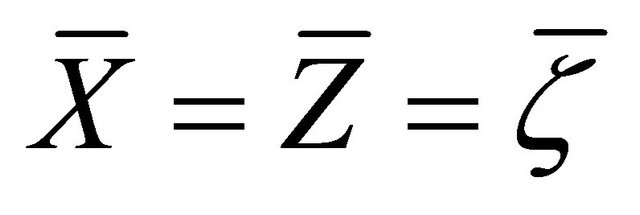 in (3.5), taking Theorem 2.5 into account, we immediately get
in (3.5), taking Theorem 2.5 into account, we immediately get
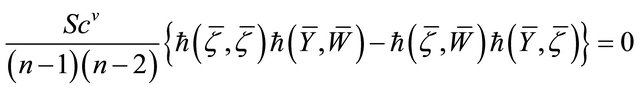
Taking the trace of the above equation, we have
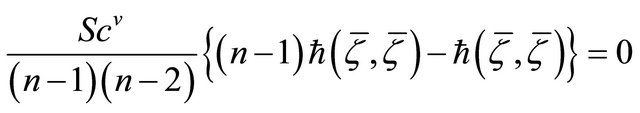
Consequently,

From which, since  (Lemma 3.1(e)), the vertical scalar curvature
(Lemma 3.1(e)), the vertical scalar curvature 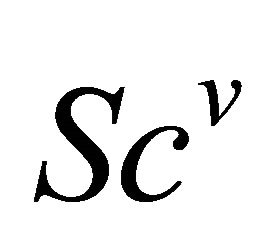 vanishes. Now, again, from (3.5), the result follows. □
vanishes. Now, again, from (3.5), the result follows. □
Definition 4.9. A Finsler manifold , where
, where , is said to be:
, is said to be:
a)  -like if the hv-curvature tensor
-like if the hv-curvature tensor 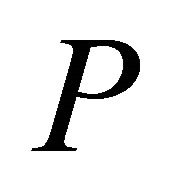 has the form:
has the form:
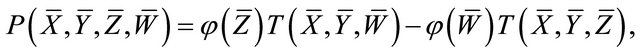 (6)
(6)
where  is
is 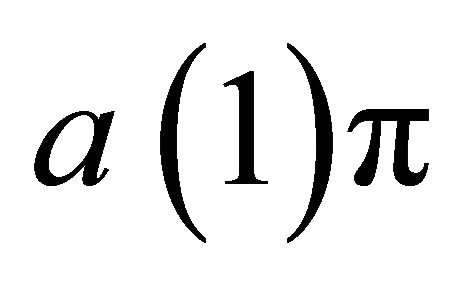 -form, positively homogeneous of degree
-form, positively homogeneous of degree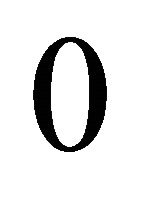 .
.
b) p-reducible if the π-tensor field
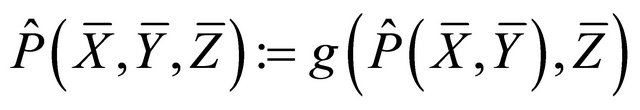 has the form
has the form
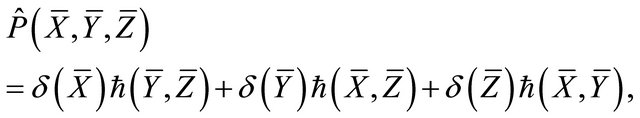 (7)
(7)
where  is the
is the  -form defined by
-form defined by
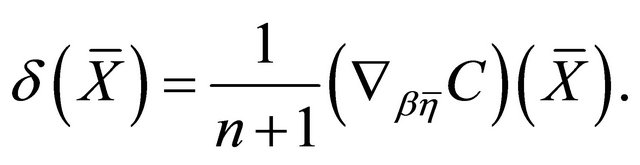
Theorem 4.10. Let 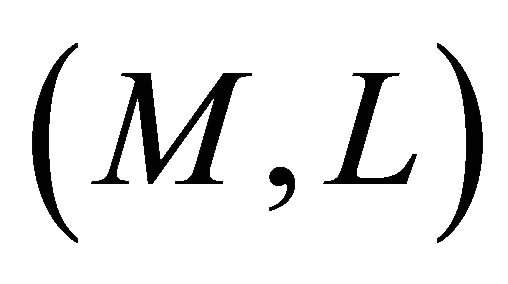 be a Finsler manifold
be a Finsler manifold  admitting a concircular
admitting a concircular  -vector field
-vector field .
.
a) If 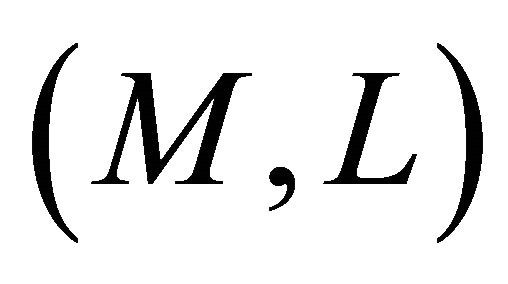 is
is 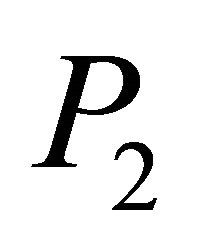 -like, then it is Riemannian, provided that
-like, then it is Riemannian, provided that .
.
b) If 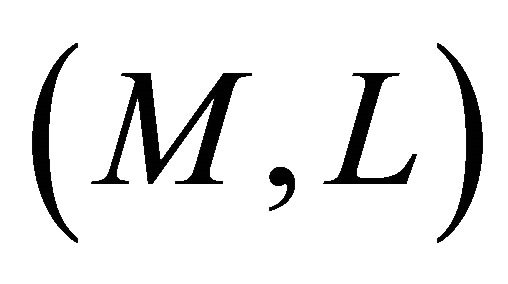 is
is 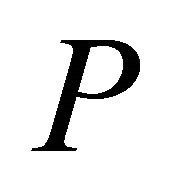 -reducible, then it is Landsbergian.
-reducible, then it is Landsbergian.
Proof.
a) Setting 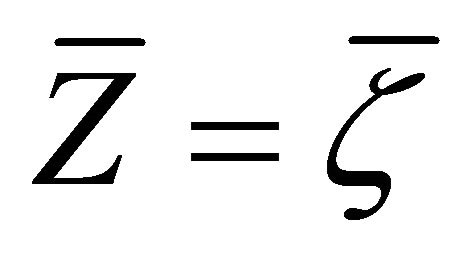 in (3.6), taking into account Theorem 2.5 and Proposition 2.7, we immediately get
in (3.6), taking into account Theorem 2.5 and Proposition 2.7, we immediately get
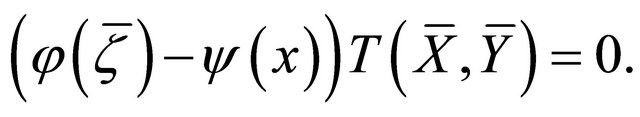
Hence, the result follows.
b) Setting  in (3.7) and using the identity
in (3.7) and using the identity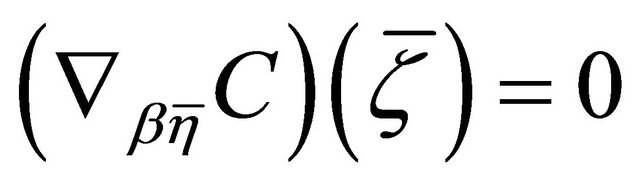 , we conclude that
, we conclude that
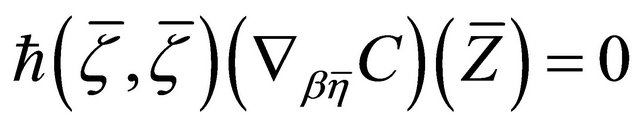 , with
, with 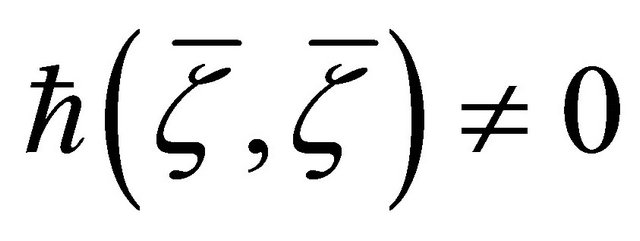 (Lemma 3.1
(Lemma 3.1
(e)). Consequently,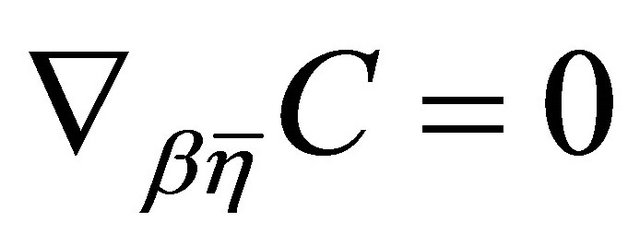 . Hence, again, from Definition 3.9(b), the (v)hv-torsion tensor
. Hence, again, from Definition 3.9(b), the (v)hv-torsion tensor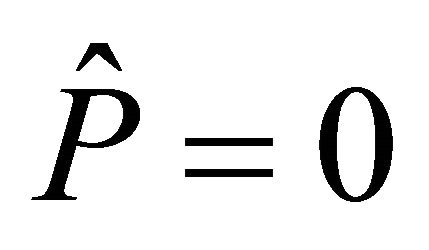 . □
. □
Definition 4.11. A Finsler manifold 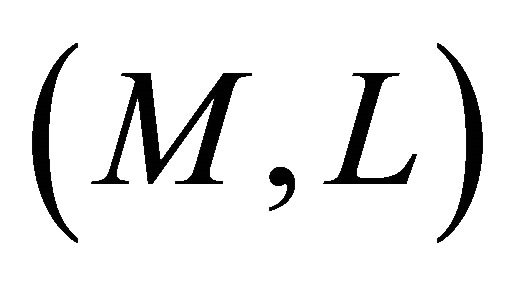 of
of 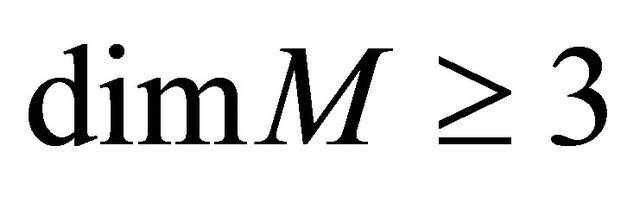 is said to be
is said to be 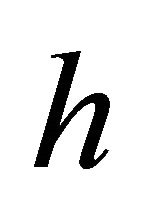 -isotropic if there exists a scalar function
-isotropic if there exists a scalar function  such that the horizontal curvature tensor
such that the horizontal curvature tensor  has the form
has the form
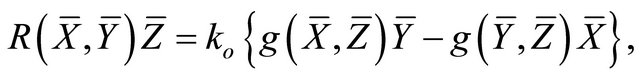
where 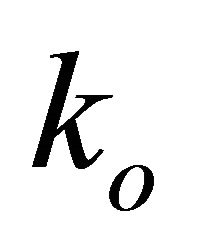 is called the scalar curvature.
is called the scalar curvature.
Theorem 4.12. For an 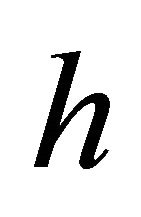 -isotropic Finsler manifold admitting a concircular
-isotropic Finsler manifold admitting a concircular  -vector field
-vector field , the scalar curvature
, the scalar curvature 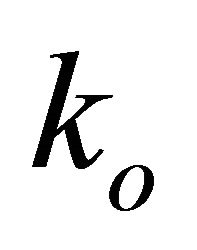 is given by
is given by

where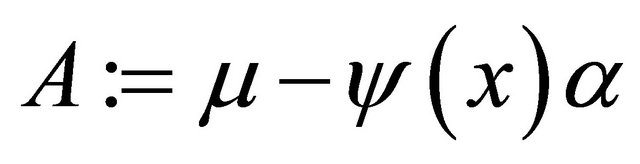 .
.
Proof. From Definition 3.11, by setting 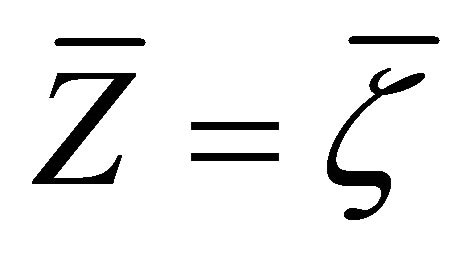 and
and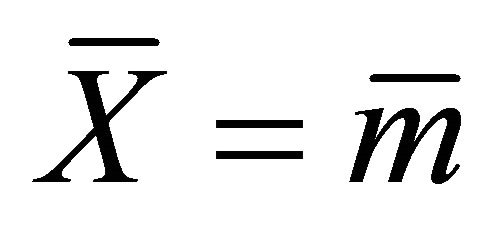 , we have
, we have
 (8)
(8)
On the other hand, using Theorem 2.5(i), we have
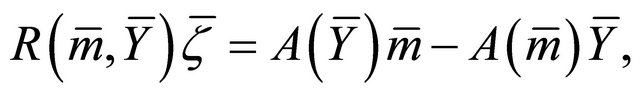 (9)
(9)
From (8) and (9), it follows that
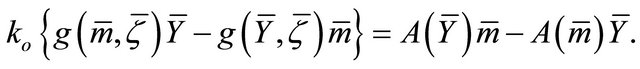
Taking the trace of the above equation, we get

Hence, the scalar 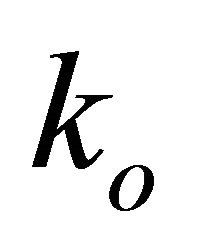 is given by
is given by
 (10)
(10)
This completes the proof. □
Corollary 4.13. For an h-isotropic Finsler manifold admitting a concurrent π-vector field , the hcurvature
, the hcurvature  vanishes.
vanishes.
Proof. If  is concurrent, then the
is concurrent, then the  -form
-form  vanishes. Hence, using (10), the scalar
vanishes. Hence, using (10), the scalar 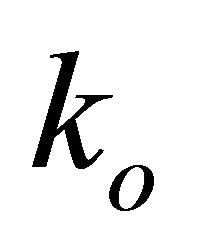 vanishes. Consequently, from Definition 3.11, the
vanishes. Consequently, from Definition 3.11, the 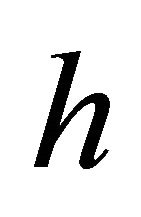 -curvature
-curvature 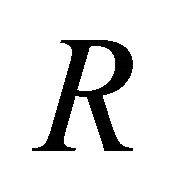 vanishes. □
vanishes. □
5. Different Types of Recurrent Finsler Manifolds Admitting Concircular π-Vector Fields
In this section, we investigate intrinsically the effect of the existence of a concircular π-vector field on recurrent Finsler manifolds. We study different types of recurrence (with respect to Cartan connection).
Let us begin with the first type of recurrence related to the Cartan tensor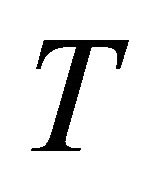 .
.
Definition 5.1. A Finsler manifold 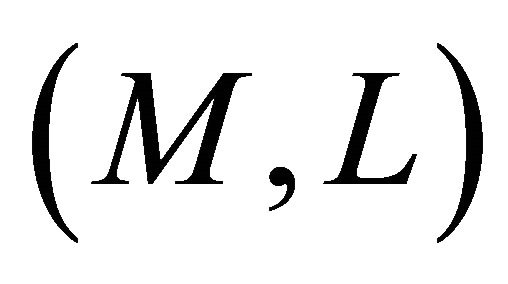 is said to be
is said to be 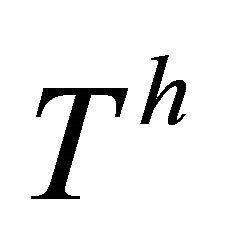 -recurrent if the (h)hv-torsion tensor
-recurrent if the (h)hv-torsion tensor 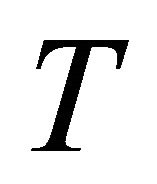 has the property that
has the property that

where 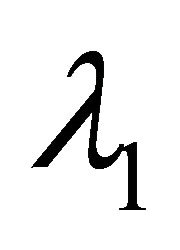 is a scalar (1)π-form, positively homogenous of degree zero in
is a scalar (1)π-form, positively homogenous of degree zero in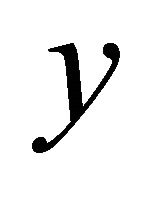 , called the
, called the 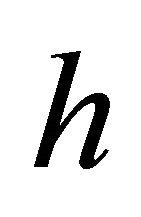 -recurrence form.
-recurrence form.
Similarly,  is called
is called 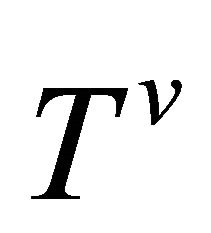 -recurrent if the (h)hv-torsion tensor
-recurrent if the (h)hv-torsion tensor 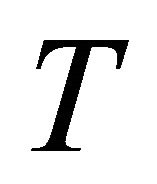 has the property that
has the property that
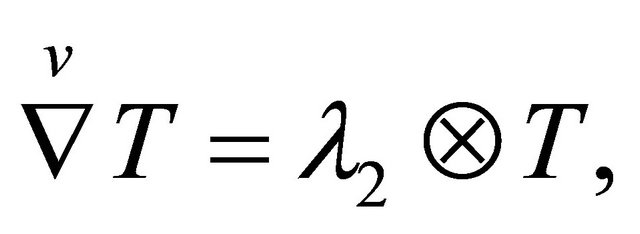
where  is a scalar (1) π-form, positively homogenous of degree
is a scalar (1) π-form, positively homogenous of degree 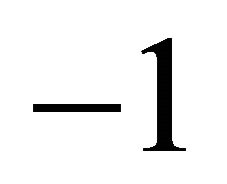 in
in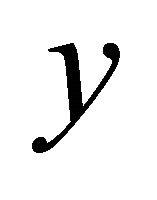 , called the
, called the 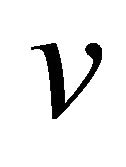 -recurrence form.
-recurrence form.
Theorem 5.2. If a 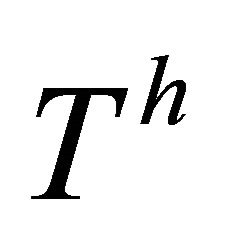 -recurrent Finsler manifold admits a concircular π-vector field
-recurrent Finsler manifold admits a concircular π-vector field , then it is Riemannian, provided that
, then it is Riemannian, provided that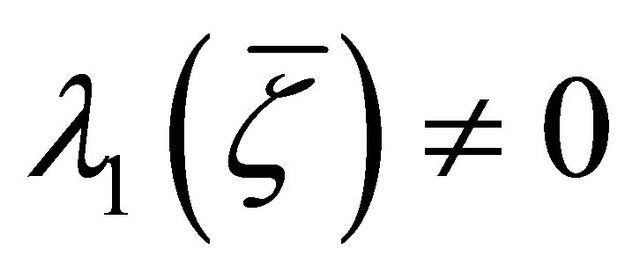 .
.
Proof. We have [10]
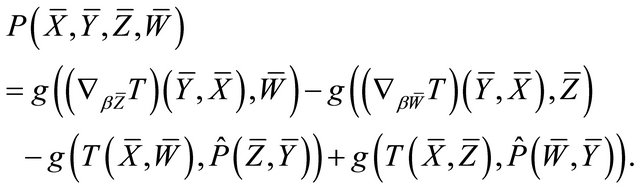
Setting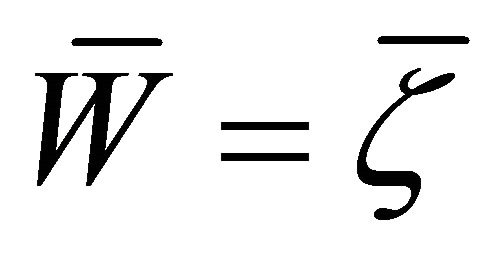 , making use of Theorem 2.5, Proposition 2.7 and the identity [10]
, making use of Theorem 2.5, Proposition 2.7 and the identity [10]
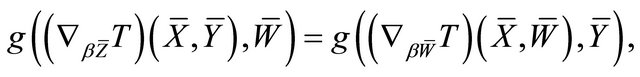
we get
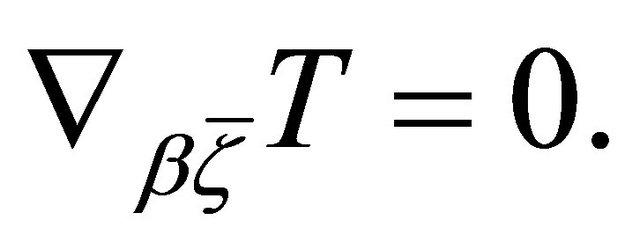
On the other hand, Definition 4.1 yields
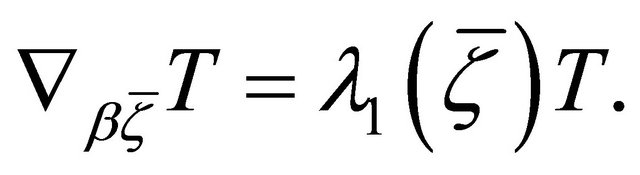
Under the given assumption, the above two equations imply that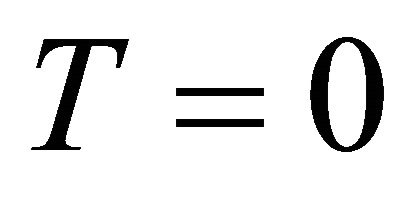 . Hence,
. Hence,  is Riemannian. □
is Riemannian. □
In view of the above theorem, we have.
Corollary 5.3. In the presence of a concircular  - vector field
- vector field , the three notions of being
, the three notions of being 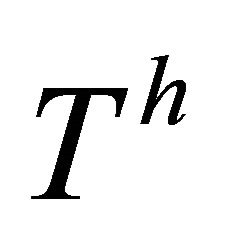 -recurrent,
-recurrent, 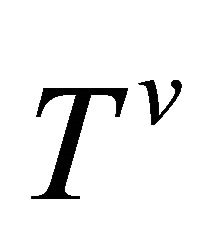 -recurrent and Riemannian coincide, provided that
-recurrent and Riemannian coincide, provided that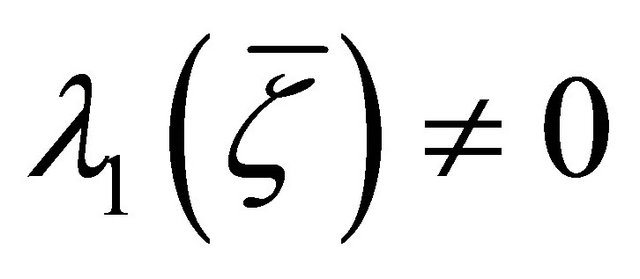 .
.
Proof. By Theorem 4.7 of [7], regardless of the existence of concircular  -vector fields, a
-vector fields, a  -recurrent Finsler space is necessarily Riemannian. On the other hand, a Riemannian space is trivially both
-recurrent Finsler space is necessarily Riemannian. On the other hand, a Riemannian space is trivially both 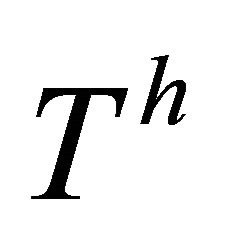 -recurrent and
-recurrent and 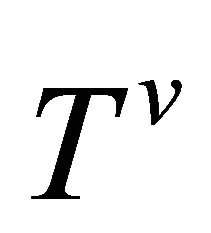 -recurrent. □
-recurrent. □
Remark 5.4. Corollary 4.3 remains true if in particular a concircular  -vector field replaced by a concurrent
-vector field replaced by a concurrent  -vector field [4].
-vector field [4].
The following definition gives the second type of recurrence related to the 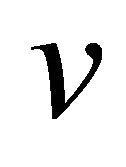 -curvature tensor
-curvature tensor .
.
Definition 5.5. If we replace  by
by 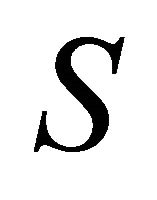 in Definition 4.1, then
in Definition 4.1, then 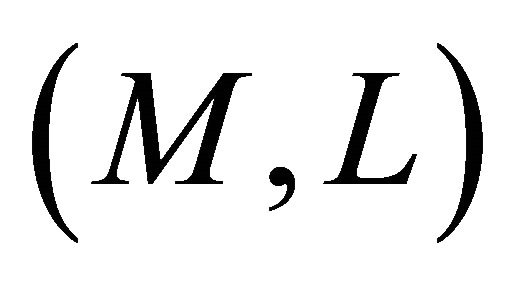 is said to be
is said to be 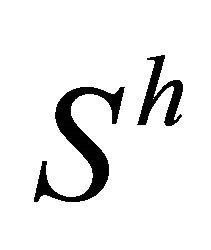 -recurrent (
-recurrent ( -recurrent).
-recurrent).
Theorem 5.6. If an 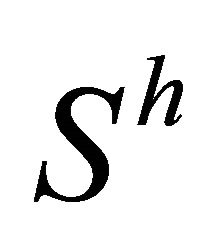 -recurrent Finsler manifold admits a concircular
-recurrent Finsler manifold admits a concircular  -vector field
-vector field , then its
, then its 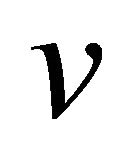 - curvature tensor
- curvature tensor 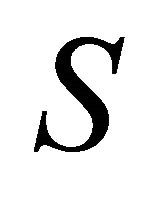 vanishes.
vanishes.
Proof. Suppose that 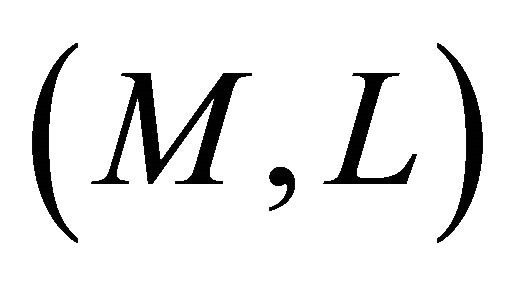 is an
is an 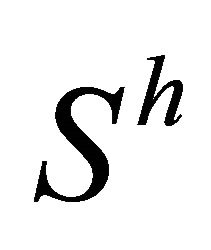 -recurrent manifold which admits a concircular
-recurrent manifold which admits a concircular  -vector field
-vector field . Then, by Definition 4.5 and Theorem 2.5(a), we have
. Then, by Definition 4.5 and Theorem 2.5(a), we have
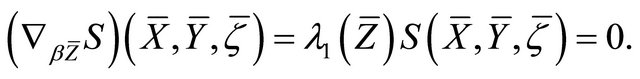
On the other hand, by Theorem 2.5(c), we get
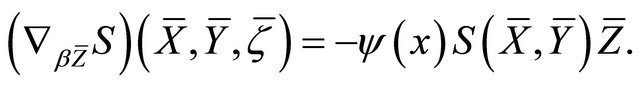
From the above two equations, since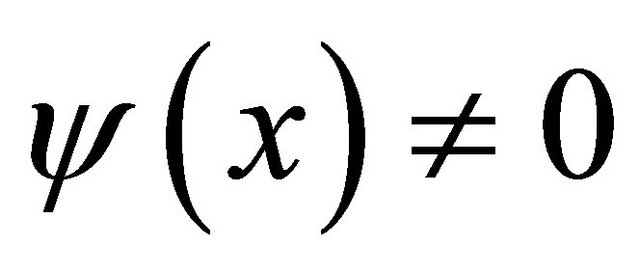 , the
, the 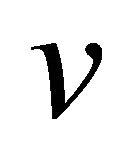 -curvature tensor
-curvature tensor 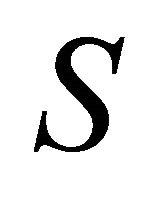 vanishes. □
vanishes. □
Corollary 5.7. Let 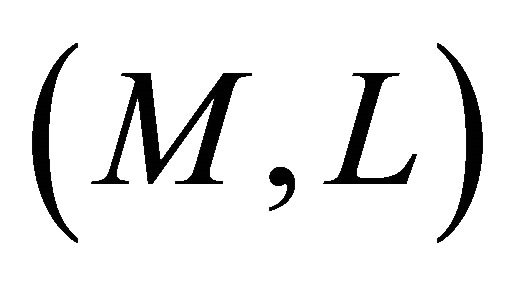 be a Finsler manifold which admits a concircular
be a Finsler manifold which admits a concircular  -vector field. The following assertions are equivalent:
-vector field. The following assertions are equivalent:
a) 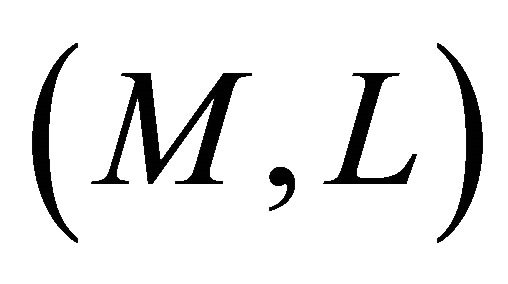 is
is 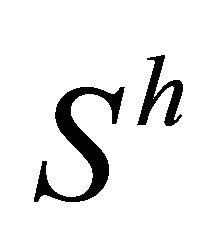 -recurrent, b)
-recurrent, b) 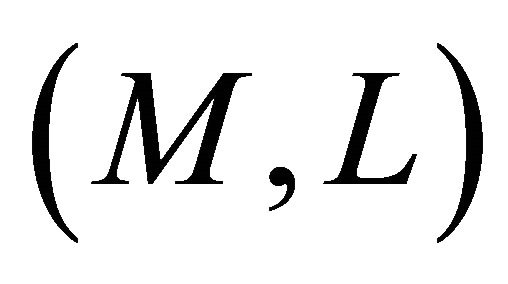 is
is 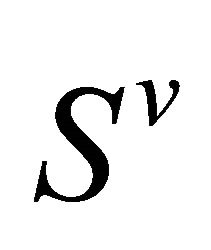 -recurrent, c) the
-recurrent, c) the 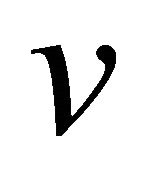 -curvature tensor
-curvature tensor 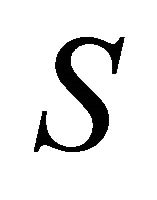 vanishes.
vanishes.
In fact, for an 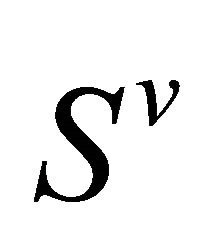 -recurrent Finsler manifold the
-recurrent Finsler manifold the 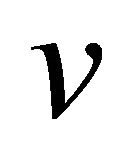 - curvature tensor
- curvature tensor 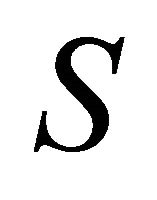 vanishes [7] regardless of the existence of concircular
vanishes [7] regardless of the existence of concircular  -vector fields.
-vector fields.
Remark 5.8. We retrieve here a result of [4] concerning concurrent  -vector fields: Corollary 4.7 remains true if in particular a concircular
-vector fields: Corollary 4.7 remains true if in particular a concircular  -vector field replaced by a concurrent
-vector field replaced by a concurrent  -vector field.
-vector field.
In the following we give the third type of recurrence related to the  -curvature tensor
-curvature tensor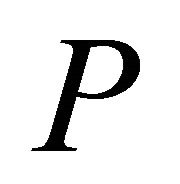 .
.
Definition 5.9. If we replace 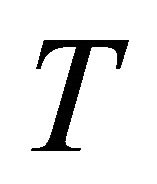 by
by 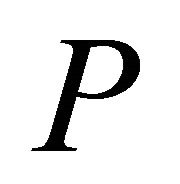 in Definition 4.1, then
in Definition 4.1, then 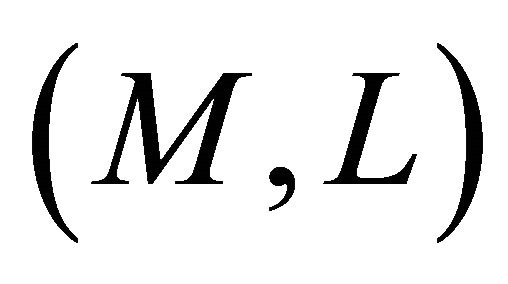 is said to be
is said to be 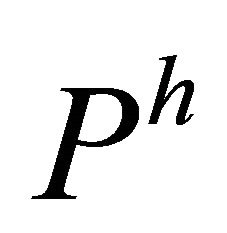 -recurrent (
-recurrent (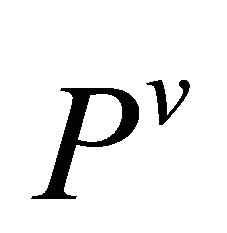 - recurrent).
- recurrent).
In view of the above definition, we have Theorem 5.10. Let  be a
be a 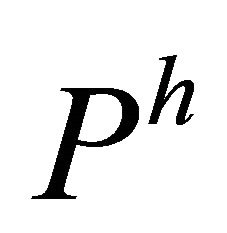 -recurrent Finsler manifold admitting a concircular
-recurrent Finsler manifold admitting a concircular  -vector field
-vector field . Theneither (a)
. Theneither (a) 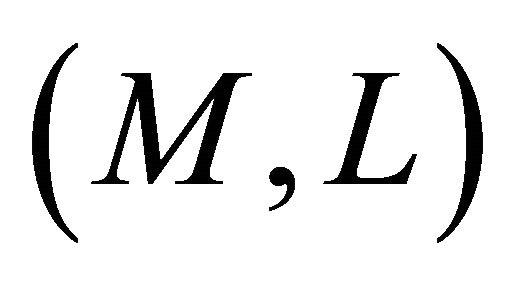 is Riemannian, or
is Riemannian, or
(b)  has the property that
has the property that
 .
.
Proof. By Theorem 2.5(g), we have
 (1)
(1)
On the other hand, by Definition 4.9 and Theorem 2.5(e), we get
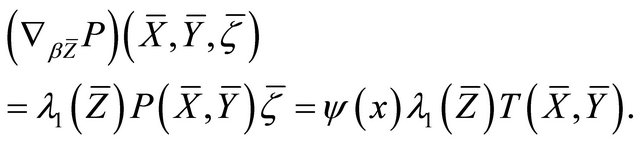
From which together with (1), it follows that
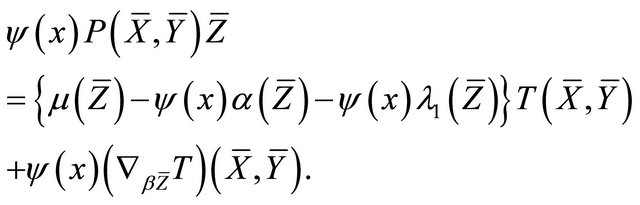
By setting 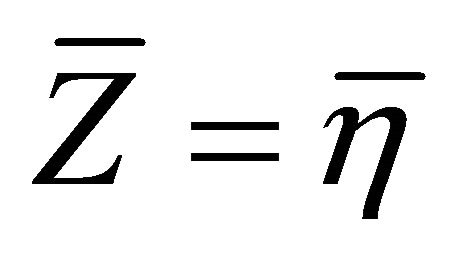 and noting that
and noting that
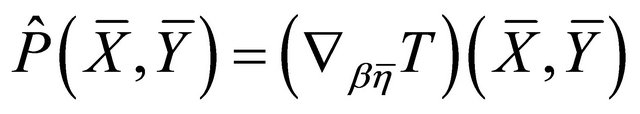 [10], the above equation gives
[10], the above equation gives
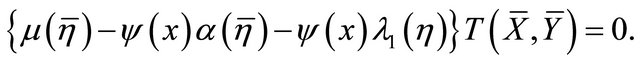
Now, we have two cases: either  and consequently
and consequently  is Riemannian, or
is Riemannian, or
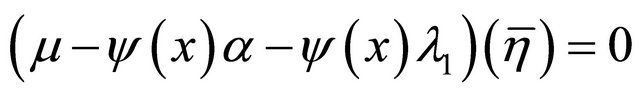 . This completes the proof. □
. This completes the proof. □
Lemma 5.11. For a 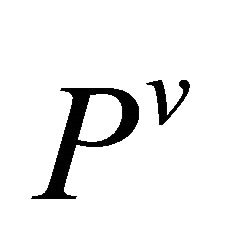 -recurrent Finsler manifold, the
-recurrent Finsler manifold, the 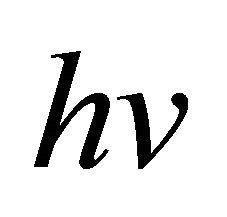 -curvature tensor
-curvature tensor 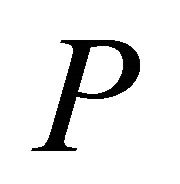 vanishes.
vanishes.
Proof. Suppose that  is
is 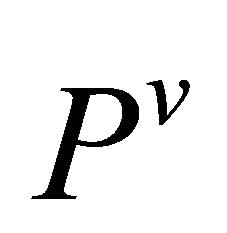 -recurrent, then, by Definition 4.9, we get
-recurrent, then, by Definition 4.9, we get
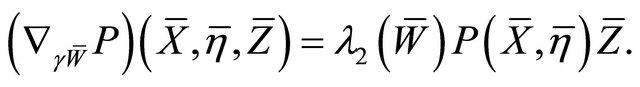
From which, together with the fact that 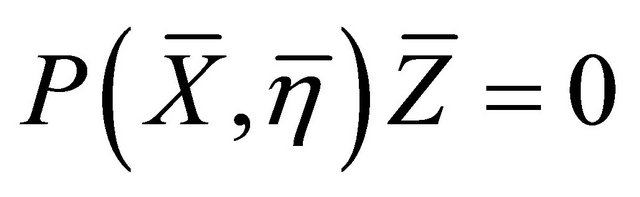 [10] and
[10] and , the result follows. □
, the result follows. □
In view of Theorem 4.10 and Lemma 4.11, we have Theorem 5.12. Let 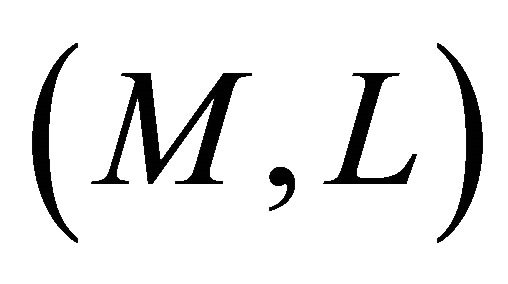 be a Finsler manifold admitting a concircular
be a Finsler manifold admitting a concircular  -vector field. Then, the following assertions are equivalent:
-vector field. Then, the following assertions are equivalent:
a) 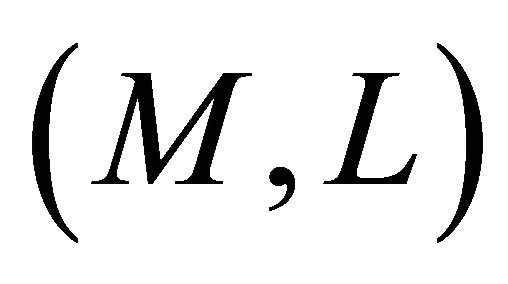 is
is  -recurrent;
-recurrent;
b) 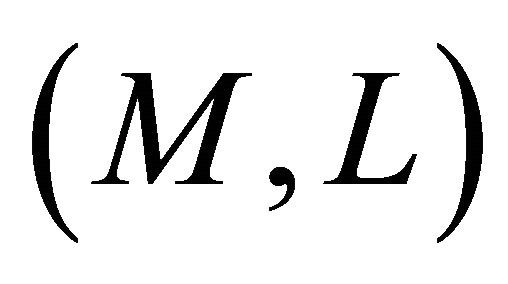 is
is  -recurrent;
-recurrent;
c)  is Riemannianprovided that
is Riemannianprovided that  in the
in the 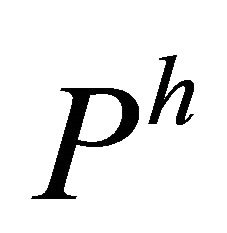 -recurrence case.
-recurrence case.
Remark 5.13. In view of Theorem 4.12, we conclude that under the presence of a concurrent  -vector field
-vector field , the three notions of being
, the three notions of being 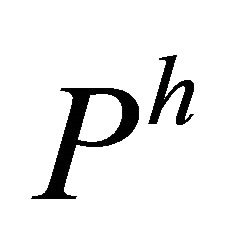 -recurrent,
-recurrent, 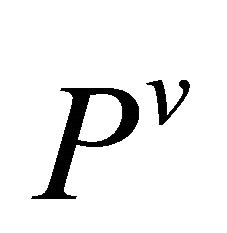 -recurrent and Riemannian coincide, provided that
-recurrent and Riemannian coincide, provided that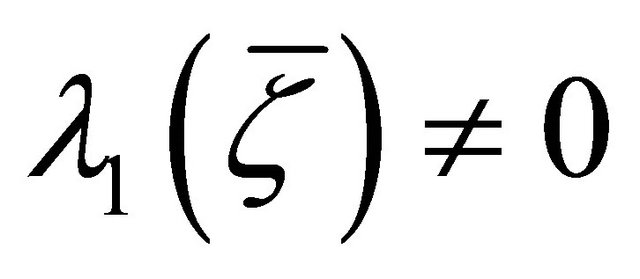 .
.
Finally, we focus our attention to the fourth type of recurrent Finsler manifolds related to the 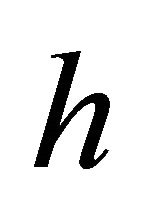 -curvature tensor
-curvature tensor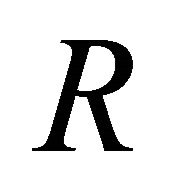 .
.
Definition 5.14. If we replace  by
by  in Definition 4.1, then
in Definition 4.1, then 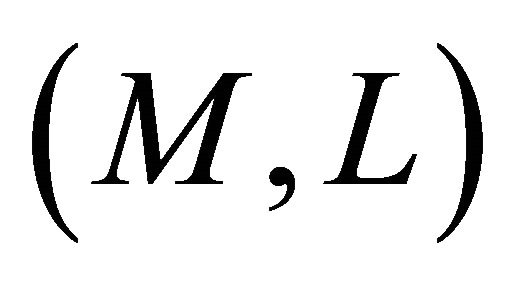 is said to be
is said to be 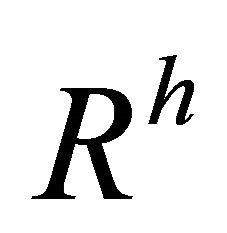 -recurrent (
-recurrent (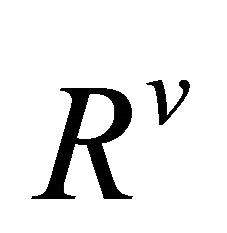 - recurrent).
- recurrent).
Theorem 5.15. An  -recurrent Finsler manifold admitting a concircular
-recurrent Finsler manifold admitting a concircular  -vector field
-vector field  is
is 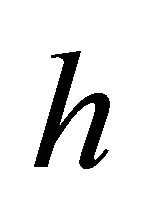 -isotropic with scalar curvature
-isotropic with scalar curvature
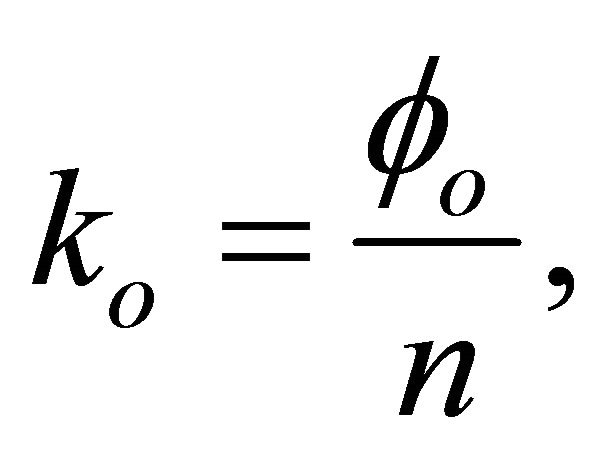
where
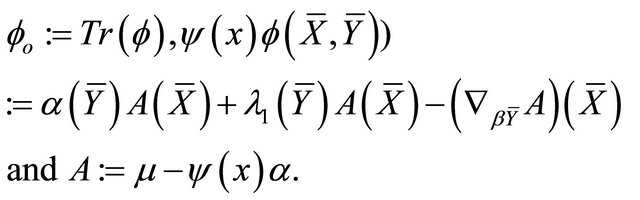
Moreover, if  is
is 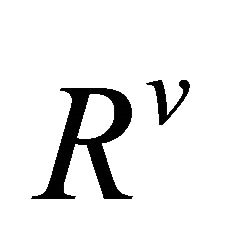 -recurrent with
-recurrent with
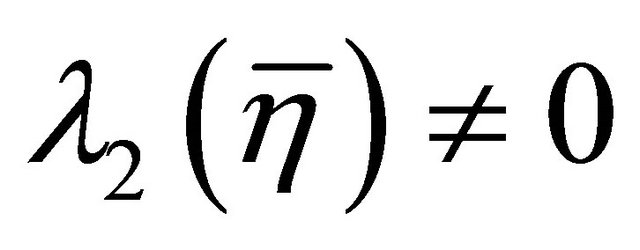 , then the
, then the  -curvature tensor
-curvature tensor  vanishes.
vanishes.
Proof. Firstly, suppose that  is an
is an 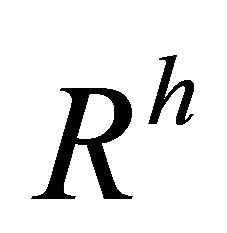 - recurrent manifold which admits a concircular
- recurrent manifold which admits a concircular  -vector field
-vector field . Then, by Theorem 2.5 (l), we have
. Then, by Theorem 2.5 (l), we have

On the other hand, by Definition 4.14 and Theorem 2.5(i), we get
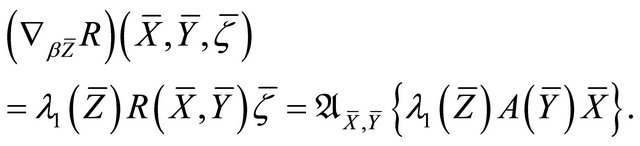
The above two equations imply that
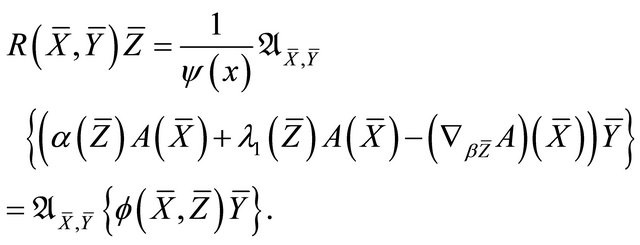
Consequently,
 (2)
(2)
Hence,
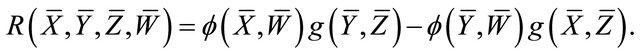
From the above two relations, noting that
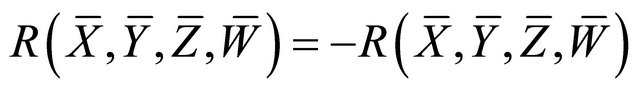 [10], we get
[10], we get
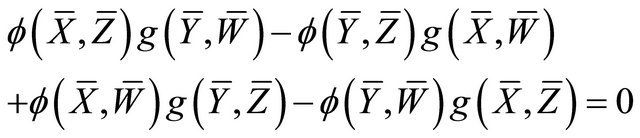
Taking the trace of the above relation with respect to the two arguments  and
and , we obtain
, we obtain
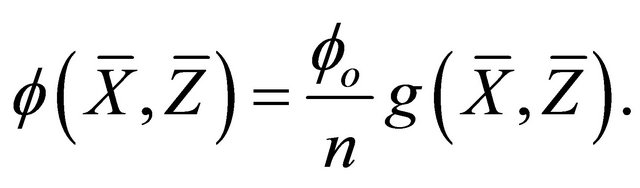
From which, together with (4.2), we obtain

This means that 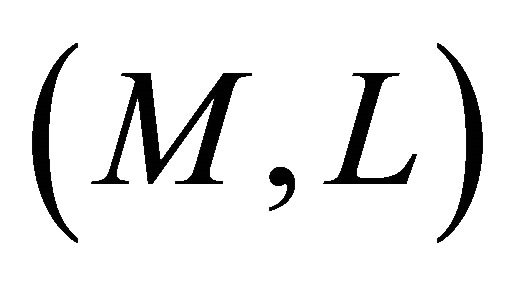 is
is 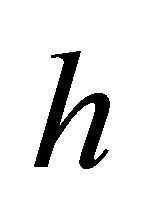 -isotropic (Definition 3.11) with scalar curvature
-isotropic (Definition 3.11) with scalar curvature 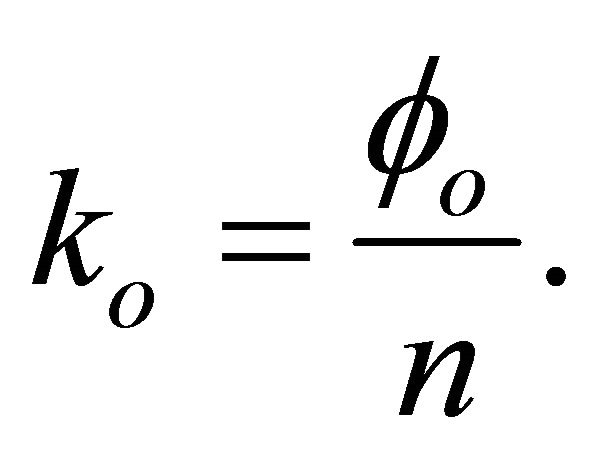
Finally, the second part of the theorem follows from Definition 4.14 and the identity  [10]. □
[10]. □
As a consequence of the above theorem, we have Corollary 5.16. For an 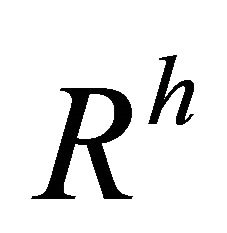 -recurrent Finsler manifold admitting a concurrent
-recurrent Finsler manifold admitting a concurrent  -vector field
-vector field , the
, the  - curvature tensor
- curvature tensor 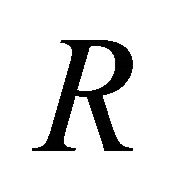 vanishes.
vanishes.
• 6. Concluding Remarks
• The concept of a concircular  -vector field in Finsler geometry has been introduced and investigated from a global point of view. This generalizes, on one hand, the concept of a concircular vector field in Riemannian geometry and, on the other hand, the concept of a concurrent vector field in Finsler geometry. Various properties of concircular
-vector field in Finsler geometry has been introduced and investigated from a global point of view. This generalizes, on one hand, the concept of a concircular vector field in Riemannian geometry and, on the other hand, the concept of a concurrent vector field in Finsler geometry. Various properties of concircular  -vector fields have been obteined.
-vector fields have been obteined.
• The effect of the existence of concircular  -vector fields on some of the most important special Finsle spaces has been investigated.
-vector fields on some of the most important special Finsle spaces has been investigated.
• Different types of recurrent Finsler manifolds admitting concircular  -vector fields have been studied.
-vector fields have been studied.
• Almost all results of this work have been obtained in a coordinate-free form, without being trapped into the complications of indices.
REFERENCES
- K. Yano, “Sur le Prarallélisme et la Concourance Dans l’Espaces de Riemann,” Proceedings of the Imperial Academy of Japan, Vol. 19, No. 4, 1943, pp. 189-197. doi:10.3792/pia/1195573583
- S. Tachibana, “On Finsler Spaces which Admit a Concurrent Vector Field,” Tensor, N. S., Vol. 1, 1950, pp. 1-5.
- M. Matsumoto and K. Eguchi, “Finsler Spaces Admitting a Concurrent Vector Field,” Tensor, N. S., Vol. 28, 1974, pp. 239-249.
- N. L. Youssef, S. H. Abed and A. Soleiman, “Concurrent π-Vector Fields and Eneregy β-Change,” International Journal of Geometric Methods in Modern Physics, Vol. 6, No. 6, 2009, pp. 1003-1031. doi:10.1142/S0219887809003904
- T. Adat and T. Miyazawa, “On Riemannian Spaces which Admit a Concircular Vector Field,” Tensor, N. S., Vol. 18, No. 3, 1967, pp. 335-341.
- B. N. Prasad, V. P. Singh and Y. P. Singh, “On Concircular Vector Fields in Finsler Spaces,” Indian Journal of Pure and Applied Mathematics, Vol. 17, No. 8, 1986, pp. 998-1007.
- N. L. Youssef, S. H. Abed and A. Soleiman, “A Global Approach to the Theory of Special Finsler Manifolds,” Kyoto Journal of Mathematics, Vol. 48, No. 4, 2008, pp. 857-893.
- N. L. Youssef, S. H. Abed and A. Soleiman, “A Global Approach to the Theory of Connections in Finsler Geometry,” Tensor, N. S., Vol. 71, No. 3, 2009, pp. 187-208.
- N. L. Youssef, S. H. Abed and A. Soleiman, “Cartan and Berwald Connections in the Pullback Formalism,” Algebras, Groups and Geometries, Vol. 25, No. 4, 2008, pp. 363-386.
- N. L. Youssef, S. H. Abed and A. Soleiman, “Geometric Objects Associated with the Fundumental Connections in Finsler Geometry,” Journal of the Egyptian Mathematical Society, Vol. 18, No. 1, 2010, pp. 67-90.
- F. Brickell, “A New Proof of Deicke’s Theorem on Homogeneous Functions,” Proceedings of the American Mathematical Society, Vol. 16, No. 2, 1965, pp. 190-191.
NOTES
*ArXiv Number: 1208.2838 [math.DG].
1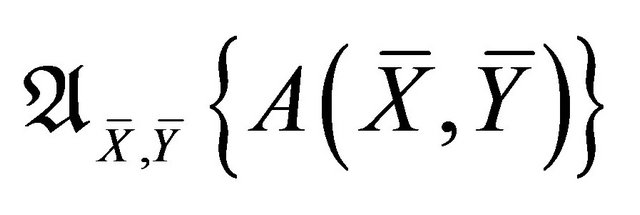 denotes the alternate sum
denotes the alternate sum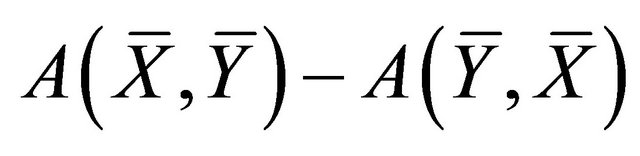 .
.
2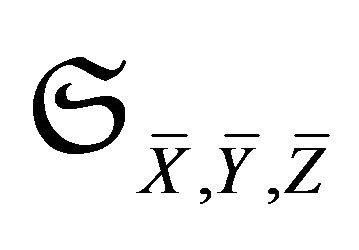 denotes the cyclic sum over the arguments
denotes the cyclic sum over the arguments 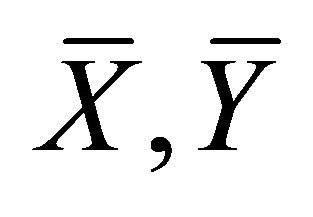 and
and .
.

