ABSTRACT

In this paper, we prove introduce some fixed point theorems for quasi-contraction under the cyclical conditions. Then, we point out that a common fixed point extension is also applicable via our earlier results equipped together with a weaker cyclical properties, namely a co-cyclic representation. Examples are as well provided along this paper.

1. Introduction

Since Banach [1] proved his contraction principle in 1922, many authors have improved, extended and generalized Banach’s contraction principle in several ways and applied the principle to differential and integral equations, variational inequality theory, complementarity problems, equilibrium problems, optimization problems, convex analysis and many others.

Theorem 1.1 [1] Let 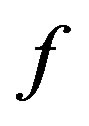be a self-mapping on a complete metric space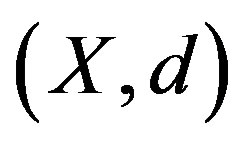. If there exists 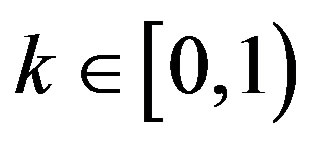such that

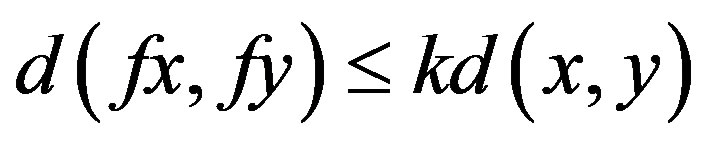
for all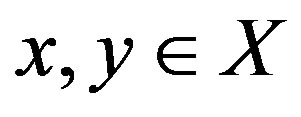, then f has a unique fixed point in X.

In 1971, Ććirić [2] generalized Banach’s contraction principle theorem to a more general contraction as follows:

Theorem 1.2 [2] Let 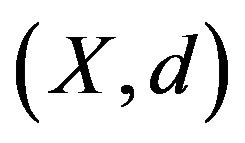be a complete metric space and 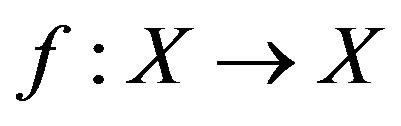be a mapping such that, for all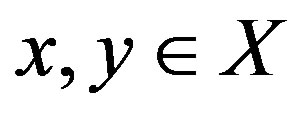, there exists 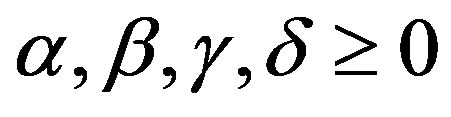with 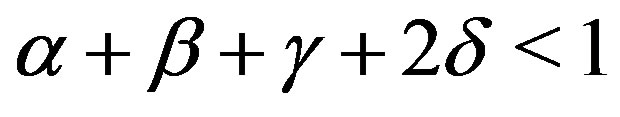such that

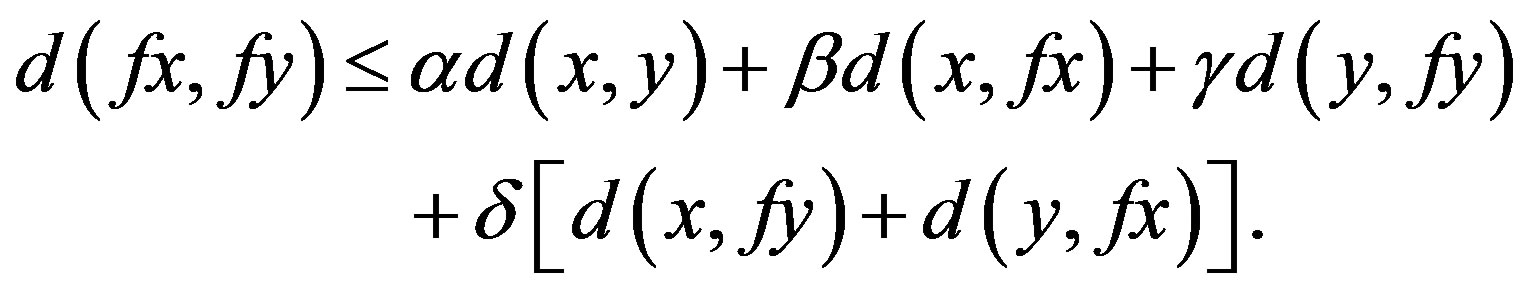
Then f has a unique fixed point.

Also, in 1974, Ććirić [3] generalized his own result [2] by introducing the quasi-contraction and proved a fixed point theorem under this condition as follows:

Definition 1.3 [3] A mapping 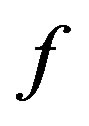of a metric space 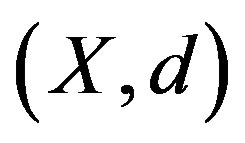into itself is said to be a quasi-contraction if there exists a number 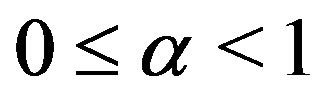such that

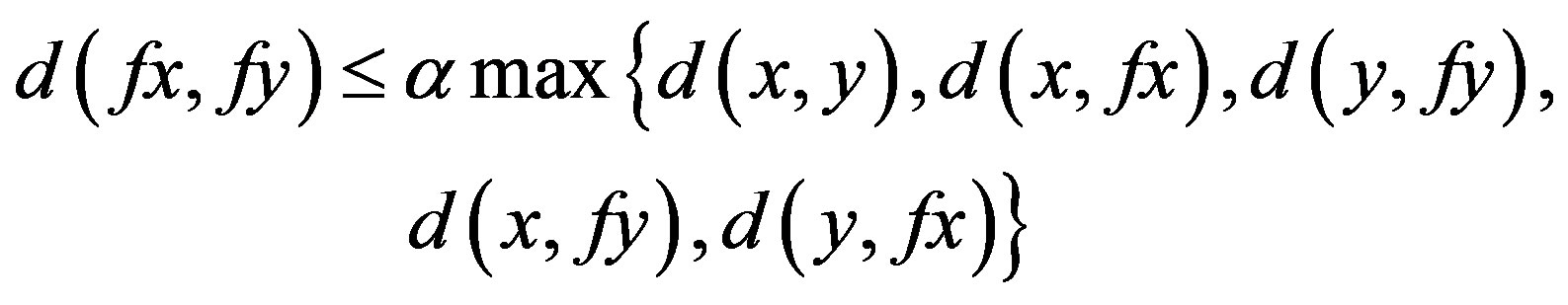
for all.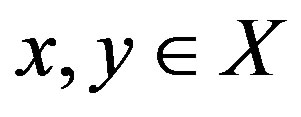

Theorem 1.4. [3] Let 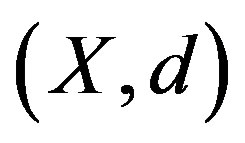be a complete metric space and 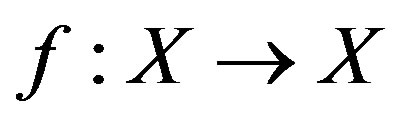be a quasi-contraction. Then f has a unique fixed point in X.

In 2005, Rus [4] introduced the cyclical condition in metric spaces. For some results on fixed point theory, we refer the readers to [5-7]. Throughout this paper, we denote the set 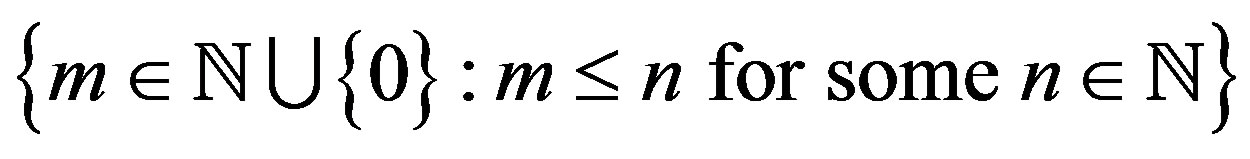by.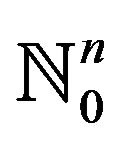

Definition 1.5. [4] Let 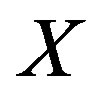be a nonempty set and

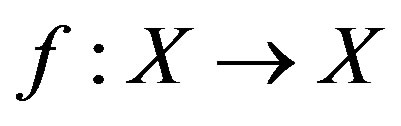be a mapping. The set 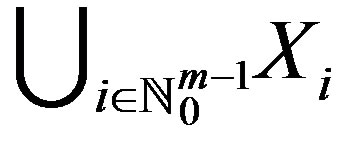is called a cyclic representation of X with respect to f if the following conditions hold:

1);

2) 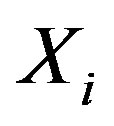is a nonempty subset of 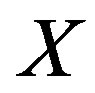for all;

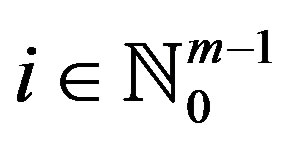3) 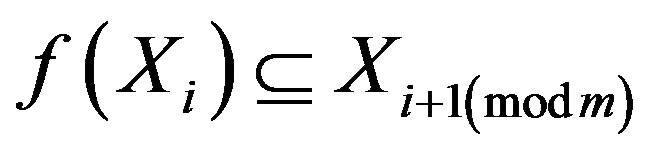for all.

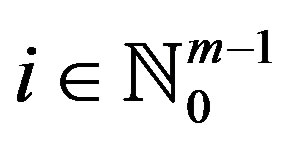Definition 1.6. Let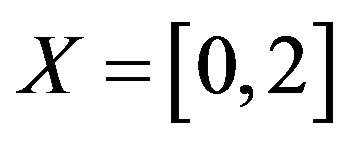, , 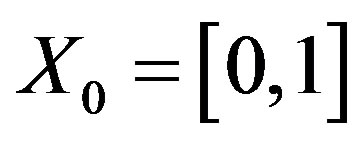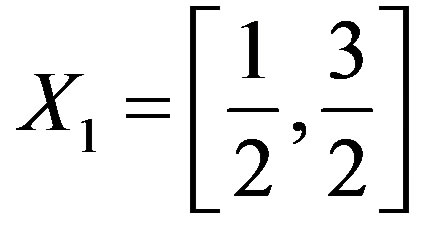and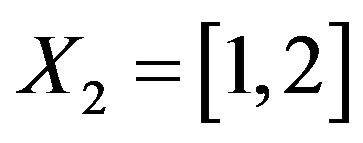. Now, we define a selfmapping f on X by

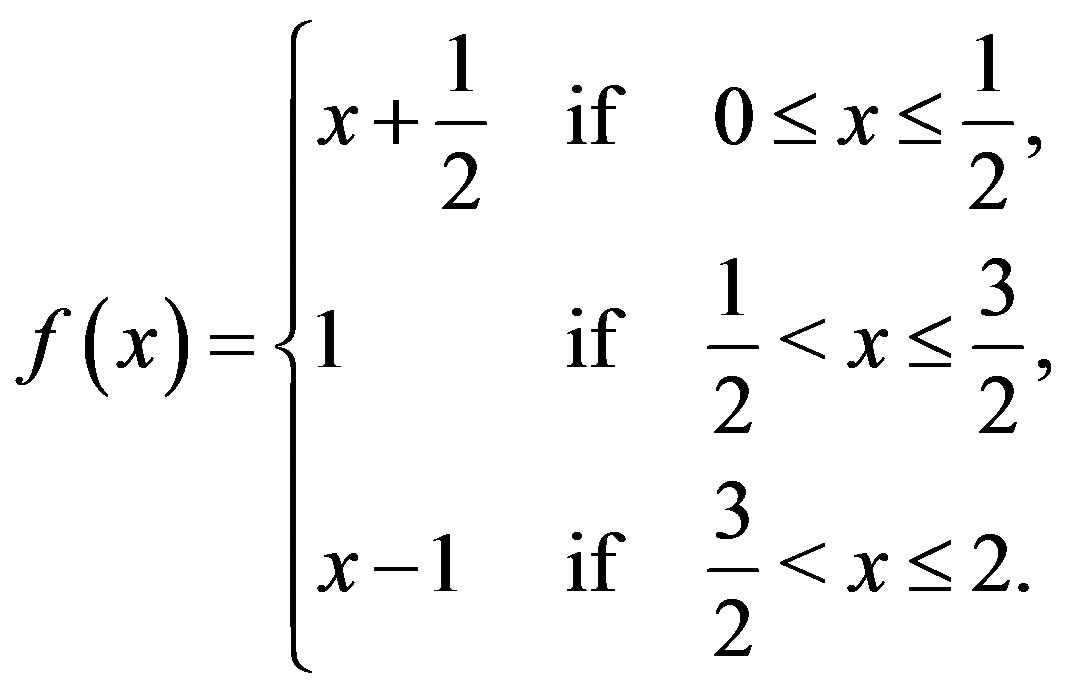
Now, we see that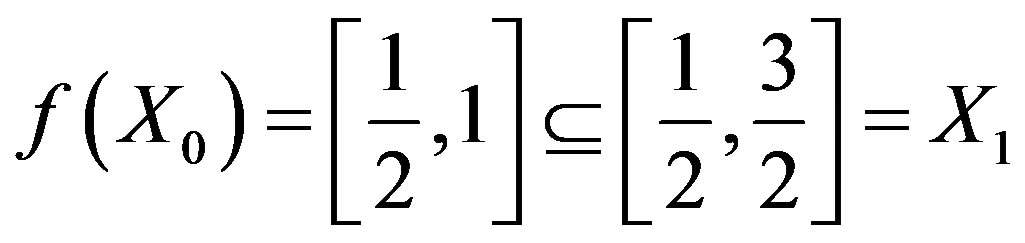, 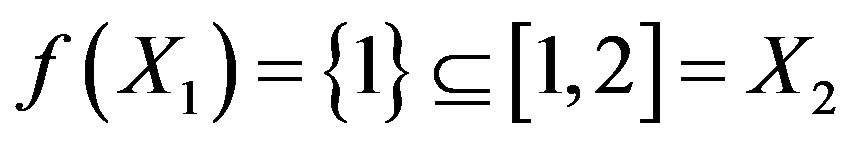and 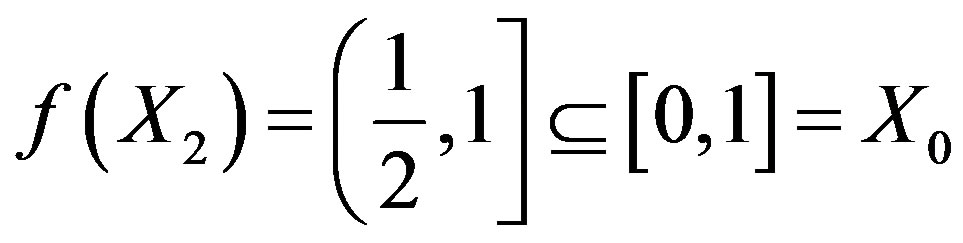. Therefore, the set 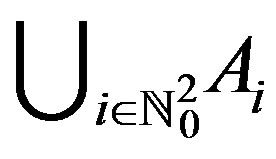is a cyclic representation of X with respect to f.

Definition 1.7. Let X be a nonempty set,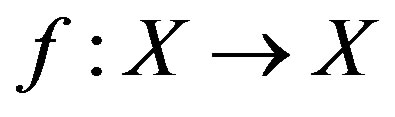

be a mapping and the set 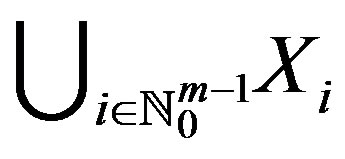be a cyclic representation of X with respect to f. If 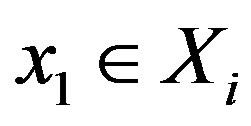and 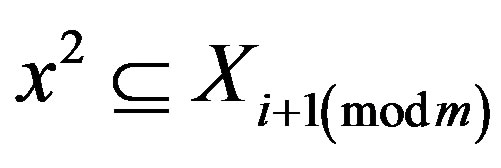for some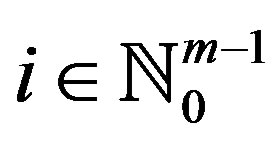, we say that x₁ and x₂ are descendants in Y.

The purpose of this paper is to extend Ććirić’s quasicontraction to a cyclic quasi-contraction, establish some fixed point theorems and give an example to illustrate the main result. We also introduce the notion of co-cyclic quasi-contraction and prove some common fixed point theorems.

2. Fixed Point Theorems

In this section, we introduce a generalization of Ććirić’s quasi-contraction, say, a cyclic quasi-contraction, and prove some fixed point theorems.

Definition 2.1. Let 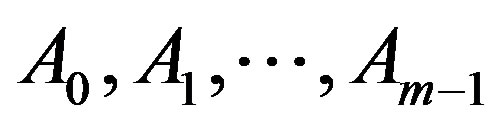be nonempty closed subsets of a metric space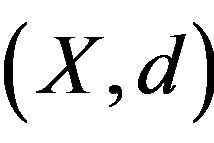, and

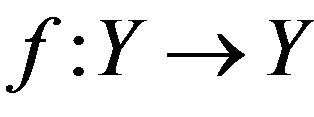be a mapping. If the following conditions are satisfied:

1) 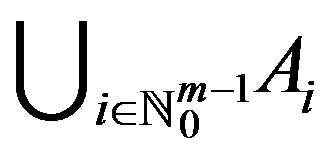is a cyclic representation of Y with respect to f;

2) there exists 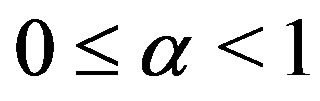such that

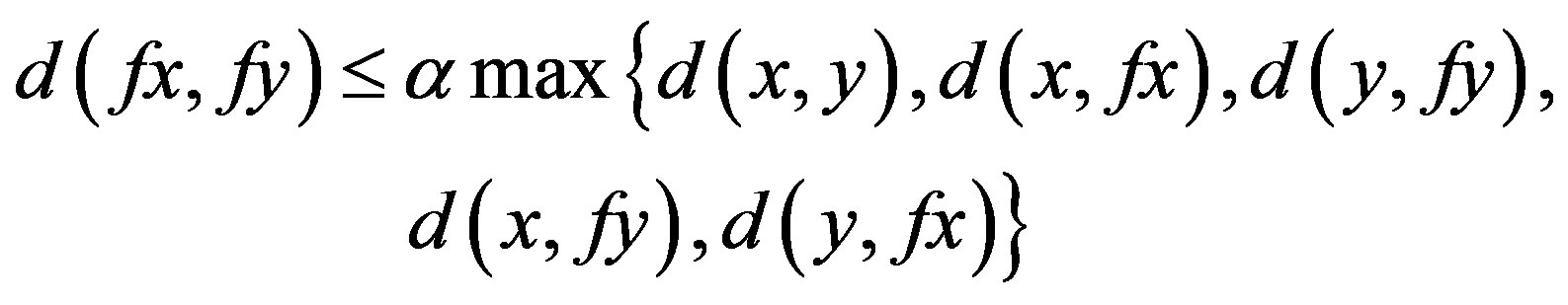
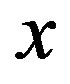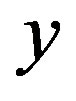whenever and are descendants in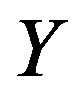, then 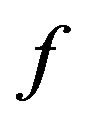is called a cyclic quasi-contraction.

Remark 2.2. To reduce a cyclic quasi-contraction to a quasi-contraction, simply take each 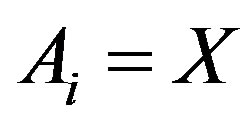and the result directly emerges.

Now, we can construct some fixed point theorems, which generalize the further results, as follows:

Theorem 2.3. Let 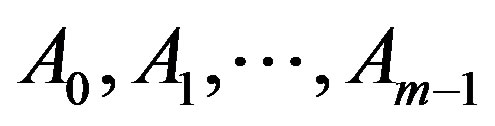be nonempty closed subsets of a complete metric space 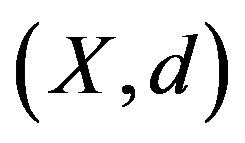and

. Suppose that 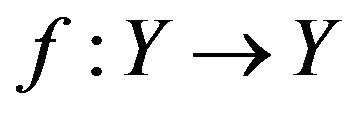is a cyclic quasi-contraction with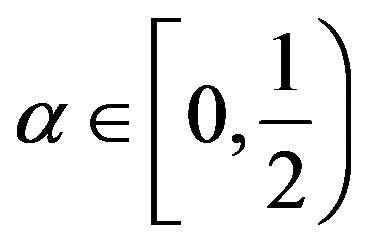. Then f has a unique fixed point and the sequence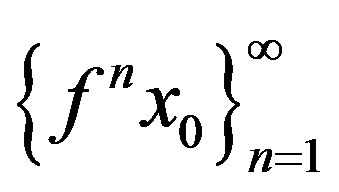

converges to 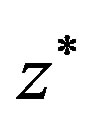for any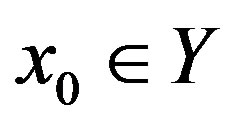

Notice that the 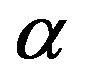-constant in the quasi-contraction is restricted to the set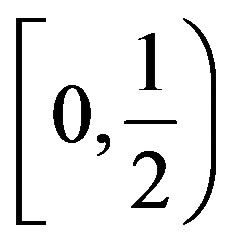. Next, we can drop this restriction and develop a theorem in an ultrametric space. The result follows from the additional assumption of an ultrametric space. Before we give the result, we now give the definition of an ultrametric space.

Definition 2.4. Let 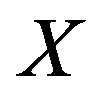be a nonempty set. A function 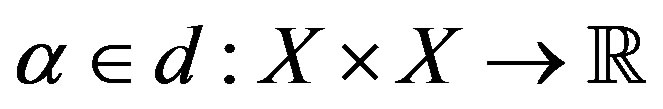is called an ultrametric if it satisfies the following conditions:

1) 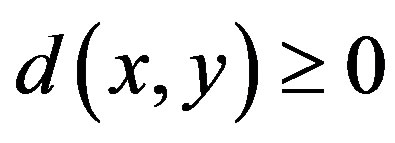and 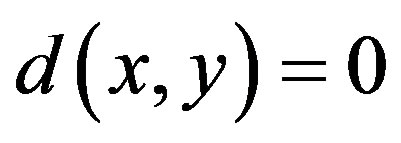if and only if x = y for all;

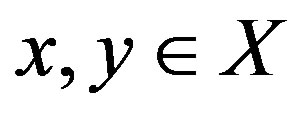2) 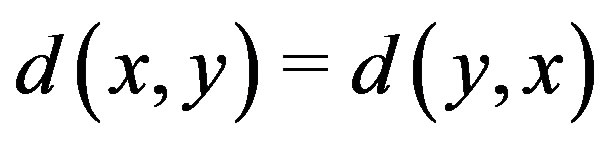for all;

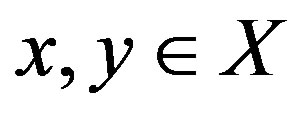3) 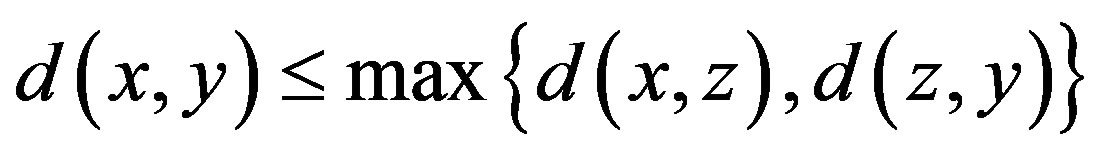for all .

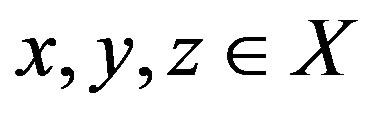A set X equipped with this ultrametric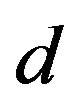, denoted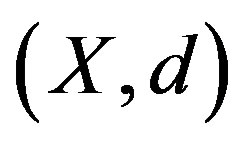, is called an ultrametric space.

Remark 2.5. Note that an ultrametric space is also a metric space. We can simply prove this. In fact, for any,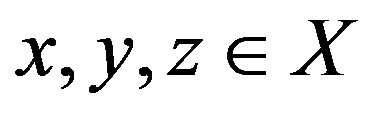

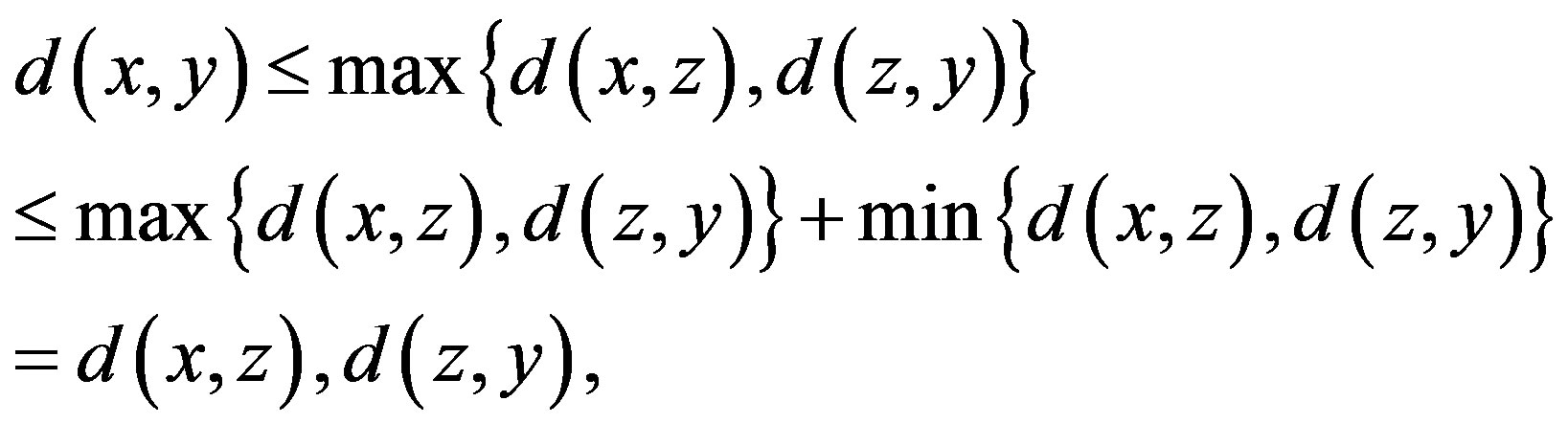
which in turn is a metric.

Theorem 2.6. Let 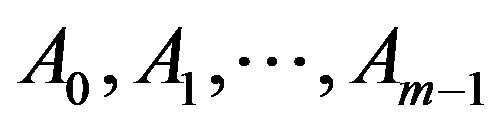be nonempty closed subsets of a complete ultrametric space 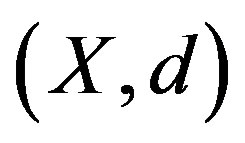and

. Suppose that 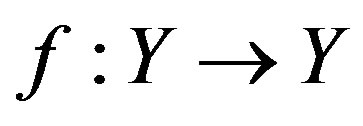is a cyclic quasi-contraction. Then 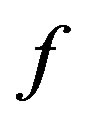has a unique fixed point 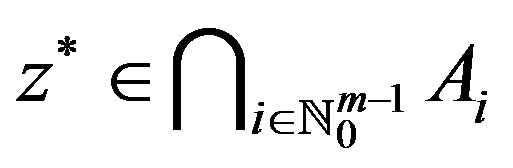and the sequence converges to 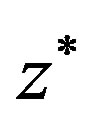for any.

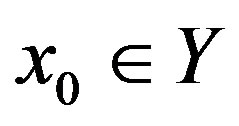Now, we prove Theorem 2.3. The proof of Theorem 2.6 is quite similar to the proof of Theorem 2.3, we omit to prove this theorem.

Proof of Theorem 2.3. Let 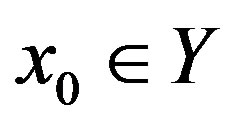be arbitrarily chosen. Define a sequence 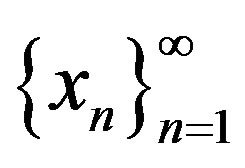by 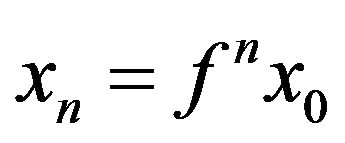for all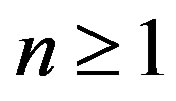. If there exists a positive integer n₀ such that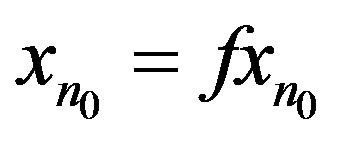, the the proof is finished. So, assume that

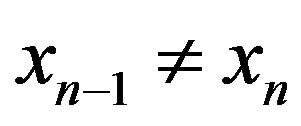for all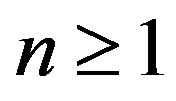. Since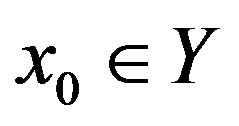, there exists

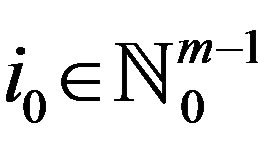such that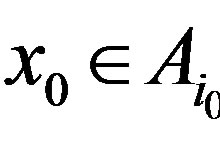. Therefore, 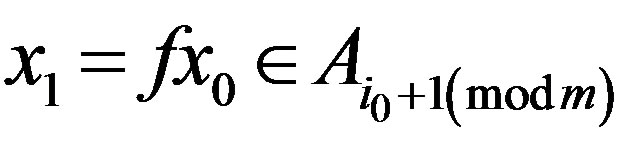and, by induction, we have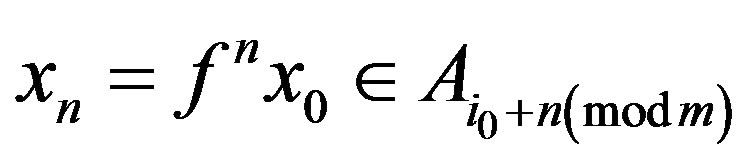. Hence we have

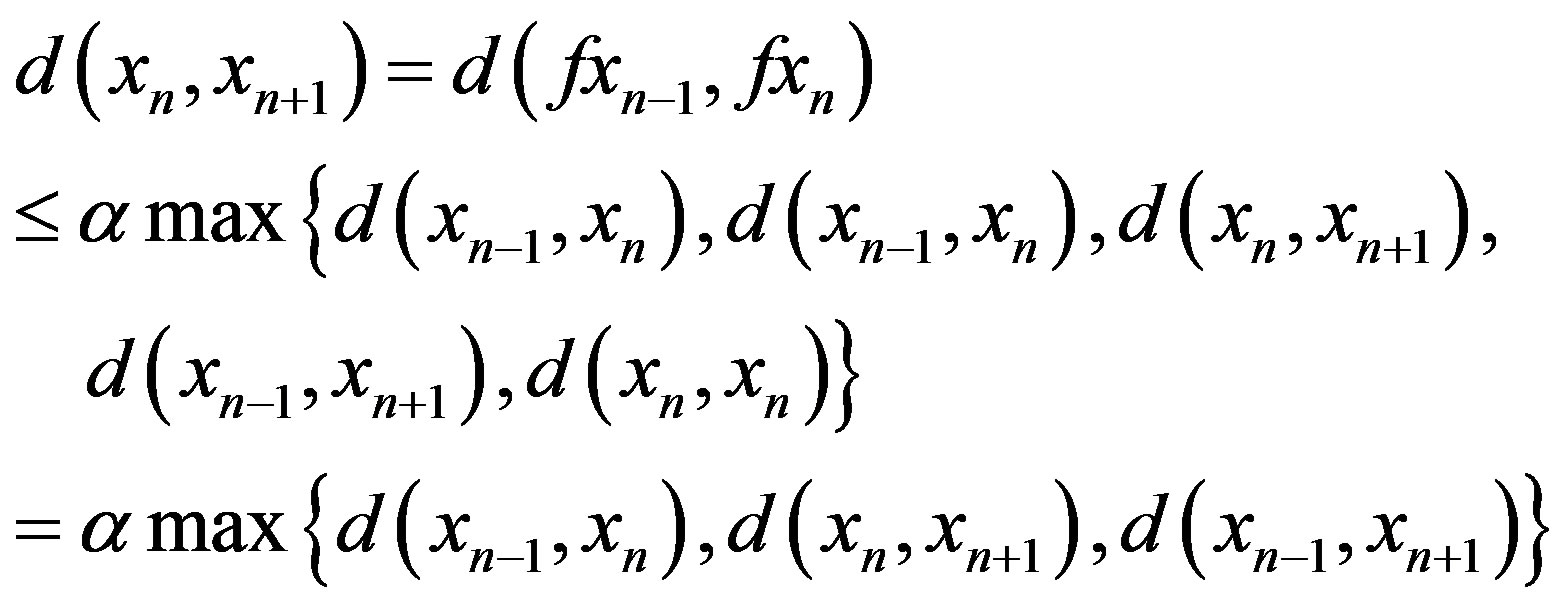(1)

Assume that

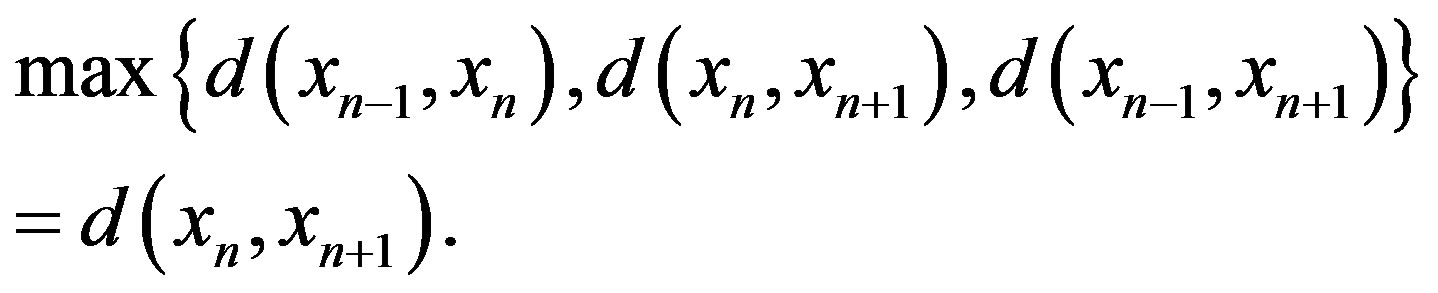
Then we can see that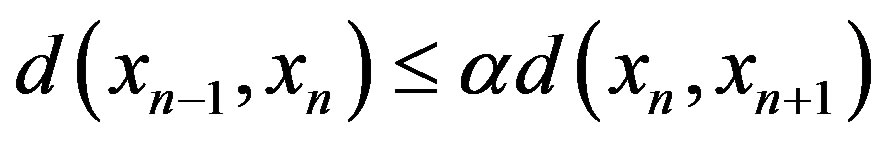, which is a contradiction. Therefore, from (1), it follows that

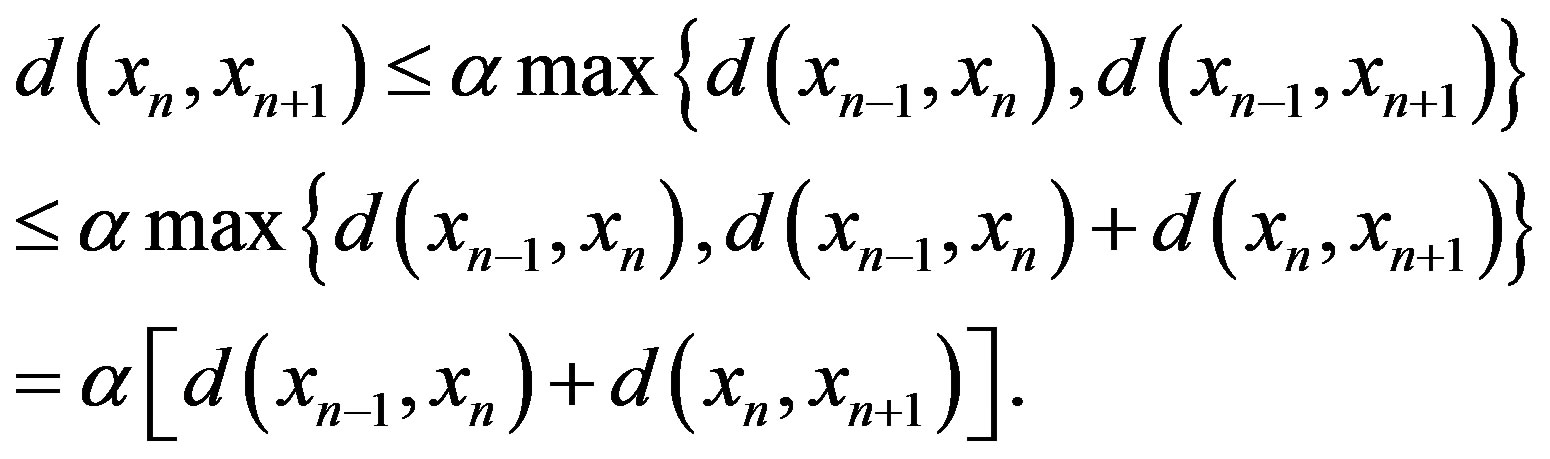
Consequently, we can deduce that

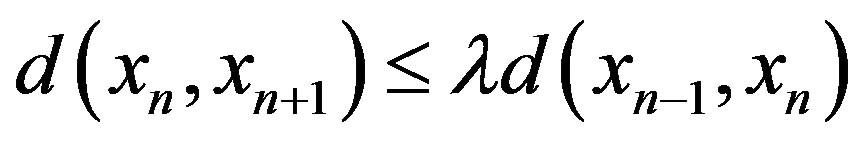, where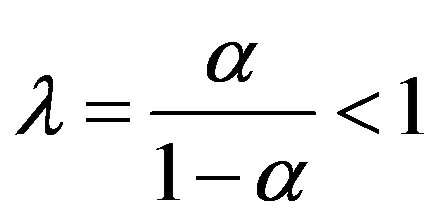. By repeating this process, we have.

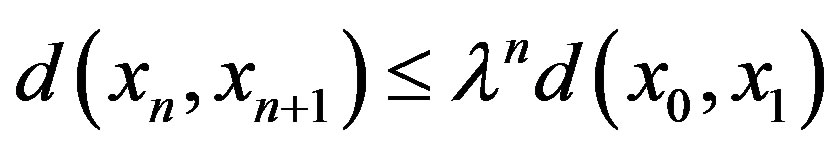Thus it is easily seen that 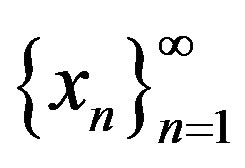is a Cauchy sequence in Y. Since Y is closed in X, Y is a complete subspace of X and so 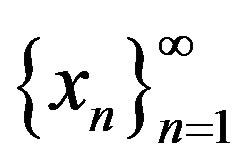converges to some point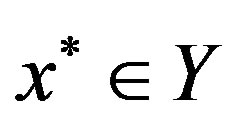. Denote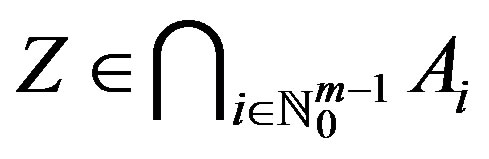. Now, we show that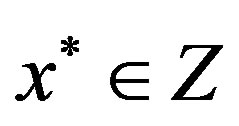. Sincefor each, we have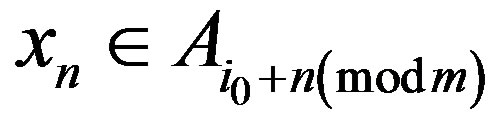, it is easy to see that, for each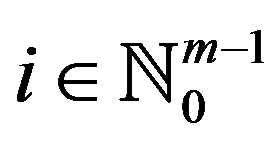, A_i contains infinitely many points of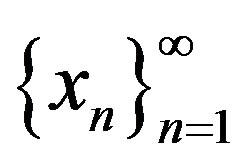. Since A_i is closed for each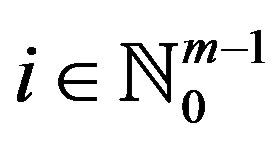, we can construct a subsequence of 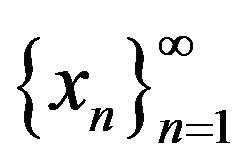in A_i which converges to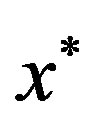. Therefore,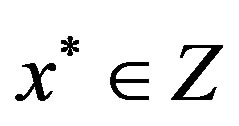. In other words, Z is nonempty.

Consider the restriction 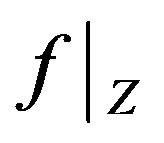of the function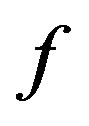. We can see that it maps 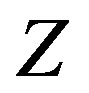into itself, i.e.,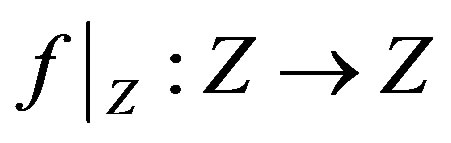. Then it is easily proved, by applying Theorem 1.4, that 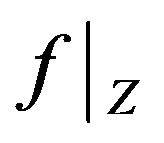has a unique fixed point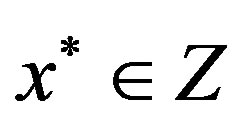. Thus is also a fixed point of.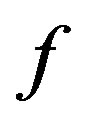

Now, assume that there exists another fixed point of 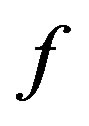denoted by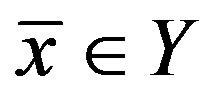. Since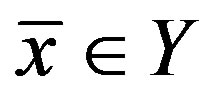, we have 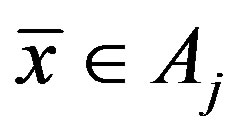for some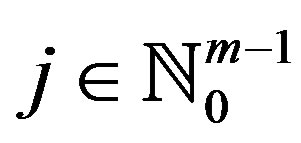. Therefore, 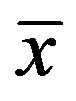and 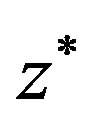are descendants in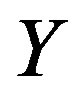. Hence we have

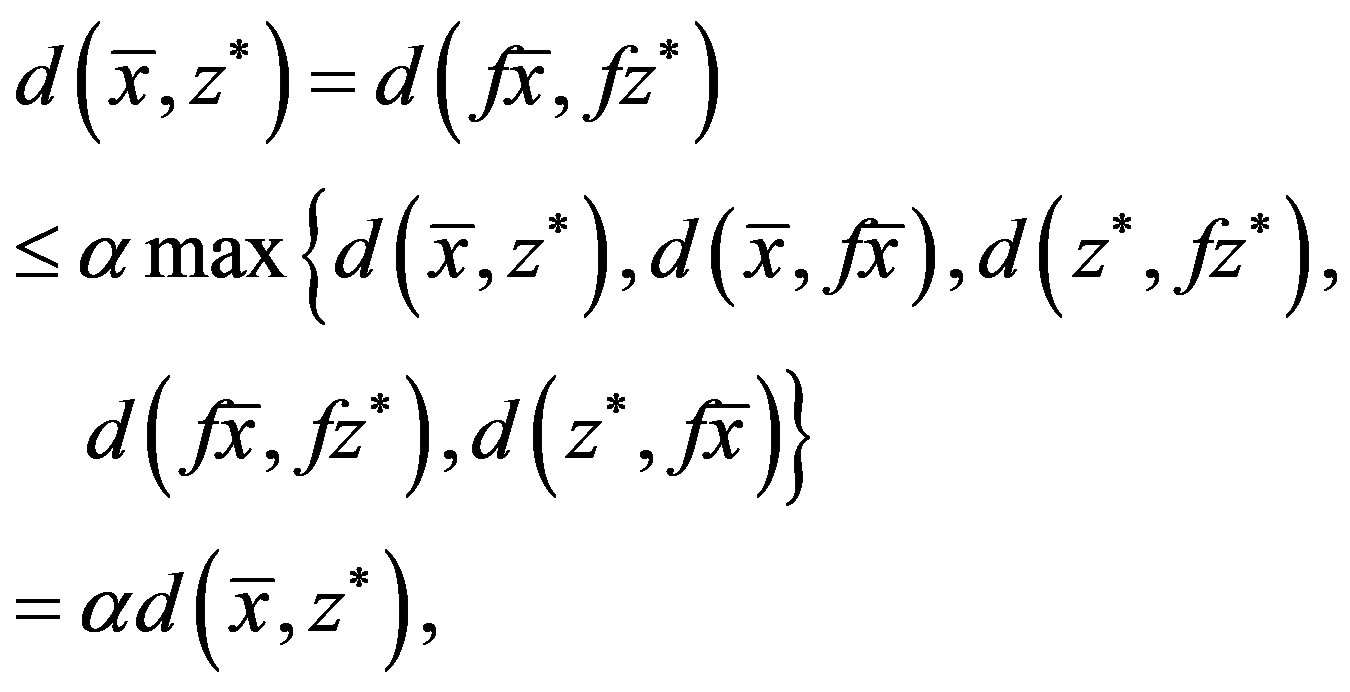
which implies that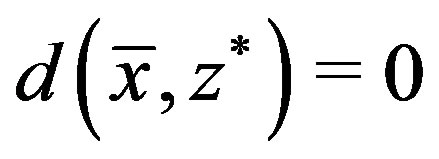, that is, 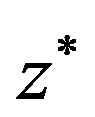is the unique fixed point of.

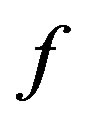Next, we show that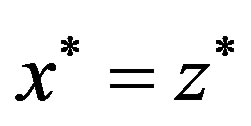. Since Z and 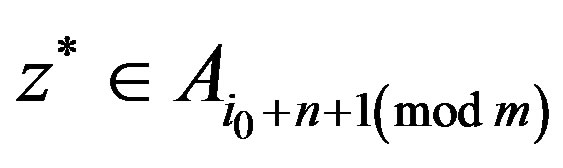, we have

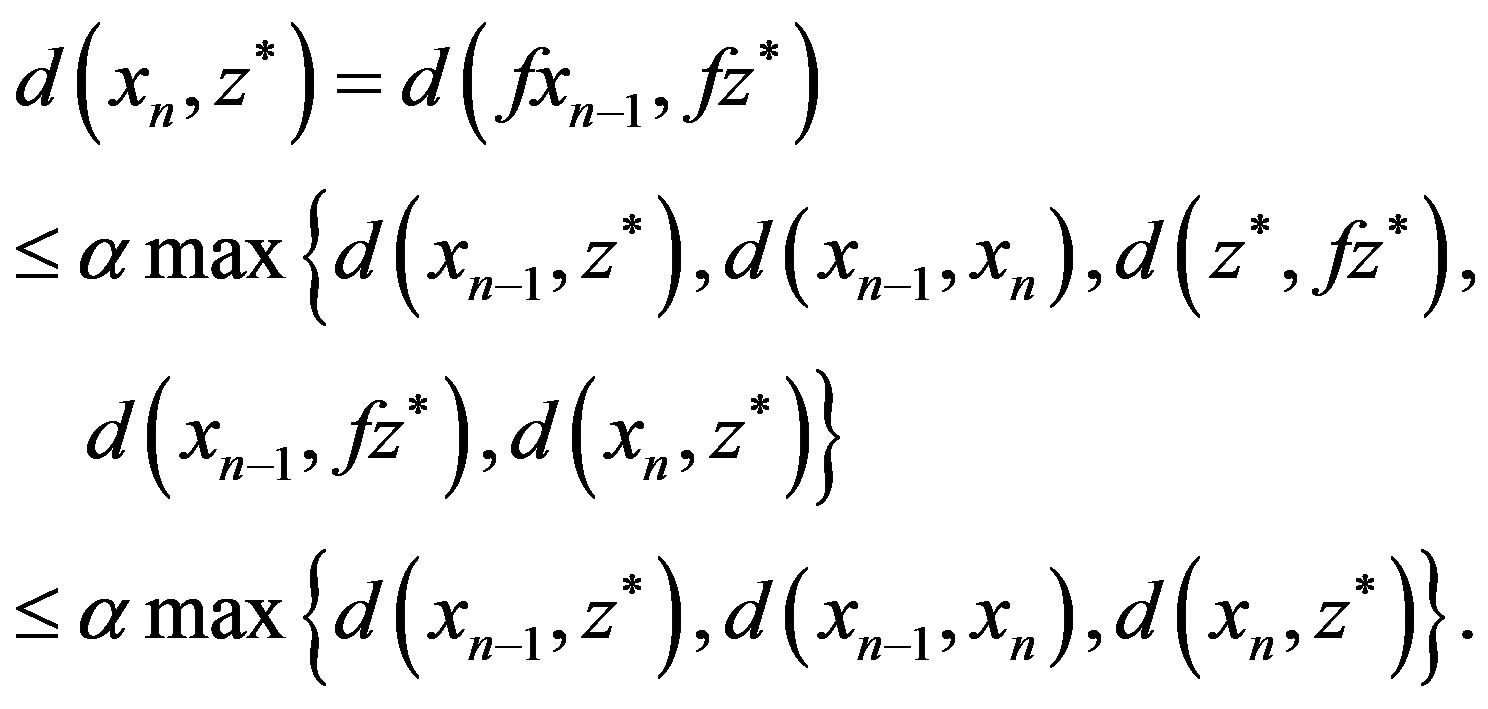(2)

We have a contradiction if

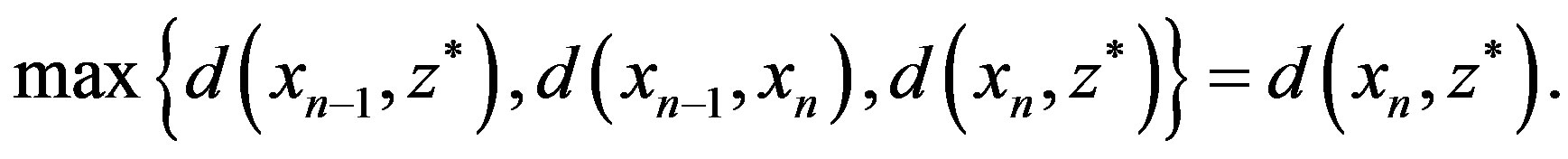
So, we claim that

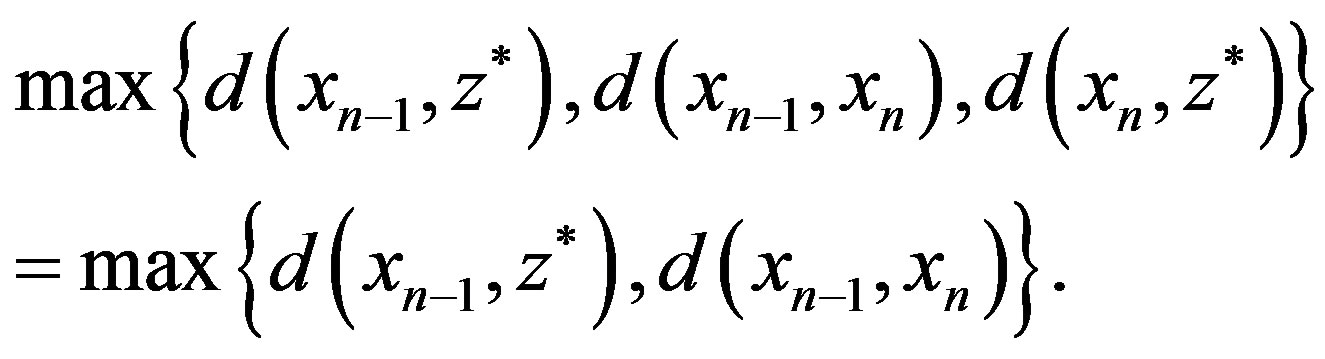
Hence, from (2), it follows that

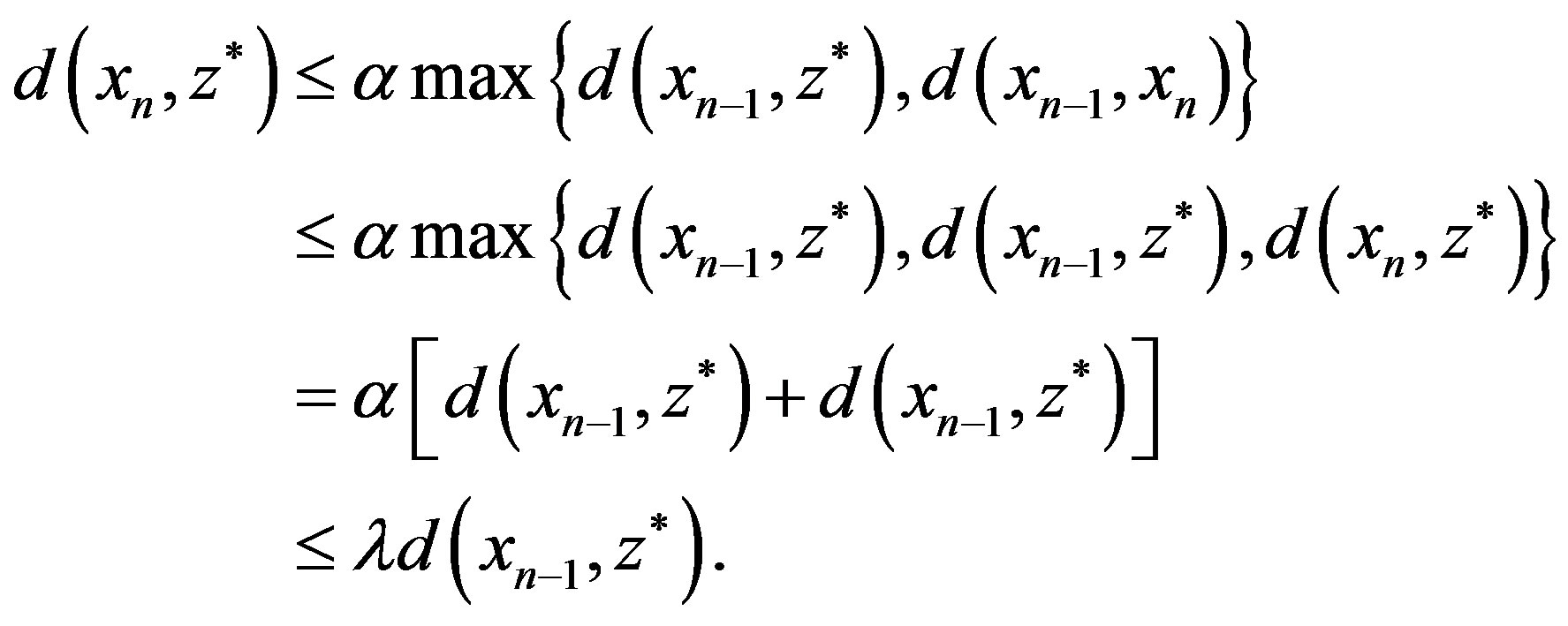
Thus, by repeating this process, we obtain

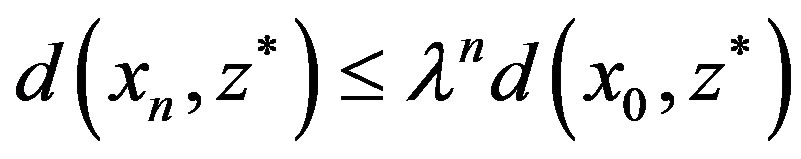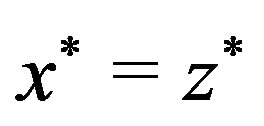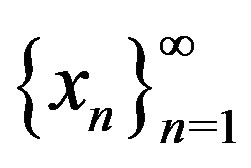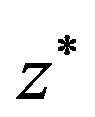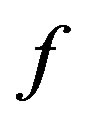. Therefore, we have, that is, converges to the unique fixed point of in 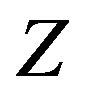for any initial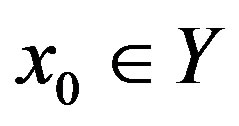. This complete the proof.                                        ■

Proof of Theorem 2.6. Let 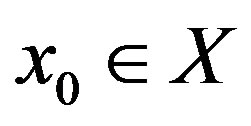be arbitrary. Define a sequence 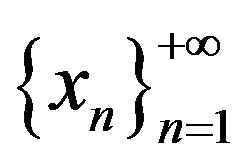as in the proof of Theorem 2.3. Following the proof lines, we obtain

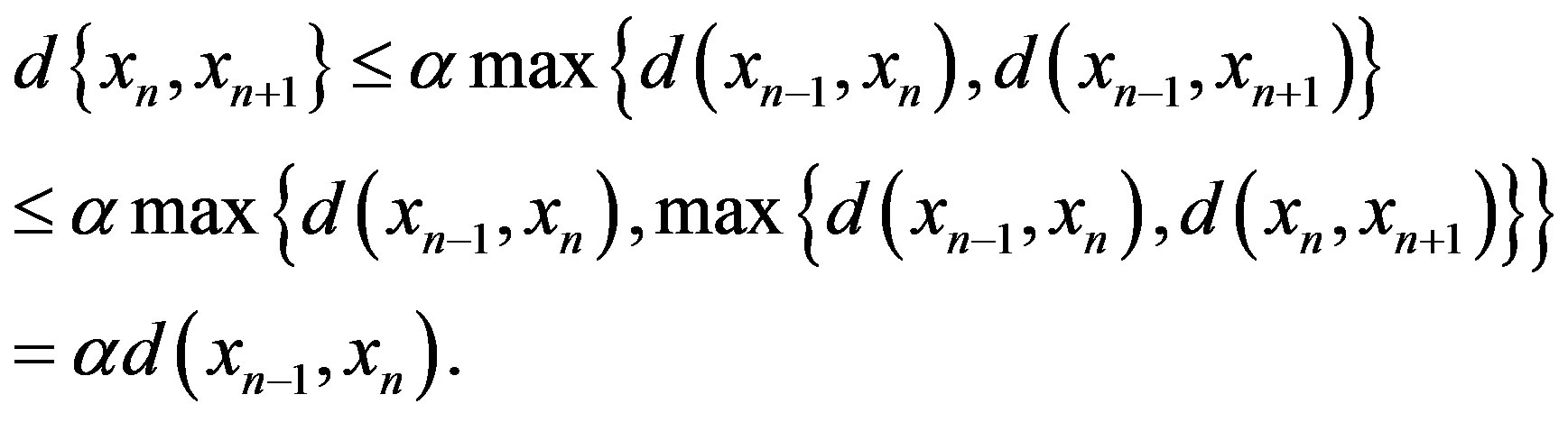
By repeating this process, we get

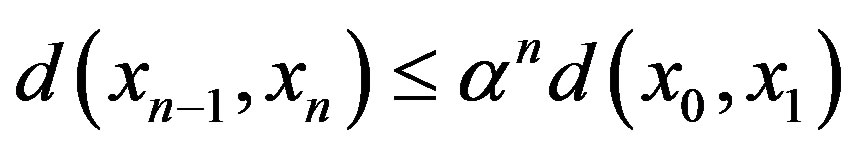. Then it is easily seen that the sequence 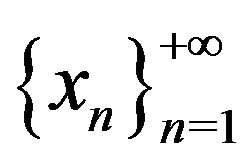is a Cauchy sequence and so, from the completeness of, 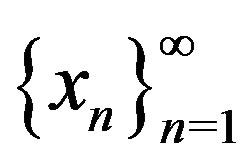converges to some point

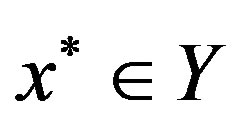. We can show, by using the proof of Theorem 2.3, that 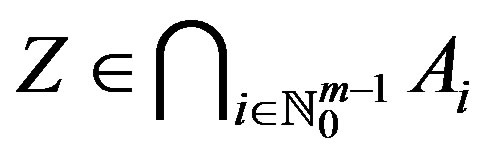is not empty. More precisely, .

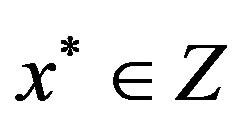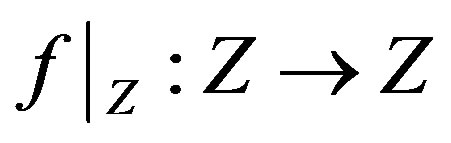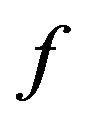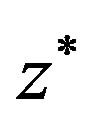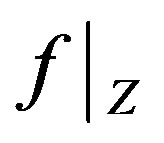Now, we consider the restriction of the function. Note that the strong triangle inequality also implies the ordinary triangle inequality. Hence Theorem 1.4 can be applied to confirm the existence of a unique fixed point of in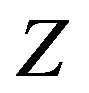. By the proof of Theorem 2.3, we can show that 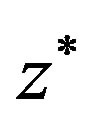is also the unique fixed point of.

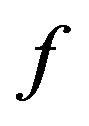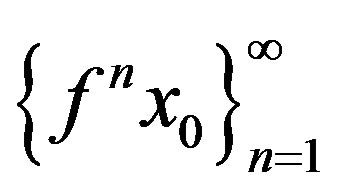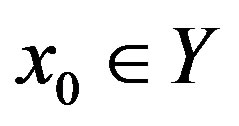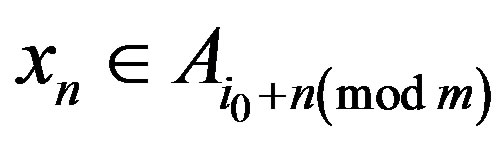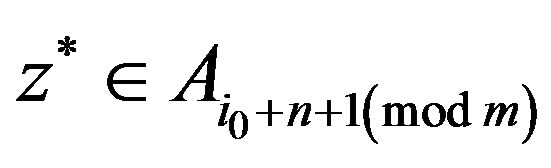Now, we show that the sequence converges to z^* for any. Since and, we have

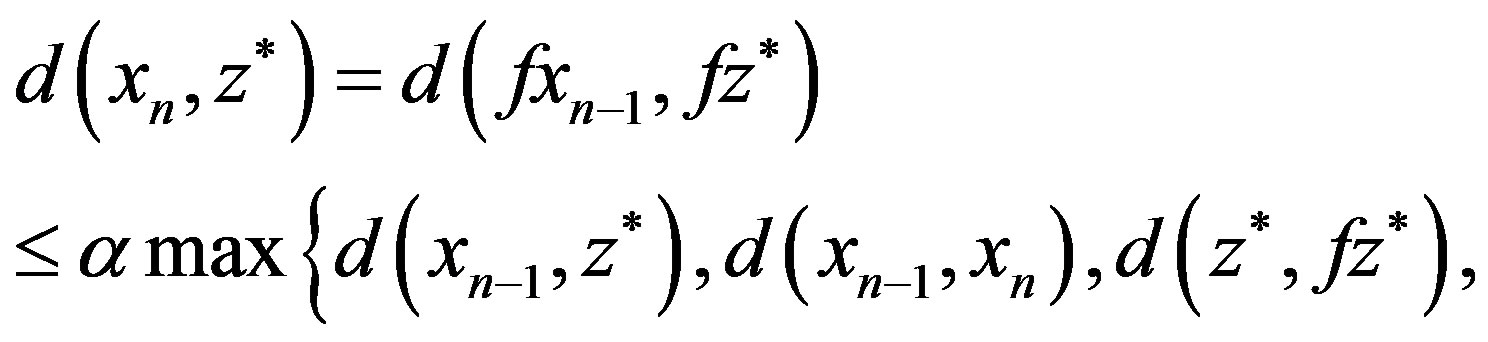
We can see that

.

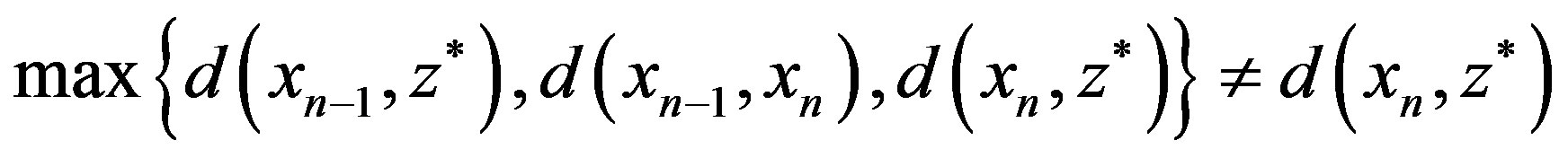Otherwise, we have a contradiction. Hence we have

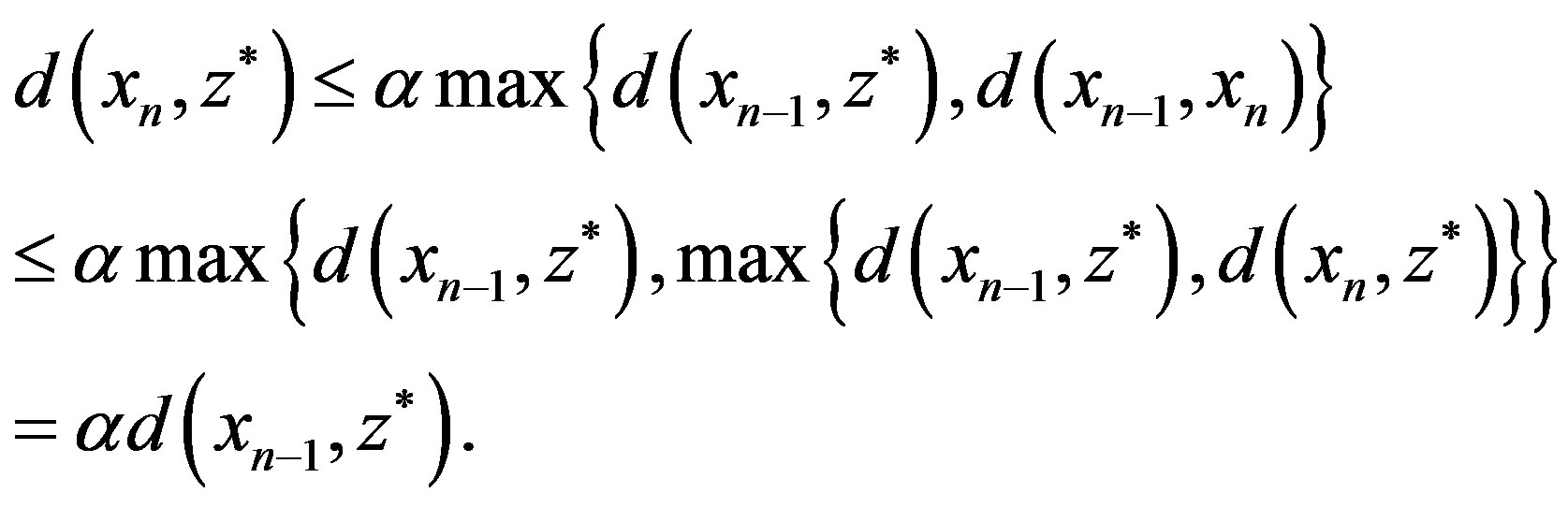
Again, by repeating this procedure, we obtain

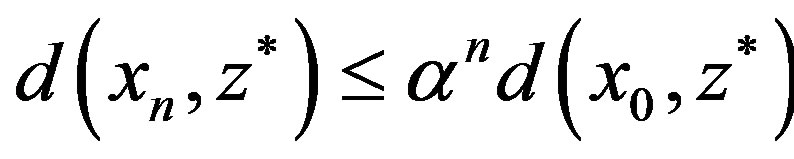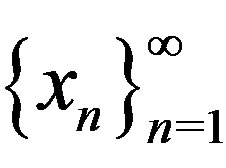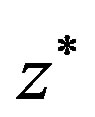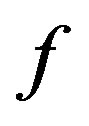. Then the sequence converges to the unique fixed point of in 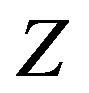for any initial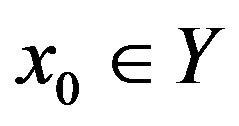. This completes the proof.        ■

Notice that our results do not only generalize Ććirić’s result, but also make it easier to determine the fixed point of a given mapping as in the following example:

Example 2.7. Consider a weighted graph

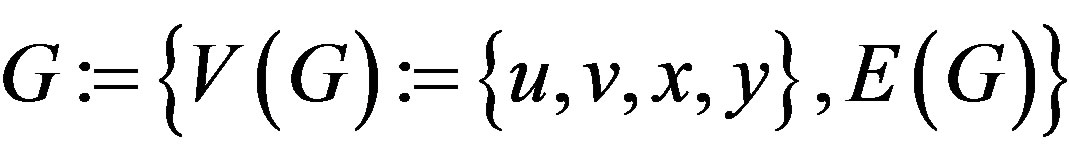whose 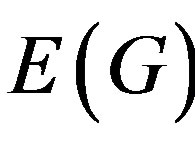makes G a complete K₄ graph with weights 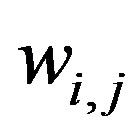for each 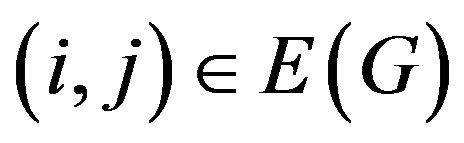given as follows:

For the understanding of the readers, we illustrate G as a figure in the following:

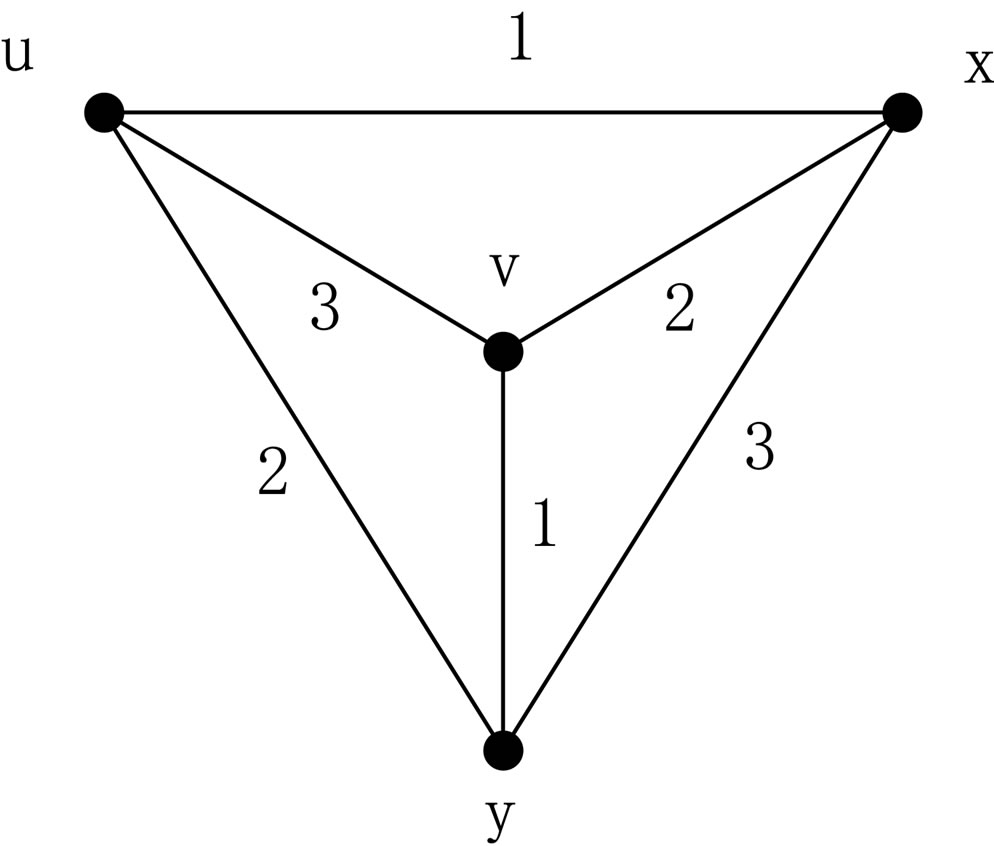
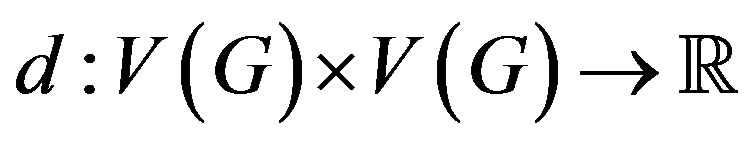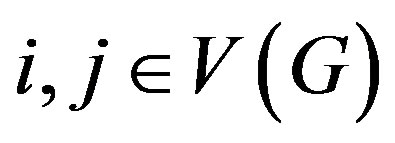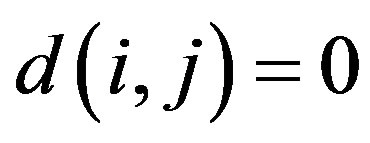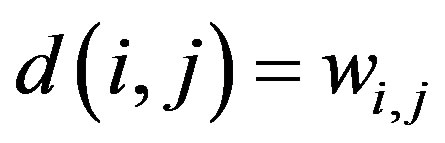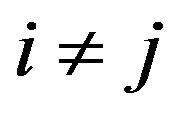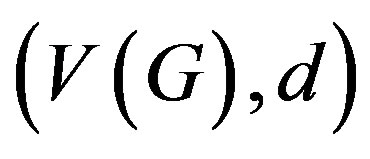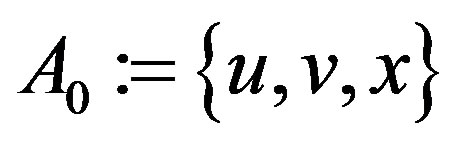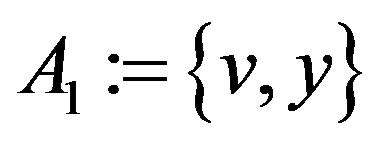Now, define a function by letting, for all, if i = j and if (we can do this because the graph G is complete). By this setting, it is easy to verify that is a complete metric space. Set and, we have A₀ and A₁ being two closed subsets of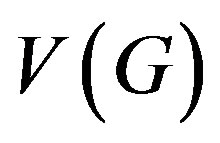. Suppose that the mapping 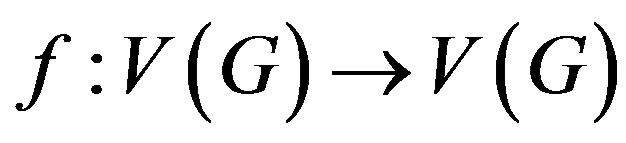given by the following:

By a careful calculation, we may obtain that 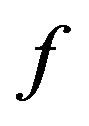is a cyclic quasi-contraction on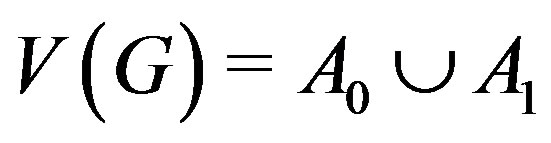. Thus, 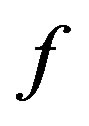has a unique fixed point 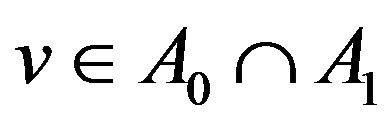and 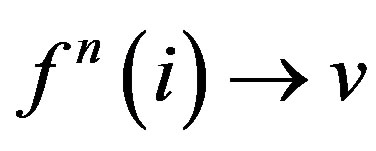for every.

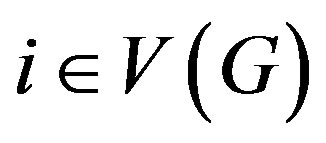3. Common Fixed Point Theorems

In this section, we prove some common fixed points theorems for the co-cyclic conditions. Before we can prove our results, we also need the following, which is an extension of Definition 2.

Definition 3.1. Let X be a nonempty set and

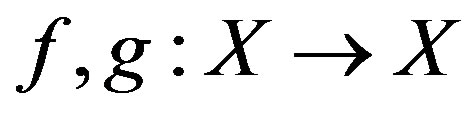be two mappings. The set 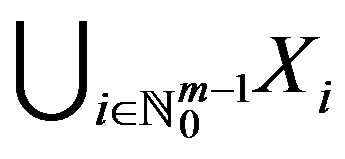is called a co-cyclic representation of X between f and g if the following conditions are satisfied:

1);

2) 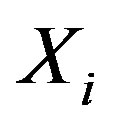is a non-empty subset of 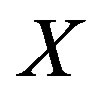for all;

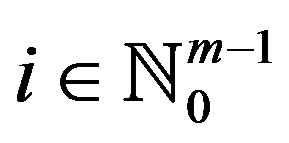3) 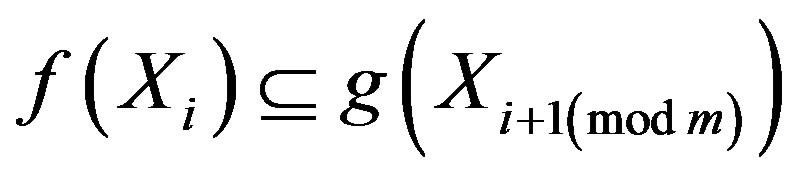for all.

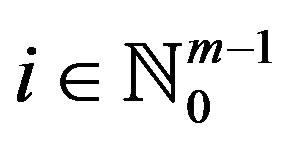Example 3.2. Let, ,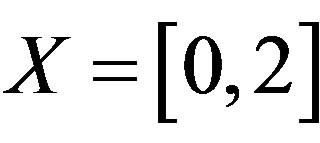

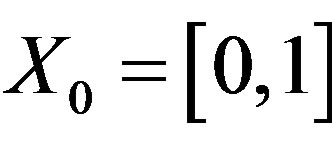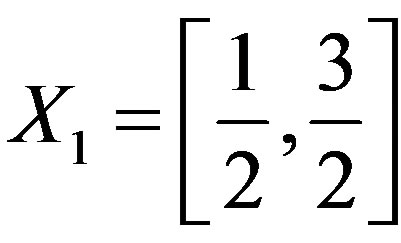
and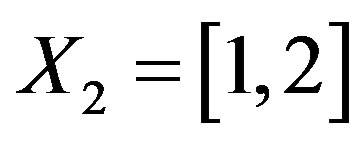. Now, define two self-mappings f, g on X by

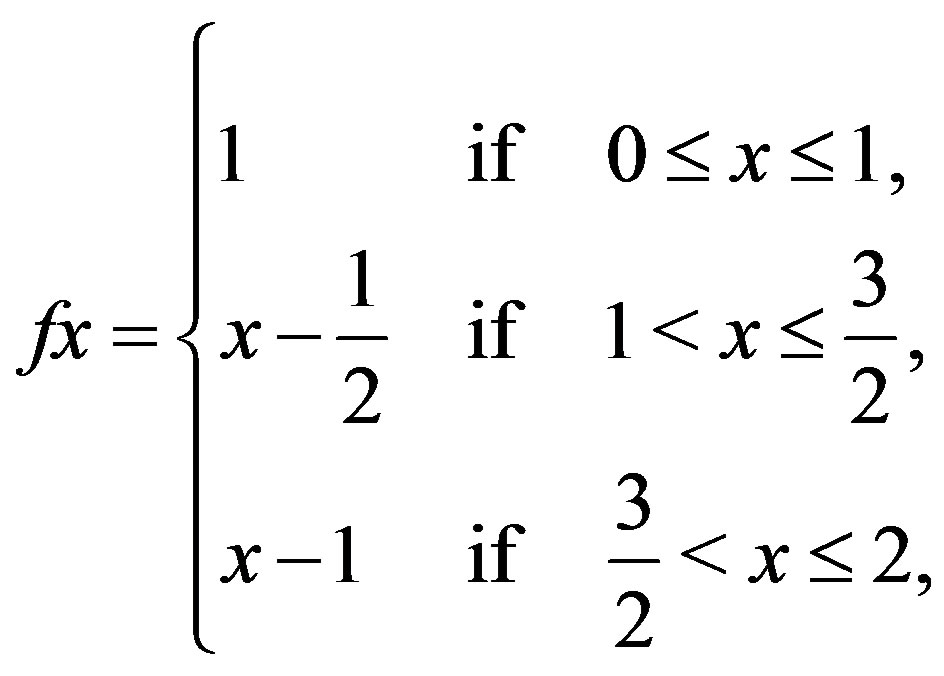
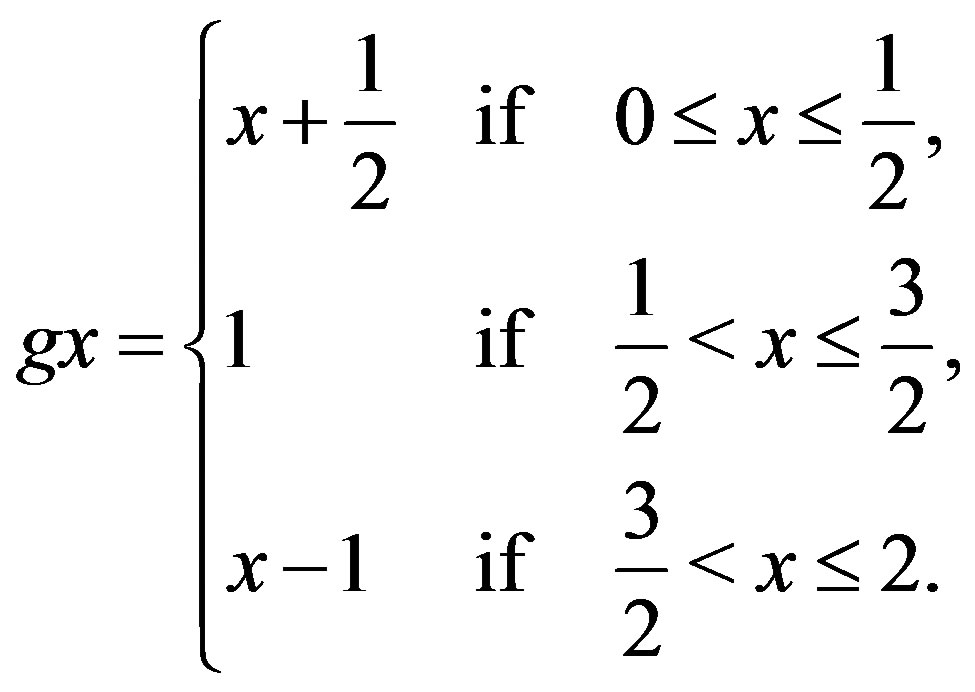
Now, we see that

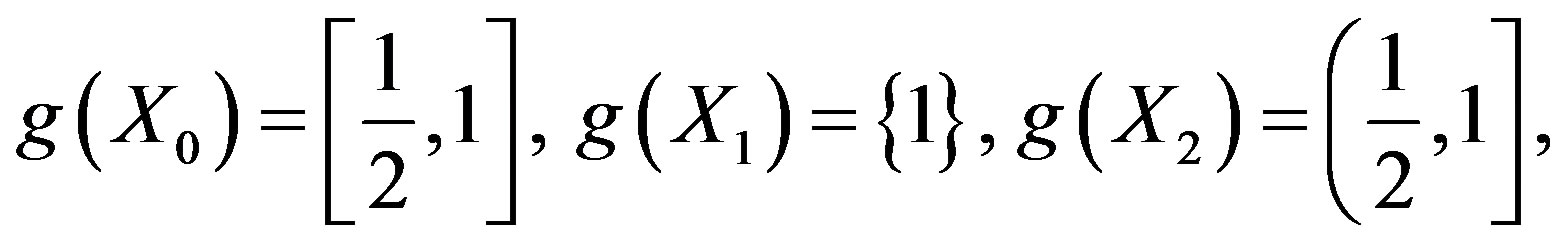
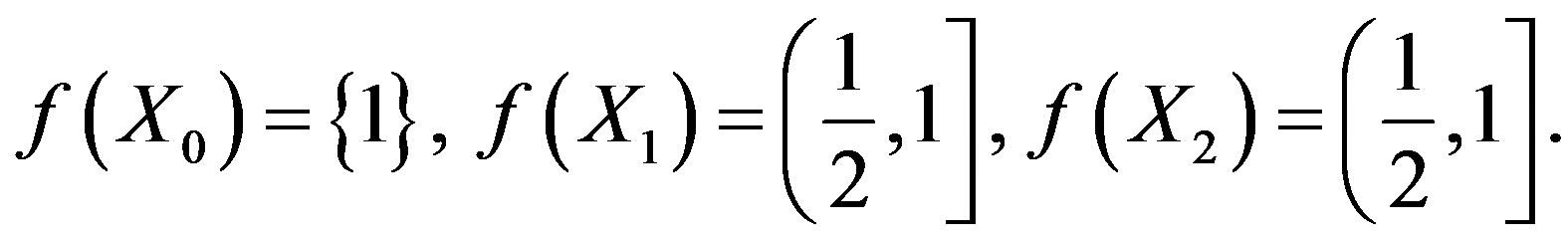
Therefore, 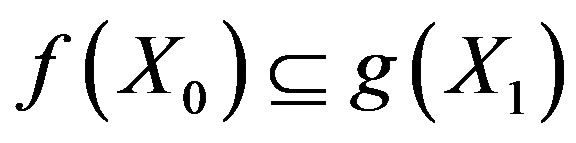, 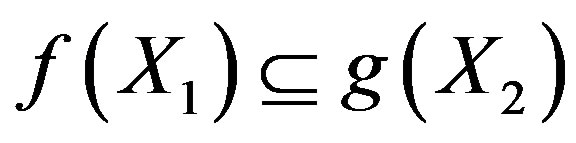and

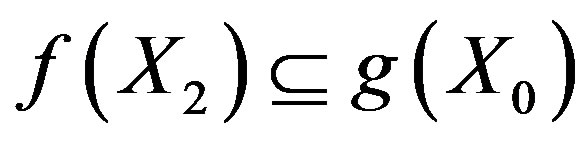. That is, 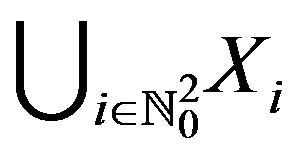is a co-cyclic representation of X between f and g.

Definition 3.3. Let 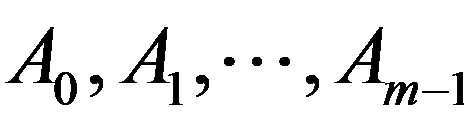be nonempty closed subsets of a metric space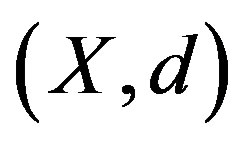, and

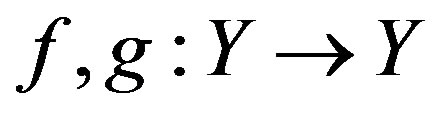be two mappings. If the following conditions are satisfied:

1) 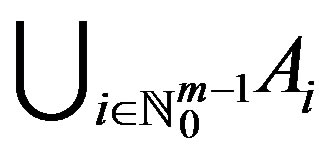is a co-cyclic representation of Y between f and g;

2) there exists 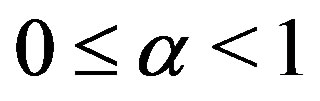such that

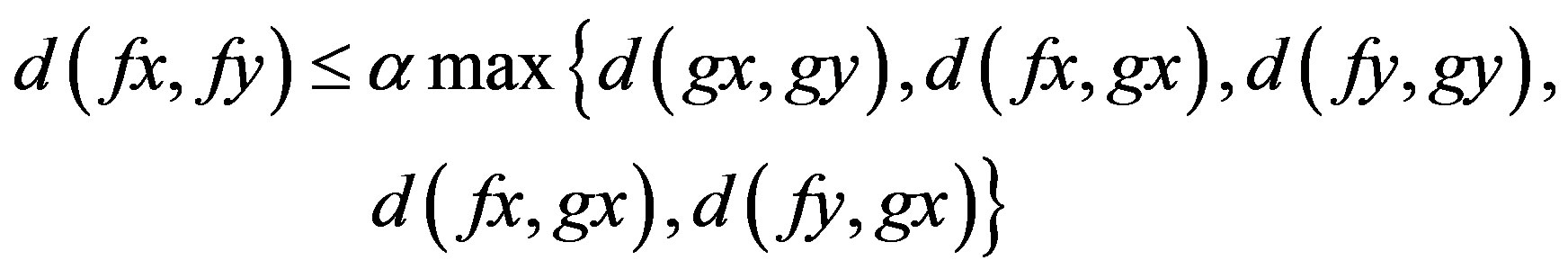
whenever x and y are descendants in Y, then we say that f and g are 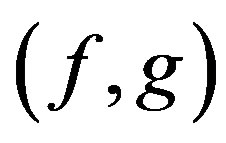-co-cyclic quasi-contraction.

Remark 3.4. The notions and results in this section can be reduced from the results of the previous section if the mapping g is the identity mapping.

Now, we are ready to give some extensions of the results in Section 2.

Theorem 3.5. Let 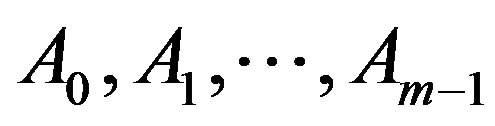be nonempty closed subsets of a complete metric space 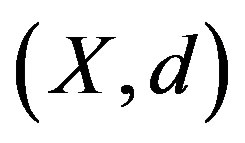and

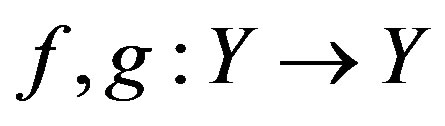. Suppose that are 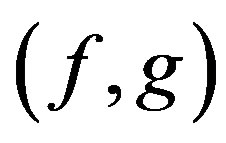- co-cyclic quasi-contraction with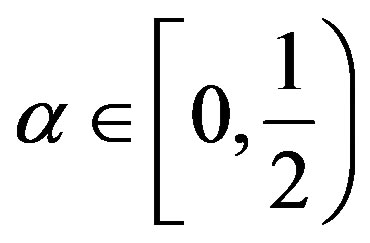, 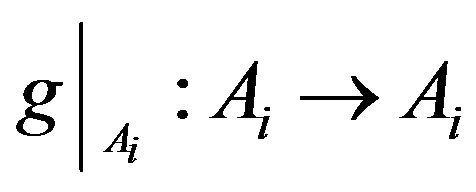is a mapping and 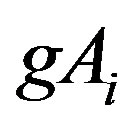is closed for all

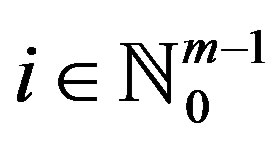. Then f and g have a unique point of coincidence in.

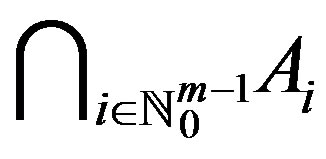Theorem 3.5 can be proved using the analogous ideas of the proofs in Section 2. However, we prove Theorem 3.5 differently by using the following lemma ([8]):

Lemma 3.6. [8] Let 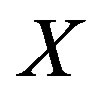be a nonempty set and 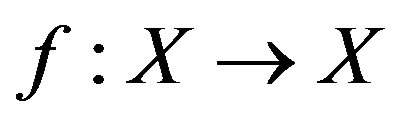be a mapping. Then there exists a subset 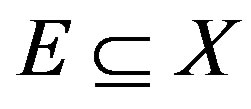such that 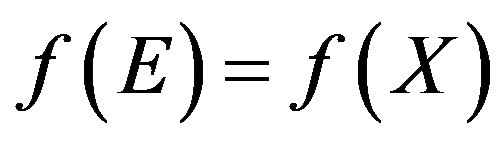and 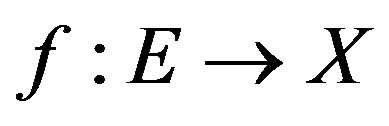is an injection.

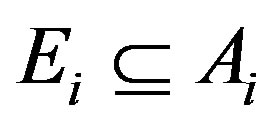Proof of Theorem 3.5. By Lemma 3.2, for each, there exists such that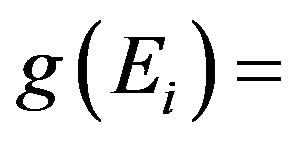 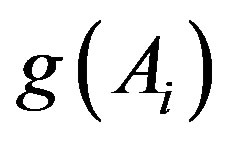and 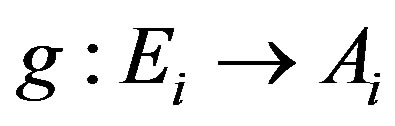is an injection. Define

and a mapping 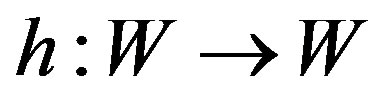by hgx = fx. It is easy to see that

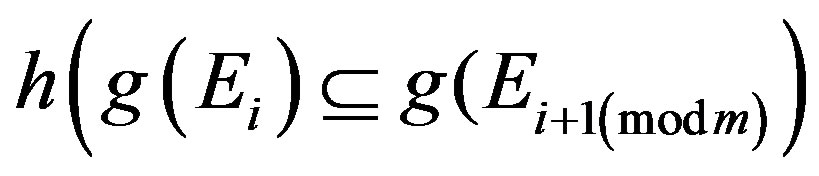
for each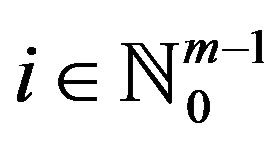, which further implies that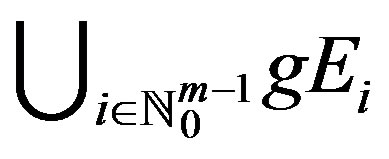

is a cyclic representation of W with respect to h. Moreover, we can write the 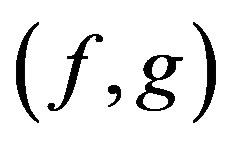-co-cyclic quasi-contraction with 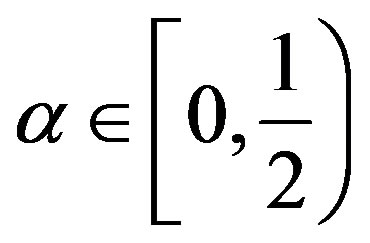in terms of a cyclic quasi-contraction as follow:

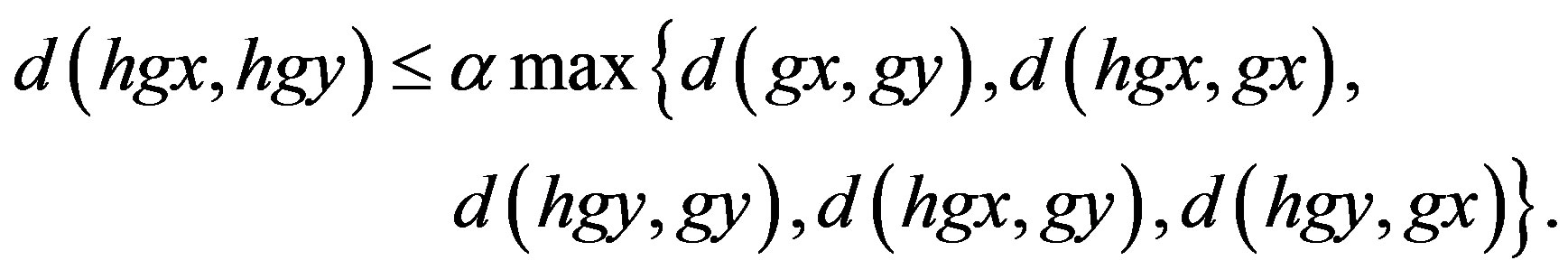
Since W is complete, by using Theorem 2.3, we show that there exists a unique fixed point 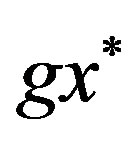of h in

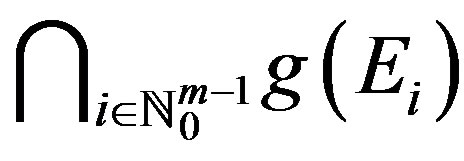. In fact, this means.

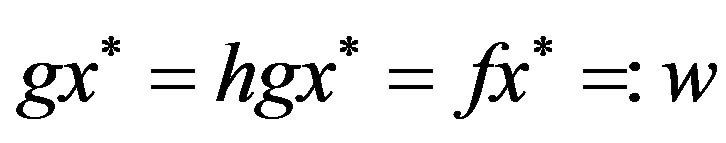Furthermore, we can see that w is also the unique point of coincidence of f and g in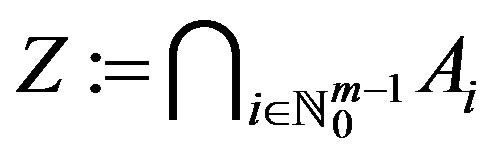. This completes the proof.

Note that our conditions are not strong enough to show the existence of a common fixed point of two mappings. To guarantee the existence and uniqueness of a common fixed point, we need an additional condition, namely, a weak compatibility, which is defined as follows:

Definition 3.7. [9] Let X be a nonempty set. Two mappings 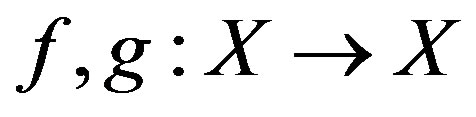are said to be weakly compatible if they commute at their point of coincidences, i.e., if 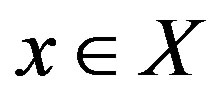is such that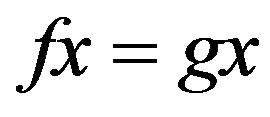, then.

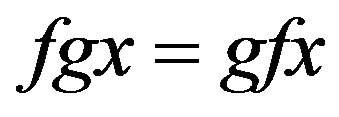Theorem 3.8. Suppose that all the conditions in Theorem 3.5 hold. If f and g are weakly compatible, then f and g have a unique common fixed point.

Proof. Since all the conditions in Theorem 3.5 hold, it follows that f and g have a unique point of coincidence w of f and g, that is, 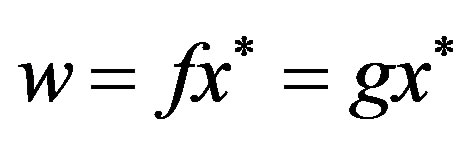in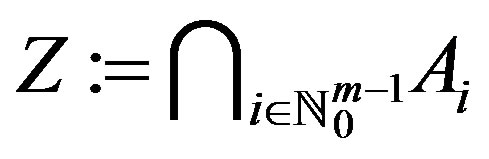. If f and g are weakly compatible, we have

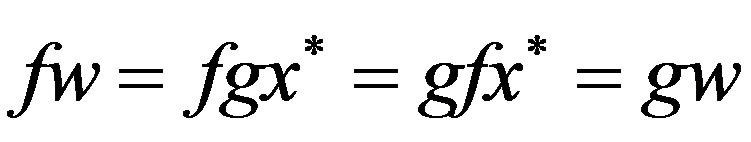. This means 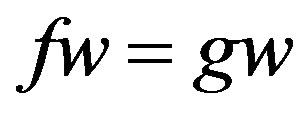is also a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we have that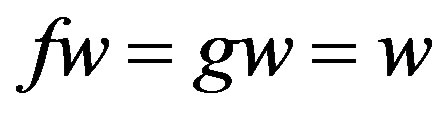, that is, w is a common fixed point between f and g.

For the uniqueness of the point w, suppose that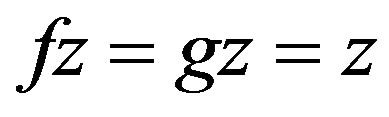. Hence z is a point of coincidence of f and g. Since the point of coincidence of f and g is unique, we conclude that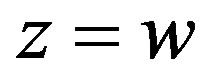. Thus f and g have a unique common fixed point w in Z. This completes the proof.

Theorem 3.9. Let 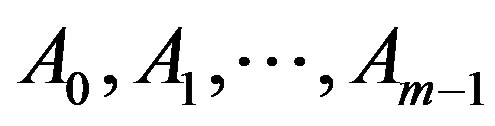be nonempty closed subsets of a complete ultrametric space 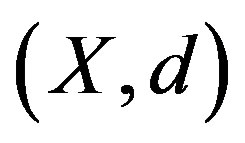and

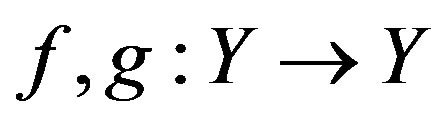. Suppose that are 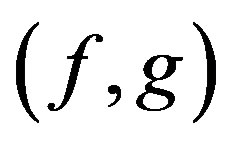- co-cyclic quasi-contraction, 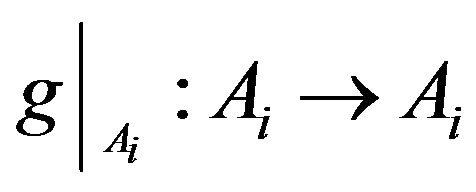is a mapping and 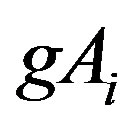is closed for all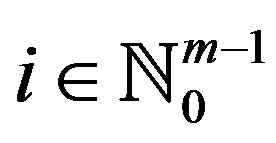. Then f and g have a unique point of coincidence in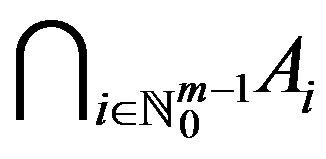. Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.

The proof of this theorem can be completed using the proof of Theorems 2.6, 3.5 and 3.8 and so we omit here.

Corollary 3.10. Let 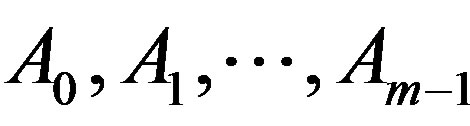be nonempty closed subsets of a complete metric space and

. Let f and g be two self-mappings on Y.

Suppose that there exist 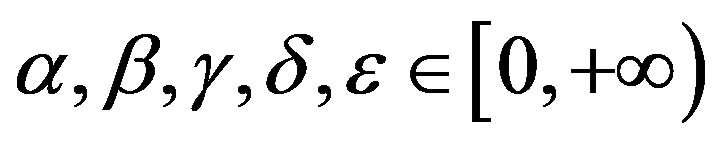such that

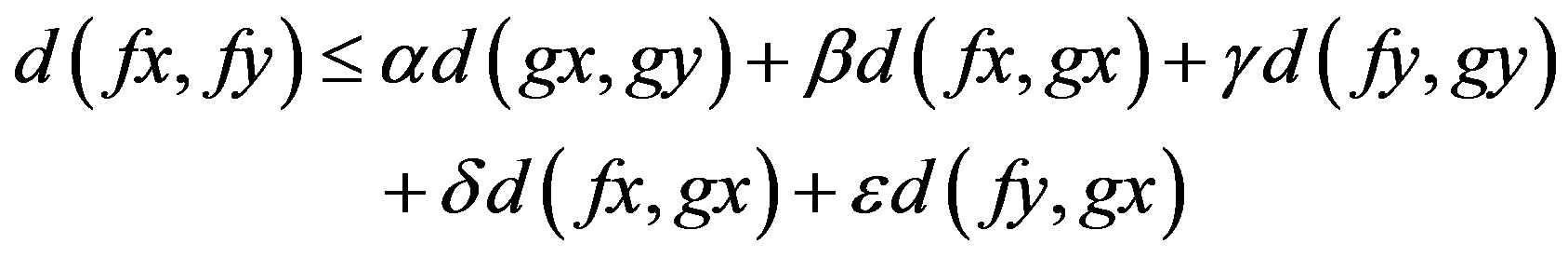(3)

whenever x and y are descendants in Y, where

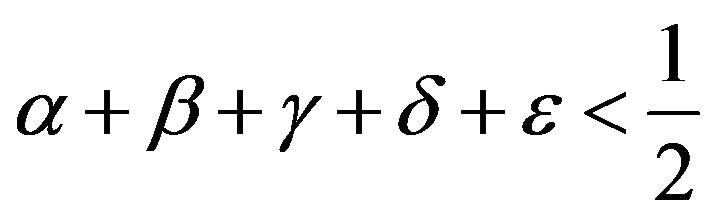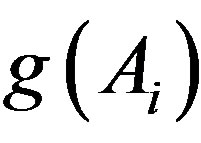, is a mapping and is closed for all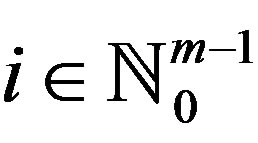. Suppose that 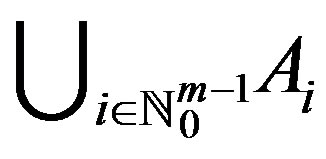is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in.

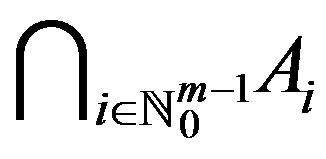Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.

Proof. Since f and g satisfy the inequality (3), we can deduce that

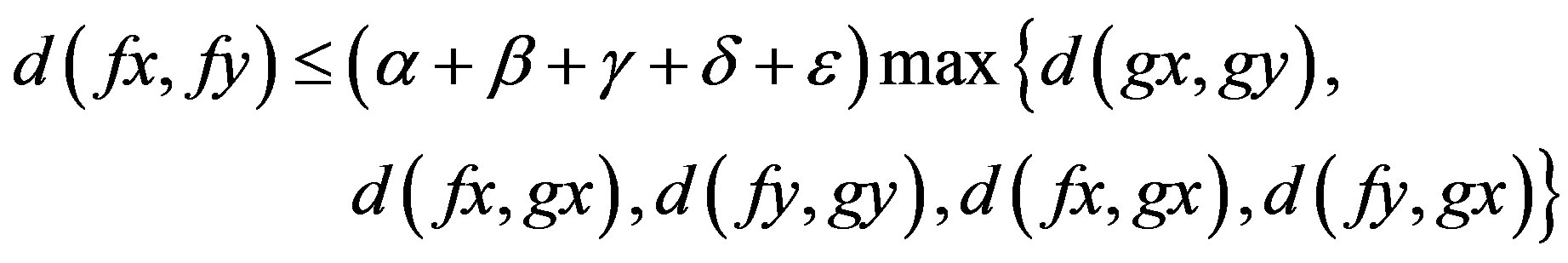
Now, since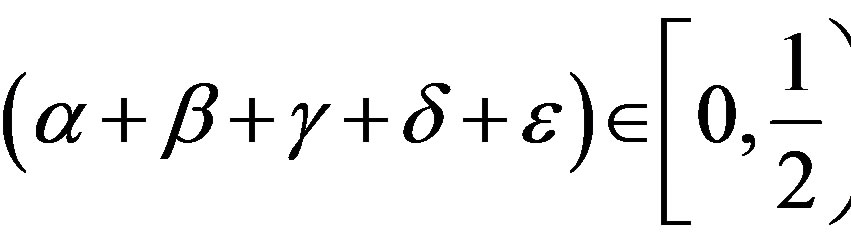, applying Theorems 3.5 and 3.8, we obtain the result.

Corollary 3.11. Let 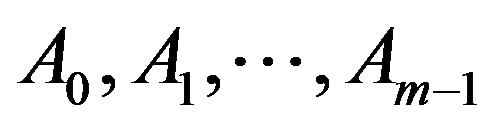be nonempty closed subsets of a complete ultrametric space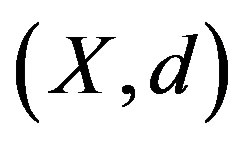

and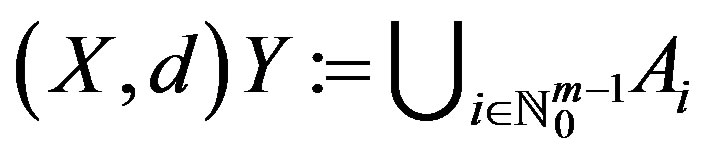. Let f and g be two self-mappings on Y. Suppose that there exist

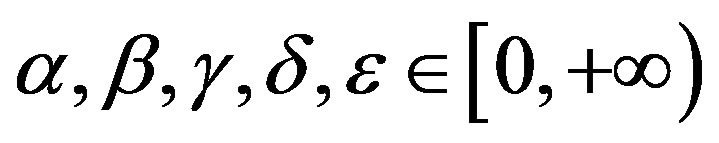such that

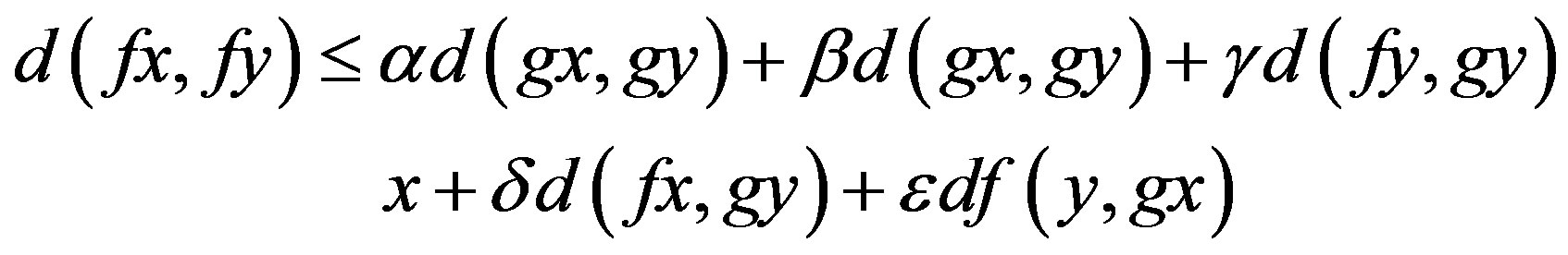
whenever x and y are descendants in Y, where

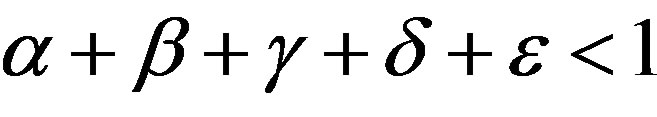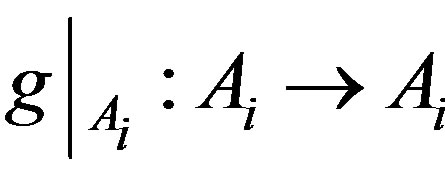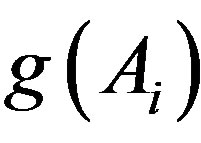, and is closed for all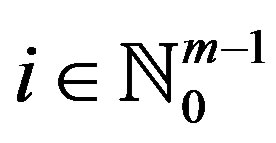. Suppose that 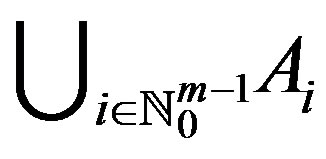is a co-cyclic representation of Y between f and g. Then f and g have a unique point of coincidence in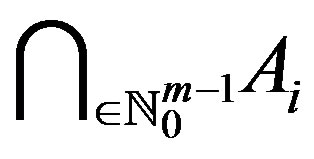. Moreover, if f and g are weakly compatible, then f and g have a unique common fixed point.

Proof. Since f and g satisfy the inequality (3), it follows that

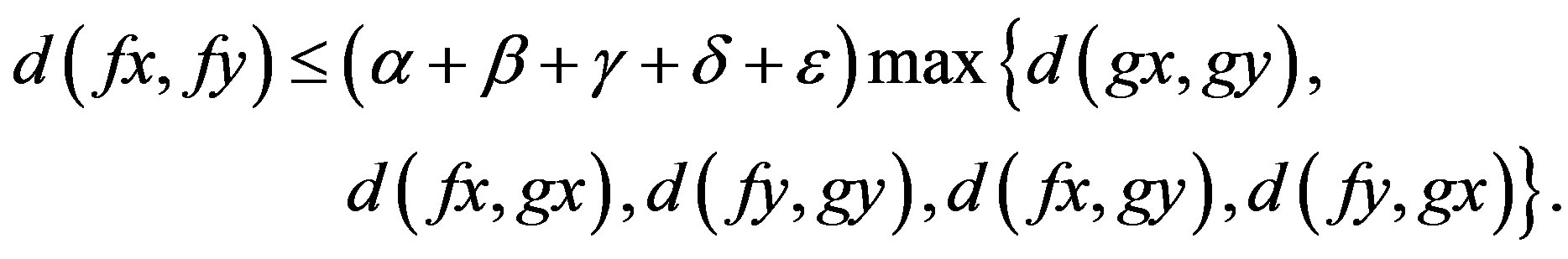
Now, since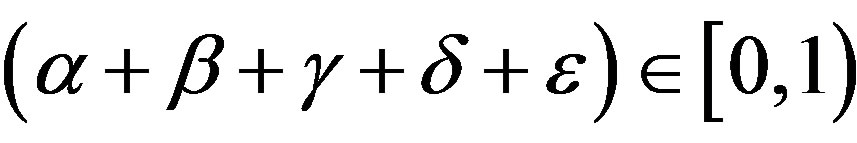, applying Theorem 3.4, we obtain the result.

If g is the identity mapping in Corollaries 3.5 and 3.6, we have the following:

Corollary 3.12. Let 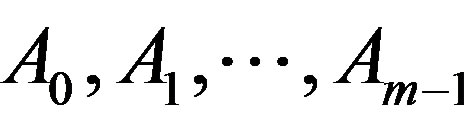be nonempty closed subsets of a complete metric space 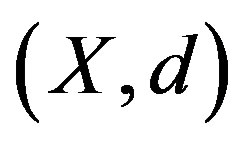and

. Let f be a self-mapping on Y. Suppose that there exist 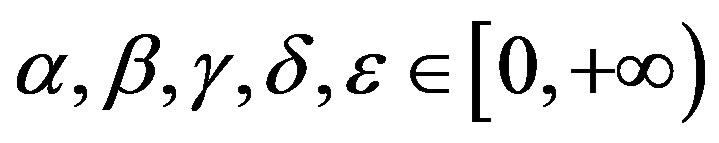such that

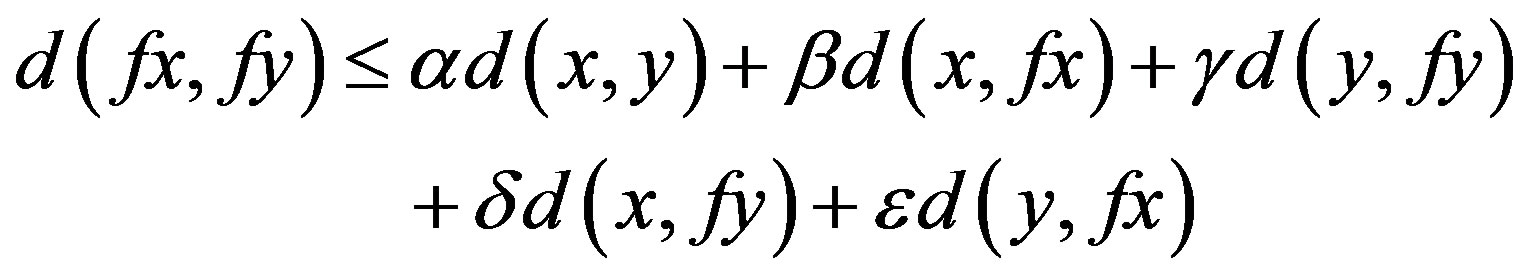
whenever x and y are descendants in Y, where

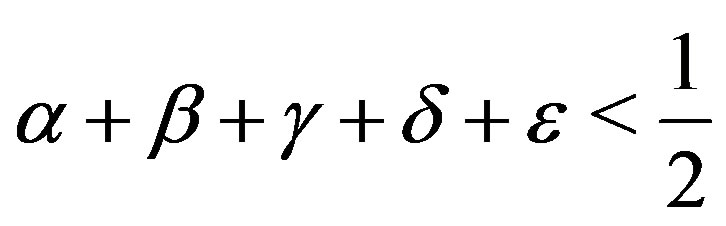. Suppose that 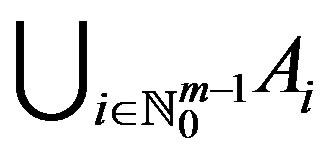is a cyclic representation of Y with respect to f. Then f has a unique fixed point in.

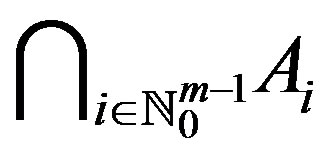Corollary 3.13. Let 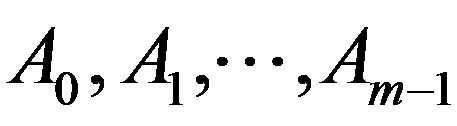be nonempty closed subsets of a complete ultrametric space 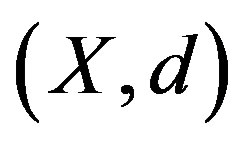and

. Let f be a self-mapping on Y. Suppose that there exist 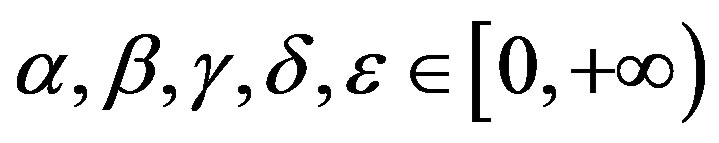such that

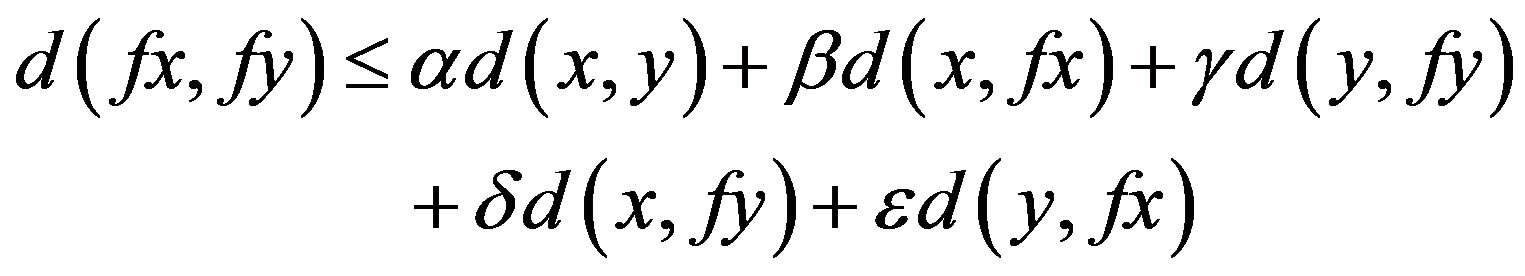
whenever x and y are descendants in Y, where

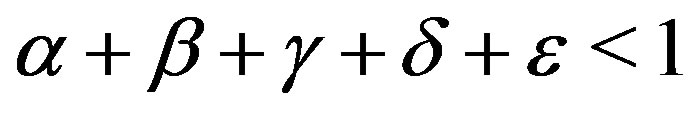. Suppose that 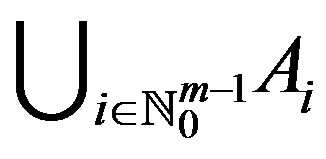is a cyclic representation of Y with respect to f. Then f has a unique fixed point in.

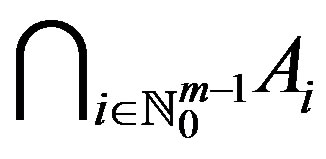Remark 3.14. Notice that Corollary 3.12 also generalizes the condition 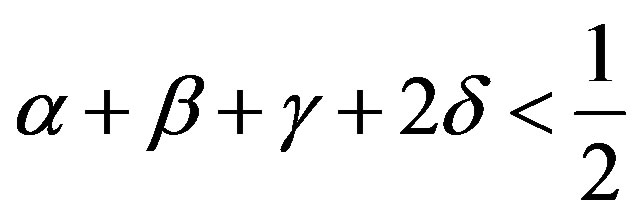of Theorem 1.2.

4. Conclusion

For the single-mapping case, the existence and uniqueness of a fixed points for a quasi-contraction in cyclic sense is proved with a restriction that the contraction constant have to be less than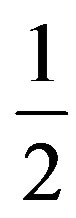. We further showed that if X is an ultrametric space, such a restriction may be dropped. Further, with the notion of a co-cyclic representation, we point out that the two-mapping case may be extended from our results proved earlier.

5. Acknowledgements

The authors were supported by the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission (NRU-CSEC No.55000613). The second author was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science, and Technology (Grant no. 2011-0021821). The Third author would like to thank the Research Professional Development Project Under the Science Achievement Scholarship of Thailand (SAST).

REFERENCES

NOTES

^*Corresponding authors.