World Journal of Condensed Matter Physics
Vol.06 No.01(2016), Article ID:64012,7 pages
10.4236/wjcmp.2016.61008
Direct Current Generation in Carbon Nanotubes by Terahertz Field
Sulemana S. Abukari1*, Frederick Sam1, Samuel Y. Mensah1, Natalia G. Mensah2, Rabiu Musah3, Anthony Twum1, Patrick M. Amoah1, Alfred Owusu1
1Department of Physics, Laser and Fibre Optics Centre, University of Cape Coast, Cape Coast, Ghana
2Department of Mathematics, University of Cape Coast, Cape Coast, Ghana
3Department of Applied Physics, University for Development Studies, Navorongo, Ghana

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 September 2015; accepted 26 February 2016; published 29 February 2016
ABSTRACT
We report on a theoretical investigation of a direct current generation in carbon nanotubes (CNTs) that are stimulated axially by terahertz (THz) field. We consider the kinetic approach based on the semiclassical Boltzmann’s transport equation with constant relaxation time approximation, together with the energy spectrum of an electron in the tight-binding approximation. Our results indicate that for strong THz-fields, there is simultaneous generation of DC current in the axial and circumferential directions of the CNTs, even at room temperature. We found that a THz-field can induce a negative conductivity in the CNTs that leads to the THz field induced DC current. For varying amplitude of the THz-field, the current density decreases rapidly and modulates around zero with interval of negative conductivity. The interval decreases with increasing the amplitude of the THz-field. We show that the THz-field can cause fast switching from a zero DC current to a finite DC current due to the quasi-ballistic transport, and that electron scattering is a necessary condition for switching.
Keywords:
Carbon Nanotubes, Terahertz Fields, DC Voltage Generation, Negative Conductivity, Electron Scattering, Ballistic Transport

1. Introduction
Investigation into the electronic properties of carbon nanotubes (CNTs) has attracted a great deal of interests ever since the discovery of these quasi-one-dimensional monomolecular structures by Iijima [1] . This may be due to their intriguing properties. The oscillatory response of the CNTs to moderate electric field strength makes CNTs inherently nonlinear, and as such, can exhibit plethora of transport phenomena. Under different conditions of an external electric field, an electron in CNT is predicted to reveal a variety of physical effects such as Bloch oscillations, self-induced transparency, negative differential conductivity, absolute negative conductance [2] - [9] , and many more. Furthermore, CNTs have been shown to exhibit ballistic transport [10] - [12] , Coulomb-blockade [13] [14] , Luttinger Liquid [15] [16] and superconductivity [17] [18] . The unique architecture and physicochemical properties have undoubtedly led to CNT which has been identified as a promising candidate for the fundamental building block of new generation of nanoelectronics [19] - [22] , sensors [23] [24] , electrochemical capacitors [25] -[27] , Li-ion batteries [28] - [30] and terahertz (THz) generation and amplification [31] - [35] , just to mention a few. There are several reports on CNTs for THz application [31] - [35] . Most of these reports focus on room temperature generation of THz radiation. Different proposals of CNTs for THz applications have been made. These ranges from multipliers [31] [32] , amplifies [33] , switches [34] to antennas [35] (see also [36] - [41] ).
However, there are very limited reports on the effect of THz-fields on the transport properties of CNTs.
In this report, we present a theoretical investigation of the influence of THz-fields on the conductivity of CNTs that are stimulated axially, by considering the kinetic approach based on the semiclassical Boltzmann’s transport equation with constant relaxation time approximation, together with the energy spectrum of electron in the tight-binding approximation, and predict the generation of DC current in both axial and circumferential directions of the CNTs.
2. Theory
We start with the Boltzmann equation and proceed as in refs [42] -[44] ,
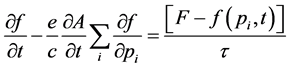 (1)
(1)
In accordance with ref. [4] - [6] [11] , we find that the distribution function is periodic in the quasimomentum and can be written in Fourier series as;
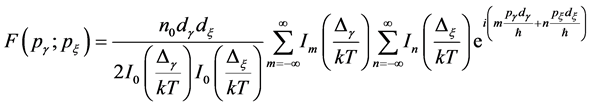 (2)
(2)
where e is electronic charge, the index 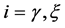 ;
; 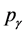 and
and 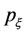 are components of the electron dynamical momentum along the axial and tubular axes respectively;
are components of the electron dynamical momentum along the axial and tubular axes respectively; 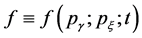 is the distribution function, and
is the distribution function, and 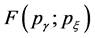 is the equilibrium distribution function; while
is the equilibrium distribution function; while 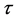 is the electron relaxation time and assumed to be
is the electron relaxation time and assumed to be
constant. The electric field is related to the vector potential A as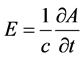 .
. 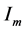 is the modified Bessel function
is the modified Bessel function
of the order m and 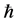 is Planck’s constant, finally
is Planck’s constant, finally  and
and 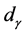 are the distances between along the axis and
are the distances between along the axis and
helix respectively.
The solution of Equation (1) by the method of characteristics is obtained in [5] [6] [11] as;
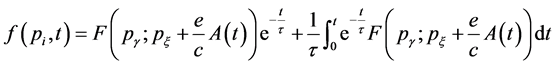 (3)
(3)
Interesting to us is the situation that 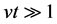 and Equation (2) reduces to the form
and Equation (2) reduces to the form

We proceed as in [5] [6] by considering an infinitely long chain of carbon atoms wrapped along a base helix as a model of a SWNT. This phenomenological model gives analytical tractability, which easily provides physically interpretable results. Also, the model gives a correct qualitative description of various electronic processes which are corroborated by the first principle numerical simulations. Thus, using the simple model of the tight- binding approximation, we describe the energy spectrum of the CNTs as ref [5] [6] .

where 


The electron quasi classical velocity components for 



and the electron fluxes along the tubular axis and the base helix are given by after making the transformation 


where the integration is done over the first Brilloiun zone. The expressions for the axial and the circumferential components are as in [5] ;


where 





where

If we re-write expressions (9) in the form of ref [44] and using the simplest case for [5] [6] that




and

respectively.
where 
Equation (10) show the ac field can open up new transport channel for DC current as a result of multiphoton absorption or emission with probability of emission or absorption of photon given by 
For quasi static case i.e.


here 
From Equation (11) we obtain the normalized differential conductivity as;

where
3. Results and Discussion
We present the results of the kinetic equation approach of a CNT subjected to inhomogeneous THz field of the form



In Figure 1, we show the dependence of the current density 









Figure 1. A plot of a normalized DC current density 


Figure 2. A plot of a DC conductivity 

4. Conclusion
In conclusion, we considered the nonlinear electronic properties in CNTs stimulated by a high frequency THz field, i.e., 
Cite this paper
Sulemana S.Abukari,FrederickSam,Samuel Y.Mensah,Natalia G.Mensah,RabiuMusah,AnthonyTwum,Patrick M.Amoah,AlfredOwusu, (2016) Direct Current Generation in Carbon Nanotubes by Terahertz Field. World Journal of Condensed Matter Physics,06,56-62. doi: 10.4236/wjcmp.2016.61008
References
- 1. Iijima, S. (1991) Helical Microtubules of Graphitic Carbon. Nature, 354, 56-58.
http://dx.doi.org/10.1038/354056a0 - 2. Jódar, E., Pérez-Garrido, A. and Rojas, F. (2009) Fast Track Communication: Bloch Oscillations in Carbon Nanotubes. Journal of Physics: Condensed Matter, 21, Article ID: 212202.
http://dx.doi.org/10.1088/0953-8984/21/21/212202 - 3. Abukari, S.S., et al. (2013) External Electric Field Effect on Electrons Transport in Carbon Nanotubes. World Journal of Condensed Matter Physics, 3, 169-172.
http://dx.doi.org/10.4236/wjcmp.2013.34027 - 4. Maksimenko, A.S. and Slepyan, G.Y. (2000) Negative Differential Conductivity in Carbon Nanotubes. Physical Review Letters, 84, 362.
http://dx.doi.org/10.1103/PhysRevLett.84.362 - 5. Slepyan, G.Y., et al. (1998) Electronic and Electromagnetic Properties of Nanotubes. Physical Review B, 57, 9485.
http://dx.doi.org/10.1103/PhysRevB.57.9485 - 6. Yevtushenko, O.M. (1997) Nonlinear Electron Transport Effects in a Chiral Carbon Nanotube. Physical Review Letters, 79, 1102.
http://dx.doi.org/10.1103/PhysRevLett.79.1102 - 7. Abukari, S.S., et al. (2013) Rectification Due to Harmonic Mixing of Two Coherent Electromagnetic Waves with Commensurate Frequencies in Carbon Nanotubes. European Physical Journal B, 86, 106.
http://dx.doi.org/10.1140/epjb/e2013-30011-3 - 8. Kibis, O.V. (1992) Electron-Electron Interaction in a Spiral Quantum Wire. Physics Letters A, 166, 393-394.
http://dx.doi.org/10.1016/0375-9601(92)90730-A - 9. Miyamoto, Y., Louie, S.G. and Cohen, M.L. (1996) Chiral Conductivities of Nanotubes. Physical Review Letters, 76, 2121.
http://dx.doi.org/10.1103/PhysRevLett.76.2121 - 10. Li, H.J., et al. (2005) Multichannel Ballistic Transport in Multiwall Carbon Nanotubes. Physical Review Letters, 95, Article ID: 086601.
http://dx.doi.org/10.1103/PhysRevLett.95.086601 - 11. Kajiura, H., Nandyala, A. and Bezryadin, A. (2005) Quasi-Ballistic Electron Transport in As-Produced and Annealed Multiwall Carbon Nanotubes. Carbon, 43, 1317-1319.
http://dx.doi.org/10.1016/j.carbon.2004.12.004 - 12. Kajiura, H., Huang, H. and Bezryadin, A. (2004) Quasi-Ballistic Electron Transport in Double-Wall Carbon Nanotubes. Chemical Physics Letters, 398, 476-479.
http://dx.doi.org/10.1016/j.cplett.2004.09.115 - 13. Hsiou, Y.F., Yang, Y.J., Chen, C.D. and Chan, C.H. (2006) Coulomb Blockade Behavior in Individual Multiwalled Carbon Nanotubes. Journal of Vacuum Science & Technology B, 24, 143.
http://dx.doi.org/10.1116/1.2151216 - 14. Haruyama, J., Takesue, I. and Sato, Y. (2000) Coulomb Blockade in a Single Tunnel Junction Directly Connected to a Multiwalled Carbon Nanotube. Applied Physics Letters, 77, 2891-2893.
http://dx.doi.org/10.1063/1.1312254 - 15. Bockrath, M., Cobden, D.H., Lu, J., et al. (1999) Luttinger-Liquid Behaviour in Carbon Nanotubes. Nature, 397, 598-601.
http://dx.doi.org/10.1038/17569 - 16. Shiraishi, M. and Ata, M. (2003) Tomonaga-Luttinger-Liquid Behavior in Single-Walled Carbon Nanotube Networks. Solid State Communications, 127, 215-218.
http://dx.doi.org/10.1016/S0038-1098(03)00417-4 - 17. Kociak, M., Kasumov, A.Y., Guéron, S., et al. (2001) Superconductivity in Ropes of Single-Walled Carbon Nanotubes. Physical Review Letters, 86, 2416-2419.
http://dx.doi.org/10.1103/PhysRevLett.86.2416 - 18. Southard, A., Sangwan, V., Cheng, J., et al. (2009) Solution-Processed Single Walled Carbon Nanotube Electrodes for Organic Thin-Film Transistors. Organic Electronics, 10, 1556-1561.
http://dx.doi.org/10.1016/j.orgel.2009.09.001 - 19. Hong, K., Nam, S., Yang, C., et al. (2009) Solution-Processed Organic Field-Effect Transistors Composed of Poly(4-styrene sulfonate) Wrapped Multiwalled Carbon Nanotube Source/Drain Electrodes. Organic Electronics, 10, 363-367.
http://dx.doi.org/10.1016/j.orgel.2008.11.008 - 20. Aguirre, C.M., Ternon, C., Paillet, M., et al. (2009) Carbon Nanotubes as Injection Electrodes for Organic Thin Film Transistors. Nano Letters, 9, 1457-1461.
http://dx.doi.org/10.1021/nl8033152 - 21. Novak, J.P., Snow, E.S., Houser, E.J., et al. (2009) Nerve Agent Detection Using Networks of Single-Walled Carbon Nanotubes. Applied Physics Letters, 83, 4026-4028.
http://dx.doi.org/10.1063/1.1626265 - 22. Kong, J., et al. (2000) Nanotube Molecular Wires as Chemical Sensors. Science, 287, 622-625.
http://dx.doi.org/10.1126/science.287.5453.622 - 23. Robinson, J.A., Snow, E.S. and Badescu, S.C. (2006) Role of Defects in Single-Walled Carbon Nanotube Chemical Sensors. Nano Letters, 6, 1747-1751.
http://dx.doi.org/10.1021/nl0612289 - 24. Signorelli, R., Ku, D.C., Kassakian, J.G. and Schindall, J.E. (2009) Electrochemical Double-Layer Capacitors Using Carbon Nanotube Electrode Structures. Proceedings of IEEE, 97, 1837-1847.
http://dx.doi.org/10.1109/JPROC.2009.2030240 - 25. Du, C.S. and Pan, N. (2006) High Power Density Supercapacitor Electrodes of Carbon Nanotube Films by Electrophoretic Deposition. Nanotechnology, 17, 5314-5318.
http://dx.doi.org/10.1088/0957-4484/17/21/005 - 26. Du, C.S. and Pan, N. (2006) Supercapacitors Using Carbon Nanotubes Films by Electrophoretic Deposition. Journal of Power Sources, 160, 1487-1494.
http://dx.doi.org/10.1016/j.jpowsour.2006.02.092 - 27. Zhao, J.J., Buldum, A., Han, J. and Lu, J.P. (2000) First-Principles Study of Li-Intercalated Carbon Nanotube Ropes. Physical Review Letters, 85, 1706-1709.
http://dx.doi.org/10.1103/PhysRevLett.85.1706 - 28. Udomvech, A., Kerdcharoen, T. and Osotchan, T. (2005) First Principles Study of Li and Li+ Adsorbed on Carbon Nanotube: Variation of Tubule Diameter and Length. Chemical Physics Letters, 406, 161-166.
http://dx.doi.org/10.1016/j.cplett.2005.02.084 - 29. Chen, J., Liu, Y., Minett, A.I., et al. (2007) Flexible, Aligned Carbon Nanotube/Conducting Polymer Electrodes for a Lithium-Ion Battery. Chemistry of Materials, 19, 3595-3597.
http://dx.doi.org/10.1021/cm070991g - 30. Tang, Z.K., et al. (2001) Superconductivity in 4 Angstrom Single-Walled Carbon Nanotubes. Science, 292, 2462-2465.
http://dx.doi.org/10.1126/science.1060470 - 31. Slepyan, G.Y., Maksimenko, S.A., Kalosha, V.P., et al. (1999) Highly Efficient High-Order Harmonic Generation by Metallic Carbon Nanotubes. Physical Review A, 60, 777-780.
http://dx.doi.org/10.1103/PhysRevA.60.R777 - 32. Ferguson, B. and Zhang, X.C. (2002) Materials for Terahertz Science and Technology. Nature Materials, 1, 26-33.
http://dx.doi.org/10.1038/nmat708 - 33. Slepyan, G.Y., Maksimenko, S.A., Kalosha, V.P., et al. (2001) High-Order Harmonic Generation by Conduction Electrons in Carbon Nanotube Ropes. Physical Review A, 63, Article ID: 053808.
http://dx.doi.org/10.1103/PhysRevA.63.053808 - 34. Dragoman, D. and Dragoman, M. (2005) Terahertz Continuous Wave Amplification in Semiconductor Carbon Nanotubes. Physica E, 25, 492-496.
http://dx.doi.org/10.1016/j.physe.2004.08.001 - 35. Dragoman, M., Cismaru, A., Hartnagel, H. and Plana, R. (2006) Reversible Metal-Semiconductor Transitions for Microwave Switching Applications. Applied Physics Letters, 88, Article ID: 073503. http://dx.doi.org/10.1063/1.2177369
- 36. Maksimenko, A.S., et al, (2007) Electrodynamics of Chiral Carbon Nanotubes in the Helical Parametrization Scheme. Journal of Nanophotonics, 1, Article ID: 013505.
http://dx.doi.org/10.1117/1.2710766 - 37. Kibis, O.V., Parfitt, D.G.W. and Portnoi, M.E. (2005) Superlattice Properties of Carbon Nanotubes in a Transverse Electric Field. Physical Review B, 71, Article ID: 035411.
http://dx.doi.org/10.1103/PhysRevB.71.035411 - 38. Kibis, O.V., Malevannyy, S.V., Huggett, L., et al. (2005) Superlattice Properties of Helical Nanostructures in a Transverse Electric Field. Electromagnetics, 25, 425-435.
http://dx.doi.org/10.1080/02726340590957416 - 39. Hartmann, R.R., Kono, J. and Portnoi, M.E. (2014) Terahertz Science and Technology of Carbon Nanomaterials. Nanotechnology, 25, Article ID: 322001.
http://dx.doi.org/10.1088/0957-4484/25/32/322001 - 40. Batrakov, K.G., Kibis, O.V., Kuzhir, P.P., et al. (2010) Terahertz Processes in Carbon Nanotubes. Journal of Nanophotonics, 4, Article ID: 041665.
http://dx.doi.org/10.1117/1.3436585 - 41. Portnoi, M.E., Kibis, O.V., da Costa, M.R., et al. (2008) Terahertz Applications of Carbon Nanotubes. Superlattices and Microstructures, 43, 399-407.
http://dx.doi.org/10.1016/j.spmi.2007.07.026 - 42. Bass, F.G., Bulgakov, A.A. and Tetervov, A.P. (1997) High-Frequency Properties of Semiconductors with Superlattices. Nova Science, New York.
- 43. Lifshits, I.M., Azbel, M. and Kaganov, M.I. (1973) Electron Theory of Metals. Consultants Bureau, New York.
- 44. Ignatov, A.A., Schomburg, E., Grenzer, J., Renk, K.F. and Dodin, E.P. (1995) THz-Field Induced Nonlinear Transport and DC Voltage Generation in a Semiconductor Superlattice Due to Bloch Oscillations. Zeitschrift für Physik B, 98, 187-195.
http://dx.doi.org/10.1007/BF01324524
NOTES
*Corresponding author.







