Received 9 April 2015; accepted 4 August 2015; published 7 August 2015

ABSTRACT

The mixed spin-2 and spin-3/2 Blume-Emery-Griffiths (BEG) Ising ferrimagnetic system is studied by the Bethe lattice approach. The ground-state phase diagram is constructed. The influence of the crystal-field and the biquadratic interactions among neighboring spins on the thermal behaviors of the system is singled out. The system displays very rich critical behaviors with the existence of tricritical points. Compensation points where the global magnetization of the system vanishes have been detected for appropriate values of the system parameters.

Keywords:

BEG Model, Tricritical Point, Compensation Points, Bethe Lattice

1. Introduction

Ising systems have attracted much interest in the three last decades because of their critical behaviors. Mixed Ising systems, beyond their theoretical purposes, have been proposed as possible systems to describe ferrimagnetic materials [1] . Moreover, the increasing interest in these systems is mainly related to their technological applications in the area of thermomagnetic recording [2] . They have less translational symmetry than their single spin counterparts; therefore, they exhibit many novel phenomena. The study of these systems can be relevant for the understanding of bimetallic molecular based magnetic materials [3] . They are also useful to study the effect of inhomogeneities on the phase diagram of Ising systems. When defined on hierarchical graphs as the Bethe lattice or the Cayley tree, interesting statistical properties are expected.

One of the earliest, simplest and the most extensively studied mixed-spin Ising model is the spin-1/2 and spin-1 mixed system. Different approaches have been used: renormalization-group technique [4] , high-temper- ature series expansions [5] , the free-fermion approximation [6] , the recursion method [7] , the Bethe-Peierls approximation [8] , the Monte-Carlo simulation [9] [10] , the numerical transfer matrix study [11] and the cluster method in pair-approximation [12] . Most of these studies have focused on the mixed spin-1/2 and spin-s Ising systems. Mixed-spin Ising systems consisting of higher spins are not without interest. Indeed, several theoretical studies of mixed spin-1 and spin-3/2 Ising models have been reported, based on different approaches: the effective-field theory, on the simple cubic, honeycomb and square lattices, mean-field theory based on the Bogoliubov inequality for Gibbs free energy [13] and by the means of recursion relations on the Bethe lattice [14] - [16] .

Recently, these investigations have been extended to high order mixed spin ferrimagnetic systems in order to study their magnetic properties. Bobak et al. [13] investigated the effect of the crystal-field on the phase diagrams of the mixed spin-2 and spin-3/2 Ising system by the use of mean-field theory based on the Bogoliubov inequality for the energy. By means of exact recursion equations, Albayrak investigated the magnetic properties of the mixed spin-2 and spin-3/2 Blume Capel (BC) Ising model with different crystal-fields on the Bethe lattice [17] . Deviren et al. [18] used the effective field-theory to study the magnetic properties of the ferrimagnetic mixed spin-2 and spin-3/2 BC Ising model with equal crystal-field in a longitudinal magnetic field on the honeycomb and a square lattice and got interesting results. Fathi [19] studied the same model with different crystal-fields for the two sublattices arranged alternatively using the mean-field theory based on the Bogoliubov inequality for the Gibbs free energy. It should be emphasized that all these above mentioned works don’t include the biquadratic exchange interactions.

In this work, we study the mixed spin-2 and spin-3/2 Blume-Emery-Griffiths (BEG) ferrimagnetic system on the Bethe lattice in terms of exact recursion equations to investigate the influence of the crystal-field and biquadratic spin interactions on the critical behaviors of the model. It has been shown that the partition function in the Bethe lattice approach is that of an Ising model in the Bethe-Peierls approximation [20] . The Bethe lattice approach calculations provide exact solutions and results that are qualitatively better for the regular lattices than those obtained by the conventional mean-field theories [21] .

The remainder of this work is organized as follows. In Section 2, a brief formulation of the Bethe lattice approach is given. Section 3 is devoted to the formulation of the critical temperatures of the model. In Section 4, besides the ground-state phase diagram, the thermal properties of the model are presented and discussed in details in the model parameters’ space. Some concluding remarks are given in the last section.

2. The Bethe Lattice Approach Formulation

A Bethe lattice is an infinite Cayley tree, i.e. a connected graph without circuits. It consists of a central spin which may be called the first generation of spins. 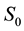has a number q of nearest-neighbors which form the second generation of spins. Each site of the second generation is joined to 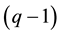nearest-neighbors. Thus, the second generation has 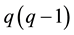nearest-neighbors which form the third generation and so on to infinity as shown in Figure 1.

The Hamiltonian of the system is given by:

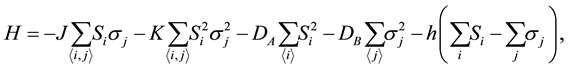(1)

where each spin 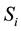located at site i on the lattice is a spin of type 1 and each spin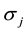, located at site j is a spin of type 2. The Bethe lattice is arranged such that the central spin is a spin of type 1, the next generation spins are of type 2, and the next generation spins are again, spins of type 1 and so on. The first sum runs over all nearest-neighbor pairs of the bipartite lattice. J and K are the bilinear exchange and the biquadratic coupling interaction stengths respectively. 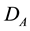and 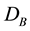are the crystal-fields acting on spins of sublattices A and B respectively. h is the external field.

The partition function of the model reads:

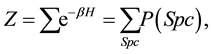
where 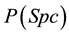is taken as an unnormalized probability distribution over the spin configuration, Spc (e.g.

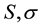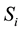). and 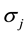indicate the spins’ values at sites i and j respectively. If the Bethe lattice is cut in some central point with a spin, spin of type 1, then it splits up into q identical branches; i.e. disconnected pieces. Each of these is a rooted tree at a central spin. This implies that, i.e., of a spin configuration with the spin value at the central site, can be written as:

(2)

(3)

where, is the central spin value of the lattice, the partition function of an individual branch and the suffix n represents the fact that the sub-tree has n shells, i.e., n steps from the root to the boundary sites. Therefore, is written in terms of summation over spins set as:

(4)

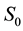
Advancing along any branch, we get a site that is next-nearest to the central spin, hence is expressed:

(5)

Let us give some examples of the calculated and:

(6)

(7)

In order to find the recursion relations, we introduce the following variables as a ratio of functions for the spin-2 as follows:

(8)

and for the spin- as the ratio of functions

(9)

The BEG model is characterized by two order parameters, the magnetization M and the quadrupolar moment Q. Four order parameters: and, where A, B refer to the two sublattices may be considered. Their expressions follow:

(10)

They are easily expressed in terms of the recursion relations, namely Equation (10), and calculated as:

Similarly, we get:

The energy F of the system is defined as and its expression in the thermodynamic limit as is given in terms of the recursion relations by setting and [14] as follows [22]

(11)

Then, the phase diagrams of the system for a given coordination number q are obtained by studying the thermal variations of the order parameters and the free energy.

In the thermodynamic limit, converges to the fixed point. Thus one rewrites Equation (9) as:

;;.

Also, in this case, substituting;;;; A; B and C in the Equations (11)-(15), one obtains:

;;;;.

Usually, multiple solutions of may exist. The solution that minimizes the free energy is the thermodynamically stable one. Technically, we use peaks in the magnetic susceptibility of the system defined by:

to detect phase transition. These new curves simultaneously show a maximum at the same tem-

perature that we take as when no anomalous behaviour is observed in the thermal behaviour of free energy F at this moment. The first order transition is obtained when a sharp jump occurs in the thermal behaviors of the sublattice magnetizations followed by a discontinuity of the first derivative of F.

3. Formulation of the Critical Temperatures

The most common phase transitions are of second or first order type for all kind of systems.

The second order phase transition (SOT) temperature is the temperature at which both sublattice magnetizations become zero continuously. separates the ferrimagnetic phase from the paramagnetic phase. Therefore, by using the expressions for the magnetizations, one can obtain the exact formulation of the second-order phase transition temperatures by setting or separately equal to zero:

(12)

and

(13)

At, The condition and, must be satistied, which implies and. In the same way, for the sublattice B, one has a simple solution given by and which implies that, and must be satisfied. It’s should be mentioned that the latter condition is readily obtained from the first condition and at the transition, we obtain:

(14)

(15)

(16)

In order to calculate the first-order phase transition (FOT) temperature, we need an analysis of the free energy expression given above in terms of the recursion relations.

We have also investigated the compensation temperature which corresponds to the crossing point of sublattice magnetization curves i.e.:

(17)

The real compensation occurs when and this only happens in the ferrimagnetic coupling case at the same value. In the spirit of the above definitions of the critical temperatures, one can then study in depth the phase diagrams of the mixed spin-2 and spin-3/2 BEG ferrimagnetic system in the plane at constant values of and also in the plane for fixed values of for all values of q.

4. Results and Discussions

4.1. Phase Diagram at T = 0

It is instructive to analytically analyze the ground-state phase diagrams from the ground-state energies of the model Hamiltonian. The ground-state configuration is that with the lowest ground state energy. Here, we have six different ground-state configurations as in ref. [19] . They are written in the following as

:, , ,.

Two disordered phases are obtained,. For the two latter phases, and one half of the lattice B has spins in state whereas the other half has spins in the state, so

. A similar structure is observed for the phase. The ground phase diagram shows five multicritical points whose coordinates are:;;;;. At these points, more than one phase coexist. All transition lines of the ground-state diagrams are of first order.

4.2. Sublattice Magnetizations

Thermal magnetic properties of the system, namely the sublattice magnetiztions are presented. It’s worthwhile to first mention that the disordered phases and found in Figure 2 are thermally unstable and have not been observed during the simulation at non-zero temperature. Figure 3 shows typical sublattice magnetization curves for different values of for (panel a) and for different values of for (panel b) and. In Figure 3(a), one observes that and decrease from their saturation values at with the increase of the temperature. Thermal fluctuations disorder magnetic moments orientation is the system. shows three saturation values whereas shows a unique saturation value. The sublattice magnetizations and show a standard characteristic convex chape. We notice the existence of an hybrid ferrimagnetic phase and, where on the sublattice A, half of the spins are in the state 2 whereas the second half is in the state 1; hence. This hybrid phase is located at

the boundary of phases and. Also, for selected values of, exhibits interesting behaviors. Indeed, for, decreases rapidly from its saturation values 2, 1 respectively when the temperature increase from to the critical temperature where vanishes. For, exhibits a rather increase before decreasing to vanish at the critical temperature. It’s should be interesting to indicate for, shows a rapid decrease before presenting a jump at the critical temperature which indicate a first-order transition. As shown in Figure 3(b), one notices again the existence of an hybrid ferrimagnetic phase and where on the sublattice B, half of the spins are in the state and the the second half spins are in the state, hence. This hybrid phase is also located at the boundary of the phase and. Also for the selected values of, exhibits interesting behaviors. For, decreases rapidly from its saturation value with the increase temperature from to the critical temperature where vanishes. For, exhibits a rapid increase before decreases and cancels at the critical temperature. Figure 4(a) shows typical sublattice magnetization curves for five different values of the biquadratic field of the model when and the coordination number. For, one observes that and decrease from their saturation values and at with the increase of the temperature. Indeed, for, decreases rapidly from its saturation values 2 and 1 respectively when the temperature increases from to the critical temperature where the vanishes. It’s should be interesting to indicate that for, shows a rapid decrease before showing a jump at the critical temperature which indicates a first-order transition. Figure 4(b) shows typical sublattice magnetization curves for five different values of the crystal field of the model when and the coordination number. For these values, one observes different values of saturation of and a single saturation value for. These results are in perfect agreement with the phase diagram at.

4.3. Magnetic Susceptibilities and Phase Diagrams

In Figure 5(a), the temperature dependence of total and sublattice susceptibilities is presented for constant values of and. It is easy to see from this figure that the variation of the total

susceptibility in the low-temperature region originates from the behaviour of the sublattice susceptibility. It is also seen that the sublattice susceptibility exhibits the usual temperature dependence in the vicinity of, while the sublattice susceptibility takes negative values.

Now, in order to explain the appearance of the broad maximum in the susceptibility of the sublattice B in the low-temperature region (Figure 5(a)), we consider the temperature dependence of the sublattice magnetizations and (as shown in Figure 3(c)) for the system with and, when (solid lines) and when (dashed lines). In the figure, it is seen that there is a rapid decrease in from its saturation value with the increase in T and it is clear that at any temperature in this region, there is a jump in from a certain value, when to a lower value, when resulting in the broad maximum of.

In Figure 5(b), we show the thermal variation of initial susceptibilities (total and sublattices). For the system with and. It is seen from this figure that the divergence of the total susceptibility at zero temperature originates from the divergence of the sublattice susceptibility.

To explain the physical scenario for the appearance of the divergence of the susceptibility of the sublattice B (Figure 5(b)), we consider the temperature dependence of the sublattice magnetization and (as shown in Figure 3(d)) for the system with and, when (solid lines) and when (dashed lines). In this figure, there is a mixed-spin state on the sublattice B in the ground state, for and, consisting from and with equal probabilities.

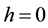
In Figure 6, phase diagrams are illustrated at and varying when. The solid and dashed lines indicate SOT and the FOT lines respectively. The black triangle indicates the tricritical point (TCP). As it’s seen in this figure, it’s clear that the SOT and FOT lines separate the ferrimagnetic phase F from the paramagnetic phase P. Some interesting phenomena are observed on the phase diagrams. First, the model exhibits for all values of q, a TCP where a SOT and a FOT lines are connected. Second, for larger than its tricritical value, the SOT occurs from the ferrimagnetic phase to the paramagnetic phase P. But for lower values, the first order phase transition occurs from the same ferrimagnetic phase to the paramagnetic phase P. Third, by increasing q, most of the transition lines become of first order. These results appear in perfect agreement with the ground-state phase diagram and bear some resemblance with those displayed in Figure 3 of Ref. [19] .

Figure 7 displays the phase diagrams of the model for four different values of the parameter: 0.0, −0.1, −0.25 and −1.2. The coordination number is still set to 3. The dotted lines indicate compensation lines. From this figure, several features of the model emerge. In panel (a) for example, for, one observes the

existence of a TCP and a compensation line with two end-points indicated by full squares. The ordered domain F is not homogeneous in the sense that it does not consist of only one ferrimagnetic phase. Indeed, one gets three ferrimagnetic phase, and in this domain F. The other panels (b, c and d) present similar features with the previous case with no existence of TCP.

In order to check the obtained compensation temperatures, we have illustrated the thermal behavior of the net magnetization (see Figure 8).

It is important to mention that the model shows interesting numerical behavior when. Figure 9 is displayed to extend Figure 6 and Figure 7 to other values of the fixed parameters and. It illustrates almost the same properties of the model. Some particularities are however noticed: transition lines always show a TCP and compensation temperature are absent from both panels. In panel (a), one can remark that TCP are found for and for appropriate positive values of. With increasing values of, most of the transition lines become of second order. In panel (b), TCP are found for and appropriate positive values of. With increasing, the portion of SOT line becomes important. From Figure 9, it appears that a tricritical line can be drawn by connecting tricritical points of different transition lines in both panels

5. Conclusion

In summary, the mixed spin-2 and spin-3/2 BEG Ising ferrimagnetic system is studied on the Bethe lattice using exact recursion equations. The ground phase diagram of the model was constructed in (,) plane. There, one found four ordered phases and two disordered phases. We have investigated the thermal variations of

the magnetizations and susceptibility curves and found interesting behavior results. Finally, the influences of the crystal field and the biquadratic interactions are investigated by obtaining the phase diagrams on the (,) and (,) planes, respectively, with equal crystal field interactions for the sublattices. The model presents very rich critical behaviors, which include first and second order transitions and tricritical points. We have also found that the model exhibits compensation temperatures for appropriate values of the system parameters.

Cite this paper

M.Karimou,R.Yessoufou,F.Hontinfinde, (2015) Mixed Spin-2 and Spin-3/2 Blume-Emery-Griffiths (BEG) Model on the Bethe Lattice. World Journal of Condensed Matter Physics,05,187-200. doi: 10.4236/wjcmp.2015.53020

References