World Journal of Condensed Matter Physics
Vol.3 No.4(2013), Article ID:38957,4 pages DOI:10.4236/wjcmp.2013.34032
Double Quantum Entanglement to Understand Superconductivity
![]()
Birkenweg 2, Elmenhorst, Germany.
Email: Jens.Cordelair@freenet.de
Copyright © 2013 Jens Cordelair. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 15th, 2013; revised September 21st, 2013; accepted October 14th, 2013
Keywords: Quantum Entanglement; Superconductivity
ABSTRACT
The feature of quantum entanglement in doublet and multiplet systems is briefly described and used to create a new model for the superconducting phase.
1. Introduction
A fundamental aspect of physical thoughts is the principle of a homogenous time development. This regularity of time over the whole extension of our cosmos is so deeply impressed in our experience, that we can only hardly envisage it can’t be true in general. As a result, its influence on the interpretation of natural phenomena is very imperative. Formally the principal of a homogenous time will be represented by the law of conservation of energy and play a central role not only in all parts of physics but also as irreplaceable element of almost all natural sciences. For example, Einstein [1] showed in his theory of special relativity that the mass of a body is equivalent to the energy in a proper measure. This means one can convert mass into energy (nuclear fission in the sun) and energy into mass (particle generation in high energy physics).
Louis de Broglie [2] postulated 1924 that matter behaves like light waves, also featuring interference. The simplest type of these matter waves is a plain and monochrome wave, where the energyand momentum-distribution is restricted to a single value
 (1)
(1)
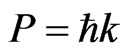 . (2)
. (2)
In general, all matter-waves ψ, describing a particle or a quantum mechanical system, are elements of a Hilbertspace. Therefore they are subjected to the principle of superposition with interesting effects.
Figure 1 shows, as virtual holography-experiment,

Figure 1. Interference between matter-waves of a single particle like an electron.
how the principle of superposition leads to interference between matter-waves of a single particle like an electron.
The particle wave (a single electron), injected from the top, can pass the very thin wire to the right and to the left. Accordingly, the matter-wave underneath the wire is the superposition of both single waves
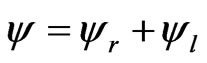 . (3)
. (3)
The probability of finding independent particles in separated experiments performing a punctual interaction with the screen at point x is equivalent to the square of the matter-wave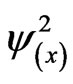 . Due to the fact that the single waves
. Due to the fact that the single waves 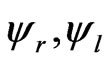 differ in their path and phase, the phenomenon that a single particle can interfere with itself, occur.
differ in their path and phase, the phenomenon that a single particle can interfere with itself, occur.
In this sense, an electron in a compound may be roughly viewed as the surface excitation of water in a basin with many pillars (atoms), when we throw a stone into it. After a very little time the initial wave is spread out over the whole tank and only the wave components conform with the walls and the pillars persist (Blochwaves).
2. Model Description
2.1. Quantum Entanglement
Another characteristic which doesn’t agree with our imagination of how nature works is the capacity of quantum entanglement. In our classical view of the world one is able to select a single particle out of a set and perform separate measurements of its properties (energy, momentum, position, spin, ···). In quantum mechanics this is not in general possible. If quantum entanglement is present in a system, the collective wave function can’t be composed of its individual subsystems, with the effect that each change of a property of a subsystem, like the change of state due to a measurement, has a direct influence on the properties of the whole collective.
In spacious systems the entanglement induce a spooky distant effect [3]. If, for example, a two atomic molecule gets dissociated by an excitation (Figure 2), the atoms may remain entangled by their spins. If we measure the spin of both Atoms, one will show spin 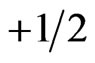 and the other
and the other , but it is not possible to predict which one will have the positive and negative sign. If we carefully align the spin of one atom in a magnetic field, the other must be oriented simultaneously in the opposite direction, even though it is not in the vicinity. In other words, you can play with Schrödinger’s cat while it’s in the box.
, but it is not possible to predict which one will have the positive and negative sign. If we carefully align the spin of one atom in a magnetic field, the other must be oriented simultaneously in the opposite direction, even though it is not in the vicinity. In other words, you can play with Schrödinger’s cat while it’s in the box.
Also in many body systems the phenomenon of entanglement may occur. For example, the atoms in a solid oscillate around their position of rest. When these atoms absorb or emit a photon, they can transfer the rebound to the lattice by inciting a vibration. At low temperatures many of the Atoms in a solid are in the ground state. These can form an entangled consolidated base vibration, which allow only definite vibration energies to occur. During the emission or absorption of a gamma quantum it may happen that the rebound of an atom from the entangled base state, can’t incite a vibration, thus the whole entanglement has to carry the momentum. Due to the fact that the mass of the entangled lattice is much larger than the mass of an atom, the emission or absorption is carried out nearly without rebound. This effect was first observed by Mößbauer in 1958 [4].
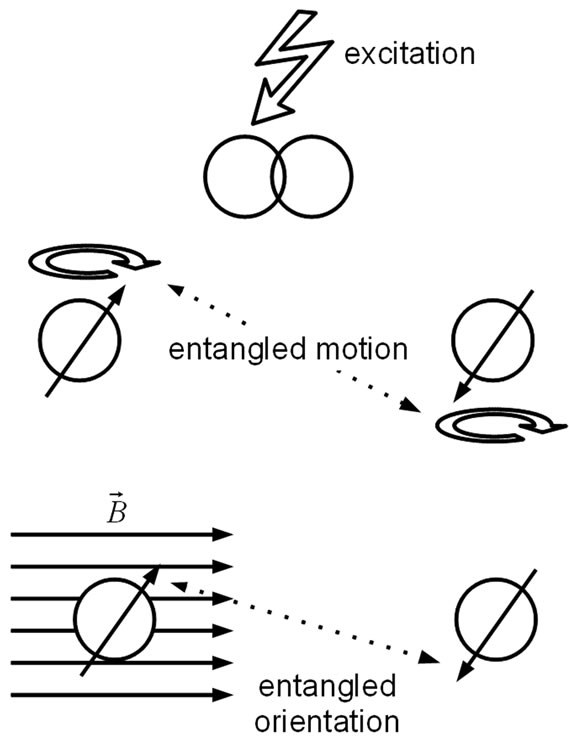
Figure 2. Spin entanglement between two atoms.
2.2. Bose-Einstein-Condensate
In nature we find 2 different types of particles, we call them Bosons and Fermions. When a couple of Bosons or Fermions meet, they show different social behavior. While Bosons are chummy and like to come together as close as possible, Fermions are loner avoiding the contact to one’s peer. At very low temperatures the social behavior of the Bosons cause a new aggregate state, the BoseEinstein-Condensate [5,6], with astonishing properties, like super-fluidity, superconductivity or long ranged coherence. Figure 3 shows the development of the wavefunction in a Boson gas having different temperatures compared with the critical temperature Tc where a good portion of the Bosons are condensed in the collective wave-function ψBEC. At elevated temperatures  the extension of the wave-function is small, thus the Bosons can be regarded as classical point-shaped particles.
the extension of the wave-function is small, thus the Bosons can be regarded as classical point-shaped particles.
Reducing the temperature close to but above 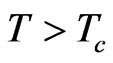 cause the wave-function of the Bosons to expand. Accordingly the wave-functions start to overlap, inducing an attractive interaction. The gas can any longer be regarded as classical Boson-gas and quantum mechanical characteristics start to dominate its behavior.
cause the wave-function of the Bosons to expand. Accordingly the wave-functions start to overlap, inducing an attractive interaction. The gas can any longer be regarded as classical Boson-gas and quantum mechanical characteristics start to dominate its behavior.
Below the critical temperature 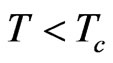 the extension of the wave-function is larger than the average distance between the Bosons. The wave-functions are overlapping, forming a consolidated base-function, the Bose-EinsteinCondensate.
the extension of the wave-function is larger than the average distance between the Bosons. The wave-functions are overlapping, forming a consolidated base-function, the Bose-EinsteinCondensate.
At temperatures T ~0˚K all Bosons are condensed in the collective wave-function ψBEC.
2.3. Electrical Conductivity
When the temperature is high enough , the electrons in a solid behave like a gas of Fermions [7]. Observing a single Atom, the binding energies En of the
, the electrons in a solid behave like a gas of Fermions [7]. Observing a single Atom, the binding energies En of the
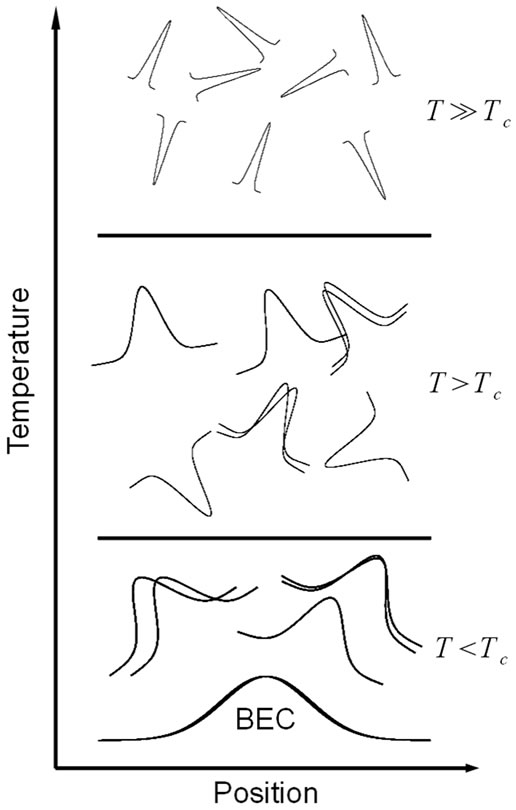
Figure 3. Schematic outline of boson wave-functions at different temperatures.
electron exist in discrete form (Figure 4). Nearing a second Atom, the wave-function of the electrons begin to overlap. Due to the fact that electrons are Fermions which don’t like each other, the binding energies of the single atoms are split into two levels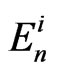 . In doing so the electrons are not bound to a single energy, but rather all electrons are in all energy states, in general in all available states. The single electrons loose their identity due to the overlap with respect to the principle of superposition and the system of electrons should be described by an overall wave-function
. In doing so the electrons are not bound to a single energy, but rather all electrons are in all energy states, in general in all available states. The single electrons loose their identity due to the overlap with respect to the principle of superposition and the system of electrons should be described by an overall wave-function
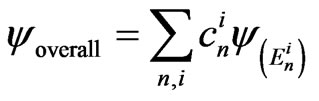 . (4)
. (4)
The further approach of atoms (Figures 4(c) and (d)) constitute further splitting of the overall wave-function thus for a large number of atoms the distribution of energies is quasi-continuous, forming energy-bands. In general the splitting also depends on the angular momentum (s, p, d··· orbitals), where the different extensions of the wavefunctions generate different overlaps with different energy splittings.
Decreasing the temperature below a critical temperature  evokes the phenomenon of Cooper-pairing [8] as spooky synchronization. This effect can be compared with the experiment in Figure 2 describing the quantum entanglement. In this case we use the wavefunctions with antipodal spin S and momentum P as entangled partners
evokes the phenomenon of Cooper-pairing [8] as spooky synchronization. This effect can be compared with the experiment in Figure 2 describing the quantum entanglement. In this case we use the wavefunctions with antipodal spin S and momentum P as entangled partners
 . (5)
. (5)
This pairing has a drastic impact on the social behavior of the electrons.
It transforms the single fermion-wave-functions into paired boson-wave-functions ψCP. These bosons like each
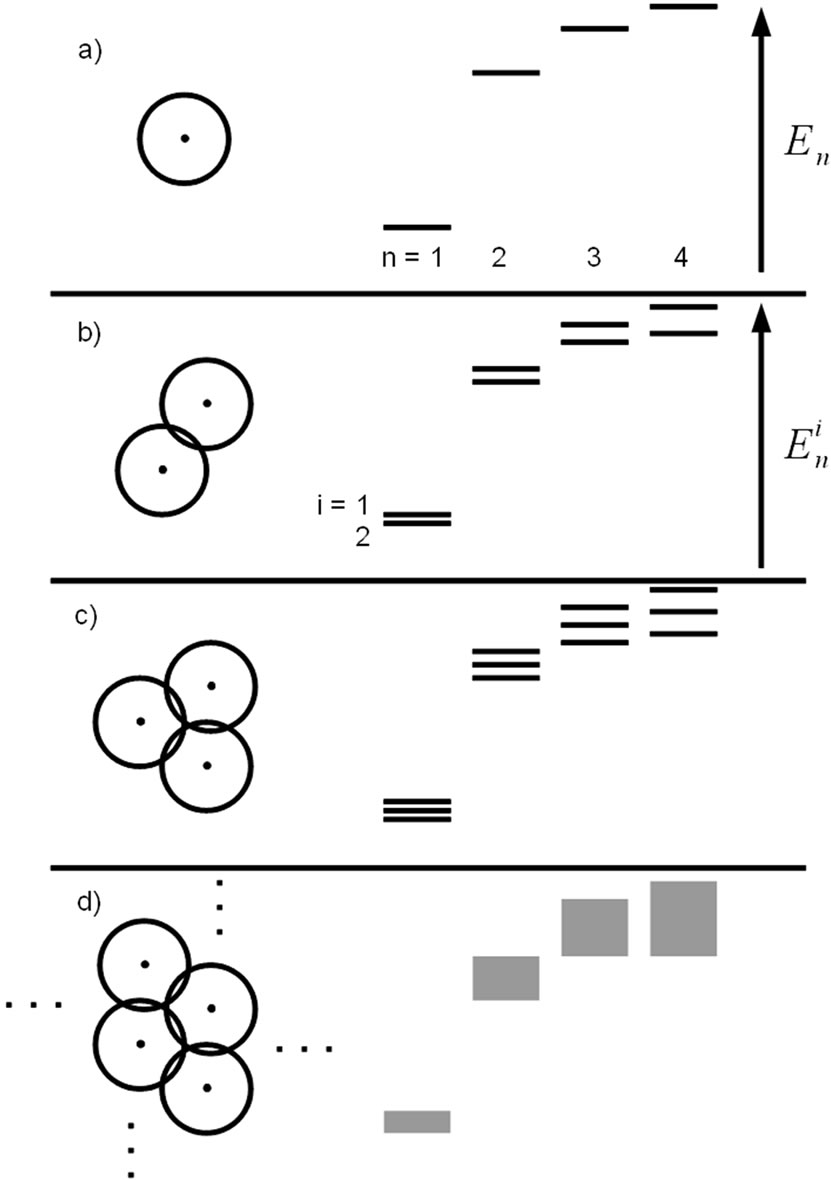
Figure 4. Basic concept of electronic band structure.
other and don’t contribute to the energy-bands. Due to the long range of influence (coherence-length ~50 - 1500 nm), the Cooper-pairs can, also at low fractions, easily condensate into the consolidated entangled base-wavefunction, the BCS ground state [9].
A constitutive feature of the BCS ground state is, that all Cooper-pairs are entangled analogous to the atoms in the Mößbauer experiment: if a voltage is applied to a sample, all Cooper-pairs move in the same manner. When one Cooper-pair gets scattered, all pairs would also be scattered. This process is very infrequent, whereby a once excited current of Cooper-pairs will persist resistance-less for a very long time. This behavior we call superconductivity.
At absolute zero temperature, there is no energy-band present and all electron wave-functions are bound in Cooper-pairs where all pairs are condensed in the BCS base-function.
3. Conclusions
It has been shown that the phenomenon of superconductivity can be consistently explained in terms of double entangled electrons. Simple spin-entanglement results in cooper-pairs and the boson-gas of cooper-pairs condensate into the entangled BCS ground state. This novel model may give a new intuitive understanding of superconductivity.
I think this paper is also a beautiful paradigm for the quantum-mechanical wave-particle dualism. The wavy nature of matter is forced to interact like a particle in discrete quanta due to the constriction of quantum entanglement.
REFERENCES
- A. Einstein, “Zur Elektrodynamik Bewegter Körper,” Annalen der Physik und Chemie, Vol. 17, 1905, pp. 891- 921.
- L. de Broglie, “The Wave Nature of the Electron,” Nobel Lecture, Vol. 12, 1929.
- A. Einstein, B. Podolsky and N. Rosen, “Can QuantumMechanical Description of Physical Reality Be Considered Complete?” Physical Review, Vol. 47, No. 10, 1935, pp. 777-780. http://dx.doi.org/10.1103/PhysRev.47.777
- R. L. Mößbauer, “Kernresonanzfluoreszenz von Gammastrahlung in Ir191,” Zeitschrift für Physik A, Vol. 151, No. 2, 1958, pp. 124-143. http://dx.doi.org/10.1007/BF01344210
- A. Einstein, “Quantentheorie des Einatomigen Idealen Gases,” Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1925, pp. 3-10.
- I. Bloch, “Atomlaser und Phasenkohärenz Atomarer Bose-Einstein-Kondensate,” PhD Thesis in Physics, Ludwig-Maximilians-Universität München, 2000.
- C. Kittel, “Introduction to Solid State Physics,” Oldenbourg Publishing House, 2004.
- L. N. Cooper, “Bound Electron Pairs in a Degenerate Fermi Gas,” Physical Review, Vol. 104, No. 4, 1956, pp. 1189-1190. http://dx.doi.org/10.1103/PhysRev.104.1189
- J. Bardeen, L. N. Cooper and J. R. Schriffer, “Microscopic Theory of Superconductivity,” Physical Review, Vol. 106, No. 1, 1957, pp. 162-164. http://dx.doi.org/10.1103/PhysRev.106.162

