World Journal of Condensed Matter Physics
Vol.1 No.4(2011), Article ID:8777,8 pages DOI:10.4236/wjcmp.2011.14025
Study of Molecular Polarizabilities and Orientational Order Parameter in the Nematic Phase of 6.O12O.6 and 7.O12O.7
![]()
1Department of Physics, North Eastern Regional Institute of Science and Technology, Itanagar, India; 2Department of Physics, The Hindu College, Machilipatnam, India; 3ECE Department, Liquid Crystal Research Centre (LCRC), K. L. University, Vaddeswaram, India.
Email: *snigsam@yahoo.co.in
Received August 19th, 2011; revised September 26th, 2011; accepted October 9th, 2011.
Keywords: Symmetric Liquid Crystal Dimers, Refractive Index, Orientational Order Parameter, Molecular Polarizability
ABSTRACT
As a part of our systematic study of the physical properties of the compounds of symmetric liquid crystal dimer homologous series, α,ω-bis-(4-n-alkylaniline benzylidene-4’-oxy) alkanes (m.OnO.m), we report here an optical study of two nematogenic compounds of this series viz., 6.O12O.6 and 7.O12O.7 by carrying out the measurement of extraordinary and ordinary refractive indices using modified spectrometer. The molecular polarizability anisotropies are evaluated using Lippincott δ-function model, the molecular vibration method, Haller’s extrapolation method and scaling factor method. The molecular polrizabilities, αe and αo are calculated using Vuks’ isotropic field model and Neugebauer’s anisotropic field model. The orientational order parameter, S, is estimated by using the molecular polarizability values calculated from refractive index and denstity data as well as polarizability anisotropy values calculated as a function of temperature in the nematic phase of both of the dimers. These values are discussed with reference to the order parameter values obtained directly from the optical birefringence, Δn, data without assuming any internal field. A comparison of the order parameter values from all of these methods was carried out in the light of available literature data.
1. Introduction
In liquid crystals, the molecular polarizabilities and their anisotropy are considered to be important characteristic inherent molecular properties because the intermolecular interaction energies, according to different theoretical models are dependent on them. The liquid crystal display technology is a major area which requires complete knowledge on the liquid crystalline materials, their response to electric fields and the study regarding optical anisotropies. Hence, it is important to gain knowledge of the temperature dependence of refractive indices, optical anisotropies, molecular polarizabilities and the order parameter of the liquid crystalline materials.
In recent years, liquid crystal dimers, which are prepared by joining two mesogenic units through a flexible alkyl spacer, are attracting much interest because of their unusual properties compared with monomeric liquid crystals as well as their capability to act as model compounds for semi-flexible main chain liquid crystal polymers [1-4]. They are classified into two categories: symmetric and non-symmetric dimers. In the former class of dimers, the mesogenic groups are identical and in the later, the mesogenic groups are not identical. The liquid crystalline properties as well as the structure of different mesophases of these class of compounds are found to be dependent on the number of carbon atoms in the spacer. The nematic-isotropic transition temperatures are found to exhibit a dramatic alternation as the number of carbon atoms in the alkyl spacer changes from odd to even. However, the alternation is attenuated as the spacer grows in length. In contrast, the alternation in the entropy of nematic-isotropic transition is essentially unattenuated:
at least for spacers containing upto twelve carbon atoms [5]. In addition the entropy change at the nematic-isotropic transition for dimers with odd spacers is comparable to that of monomers while for even spacers the translational entropy is typically three times larger. The behavior of the translational entropy suggest that the orientational order for even spacer dimer should be significantly greater than that for odd spacer dimers. Further, in case of non-symmetric liquid crystal dimers, the thermal stability of the smectic phase shows different behavior with long and short terminal alkyl chains. This surprising observation was rationalized by proposing a novel intercalated structure for the smectic. A phase exhibited by short chain lengths and the conventional interdigitated structure for long chain lengths. The driving force for the intercalated structure was considered to be mixed mesogenic unit-mesogenic unit interaction, while for the interdigitated phase, the driving force for association was thought to be electrostatic interaction between polar and polarizable cyanobiphenyl groups and the smectic phase resulted from the molecular inhomogenity produced by the long terminal alkyl chains [3]. As a part of our systematic study of the physical properties of the homologues of Schiff base symmetric liquid crystal dimers viz., α,ω-bis-(4-n-alkylaniline benzylidene-4’-oxy) alkanes (m.OnO.m), in this paper, optical anisotropy as a function of temperature in the nematic phase of two dimers, 6.O12O.6 and 7.O12O.7, using a modified spectrometer was measured. Further, the molecular polarizability anisotropies were evaluated using Lippincott δ-function model, the molecular vibration method, Haller’s extrapolation method and scaling factor method. Also, orientational order parameter was evaluated using different methods have been discussed in the nematic phase of these two compounds.
2. Experimental
The compounds 6.O12O.6 and 7.O12O.7 were synthesized following a standard method available in literature [1]. Differential Scanning Calorimetry measurements were carried out using Shimadju DSC-60. The refractive indices of the liquid crystals were measured with a wedge shaped glass cell, similar to the one used to obtain birefringence by Haller et al. [6] using a modified spectrometer. The liquid crystal sample was sandwiched between two optically flat rectangular glass plates (50 mm × 25 mm) made into a wedge shape by inserting a thin glass plate (0.40 mm) at one edge which acts as a wedge spacer. The optical flats were uniformly rubbed along the short edge to achieve the alignment of the liquid crystal molecules. After filling the liquid crystal sample the cell acts as a uniaxial crystal with its optic axis parallel to the edge of the spacer glass plate. The temperature of the heating block used was measured to an accuracy of ±0.1˚C.
The accuracy in the measurement of refractive indices was ±0.0005. The extraordinary and ordinary refractive indices, ne and no, were measured using a source of wave length 589.3 nm.
3. Results and Discussion
The general molecular structure of the compounds is shown below.
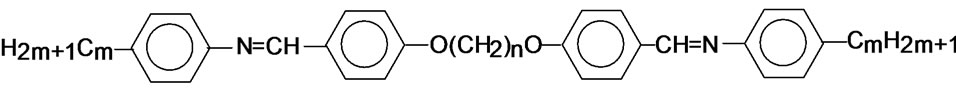
6.O12O.6: m = 6 and n = 12
7.O12O.6: m = 7 and n = 12
The transition temperatures observed for these compounds were measured using DSC and polarizing thermal microscopy and found that they are in good agreement with those reported in literature [1]. The observed transition temperatures are shown in the Table 1.
The variation of refractive index with temperature in 6.O12O.6 and 7.O12O.7 are shown in Figures 1 and 2. It can be observed that while cooling the sample from isotropic phase, the value of refractive index in isotropic phase (niso) is constant in both of the compounds. At the I-N transition the isotropic refractive index value splits into two, extraordinary refractive index (ne > niso) and ordinary refractive index (no < niso). This splitting is clearly observed in the telescope of the modified spectrometer at the position of angle of minimum deviation at the I-N
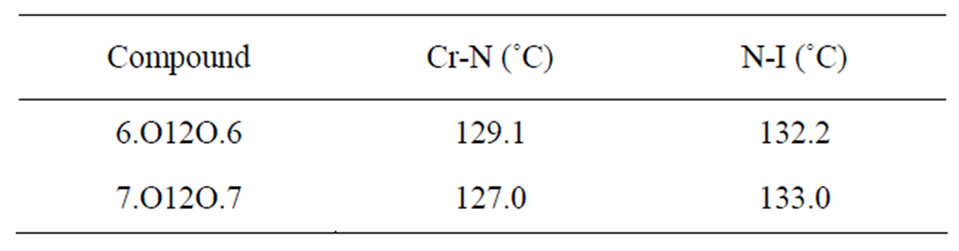
Table 1. Transition temperatures of the phase transitions exhibited by 6.O12O.6 and 7.O12O.7.
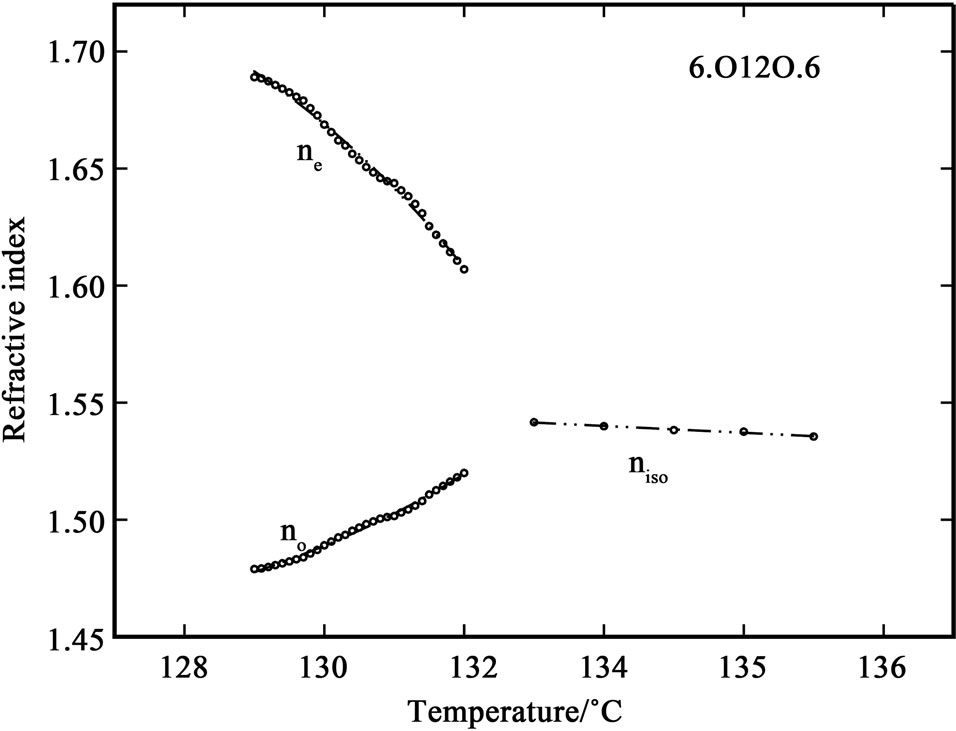
Figure 1. Variation of refractive indices ne and no with temperature in the compound 6.O12O.6.

Figure 2. Variation of refractive indices ne and no with temperature in the compound 7.O12O.7.
transition. When the temperature is further decreased, the value of ne increases while the value of no decreases slightly; and when the temperature is further decreased, deep in the nematic phase, the values of both components of refractive index saturates. The I-N temperatures observed in the birefringence measurements are in good agreement with those observed in DSC and density measurements [7,8]. Also, the density data reported in these references was used for calculating the molecular polarizability values, αe and αo.
3.1. Estimation of Order Parameter
3.1.1. Estimation of Molecular Polarizability Anisotropy from Lippincott δ-Function Model and the Molecular Vibrational Methods
The principal molecular polarizability anisotropy and the mean polarizability are evaluated for the compounds 6.O12O.6 and 7.O12O.7 using the Lippincott δ-function model [8,9] and the molecular vibration method [10]. The principal molecular polarizability components as well as mean polarizabilities for the compounds 6.O12O.6 and 7.O12O.7 using these two methods are given in Table 2.
3.1.2. Estimation of molecular polarizabilities from Refractive Indices and Densities Employing Vuks and Neugebaur Methods
3.1.2.1. Vuks Method
This model was first applied to liquid crystal molecules by Chandrasekhar et al. [11] in which the internal field is assumed to be isotropic even in anisotropic crystal. These assumptions lead to the following equations
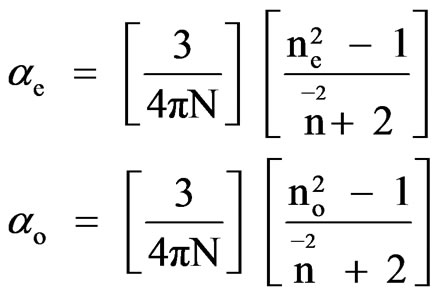 (1)
(1)
where N is the number of molecules per unit volume, ne and no are the extraordinary and ordinary refractive indi-

Table 2. Principal parallel, perpendicular components and mean polarizabilities of (×10–24 cm3) 6.O12O.6 and 7.O12O.7.
ces of the LC molecule,
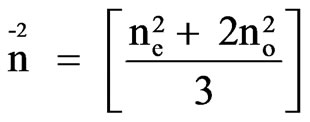
and N = NAr/M where NA is the Avogadro number, r is the density and M is the molecular weight.
3.1.2.2. Neugebauer Method
Saupe and Maier [12] and Subramanyam et al. [13] applied this method to liquid crystal molecule in which the internal field is assumed to be anisotropic. According to this method the molecular polarizabilities are
 (2)
(2)
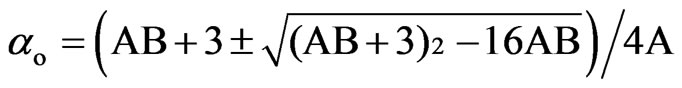 (3)
(3)
where
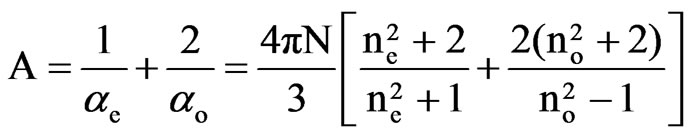 (4)
(4)
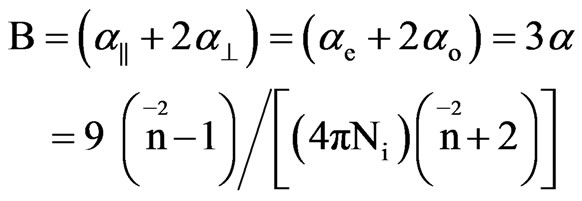 (5)
(5)
and Ni is the number of molecules per unit volume in the isotropic phase.
Using the two models the molecular polarizabilities (αe and αo) and the polarizability anisotropy (ae – ao) in nematic phase of the compounds 6.O12O.6 and 7.O12O.7 were calculated at different temperatures and the values are presented in Tables 3 and 4, respectively.
From these two tables following observations can be made: the calculated values of αe, αo and (αe – αo) using both Vuks and Neugebaur methods are marginally larger for 7.O12O.7 than those for 6.O12O.6 and the values obtained for any single compound using these two methods are almost similar. This is rather surprising as it was assumed that the molecular distribution in the Vuks model to be isotropic even in the anisotropic crystal which was applied to anisotropic liquid crystals [10], whereas, the Neugebaur model assumes anisotropy of the internal field in a crystal [14] which was applied to liquid crystals [11,12].

Table 3. The molecular polariziabilities and the polarizability anisotropy (αe – αo) in 6.O12O.6.
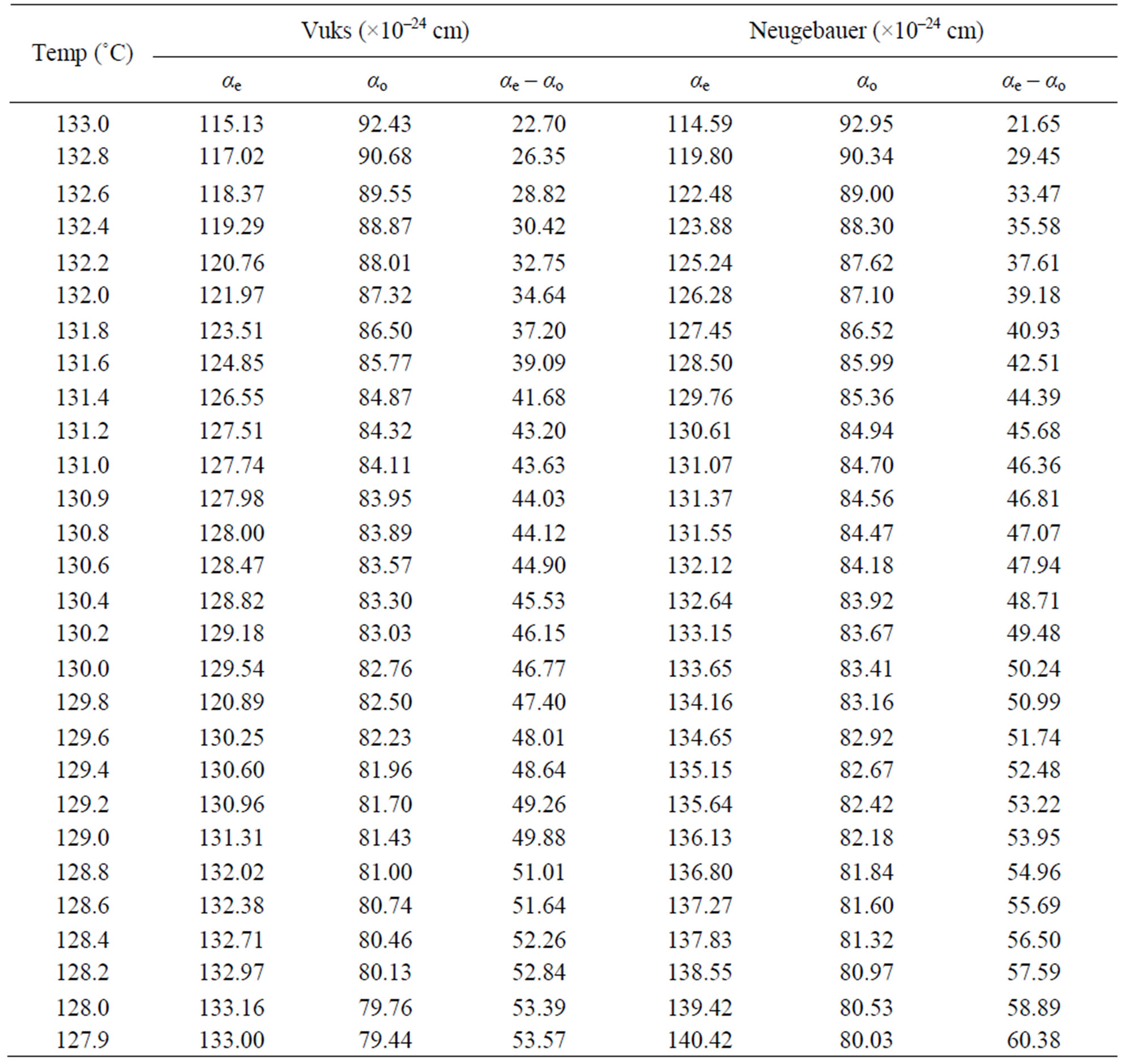
Table 4. The molecular polarizabilities and the polarizability anisotropy (αe – αo) in 7.O12O.7.
However, the molecules are assumed as point polariza-bilities distributed anisotropically in space. Also, if the small difference in the length of these two molecules is considered, the molecular polarizability values appears to be almost same in the nematic phase of both of these two compounds. The anisotropy in the molecular polarizabilities calculated using both Vuks and Neugebauer models increases with decrease of temperature in both 6.O12O.6 and 7.O12O.7. This could be explained as follows: at molecular level, if the motion of different parts of a molecule are considered viz., the possible free rotation about the single bonds of the methylene units present in both spacer as well as end groups, the hindered rotation due to the presence of bulk groups or double bonds as well as non-coplanarity of benzene rings reducing the conjugation effects are possible in liquid crystalline phase. The number of molecules in which such motions take place and decrease of the amplitudes of such motions with decreasing temperature are possible leading to the increase of polarizability anisotropy as the temperature is decreased. Finally, the calculated values of αe and αo in the nematic phase of both 6.O12O.6 and 7.O12O.7 are nearly 2.5 times to those observed for the compounds of n.Om series viz., 6O.4, 6O.2 and 7O.1 [15] which are the precursors of these dimers with slightly different end chain lengths and those of other monomers (nO.Om) reported recently [16].
3.1.3. Estimation of Order Parameter, S, from Molecular Polarizability Anisotropies and Mean Polarizabilities in Different Ways from Different Methods
In uniaxial liquid crystal phase the extraordinary (ae) and ordinary (ao) polarizabilities corresponding to the electric vector parallel and perpendicular to the optic axis are given as
 (6)
(6)
where S is the order parameter a|| and 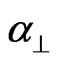 are principal polarizabilities of the molecule parallel and perpendicular to the long molecular axis of the liquid crystal molecule. The average molecular polarizability
are principal polarizabilities of the molecule parallel and perpendicular to the long molecular axis of the liquid crystal molecule. The average molecular polarizability 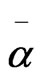 is given as
is given as
 (7)
(7)
Combining the above two equations the order parameter, S, is
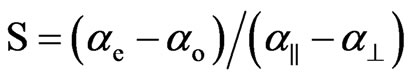 (8)
(8)
The principal polarizabilities a|| and a^ are estimated using different methods and the S is estimated for both cases viz., Vuks and Neugebauer. The methods used for obtaining principal polarizabilities are Lippincott d-function method [8,9], molecular vibrational method [10], Haller [17] extrapolation method and scaling factor method. Therefore, the order parameter, S, using Vuks and Neugebauer methods is obtained in different ways employing the four different principle polarizabilities for both of the compounds, 6.O12O.6 and 7.O12O.7.
In the Vuks method the order parameter is given by [18,19]
 (9)
(9)
where
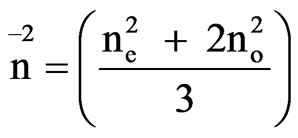
In the Neugebauer method the order parameter S [18] is given by
 (10)
(10)
where

and
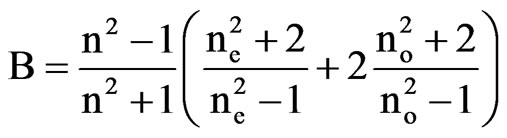
The scaling factors for the determination of order parameter are obtained in both the cases by plotting loglog plots between 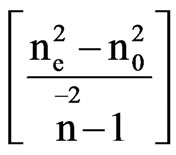 and f(B) in Vuks and Neugebauer methods respectively against the reduced temperature (TNI – T)/( TNI – TNI/NCr) (where TNI and TNCr are isotropic-nematic and nematic-crystal transition temperatures, respectively) .
and f(B) in Vuks and Neugebauer methods respectively against the reduced temperature (TNI – T)/( TNI – TNI/NCr) (where TNI and TNCr are isotropic-nematic and nematic-crystal transition temperatures, respectively) .
The order parameter, S, from molecular polarizabilities is estimated by assuming Vuks and Neugebauer internal field models. The denominator i.e., the principal polarizabilities used are obtained by four different methods as stated above. The order parameter, S, calculated using these methods are shown in Figures 3 and 4 for 6.O12O.6 and 7.O12O.7, respectively. The S values calculated directly from optical anisotropy are also included for the sake of comparison (In figures, 1:S calculated from Lippincott δ-function model; 2:S calculated from molecular vibration method; 3:S calculated from Haller extrapolation method; 4:S calculated from scalling factor method).
 (a)
(a) (b)
(b)
Figure 3. (a) Variation of order parameter, S versus the normalized nematic range for the compound 6.O12O.6 using Vuks model; (b) Variation of order parameter, S versus the normalized nematic range for the compound 6.O12O.6 using Neugebauer model.
 (a)
(a) (b)
(b)
Figure 4. Variation of order parameter, S versus the normalized nematic range for the compound 7.O12O.7 using (a) Vuks model and (b) Neugebauer model.
Table 5 shows the percentage of deviation of the S values calculated using Vuks and Neugebauer models using all methods from that calculated directly from optical anisotropy values, Δn, the birefringence in perfect order [19-22]. The values are underlined if the deviation is less than or equal to 10% which are considered in agreement with S calculated from Δn and is within the experimental error (which is be between –5% to +5%). From the figures 3 and 4 as well as from Table 5, following conclusions can be drawn: The S values obtained from Vuks model using the polarizability anisotropies calculated from Lippincott δ-function model, vibrational method, Haller extrapolation method and from scaling factor method are slightly larger than those calculated directly from optical birefringence (Δn) in both 6.O12O.6
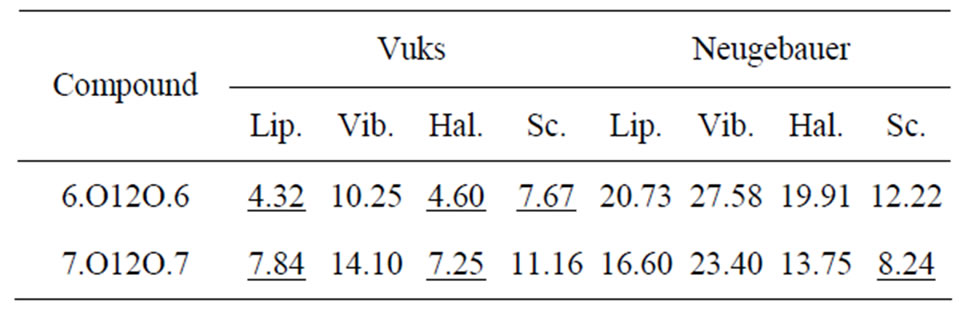
Table 5. Prcentage of deviation of order parameter, S estimated assuming the two field models and using different methods from that obtained using ∆n, the birerefringence in perfact order in the two dimeric compounds.
and 7.O12O.7 as well as in reasonably good agreement with with S values calculated from Δn directly. Whereas, in the case of S values obtained from Neugebauer model, the S values calculated from scaling factor method are slightly smaller than those calculated from Δn values directly and S values calculated from all other methods are slightly larger than those obtained from Δn values for both of the compounds. Also, the percent of deviation observed is rather large, except in case of the values obtained from scaling factor method for 6.O12O.6 and Haller’s extrapolation and scaling factor methods in case of 7.O12O.7. From all the methods employed, it can be seen that the largest value of S attained in N phase of 7.O12O.7 is slightly higher compared with that for 6.O12O.6. From this analysis a good agreement can be observed in the S values obtained from Δn directly with S values obtained from other methods using Vuks model in the N phase of both of the compounds studied. Whereas this kind of agreement is rather poor in case of the calculated S values Using Neugebauer method with those obtained from Δn values directly except in case of S values obtained from scaling factor method. Our results show that the application of Vuks model for calculating molecular polarizabilities and order parameter gives good results in these two dimers than the Neugebauer model which indicates that the assumption of isotropic model even in the anisotropic environment in these dimers is giving better results of S values than the assumption of anisotropic environment.
4. Acknowledgements
P. R. Alapati expresses his gratitude to CSIR, New Delhi, India for providing financial support. The authors D. Madhavi Latha and V. G. K. M. Pisipati express their thanks to the management of K. L. University, Vaddeswaram, India as well as financial support from DST, New Delhi, India. Authors P. V. Datta Prasad and P. Pardhasaradhi express their gratitude to the management of The Hindu College, Machilipatnam, India for providing computational facilities.
REFERENCES
- R. W. Date, C. T. Imrie, G. R. Luckhurst and J. M. Seddon, “Smectogenic Dimeric Liquid Crystals. The Preparation and Properties of α,ω-Bis-(4-N-alkylaniline benzylidene-4’-oxy) Alkanes,” Liqid Crystals, vol. 12, No. 2, 1992, pp. 203-235. doi:10.1080/02678299208030393
- S. K. Heeks and G. R. Luckhurst, “On the Molecular Organization within the Nematic Phase of Liquid Crystal Dimmers,” Journal of the Chemical Society, Faraday Transctions, vol. 89, 1993, pp. 3289-3296. doi:10.1039/ft9938903289
- G. S. Attard, R. W. Date, C. T. Imrie, G. R. Luckhurst, S. J. Roskilly, J. M. Seddon and L. Taylor, “Non-Symmetric Dimeric Liquid Crystals. The Preparation and Properties of α-(4-Cyanobiphenyl-4’-oxy) Alkanes,” Liqid Crystals, vol. 16, No. 4, 1994, pp. 529-551. doi:10.1080/02678299408036531
- R. W. Date, G. R. Luckhurst, M. Schuman and J. M. Seddon, “Novel Modulated Hexatic Phases in Symmetric Liquid Crystal Dimmers,” Journal of de Physique II, vol. 5, No. 4, 1995, pp. 587-605. doi:10.1051/jp2:1995151
- A. Ferrarini, G. R. Luckhurst, P. L. Nordio and S. J. Roskilly, “Understanding the Unusual Transitional Behaviour of Liquid Crystal Dimmers,” Chemical Physics Letters, vol. 214, No. 1-4, 1993, pp. 409-417. doi:10.1016/0009-2614(93)85658-B
- I. Haller, H. A. Huggins, H. R. Lilienthal and T. R. McGuire, “Order-Related Properties of Some Nematic Liquids,” Chemical Physics Letters, vol. 77, No. 7, 1973, pp. 950-954. doi:10.1021/j100626a020
- D. Bhuyan, P. Pardhasaradhi, B. Gogoi, P. V. Datta Prasad, P. R. Alapati and V. G. K. M. Pisipati, “Phase Transition Studies of 6.O12O.6 and 7.O6O.7 by Using Density Measurements,” Molecular Crystals and Liquid Crystals, vol. 540, No. 1, 2011, pp. 205-212. doi:10.1080/15421406.2011.568882
- E. R. Lippincott and M. O. Dayhoff, “Delta-function Model of Chemical Binding,” Spectrochimica Acta, vol. 16, No. 1, 1960, pp. 807-834.
- E. R. Lippincott, G. Nagarajan and J. M. Stutman, “Polarizabilities from the δ-Function Model of Chemical Binding II. Molecules with Polar Bonds,” The Journal Physical Chemistry, vol. 70, No. 1, 1966, pp. 78-84. doi:10.1021/j100873a012
- Y. N. Muthi, V. R. Murthi and R. N. V. Ranga Reddy, “Molecular Vibration Approach to Polarizability of Methyl Cinnamate Liquid Crystal Compounds,” Acta Physica Polonica A, vol. 91, 1997, pp. 1069-1079.
- S. Chandrasekhar and N. V. Madhusudhana, “Orientational order in p-Azoxyanisole, p-Azoxyphenetole and Their Mixtures in Nematic Phase,” Journal of de Physique Colloques, Vol. 30, Supplement 11, 1969, pp. 24-27.
- A. Saupe and W. Maier, Zeitschrift fur Naturforschung, vol. 16a, 1961, p. 816.
- H. S. Subrahmanyam and D. Krishnamurthi, “Polarization Field and Molecular Order in Nematic Liquid Crystals,” Molecular Crystals and Liquid Crystals, vol. 22, No. 3-4, 1973, pp. 239-248. doi:10.1080/15421407308083347
- H. E. J. Neugebauer, “Clausius-Mosotti Equation for Certain Types of Anisotropic Crystals,” Canadian Journal of Physics, Vol. 32, No. 1, 1954, pp. 1-8. doi:10.1139/p54-001
- N. V. S. Rao, V. G. K. M. Pisipati, P. V. Datta Prasad and P. R. Alapati, “Order Parameter and Molecular Polarizabilities in 6O.4, 6O.2 and 7O.1,” Molecular Crystals and Liquid Crystals, vol. 132, No. 1-2, 1986, pp. 1-21. doi:10.1080/00268948608079523
- P. Pardhasaradhi, C. S. V. S. Murthy, J. L. Kumari, P. V. Datta Prasad, M. Srinivasulu and V. G. K. M. Pisispati, “Orientational Order Parameter-II—A Birefringence Study,” Molecular Crystals and Liquid Crystals, vol. 511, No. 1-2, 2009, pp. 121-132. doi:10.1080/15421400903053644
- I. Haller, H. A. Huggins and M. J. Freisner, “On the Measurement of Indices of Refraction of Nematic Liquid Crystals,” Molecular Crystals and Liquid Crystals, vol. 16, No. 1-2, 1972, pp. 53-59. doi:10.1080/15421407208083579
- R. G. Horn, “Refractive Indices and Order Parameters of Two Liquid Crystals,” Journal of Physics, vol. 39, No. 1, 1978, pp. 105-109. doi:10.1051/jphys:01978003901010500
- P. G. de Gennes and J. Prost, “The Physics of Liquid Crystals,” Oxford University Press, New York, 1993.
- W. H. de Jeu, “Physical Properties of Liquid Crystalline Materials,” Gordon and Breach Publishers, New York, 1980.
- B. J. Zywucki and W. Kuczynski, IEEE Transactions, Vol. 8, 2001, p. 512.
- W. Kuczyncki, B. J. Zywucki and J. Malecki, “Determination of Orientational Order Parameter in Various Liquid Crystalline Phases,” Molecular Crystals and Liquid Crystals, vol. 381, No. 1, 2002, pp. 1-19. doi:10.1080/713738745

