Atmospheric and Climate Sciences
Vol.05 No.04(2015), Article ID:60203,8 pages
10.4236/acs.2015.54035
Local Altruism as an Environmental Ethic in CO2 Emissions Control
Masayuki Otaki
The Institute of Social Sciences, The University of Tokyo, Tokyo, Japan
Email: ohtaki@iss.u-tokyo.ac.jp
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2015; accepted 9 October 2015; published 12 October 2015
ABSTRACT
When considering emissions control problems associated with carbon dioxide (CO2), social planning over quite a long-term horizon is usually considered to be necessary because it takes much time for the full absorption of CO2 by oceans and forests. Sometimes the required time horizon even becomes infinite. Such a fact seems to impose patience beyond the limits of human cognition. However, this study proves that the first-best emissions scenario can be achieved only by local altruism, which is dubbed parentage. Parentage is defined as the action of applying zero social discount rate to its subsequent generation, and discounting the utility of generations thereafter infinitely. In this sense, the nearly first-best emissions scenario is feasible within the ordinal cognition and benevolence of human beings. This paper also examines the definition of egalitarian sustainability, in which the utility of every generation must be kept constant, and reveals that such a definition of sustainability possibly provokes the inefficient intergenerational allocation of CO2. This is because the vested interest of the predecessors is put much importance in the process of the planning. It is required more rigid sustainability concept, in which the utility of each generation is no less decreasing through time and at least strictly increasing locally, to achieve the efficient allocation of CO2. One will find that the intergenerational allocation by the local altruism satisfies this property.
Keywords:
Parentage as Local Altruism, Social Discount Rate, Environmental Ethics, Sustainability

1. Introduction
CO2 emissions control is a difficult problem since it requires consistent decisions across generations. There are serious conflicts between the generations. For example, as long as individuals’ economic concerns are limited to their own lives, they ruthlessly discount future generations’ wellbeing. Their resultant excessive consumption is certainly connected to excessive emissions of CO2, which have become a serious cause of global warming.
Nevertheless, even though we can overcome such a difficulty in principle, to achieve the precise control requires exorbitant information. By virtue of dynamic programming, we must determine beforehand the terminal condition that corresponds to the wellbeing of generations belonging to the far future in the context of emissions control. Obviously, this is beyond the cognitive ability of human beings.
This study provides an effective control method presuming that the time horizon of an individual is far shorter than the whole length of the time horizon of the history of human beings. Parentage, which implies that love for children does not contradict parents’ own economic concern, plays a crucial role. That is, individuals are assumed to be myopic in the sense that their economic concern is limited to themselves and their children. Parents are called devoted to their children whenever they apply the zero discount rate to the children’s wellbeing. As precisely analyzed below, this is a crucial condition for the global stability of CO2 emissions that requires no information concerning the economic situations of far descendants. That is, the concept of devotion, which is a stronger concept than parentage yet still remains within the cognitive ability of people with common sense, can ultimately hinder excess consumption and emissions that stem from selfish economic motives1.
The rest of paper is constructed as follows. Section 2 deals with a laissez faire economy, in which there is no emissions control, based on the concept of the sequential equilibrium proposed by Kreps and Wilson (1982) [1] . Section 3 defines the first-best emissions control under the stationary state originated by Otaki (2013) [4] . In addition, this section reveals the extent of divergence between the stationary state of the laissez faire economy and that of the properly controlled economy. This fact acutely conveys the importance of CO2 emissions control. Section 4 considers how the economy can reach the first-best allocation without imposing transcendent and stringent morals beyond the cognitive ability of human beings. The concept of parentage and devotion play crucial roles. Section 5 provides brief concluding remarks. Appendix shows the desired property which the transition periods should satisfy, that is dubbed sustainability.
2. The Basic Structure of the Model and the Laissez Faire Economy
2.1. The Basic Structure of the Model
It is assumed that every individual lives in one period, and his or her utility function
 is defined as
is defined as
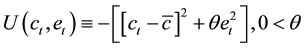 (1)
(1)
where
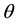 represents how much importance individuals, who belong to generation
represents how much importance individuals, who belong to generation , put on the direct disutility from the accumulated emission of CO2,
, put on the direct disutility from the accumulated emission of CO2,
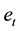 , relatively to current consumption,
, relatively to current consumption, . While such a quadratic function seems quite a naïve formulation, it can exclude inessential phenomena, which are peculiar to nonlinear difference equations, such as limit cycle and chaos, completely. In terms of economics, the nonlinearity, which stems from the complexity of the utility function, is regarded as a less relevant problem compared with the problem that shall be deal with hereafter.
. While such a quadratic function seems quite a naïve formulation, it can exclude inessential phenomena, which are peculiar to nonlinear difference equations, such as limit cycle and chaos, completely. In terms of economics, the nonlinearity, which stems from the complexity of the utility function, is regarded as a less relevant problem compared with the problem that shall be deal with hereafter.
By the same token, the emission dynamics is assumed to obey the following simple linear first order difference equation.
 (2)
(2)
2.2. The Laissez Faire Economy as a Sequential Equilibrium
This subsection deals with the consumption/emission dynamics within the laisses faire economy. The laissez faire economy is defined as a sequential equilibrium in the sense of Kreps and Wilson (1982) [1] . That is, it is assumed that generation
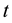 maximizes its utility for a given previously accumulated CO2,
maximizes its utility for a given previously accumulated CO2,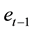 . The first-order condition, which is derived from (1) and (2), implies the following linear difference equation.
. The first-order condition, which is derived from (1) and (2), implies the following linear difference equation.
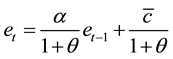 (3)
(3)
It is clear that this equation is stable and monotonously converges to the stationary state:
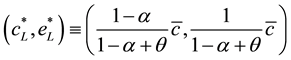 (4)
(4)
The values in (4) comprise the pivotal point for acknowledging the acute necessity for the emissions control.
3. The First-Best Allocation in the Stationary State
This section calculates the first-best allocation of consumption/accumulated emissions in accordance with the method developed by Otaki (2013) [4] . By assuming a proportional carbon tax under the stationary state, it is straightforward from Figure 1 that the marginal substitution rate must be equal to the correct effective relative
price of CO2,
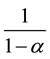 , to the consumption good for achieving the first-best allocation2. This implies the following formula that the optimal planning must satisfy:
, to the consumption good for achieving the first-best allocation2. This implies the following formula that the optimal planning must satisfy:
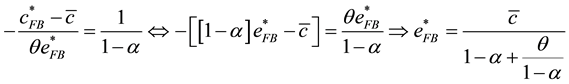 (5)
(5)
Thus, the fist-best allocation at the stationary equilibrium is
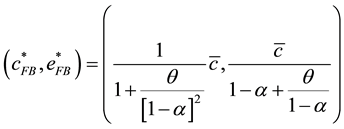 (6)
(6)
Figure 1. Optimal stationary state.
Compared with (4), the consumption level of the lasses faire economy exceeds that of the first-best allocation by

times. As discussed below, it should be noted that

4. Parentage as the Minimum Environmental Ethic
The first-best allocation shown in Section 3 imposes quite stringent and transcendent ethics on human beings. Every generation must have deep sympathy for their unforeseen far descendants in order to achieve the idealistic allocation. This criterion is too strict and unfeasible in reality. Instead this section introduces the concept of parentage, which implies that the concern of an individual with well being is limited to those of his/herself and their children. This concept is realistic and coheres with human beings’ cognitive limits in the sense that people can hold sympathy only with the next generation, with whom they can communicate directly. This section analyzes how such parentage contributes to emissions problem.
By using the utility function (1), parentage can be represented as the fact that each individual possesses the following utility function,


where


The maximization of (8) under the constraint of (2) yields the following second-order difference equation:

The eigen value,


The corresponding stationary state


It should be noted that, by comparing (11) with (6), the first-best allocation in the stationary state is achieved if parents possess deep parentage enough that they are devoted to their children
Definition 1
The economy is stable if and only if it converges to the stationary state


Such a definition of stability implies that even though the initial parents face unchangeable past accumulation of CO2 within the rational expectations equilibrium, the economy converges to its stationary state if sufficient parentage is embedded to the mind of an individual. In this sense, we, hereafter, search for the minimum ethic that enables the economy to stabilize CO2 emissions autonomously.
Mathematically, Definition 1 is equivalent to the property that the smaller eigen values,




(12) is equivalent to

In addition, the following condition is necessary for keeping the stationary state (11) is well defined.

The reason why


Theorem 1
Parents should be devoted to their children in the sense that they should apply zero social discount rate (i.e.,
Theorem 1 implies that it is an acute environmental ethic for parents to have as much concern for their children’s wellbeing as that for themselves to stabilize emissions of CO2, and this achieves the first-best allocation in the stationary equilibrium although such a long-run problem might be out of their scope.
In addition, some discussions are necessary about the properties of the social discount rate. First, excess devotion is harmful conversely in the sense that parents apply the negative discount rate to their children’s wellbeing at least in the long run. This is because such self-sacrifice thwarts consumption excessively, even though emissions of CO2 are controlled stringently.
Second, although a reliable value of the crucial parameter,

Third, as exhibited in (6) and (11), the allocation approaches the first best together with a decrease in the gross social discount rate


Finally, although this is the most serious problem, even though the laissez faire economy converges to the stationary state, it should be emphasized that there is no guarantee that such a stationary state is harmonious with the viability of human beings. This implies that not only the parameter of the remaining ratio,


5. Concluding Remarks
This study considers how CO2 emissions should be effectively controlled within the cognitive abilities of human beings. The role of parentage, which is defined as parents’ partial altruism to their children, plays a crucial role. If parentage is perfect, parents are devoted to their children. This means that parents apply zero local social discount rate limited to their children. Then, the first-best resource allocation is achieved in the stable stationary state. Otherwise, some incentive schemes should be constructed for the efficient control of CO2 emissions.
This theorem advocated that artificial carbon tax schemes and/or emissions trading, properties of which are analyzed by Otaki (2013, 2013) [4] [5] , play only subsidiary roles as measures of emissions control. The most important role should be ascribed to the establishment of environmental ethics that are deeply rooted in love for children.
Cite this paper
MasayukiOtaki, (2015) Local Altruism as an Environmental Ethic in CO2 Emissions Control. Atmospheric and Climate Sciences,05,433-440. doi: 10.4236/acs.2015.54035
References
- 1. Kreps, D.M. and Wilson, R. (1982) Sequential Equilibrium. Econometrica, 50, 863-894.
http://dx.doi.org/10.2307/1912767 - 2. Houghton, J.T., Jenkins, G.J. and Ephraums, J.J. (Eds.) (1990) Climate Change. Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge.
- 3. Nordhaus, W.D. (2014) Dice-2013R Model of as of November 15, 2013.
http://www.econ.yale.edu/~nordhaus/homepage/Web-DICE-2013-April.htm - 4. Otaki, M. (2013) The Endogenous Social Discount Rate, Proportional Carbon Tax, and Sustainability: Do We Have the Right to Discount Future Generations’ Utility? Environmental Systems Research, 2, 1-8.
http://dx.doi.org/10.1186/2193-2697-2-1 - 5. Otaki, M. (2013) Emission Trading or Proportional Carbon Tax: A Quest for More Efficacious Emission Control. Environmental Systems Research, 2, 1-6.
http://dx.doi.org/10.1186/2193-2697-2-1 - 6. Pezzy, J. (1997) Sustainability Constraint versus “Optimality” versus Intertemporal Concern, and Axiom versus Data. Land Economics, 73, 448-466.
http://dx.doi.org/10.2307/3147239 - 7. Ramsey, F.P. (1928) A Mathematical Theory of Saving. Economic Journal, 38, 543-559.
http://dx.doi.org/10.2307/2224098 - 8. Tanaka, M. (1993) Chikyu ondanka no mekanizumu (The Mechanism of Global Warming). In: Uzawa, H. and Kuninori, M., Eds., Chikyu ondamka no Keizai bunseki (Economic Analysis of Global Warming), University of Tokyo Press, Tokyo, 37-72.
- 9. Vanderheiden, S. (2008) Atmospheric Justice: Apolitical Theory of Climate Change. Oxford University Press, Oxford.
http://dx.doi.org/10.1093/acprof:oso/9780195334609.001.0001
Appendix
Since the problem of stabilizing CO2 emissions contains a serious conflict between generations, it should be some minimum guarantee for the utility acquired by each generation. We dub this guarantee of the minimum utility sustainability. This notion is specifically important when one analyzes the transition path to the stationary state.
In this Appendix, two concepts of sustainability are examined. One is a seemingly egalitarian standard that requires that every generation should enjoy the same utility proposed by Pezzy (1997) [6] and Vanderheiden (2008) [9] in the separate contexts. The other is based on a more stringent definition than Pezzy-Venderheiden’s definition. That is, we call that the economy is sustainable whenever the subsequent generations can enjoy not less utility than current generation. One would find that the equilibrium path derived by this paper satisfies this criterion.
1. Egalitarian Allocation Does Not Imply Justice as Fairness
Sustainability in the sense of Pezzy (1997) [6] and Vanderheiden (2008) [9] does not imply non-discounting future generations’ utility.
Such sustainability is defined by the following egalitarian inequalities:

Since under the initial condition
and the feasibility condition
(1) requires that the economy should stay at the initial position. That is,

It is assumed that the allocation of the economic is initially located at an excess consumption/emission stationary equilibrium, and thus,

holds.
The definition of sustainability (1) is advantageous for the initial generation and conservative in the sense that the incumbent interests are reflected as much as possible when the intertemporal emissions allocation is considered. Since the optimized utility of each generation must satisfies

And the conditions (2) and (3), the Lagrangean multipliers satisfy

(5) implies that the seemingly egalitarian allocation represented by (1), does not mean that the current generation, who plans the emissions control, takes future generations’ utility fairly. Since (1) implies that it makes possible for the current generation, who faces excess consumption/emission, to advocate the status quo even though more desirable allocations exist in the future, the applied social discount rate becomes positive as shown by (5). As such, the progress of emissions control is hindered if we accept the Pezzy-Vanderheiden’s definition of sustainability5 [4] .
2. Priorities of the Value Judgment Concerning CO2 Emissions Control and the Role of Parentage
We assume that value judgments concerning CO2 emissions control obey the following order.
I. An economy must converge to a stable stationary state.
II. The path of CO2 emissions must satisfy the sustainability in the following progressive sense. That is,

where


III. As long as I and II are satisfied, the planning that achieves higher

The first value judgment is imperative for stabilizing the atmosphere and the climate change. The second order judgment concerning sustainability implies that the emissions control should progress incessantly as long as excess consumption/emission prevails in an economy. The third order judgment asserts the importance of the efficiency of the long-run emissions control. An economy will reach the vicinity of the stationary state sooner or later, and stays there during all time thereafter. Accordingly, for the future generations’ wellbeing, this condition should be entailed.
It is already shown the local altruism, which we call parentage, satisfies the conditions I and III. What is left is to check whether such an ingenious emissions control satisfies Condition II. Thus, the following theorem is obtained.
Theorem 2
If


Proof
By Equation (2), the total derivative of the utility of an individual who belongs to generation

From Equation (5) and the assumption, it is clear that



Then let


By the definition of the eigen value,
holds. Figure A1 illustrates the locus of


Figure A1. Characteristic equation.
NOTES
1Ramsey (1928) [7] argues that discounting future consumptions is not ethically permissible. He solves the optimal growth path without discounting. My study provides a utilitarian foundation of his assertion. Against Ramsey’s merciful thought, almost all recent research (e.g., Nordhaus (2014) [3] ) presumes the discounting uncritically. This tendency is based on both political and technical reasons. From the political view, the discounting justifies the ephemeral and over consuming prosperity of the current generation to some extent. A technical aspect of model building requires that a utility integral (or summation) over the infinite horizon should remain finite. Without discounting, such a value surely diverges and the analysis becomes meaningless. No discounting is permissible only when a model is formatted based either on the bounded instantaneous utility function (Ramsey’s case) or the limited time horizon for the planning (my case). There seems to be no other attempt to capture the CO2 emissions problem by the infinite chain of individuals whose lives are finite than this study.
2In addition, evaluating the correct (or socially justified) price of CO2 as
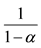 implies that the optimal social discount is unity in the stationary state. For more detail, see Otaki (2013) [4] .
implies that the optimal social discount is unity in the stationary state. For more detail, see Otaki (2013) [4] .
3According to Tanaka (1993) [8] , CO2 emissions from fossil fuel combustion are estimated at



4By an elementary calculus, it can be ascertained that


5Otaki (2013) [4] shows that if an economy can converges to the optimal stationary state, the optimal social discount rate becomes zero.












